1. Introduction
One of the main goals of inertial confinement fusion (ICF)[Reference Lindl1–Reference Atzeni and Meyer-ter-Vehn3] concerns the ignition of the thermonuclear fusion reactions in a mixture of deuterium–tritium (DT) nuclear fuel. After the ignition phase, it is expected that propagation of a thermonuclear burn wave – dominated by the fusion reaction with larger cross section
![]() $D+T=>\alpha +n+17.6$
MeV – throughout the compressed fuel should generate a large energy gain
$D+T=>\alpha +n+17.6$
MeV – throughout the compressed fuel should generate a large energy gain
![]() $G=E_{\mathrm{fus}}/E_{\mathrm{in}}$
(ratio between thermonuclear fusion and the invested energy). To this aim two schemes have been proposed, namely: direct drive and indirect drive. In both cases a spherical capsule containing the DT nuclear fuel is considered. In the direct drive[Reference Bodner, Colombant, Gardner, Lehmberg, Obenschain, Phillips, Schmitt, Sethian, McCrory, Seka, Verdon, Knauer, Afeyan and Powell4] scheme the spherical capsule is irradiated by a large number of laser beams, whilst in the indirect drive[Reference Lindl1] scheme the laser energy is first converted into an x-ray field (confined into a high-
$G=E_{\mathrm{fus}}/E_{\mathrm{in}}$
(ratio between thermonuclear fusion and the invested energy). To this aim two schemes have been proposed, namely: direct drive and indirect drive. In both cases a spherical capsule containing the DT nuclear fuel is considered. In the direct drive[Reference Bodner, Colombant, Gardner, Lehmberg, Obenschain, Phillips, Schmitt, Sethian, McCrory, Seka, Verdon, Knauer, Afeyan and Powell4] scheme the spherical capsule is irradiated by a large number of laser beams, whilst in the indirect drive[Reference Lindl1] scheme the laser energy is first converted into an x-ray field (confined into a high-
![]() $Z$
casing; see hohlraum) that irradiates the capsule. The energy deposited in the external capsule shell provides a series of strong shock waves that induces the capsule implosion. In the classical central ignition scheme[Reference Nuckolls, Wood, Thiessen and Zimmermann5] the DT fuel is accelerated to high implosion velocities (hundreds of
$Z$
casing; see hohlraum) that irradiates the capsule. The energy deposited in the external capsule shell provides a series of strong shock waves that induces the capsule implosion. In the classical central ignition scheme[Reference Nuckolls, Wood, Thiessen and Zimmermann5] the DT fuel is accelerated to high implosion velocities (hundreds of
![]() ${\rm km}\ {\rm s}^{-1}$
) before stagnating to produce a high-density (hundreds of
${\rm km}\ {\rm s}^{-1}$
) before stagnating to produce a high-density (hundreds of
![]() ${\rm g}\ {\rm cm}^{-3}$
) shell that confines a fraction of the DT fuel (hundreds of
${\rm g}\ {\rm cm}^{-3}$
) shell that confines a fraction of the DT fuel (hundreds of
![]() $\mu {\rm g}$
). The ignition conditions require that the central mass, called the hot-spot, is heated to high temperature (10 keV) and confined into a volume with an areal density comparable with the
$\mu {\rm g}$
). The ignition conditions require that the central mass, called the hot-spot, is heated to high temperature (10 keV) and confined into a volume with an areal density comparable with the
![]() $\alpha $
-particle range (
$\alpha $
-particle range (
![]() ${\approx }0.3\ \mathrm{g\ cm}^{-2}$
).
${\approx }0.3\ \mathrm{g\ cm}^{-2}$
).

Figure 1. Angular coordinate of the 40 quads (blue and red boxes) distributed to the first and second ring of the LMJ facility. The gray circles represent the polar coordinates of the 10 long-pulse beams of the Orion facility.
A crucial issue concerns the uniformity of the capsule irradiation. A successful capsule implosion requires a very uniform irradiation and capsule target; otherwise, the imploding shell suffers the growth of dangerous hydrodynamic instabilities (Richtmyer–Meshkov[Reference Richtmyer6, Reference Meshkov7] and Rayleigh–Taylor (RT)[Reference Rayleigh8, Reference Taylor9]) and shell deformations that could even destroy the hot-spot. A way to reduce the growth of RT instability consists of compressing the capsule fuel at low implosion velocity
![]() $V$
. This causes a detriment of the energy gain
$V$
. This causes a detriment of the energy gain
![]() $G$
which scales[Reference Betti and Zhou10] as
$G$
which scales[Reference Betti and Zhou10] as
![]() $\varphi /(V^{5/4}I^{1/4})$
, where
$\varphi /(V^{5/4}I^{1/4})$
, where
![]() $\varphi =\rho R/(\rho R+7)$
is the fractional burn-up[Reference Lindl1, Reference Atzeni and Meyer-ter-Vehn3] with
$\varphi =\rho R/(\rho R+7)$
is the fractional burn-up[Reference Lindl1, Reference Atzeni and Meyer-ter-Vehn3] with
![]() $\rho R$
the fuel areal density, and
$\rho R$
the fuel areal density, and
![]() $I$
the incident laser intensity.
$I$
the incident laser intensity.
Alternative schemes are currently under study, such as fast ignition induced by laser accelerated electrons[Reference Basov, Gus’kov and Feoktistov11, Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason12], protons[Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks, Yasuike, Ruhl, Pegoraro, Bulanov, Campbell, Perry and Powell13–Reference Temporal, Honrubia and Atzeni15], or heavier ions[Reference Hegelich, Albright, Cobble, Flippo, Letzring, Paffett, Ruhl, Schreiber, Schulze and Fernandez16, Reference Fernandez, Honrubia, Albright, Flippo, Gautier, Hegelich, Schmitt, Temporal and Yin17]. More recently, the shock ignition (SI) scheme[Reference Shcherbakov18, Reference Betti, Zhou, Anderson, Perkins, Theobald and Solodov19] has been proposed as an alternative to the classical central ignition in the context of the inertial confinement fusion scenario. In this case, the capsule is directly irradiated by the laser beams providing the compression of the DT fuel. The implosion velocity of the compressed shell is set under the ignition threshold
![]() $(V<2\mbox{--}3\times 10^{7}\ \mathrm{cm\ s}^{-1})$
and does not allow for the generation of an efficient hot-spot. In the SI scheme, a second high-power (hundreds of TW) laser pulse irradiates the capsule and drives a strong shock wave that reaches the compressed shell providing the fuel ignition. The SI pulse must be carefully tuned in time to synchronize the strong shock wave with the compression shock rebounded from the centre after stagnation. This new scheme promises higher gain[Reference Shcherbakov18–Reference Lafon, Ribeyre and Schurtz21] in comparison to central ignition, and the separation between the compression and the ignition phase allows for less stringent conditions in terms of irradiation uniformity[Reference Hallo, Olazabal-Loume, Ribeyre, Drean, Schurtz, Feugeas, Breil, Nicolai and Maire22, Reference Ribeyre, Schurtz, Lafon, Galera and Weber23]. Moreover, this two-step irradiation would benefit also from the zooming technique[Reference Lehmberg and Goldhar24, Reference Canaud and Garaude25] in order to increase the laser–capsule coupling efficiency. Nevertheless, caution is necessary due to the uncertainties related to laser–plasma instabilities such as stimulated Raman scattering (SRS)[Reference Rose, DuBois and Bezzerides26], stimulated Brillouin scattering (SBS)[Reference Estabrook, Harte, Campbell, Ze, Phillion, Rosen and Larsen27], and the two-plasmon decay (TPD)[Reference Yan, Maximov, Ren and Tsung28] expected at the high laser intensities
$(V<2\mbox{--}3\times 10^{7}\ \mathrm{cm\ s}^{-1})$
and does not allow for the generation of an efficient hot-spot. In the SI scheme, a second high-power (hundreds of TW) laser pulse irradiates the capsule and drives a strong shock wave that reaches the compressed shell providing the fuel ignition. The SI pulse must be carefully tuned in time to synchronize the strong shock wave with the compression shock rebounded from the centre after stagnation. This new scheme promises higher gain[Reference Shcherbakov18–Reference Lafon, Ribeyre and Schurtz21] in comparison to central ignition, and the separation between the compression and the ignition phase allows for less stringent conditions in terms of irradiation uniformity[Reference Hallo, Olazabal-Loume, Ribeyre, Drean, Schurtz, Feugeas, Breil, Nicolai and Maire22, Reference Ribeyre, Schurtz, Lafon, Galera and Weber23]. Moreover, this two-step irradiation would benefit also from the zooming technique[Reference Lehmberg and Goldhar24, Reference Canaud and Garaude25] in order to increase the laser–capsule coupling efficiency. Nevertheless, caution is necessary due to the uncertainties related to laser–plasma instabilities such as stimulated Raman scattering (SRS)[Reference Rose, DuBois and Bezzerides26], stimulated Brillouin scattering (SBS)[Reference Estabrook, Harte, Campbell, Ze, Phillion, Rosen and Larsen27], and the two-plasmon decay (TPD)[Reference Yan, Maximov, Ren and Tsung28] expected at the high laser intensities
![]() $I\lambda ^{2}>10^{15}\ \mathrm{W\ cm}^{-2}\ \mu \mathrm{m}^{2}$
[Reference Klimo, Tikhonchuk, Ribeyre, Schurtz, Riconda, Weber and Limpouch29] provided during the shock ignition pulse. These dangerous instabilities act to reduce the energy deposition efficiency and generate high-energetic (
$I\lambda ^{2}>10^{15}\ \mathrm{W\ cm}^{-2}\ \mu \mathrm{m}^{2}$
[Reference Klimo, Tikhonchuk, Ribeyre, Schurtz, Riconda, Weber and Limpouch29] provided during the shock ignition pulse. These dangerous instabilities act to reduce the energy deposition efficiency and generate high-energetic (
![]() $\approx $
10–40 keV) electrons[Reference Yan, Maximov and Ren30–Reference Klimo, Weber, Tikhonchuk and Limpouch32]. The uncertainties concerning the laser–plasma interaction correlated to the shock ignition scheme have also motivated great interest in experimental activities[Reference Theobald, Betti, Stoeckl, Anderson, Delettrez, Glebov, Goncharov, Marshall, Maywar, McCrory, Meyerhofer, Radha, Sangster, Seka, Shvarts, Smalyuk, Solodov, Yaakobi, Zhou, Frenje, Li, Séguin, Petrasso and Perkins33–Reference Goyon, Depierreux, Yahia, Loisel, Baccou, Courvoisier, Borisenko, Orekhov, Rosmej and Labaune39]. Moreover, large laser facilities such as the National Ignition Facility (NIF)[Reference Miller, Moses and Wuest40, Reference Moses, Boyd, Remington, Keane and Al-Ayat41] in the USA and the Laser MegaJoule (LMJ) facility[Reference Cavailler, Fleurot, Lonjaret and Di-Nicola42, Reference Lion43] in France as well as the smaller Orion facility[Reference Hopps, Danson, Duffield, Egan, Elsmere, Girling, Harvey, Hillier, Norman, Parker, Treadwell, Winter and Bett44] in the UK – all of them devoted to the indirect drive scheme – could be used to test relevant aspects inherent to the shock ignition scheme.
$\approx $
10–40 keV) electrons[Reference Yan, Maximov and Ren30–Reference Klimo, Weber, Tikhonchuk and Limpouch32]. The uncertainties concerning the laser–plasma interaction correlated to the shock ignition scheme have also motivated great interest in experimental activities[Reference Theobald, Betti, Stoeckl, Anderson, Delettrez, Glebov, Goncharov, Marshall, Maywar, McCrory, Meyerhofer, Radha, Sangster, Seka, Shvarts, Smalyuk, Solodov, Yaakobi, Zhou, Frenje, Li, Séguin, Petrasso and Perkins33–Reference Goyon, Depierreux, Yahia, Loisel, Baccou, Courvoisier, Borisenko, Orekhov, Rosmej and Labaune39]. Moreover, large laser facilities such as the National Ignition Facility (NIF)[Reference Miller, Moses and Wuest40, Reference Moses, Boyd, Remington, Keane and Al-Ayat41] in the USA and the Laser MegaJoule (LMJ) facility[Reference Cavailler, Fleurot, Lonjaret and Di-Nicola42, Reference Lion43] in France as well as the smaller Orion facility[Reference Hopps, Danson, Duffield, Egan, Elsmere, Girling, Harvey, Hillier, Norman, Parker, Treadwell, Winter and Bett44] in the UK – all of them devoted to the indirect drive scheme – could be used to test relevant aspects inherent to the shock ignition scheme.
Due to its indirect drive design, the LMJ facility does not provide a favourable laser beam configuration for direct drive irradiation. Nevertheless, this large facility is very attractive for direct drive studies because of its large available energy. In this context, this paper aims to chart a path starting from the current characteristics of the LMJ facility and exploring the potential of the shock ignition scheme. After summarizing the main characteristics of the LMJ facility in Section 2, the paper analyses two different aspects: the requirement in the maximum power on the shock ignition scheme together with possible consequences due by laser–plasma instabilities in Section 3, and the study of the uniformity of the irradiation during the foot pulse of the imprint phase in Section 4, while in Section 5 some three-dimensional (3D) aspects of the hydrodynamics of the implosion are discussed. Then, conclusions are drawn in Section 6.
2. The Laser MegaJoule configuration
The configuration of the Laser MegaJoule facility considered in this paper consists of 176 high-power laser beams. These beams are grouped in 44 identical quads, each one composed by four beams. 40 quads are distributed into the spherical experimental chamber in four axial symmetric rings, and the two hemispheres are rotated by
![]() $18^{\circ }$
. The two rings closer to the polar axis have an angle of
$18^{\circ }$
. The two rings closer to the polar axis have an angle of
![]() $33.2^{\circ }$
and
$33.2^{\circ }$
and
![]() $146.8^{\circ }$
with each having 10 quads; another 20 quads are located in the rings at
$146.8^{\circ }$
with each having 10 quads; another 20 quads are located in the rings at
![]() $49^{\circ }$
and
$49^{\circ }$
and
![]() $131^{\circ }$
, as shown in Figure 1. The last four quads, not shown in the figure, will be located in two additional rings at
$131^{\circ }$
, as shown in Figure 1. The last four quads, not shown in the figure, will be located in two additional rings at
![]() $59.5^{\circ }$
and
$59.5^{\circ }$
and
![]() $120.5^{\circ }$
. The LMJ architecture is designed to provide a maximum laser energy (power) of 7.5 kJ (2.5 TW) for each beam. Consequently, this corresponds to a total energy (power) of 30 kJ (10 TW) per quad, and each pair of rings will provide a maximum energy (power) of 600 kJ (200 TW). This makes the LMJ a large laser facility, able to drive a total energy of about 1.3 MJ with a maximum power of 440 TW delivered by laser beams with a wavelength of
$120.5^{\circ }$
. The LMJ architecture is designed to provide a maximum laser energy (power) of 7.5 kJ (2.5 TW) for each beam. Consequently, this corresponds to a total energy (power) of 30 kJ (10 TW) per quad, and each pair of rings will provide a maximum energy (power) of 600 kJ (200 TW). This makes the LMJ a large laser facility, able to drive a total energy of about 1.3 MJ with a maximum power of 440 TW delivered by laser beams with a wavelength of
![]() $\lambda =351\ \mathrm{nm}$
(
$\lambda =351\ \mathrm{nm}$
(
![]() $3\omega $
)[Reference Jacquemot, Amiranoff, Baton, Chanteloup, Labaune, Koenig, Michel, Perez, Schlenvoigt, Canaud, Cherfils Clerouin, Debras, Depierreux, Ebrardt, Juraszek, Lafitte, Loiseau, Miquel, Philippe, Rousseaux, Blanchot, Edwards, Norreys, Atzeni, Schiavi, Breil, Feugeas, Hallo, Lafon, Ribeyre, Santos, Schurtz, Tikhonchuk, Debayle, Honrubia, Temporal, Batani, Davies, Fiuza, Fonseca, Silva, Gizzi, Koester, Labate, Badziak and Klimo45]. The facility design energy is appropriate for indirect drive central ignition, but both direct drive and shock ignition schemes are expected to lower the energy threshold for ignition. Thus the total available energy at the LMJ facility largely exceeds the needs in the direct drive approach.
$3\omega $
)[Reference Jacquemot, Amiranoff, Baton, Chanteloup, Labaune, Koenig, Michel, Perez, Schlenvoigt, Canaud, Cherfils Clerouin, Debras, Depierreux, Ebrardt, Juraszek, Lafitte, Loiseau, Miquel, Philippe, Rousseaux, Blanchot, Edwards, Norreys, Atzeni, Schiavi, Breil, Feugeas, Hallo, Lafon, Ribeyre, Santos, Schurtz, Tikhonchuk, Debayle, Honrubia, Temporal, Batani, Davies, Fiuza, Fonseca, Silva, Gizzi, Koester, Labate, Badziak and Klimo45]. The facility design energy is appropriate for indirect drive central ignition, but both direct drive and shock ignition schemes are expected to lower the energy threshold for ignition. Thus the total available energy at the LMJ facility largely exceeds the needs in the direct drive approach.
The polar coordinates of the quads have been optimized for the indirect drive scheme. Nevertheless, this laser beam distribution could be helpful also in the direct drive shock ignition scheme. Indeed, as already mentioned, this scheme involves two laser pulses: one for the capsule compression and a second one for the fuel ignition. Thus, there are several options in order to use the LMJ facility as a direct drive facility in the context of the SI scheme. Hereafter, we will consider two options: option A, where 20 quads of the second ring are devoted to the compression of the capsule and with the other 24 quads driving the high-power shock ignition pulse; and option B, with only 10 quads of the second ring devoted to the foot pulse while together with the remaining 34 quads contributing to the drive and the igniting pulse. The main difference between the two options concerns the role of the different quads in the partition of laser power during the low-power foot pulse, the main drive of the compression phase, and the shock ignition phase.

Figure 2. Sketch of the temporal power profile partition for the two LMJ options, A (left) and B (right), in the shock ignition scheme.
Of course, the choice of the irradiation configuration also has consequences on the irradiation uniformity. Details of these configurations are given in the temporal power pulse sketched in Figure 2. In option A, the whole 600 kJ (200 TW) of the laser beams of the second ring are available for the compression phase and quads of the first ring are almost entirely associated to the shock ignition pulse. In option B, only 300 kJ (100 TW) – half the laser beams of the second ring – are devoted to the foot pulse and part of the compression phase, while part of the drive and the shock ignition pulse operate with the 34 quads located in the three rings. In both cases the maximum available power for the shock ignition pulse will be the totality of the 440 TW.
The division of tasks among the different quads also allows implementing in a natural way both the polar direct drive (PDD)[Reference Skupsky, Marozas, Craxton, Betti, Collins, Delettrez, Goncharov, McKenty, Radha, Knauer, Marshall, Harding, Kilkenny, Meyerhofer, Sangster and McCrory46, Reference Craxton, Marshall, Bonino, Epstein, McKenty, Skupsky, Delettrez, Igumenshchev, Jacobs-Perkins, Knauer, Marozas, Radha and Seka47] and the zooming technique. The purpose of the PDD is to adapt a non-optimal configuration of laser beams in order to optimize the uniformity of the capsule irradiation. To this purpose, in the PDD technique the laser beam directions are modified in order to optimize the direct drive capsule irradiation[Reference Canaud, Fortin, Garaude, Meyer and Philippe48–Reference Radha, Marshall, Marozas, Shvydky, Gabalski, Boehly, Collins, Craxton, Edgell, Epstein, Frenje, Froula, Goncharov, Hohenberger, McCrory, McKenty, Meyerhofer, Petrasso, Sangster and Skupsky51]. The use – as a direct drive – of the quads in the second rings of the LMJ facility leads to an over-irradiation of the capsule polar regions, whilst the equatorial area is under-irradiated. Thus, applying the PDD by displacing the quad toward the equator improves the capsule illumination uniformity considerably.
It is worth noting that the Orion facility in the UK is composed of 12 beams: two laser beams provide 500 J each at
![]() $1\omega $
(1054 nm) in a short pulse of 0.5 ps and the other ten provide a total energy of 5 kJ (
$1\omega $
(1054 nm) in a short pulse of 0.5 ps and the other ten provide a total energy of 5 kJ (
![]() $3\omega $
,
$3\omega $
,
![]() $\lambda =351$
nm) in 1–5 ns long pulses. The angular positions of these ten beams are indicated by gray circles in Figure 1. These
$\lambda =351$
nm) in 1–5 ns long pulses. The angular positions of these ten beams are indicated by gray circles in Figure 1. These
![]() $5+5$
beams are located in two rings at
$5+5$
beams are located in two rings at
![]() $50^{\circ }$
and
$50^{\circ }$
and
![]() $130^{\circ }$
with respect to the polar angle. This beam distribution is very similar to the one provided by the second ring of the LMJ facility. This makes the Orion facility the natural choice to test relevant aspects inherent to the LMJ facility such as the laser absorption and the improvement of the irradiation uniformity promised by the PDD technique. Indeed, despite the relatively small dimensions, 5 kJ in 5 ns for 1 TW, this facility is perfectly matched to the requirements of experiments dedicated to the study of the imprint phase, where the first shock wave is driven by a low-power (
$130^{\circ }$
with respect to the polar angle. This beam distribution is very similar to the one provided by the second ring of the LMJ facility. This makes the Orion facility the natural choice to test relevant aspects inherent to the LMJ facility such as the laser absorption and the improvement of the irradiation uniformity promised by the PDD technique. Indeed, despite the relatively small dimensions, 5 kJ in 5 ns for 1 TW, this facility is perfectly matched to the requirements of experiments dedicated to the study of the imprint phase, where the first shock wave is driven by a low-power (
![]() $\approx $
TW) foot pulse.
$\approx $
TW) foot pulse.
3. Shock ignition calculations
A relatively large direct drive capsule characterized by an initial aspect ratio
![]() $A=3$
has been considered. This capsule is part of a family of capsules that have been recently studied[Reference Brandon, Canaud, Primout, Laffite and Temporal52]. This spherical capsule has an external radius of
$A=3$
has been considered. This capsule is part of a family of capsules that have been recently studied[Reference Brandon, Canaud, Primout, Laffite and Temporal52]. This spherical capsule has an external radius of
![]() $815\ \mu {\rm m}$
and contains a DT fuel mass of
$815\ \mu {\rm m}$
and contains a DT fuel mass of
![]() $300\ \mu $
g. The cryogenic nuclear fuel
$300\ \mu $
g. The cryogenic nuclear fuel
![]() $(\rho _{\mathrm{DT}}=0.25\ \mathrm{g\ cm}^{-3})$
is surrounded by a thin (
$(\rho _{\mathrm{DT}}=0.25\ \mathrm{g\ cm}^{-3})$
is surrounded by a thin (
![]() $24\ \mu {\rm m}$
) shell of plastic (
$24\ \mu {\rm m}$
) shell of plastic (
![]() $\rho _{\mathrm{CH}}=1.07\ \mathrm{g\ cm}^{-3})$
devoted to the laser energy absorption. Detailed parametric studies have been performed showing that the self-ignition threshold in the implosion velocity is about
$\rho _{\mathrm{CH}}=1.07\ \mathrm{g\ cm}^{-3})$
devoted to the laser energy absorption. Detailed parametric studies have been performed showing that the self-ignition threshold in the implosion velocity is about
![]() $3\times 10^{7}\ \mathrm{cm\ s}^{-1}$
[Reference Brandon, Canaud, Temporal and Ramis53] and that the maximum energy gain is
$3\times 10^{7}\ \mathrm{cm\ s}^{-1}$
[Reference Brandon, Canaud, Temporal and Ramis53] and that the maximum energy gain is
![]() $G=44$
with an incident energy of about 500 kJ and laser peak power of 230 TW[Reference Temporal, Brandon, Canaud, Didelez, Fedosejevs and Ramis54]. In the considered LMJ design, the available energy (1.3 MJ) is above that needed by the capsule, which means we retain some energy margin against constraints mainly related to the required irradiation uniformity.
$G=44$
with an incident energy of about 500 kJ and laser peak power of 230 TW[Reference Temporal, Brandon, Canaud, Didelez, Fedosejevs and Ramis54]. In the considered LMJ design, the available energy (1.3 MJ) is above that needed by the capsule, which means we retain some energy margin against constraints mainly related to the required irradiation uniformity.
Here, the capsule has been used in the context of the shock ignition scheme, and a series of 1D numerical calculations has been performed with the hydro-radiative MULTI code[Reference Ramis, Schmaltz and Meyer-ter-Vehn55, Reference Ramis, Eidmann, Meyer-ter-Vehn and Hüller56]. In this version, the MULTI code takes into account the tabulated equation of state, heat conduction (Spitzer–Harm flux limited 8%) and a 3D ray-tracing package that manage the laser energy absorption via an inverse bremsstrahlung mechanism. A laser beam characterized by a Gaussian intensity profile with a full-width at half-maximum of 1356
![]() $\mu {\rm m}$
– the intensity is reduced to
$\mu {\rm m}$
– the intensity is reduced to
![]() $1/e$
at the initial capsule radius – has been considered. The laser pulse is composed of a low-power foot pulse (
$1/e$
at the initial capsule radius – has been considered. The laser pulse is composed of a low-power foot pulse (
![]() ${\approx }7$
ns at
${\approx }7$
ns at
![]() $\approx $
TW) followed by the main pulse with a maximum power
$\approx $
TW) followed by the main pulse with a maximum power
![]() $P_{\mathrm{C}}=180$
TW (see the shadow area in Figure 3) which drives the capsule compression. This laser pulse does not provide self-ignition but only serves to compress the DT fuel. Indeed, ignition is achieved by the action of an additional high-power shock ignition spike. In this case, the igniting SI pulse starts at time
$P_{\mathrm{C}}=180$
TW (see the shadow area in Figure 3) which drives the capsule compression. This laser pulse does not provide self-ignition but only serves to compress the DT fuel. Indeed, ignition is achieved by the action of an additional high-power shock ignition spike. In this case, the igniting SI pulse starts at time
![]() $t_{\mathrm{SI}}$
and the power grows linearly, reaching the maximum power
$t_{\mathrm{SI}}$
and the power grows linearly, reaching the maximum power
![]() $P_{\mathrm{SI}}$
in 100 ps; the maximum power holds for 300 ps and then goes down to zero in another 100 ps.
$P_{\mathrm{SI}}$
in 100 ps; the maximum power holds for 300 ps and then goes down to zero in another 100 ps.
In Figure 3 are shown details of a numerical calculation performed with a compression pulse which is maintained until time
![]() $t_{\mathrm{SI}}=12.6$
ns, where the shock ignition pulse began. The maximum incident laser power during the compression phase is
$t_{\mathrm{SI}}=12.6$
ns, where the shock ignition pulse began. The maximum incident laser power during the compression phase is
![]() $P_{\mathrm{C}}=180$
TW, which then grows to
$P_{\mathrm{C}}=180$
TW, which then grows to
![]() $P_{\mathrm{SI}}=350$
TW during the shock ignition pulse. In this case, the calculation provides a fusion energy of
$P_{\mathrm{SI}}=350$
TW during the shock ignition pulse. In this case, the calculation provides a fusion energy of
![]() $E_{\mathrm{FUS}}=24.3$
MJ while the total incident laser energy is
$E_{\mathrm{FUS}}=24.3$
MJ while the total incident laser energy is
![]() $E_{\mathrm{INC}}=560$
kJ, of which 360 kJ are invested in the compression phase (
$E_{\mathrm{INC}}=560$
kJ, of which 360 kJ are invested in the compression phase (
![]() $t<t_{\mathrm{SI}}$
) and 200 kJ in the shock ignition pulse (
$t<t_{\mathrm{SI}}$
) and 200 kJ in the shock ignition pulse (
![]() $t>t_{\mathrm{SI}}$
). The energy gain is
$t>t_{\mathrm{SI}}$
). The energy gain is
![]() $G=E_{\mathrm{FUS}}/E_{\mathrm{INC}}=43$
. The incident and absorbed laser powers are shown by the two shadowed areas (that correspond to the linear scale) in Figure 3. As can be seen, the absorbed power is almost the half of the incident laser power, and the total energy absorption fraction is
$G=E_{\mathrm{FUS}}/E_{\mathrm{INC}}=43$
. The incident and absorbed laser powers are shown by the two shadowed areas (that correspond to the linear scale) in Figure 3. As can be seen, the absorbed power is almost the half of the incident laser power, and the total energy absorption fraction is
![]() $\eta =59\%$
. It is worth noticing that this capsule provides similar performance when is used in the central ignition scheme. Nevertheless, the shock ignition scheme benefits from a larger tolerance with respect to the fuel compression uniformity, which is the drawback at the LMJ facility.
$\eta =59\%$
. It is worth noticing that this capsule provides similar performance when is used in the central ignition scheme. Nevertheless, the shock ignition scheme benefits from a larger tolerance with respect to the fuel compression uniformity, which is the drawback at the LMJ facility.

Figure 3. Capsule dimensions and temporal evolution of the Lagrangean radii. The temporal profile of the incident and absorbed power are shown by the two shadowed areas. The position of the critical density (
![]() $\rho _{\mathrm{c}}$
) and evolution of the maximum incident laser intensity (
$\rho _{\mathrm{c}}$
) and evolution of the maximum incident laser intensity (
![]() $I_{\mathrm{INC}}$
) are also shown as a function of time.
$I_{\mathrm{INC}}$
) are also shown as a function of time.
The radial position
![]() $r_{\mathrm{c}}$
where the density is equal to the critical value
$r_{\mathrm{c}}$
where the density is equal to the critical value
![]() $\rho _{\mathrm{c}}\; [\mathrm{g\ cm}^{{-3}}] = 1.865\times 10^{-3}(A/Z)/\lambda ^{2}$
[
$\rho _{\mathrm{c}}\; [\mathrm{g\ cm}^{{-3}}] = 1.865\times 10^{-3}(A/Z)/\lambda ^{2}$
[
![]() $\mu {\rm m}$
] has also been calculated, and it is shown by the dashed red curve in Figure 3. The surface associated with the radius
$\mu {\rm m}$
] has also been calculated, and it is shown by the dashed red curve in Figure 3. The surface associated with the radius
![]() $r_{\mathrm{c}}$
has been used to estimate the maximum incident laser intensity
$r_{\mathrm{c}}$
has been used to estimate the maximum incident laser intensity
![]() $I_{\mathrm{INC}}=P_{\mathrm{INC}}/(4\pi r_{\mathrm{c}}^{2})$
, shown by the blue curve. As usual in the shock ignition scheme, a very high laser intensity
$I_{\mathrm{INC}}=P_{\mathrm{INC}}/(4\pi r_{\mathrm{c}}^{2})$
, shown by the blue curve. As usual in the shock ignition scheme, a very high laser intensity
![]() $I_{\mathrm{INC}}$
is needed during the shock ignition pulse, but there is some concern that the laser–plasma interaction at high intensities (
$I_{\mathrm{INC}}$
is needed during the shock ignition pulse, but there is some concern that the laser–plasma interaction at high intensities (
![]() $I\lambda ^{2}>10^{15}\; \mathrm{W\ cm}^{-2}\; \mu \mathrm{m}^{2}$
) is dominated by laser–plasma instabilities that considerably modify the absorption mechanism[Reference Kruer57] and negatively impact coupling of the ignition pulse energy to the capsule. In our case, the maximum intensity is larger than
$I\lambda ^{2}>10^{15}\; \mathrm{W\ cm}^{-2}\; \mu \mathrm{m}^{2}$
) is dominated by laser–plasma instabilities that considerably modify the absorption mechanism[Reference Kruer57] and negatively impact coupling of the ignition pulse energy to the capsule. In our case, the maximum intensity is larger than
![]() $10^{16}\ \mathrm{W\ cm}^{-2}$
, although the true value may not be quite this high, since not all the incident power
$10^{16}\ \mathrm{W\ cm}^{-2}$
, although the true value may not be quite this high, since not all the incident power
![]() $P_{\mathrm{INC}}$
reaches the critical density surface, also due to beam refraction. Nevertheless, these intensities are still in excess of the thresholds for laser plasma instabilities. It is likely that a large part (
$P_{\mathrm{INC}}$
reaches the critical density surface, also due to beam refraction. Nevertheless, these intensities are still in excess of the thresholds for laser plasma instabilities. It is likely that a large part (
![]() $\approx $
50%) of the photon energy is converted into energetic electrons (
$\approx $
50%) of the photon energy is converted into energetic electrons (
![]() $\approx $
30 keV) and the laser light does not penetrate until the classical critical density,
$\approx $
30 keV) and the laser light does not penetrate until the classical critical density,
![]() $\rho _{\mathrm{c}}$
, but reaches only
$\rho _{\mathrm{c}}$
, but reaches only
![]() $\rho _{\mathrm{c}}/4$
[Reference Riconda, Weber, Tikhonchuk and Heron58–Reference Theobald, Nora, Lafon, Casner, Ribeyre, Anderson, Betti, Delettrez, Frenje, Glebov, Gotchev, Hohenberger, Hu, Marshall, Meyerhofer, Sangster, Schurtz, Seka, Smalyuk, Stoeckl and Yaakobi61] where the laser light is absorbed by collective effects. The physics involving these high laser intensities and electronic transport are not included in our hydrodynamic code. Nevertheless, we tried to mimic the reduced critical density assuming a laser wavelength (
$\rho _{\mathrm{c}}/4$
[Reference Riconda, Weber, Tikhonchuk and Heron58–Reference Theobald, Nora, Lafon, Casner, Ribeyre, Anderson, Betti, Delettrez, Frenje, Glebov, Gotchev, Hohenberger, Hu, Marshall, Meyerhofer, Sangster, Schurtz, Seka, Smalyuk, Stoeckl and Yaakobi61] where the laser light is absorbed by collective effects. The physics involving these high laser intensities and electronic transport are not included in our hydrodynamic code. Nevertheless, we tried to mimic the reduced critical density assuming a laser wavelength (
![]() $\lambda _{\mathrm{SI}}$
) twice the nominal value (
$\lambda _{\mathrm{SI}}$
) twice the nominal value (
![]() $\lambda _{\mathrm{SI}}=2\lambda =702$
nm) during the shock ignition pulse, i.e., for
$\lambda _{\mathrm{SI}}=2\lambda =702$
nm) during the shock ignition pulse, i.e., for
![]() $t>t_{\mathrm{SI}}$
. Of course, this is just an attempt to evaluate the effect of the reduction by a factor of four (
$t>t_{\mathrm{SI}}$
. Of course, this is just an attempt to evaluate the effect of the reduction by a factor of four (
![]() $\rho _{\mathrm{c}}\alpha \lambda ^{-2}$
) in the maximum density reached by the photons. Detailed hydrodynamic calculations that also include the high-energetic electron transport will be needed to give a more complete treatment of the problem.
$\rho _{\mathrm{c}}\alpha \lambda ^{-2}$
) in the maximum density reached by the photons. Detailed hydrodynamic calculations that also include the high-energetic electron transport will be needed to give a more complete treatment of the problem.

Figure 4. Gain as a function of the starting time
![]() $t_{\mathrm{SI}}$
and of the maximum power
$t_{\mathrm{SI}}$
and of the maximum power
![]() $P_{\mathrm{SI}}$
of the shock ignition pulse. (a) Gain
$P_{\mathrm{SI}}$
of the shock ignition pulse. (a) Gain
![]() $G$
, calculated with
$G$
, calculated with
![]() $\lambda _{\mathrm{SI}}=\lambda $
; (b) Gain
$\lambda _{\mathrm{SI}}=\lambda $
; (b) Gain
![]() $G^{\ast }$
, calculated assuming
$G^{\ast }$
, calculated assuming
![]() $\lambda _{\mathrm{SI}}=2\lambda $
. The white curves represent isovalues of the absorption,
$\lambda _{\mathrm{SI}}=2\lambda $
. The white curves represent isovalues of the absorption,
![]() $\eta $
[%].
$\eta $
[%].
Two parametric studies have been performed, varying the starting time,
![]() $t_{\mathrm{SI}}$
, of the shock ignition pulse and the maximum incident power,
$t_{\mathrm{SI}}$
, of the shock ignition pulse and the maximum incident power,
![]() $P_{\mathrm{SI}}$
. In a first case, we used the usual laser wavelength
$P_{\mathrm{SI}}$
. In a first case, we used the usual laser wavelength
![]() $\lambda =351$
nm during the whole calculations and for each couple of parameters,
$\lambda =351$
nm during the whole calculations and for each couple of parameters,
![]() $t_{\mathrm{SI}}$
and
$t_{\mathrm{SI}}$
and
![]() $P_{\mathrm{SI}}$
, the final energy gain
$P_{\mathrm{SI}}$
, the final energy gain
![]() $G$
has been calculated. In a second set of calculations the laser wavelength has been doubled during the shock ignition pulse – i.e., when
$G$
has been calculated. In a second set of calculations the laser wavelength has been doubled during the shock ignition pulse – i.e., when
![]() $t<t_{\mathrm{SI}}$
– providing the gain
$t<t_{\mathrm{SI}}$
– providing the gain
![]() $G^{\ast }(t_{\mathrm{SI}},P_{\mathrm{SI}})$
. The colour maps in Figure 4 shown the gain
$G^{\ast }(t_{\mathrm{SI}},P_{\mathrm{SI}})$
. The colour maps in Figure 4 shown the gain
![]() $G$
and
$G$
and
![]() $G^{\ast }$
as a function of the two parameters
$G^{\ast }$
as a function of the two parameters
![]() $t_{\mathrm{SI}}$
and
$t_{\mathrm{SI}}$
and
![]() $P_{\mathrm{SI}}$
. In the same figures the white contour curves show the total absorbed energy fraction,
$P_{\mathrm{SI}}$
. In the same figures the white contour curves show the total absorbed energy fraction,
![]() $\eta $
. The case of the gain
$\eta $
. The case of the gain
![]() $G$
– Figure 4(a), evaluated using always the same wavelength
$G$
– Figure 4(a), evaluated using always the same wavelength
![]() $\lambda $
– shows two regions with high gain. In the first maximum, at smaller parameter
$\lambda $
– shows two regions with high gain. In the first maximum, at smaller parameter
![]() $t_{\mathrm{SI}}$
and characterized by a lower gain, the high-power laser pulse arrives too early and generates a Kidder-like exponential laser pulse[Reference Kidder62] that induces the classical central ignition. In contrast, the shock ignition mechanism is responsible for the second stronger signal at larger times,
$t_{\mathrm{SI}}$
and characterized by a lower gain, the high-power laser pulse arrives too early and generates a Kidder-like exponential laser pulse[Reference Kidder62] that induces the classical central ignition. In contrast, the shock ignition mechanism is responsible for the second stronger signal at larger times,
![]() $t_{\mathrm{SI}}$
. It is found that for this specific laser–capsule configuration the threshold in the power
$t_{\mathrm{SI}}$
. It is found that for this specific laser–capsule configuration the threshold in the power
![]() $P_{\mathrm{SI}}$
is about 250 TW. The ignition region is reduced in the case of the gain
$P_{\mathrm{SI}}$
is about 250 TW. The ignition region is reduced in the case of the gain
![]() $G^{\ast }$
when the laser wavelength has been artificially doubled during the shock ignition pulse. In this case, the threshold moves to higher powers at around 400 TW. In both cases,
$G^{\ast }$
when the laser wavelength has been artificially doubled during the shock ignition pulse. In this case, the threshold moves to higher powers at around 400 TW. In both cases,
![]() $G$
and
$G$
and
![]() $G^{\ast }$
, the energy absorption is around 60%, and the modification in the threshold comes from the fact that the laser energy is deposited far from the compressed fuel. We are aware that our calculations do not deal with the correct laser–plasma interaction mechanisms; thus these results are not conclusive and just indicate a trend. It is also worth noting that the energetic electrons, neglected in our calculations, can transport some energy[Reference Bell and Tzoufras63, Reference Gus’kov, Ribeyre, Touati, Feugeas, Nicolai and Tikhonchuk64] between the deposition region (
$G^{\ast }$
, the energy absorption is around 60%, and the modification in the threshold comes from the fact that the laser energy is deposited far from the compressed fuel. We are aware that our calculations do not deal with the correct laser–plasma interaction mechanisms; thus these results are not conclusive and just indicate a trend. It is also worth noting that the energetic electrons, neglected in our calculations, can transport some energy[Reference Bell and Tzoufras63, Reference Gus’kov, Ribeyre, Touati, Feugeas, Nicolai and Tikhonchuk64] between the deposition region (
![]() $\rho <\rho _{\mathrm{C}}/4$
) and the ablation front that should favourably reduce the incident power threshold. In fact the high-energy electrons may not be as detrimental as in the central ignition scheme, and it is possible they may even contribute positively towards driving the ignition shock[Reference Ribeyre, Gus’kov, Feugeas, Nicolai and Tikhonchuk65].
$\rho <\rho _{\mathrm{C}}/4$
) and the ablation front that should favourably reduce the incident power threshold. In fact the high-energy electrons may not be as detrimental as in the central ignition scheme, and it is possible they may even contribute positively towards driving the ignition shock[Reference Ribeyre, Gus’kov, Feugeas, Nicolai and Tikhonchuk65].
4. Illumination non-uniformity
The shock ignition scheme is less demanding than the central ignition one with respect to the uniformity of the irradiation[Reference Canaud, Laffite, Brandon and Temporal66, Reference Atzeni, Schiavi and Marocchino67]. However, the spike power needed to ignite the target is sensitive to the uniformity of the fuel assembly[Reference Weber, Riconda, Klimo, Heron and Tikhonchuk59], and it is necessary to control the irradiation uniformity during the whole duration of the laser pulse. This is in general also difficult, because the plasma corona evolves during this time, and laser parameters optimized at the beginning of the irradiation could be no longer appropriate later during the implosion[Reference Temporal and Canaud68]. Nevertheless, special care must be paid to minimize the initial irradiation non-uniformity that generates the first shock wave of the implosion and dominates the so-called imprint phase.
In this section, we analyse some of the behaviour of the irradiation by using the illumination model[Reference Skupsky and Lee69, Reference Schmitt70]. In the model, the capsule is assumed stationary – expansion of the plasma corona is neglected – and is characterized only by the external radius
![]() $r_{\mathrm{0}}$
. For a given number of incident laser beams characterized by an arbitrary laser intensity profiles, the model calculates the intensity of the illumination
$r_{\mathrm{0}}$
. For a given number of incident laser beams characterized by an arbitrary laser intensity profiles, the model calculates the intensity of the illumination
![]() $I(\theta ,\phi )$
over the spherical surface. It is thus assumed that laser parameters that optimize the illumination uniformity also minimize the non-uniformity transmitted to the first shock wave[Reference Temporal, Canaud, Garbett and Ramis71]. Generally, the quality of the illumination is measured by the root-mean-square deviation,
$I(\theta ,\phi )$
over the spherical surface. It is thus assumed that laser parameters that optimize the illumination uniformity also minimize the non-uniformity transmitted to the first shock wave[Reference Temporal, Canaud, Garbett and Ramis71]. Generally, the quality of the illumination is measured by the root-mean-square deviation,
![]() $\sigma _{\mathrm{0}}$
, associated to the function
$\sigma _{\mathrm{0}}$
, associated to the function
![]() $I(\theta ,\phi )$
; this is given by
$I(\theta ,\phi )$
; this is given by
where
![]() $\langle I\rangle $
is the average intensity over the surface of the spherical target. The intrinsic non-uniformity
$\langle I\rangle $
is the average intensity over the surface of the spherical target. The intrinsic non-uniformity
![]() $\sigma _{0}$
is a characteristic of a given laser–capsule configuration and assumes perfectly ideal laser beams not affected by any imperfections.
$\sigma _{0}$
is a characteristic of a given laser–capsule configuration and assumes perfectly ideal laser beams not affected by any imperfections.
In reality, laser beams suffer from unavoidable errors such as beam-to-beam power imbalance
![]() $\sigma _{\mathrm{PI}}$
, laser pointing error
$\sigma _{\mathrm{PI}}$
, laser pointing error
![]() $\sigma _{\mathrm{PE}}$
, and error in the target positioning
$\sigma _{\mathrm{PE}}$
, and error in the target positioning
![]() $\sigma _{\mathrm{TP}}$
. These errors are statistical quantities that in the case of the LMJ facility are estimated by the standard deviations:
$\sigma _{\mathrm{TP}}$
. These errors are statistical quantities that in the case of the LMJ facility are estimated by the standard deviations:
![]() $\sigma _{\mathrm{PI}}=10$
% (beam-to-beam),
$\sigma _{\mathrm{PI}}=10$
% (beam-to-beam),
![]() $\sigma _{\mathrm{PE}}=50\ \mu {\rm m}$
, and
$\sigma _{\mathrm{PE}}=50\ \mu {\rm m}$
, and
![]() $\sigma _{\mathrm{TP}}=20\ \mu {\rm m}$
. In the LMJ facility, the laser beams are grouped in quads; thus the power imbalance benefits from a statistical factor which reduces it to
$\sigma _{\mathrm{TP}}=20\ \mu {\rm m}$
. In the LMJ facility, the laser beams are grouped in quads; thus the power imbalance benefits from a statistical factor which reduces it to
![]() $\sigma _{\mathrm{PI}}=5\%$
(quad-to-quad). The illumination non-uniformity, evaluated taking into account these beam uncertainties, is usually measured as an average value (
$\sigma _{\mathrm{PI}}=5\%$
(quad-to-quad). The illumination non-uniformity, evaluated taking into account these beam uncertainties, is usually measured as an average value (
![]() $\underline{\sigma }$
) estimated over a large number of calculations[Reference Murakami72–Reference Temporal, Ramis, Canaud, Brandon, Laffite and Le Garrec77]. In these calculations, each of the three parameters (laser power, laser pointing, and target position) varies randomly and follows a Gaussian distribution centred to their nominal values and characterized by the corresponding standard deviation
$\underline{\sigma }$
) estimated over a large number of calculations[Reference Murakami72–Reference Temporal, Ramis, Canaud, Brandon, Laffite and Le Garrec77]. In these calculations, each of the three parameters (laser power, laser pointing, and target position) varies randomly and follows a Gaussian distribution centred to their nominal values and characterized by the corresponding standard deviation
![]() $\sigma _{\mathrm{PI}}$
,
$\sigma _{\mathrm{PI}}$
,
![]() $\sigma _{\mathrm{PE}}$
, or
$\sigma _{\mathrm{PE}}$
, or
![]() $\sigma _{\mathrm{TP}}$
.
$\sigma _{\mathrm{TP}}$
.
As has been already said, the LMJ facility is devoted to the indirect drive scheme. This means that the laser beam directions as well as their intensity profile fit with the hohlraum requirements. As a consequence, the geometrical shape of the laser intensity profile is elliptical. Thus, the intensity profile has been parameterized by the super-Gaussian function:
![]() $I(x,y)=I_{0}\exp -[(x/\Delta _{\mathrm{a}})^{2} + (y/\Delta _{\mathrm{b}})^{2}]^{m/2}$
, characterized by the parameters
$I(x,y)=I_{0}\exp -[(x/\Delta _{\mathrm{a}})^{2} + (y/\Delta _{\mathrm{b}})^{2}]^{m/2}$
, characterized by the parameters
![]() $\Delta _{\mathrm{a}}$
and
$\Delta _{\mathrm{a}}$
and
![]() $\Delta _{\mathrm{b}}$
(half width at
$\Delta _{\mathrm{b}}$
(half width at
![]() $1/e$
) and by the exponent
$1/e$
) and by the exponent
![]() $m$
. In our calculations we considered an elliptical laser intensity profile characterized with
$m$
. In our calculations we considered an elliptical laser intensity profile characterized with
![]() $\Delta _{\mathrm{a}}=2\Delta _{\mathrm{b}}$
,
$\Delta _{\mathrm{a}}=2\Delta _{\mathrm{b}}$
,
![]() $\Delta _{\mathrm{b}}=320\ \mu {\rm m}$
, and an exponent
$\Delta _{\mathrm{b}}=320\ \mu {\rm m}$
, and an exponent
![]() $m=4$
. Because of specific needs inherent to the indirect drive scheme in the LMJ facility (the same applies also for the Orion facility), the minor axis
$m=4$
. Because of specific needs inherent to the indirect drive scheme in the LMJ facility (the same applies also for the Orion facility), the minor axis
![]() $(\Delta _{\mathrm{b}})$
of the elliptical intensity profile is located in the meridian defined by the polar and beam axes.
$(\Delta _{\mathrm{b}})$
of the elliptical intensity profile is located in the meridian defined by the polar and beam axes.
In the first set of calculations we considered the non-uniformity provided by the 20 quads located in the second ring of the LMJ facility (option A in Section 2). The results are shown in the Figure 5 as a function of the target radius
![]() $r_{\mathrm{0}}$
. The cloud of dots in the figure represents the results obtained with the elliptical profile for a large number of calculations assuming a random Gaussian distribution for the power imbalance, pointing error, and target positioning. The continuous red curve is the average non-uniformity
$r_{\mathrm{0}}$
. The cloud of dots in the figure represents the results obtained with the elliptical profile for a large number of calculations assuming a random Gaussian distribution for the power imbalance, pointing error, and target positioning. The continuous red curve is the average non-uniformity
![]() $\underline{\sigma }$
, while the blue curve shows the intrinsic non-uniformity
$\underline{\sigma }$
, while the blue curve shows the intrinsic non-uniformity
![]() $\sigma _{0}$
evaluated neglecting any beam–capsule uncertainties. As can be seen, for small capsule radii, some configurations with capsule centre, laser powers, and pointing randomly assigned can provide better results with respect to the intrinsic values. For the given elliptical LMJ laser intensity profile, an optimum capsule radius of
$\sigma _{0}$
evaluated neglecting any beam–capsule uncertainties. As can be seen, for small capsule radii, some configurations with capsule centre, laser powers, and pointing randomly assigned can provide better results with respect to the intrinsic values. For the given elliptical LMJ laser intensity profile, an optimum capsule radius of
![]() $r_{0}=320\ \mu {\rm m}$
is found for which the average non-uniformity assumes the minimum value
$r_{0}=320\ \mu {\rm m}$
is found for which the average non-uniformity assumes the minimum value
![]() $\underline{\sigma }=6.2$
%, while the minimum intrinsic non-uniformity, evaluated neglecting any beam uncertainties, is
$\underline{\sigma }=6.2$
%, while the minimum intrinsic non-uniformity, evaluated neglecting any beam uncertainties, is
![]() $\sigma _{\mathrm{0}}=4.6$
%.
$\sigma _{\mathrm{0}}=4.6$
%.

Figure 5. Average illumination non-uniformities
![]() $\underline{\sigma }$
(red curves) and intrinsic non-uniformities
$\underline{\sigma }$
(red curves) and intrinsic non-uniformities
![]() $\sigma _{0}$
(blue curves) as a function of the capsule radius
$\sigma _{0}$
(blue curves) as a function of the capsule radius
![]() $r_{0}$
evaluated for the LMJ configuration (option A). Continuous and dashed curves refer to the elliptical and circular laser intensity profile, respectively.
$r_{0}$
evaluated for the LMJ configuration (option A). Continuous and dashed curves refer to the elliptical and circular laser intensity profile, respectively.

Figure 6. Polar plot of the intensity profile
![]() $I(\theta )$
provided by two axis-symmetric laser beams illuminating a capsule of radius
$I(\theta )$
provided by two axis-symmetric laser beams illuminating a capsule of radius
![]() $r_{0}=320\ \mu {\rm m}$
. The laser intensity profiles are elliptical (red) and circular (blue), while the dashed circle is the reference of a perfectly uniform irradiation.
$r_{0}=320\ \mu {\rm m}$
. The laser intensity profiles are elliptical (red) and circular (blue), while the dashed circle is the reference of a perfectly uniform irradiation.
It has been already shown[Reference Temporal, Canaud, Garbett and Ramis78, Reference Temporal, Canaud, Garbett, Philippe and Ramis79] that, in the case of axis-symmetric beam distributions as in the LMJ or Orion facilities, the elliptical laser intensity profile allows for better non-uniformities with respect to circular shapes. For the sake of comparison we have also shown in Figure 5 the average (red dashed curve) and the intrinsic non-uniformities (blue dashed curve) calculated using a circular intensity profile. In this case it is assumed that
![]() $\Delta _{\mathrm{a}} = \Delta _{\mathrm{b}} = 450\ \mu {\rm m}$
in such a way as to have the same focal spot surface at
$\Delta _{\mathrm{a}} = \Delta _{\mathrm{b}} = 450\ \mu {\rm m}$
in such a way as to have the same focal spot surface at
![]() $I_{0}/e$
(
$I_{0}/e$
(
![]() $450^{2}=320\times 640$
). It is found that for the capsule radius
$450^{2}=320\times 640$
). It is found that for the capsule radius
![]() $r_{0}=320\ \mu {\rm m}$
the non-uniformity provided by the circular profile is almost double that of the elliptical case. These results confirm that the elliptical profile provides better results than the circular one for capsule radius
$r_{0}=320\ \mu {\rm m}$
the non-uniformity provided by the circular profile is almost double that of the elliptical case. These results confirm that the elliptical profile provides better results than the circular one for capsule radius
![]() $r_{0}<450\ \mu {\rm m}$
.
$r_{0}<450\ \mu {\rm m}$
.
The specific configurations given by the 10 or 20 quads located in the second ring (
![]() $49^{\circ }$
) of the LMJ facility are not optimized for direct drive irradiation. Nevertheless, it is worth noting that the polar angle of
$49^{\circ }$
) of the LMJ facility are not optimized for direct drive irradiation. Nevertheless, it is worth noting that the polar angle of
![]() $49^{\circ }$
is relatively close to the optimum value,
$49^{\circ }$
is relatively close to the optimum value,
![]() $\theta _{\mathrm{S}}=54.7^{\circ }$
, as found by Schmitt[Reference Schmitt70] for optimization of a two-ring configuration assuming that the energy deposition is given by a
$\theta _{\mathrm{S}}=54.7^{\circ }$
, as found by Schmitt[Reference Schmitt70] for optimization of a two-ring configuration assuming that the energy deposition is given by a
![]() $\cos ^{2}(\theta )$
distribution. Indeed, the LMJ configuration provides an over-irradiation of the two polar caps in detriment of the under-irradiation of the equatorial band. This is shown in the polar plot of Figure 6, where the radial distance – which has been set proportionally to the intensity
$\cos ^{2}(\theta )$
distribution. Indeed, the LMJ configuration provides an over-irradiation of the two polar caps in detriment of the under-irradiation of the equatorial band. This is shown in the polar plot of Figure 6, where the radial distance – which has been set proportionally to the intensity
![]() $I(\theta )$
– is shown as a function of capsule latitude
$I(\theta )$
– is shown as a function of capsule latitude
![]() $\theta \epsilon [0,\pi ]$
. The calculations have been performed for an axis-symmetric beam distribution for the elliptical and circular laser intensity profiles and a capsule radius
$\theta \epsilon [0,\pi ]$
. The calculations have been performed for an axis-symmetric beam distribution for the elliptical and circular laser intensity profiles and a capsule radius
![]() $r_{0}=320\ \mu {\rm m}$
. Both intensity profiles cause an under-irradiation of the equatorial area but – due to geometrical factors – the elliptical laser spot provides a more uniform radial intensity that better approximates the perfectly spherical symmetry which is represented by the dashed circle.
$r_{0}=320\ \mu {\rm m}$
. Both intensity profiles cause an under-irradiation of the equatorial area but – due to geometrical factors – the elliptical laser spot provides a more uniform radial intensity that better approximates the perfectly spherical symmetry which is represented by the dashed circle.
As previously mentioned, to improve the laser–capsule coupling, the polar direct drive technique has been proposed. In this case, the laser beams are re-directed towards the equator by a quantity
![]() $\delta $
in order to balance the irradiation between polar and equatorial areas. The displacement
$\delta $
in order to balance the irradiation between polar and equatorial areas. The displacement
![]() $\delta $
is also indicated in the sketch of Figure 6. A parametric study varying the PDD parameter between 0 and 100
$\delta $
is also indicated in the sketch of Figure 6. A parametric study varying the PDD parameter between 0 and 100
![]() $\mu {\rm m}$
has been performed looking for the optimal PDD parameter
$\mu {\rm m}$
has been performed looking for the optimal PDD parameter
![]() $\delta $
that minimizes the average illumination non-uniformity,
$\delta $
that minimizes the average illumination non-uniformity,
![]() $\underline{\sigma }$
. These non-uniformities
$\underline{\sigma }$
. These non-uniformities
![]() $\underline{\sigma }$
are shown as a function of the capsule radius
$\underline{\sigma }$
are shown as a function of the capsule radius
![]() $r_{0}$
in Figure 7 for the two cases A and B. The dashed curves refer to the calculations without PDD (
$r_{0}$
in Figure 7 for the two cases A and B. The dashed curves refer to the calculations without PDD (
![]() $\delta =0$
), whilst the continuous curves account for the PDD optimization; in these last cases, the corresponding optimal PDD parameter
$\delta =0$
), whilst the continuous curves account for the PDD optimization; in these last cases, the corresponding optimal PDD parameter
![]() $\delta /r_{0}$
is also shown. In both configurations, the PDD technique improves the results and reduces the minimum non-uniformities by about 40%. The minimum illumination non-uniformities
$\delta /r_{0}$
is also shown. In both configurations, the PDD technique improves the results and reduces the minimum non-uniformities by about 40%. The minimum illumination non-uniformities
![]() $\underline{\sigma }_{\mathrm{A}}=3.6$
% and
$\underline{\sigma }_{\mathrm{A}}=3.6$
% and
![]() $\underline{\sigma }_{\mathrm{B}}=4.9$
% are reached at the capsule radius
$\underline{\sigma }_{\mathrm{B}}=4.9$
% are reached at the capsule radius
![]() $r_{0}=270\ \mu {\rm m}$
, for which the associated optimum PDD parameter is
$r_{0}=270\ \mu {\rm m}$
, for which the associated optimum PDD parameter is
![]() $\delta /r_{0}=15$
%.
$\delta /r_{0}=15$
%.

Figure 7. Average irradiation non-uniformity
![]() $\bar{\sigma }$
as a function of the capsule radius
$\bar{\sigma }$
as a function of the capsule radius
![]() $r_{0}$
for the LMJ options A (blue) and B (red) with (continuous) and without (dashed) applying PDD. In the cases applying PDD, the optimum PDD parameter
$r_{0}$
for the LMJ options A (blue) and B (red) with (continuous) and without (dashed) applying PDD. In the cases applying PDD, the optimum PDD parameter
![]() $\delta /r_{0}$
is also shown.
$\delta /r_{0}$
is also shown.
Another set of calculations has been performed to evaluate the sensitivity of the illumination non-uniformity with respect to a variation of the beam uncertainties
![]() $\sigma _{\mathrm{PI}}$
,
$\sigma _{\mathrm{PI}}$
,
![]() $\sigma _{\mathrm{PE}}$
, and
$\sigma _{\mathrm{PE}}$
, and
![]() $\sigma _{\mathrm{TP}}$
. These calculations use the laser intensity profile envisaged for the LMJ facility (
$\sigma _{\mathrm{TP}}$
. These calculations use the laser intensity profile envisaged for the LMJ facility (
![]() $\Delta _{\mathrm{a}}=640\ \mu {\rm m}$
,
$\Delta _{\mathrm{a}}=640\ \mu {\rm m}$
,
![]() $\Delta _{\mathrm{b}}=320\ \mu {\rm m}$
), a capsule radius
$\Delta _{\mathrm{b}}=320\ \mu {\rm m}$
), a capsule radius
![]() $r_{0}=270\ \mu {\rm m}$
, and a PDD parameter
$r_{0}=270\ \mu {\rm m}$
, and a PDD parameter
![]() $\delta /r_{0}=15$
%. The average non-uniformities
$\delta /r_{0}=15$
%. The average non-uniformities
![]() $\underline{\sigma }$
are shown in Figure 8 as a function of an uncertainty scaling parameter
$\underline{\sigma }$
are shown in Figure 8 as a function of an uncertainty scaling parameter
![]() $f$
, which varies between 0 and 2. Three series of calculations have been done: (I) keeping constant pointing error (
$f$
, which varies between 0 and 2. Three series of calculations have been done: (I) keeping constant pointing error (
![]() $\sigma _{\mathrm{PE}}=50\ \mu {\rm m}$
) and target positioning (
$\sigma _{\mathrm{PE}}=50\ \mu {\rm m}$
) and target positioning (
![]() $\sigma _{\mathrm{TP}}=20\ \mu {\rm m}$
) while varying the power imbalance from zero to double the nominal value (
$\sigma _{\mathrm{TP}}=20\ \mu {\rm m}$
) while varying the power imbalance from zero to double the nominal value (
![]() $\sigma _{\mathrm{PI}}=5\%$
), i.e., considering
$\sigma _{\mathrm{PI}}=5\%$
), i.e., considering
![]() $f\sigma _{\mathrm{PI}}$
,
$f\sigma _{\mathrm{PI}}$
,
![]() $\sigma _{\mathrm{PE}}$
, and
$\sigma _{\mathrm{PE}}$
, and
![]() $\sigma _{\mathrm{TP}}$
; (II) varying only the pointing error (
$\sigma _{\mathrm{TP}}$
; (II) varying only the pointing error (
![]() $\sigma _{\mathrm{PI}}$
,
$\sigma _{\mathrm{PI}}$
,
![]() $f\sigma _{\mathrm{PE}}$
,
$f\sigma _{\mathrm{PE}}$
,
![]() $\sigma _{\mathrm{TP}})$
; and (III) with only variation of the target positioning (
$\sigma _{\mathrm{TP}})$
; and (III) with only variation of the target positioning (
![]() $\sigma _{\mathrm{PI}}$
,
$\sigma _{\mathrm{PI}}$
,
![]() $\sigma _{\mathrm{PE}}$
,
$\sigma _{\mathrm{PE}}$
,
![]() $f\sigma _{\mathrm{TP}}$
). The ensemble of the results is shown in Figure 8. As a comparison the two intrinsic values
$f\sigma _{\mathrm{TP}}$
). The ensemble of the results is shown in Figure 8. As a comparison the two intrinsic values
![]() $\sigma _{0}$
(horizontal gray lines) evaluated for the LMJ options A and B have been added. The largest gradient of the average non-uniformity
$\sigma _{0}$
(horizontal gray lines) evaluated for the LMJ options A and B have been added. The largest gradient of the average non-uniformity
![]() $\underline{\sigma }$
is associated with the variation of the pointing error. This makes these two laser–capsule configurations more sensitive to the pointing error
$\underline{\sigma }$
is associated with the variation of the pointing error. This makes these two laser–capsule configurations more sensitive to the pointing error
![]() $(\sigma _{\mathrm{PE}})$
rather than the other two error sources (power imbalance and target positioning).
$(\sigma _{\mathrm{PE}})$
rather than the other two error sources (power imbalance and target positioning).

Figure 8. Variation of the average non-uniformity with respect to the laser–capsule uncertainties. Continuous (dashed) curves refer to LMJ option A (B).
A final detailed parametric study has been performed to evaluate the sensitivity of the average illumination non-uniformity to a variation of the PDD parameter
![]() $\delta $
and of the super-Gaussian exponent
$\delta $
and of the super-Gaussian exponent
![]() $m$
of the laser intensity profile. As in the previous case, the capsule radius has been set to
$m$
of the laser intensity profile. As in the previous case, the capsule radius has been set to
![]() $r_{0}=270\ \mu {\rm m}$
and the elliptical intensity profile is characterized by the widths
$r_{0}=270\ \mu {\rm m}$
and the elliptical intensity profile is characterized by the widths
![]() $\Delta _{\mathrm{b}}=320\ \mu {\rm m}$
and
$\Delta _{\mathrm{b}}=320\ \mu {\rm m}$
and
![]() $\Delta _{\mathrm{a}}=2\Delta _{\mathrm{b}}$
. The average non-uniformity, which takes into account the beam uncertainties, is shown as a function of the parameters
$\Delta _{\mathrm{a}}=2\Delta _{\mathrm{b}}$
. The average non-uniformity, which takes into account the beam uncertainties, is shown as a function of the parameters
![]() $\delta $
and
$\delta $
and
![]() $m$
in Figure 9 for LMJ option A (top frame) and B (bottom). The shadowed areas indicate the regions where the non-uniformities are within 10% closer to their minimum values
$m$
in Figure 9 for LMJ option A (top frame) and B (bottom). The shadowed areas indicate the regions where the non-uniformities are within 10% closer to their minimum values
![]() $\underline{\sigma }_{\mathrm{min}}$
(3.6% for option A and 4.9% for option B). It is thus shown that both systems tolerate a relatively large variation of the super-Gaussian exponent
$\underline{\sigma }_{\mathrm{min}}$
(3.6% for option A and 4.9% for option B). It is thus shown that both systems tolerate a relatively large variation of the super-Gaussian exponent
![]() $3<m<5$
and a variation of about
$3<m<5$
and a variation of about
![]() $\pm $
10
$\pm $
10
![]() $\mu {\rm m}$
of the PDD parameter while still providing a non-uniformity smaller than 1.1
$\mu {\rm m}$
of the PDD parameter while still providing a non-uniformity smaller than 1.1
![]() $\underline{\sigma }_{\min }$
.
$\underline{\sigma }_{\min }$
.

Figure 9. Average non-uniformity as a function of the PDD parameter
![]() $\delta $
and of the super-Gaussian exponent
$\delta $
and of the super-Gaussian exponent
![]() $m$
of the laser intensity profile.
$m$
of the laser intensity profile.

Figure 10.
![]() $\sigma _{\mathrm{3D}}$
(black squares,
$\sigma _{\mathrm{3D}}$
(black squares,
![]() $\blacksquare $
) and
$\blacksquare $
) and
![]() $\sigma _{\varphi }$
(white squares,
$\sigma _{\varphi }$
(white squares,
![]() $\square $
) at
$\square $
) at
![]() $t=12$
ns, as a function of the number of quads,
$t=12$
ns, as a function of the number of quads,
![]() $N$
. Rings of opposite hemispheres are rotated against each other by an angle of
$N$
. Rings of opposite hemispheres are rotated against each other by an angle of
![]() $180^{\circ }/N$
.
$180^{\circ }/N$
.
5. 3D hydrodynamic simulations
Detailed two-dimensional (2D) hydrodynamic numerical simulations are usually employed to analyse the irradiation, compression, ignition, and thermonuclear burn wave propagation in an ICF capsule. Nevertheless, most actual laser–target configurations are intrinsically three-dimensional (3D) systems, and these have motivated the development of 3D hydrodynamic numerical tools[Reference Ramis80–Reference Lia, Zhai, Li, Li, Zheng, Yong, Zeng, Hang, Qi, Yang, Cheng, Song, Gu, Zhang, An, Xu, Guo, Cao, Mo, Pei, Jiang and Zhu85]. Three-dimensional aspects can play a role also in the present cases considered in this paper that use a limited number of quads. This is especially true in option B, where only five beams are located in each axis-symmetric ring. Recently, using the 3D version of the MULTI[Reference Ramis, Schmaltz and Meyer-ter-Vehn55] code, the uniformity of the irradiation provided by the LMJ facility has been analysed. Here, we report only on a few results of a much larger and detailed analysis[Reference Ramis, Temporal, Canaud, Brandon and Laffite86]. The 3D version of the MULTI code assumes a non-structured Lagrangian mesh (tetrahedral elements) and accounts for flux-limited (10%) thermal heat conduction, tabulated equations of state, and a 3D ray-tracing package for the laser energy deposition.
A first issue is when a 3D configuration can be correctly described as a 2D axis-symmetric problem. For this purpose, a configuration with a number
![]() $N$
of laser beams in each ring has been considered. In these calculations, the spherical capsule described in Section 3 is illuminated by beams from rings at
$N$
of laser beams in each ring has been considered. In these calculations, the spherical capsule described in Section 3 is illuminated by beams from rings at
![]() $49^{\circ }$
and
$49^{\circ }$
and
![]() $131^{\circ }$
, aligned to the target centre (
$131^{\circ }$
, aligned to the target centre (
![]() $\delta =0$
), and with a Gaussian radial shape characterized by a full width at half maximum (FWHM) of 1356
$\delta =0$
), and with a Gaussian radial shape characterized by a full width at half maximum (FWHM) of 1356
![]() $\mu {\rm m}$
. The DT shell is followed in time and a mean radial position is defined as
$\mu {\rm m}$
. The DT shell is followed in time and a mean radial position is defined as
For a pure axis-symmetric problem,
![]() $R$
does not depend on azimuthal angle
$R$
does not depend on azimuthal angle
![]() $\varphi $
. Here, it is assumed that departure from perfectly sphericity of the surface defined by the radius
$\varphi $
. Here, it is assumed that departure from perfectly sphericity of the surface defined by the radius
![]() $R$
is representative of the non-uniformity produced by the laser energy deposition. This surface has been decomposed in spherical harmonics providing the corresponding time-dependent coefficients. Then, these coefficients have been used to measure the azimuthal
$R$
is representative of the non-uniformity produced by the laser energy deposition. This surface has been decomposed in spherical harmonics providing the corresponding time-dependent coefficients. Then, these coefficients have been used to measure the azimuthal
![]() $\sigma _{\varphi }(t)$
and the polar
$\sigma _{\varphi }(t)$
and the polar
![]() $\sigma _{\theta }(t)$
components of the total root-mean-square non-uniformity
$\sigma _{\theta }(t)$
components of the total root-mean-square non-uniformity
![]() $\sigma _{3D}^{2} = \sigma _{\varphi }^{2} + \sigma _{\theta }^{2}$
associated to this interface.
$\sigma _{3D}^{2} = \sigma _{\varphi }^{2} + \sigma _{\theta }^{2}$
associated to this interface.
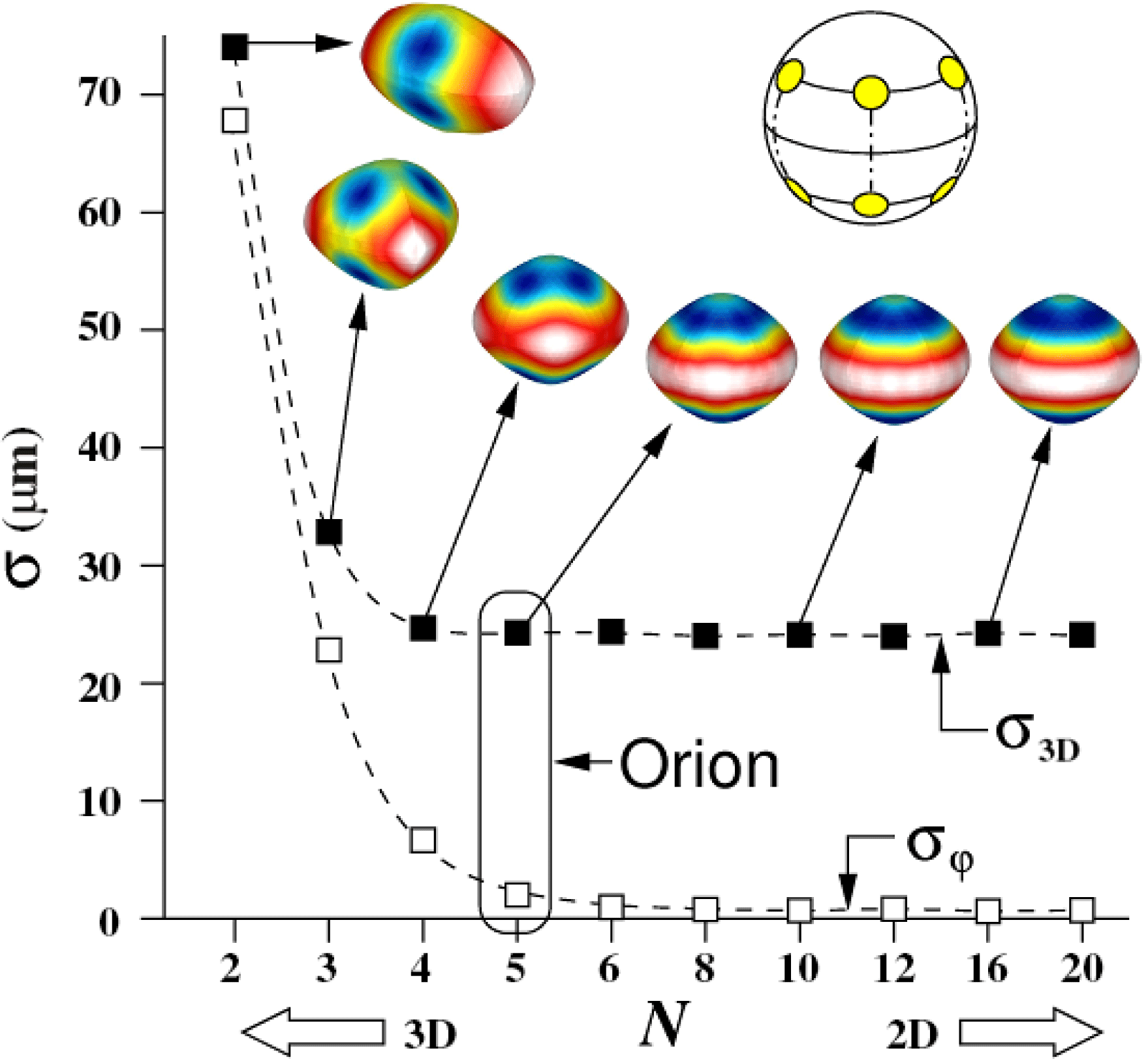
Figure 11.
![]() $\sigma _{\mathrm{3D}}$
(
$\sigma _{\mathrm{3D}}$
(
![]() $\blacksquare $
) and
$\blacksquare $
) and
![]() $\sigma _{\varphi }$
(
$\sigma _{\varphi }$
(
![]() $\square $
) evaluated at
$\square $
) evaluated at
![]() $t=12$
ns, as a function of the number of quads,
$t=12$
ns, as a function of the number of quads,
![]() $N$
. Rings of opposite hemispheres are symmetric with respect to the equatorial plane.
$N$
. Rings of opposite hemispheres are symmetric with respect to the equatorial plane.
The results of these 3D calculations are summarized in Figures 10 and 11, where we show the values of
![]() $\sigma _{\mathrm{3D}}$
and
$\sigma _{\mathrm{3D}}$
and
![]() $\sigma _{\phi }$
evaluated at
$\sigma _{\phi }$
evaluated at
![]() $t=12$
ns, approximately the time when the shell radius reduces to one half of its initial value. Figure 10 corresponds to laser beams arrangements where the rings of opposite hemispheres are rotated each other by an angle
$t=12$
ns, approximately the time when the shell radius reduces to one half of its initial value. Figure 10 corresponds to laser beams arrangements where the rings of opposite hemispheres are rotated each other by an angle
![]() $18^{\circ }/N$
(e.g., the LMJ facility with
$18^{\circ }/N$
(e.g., the LMJ facility with
![]() $N=10$
), while Figure 11 corresponds to symmetric arrangements (e.g., the Orion facility,
$N=10$
), while Figure 11 corresponds to symmetric arrangements (e.g., the Orion facility,
![]() $N=5$
). The insets in the figures show the shape of the DT–ablator interface evaluated at
$N=5$
). The insets in the figures show the shape of the DT–ablator interface evaluated at
![]() $t=12$
ns. The colours indicate the distortion – inversely related to the driver pressure – in terms of radius (white/blue for large/small values). For extremely small number of beams, there is a clear triaxiality. In Figure 10 one can recognize tetrahedral (
$t=12$
ns. The colours indicate the distortion – inversely related to the driver pressure – in terms of radius (white/blue for large/small values). For extremely small number of beams, there is a clear triaxiality. In Figure 10 one can recognize tetrahedral (
![]() $N=2$
) and hexahedral (
$N=2$
) and hexahedral (
![]() $N=3$
) shapes. In Figure 11, for
$N=3$
) shapes. In Figure 11, for
![]() $N=2$
, the four quads are in the same meridian plane, and the compressed shape is elongated along the perpendicular direction. In all these cases, polar, azimuthal, and total distortions are of the same order. For large values of
$N=2$
, the four quads are in the same meridian plane, and the compressed shape is elongated along the perpendicular direction. In all these cases, polar, azimuthal, and total distortions are of the same order. For large values of
![]() $N$
, the configuration converges to an axis-symmetric one, the same for both types of laser arrangement. These calculations have been done without PDD correction (
$N$
, the configuration converges to an axis-symmetric one, the same for both types of laser arrangement. These calculations have been done without PDD correction (
![]() $\delta =0$
), and as a consequence a polar overpressure appears. The small residual value
$\delta =0$
), and as a consequence a polar overpressure appears. The small residual value
![]() $\sigma _{\varphi }\le 1\ \mu {\rm m}$
, for large
$\sigma _{\varphi }\le 1\ \mu {\rm m}$
, for large
![]() $N$
, is due to the spatial discretization and the numerical noise associated to the Monte Carlo nature of the ray-tracing algorithm. It is noteworthy that the transition between three-dimensionality and two-dimensionality occurs at relatively small laser beam numbers,
$N$
, is due to the spatial discretization and the numerical noise associated to the Monte Carlo nature of the ray-tracing algorithm. It is noteworthy that the transition between three-dimensionality and two-dimensionality occurs at relatively small laser beam numbers,
![]() $N$
. For
$N$
. For
![]() $N=5$
, the values of
$N=5$
, the values of
![]() $\sigma _{\phi }$
are 1.55
$\sigma _{\phi }$
are 1.55
![]() $\mu {\rm m}$
and 2.0
$\mu {\rm m}$
and 2.0
![]() $\mu {\rm m}$
, just above the numerical noise. For
$\mu {\rm m}$
, just above the numerical noise. For
![]() $N\ge 8$
, the results are no longer distinguishable. This fast approach to the 2D axial symmetry justifies the use of 2D codes to treat accurately option A and, in an approximate but reasonable way, option B. These conclusions hold when spots of adjacent beams have enough overlapping, provided that uncertainties in beam power balance and pointing accuracy can be neglected. It must be mentioned that, for configurations where the beam size has been reduced (FWHM
$N\ge 8$
, the results are no longer distinguishable. This fast approach to the 2D axial symmetry justifies the use of 2D codes to treat accurately option A and, in an approximate but reasonable way, option B. These conclusions hold when spots of adjacent beams have enough overlapping, provided that uncertainties in beam power balance and pointing accuracy can be neglected. It must be mentioned that, for configurations where the beam size has been reduced (FWHM
![]() $\approx $
1000
$\approx $
1000
![]() $\mu {\rm m}$
), 3D effects occur, and azimuthal distortions can becomes significant even for
$\mu {\rm m}$
), 3D effects occur, and azimuthal distortions can becomes significant even for
![]() $N\approx 5$
[Reference Ramis, Temporal, Canaud, Brandon and Laffite86].
$N\approx 5$
[Reference Ramis, Temporal, Canaud, Brandon and Laffite86].
6. Conclusions
The Laser MegaJoule facility has been considered in the context of the shock ignition scheme. Two laser beam configurations have been analysed. A first option (A) uses 20 quads – 80 laser beams (600 kJ, 200 TW) locate at the second ring of the LMJ facility – for the compression of the capsule, making available the remaining 24 quads – 96 laser beams (720 kJ, 240 TW) – for the additional shock ignition pulse. A second option (B) envisages the possibility to use only 10 quads for the compression phase and 34 quads for the compression and SI phases. The total available laser power is 440 TW at
![]() $3\omega $
(
$3\omega $
(
![]() $\lambda =351$
nm).
$\lambda =351$
nm).
A classical ICF capsule – devoted to the central ignition scheme – has been used in the context of the shock ignition scheme. A set of mono-dimensional numerical simulations has been performed to enlighten some aspect of the shock ignition scheme. For this specific capsule it is found that the threshold power in the shock ignition pulse is about 250 TW. Nevertheless, assuming that all this power is incident to the surface of the critical density provides incident intensity larger than
![]() $10^{16}\ \mathrm{TW\ cm}^{-2}$
. At these large intensities (
$10^{16}\ \mathrm{TW\ cm}^{-2}$
. At these large intensities (
![]() $I\lambda ^{2}>10^{15}\ \mathrm{W\ cm}^{-2}\ \mu \mathrm{m}^{2}$
) we expect saturation of dangerous laser–plasma instabilities (SRS, SBS, and TPD) that modify the laser energy deposition mechanism. In this new regime, a large fraction of the laser energy is transferred to high-energetic electrons, and the photon penetration depth is limited to a quarter of the critical density (
$I\lambda ^{2}>10^{15}\ \mathrm{W\ cm}^{-2}\ \mu \mathrm{m}^{2}$
) we expect saturation of dangerous laser–plasma instabilities (SRS, SBS, and TPD) that modify the laser energy deposition mechanism. In this new regime, a large fraction of the laser energy is transferred to high-energetic electrons, and the photon penetration depth is limited to a quarter of the critical density (
![]() $\rho _{\mathrm{c}}/4$
), instead of the classical limit,
$\rho _{\mathrm{c}}/4$
), instead of the classical limit,
![]() $\rho _{\mathrm{c}}$
. These physical mechanisms are not included in our numerical tools; however, we performed some calculations to estimate the effect caused by limiting the deposition of the laser energy in the region at lower density (
$\rho _{\mathrm{c}}$
. These physical mechanisms are not included in our numerical tools; however, we performed some calculations to estimate the effect caused by limiting the deposition of the laser energy in the region at lower density (
![]() $\rho <\rho _{\mathrm{c}}/4$
). To mimic this effect, the light wavelength during the shock ignition pulse has been artificially doubled (
$\rho <\rho _{\mathrm{c}}/4$
). To mimic this effect, the light wavelength during the shock ignition pulse has been artificially doubled (
![]() $\lambda _{\mathrm{SI}}=2\lambda $
); thus, because
$\lambda _{\mathrm{SI}}=2\lambda $
); thus, because
![]() $\rho _{\mathrm{c}}\alpha \lambda ^{-2}$
, the critical density becomes a quarter. As expected, this affects negatively the power threshold in the shock ignition pulse that now increases to about 400 TW. This should be considered as a pessimistic estimation. In fact, none of the positive effects associated with the high-energetic electrons are included in our calculations.
$\rho _{\mathrm{c}}\alpha \lambda ^{-2}$
, the critical density becomes a quarter. As expected, this affects negatively the power threshold in the shock ignition pulse that now increases to about 400 TW. This should be considered as a pessimistic estimation. In fact, none of the positive effects associated with the high-energetic electrons are included in our calculations.
The second issue addressed in the paper concerns the irradiation uniformity provided during the first few ns of the foot pulse. First, it has been shown that the elliptical laser intensity profile of the LMJ facility provides better results in comparison to the usually circular profile. The two LMJ options A and B have been considered, taking into account beam uncertainties such as quad-to-quad power imbalance (
![]() $\sigma _{\mathrm{PI}}=5$
%), pointing error (
$\sigma _{\mathrm{PI}}=5$
%), pointing error (
![]() $\sigma _{\mathrm{PE}}=50\ \mu {\rm m}$
), and target positioning (
$\sigma _{\mathrm{PE}}=50\ \mu {\rm m}$
), and target positioning (
![]() $\sigma _{\mathrm{TP}}=20\ \mu {\rm m}$
). Both of these configurations cause an over-irradiation of the capsule polar regions in detriment to the equatorial area. In order to improve these schemes, the polar direct drive technique has been applied to optimize the irradiation uniformity. It has been found that for the elliptical laser intensity profile (
$\sigma _{\mathrm{TP}}=20\ \mu {\rm m}$
). Both of these configurations cause an over-irradiation of the capsule polar regions in detriment to the equatorial area. In order to improve these schemes, the polar direct drive technique has been applied to optimize the irradiation uniformity. It has been found that for the elliptical laser intensity profile (
![]() $\Delta _{\mathrm{b}}=320\ \mu {\rm m}$
,
$\Delta _{\mathrm{b}}=320\ \mu {\rm m}$
,
![]() $\Delta _{\mathrm{a}}=2\ \Delta _{\mathrm{b}}$
,
$\Delta _{\mathrm{a}}=2\ \Delta _{\mathrm{b}}$
,
![]() $m=4$
) expected at the LMJ facility the optimal capsule radius is
$m=4$
) expected at the LMJ facility the optimal capsule radius is
![]() $r_{0}=270\ \mu {\rm m}$
, and this provides an average illumination non-uniformity of
$r_{0}=270\ \mu {\rm m}$
, and this provides an average illumination non-uniformity of
![]() $\underline{\sigma }=3.6$
% and 4.9% in case A and case B, respectively. These minimum non-uniformities correspond to the use of a PDD parameter
$\underline{\sigma }=3.6$
% and 4.9% in case A and case B, respectively. These minimum non-uniformities correspond to the use of a PDD parameter
![]() $\delta /r_{0}=15$
%. This capsule radius is relatively small in comparison to the available LMJ energy and the requirements for typical ignition capsule designs; however, bigger capsules could be envisaged assuming larger focal spots provided by either defocusing of the laser beams or using an alternative set of phase plates.
$\delta /r_{0}=15$
%. This capsule radius is relatively small in comparison to the available LMJ energy and the requirements for typical ignition capsule designs; however, bigger capsules could be envisaged assuming larger focal spots provided by either defocusing of the laser beams or using an alternative set of phase plates.
A 3D version of the code MULTI has been used to perform a set of preliminary hydrodynamic calculations. The LMJ options A and B have been considered in these calculations, and the laser irradiation uniformity has been split into the azimuthal and polar components by means of decomposition in spherical harmonics. For the analysed laser–capsule configuration – with the laser intensity profile that reduces to
![]() $1/e$
at the initial capsule radius – it is found that the azimuthal component is negligible in the case of option A (ten beams per hemisphere). This encouraging result seems indicates that a 2D analysis is appropriate in option A, while in the second case, option B, it may not be. Of course these conclusions depend on the beam and capsule sizes, and further investigations are needed for specific configurations.
$1/e$
at the initial capsule radius – it is found that the azimuthal component is negligible in the case of option A (ten beams per hemisphere). This encouraging result seems indicates that a 2D analysis is appropriate in option A, while in the second case, option B, it may not be. Of course these conclusions depend on the beam and capsule sizes, and further investigations are needed for specific configurations.
Finally, the two LMJ options A and B involve the use of 10 or 20 quads located in the second rings characterized by the polar angles
![]() $49^{\circ }$
and
$49^{\circ }$
and
![]() $131^{\circ }$
. These options are in many aspects similar to the configuration already available at the Orion facility, where ten laser beams are located at
$131^{\circ }$
. These options are in many aspects similar to the configuration already available at the Orion facility, where ten laser beams are located at
![]() $50^{\circ }$
and
$50^{\circ }$
and
![]() $130^{\circ }$
. In addition, these ten ns-long laser beams operate at the wavelength
$130^{\circ }$
. In addition, these ten ns-long laser beams operate at the wavelength
![]() $\lambda =0.351\ \mu {\rm m}$
(
$\lambda =0.351\ \mu {\rm m}$
(
![]() $3\omega $
) as in the LMJ facility. The similarity between the two installations motivates us to stress the opportunity to perform Orion’s experiments addressed to PDD issues of interest also for future direct drive LMJ campaigns. Indeed, although of relatively small energy – 5 kJ in few ns for the ten long-pulse Orion beams – this installation is fully adequate for direct drive experiments that may explore the laser–capsule coupling as well as the uniformity and timing of the first shock wave generated during the low-power (
$3\omega $
) as in the LMJ facility. The similarity between the two installations motivates us to stress the opportunity to perform Orion’s experiments addressed to PDD issues of interest also for future direct drive LMJ campaigns. Indeed, although of relatively small energy – 5 kJ in few ns for the ten long-pulse Orion beams – this installation is fully adequate for direct drive experiments that may explore the laser–capsule coupling as well as the uniformity and timing of the first shock wave generated during the low-power (
![]() $\approx $
TW) ns-long foot pulse needed to control the initial imprint phase of an ICF implosion, thus helping to underwrite modelling of polar direct drive implosions.
$\approx $
TW) ns-long foot pulse needed to control the initial imprint phase of an ICF implosion, thus helping to underwrite modelling of polar direct drive implosions.
Acknowledgements
M. T. and B. C. express their thanks to Daniel Bouche for the support given to this work. R. R. was partially supported by the EURATOM/CIEMAT association in the framework of the ‘IFE Keep-in-Touch Activities’. S. W. acknowledges support from the Czech Science Foundation (Project No. CZ.1.07/2.3.00/20.0279) and from ELI (Project No. CZ.1.05/1.1.00/02.0061).













