1. Introduction
Heat flows from hot to cold: it is the (second) law. This common-sense observation can be put into mathematical terms with the formula
That is, the heat flux vector  $\boldsymbol {f}$ is proportional and opposite to the gradient of the temperature field
$\boldsymbol {f}$ is proportional and opposite to the gradient of the temperature field  $\theta (\boldsymbol {x},t)$, with proportionality constant given by the thermal diffusivity of the medium. Equation (1.1) applies in solids and quiescent fluids, and also to scalar quantities other than heat, such as the concentration of a pollutant; in that case (1.1) is known as Fick's law and
$\theta (\boldsymbol {x},t)$, with proportionality constant given by the thermal diffusivity of the medium. Equation (1.1) applies in solids and quiescent fluids, and also to scalar quantities other than heat, such as the concentration of a pollutant; in that case (1.1) is known as Fick's law and  $\kappa$ is simply a diffusivity, without the adjective ‘thermal’.
$\kappa$ is simply a diffusivity, without the adjective ‘thermal’.
Everyday experience suggests that (1.1) can not be quite right, since the thermal diffusivity of air is minuscule, and yet we can still heat our houses in the winter. The reason is that heat is transported predominantly by the motion of the fluid – small air currents in a room, driven by buoyancy and other processes, lead to a much more rapid homogenization of temperature than expected. In fact, it almost seems as though
that is, the average heat flux is linear in gradients of the average temperature, with an effective diffusivity  $\kappa _{{eff}}$ that can be much, much larger than the molecular value
$\kappa _{{eff}}$ that can be much, much larger than the molecular value  $\kappa$. (The meaning of the average in (1.2) will be discussed below.) The ansatz (1.2), which dates back to the early days of turbulence theory, expresses the beautiful dream that turbulence functions as a random process similar to molecular collisions, only with a much longer effective mean free path. And indeed, this viewpoint has proved immensely successful in many physical systems; the problem is that real flows, and real turbulence, contain a mixture of scales and processes, including waves, coherent structures, boundary effects and eddies, all of which can lead to correlations locally and globally. (See the lectures by Young (Reference Young1999) for a nice introduction, or the reviews by Ottino (Reference Ottino1990) and Warhaft (Reference Warhaft2000).)
$\kappa$. (The meaning of the average in (1.2) will be discussed below.) The ansatz (1.2), which dates back to the early days of turbulence theory, expresses the beautiful dream that turbulence functions as a random process similar to molecular collisions, only with a much longer effective mean free path. And indeed, this viewpoint has proved immensely successful in many physical systems; the problem is that real flows, and real turbulence, contain a mixture of scales and processes, including waves, coherent structures, boundary effects and eddies, all of which can lead to correlations locally and globally. (See the lectures by Young (Reference Young1999) for a nice introduction, or the reviews by Ottino (Reference Ottino1990) and Warhaft (Reference Warhaft2000).)
For modern applications, a model such as (1.2) is needed in any computer code for the simulation of large-scale ocean and atmospheric processes. We do not have access to measurements of the smallest scales in the ocean, and even if we did we would not have the capacity to simulate their effect. Therefore, all modern computer codes parametrize the small scales in a flow in some effective manner, with the crudest being (1.2). This approach will work well if there is a clear scale separation: if we can see where the large-scale ends, and where the small scales begin. And even then, we have to properly take into account the couplings between the scales.
What Souza et al. propose is to do away with this ad hoc scale separation, and instead view the effective diffusivity as an operator,
where  $\mathcal {K}$ is a tensorial kernel, allowing for anisotropic diffusion. They use a series of increasingly complex examples where they can compute
$\mathcal {K}$ is a tensorial kernel, allowing for anisotropic diffusion. They use a series of increasingly complex examples where they can compute  $\mathcal {K}$ explicitly or numerically. The structure of
$\mathcal {K}$ explicitly or numerically. The structure of  $\mathcal {K}$ then tells us much about the nature of transport in the system. For example, if
$\mathcal {K}$ then tells us much about the nature of transport in the system. For example, if  $\mathcal {K}$ is a delta function, or close to it, then a description using a local effective diffusivity will work well.
$\mathcal {K}$ is a delta function, or close to it, then a description using a local effective diffusivity will work well.
2. The closure problem
Let us briefly review the mathematical model used in Souza et al.. The concentration field  $\theta (\boldsymbol {x},t)$ of a passive scalar, advected by a random velocity field
$\theta (\boldsymbol {x},t)$ of a passive scalar, advected by a random velocity field  $\boldsymbol {u}(\boldsymbol {x},t)$, with constant scalar diffusivity
$\boldsymbol {u}(\boldsymbol {x},t)$, with constant scalar diffusivity  $\kappa$ and a source
$\kappa$ and a source  $s(\boldsymbol {x})$, obeys the advection–diffusion equation
$s(\boldsymbol {x})$, obeys the advection–diffusion equation
We can average this equation over realizations of the random field  $\boldsymbol {u}$, and obtain an equation for the average
$\boldsymbol {u}$, and obtain an equation for the average  $\langle \theta \rangle (\boldsymbol {x},t)$,
$\langle \theta \rangle (\boldsymbol {x},t)$,
The average here is an ensemble average over realizations of  $\boldsymbol {u}$. The closure problem arises because in general we don't know how to deal with the term
$\boldsymbol {u}$. The closure problem arises because in general we don't know how to deal with the term  $\langle \boldsymbol {u}\theta \rangle$: (2.2) is not a closed equation for
$\langle \boldsymbol {u}\theta \rangle$: (2.2) is not a closed equation for  $\langle \theta \rangle$. The goal of a closure is to rewrite
$\langle \theta \rangle$. The goal of a closure is to rewrite
where  ${O}$ is a linear operator, in general an integro-differential operator.
${O}$ is a linear operator, in general an integro-differential operator.
We isolate the issue by rewriting  $\theta$ and
$\theta$ and  $\boldsymbol {u}$ in terms of their ensemble mean and fluctuations:
$\boldsymbol {u}$ in terms of their ensemble mean and fluctuations:
Then, subtracting (2.1) from (2.2), we find
This last equation should be interpreted with care: on the left-hand side is a linear operator acting on  $\theta '$, including the ensemble average
$\theta '$, including the ensemble average  $\langle \boldsymbol {u}'\theta '\rangle$, which can be expressed as
$\langle \boldsymbol {u}'\theta '\rangle$, which can be expressed as
where now we explicitly denote ensemble members by a subscript  ${\omega }$, and the probability measure
${\omega }$, and the probability measure  $\mu _{\omega }$ gives the relative weight of the ensemble member
$\mu _{\omega }$ gives the relative weight of the ensemble member  ${\omega }$. Equation (2.6) indicates that the left-hand side of (2.5) is an integro-differential operator involving the variables
${\omega }$. Equation (2.6) indicates that the left-hand side of (2.5) is an integro-differential operator involving the variables  $({\omega },\boldsymbol {x},t)$, where
$({\omega },\boldsymbol {x},t)$, where  ${\omega }$ itself could be countable to indicate an atlas of fixed velocity fields, or perhaps a continuous multidimensional variable that parametrizes the velocity field. Assuming that this operator is invertible (i.e. it admits a Green's function
${\omega }$ itself could be countable to indicate an atlas of fixed velocity fields, or perhaps a continuous multidimensional variable that parametrizes the velocity field. Assuming that this operator is invertible (i.e. it admits a Green's function  $\mathcal {G}_{{\omega }{\omega }_0}(\boldsymbol {x},t\,|\,\boldsymbol {x}_0,t_0)$), then the solution to (2.5) is
$\mathcal {G}_{{\omega }{\omega }_0}(\boldsymbol {x},t\,|\,\boldsymbol {x}_0,t_0)$), then the solution to (2.5) is
where a zero subscript denotes a function of  $({\omega }_0,\boldsymbol {x}_0,t_0)$. Armed with (2.7), we can compute the flux
$({\omega }_0,\boldsymbol {x}_0,t_0)$. Armed with (2.7), we can compute the flux  $\langle \boldsymbol {u}'\theta '\rangle$. Souza et al. show that things simplify elegantly if we assume that the fluid is incompressible,
$\langle \boldsymbol {u}'\theta '\rangle$. Souza et al. show that things simplify elegantly if we assume that the fluid is incompressible,  $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {u}=0$ and that the statistics of
$\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {u}=0$ and that the statistics of  $\boldsymbol {u}$ are stationary; in that case, let
$\boldsymbol {u}$ are stationary; in that case, let
then
We have thus found the operator  ${O}$ for the closure (2.3), with an ‘effective diffusivity operator’ given by
${O}$ for the closure (2.3), with an ‘effective diffusivity operator’ given by  $\int \mathcal {K}(\boldsymbol {x}\,|\,\boldsymbol {x}_0)\boldsymbol {\cdot }\bullet {\rm d}\boldsymbol {x}_0$. The case of an isotropic, purely local effective diffusivity is recovered when
$\int \mathcal {K}(\boldsymbol {x}\,|\,\boldsymbol {x}_0)\boldsymbol {\cdot }\bullet {\rm d}\boldsymbol {x}_0$. The case of an isotropic, purely local effective diffusivity is recovered when  $\mathcal {K}(\boldsymbol {x}\,|\,\boldsymbol {x}_0) = \kappa _{{eff}}\,\delta (\boldsymbol {x} - \boldsymbol {x}_0)\,\mathbb {I}$, with
$\mathcal {K}(\boldsymbol {x}\,|\,\boldsymbol {x}_0) = \kappa _{{eff}}\,\delta (\boldsymbol {x} - \boldsymbol {x}_0)\,\mathbb {I}$, with  $\mathbb {I}$ the identity tensor; clearly in general there is no reason to expect such a simple kernel. In fact the general kernel can even be non-symmetric, which indicates an induced drift, in addition to the mean drift
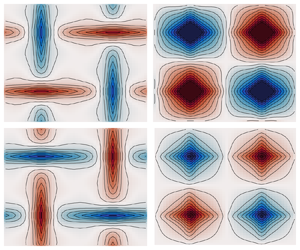
$\mathbb {I}$ the identity tensor; clearly in general there is no reason to expect such a simple kernel. In fact the general kernel can even be non-symmetric, which indicates an induced drift, in addition to the mean drift  $\langle \boldsymbol {u}\rangle$. Indeed, figure 1(a) depicts
$\langle \boldsymbol {u}\rangle$. Indeed, figure 1(a) depicts  $\mathcal {K}(\boldsymbol {x}\,|\,\boldsymbol {x}_0)$ for a simple model system. If the effective diffusivity were purely local, the figure would show non-zero values only on the diagonal. We can see abundant coupling away from the diagonal, and the kernel is manifestly not symmetric.
$\mathcal {K}(\boldsymbol {x}\,|\,\boldsymbol {x}_0)$ for a simple model system. If the effective diffusivity were purely local, the figure would show non-zero values only on the diagonal. We can see abundant coupling away from the diagonal, and the kernel is manifestly not symmetric.
Figure 1. (a) A graphical representation of the kernel  $\mathcal {K}(x,z\,|\,x_0,z_0)$ for a model flow, with
$\mathcal {K}(x,z\,|\,x_0,z_0)$ for a model flow, with  $(x,z)$ unwrapped as a one-dimensional coordinate on each axis. (b) A comparison of the ensemble mean
$(x,z)$ unwrapped as a one-dimensional coordinate on each axis. (b) A comparison of the ensemble mean  $\langle \theta \rangle$ computed using the exact equations, and with a local diffusivity approximation K, from (3.8). From Souza, Lutz & Flierl (Reference Souza, Lutz and Flierl2023).
$\langle \theta \rangle$ computed using the exact equations, and with a local diffusivity approximation K, from (3.8). From Souza, Lutz & Flierl (Reference Souza, Lutz and Flierl2023).
As pointed out by Souza et al., a great benefit of (2.9) is that it is exact, given the model assumptions. For many applications, the form of (2.9) is probably too complicated to be of direct use. However, a proposed closure can now be couched as an approximation to  $\mathcal {K}$, and having access to an exact expression should greatly help with validation. In an earlier recent paper, some of the same authors used this formalism to numerically compute the exact kernel
$\mathcal {K}$, and having access to an exact expression should greatly help with validation. In an earlier recent paper, some of the same authors used this formalism to numerically compute the exact kernel  $\mathcal {K}$ for a passive scalar in the ocean mixed layer (Bhamidipati, Souza & Flierl Reference Bhamidipati, Souza and Flierl2020).
$\mathcal {K}$ for a passive scalar in the ocean mixed layer (Bhamidipati, Souza & Flierl Reference Bhamidipati, Souza and Flierl2020).
3. A stochastic process and conditional means
In the present paper, Souza et al. probe the effective diffusivity kernel by computing it exactly for some model problems. Inspired by Hopf (Reference Hopf1952), their approach starts by specifying the ensemble  ${\omega }$ as arising from a stochastic process
${\omega }$ as arising from a stochastic process  ${\varOmega }(t)$, with a probability density
${\varOmega }(t)$, with a probability density  $p_\alpha (t) = \mathbb {P}({\varOmega }(t) \in [\alpha,\alpha + {\rm d}\alpha ])$ that follows a master equation
$p_\alpha (t) = \mathbb {P}({\varOmega }(t) \in [\alpha,\alpha + {\rm d}\alpha ])$ that follows a master equation
for some generator  $\mathcal {L}_\alpha$. Then they show that the weighted conditional mean
$\mathcal {L}_\alpha$. Then they show that the weighted conditional mean
obeys the equation
The mean is then recovered with  $\langle \theta \rangle = \int \varTheta _\alpha \,\mathrm {d}\mu _\alpha$, as is the advective flux
$\langle \theta \rangle = \int \varTheta _\alpha \,\mathrm {d}\mu _\alpha$, as is the advective flux  $\langle \boldsymbol {u}\,\theta \rangle$. Note that (3.3) itself is deterministic, even though there is an underlying random process, and is also autonomous – time does not appear explicitly and we are looking for a steady solution.
$\langle \boldsymbol {u}\,\theta \rangle$. Note that (3.3) itself is deterministic, even though there is an underlying random process, and is also autonomous – time does not appear explicitly and we are looking for a steady solution.
As a simple example, Souza et al. look at a stochastic Rossby wave system from Flierl & McGillicuddy (Reference Flierl and McGillicuddy2002), where the velocity  $\boldsymbol {u}_\alpha$ is given by a stream function
$\boldsymbol {u}_\alpha$ is given by a stream function
where  $\omega$ is a random phase angle, which obeys the stochastic process
$\omega$ is a random phase angle, which obeys the stochastic process  $\omega = \varOmega (t)$:
$\omega = \varOmega (t)$:
Here  $c$ is a constant angular velocity, and
$c$ is a constant angular velocity, and  $W(t)$ is a standard Brownian motion. The master equation (3.1) is taken to be a Fokker–Planck equation
$W(t)$ is a standard Brownian motion. The master equation (3.1) is taken to be a Fokker–Planck equation
The Fokker–Planck equation (3.6) together with (3.3), with source
can then be solved in various ways, for instance by discretization of the flow pattern into a finite set of states. Souza et al. extract an effective diffusivity operator, which can then be compared with the Taylor–Green–Kubo approximation for the local diffusivity (Taylor Reference Taylor1921),
Figure 1 compares the ‘exact’ (numerically obtained) mean  $\langle \theta \rangle$ with the mean obtained using the local diffusivity approximation (3.8). Indeed, there are visible deviations, indicating that the local approximation is flawed.
$\langle \theta \rangle$ with the mean obtained using the local diffusivity approximation (3.8). Indeed, there are visible deviations, indicating that the local approximation is flawed.
Of course, there remains an important problem: how to take a real time-dependent velocity field, either observed or numerically simulated, and model it as a series of random states. The authors discuss this by showing that what are essentially Koopman modes (Budišić, Mohr & Mezić Reference Budišić, Mohr and Mezić2012) can be used to break up a system into a discrete set of states. (Souza (Reference Souza2023) explores this idea further in a new preprint.) The strength of the current paper is that it builds a strong mathematical foundation for further study – after all, experience shows that ad hoc models are short lived and easily replaced, whereas models grounded in mathematics, even if imperfect, are revisited over and over again and eventually lead to significant breakthroughs. A precise definition of the effective diffusivity operator should help clarify the quality of a closure approximation, by testing in simple cases and then in more complex ones. Finally, a precise definition opens the way to more refined mathematical analysis, either by allowing a systematic use of asymptotics to derive closure models, or by providing an impetus for rigorous mathematical work.

 $\mathcal {K}(x,z\,|\,x_0,z_0)$ for a model flow, with
$\mathcal {K}(x,z\,|\,x_0,z_0)$ for a model flow, with  $(x,z)$ unwrapped as a one-dimensional coordinate on each axis. (b) A comparison of the ensemble mean
$(x,z)$ unwrapped as a one-dimensional coordinate on each axis. (b) A comparison of the ensemble mean  $\langle \theta \rangle$ computed using the exact equations, and with a local diffusivity approximation K, from (3.8). From Souza, Lutz & Flierl (2023).
$\langle \theta \rangle$ computed using the exact equations, and with a local diffusivity approximation K, from (3.8). From Souza, Lutz & Flierl (2023).



1. Introduction
Heat flows from hot to cold: it is the (second) law. This common-sense observation can be put into mathematical terms with the formula
That is, the heat flux vector $\boldsymbol {f}$ is proportional and opposite to the gradient of the temperature field
$\boldsymbol {f}$ is proportional and opposite to the gradient of the temperature field  $\theta (\boldsymbol {x},t)$, with proportionality constant given by the thermal diffusivity of the medium. Equation (1.1) applies in solids and quiescent fluids, and also to scalar quantities other than heat, such as the concentration of a pollutant; in that case (1.1) is known as Fick's law and
$\theta (\boldsymbol {x},t)$, with proportionality constant given by the thermal diffusivity of the medium. Equation (1.1) applies in solids and quiescent fluids, and also to scalar quantities other than heat, such as the concentration of a pollutant; in that case (1.1) is known as Fick's law and  $\kappa$ is simply a diffusivity, without the adjective ‘thermal’.
$\kappa$ is simply a diffusivity, without the adjective ‘thermal’.
Everyday experience suggests that (1.1) can not be quite right, since the thermal diffusivity of air is minuscule, and yet we can still heat our houses in the winter. The reason is that heat is transported predominantly by the motion of the fluid – small air currents in a room, driven by buoyancy and other processes, lead to a much more rapid homogenization of temperature than expected. In fact, it almost seems as though
that is, the average heat flux is linear in gradients of the average temperature, with an effective diffusivity $\kappa _{{eff}}$ that can be much, much larger than the molecular value
$\kappa _{{eff}}$ that can be much, much larger than the molecular value  $\kappa$. (The meaning of the average in (1.2) will be discussed below.) The ansatz (1.2), which dates back to the early days of turbulence theory, expresses the beautiful dream that turbulence functions as a random process similar to molecular collisions, only with a much longer effective mean free path. And indeed, this viewpoint has proved immensely successful in many physical systems; the problem is that real flows, and real turbulence, contain a mixture of scales and processes, including waves, coherent structures, boundary effects and eddies, all of which can lead to correlations locally and globally. (See the lectures by Young (Reference Young1999) for a nice introduction, or the reviews by Ottino (Reference Ottino1990) and Warhaft (Reference Warhaft2000).)
$\kappa$. (The meaning of the average in (1.2) will be discussed below.) The ansatz (1.2), which dates back to the early days of turbulence theory, expresses the beautiful dream that turbulence functions as a random process similar to molecular collisions, only with a much longer effective mean free path. And indeed, this viewpoint has proved immensely successful in many physical systems; the problem is that real flows, and real turbulence, contain a mixture of scales and processes, including waves, coherent structures, boundary effects and eddies, all of which can lead to correlations locally and globally. (See the lectures by Young (Reference Young1999) for a nice introduction, or the reviews by Ottino (Reference Ottino1990) and Warhaft (Reference Warhaft2000).)
For modern applications, a model such as (1.2) is needed in any computer code for the simulation of large-scale ocean and atmospheric processes. We do not have access to measurements of the smallest scales in the ocean, and even if we did we would not have the capacity to simulate their effect. Therefore, all modern computer codes parametrize the small scales in a flow in some effective manner, with the crudest being (1.2). This approach will work well if there is a clear scale separation: if we can see where the large-scale ends, and where the small scales begin. And even then, we have to properly take into account the couplings between the scales.
What Souza et al. propose is to do away with this ad hoc scale separation, and instead view the effective diffusivity as an operator,
where $\mathcal {K}$ is a tensorial kernel, allowing for anisotropic diffusion. They use a series of increasingly complex examples where they can compute
$\mathcal {K}$ is a tensorial kernel, allowing for anisotropic diffusion. They use a series of increasingly complex examples where they can compute  $\mathcal {K}$ explicitly or numerically. The structure of
$\mathcal {K}$ explicitly or numerically. The structure of  $\mathcal {K}$ then tells us much about the nature of transport in the system. For example, if
$\mathcal {K}$ then tells us much about the nature of transport in the system. For example, if  $\mathcal {K}$ is a delta function, or close to it, then a description using a local effective diffusivity will work well.
$\mathcal {K}$ is a delta function, or close to it, then a description using a local effective diffusivity will work well.
2. The closure problem
Let us briefly review the mathematical model used in Souza et al.. The concentration field $\theta (\boldsymbol {x},t)$ of a passive scalar, advected by a random velocity field
$\theta (\boldsymbol {x},t)$ of a passive scalar, advected by a random velocity field  $\boldsymbol {u}(\boldsymbol {x},t)$, with constant scalar diffusivity
$\boldsymbol {u}(\boldsymbol {x},t)$, with constant scalar diffusivity  $\kappa$ and a source
$\kappa$ and a source  $s(\boldsymbol {x})$, obeys the advection–diffusion equation
$s(\boldsymbol {x})$, obeys the advection–diffusion equation
We can average this equation over realizations of the random field $\boldsymbol {u}$, and obtain an equation for the average
$\boldsymbol {u}$, and obtain an equation for the average  $\langle \theta \rangle (\boldsymbol {x},t)$,
$\langle \theta \rangle (\boldsymbol {x},t)$,
The average here is an ensemble average over realizations of $\boldsymbol {u}$. The closure problem arises because in general we don't know how to deal with the term
$\boldsymbol {u}$. The closure problem arises because in general we don't know how to deal with the term  $\langle \boldsymbol {u}\theta \rangle$: (2.2) is not a closed equation for
$\langle \boldsymbol {u}\theta \rangle$: (2.2) is not a closed equation for  $\langle \theta \rangle$. The goal of a closure is to rewrite
$\langle \theta \rangle$. The goal of a closure is to rewrite
where ${O}$ is a linear operator, in general an integro-differential operator.
${O}$ is a linear operator, in general an integro-differential operator.
We isolate the issue by rewriting $\theta$ and
$\theta$ and  $\boldsymbol {u}$ in terms of their ensemble mean and fluctuations:
$\boldsymbol {u}$ in terms of their ensemble mean and fluctuations:
Then, subtracting (2.1) from (2.2), we find
This last equation should be interpreted with care: on the left-hand side is a linear operator acting on $\theta '$, including the ensemble average
$\theta '$, including the ensemble average  $\langle \boldsymbol {u}'\theta '\rangle$, which can be expressed as
$\langle \boldsymbol {u}'\theta '\rangle$, which can be expressed as
where now we explicitly denote ensemble members by a subscript ${\omega }$, and the probability measure
${\omega }$, and the probability measure  $\mu _{\omega }$ gives the relative weight of the ensemble member
$\mu _{\omega }$ gives the relative weight of the ensemble member  ${\omega }$. Equation (2.6) indicates that the left-hand side of (2.5) is an integro-differential operator involving the variables
${\omega }$. Equation (2.6) indicates that the left-hand side of (2.5) is an integro-differential operator involving the variables  $({\omega },\boldsymbol {x},t)$, where
$({\omega },\boldsymbol {x},t)$, where  ${\omega }$ itself could be countable to indicate an atlas of fixed velocity fields, or perhaps a continuous multidimensional variable that parametrizes the velocity field. Assuming that this operator is invertible (i.e. it admits a Green's function
${\omega }$ itself could be countable to indicate an atlas of fixed velocity fields, or perhaps a continuous multidimensional variable that parametrizes the velocity field. Assuming that this operator is invertible (i.e. it admits a Green's function  $\mathcal {G}_{{\omega }{\omega }_0}(\boldsymbol {x},t\,|\,\boldsymbol {x}_0,t_0)$), then the solution to (2.5) is
$\mathcal {G}_{{\omega }{\omega }_0}(\boldsymbol {x},t\,|\,\boldsymbol {x}_0,t_0)$), then the solution to (2.5) is
where a zero subscript denotes a function of $({\omega }_0,\boldsymbol {x}_0,t_0)$. Armed with (2.7), we can compute the flux
$({\omega }_0,\boldsymbol {x}_0,t_0)$. Armed with (2.7), we can compute the flux  $\langle \boldsymbol {u}'\theta '\rangle$. Souza et al. show that things simplify elegantly if we assume that the fluid is incompressible,
$\langle \boldsymbol {u}'\theta '\rangle$. Souza et al. show that things simplify elegantly if we assume that the fluid is incompressible,  $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {u}=0$ and that the statistics of
$\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {u}=0$ and that the statistics of  $\boldsymbol {u}$ are stationary; in that case, let
$\boldsymbol {u}$ are stationary; in that case, let
then
We have thus found the operator ${O}$ for the closure (2.3), with an ‘effective diffusivity operator’ given by
${O}$ for the closure (2.3), with an ‘effective diffusivity operator’ given by  $\int \mathcal {K}(\boldsymbol {x}\,|\,\boldsymbol {x}_0)\boldsymbol {\cdot }\bullet {\rm d}\boldsymbol {x}_0$. The case of an isotropic, purely local effective diffusivity is recovered when
$\int \mathcal {K}(\boldsymbol {x}\,|\,\boldsymbol {x}_0)\boldsymbol {\cdot }\bullet {\rm d}\boldsymbol {x}_0$. The case of an isotropic, purely local effective diffusivity is recovered when  $\mathcal {K}(\boldsymbol {x}\,|\,\boldsymbol {x}_0) = \kappa _{{eff}}\,\delta (\boldsymbol {x} - \boldsymbol {x}_0)\,\mathbb {I}$, with
$\mathcal {K}(\boldsymbol {x}\,|\,\boldsymbol {x}_0) = \kappa _{{eff}}\,\delta (\boldsymbol {x} - \boldsymbol {x}_0)\,\mathbb {I}$, with  $\mathbb {I}$ the identity tensor; clearly in general there is no reason to expect such a simple kernel. In fact the general kernel can even be non-symmetric, which indicates an induced drift, in addition to the mean drift
$\mathbb {I}$ the identity tensor; clearly in general there is no reason to expect such a simple kernel. In fact the general kernel can even be non-symmetric, which indicates an induced drift, in addition to the mean drift  $\langle \boldsymbol {u}\rangle$. Indeed, figure 1(a) depicts
$\langle \boldsymbol {u}\rangle$. Indeed, figure 1(a) depicts  $\mathcal {K}(\boldsymbol {x}\,|\,\boldsymbol {x}_0)$ for a simple model system. If the effective diffusivity were purely local, the figure would show non-zero values only on the diagonal. We can see abundant coupling away from the diagonal, and the kernel is manifestly not symmetric.
$\mathcal {K}(\boldsymbol {x}\,|\,\boldsymbol {x}_0)$ for a simple model system. If the effective diffusivity were purely local, the figure would show non-zero values only on the diagonal. We can see abundant coupling away from the diagonal, and the kernel is manifestly not symmetric.
Figure 1. (a) A graphical representation of the kernel $\mathcal {K}(x,z\,|\,x_0,z_0)$ for a model flow, with
$\mathcal {K}(x,z\,|\,x_0,z_0)$ for a model flow, with  $(x,z)$ unwrapped as a one-dimensional coordinate on each axis. (b) A comparison of the ensemble mean
$(x,z)$ unwrapped as a one-dimensional coordinate on each axis. (b) A comparison of the ensemble mean  $\langle \theta \rangle$ computed using the exact equations, and with a local diffusivity approximation K, from (3.8). From Souza, Lutz & Flierl (Reference Souza, Lutz and Flierl2023).
$\langle \theta \rangle$ computed using the exact equations, and with a local diffusivity approximation K, from (3.8). From Souza, Lutz & Flierl (Reference Souza, Lutz and Flierl2023).
As pointed out by Souza et al., a great benefit of (2.9) is that it is exact, given the model assumptions. For many applications, the form of (2.9) is probably too complicated to be of direct use. However, a proposed closure can now be couched as an approximation to $\mathcal {K}$, and having access to an exact expression should greatly help with validation. In an earlier recent paper, some of the same authors used this formalism to numerically compute the exact kernel
$\mathcal {K}$, and having access to an exact expression should greatly help with validation. In an earlier recent paper, some of the same authors used this formalism to numerically compute the exact kernel  $\mathcal {K}$ for a passive scalar in the ocean mixed layer (Bhamidipati, Souza & Flierl Reference Bhamidipati, Souza and Flierl2020).
$\mathcal {K}$ for a passive scalar in the ocean mixed layer (Bhamidipati, Souza & Flierl Reference Bhamidipati, Souza and Flierl2020).
3. A stochastic process and conditional means
In the present paper, Souza et al. probe the effective diffusivity kernel by computing it exactly for some model problems. Inspired by Hopf (Reference Hopf1952), their approach starts by specifying the ensemble ${\omega }$ as arising from a stochastic process
${\omega }$ as arising from a stochastic process  ${\varOmega }(t)$, with a probability density
${\varOmega }(t)$, with a probability density  $p_\alpha (t) = \mathbb {P}({\varOmega }(t) \in [\alpha,\alpha + {\rm d}\alpha ])$ that follows a master equation
$p_\alpha (t) = \mathbb {P}({\varOmega }(t) \in [\alpha,\alpha + {\rm d}\alpha ])$ that follows a master equation
for some generator $\mathcal {L}_\alpha$. Then they show that the weighted conditional mean
$\mathcal {L}_\alpha$. Then they show that the weighted conditional mean
obeys the equation
The mean is then recovered with $\langle \theta \rangle = \int \varTheta _\alpha \,\mathrm {d}\mu _\alpha$, as is the advective flux
$\langle \theta \rangle = \int \varTheta _\alpha \,\mathrm {d}\mu _\alpha$, as is the advective flux  $\langle \boldsymbol {u}\,\theta \rangle$. Note that (3.3) itself is deterministic, even though there is an underlying random process, and is also autonomous – time does not appear explicitly and we are looking for a steady solution.
$\langle \boldsymbol {u}\,\theta \rangle$. Note that (3.3) itself is deterministic, even though there is an underlying random process, and is also autonomous – time does not appear explicitly and we are looking for a steady solution.
As a simple example, Souza et al. look at a stochastic Rossby wave system from Flierl & McGillicuddy (Reference Flierl and McGillicuddy2002), where the velocity $\boldsymbol {u}_\alpha$ is given by a stream function
$\boldsymbol {u}_\alpha$ is given by a stream function
where $\omega$ is a random phase angle, which obeys the stochastic process
$\omega$ is a random phase angle, which obeys the stochastic process  $\omega = \varOmega (t)$:
$\omega = \varOmega (t)$:
Here $c$ is a constant angular velocity, and
$c$ is a constant angular velocity, and  $W(t)$ is a standard Brownian motion. The master equation (3.1) is taken to be a Fokker–Planck equation
$W(t)$ is a standard Brownian motion. The master equation (3.1) is taken to be a Fokker–Planck equation
The Fokker–Planck equation (3.6) together with (3.3), with source
can then be solved in various ways, for instance by discretization of the flow pattern into a finite set of states. Souza et al. extract an effective diffusivity operator, which can then be compared with the Taylor–Green–Kubo approximation for the local diffusivity (Taylor Reference Taylor1921),
Figure 1 compares the ‘exact’ (numerically obtained) mean $\langle \theta \rangle$ with the mean obtained using the local diffusivity approximation (3.8). Indeed, there are visible deviations, indicating that the local approximation is flawed.
$\langle \theta \rangle$ with the mean obtained using the local diffusivity approximation (3.8). Indeed, there are visible deviations, indicating that the local approximation is flawed.
Of course, there remains an important problem: how to take a real time-dependent velocity field, either observed or numerically simulated, and model it as a series of random states. The authors discuss this by showing that what are essentially Koopman modes (Budišić, Mohr & Mezić Reference Budišić, Mohr and Mezić2012) can be used to break up a system into a discrete set of states. (Souza (Reference Souza2023) explores this idea further in a new preprint.) The strength of the current paper is that it builds a strong mathematical foundation for further study – after all, experience shows that ad hoc models are short lived and easily replaced, whereas models grounded in mathematics, even if imperfect, are revisited over and over again and eventually lead to significant breakthroughs. A precise definition of the effective diffusivity operator should help clarify the quality of a closure approximation, by testing in simple cases and then in more complex ones. Finally, a precise definition opens the way to more refined mathematical analysis, either by allowing a systematic use of asymptotics to derive closure models, or by providing an impetus for rigorous mathematical work.
Declaration of interests
The authors report no conflict of interest.