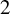1 Introduction
For
![]() $d\ge 2$
, denote by
$d\ge 2$
, denote by
![]() $\mathrm {Rat}_d$
the space of rational maps of degree d in one complex variable. Via parameterizing coefficients, the space
$\mathrm {Rat}_d$
the space of rational maps of degree d in one complex variable. Via parameterizing coefficients, the space
![]() $\mathrm {Rat}_d$
is an open dense subset of the
$\mathrm {Rat}_d$
is an open dense subset of the
![]() $2d+1$
-dimensional complex projective space
$2d+1$
-dimensional complex projective space
![]() $\mathbb {P}^{2d+1}$
. The boundary
$\mathbb {P}^{2d+1}$
. The boundary
![]() $\partial \mathrm {Rat}_d:= {\mathbb P}^{2d+1}\setminus \mathrm {Rat}_d$
consists of so-called degenerate rational maps. A sequence in
$\partial \mathrm {Rat}_d:= {\mathbb P}^{2d+1}\setminus \mathrm {Rat}_d$
consists of so-called degenerate rational maps. A sequence in
![]() $\mathrm {Rat}_d$
is degenerate if its limit is a degenerate rational map. It is of interest to understand the interplay of dynamics for a degenerate sequence and its limit. The goal of this paper is to explore this interplay in a significant slice of
$\mathrm {Rat}_d$
is degenerate if its limit is a degenerate rational map. It is of interest to understand the interplay of dynamics for a degenerate sequence and its limit. The goal of this paper is to explore this interplay in a significant slice of
![]() $\mathrm {Rat}_d$
, namely Newton family. We show that under natural assumptions, the dynamics preserves stably when Newton maps approach to
$\mathrm {Rat}_d$
, namely Newton family. We show that under natural assumptions, the dynamics preserves stably when Newton maps approach to
![]() $\partial \mathrm {Rat}_d$
. Once this result is at our disposal, we can describe completely the boundedness of hyperbolic components in the moduli space of quartic Newton maps.
$\partial \mathrm {Rat}_d$
. Once this result is at our disposal, we can describe completely the boundedness of hyperbolic components in the moduli space of quartic Newton maps.
1.1 Statements of main results
For a degree
![]() $d\ge 2$
complex polynomial
$d\ge 2$
complex polynomial
![]() $P(z)$
with simple roots, its Newton map is defined by
$P(z)$
with simple roots, its Newton map is defined by
Denote by
![]() $\mathrm {NM}_d$
the space of degree d Newton maps. Then
$\mathrm {NM}_d$
the space of degree d Newton maps. Then
![]() $\mathrm {NM}_d$
is a d-dimensional subspace in
$\mathrm {NM}_d$
is a d-dimensional subspace in
![]() $\mathrm {Rat}_d$
and hence in
$\mathrm {Rat}_d$
and hence in
![]() $\mathbb {P}^{2d+1}$
. Let
$\mathbb {P}^{2d+1}$
. Let
![]() $\overline {\mathrm {NM}}_d$
be the closure of
$\overline {\mathrm {NM}}_d$
be the closure of
![]() $\mathrm {NM}_d$
in
$\mathrm {NM}_d$
in
![]() $\mathbb {P}^{2d+1}$
. For
$\mathbb {P}^{2d+1}$
. For
![]() $f\in \overline {\mathrm {NM}}_d$
, denote by
$f\in \overline {\mathrm {NM}}_d$
, denote by
![]() $\hat f$
the reduction of f, see §2.1. We are interested in the case where
$\hat f$
the reduction of f, see §2.1. We are interested in the case where
![]() $\hat f$
has degree at least
$\hat f$
has degree at least
![]() $2$
, see Lemma 5.6. Then
$2$
, see Lemma 5.6. Then
![]() $\hat f$
is a Newton map for a polynomial with possible multiple roots. For more details, we refer the reader to [Reference Nie21].
$\hat f$
is a Newton map for a polynomial with possible multiple roots. For more details, we refer the reader to [Reference Nie21].
Now consider the basin of roots of
![]() $\hat f$
. Let
$\hat f$
. Let
![]() $\mathcal {U}$
be a set consisting of finitely many components of such basins. The boundary of each
$\mathcal {U}$
be a set consisting of finitely many components of such basins. The boundary of each
![]() $U\in \mathcal {U}$
is locally connected [Reference Drach and Schleicher5, Reference Wang, Yin and Zeng29]. Provided that
$U\in \mathcal {U}$
is locally connected [Reference Drach and Schleicher5, Reference Wang, Yin and Zeng29]. Provided that
![]() $\hat f$
is forward invariant and post-critically finite on
$\hat f$
is forward invariant and post-critically finite on
![]() $\bigcup _{U\in \mathcal {U}}U$
, each
$\bigcup _{U\in \mathcal {U}}U$
, each
![]() $U\in \mathcal {U}$
carries landed internal rays
$U\in \mathcal {U}$
carries landed internal rays
![]() $I_{(U,u)}(t)$
of
$I_{(U,u)}(t)$
of
![]() $\hat f$
for
$\hat f$
for
![]() $t\in \mathbb {R}/\mathbb {Z}$
, where
$t\in \mathbb {R}/\mathbb {Z}$
, where
![]() $u\in U$
is the center of U. Let
$u\in U$
is the center of U. Let
![]() $\Gamma $
be a (not necessarily connected) graph consisting of finitely many (pre)periodic internal rays in
$\Gamma $
be a (not necessarily connected) graph consisting of finitely many (pre)periodic internal rays in
![]() $\bigcup _{U\in \mathcal {U}}U$
, that is,
$\bigcup _{U\in \mathcal {U}}U$
, that is,
 $$ \begin{align*} \Gamma:=\bigcup_{U\in\mathcal{U},t\in T_{ U}}I_{(U,u)}(t), \end{align*} $$
$$ \begin{align*} \Gamma:=\bigcup_{U\in\mathcal{U},t\in T_{ U}}I_{(U,u)}(t), \end{align*} $$
with
![]() $T_{ U}\subseteq \mathbb {Q}$
for every
$T_{ U}\subseteq \mathbb {Q}$
for every
![]() $U\in {\mathcal U}$
. Here we allow
$U\in {\mathcal U}$
. Here we allow
![]() $T_{ U}=\emptyset $
for some
$T_{ U}=\emptyset $
for some
![]() $U\in {\mathcal U}$
. The canonical paradigms of such graphs are the Newton graphs (see §4.1) formulated recently by Drach et al [Reference Drach, Mikukich, Rückert and Schleicher4] and the alternative graphs for cubic Newton maps (see §4.2) based on Roesch’s work in [Reference Roesch25].
$U\in {\mathcal U}$
. The canonical paradigms of such graphs are the Newton graphs (see §4.1) formulated recently by Drach et al [Reference Drach, Mikukich, Rückert and Schleicher4] and the alternative graphs for cubic Newton maps (see §4.2) based on Roesch’s work in [Reference Roesch25].
Let
![]() $\{f_n\}_{n\ge 1}\subset {\mathrm {NM}}_d$
be a sequence such that
$\{f_n\}_{n\ge 1}\subset {\mathrm {NM}}_d$
be a sequence such that
![]() $f_n$
converges to f. As we will see in §3.1, each
$f_n$
converges to f. As we will see in §3.1, each
![]() $(U,u)\in {\mathcal U}$
has a deformation
$(U,u)\in {\mathcal U}$
has a deformation
![]() $(U_n,u_n)$
at
$(U_n,u_n)$
at
![]() $f_n$
and the map
$f_n$
and the map
![]() $f_n:(U_n,u_n)\to {\mathbb C}$
converges to
$f_n:(U_n,u_n)\to {\mathbb C}$
converges to
![]() $\hat f:(U,u)\to {\mathbb C}$
under the Carathéodory topology in the sense of McMullen [Reference McMullen16, §5.1]. If, in addition, the local degrees
$\hat f:(U,u)\to {\mathbb C}$
under the Carathéodory topology in the sense of McMullen [Reference McMullen16, §5.1]. If, in addition, the local degrees
![]() $\deg _{u_n}f_n=\deg _u\hat f$
for every
$\deg _{u_n}f_n=\deg _u\hat f$
for every
![]() $(U,u)\in {\mathcal U}$
, we denote
$(U,u)\in {\mathcal U}$
, we denote
![]() $f_n\xrightarrow {\deg }f$
on
$f_n\xrightarrow {\deg }f$
on
![]() ${\mathcal U}$
. In this case, the deformation
${\mathcal U}$
. In this case, the deformation
![]() $(U_n,u_n)$
is unique at
$(U_n,u_n)$
is unique at
![]() $f_n$
. Moreover, a Böttcher coordinate of
$f_n$
. Moreover, a Böttcher coordinate of
![]() $\hat f$
on
$\hat f$
on
![]() $U\in \mathcal {U}$
naturally deduces a Böttcher coordinate of
$U\in \mathcal {U}$
naturally deduces a Böttcher coordinate of
![]() $f_n$
on the deformation
$f_n$
on the deformation
![]() $(U_n,u_n)$
of
$(U_n,u_n)$
of
![]() $(U,u)$
, see §3.1. Then we can define the corresponding internal rays in
$(U,u)$
, see §3.1. Then we can define the corresponding internal rays in
![]() $U_n$
, which either land on
$U_n$
, which either land on
![]() $\partial U_n$
or terminate at
$\partial U_n$
or terminate at
![]() $f_n$
-iterated preimages of critical points in
$f_n$
-iterated preimages of critical points in
![]() $U_n$
, see §3.2. For examples satisfying the above conditions, see Lemma 3.5.
$U_n$
, see §3.2. For examples satisfying the above conditions, see Lemma 3.5.
Our first result concerns the perturbations of
![]() $\Gamma $
.
$\Gamma $
.
Theorem 1.1. Let
![]() $f\in \overline {\mathrm {NM}}_d$
with
$f\in \overline {\mathrm {NM}}_d$
with
![]() ${\mathcal U},\Gamma $
defined as above. Let
${\mathcal U},\Gamma $
defined as above. Let
![]() $\{f_n\}_{n\ge 1}\subset {\mathrm {NM}}_d$
be a sequence such that
$\{f_n\}_{n\ge 1}\subset {\mathrm {NM}}_d$
be a sequence such that
![]() $f_n\xrightarrow {\deg }f$
on
$f_n\xrightarrow {\deg }f$
on
![]() ${\mathcal U}$
. Suppose that for each
${\mathcal U}$
. Suppose that for each
![]() $U\in \mathcal {U}$
and
$U\in \mathcal {U}$
and
![]() $t\in T_{U}$
:
$t\in T_{U}$
:
-
(i) the orbit of the landing point of
 $I_{(U,u)}(t)$
is eventually repelling periodic and avoids the critical points of
$I_{(U,u)}(t)$
is eventually repelling periodic and avoids the critical points of
 $\hat {f}$
; and
$\hat {f}$
; and -
(ii) the corresponding internal ray
 $I_{(U_n,u_n)}(t)$
lands on
$I_{(U_n,u_n)}(t)$
lands on
 $\partial U_n$
for all large n.
$\partial U_n$
for all large n.
Then for all large n, the graph
 $$ \begin{align*} \Gamma_n:=\bigcup_{U\in\mathcal{U},t\in T_{U}}I_{(U_n,u_n)}(t) \end{align*} $$
$$ \begin{align*} \Gamma_n:=\bigcup_{U\in\mathcal{U},t\in T_{U}}I_{(U_n,u_n)}(t) \end{align*} $$
is homeomorphic to
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $\Gamma _n$
converges to
$\Gamma _n$
converges to
![]() $\Gamma $
, as
$\Gamma $
, as
![]() $n\to \infty $
, in the Hausdorff metric topology.
$n\to \infty $
, in the Hausdorff metric topology.
Furthermore, if
![]() $\Gamma $
is
$\Gamma $
is
![]() $\hat {f}$
-invariant, then there exist homeomorphisms
$\hat {f}$
-invariant, then there exist homeomorphisms
![]() $\varphi _n:\Gamma \to \Gamma _n$
such that
$\varphi _n:\Gamma \to \Gamma _n$
such that
![]() $\varphi _n\circ f=f_n\circ \varphi _n$
on
$\varphi _n\circ f=f_n\circ \varphi _n$
on
![]() $\Gamma $
for all large n.
$\Gamma $
for all large n.
Remark 1.2
-
(1) In Theorem 1.1, the assumption (i) guarantees that the perturbations of the orbit of the landing point of
 $I_{(U,u)}(t)$
are well controlled, see Proposition 2.4. In Proposition 3.9, we provide sufficient condition for the assumption (ii).
$I_{(U,u)}(t)$
are well controlled, see Proposition 2.4. In Proposition 3.9, we provide sufficient condition for the assumption (ii). -
(2) In the present paper, we mainly use the first part of the conclusion in Theorem 1.1 to classify the bounded hyperbolic components. In the sequel [Reference Gao and Nie11], we will apply the both parts of the conclusion in Theorem 1.1 to characterize the unbounded hyperbolic components.
The technique of perturbations of internal rays already appear in complex dynamics for the non-degenerate maps, see e.g. [Reference Gao and Giulio10, Reference Goldberg and Milnor12, Reference Roesch24]. Theorem 1.1 generalizes it to the degenerate case within the Newton family. The key point of the proof, differing from the non-degenerate case, is an elaborate argument to the internal rays landing at holes of f, where the locally uniform convergence fails.
In principle, our above theorem provides a combinational method to study degenerate sequences of Newton maps in the parameter space and hence that in moduli space. In a certain sense it asserts that, under the assumptions, part of the dynamics of the degenerate map
![]() $\hat f$
embeds into the dynamics of non-degenerate maps
$\hat f$
embeds into the dynamics of non-degenerate maps
![]() $f_n$
. Thus it allows us to control the dynamics of
$f_n$
. Thus it allows us to control the dynamics of
![]() $f_n$
by that of
$f_n$
by that of
![]() $\hat f$
.
$\hat f$
.
Now we apply Theorem 1.1 to study the boundedness of hyperbolic components in the moduli space of quartic Newton maps. Since the point
![]() $\infty $
is the unique repelling fixed point for Newton maps, the moduli space of degree d Newton maps is defined by
$\infty $
is the unique repelling fixed point for Newton maps, the moduli space of degree d Newton maps is defined by
modulo the action by conjugation of the group of affine maps. We mention here that the space
![]() $\mathrm {nm}_d$
has complex dimension
$\mathrm {nm}_d$
has complex dimension
![]() $d-2$
. Recall that a rational map is hyperbolic if each critical point converges under iteration to a (super)attracting cycle, equivalently, it is uniformly expanding in a neighborhood of its Julia set, see [Reference McMullen16, §3.4]. The space of hyperbolic Newton maps descends an open subset in
$d-2$
. Recall that a rational map is hyperbolic if each critical point converges under iteration to a (super)attracting cycle, equivalently, it is uniformly expanding in a neighborhood of its Julia set, see [Reference McMullen16, §3.4]. The space of hyperbolic Newton maps descends an open subset in
![]() $\mathrm {nm}_d$
, and each component of this subset is a hyperbolic component in
$\mathrm {nm}_d$
, and each component of this subset is a hyperbolic component in
![]() $\mathrm {nm}_d$
. Endowing
$\mathrm {nm}_d$
. Endowing
![]() $\mathrm {nm}_d$
the quotient topology, we say a hyperbolic component in
$\mathrm {nm}_d$
the quotient topology, we say a hyperbolic component in
![]() $\mathrm {nm}_d$
is bounded if it has compact closure in
$\mathrm {nm}_d$
is bounded if it has compact closure in
![]() $\mathrm { nm}_d$
, and unbounded otherwise.
$\mathrm { nm}_d$
, and unbounded otherwise.
A hyperbolic component
![]() $\mathcal {H}\subset \mathrm {nm}_d$
is of immediate escaping type if each element in
$\mathcal {H}\subset \mathrm {nm}_d$
is of immediate escaping type if each element in
![]() $\mathcal {H}$
is the conjugacy class of a Newton map having degree at least
$\mathcal {H}$
is the conjugacy class of a Newton map having degree at least
![]() $3$
in the immediate basin of some root.
$3$
in the immediate basin of some root.
Theorem 1.3. Let
![]() $\mathcal {H}\subset \mathrm {nm}_4$
be a hyperbolic component. Then
$\mathcal {H}\subset \mathrm {nm}_4$
be a hyperbolic component. Then
![]() $\mathcal {H}$
is unbounded if and only if
$\mathcal {H}$
is unbounded if and only if
![]() $\mathcal {H}$
is of immediate escaping type (see Figure 1).
$\mathcal {H}$
is of immediate escaping type (see Figure 1).

Figure 1 The c-plane for the family of Newton maps
![]() $f_{P_c}$
for the polynomials
$f_{P_c}$
for the polynomials
![]() $P_c(z)=z^4/12-cz^3/6+(4c-3)z/12+(3-4c)/12$
, see [Reference Nie and Pilgrim22, Figure 1]. The critical points of
$P_c(z)=z^4/12-cz^3/6+(4c-3)z/12+(3-4c)/12$
, see [Reference Nie and Pilgrim22, Figure 1]. The critical points of
![]() $f_{P_c}$
are the four roots of
$f_{P_c}$
are the four roots of
![]() $P_c(z)$
,
$P_c(z)$
,
![]() $0$
and c. The map
$0$
and c. The map
![]() $f_{P_c}$
has a superattracting
$f_{P_c}$
has a superattracting
![]() $2$
-cycle
$2$
-cycle
![]() $0\to 1\to 0$
. The letters indicate the types of hyperbolic components, see §5.1. Our result asserts that the hyperbolic components indicated by A, B, C, or FE1 are bounded in
$0\to 1\to 0$
. The letters indicate the types of hyperbolic components, see §5.1. Our result asserts that the hyperbolic components indicated by A, B, C, or FE1 are bounded in
![]() $\mathrm {nm}_4$
.
$\mathrm {nm}_4$
.
For the boundedness of hyperbolic components, motivated by a result of Kleinian groups [Reference Thurston28, Theorem 1.2], McMullen [Reference McMullen15] conjectures that every hyperbolic component with Sierpínski Julia set is bounded in the moduli space of degree d rational maps. In his celebrated work [Reference Milnor17, Remark 7.2], Milnor proposed the study of this topic in quadratic case. If the moduli space has complex dimension at least
![]() $2$
, there are only few already known results: for a hyperbolic component in the moduli space of bicritical rational maps, if each element possesses two distinct (super)attracting cycles of period at least
$2$
, there are only few already known results: for a hyperbolic component in the moduli space of bicritical rational maps, if each element possesses two distinct (super)attracting cycles of period at least
![]() $2$
, then it is bounded, see [Reference Epstein6, Theorem 1] and [Reference Nie and Pilgrim23, Theorem 1.1]; for quartic Newton maps, the second author and Pilgrim proved that a hyperbolic component in
$2$
, then it is bounded, see [Reference Epstein6, Theorem 1] and [Reference Nie and Pilgrim23, Theorem 1.1]; for quartic Newton maps, the second author and Pilgrim proved that a hyperbolic component in
![]() $\mathrm {nm}_4$
is bounded if each element has two distinct (super)attracting cycles of period at least
$\mathrm {nm}_4$
is bounded if each element has two distinct (super)attracting cycles of period at least
![]() $2$
[Reference Nie and Pilgrim22, Main Theorem].
$2$
[Reference Nie and Pilgrim22, Main Theorem].
All the previous known bounded hyperbolic components are of so-called type D, that is, each element has maximal number of (super)attracting cycles. We point out here that the type-D components are semi-algebraic, but the components of other types are possible transcendental objects, see [Reference Milnor20, Theorem 1 and Conjecture 2]. Our boundedness result gives the first non-semi-algebraic bounded hyperbolic components in a complex two-dimensional moduli space. Moreover, it strengthens the result [Reference Nie and Pilgrim22, Theorem 1.3].
1.2 Strategy of the proof of Theorem 1.3
One direction of Theorem 1.3 is the result [Reference Nie and Pilgrim22, Theorem 1.4]: if
![]() $\mathcal {H}$
is of immediate escaping type, then
$\mathcal {H}$
is of immediate escaping type, then
![]() $\mathcal {H}$
is unbounded. Now we give an overview of the proof of the reverse implication. Differing from the analytic argument in [Reference Epstein6] and the arithmetic argument in [Reference Nie and Pilgrim22, Reference Nie and Pilgrim23], our argument relies on the combinatorial properties of Newton maps and applies Theorem 1.1. The proof goes by contradiction as follows. Suppose
$\mathcal {H}$
is unbounded. Now we give an overview of the proof of the reverse implication. Differing from the analytic argument in [Reference Epstein6] and the arithmetic argument in [Reference Nie and Pilgrim22, Reference Nie and Pilgrim23], our argument relies on the combinatorial properties of Newton maps and applies Theorem 1.1. The proof goes by contradiction as follows. Suppose
![]() $\mathcal {H}$
is unbounded and not of immediate escaping type. Then we obtain an unbounded sequence
$\mathcal {H}$
is unbounded and not of immediate escaping type. Then we obtain an unbounded sequence
![]() $[f_n]\in \mathcal {H}$
. Passing to a subsequence, we can assume that
$[f_n]\in \mathcal {H}$
. Passing to a subsequence, we can assume that
![]() $[f_n]$
has a lift
$[f_n]$
has a lift
![]() $f_n\in \mathrm {NM}_4$
such that
$f_n\in \mathrm {NM}_4$
such that
![]() $f_n$
converges to
$f_n$
converges to
![]() $f\in \partial \mathrm {NM}_4$
with reduction
$f\in \partial \mathrm {NM}_4$
with reduction
![]() $\hat f$
having degree
$\hat f$
having degree
![]() $2$
or
$2$
or
![]() $3$
and no roots of
$3$
and no roots of
![]() $f_n$
collide in
$f_n$
collide in
![]() $\mathbb {C}$
as
$\mathbb {C}$
as
![]() $n\to \infty $
, see Lemma 5.6. It follows that at least one non-fixed critical point
$n\to \infty $
, see Lemma 5.6. It follows that at least one non-fixed critical point
![]() $c_n$
of
$c_n$
of
![]() $f_n$
diverges to
$f_n$
diverges to
![]() $\infty $
. We derive a contradiction case by case.
$\infty $
. We derive a contradiction case by case.
Case 1:
![]() $\deg \hat f=2$
. In this case, we consider rational internal rays in the immediate basins of the roots of
$\deg \hat f=2$
. In this case, we consider rational internal rays in the immediate basins of the roots of
![]() $\hat f$
and the corresponding perturbations for
$\hat f$
and the corresponding perturbations for
![]() $f_n$
. Theorem 1.1 implies that
$f_n$
. Theorem 1.1 implies that
![]() $\deg f_n=2$
and hence leads to a contradiction.
$\deg f_n=2$
and hence leads to a contradiction.
Case 2:
![]() $\deg \hat f=3$
and
$\deg \hat f=3$
and
![]() $\mathcal {H}$
is of type A, B, C, or D. It turns out that the Newton graphs of
$\mathcal {H}$
is of type A, B, C, or D. It turns out that the Newton graphs of
![]() $\hat f$
are disjoint with the unique non-fixed critical point c of
$\hat f$
are disjoint with the unique non-fixed critical point c of
![]() $\hat f$
. Applying Theorem 1.1 to the Newton graphs of
$\hat f$
. Applying Theorem 1.1 to the Newton graphs of
![]() $\hat f$
, we bound the immediate basins of the (super)attracting cycles of periods at least 2 for
$\hat f$
, we bound the immediate basins of the (super)attracting cycles of periods at least 2 for
![]() $f_n$
. We obtain a contradiction by arguing the location of forward orbit of the critical point
$f_n$
. We obtain a contradiction by arguing the location of forward orbit of the critical point
![]() $c_n$
.
$c_n$
.
Case 3:
![]() $\deg \hat f=3$
and
$\deg \hat f=3$
and
![]() $\mathcal {H}$
is of type FE1 or FE2. In this case, the critical point c could be an iterated preimage of
$\mathcal {H}$
is of type FE1 or FE2. In this case, the critical point c could be an iterated preimage of
![]() $\infty $
. Then we can not apply Theorem 1.1 directly to the Newton graphs as in the previous case. Alternatively, using Rosech’s results in [Reference Roesch25] on cut angles, we construct a natural Jordan curve
$\infty $
. Then we can not apply Theorem 1.1 directly to the Newton graphs as in the previous case. Alternatively, using Rosech’s results in [Reference Roesch25] on cut angles, we construct a natural Jordan curve
![]() ${\mathcal C}$
consisting of (pre)periodic internal rays of
${\mathcal C}$
consisting of (pre)periodic internal rays of
![]() $\hat f$
such that the orbit of
$\hat f$
such that the orbit of
![]() ${\mathcal C}$
is away from the critical point c. Then Theorem 1.1 works for the curve
${\mathcal C}$
is away from the critical point c. Then Theorem 1.1 works for the curve
![]() $\mathcal {C}$
. Thus, we can continue to analyze the location of the related critical points and the corresponding Fatou components of
$\mathcal {C}$
. Thus, we can continue to analyze the location of the related critical points and the corresponding Fatou components of
![]() $f_n$
, and obtain a contradiction.
$f_n$
, and obtain a contradiction.
We remark that our proof of Theorem 1.3 highly relies on the behavior of the critical point
![]() $c_n$
for
$c_n$
for
![]() $f_n$
, see Lemma 5.3. We do not expect an analogy of such behavior holding for Newton maps of higher degrees. However, it would be interesting to apply Theorem 1.1 to investigate the boundedness of hyperbolic components in
$f_n$
, see Lemma 5.3. We do not expect an analogy of such behavior holding for Newton maps of higher degrees. However, it would be interesting to apply Theorem 1.1 to investigate the boundedness of hyperbolic components in
![]() $\mathrm {nm}_d$
for
$\mathrm {nm}_d$
for
![]() $d\ge 5$
.
$d\ge 5$
.
2 Preliminaries
In this section, we give background materials. In §2.1, we provide basic definitions and properties of degenerate rational maps. Section 2.2 concerns the (degenerate) Newton maps.
2.1 Degenerate rational maps
As mentioned in §1, the space
![]() $\mathrm {Rat}_d$
is naturally identified as an open and dense subset of
$\mathrm {Rat}_d$
is naturally identified as an open and dense subset of
![]() $\mathbb {P}^{2d+1}$
. We say each element
$\mathbb {P}^{2d+1}$
. We say each element
![]() $f\in \mathbb {P}^{2d+1}\setminus \mathrm {Rat}_d$
is a degenerate rational map of degree d. For such f, there exist two homogeneous polynomials
$f\in \mathbb {P}^{2d+1}\setminus \mathrm {Rat}_d$
is a degenerate rational map of degree d. For such f, there exist two homogeneous polynomials
![]() $F(X,Y)$
and
$F(X,Y)$
and
![]() $G(X,Y)$
of degree d in
$G(X,Y)$
of degree d in
![]() $\mathbb {C}[X,Y]$
such that
$\mathbb {C}[X,Y]$
such that
![]() $f=[F:G]$
is in homogeneous coordinates and
$f=[F:G]$
is in homogeneous coordinates and
![]() $H_f:=\gcd [F,G]$
is a polynomial in
$H_f:=\gcd [F,G]$
is a polynomial in
![]() $\mathbb {C}[X,Y]$
of degree at least
$\mathbb {C}[X,Y]$
of degree at least
![]() $1$
. We can rewrite
$1$
. We can rewrite
where
![]() $\hat f$
is a rational map of degree less than d. We say each zero of
$\hat f$
is a rational map of degree less than d. We say each zero of
![]() $H_f$
is a hole of f and denote
$H_f$
is a hole of f and denote
![]() $\mathrm {Hole}(f)$
the set of holes of f. Moreover, we call
$\mathrm {Hole}(f)$
the set of holes of f. Moreover, we call
![]() $\hat f$
the reduction of f. For convenience, if f is a rational map of degree d, we define
$\hat f$
the reduction of f. For convenience, if f is a rational map of degree d, we define
![]() $H_f=1$
and then
$H_f=1$
and then
![]() $\hat f=f$
.
$\hat f=f$
.
Let
![]() $\{f_n\}_{n\ge 1}$
be a sequence of rational maps of degree
$\{f_n\}_{n\ge 1}$
be a sequence of rational maps of degree
![]() $d\ge 1$
. We say
$d\ge 1$
. We say
![]() $f_n$
converges semi-algebraically to a (degenerate) rational map f if the coefficients of
$f_n$
converges semi-algebraically to a (degenerate) rational map f if the coefficients of
![]() $f_n$
converge to the coefficients of f in
$f_n$
converge to the coefficients of f in
![]() $\mathbb {P}^{2d+1}$
. Compare to the algebraically convergence in [Reference Buff and Tan1]. Without special emphasis, we mean semi-algebraically convergence when we consider convergence for a sequence in
$\mathbb {P}^{2d+1}$
. Compare to the algebraically convergence in [Reference Buff and Tan1]. Without special emphasis, we mean semi-algebraically convergence when we consider convergence for a sequence in
![]() $\mathbb {P}^{2d+1}$
. The semi-algebraical convergence implies locally uniform convergence away from holes.
$\mathbb {P}^{2d+1}$
. The semi-algebraical convergence implies locally uniform convergence away from holes.
Lemma 2.1. [Reference DeMarco2, Lemma 4.1]
Let
![]() $\{f_n\}_{n\geq 1}$
be a sequence of degree
$\{f_n\}_{n\geq 1}$
be a sequence of degree
![]() $d\ge 1$
rational maps. If
$d\ge 1$
rational maps. If
![]() $f_n$
converges to
$f_n$
converges to
![]() $f=H_f\hat {f}\in {\mathbb P}^{2d+1}$
, then
$f=H_f\hat {f}\in {\mathbb P}^{2d+1}$
, then
![]() $f_n$
converges locally uniformly to
$f_n$
converges locally uniformly to
![]() $\hat {f}$
outside
$\hat {f}$
outside
![]() $\mathrm {Hole}(f)$
.
$\mathrm {Hole}(f)$
.
Suppose that each
![]() $f_n$
possesses a cycle of fixed period. If the limit of these cycles is away from the holes of f, Lemma 2.1 immediately implies that this limit is also a cycle for
$f_n$
possesses a cycle of fixed period. If the limit of these cycles is away from the holes of f, Lemma 2.1 immediately implies that this limit is also a cycle for
![]() $\hat f$
. We state as follows and omit the proof.
$\hat f$
. We state as follows and omit the proof.
Lemma 2.2. Let
![]() $\{f_n\}_{n\geq 1}$
be a sequence of degree
$\{f_n\}_{n\geq 1}$
be a sequence of degree
![]() $d\ge 2$
rational maps. Suppose that
$d\ge 2$
rational maps. Suppose that
![]() $f_n$
converges to
$f_n$
converges to
![]() $f=H_f\hat {f}\in {\mathbb P}^{2d+1}$
with
$f=H_f\hat {f}\in {\mathbb P}^{2d+1}$
with
![]() $\deg \hat f\ge 1$
. Assume
$\deg \hat f\ge 1$
. Assume
![]() $\mathcal {O}_n$
is a cycle of
$\mathcal {O}_n$
is a cycle of
![]() $f_n$
of period
$f_n$
of period
![]() $m\ge 1$
and suppose that
$m\ge 1$
and suppose that
![]() $\mathcal {O}_n$
converges to
$\mathcal {O}_n$
converges to
![]() $\mathcal {O}$
in
$\mathcal {O}$
in
![]() $\mathbb {P}^1$
. If
$\mathbb {P}^1$
. If
![]() $\mathcal {O}\cap \mathrm {Hole}(f)=\emptyset $
, then
$\mathcal {O}\cap \mathrm {Hole}(f)=\emptyset $
, then
![]() $\mathcal {O}$
is a cycle of
$\mathcal {O}$
is a cycle of
![]() $\hat f$
of period q with
$\hat f$
of period q with
![]() $q\mid m$
. Furthermore: (1) if
$q\mid m$
. Furthermore: (1) if
![]() $\mathcal {O}_n$
is attracting, then
$\mathcal {O}_n$
is attracting, then
![]() $\mathcal {O}$
is non-repelling; (2) if
$\mathcal {O}$
is non-repelling; (2) if
![]() $q<m$
, then
$q<m$
, then
![]() $\mathcal {O}$
is parabolic.
$\mathcal {O}$
is parabolic.
If the limit intersects the holes of f, we have the following basins shrinking result.
Lemma 2.3. [Reference Nie and Pilgrim22, Proposition 2.8]
Let
![]() $\{f_n\}_{n\geq 1}$
be a sequence of degree
$\{f_n\}_{n\geq 1}$
be a sequence of degree
![]() $d\ge 2$
rational maps. Assume that
$d\ge 2$
rational maps. Assume that
![]() $f_n$
converges to
$f_n$
converges to
![]() $f=H_f\hat {f}\in {\mathbb P}^{2d+1}$
. Assume
$f=H_f\hat {f}\in {\mathbb P}^{2d+1}$
. Assume
![]() ${\deg }\hat {f}\geq 2$
and
${\deg }\hat {f}\geq 2$
and
![]() $\infty \in \mathrm {Hole}(f)$
is a fixed point of
$\infty \in \mathrm {Hole}(f)$
is a fixed point of
![]() $\hat {f}$
. Let
$\hat {f}$
. Let
![]() $\{z_n^{(0)},\ldots ,z_n^{(m-1)}\}$
be a (super)attracting cycle of
$\{z_n^{(0)},\ldots ,z_n^{(m-1)}\}$
be a (super)attracting cycle of
![]() $f_n$
of period
$f_n$
of period
![]() $m\geq 2$
, and let
$m\geq 2$
, and let
![]() $U_n^{(k)}$
be the Fatou component containing
$U_n^{(k)}$
be the Fatou component containing
![]() $z_n^{(k)}$
. Suppose
$z_n^{(k)}$
. Suppose
![]() $z_n^{(k)}\to z^{(k)}$
for
$z_n^{(k)}\to z^{(k)}$
for
![]() $k=0,\ldots ,m-1$
with
$k=0,\ldots ,m-1$
with
![]() $z^{(0)}=\infty $
and
$z^{(0)}=\infty $
and
![]() $z^{(i)}\not =\infty $
for some
$z^{(i)}\not =\infty $
for some
![]() $1\leq i\leq m-1$
. Then:
$1\leq i\leq m-1$
. Then:
-
(1)
 $U_n^{(0)}$
converges to
$U_n^{(0)}$
converges to
 $\infty $
in the sense that, for any
$\infty $
in the sense that, for any
 $\epsilon>0$
, the component
$\epsilon>0$
, the component
 $U_n^{(0)}$
is contained in the disk
$U_n^{(0)}$
is contained in the disk
 $\{z:\rho (z,\infty )<\epsilon \}$
for all large n, where
$\{z:\rho (z,\infty )<\epsilon \}$
for all large n, where
 $\rho $
is the sphere metric; and
$\rho $
is the sphere metric; and -
(2) there exists a neighborhood V of
 $\infty $
such that
$\infty $
such that
 $U_n^{(i)}\cap V=\emptyset $
for all large n.
$U_n^{(i)}\cap V=\emptyset $
for all large n.
Now we state a straightforward result about the perturbations of periodic points.
Lemma 2.4. Let
![]() $f=H_f\hat f\in {\mathbb P}^{2d+1}$
with
$f=H_f\hat f\in {\mathbb P}^{2d+1}$
with
![]() $\deg \hat f\ge 1$
. Then the following holds.
$\deg \hat f\ge 1$
. Then the following holds.
-
(1) For
 $z_0\in \widehat {{\mathbb C}}$
and
$z_0\in \widehat {{\mathbb C}}$
and
 $j\ge 1$
, denote
$j\ge 1$
, denote
 $z_i:=\hat f^i(z_0)$
for
$z_i:=\hat f^i(z_0)$
for
 $0\le i\le j$
. Suppose
$0\le i\le j$
. Suppose
 $z_i$
avoids the critical point of
$z_i$
avoids the critical point of
 $\hat f$
for all
$\hat f$
for all
 $0\le i\le j-1$
. Let
$0\le i\le j-1$
. Let
 $z_j(g)$
be a holomorphic map defined in a neighborhood of
$z_j(g)$
be a holomorphic map defined in a neighborhood of
 $f\in {\mathbb P}^{2d+1}$
with
$f\in {\mathbb P}^{2d+1}$
with
 $z_j(f)=z_j$
. Then for each
$z_j(f)=z_j$
. Then for each
 $0\le i\le j-1$
, there exists a holomorphic map
$0\le i\le j-1$
, there exists a holomorphic map
 $z_i(g)$
defined in a neighborhood of f such that
$z_i(g)$
defined in a neighborhood of f such that
 $z_i(f)=z_i$
and
$z_i(f)=z_i$
and
 $\hat g^{j-i}(z_i(g))=z_j(g)$
. Moreover, if
$\hat g^{j-i}(z_i(g))=z_j(g)$
. Moreover, if
 $z_i$
avoids the holes of f for all
$z_i$
avoids the holes of f for all
 $0\le i\le j-1$
, then
$0\le i\le j-1$
, then
 $z_i(g)$
is the unique point near
$z_i(g)$
is the unique point near
 $z_i$
such that
$z_i$
such that
 $\hat g^{j-i}(z_i(g))=z_j(g)$
, which implies
$\hat g^{j-i}(z_i(g))=z_j(g)$
, which implies
 $z_i(g)=\hat g^i(z_0(g))$
for all
$z_i(g)=\hat g^i(z_0(g))$
for all
 $0\le i\le j-1$
.
$0\le i\le j-1$
. -
(2) Let
 $\mathcal {O}=\{\xi _0,\ldots ,\xi _{k-1}\}$
be an attracting (respectively repelling) cycle of
$\mathcal {O}=\{\xi _0,\ldots ,\xi _{k-1}\}$
be an attracting (respectively repelling) cycle of
 $\hat f$
. If
$\hat f$
. If
 $\mathcal {O}\cap \mathrm {Hole}(f)=\emptyset $
, then for each g close to f, there exists a unique attracting (respectively repelling) cycle
$\mathcal {O}\cap \mathrm {Hole}(f)=\emptyset $
, then for each g close to f, there exists a unique attracting (respectively repelling) cycle
 $\mathcal {O}(g):=\{\xi _0(g),\ldots ,\xi _{k-1}(g)\}$
of g such that each
$\mathcal {O}(g):=\{\xi _0(g),\ldots ,\xi _{k-1}(g)\}$
of g such that each
 $\xi _i(g)$
is a holomorphic map near f with
$\xi _i(g)$
is a holomorphic map near f with
 $\xi _i(f)=\xi _i$
.
$\xi _i(f)=\xi _i$
.
Proof. By pre and post composition of Möbius transformations, we can assume
![]() $z_0,\ldots ,z_j\in {\mathbb C}$
. For
$z_0,\ldots ,z_j\in {\mathbb C}$
. For
![]() $g=H_g\hat g\in \mathbb {P}^{2d+1}$
close to f, we have
$g=H_g\hat g\in \mathbb {P}^{2d+1}$
close to f, we have
![]() $\deg \hat g\ge 1$
. Then for
$\deg \hat g\ge 1$
. Then for
![]() $0\le i\le j-1$
, the iteration
$0\le i\le j-1$
, the iteration
![]() $g^{j-i}$
is well defined, see [Reference DeMarco2, Lemma 2.2]. Consider the holomorphic function
$g^{j-i}$
is well defined, see [Reference DeMarco2, Lemma 2.2]. Consider the holomorphic function
on
![]() $\Lambda _f\times D(z_j)$
, where
$\Lambda _f\times D(z_j)$
, where
![]() $\Lambda _f\subseteq {\mathbb P}^{2d+1}$
is a neighborhood of f and
$\Lambda _f\subseteq {\mathbb P}^{2d+1}$
is a neighborhood of f and
![]() $D(z_j)\subseteq {\mathbb C}$
is a neighborhood of
$D(z_j)\subseteq {\mathbb C}$
is a neighborhood of
![]() $z_j$
. By the assumptions, we have that
$z_j$
. By the assumptions, we have that
![]() $F_i(f,z_i)=0$
and
$F_i(f,z_i)=0$
and
Then the implicit function theorem implies there exists a holomorphic function
![]() $z_i(g)$
near f such that
$z_i(g)$
near f such that
![]() $\hat g^{j-i}(z_i(g))=z_j(g)$
. If
$\hat g^{j-i}(z_i(g))=z_j(g)$
. If
![]() $\{z_0,\ldots ,z_{j-1}\}\cap \mathrm {Hole}(f)=\emptyset $
, the function
$\{z_0,\ldots ,z_{j-1}\}\cap \mathrm {Hole}(f)=\emptyset $
, the function
![]() $\hat g^{j-i}(z)$
is holomorphic in z in a fixed neighborhood of
$\hat g^{j-i}(z)$
is holomorphic in z in a fixed neighborhood of
![]() $z_i$
for each g close to f. It follows from Hurwitz’s theorem (see [Reference Gamelin7]) that
$z_i$
for each g close to f. It follows from Hurwitz’s theorem (see [Reference Gamelin7]) that
![]() $g^{j-i}(z)-z_j(g)$
has a unique root near
$g^{j-i}(z)-z_j(g)$
has a unique root near
![]() $z_i$
for g close to f. Thus statement (1) follows.
$z_i$
for g close to f. Thus statement (1) follows.
For statement (2), note that the cycle
![]() $\mathcal {O}\cap \mathrm {Hole}(f)=\emptyset $
. Applying the implicit function theorem on
$\mathcal {O}\cap \mathrm {Hole}(f)=\emptyset $
. Applying the implicit function theorem on
![]() $G(g,z):= g^k(z)-z$
, we obtain the expected cycle
$G(g,z):= g^k(z)-z$
, we obtain the expected cycle
![]() $\mathcal {O}(g)$
of
$\mathcal {O}(g)$
of
![]() $ g$
for g close to f.
$ g$
for g close to f.
For
![]() $f=H_f\hat f\in \mathbb {P}^{2d+1}$
, assume
$f=H_f\hat f\in \mathbb {P}^{2d+1}$
, assume
![]() $\hat f$
has an attracting cycle
$\hat f$
has an attracting cycle
![]() $\mathcal {O}$
and denote
$\mathcal {O}$
and denote
![]() $\Omega $
the immediate basin of
$\Omega $
the immediate basin of
![]() $\mathcal {O}$
. If
$\mathcal {O}$
. If
![]() $\Omega \cap \mathrm {Hole}(f)=\emptyset $
, Lemma 2.4 implies that for g close to f, the map
$\Omega \cap \mathrm {Hole}(f)=\emptyset $
, Lemma 2.4 implies that for g close to f, the map
![]() $\hat g$
has an attracting cycle
$\hat g$
has an attracting cycle
![]() $\mathcal {O}(g)$
. Denote by
$\mathcal {O}(g)$
. Denote by
![]() $\Omega (g)$
the immediate basin of
$\Omega (g)$
the immediate basin of
![]() $\mathcal {O}(g)$
. Then we have the following lemma.
$\mathcal {O}(g)$
. Then we have the following lemma.
Lemma 2.5. Assume that
![]() $\Omega \cap \mathrm {Hole}(f)=\emptyset $
and let
$\Omega \cap \mathrm {Hole}(f)=\emptyset $
and let
![]() $E\subset \Omega $
be any compact set. Then
$E\subset \Omega $
be any compact set. Then
![]() $E\subseteq \Omega (g)$
for any g sufficiently close to f.
$E\subseteq \Omega (g)$
for any g sufficiently close to f.
This above result is well known in the case where f is a rational map of degree d, see [Reference Douady3, Lemma 6.3]. Our assumption
![]() $\Omega \cap \mathrm {Hole}(f)=\emptyset $
guarantees that the argument in the non-degenerate case also works in our case. Here we omit the proof.
$\Omega \cap \mathrm {Hole}(f)=\emptyset $
guarantees that the argument in the non-degenerate case also works in our case. Here we omit the proof.
2.2 Newton maps
For a degree
![]() $d\ge 2$
complex polynomial
$d\ge 2$
complex polynomial
![]() $P(z)$
with simple roots, its Newton map
$P(z)$
with simple roots, its Newton map
is a degree d rational map having d superattracting fixed points at the roots of P. The only other fixed point is at
![]() $\infty $
. The holomorphic index formula (see [Reference Milnor18, Theorem 12.4]) asserts that the point
$\infty $
. The holomorphic index formula (see [Reference Milnor18, Theorem 12.4]) asserts that the point
![]() $\infty $
is the unique repelling fixed point of
$\infty $
is the unique repelling fixed point of
![]() $f_P$
. The critical points of
$f_P$
. The critical points of
![]() $f_P$
are the roots of P and the zeros of
$f_P$
are the roots of P and the zeros of
![]() $P"$
. Moreover, the poles of
$P"$
. Moreover, the poles of
![]() $f_p$
are the zeros of
$f_p$
are the zeros of
![]() $P'$
.
$P'$
.
Recall that
![]() $\mathrm {NM}_d$
is the space of degree d Newton maps and
$\mathrm {NM}_d$
is the space of degree d Newton maps and
![]() $\overline {\mathrm {NM}}_d$
is the closure of
$\overline {\mathrm {NM}}_d$
is the closure of
![]() $\mathrm {NM}_d$
in
$\mathrm {NM}_d$
in
![]() $\mathbb {P}^{2d+1}$
. Then for each
$\mathbb {P}^{2d+1}$
. Then for each
![]() $f=H_f\hat f\in \overline {\mathrm {NM}}_d$
, there exists a polynomial Q degree at most d with possible multiple roots such that
$f=H_f\hat f\in \overline {\mathrm {NM}}_d$
, there exists a polynomial Q degree at most d with possible multiple roots such that
![]() $\hat f$
is the Newton map of Q. Each root r of Q is a (super)attracting fixed point of
$\hat f$
is the Newton map of Q. Each root r of Q is a (super)attracting fixed point of
![]() $\hat f$
with multiplier
$\hat f$
with multiplier
![]() $1-1/n_r$
, where
$1-1/n_r$
, where
![]() $n_r$
is the multiplicity of r as a zero of Q. Moreover, again
$n_r$
is the multiplicity of r as a zero of Q. Moreover, again
![]() $\hat f$
has only one more fixed point at
$\hat f$
has only one more fixed point at
![]() $\infty $
, which is repelling. It follows that each hole of f is either a multiple root of Q or
$\infty $
, which is repelling. It follows that each hole of f is either a multiple root of Q or
![]() $\infty $
. Furthermore,
$\infty $
. Furthermore,
![]() $\infty \in \mathrm {Hole}(f)$
if and only if
$\infty \in \mathrm {Hole}(f)$
if and only if
![]() $\deg Q<d$
. For more details about degenerate Newton maps, we refer the reader to [Reference Nie21].
$\deg Q<d$
. For more details about degenerate Newton maps, we refer the reader to [Reference Nie21].
For
![]() $f=H_f\hat f\in \overline {\mathrm {NM}}_d$
with
$f=H_f\hat f\in \overline {\mathrm {NM}}_d$
with
![]() $\deg \hat f\ge 2$
, the Fatou components of
$\deg \hat f\ge 2$
, the Fatou components of
![]() $\hat f$
have well-studied topological structure. By a result of Shishikura [Reference Shishikura27], all Fatou components of
$\hat f$
have well-studied topological structure. By a result of Shishikura [Reference Shishikura27], all Fatou components of
![]() $\hat f$
are simply connected, and hence the Julia set of
$\hat f$
are simply connected, and hence the Julia set of
![]() $\hat f$
is connected. Moreover, the boundary of each component of the basins of roots is locally connected, see [Reference Drach and Schleicher5, Reference Wang, Yin and Zeng29].
$\hat f$
is connected. Moreover, the boundary of each component of the basins of roots is locally connected, see [Reference Drach and Schleicher5, Reference Wang, Yin and Zeng29].
3 Proof of Theorem 1.1
The goal of this section is to prove Theorem 1.1. We define Böttcher coordinates on the deformations in §3.1 and prove the convergence of Böttcher coordinates (Proposition 3.7). To do that, we introduce the convergence preserving the degrees at centers (Definition 3.3). In §3.2, we use the Böttcher coordinates on the deformations to define the corresponding internal rays, and then show a convergence result on these rays (Proposition 3.8). Finally, we prove Theorem 1.1 in §3.3.
3.1 Perturbation of Böttcher coordinates
Let
![]() $f=H_f\hat f\in \overline {\mathrm {NM}}_d$
with
$f=H_f\hat f\in \overline {\mathrm {NM}}_d$
with
![]() $\deg \hat f\ge 2$
and denote by
$\deg \hat f\ge 2$
and denote by
![]() $\Omega _{\hat f}$
the union of basins of the roots of
$\Omega _{\hat f}$
the union of basins of the roots of
![]() $\hat f$
. Let
$\hat f$
. Let
![]() $\mathcal {U}$
be a finite subset of components of
$\mathcal {U}$
be a finite subset of components of
![]() $\Omega _{\hat f}$
such that if
$\Omega _{\hat f}$
such that if
![]() $U\in \mathcal {U}$
, then
$U\in \mathcal {U}$
, then
![]() $\hat f(U)\in \mathcal {U}$
. Recall that
$\hat f(U)\in \mathcal {U}$
. Recall that
![]() $\hat f$
is post-critically finite on
$\hat f$
is post-critically finite on
![]() $\bigcup _{U\in \mathcal {U}}U$
if the critical points in any
$\bigcup _{U\in \mathcal {U}}U$
if the critical points in any
![]() $U\in \mathcal {U}$
have finite orbits. For such
$U\in \mathcal {U}$
have finite orbits. For such
![]() $\hat f$
and
$\hat f$
and
![]() $\mathcal {U}$
, one can choose a system of Böttcher coordinates
$\mathcal {U}$
, one can choose a system of Böttcher coordinates
![]() $\{\phi _U:U\to \mathbb D\}_{U\in \mathcal {U}}$
satisfying
$\{\phi _U:U\to \mathbb D\}_{U\in \mathcal {U}}$
satisfying
and
![]() $u:= \phi _U^{-1}(0)$
is called the center of U. Moreover, we have the following proposition.
$u:= \phi _U^{-1}(0)$
is called the center of U. Moreover, we have the following proposition.
Proposition 3.1. The set
![]() $\bigcup _{U\in {\mathcal U}}U$
is disjoint with the holes of f.
$\bigcup _{U\in {\mathcal U}}U$
is disjoint with the holes of f.
Proof. By §2.2, a possible hole of f is either
![]() $\infty $
or a geometrically attracting fixed point of
$\infty $
or a geometrically attracting fixed point of
![]() $\hat {f}$
. Since
$\hat {f}$
. Since
![]() $\hat f$
is post-critically finite on
$\hat f$
is post-critically finite on
![]() $\bigcup _{U\in \mathcal {U}}U$
, the conclusion holds.
$\bigcup _{U\in \mathcal {U}}U$
, the conclusion holds.
To abuse notation, we denote the set of pointed sets
![]() $(U,u)$
with
$(U,u)$
with
![]() $U\in \mathcal {U}$
also by
$U\in \mathcal {U}$
also by
![]() $\mathcal {U}$
. Let
$\mathcal {U}$
. Let
![]() $\{f_n\}_{n\ge 1}$
be a sequence in
$\{f_n\}_{n\ge 1}$
be a sequence in
![]() $\mathrm {NM}_d$
such that
$\mathrm {NM}_d$
such that
![]() $f_n$
converges to f. By Proposition 3.1 and Lemma 2.5, for
$f_n$
converges to f. By Proposition 3.1 and Lemma 2.5, for
![]() $(U,u)\in \mathcal {U}$
, the point u belongs to the unique component
$(U,u)\in \mathcal {U}$
, the point u belongs to the unique component
![]() $U_n$
of
$U_n$
of
![]() $\Omega _{f_n}$
for all large n; and combining Proposition 2.4, the component
$\Omega _{f_n}$
for all large n; and combining Proposition 2.4, the component
![]() $U_n$
contains a preperiodic point
$U_n$
contains a preperiodic point
![]() $u_n$
with the same preperiod and period as that of u such that
$u_n$
with the same preperiod and period as that of u such that
![]() $u_n\to u$
as
$u_n\to u$
as
![]() $n\to \infty $
. We call such
$n\to \infty $
. We call such
![]() $(U_n,u_n)$
a deformation of
$(U_n,u_n)$
a deformation of
![]() $(U,u)$
at
$(U,u)$
at
![]() $f_n$
. Note that such
$f_n$
. Note that such
![]() $u_n$
is not necessarily unique. For example, if u is a preperiodic critical point, it possibly splits into two preperiodic points of
$u_n$
is not necessarily unique. For example, if u is a preperiodic critical point, it possibly splits into two preperiodic points of
![]() $f_n$
contained in
$f_n$
contained in
![]() $U_n$
.
$U_n$
.
To the end of this subsection, under natural assumptions, we define a Böttcher coordinate
![]() $\phi _{U_n}$
on the deformations
$\phi _{U_n}$
on the deformations
![]() $U_n$
of U and show a convergence result of
$U_n$
of U and show a convergence result of
![]() $\phi _{U_n}$
. First, we consider the convergence of deformations.
$\phi _{U_n}$
. First, we consider the convergence of deformations.
Recall the definition of Carathéodory topology on a set of pointed sets and a set of holomorphic functions respectively, following [Reference McMullen16, §5.1]. Let
![]() $\mathcal {V}$
be a set of open simply connected pointed sets
$\mathcal {V}$
be a set of open simply connected pointed sets
![]() $(V,v)$
in
$(V,v)$
in
![]() $\mathbb {C}$
. The Carathéodory topology on
$\mathbb {C}$
. The Carathéodory topology on
![]() $\mathcal {V}$
is defined by the following convergence:
$\mathcal {V}$
is defined by the following convergence:
![]() $(V_n, v_n)$
converges to
$(V_n, v_n)$
converges to
![]() $(V,v)$
if and only if:
$(V,v)$
if and only if:
-
(i)
 $v_n$
converges to v;
$v_n$
converges to v; -
(ii) for any compact
 $K\subset V$
, we have
$K\subset V$
, we have
 $K\subset V_n$
for all large n; and
$K\subset V_n$
for all large n; and -
(iii) for any domain W containing v, if
 $W\subset V_n$
for infinitely many n, then
$W\subset V_n$
for infinitely many n, then
 $W\subset V$
.
$W\subset V$
.
Denote
![]() $\mathcal {G}$
the set of holomorphic functions defined on
$\mathcal {G}$
the set of holomorphic functions defined on
![]() $(V, v)\in \mathcal {V}$
. Then the Carathéodory topology on
$(V, v)\in \mathcal {V}$
. Then the Carathéodory topology on
![]() $\mathcal {G}$
is defined as follows. Let
$\mathcal {G}$
is defined as follows. Let
![]() $g:(V, v)\to \mathbb {C}$
and
$g:(V, v)\to \mathbb {C}$
and
![]() $g_n:(V_n, v_n)\to \mathbb {C}$
be functions in
$g_n:(V_n, v_n)\to \mathbb {C}$
be functions in
![]() $\mathcal {G}$
. We say
$\mathcal {G}$
. We say
![]() $g_n$
converges to g if: (1)
$g_n$
converges to g if: (1)
![]() $(V_n, v_n)$
converges to
$(V_n, v_n)$
converges to
![]() $(V, v)$
in
$(V, v)$
in
![]() $\mathcal {V}$
; and (2)
$\mathcal {V}$
; and (2)
![]() $g_n$
converges to g uniformly on any compact subset of V as
$g_n$
converges to g uniformly on any compact subset of V as
![]() $n\to \infty $
.
$n\to \infty $
.
Proposition 3.2. Let
![]() $\{f_n\}_{n\ge 1},f=H_f\hat {f}$
and
$\{f_n\}_{n\ge 1},f=H_f\hat {f}$
and
![]() ${\mathcal U}$
be as above. For any
${\mathcal U}$
be as above. For any
![]() $(U,u)\in {\mathcal U}$
, the holomorphic maps
$(U,u)\in {\mathcal U}$
, the holomorphic maps
![]() $f_n:(U_n,u_n)\to {\mathbb C}$
converge to
$f_n:(U_n,u_n)\to {\mathbb C}$
converge to
![]() $\hat {f}:(U,u)\to {\mathbb C}$
, where
$\hat {f}:(U,u)\to {\mathbb C}$
, where
![]() $(U_n,u_n)$
is a deformation of
$(U_n,u_n)$
is a deformation of
![]() $(U,u)$
at
$(U,u)$
at
![]() $f_n$
.
$f_n$
.
Proof. We first show that
![]() $(U_n,u_n)$
converge to
$(U_n,u_n)$
converge to
![]() $(U,u)$
. By the definition of
$(U,u)$
. By the definition of
![]() $(U_n,u_n)$
, we have
$(U_n,u_n)$
, we have
![]() $u_n\to u$
as
$u_n\to u$
as
![]() $n\to \infty $
. Proposition 3.1 and Lemma 2.5 imply that any compacted set contained in U is contained in
$n\to \infty $
. Proposition 3.1 and Lemma 2.5 imply that any compacted set contained in U is contained in
![]() $U_n$
for sufficiently large n. Now pick an open and connected set
$U_n$
for sufficiently large n. Now pick an open and connected set
![]() $W\subset U_n$
for infinitely many n with
$W\subset U_n$
for infinitely many n with
![]() $u\in W$
. We assume on the contrary that
$u\in W$
. We assume on the contrary that
![]() $W\not \subset U$
. Then W contains a eventually repelling preperiodic point
$W\not \subset U$
. Then W contains a eventually repelling preperiodic point
![]() $z\in \partial U$
such that its orbit avoids the critical points and holes of
$z\in \partial U$
such that its orbit avoids the critical points and holes of
![]() $\hat {f}$
, since the repelling periodic points are dense in the boundary of any immediate basin of a root of
$\hat {f}$
, since the repelling periodic points are dense in the boundary of any immediate basin of a root of
![]() $\hat {f}$
, and the critical points and holes of
$\hat {f}$
, and the critical points and holes of
![]() $\hat {f}$
are finite. By Proposition 2.4, the point z is perturbed to an eventually repelling preperiodic point of
$\hat {f}$
are finite. By Proposition 2.4, the point z is perturbed to an eventually repelling preperiodic point of
![]() $f_n$
, which also belongs to W for sufficiently large n. It contradicts that
$f_n$
, which also belongs to W for sufficiently large n. It contradicts that
![]() $W\subset U_n$
. Thus
$W\subset U_n$
. Thus
![]() $(U_n,u_n)$
converges to
$(U_n,u_n)$
converges to
![]() $(U,u)$
. The locally uniform convergence of
$(U,u)$
. The locally uniform convergence of
![]() $f_n$
follows immediately from Lemma 2.1. This completes the proof.
$f_n$
follows immediately from Lemma 2.1. This completes the proof.
For our propose, we use the following definition.
Definition 3.3. Let
![]() $f_n$
and f be as above. We say
$f_n$
and f be as above. We say
![]() $f_n$
converges to f preserving the degrees at the centers, denoted by
$f_n$
converges to f preserving the degrees at the centers, denoted by
![]() $f_n\xrightarrow {\deg }f$
, on
$f_n\xrightarrow {\deg }f$
, on
![]() $\mathcal {U}$
if for each
$\mathcal {U}$
if for each
![]() $(U,u)\in \mathcal {U}$
, a deformation
$(U,u)\in \mathcal {U}$
, a deformation
![]() $(U_n,u_n)$
of
$(U_n,u_n)$
of
![]() $(U,u)$
satisfies the local degrees property
$(U,u)$
satisfies the local degrees property
![]() $\deg _u\hat f=\deg _{u_n} f_n$
.
$\deg _u\hat f=\deg _{u_n} f_n$
.
If
![]() $f_n\xrightarrow {\deg }f$
on
$f_n\xrightarrow {\deg }f$
on
![]() $\mathcal {U}$
, it follows immediately that any
$\mathcal {U}$
, it follows immediately that any
![]() $(U,u)\in {\mathcal U}$
has a unique deformation
$(U,u)\in {\mathcal U}$
has a unique deformation
![]() $(U_n,u_n)$
. We call such
$(U_n,u_n)$
. We call such
![]() $u_n$
a center of
$u_n$
a center of
![]() $U_n$
. In this case, set
$U_n$
. In this case, set
We mention here that the set
![]() $U_n$
may contain several distinct centers.
$U_n$
may contain several distinct centers.
Remark 3.4. If a critical point c of
![]() $\hat {f}$
is contained in the boundaries of distinct
$\hat {f}$
is contained in the boundaries of distinct
![]() $(U,u)$
and
$(U,u)$
and
![]() $(U',u')$
in
$(U',u')$
in
![]() $\mathcal {U}$
, it is possible that
$\mathcal {U}$
, it is possible that
![]() $U_n$
coincides with
$U_n$
coincides with
![]() $U_n'$
and it contains the critical point of
$U_n'$
and it contains the critical point of
![]() $f_n$
perturbed from c (see Figure 2). In this case, both
$f_n$
perturbed from c (see Figure 2). In this case, both
![]() $u_n$
and
$u_n$
and
![]() $u_n'$
are centers of
$u_n'$
are centers of
![]() $U_n=U_n'$
, and hence
$U_n=U_n'$
, and hence
![]() $f_n$
is not post-critically finite on the union of
$f_n$
is not post-critically finite on the union of
![]() $U_n$
with
$U_n$
with
![]() $(U_n,u_n)\in \mathcal {U}_n$
.
$(U_n,u_n)\in \mathcal {U}_n$
.

Figure 2 (a) The dynamical plane of the Newton map f for the polynomial
![]() $z^3-1$
. The letters indicate Fatou components
$z^3-1$
. The letters indicate Fatou components
![]() $U, U', U"$
, and
$U, U', U"$
, and
![]() $U"'$
with centers
$U"'$
with centers
![]() $u,u',u"$
, and
$u,u',u"$
, and
![]() $u"'$
respectively. The arcs indicate internal rays. The critical point
$u"'$
respectively. The arcs indicate internal rays. The critical point
![]() $c=0$
is contained in
$c=0$
is contained in
![]() $\partial U\cap \partial U'$
. (b) The dynamical plane of the Newton map
$\partial U\cap \partial U'$
. (b) The dynamical plane of the Newton map
![]() $f_n$
for the polynomial
$f_n$
for the polynomial
![]() $z^3+z/n-1$
with indicated Fatou component
$z^3+z/n-1$
with indicated Fatou component
![]() $U_n$
. The critical point
$U_n$
. The critical point
![]() $c_n\in U_n$
. The points
$c_n\in U_n$
. The points
![]() $u_n, u_n', u_n"$
, and
$u_n, u_n', u_n"$
, and
![]() $u_n"'$
are all in
$u_n"'$
are all in
![]() $U_n$
and centers of
$U_n$
and centers of
![]() $U_n$
. The set
$U_n$
. The set
![]() $(U_n,u_n)$
is the deformation of
$(U_n,u_n)$
is the deformation of
![]() $(U,u)$
; the set
$(U,u)$
; the set
![]() $(U_n,u^{\prime }_n)$
is the deformation of
$(U_n,u^{\prime }_n)$
is the deformation of
![]() $(U',u')$
; the set
$(U',u')$
; the set
![]() $(U_n,u^{\prime \prime }_n)$
is the deformation of
$(U_n,u^{\prime \prime }_n)$
is the deformation of
![]() $(U",u")$
; and the set
$(U",u")$
; and the set
![]() $(U_n,u^{\prime \prime \prime }_n)$
is the deformation of
$(U_n,u^{\prime \prime \prime }_n)$
is the deformation of
![]() $(U"',u"')$
. The corresponding rays in
$(U"',u"')$
. The corresponding rays in
![]() $U_n$
either land on
$U_n$
either land on
![]() $\partial U_n$
or terminate at the iterated preimages of
$\partial U_n$
or terminate at the iterated preimages of
![]() $c_n$
.
$c_n$
.
The following result states a natural sufficient condition for the convergence
![]() $f_n\xrightarrow {\deg }f$
, which we will use repeatedly in §5. The proof is straightforward, so we omit it.
$f_n\xrightarrow {\deg }f$
, which we will use repeatedly in §5. The proof is straightforward, so we omit it.
Lemma 3.5. Let
![]() $f_n$
, f, and
$f_n$
, f, and
![]() $\mathcal {U}$
be as above. Assume that
$\mathcal {U}$
be as above. Assume that
![]() $\hat f$
has degree
$\hat f$
has degree
![]() $2$
on every immediate basin of roots in
$2$
on every immediate basin of roots in
![]() ${\mathcal U}$
and degree
${\mathcal U}$
and degree
![]() $1$
on all other elements in
$1$
on all other elements in
![]() ${\mathcal U}$
. Then,
${\mathcal U}$
. Then,
![]() $f_n\xrightarrow {\deg }f$
on
$f_n\xrightarrow {\deg }f$
on
![]() ${\mathcal U}$
.
${\mathcal U}$
.
From now on, we assume that
![]() $f_n\xrightarrow {\deg }f$
. Since
$f_n\xrightarrow {\deg }f$
. Since
![]() $\hat f$
is post-critically finite on
$\hat f$
is post-critically finite on
![]() $\bigcup _{U\in \mathcal {U}}U$
, by Proposition 3.1 and Lemma 2.1, we have the following straightforward result and again omit the proof.
$\bigcup _{U\in \mathcal {U}}U$
, by Proposition 3.1 and Lemma 2.1, we have the following straightforward result and again omit the proof.
Lemma 3.6. If
![]() $(U_n,u_n)$
is the deformation of
$(U_n,u_n)$
is the deformation of
![]() $(U,u)\in \mathcal {U}$
at
$(U,u)\in \mathcal {U}$
at
![]() $f_n$
, then
$f_n$
, then
![]() $(f_n(U_n),f_n(u_n))$
is the deformation of
$(f_n(U_n),f_n(u_n))$
is the deformation of
![]() $(\hat {f}(U),\hat {f}(u))$
.
$(\hat {f}(U),\hat {f}(u))$
.
Lemma 3.6 suggests that for each
![]() $(U_n,u_n)\in \mathcal {U}_n$
, we have a Böttcher coordinate
$(U_n,u_n)\in \mathcal {U}_n$
, we have a Böttcher coordinate
![]() $\phi _{(U_n,u_n)}$
near
$\phi _{(U_n,u_n)}$
near
![]() $u_n$
such that
$u_n$
such that
for z near
![]() $u_n$
, and that
$u_n$
, and that
The map
![]() $\phi _{(U_n,u_n)}$
extends conformally until meeting an iterated preimage of critical points of
$\phi _{(U_n,u_n)}$
extends conformally until meeting an iterated preimage of critical points of
![]() $f_n$
. Then there exists a maximum
$f_n$
. Then there exists a maximum
![]() $r_n\le 1$
such that
$r_n\le 1$
such that
![]() $\psi _{(U_n,u_n)}:=\phi _{(U_n,u_n)}^{-1}: \mathbb {D}_{r_n}\to U_n$
is well defined.
$\psi _{(U_n,u_n)}:=\phi _{(U_n,u_n)}^{-1}: \mathbb {D}_{r_n}\to U_n$
is well defined.
Denote by
![]() $\psi _{(U,u)}$
the inverse of
$\psi _{(U,u)}$
the inverse of
![]() $\phi _{(U,u)}$
. The following result asserts that
$\phi _{(U,u)}$
. The following result asserts that
![]() $\psi _{(U_n,u_n)}$
converges to
$\psi _{(U_n,u_n)}$
converges to
![]() $\psi _{(U,u)}$
locally uniformly on
$\psi _{(U,u)}$
locally uniformly on
![]() $\mathbb {D}$
, which is well known in Carathéodory topology, see e.g. [Reference McMullen16, Theorem 5.1].
$\mathbb {D}$
, which is well known in Carathéodory topology, see e.g. [Reference McMullen16, Theorem 5.1].
Proposition 3.7. For
![]() $(U,u)\in \mathcal {U}$
, let
$(U,u)\in \mathcal {U}$
, let
![]() $(U_n,u_n)\in \mathcal {U}_n$
be the deformation of
$(U_n,u_n)\in \mathcal {U}_n$
be the deformation of
![]() $(U,u)$
. Then
$(U,u)$
. Then
![]() $\psi _{(U_n,u_n)}$
converges to
$\psi _{(U_n,u_n)}$
converges to
![]() $\psi _{(U,u)}$
locally uniformly on
$\psi _{(U,u)}$
locally uniformly on
![]() $\mathbb {D}$
.
$\mathbb {D}$
.
3.2 Perturbation of internal rays
In §3.1, we perturb a Böttcher coordinate in
![]() $(U,u)\in \mathcal {U}$
to obtain a Böttcher coordinate
$(U,u)\in \mathcal {U}$
to obtain a Böttcher coordinate
![]() $\phi _{(U_n,u_n)}$
in
$\phi _{(U_n,u_n)}$
in
![]() $(U_n,u_n)\in \mathcal {U}_n$
. In this subsection, we use the inverse map
$(U_n,u_n)\in \mathcal {U}_n$
. In this subsection, we use the inverse map
![]() $\psi _{(U_n,u_n)}$
to define the internal rays in
$\psi _{(U_n,u_n)}$
to define the internal rays in
![]() $(U_n,u_n)$
and prove a convergence result on internal rays.
$(U_n,u_n)$
and prove a convergence result on internal rays.
Now we define internal rays of
![]() $f_n$
in
$f_n$
in
![]() $(U_n,u_n)$
as follows. For each
$(U_n,u_n)$
as follows. For each
![]() $\theta \in {\mathbb R}/{\mathbb Z}$
, let
$\theta \in {\mathbb R}/{\mathbb Z}$
, let
![]() $r_{\theta }$
be the maximal radius such that
$r_{\theta }$
be the maximal radius such that
![]() $\psi _{(U_n,u_n)}$
extends along
$\psi _{(U_n,u_n)}$
extends along
![]() $(0,r_{\theta })e^{2\pi i\theta }$
. If
$(0,r_{\theta })e^{2\pi i\theta }$
. If
![]() $r_{\theta }<1$
, then arc
$r_{\theta }<1$
, then arc
![]() $\psi _{(U_n,u_n)}((0,r_{\theta })e^{2\pi i\theta })$
terminates at an iterated preimage of critical points of
$\psi _{(U_n,u_n)}((0,r_{\theta })e^{2\pi i\theta })$
terminates at an iterated preimage of critical points of
![]() $f_n$
, and if
$f_n$
, and if
![]() $r_{\theta }=1$
, the arc
$r_{\theta }=1$
, the arc
![]() $\psi _{(U_n,u_n)}((0,1)e^{2\pi i\theta })$
accumulates and factually lands on
$\psi _{(U_n,u_n)}((0,1)e^{2\pi i\theta })$
accumulates and factually lands on
![]() $\partial U_n$
. In the latter case, we call
$\partial U_n$
. In the latter case, we call
the landed internal ray in
![]() $(U_n,u_n)$
of angle
$(U_n,u_n)$
of angle
![]() $\theta $
. Note that
$\theta $
. Note that
![]() $f_n$
sends a landed internal ray of
$f_n$
sends a landed internal ray of
![]() $(U_n,u_n)$
to a landed internal ray of
$(U_n,u_n)$
to a landed internal ray of
![]() $(f(U_n),f(u_n))$
. Also, since
$(f(U_n),f(u_n))$
. Also, since
![]() $U_n$
may contain more than one center, it may possess several groups of landed interval rays. In this case, each such ray starts from a center of
$U_n$
may contain more than one center, it may possess several groups of landed interval rays. In this case, each such ray starts from a center of
![]() $U_n$
and rays from distinct groups are disjoint (see Figure 2).
$U_n$
and rays from distinct groups are disjoint (see Figure 2).
The following result asserts that the internal rays of eventually periodic angles converge.
Proposition 3.8. For
![]() $(U,u)\in \mathcal {U}$
, assume that the internal ray
$(U,u)\in \mathcal {U}$
, assume that the internal ray
![]() $I_{(U,u)}(\theta )$
of angle
$I_{(U,u)}(\theta )$
of angle
![]() $\theta $
lands at an eventually repelling periodic point. For all large n, suppose that
$\theta $
lands at an eventually repelling periodic point. For all large n, suppose that
![]() $I_{(U_n,u_n)}(\theta )$
is a landed internal ray in
$I_{(U_n,u_n)}(\theta )$
is a landed internal ray in
![]() $(U_n,u_n)\in \mathcal {U}_n$
. Then
$(U_n,u_n)\in \mathcal {U}_n$
. Then
![]() $I_{(U_n,u_n)}(\theta )\to I_{(U,u)}(\theta )$
as
$I_{(U_n,u_n)}(\theta )\to I_{(U,u)}(\theta )$
as
![]() $n\to \infty $
.
$n\to \infty $
.
Proof. To ease notation, we write
![]() $I(\theta ),I_n(\theta ),\psi $
, and
$I(\theta ),I_n(\theta ),\psi $
, and
![]() $\psi _n$
for
$\psi _n$
for
![]() $I_{(U,u)}(\theta ), I_{(U_n,u_n)}(\theta ),\psi _{(U,u)}$
, and
$I_{(U,u)}(\theta ), I_{(U_n,u_n)}(\theta ),\psi _{(U,u)}$
, and
![]() $\psi _{(U_n,u_n)}$
, respectively. Set
$\psi _{(U_n,u_n)}$
, respectively. Set
![]() $\delta :=\mathrm {deg}(\hat {f}|_U)$
and let
$\delta :=\mathrm {deg}(\hat {f}|_U)$
and let
![]() $z_0$
be the landing point of
$z_0$
be the landing point of
![]() $I(\theta )$
. It is sufficient to show that, given any
$I(\theta )$
. It is sufficient to show that, given any
![]() $\eta>0$
, for all large n, we have
$\eta>0$
, for all large n, we have
![]() $d_H(I(\theta ),I_n(\theta ))<\eta $
, where
$d_H(I(\theta ),I_n(\theta ))<\eta $
, where
![]() $d_H$
is the Hausdorff metric.
$d_H$
is the Hausdorff metric.
First assume that
![]() $I(\theta )$
is periodic of period
$I(\theta )$
is periodic of period
![]() $p\ge 1$
. Then u is a super-attracting fixed point of
$p\ge 1$
. Then u is a super-attracting fixed point of
![]() $\hat {f}$
. Define
$\hat {f}$
. Define
where
![]() $\rho $
is the spherical metric. Shrinking
$\rho $
is the spherical metric. Shrinking
![]() $\epsilon $
if necessary, we may assume
$\epsilon $
if necessary, we may assume
![]() $\hat {f}|_{D_{\epsilon }}$
is injective and
$\hat {f}|_{D_{\epsilon }}$
is injective and
![]() $\overline {D}_{\epsilon }\subseteq \hat f^p(D_{\epsilon })$
. We claim that for any sufficiently large n and any component
$\overline {D}_{\epsilon }\subseteq \hat f^p(D_{\epsilon })$
. We claim that for any sufficiently large n and any component
![]() $D^{\prime }_n$
of
$D^{\prime }_n$
of
![]() $f^{-p}_n(D_{\epsilon })$
, either
$f^{-p}_n(D_{\epsilon })$
, either
![]() $\overline {D_n'}\subseteq D_{\epsilon }$
or
$\overline {D_n'}\subseteq D_{\epsilon }$
or
![]() $\overline {D_n'}\subseteq \widehat {{\mathbb C}}\setminus \overline {D}_{\epsilon }$
. Indeed, if
$\overline {D_n'}\subseteq \widehat {{\mathbb C}}\setminus \overline {D}_{\epsilon }$
. Indeed, if
![]() $p>1$
, the landing point
$p>1$
, the landing point
![]() $z_0$
of
$z_0$
of
![]() $I(\theta )$
is not a hole of
$I(\theta )$
is not a hole of
![]() $f^p$
, see §2.1 and [Reference DeMarco2, Lemma 2.2]. It follows from Lemma 2.1 that
$f^p$
, see §2.1 and [Reference DeMarco2, Lemma 2.2]. It follows from Lemma 2.1 that
![]() $f_n^p$
converges uniformly to
$f_n^p$
converges uniformly to
![]() $\hat {f}^p$
near
$\hat {f}^p$
near
![]() $z_0$
, and hence
$z_0$
, and hence
![]() $f_n^p|_{D_{\epsilon }}$
is injective and
$f_n^p|_{D_{\epsilon }}$
is injective and
![]() $\overline {D}_{\epsilon }\subseteq f_n^p(D_{\epsilon })$
for all large n. Then in this case, the claim follows. Now we consider the case where
$\overline {D}_{\epsilon }\subseteq f_n^p(D_{\epsilon })$
for all large n. Then in this case, the claim follows. Now we consider the case where
![]() $p=1$
. Then
$p=1$
. Then
![]() $z_0=\infty $
. If
$z_0=\infty $
. If
![]() $z_0=\infty $
is not a hole of f, the claim follows by previous argument. If
$z_0=\infty $
is not a hole of f, the claim follows by previous argument. If
![]() $z_0=\infty $
is a hole of f, then
$z_0=\infty $
is a hole of f, then
![]() $f_n$
fails to converge uniformly to
$f_n$
fails to converge uniformly to
![]() $\hat {f}$
near
$\hat {f}$
near
![]() $\infty $
. In this case, we prove the claim by contradiction. Suppose that the claim fails. Then there exists a subsequence, denoted also by
$\infty $
. In this case, we prove the claim by contradiction. Suppose that the claim fails. Then there exists a subsequence, denoted also by
![]() $\{f_n\}$
, such that for each
$\{f_n\}$
, such that for each
![]() $f_n$
, there exists a component
$f_n$
, there exists a component
![]() $D_n'$
of
$D_n'$
of
![]() $f^{-1}_n(D_{\epsilon })$
with
$f^{-1}_n(D_{\epsilon })$
with
![]() $\overline {D}^{\prime }_n\cap \partial D_{\epsilon }\not =\emptyset $
. Choose a point
$\overline {D}^{\prime }_n\cap \partial D_{\epsilon }\not =\emptyset $
. Choose a point
![]() $w_n\in \overline {D}_n'\cap \partial D_{\epsilon }$
. Passing to subsequence if necessary, we may assume
$w_n\in \overline {D}_n'\cap \partial D_{\epsilon }$
. Passing to subsequence if necessary, we may assume
![]() $w_n\to w$
. Then
$w_n\to w$
. Then
![]() $w\in \partial D_{\epsilon }$
. By Lemma 2.1, the sequence
$w\in \partial D_{\epsilon }$
. By Lemma 2.1, the sequence
![]() $f_n$
converges uniformly to
$f_n$
converges uniformly to
![]() $\hat f$
on
$\hat f$
on
![]() $\partial D_{\epsilon }$
. It follows that as
$\partial D_{\epsilon }$
. It follows that as
![]() $n\to \infty $
,
$n\to \infty $
,
Note that
![]() $\overline {D}_{\epsilon }\subseteq f(D_{\epsilon })$
. Then
$\overline {D}_{\epsilon }\subseteq f(D_{\epsilon })$
. Then
We have that
![]() $f(w)\not \in \overline {D}_{\epsilon }$
. However,
$f(w)\not \in \overline {D}_{\epsilon }$
. However,
which implies
![]() $f(w)\in \overline {D}_{\epsilon }$
. It is a contradiction. Therefore, the claim holds.
$f(w)\in \overline {D}_{\epsilon }$
. It is a contradiction. Therefore, the claim holds.
Since
![]() $I(\theta )$
lands at
$I(\theta )$
lands at
![]() $z_0$
, there exists
$z_0$
, there exists
![]() $0<r<1$
such that
$0<r<1$
such that
Pick
![]() $0<s<1$
such that
$0<s<1$
such that
![]() $s^{\delta ^p}>r$
. Then the segment
$s^{\delta ^p}>r$
. Then the segment
![]() $\psi ([s^{\delta ^p},s]e^{2\pi i \theta })\subseteq I(\theta )$
belongs to
$\psi ([s^{\delta ^p},s]e^{2\pi i \theta })\subseteq I(\theta )$
belongs to
![]() $U\cap D_{\epsilon }$
. It follows from Proposition 3.7 that for all large n,
$U\cap D_{\epsilon }$
. It follows from Proposition 3.7 that for all large n,
Define
to be an arc such that
![]() $\gamma _{n,0}(0)=\psi _n(s^{\delta ^p}e^{2\pi i\theta })$
and
$\gamma _{n,0}(0)=\psi _n(s^{\delta ^p}e^{2\pi i\theta })$
and
![]() $\gamma _{n,0}(1)=\psi _n(s e^{2\pi i\theta })$
. Then,
$\gamma _{n,0}(1)=\psi _n(s e^{2\pi i\theta })$
. Then,
Note that
![]() $f_n^p(\gamma _{n,0}(1))=\gamma _{n,0}(0)$
. Lift
$f_n^p(\gamma _{n,0}(1))=\gamma _{n,0}(0)$
. Lift
![]() $\gamma _{n,0}$
to an arc
$\gamma _{n,0}$
to an arc
![]() $\gamma _{n,1}$
based at
$\gamma _{n,1}$
based at
![]() $\gamma _{n,0}(1)$
. Since
$\gamma _{n,0}(1)$
. Since
![]() $I_n(\theta )$
is landed, inductively we obtain a sequence of arcs
$I_n(\theta )$
is landed, inductively we obtain a sequence of arcs
![]() $\gamma _{n,k}$
such that
$\gamma _{n,k}$
such that
![]() $\gamma _{n,k+1}$
is a lift by
$\gamma _{n,k+1}$
is a lift by
![]() $f_n$
of
$f_n$
of
![]() $\gamma _{n,k}$
based at the endpoint of
$\gamma _{n,k}$
based at the endpoint of
![]() $\gamma _{n,k}$
which is not in
$\gamma _{n,k}$
which is not in
![]() $\gamma _{n,k-1}$
.
$\gamma _{n,k-1}$
.
Now we claim that for sufficiently large n, the arc
![]() $\gamma _{n,k}\subset D_{\epsilon }$
. We prove the claim by induction on k. The claim holds for
$\gamma _{n,k}\subset D_{\epsilon }$
. We prove the claim by induction on k. The claim holds for
![]() $k=0$
by the definition of
$k=0$
by the definition of
![]() $\gamma _{n,0}$
. Suppose that for
$\gamma _{n,0}$
. Suppose that for
![]() $k\geq 0$
, the arc
$k\geq 0$
, the arc
![]() $\gamma _{n,k}\subseteq D$
. Since
$\gamma _{n,k}\subseteq D$
. Since
![]() $\gamma _{n,k+1}$
is a preimage of
$\gamma _{n,k+1}$
is a preimage of
![]() $\gamma _{n,k}$
under
$\gamma _{n,k}$
under
![]() $f_n$
, there exists a component
$f_n$
, there exists a component
![]() $D'$
of
$D'$
of
![]() $f_n^{-1}(D_{\epsilon })$
containing
$f_n^{-1}(D_{\epsilon })$
containing
![]() $\gamma _{n,k+1}$
. Since the intersection point of
$\gamma _{n,k+1}$
. Since the intersection point of
![]() $\gamma _{n,k+1}\subseteq D'$
and
$\gamma _{n,k+1}\subseteq D'$
and
![]() $\gamma _{n,k}\subseteq D_{\epsilon }$
belongs to
$\gamma _{n,k}\subseteq D_{\epsilon }$
belongs to
![]() $D_{\epsilon }$
, it follows that
$D_{\epsilon }$
, it follows that
![]() $D'\cap D_{\epsilon }\not =\emptyset .$
By the previous claim, we have
$D'\cap D_{\epsilon }\not =\emptyset .$
By the previous claim, we have
![]() $D'\subseteq D_{\epsilon }$
, and hence
$D'\subseteq D_{\epsilon }$
, and hence
![]() $\gamma _{n,k+1}\subseteq D_{\epsilon }$
, which completes the induction.
$\gamma _{n,k+1}\subseteq D_{\epsilon }$
, which completes the induction.
Note that for all large n,
where
![]() $z_n$
is the landing point of
$z_n$
is the landing point of
![]() $I_n(\theta )$
. According to the estimate in equation (3.3) and the fact that
$I_n(\theta )$
. According to the estimate in equation (3.3) and the fact that
![]() $\gamma _{n,k}\subseteq D_{\epsilon }$
, we have
$\gamma _{n,k}\subseteq D_{\epsilon }$
, we have
By choosing
![]() $\epsilon <\eta $
, we prove the proposition under the periodicity assumption.
$\epsilon <\eta $
, we prove the proposition under the periodicity assumption.
In the strictly preperiodic case, we set
![]() $(V,v):=\hat {f}(U,u)$
and
$(V,v):=\hat {f}(U,u)$
and
![]() $I_V(\theta ')=\hat f(I(\theta ))$
. Let
$I_V(\theta ')=\hat f(I(\theta ))$
. Let
![]() $(V_n,v_n)$
be the deformation of
$(V_n,v_n)$
be the deformation of
![]() $(V,v)$
with
$(V,v)$
with
![]() $f_n(U_n,u_n)=(V_n,v_n)$
. Inductively, it is sufficient to prove
$f_n(U_n,u_n)=(V_n,v_n)$
. Inductively, it is sufficient to prove
![]() $d_H(I(\theta ),I_n(\theta ))<\epsilon $
under the assumption that
$d_H(I(\theta ),I_n(\theta ))<\epsilon $
under the assumption that
![]() $\lim \nolimits _{n\to \infty }d_H(I_V(\theta '), I_{V_n}(\theta '))=0$
.
$\lim \nolimits _{n\to \infty }d_H(I_V(\theta '), I_{V_n}(\theta '))=0$
.
Define
![]() $D_{\epsilon }$
as above. By Proposition 3.7, there exists
$D_{\epsilon }$
as above. By Proposition 3.7, there exists
![]() $0<s<1$
such that for all large n,
$0<s<1$
such that for all large n,
Set
![]() $L^{\prime }_n:=\psi _{(V_n,v_n)}([s^{\delta },1]e^{2\pi \theta '})$
and
$L^{\prime }_n:=\psi _{(V_n,v_n)}([s^{\delta },1]e^{2\pi \theta '})$
and
![]() $L':=\psi _{(V,v)}([s^{\delta },1]e^{2\pi \theta '})$
. Since
$L':=\psi _{(V,v)}([s^{\delta },1]e^{2\pi \theta '})$
. Since
![]() $I_{V_n}(\theta ')\to I_V(\theta ')$
,
$I_{V_n}(\theta ')\to I_V(\theta ')$
,
![]() $L^{\prime }_n$
and
$L^{\prime }_n$
and
![]() $L'$
are contained in
$L'$
are contained in
![]() $\hat f(D_{\epsilon })$
for large n. Since
$\hat f(D_{\epsilon })$
for large n. Since
![]() $I_n(\theta )$
is a landed internal ray for all large n, there is a lift
$I_n(\theta )$
is a landed internal ray for all large n, there is a lift
![]() $L_n$
of
$L_n$
of
![]() $L^{\prime }_n$
based at the point
$L^{\prime }_n$
based at the point
![]() $\psi _n(se^{2\pi i\theta })$
. Denote by L the lift of
$\psi _n(se^{2\pi i\theta })$
. Denote by L the lift of
![]() $L'$
based at the point
$L'$
based at the point
![]() $\psi (se^{2\pi i\theta })$
. Note that in this case, we have
$\psi (se^{2\pi i\theta })$
. Note that in this case, we have
![]() $z_0\not \in \mathrm {Hole}(f)$
. Then
$z_0\not \in \mathrm {Hole}(f)$
. Then
![]() $f_n$
converges uniformly to
$f_n$
converges uniformly to
![]() $\hat {f}$
on
$\hat {f}$
on
![]() $D_{\epsilon }$
. Thus for sufficiently large n,
$D_{\epsilon }$
. Thus for sufficiently large n,
Hence we have
![]() $L_n\subset D_{2\epsilon }$
and
$L_n\subset D_{2\epsilon }$
and
![]() $L\subseteq D_{2\epsilon }$
. Note
$L\subseteq D_{2\epsilon }$
. Note
![]() $I(\theta )=\psi ([0,s]e^{2\pi it})\cup L$
and
$I(\theta )=\psi ([0,s]e^{2\pi it})\cup L$
and
![]() $I_n(\theta )=\psi _n([0,s]e^{2\pi it})\cup L_n$
. It follows that
$I_n(\theta )=\psi _n([0,s]e^{2\pi it})\cup L_n$
. It follows that
Choose
![]() $\epsilon <\eta /2$
. This completes the proof.
$\epsilon <\eta /2$
. This completes the proof.
3.3 Proof of Theorem 1.1
Now we begin to prove Theorem 1.1 and state a sufficient condition for the assumption (ii) in Theorem 1.1.
Proof of Theorem 1.1
Under the assumptions (i) and (ii), by Proposition 3.8, we have that for each
![]() $(U,u)\in \mathcal {U}$
and
$(U,u)\in \mathcal {U}$
and
![]() $t\times T_U$
, the internal rays
$t\times T_U$
, the internal rays
![]() $I_{(U_n,u_n)}(t)$
converge to
$I_{(U_n,u_n)}(t)$
converge to
![]() $I_{(U,u)}(t)$
as
$I_{(U,u)}(t)$
as
![]() $n\to \infty $
. It follows immediately that
$n\to \infty $
. It follows immediately that
![]() $\Gamma _n$
converges to
$\Gamma _n$
converges to
![]() $\Gamma $
as
$\Gamma $
as
![]() $n\to \infty $
.
$n\to \infty $
.
We are going to check that
![]() $\Gamma _n$
is homeomorphic to
$\Gamma _n$
is homeomorphic to
![]() $\Gamma $
for large n. It is sufficient to show that for any
$\Gamma $
for large n. It is sufficient to show that for any
![]() $(U,u),(U'u')\in {\mathcal U}$
and
$(U,u),(U'u')\in {\mathcal U}$
and
![]() $t\in T_U,t'\in T_{U'}$
, the rays
$t\in T_U,t'\in T_{U'}$
, the rays
![]() $I_{(U,u)}(t)$
and
$I_{(U,u)}(t)$
and
![]() $I_{(U',u')}(t')$
land at a common point only if
$I_{(U',u')}(t')$
land at a common point only if
![]() $I_{(U_n,u_n)}(t)$
and
$I_{(U_n,u_n)}(t)$
and
![]() $I_{(U_n',u_n')}(t')$
land at a common point for all large n. Assume first that this common landing point, denoted by z, is periodic. If
$I_{(U_n',u_n')}(t')$
land at a common point for all large n. Assume first that this common landing point, denoted by z, is periodic. If
![]() $z=\infty $
, the unique possible hole of f is in the Julia set of
$z=\infty $
, the unique possible hole of f is in the Julia set of
![]() $\hat f$
, where we have
$\hat f$
, where we have
![]() $t=t'=0$
. It follows that
$t=t'=0$
. It follows that
![]() $I_{(U_n,u_n)}(t)$
and
$I_{(U_n,u_n)}(t)$
and
![]() $I_{(U_n',u_n')}(t')$
land at the fixed points of
$I_{(U_n',u_n')}(t')$
land at the fixed points of
![]() $f_n$
in the Julia set, which can be only
$f_n$
in the Julia set, which can be only
![]() $\infty $
. If
$\infty $
. If
![]() $z\not =\infty $
, the conclusion follows immediately from Lemma 2.4(2) and Proposition 3.8. In the case where z is preperiodic, we have this result by combining the periodic case, Lemma 2.4(1), and Proposition 3.8 since the orbit of z avoids the critical points of
$z\not =\infty $
, the conclusion follows immediately from Lemma 2.4(2) and Proposition 3.8. In the case where z is preperiodic, we have this result by combining the periodic case, Lemma 2.4(1), and Proposition 3.8 since the orbit of z avoids the critical points of
![]() $\hat {f}$
.
$\hat {f}$
.
Assume now that
![]() $\Gamma $
is
$\Gamma $
is
![]() $\hat {f}$
-invariant. Let
$\hat {f}$
-invariant. Let
![]() $I:=I_{(U,u)}(t)$
be a periodic internal ray in
$I:=I_{(U,u)}(t)$
be a periodic internal ray in
![]() $\Gamma $
of period p. Since
$\Gamma $
of period p. Since
![]() $I_n:=I_{(U_n,u_n)}(t)$
is landed by the assumption, the inverse
$I_n:=I_{(U_n,u_n)}(t)$
is landed by the assumption, the inverse
![]() $\psi _{(U_n,u_n)}$
of the Böttcher coordinate on
$\psi _{(U_n,u_n)}$
of the Böttcher coordinate on
![]() $(U_n,u_n)$
(defined after Lemma 3.6) can be extended to
$(U_n,u_n)$
(defined after Lemma 3.6) can be extended to
![]() $[0,1]e^{2\pi i t}$
. So we are able to define a homeomorphism
$[0,1]e^{2\pi i t}$
. So we are able to define a homeomorphism
![]() $\varphi _{n,I}:I_{(U,u)}(t)\to I_{(U_n,u_n)}(t)$
by
$\varphi _{n,I}:I_{(U,u)}(t)\to I_{(U_n,u_n)}(t)$
by
![]() $\varphi _{n,I}:=\psi _{(U_n,u_n)}\circ \phi _{(U,u)}|_I$
. It follows from equation (3.1) that
$\varphi _{n,I}:=\psi _{(U_n,u_n)}\circ \phi _{(U,u)}|_I$
. It follows from equation (3.1) that
![]() $\varphi _{n,I}\circ \hat f^p=f_n^p\circ \varphi _{n,I}$
on I. If
$\varphi _{n,I}\circ \hat f^p=f_n^p\circ \varphi _{n,I}$
on I. If
![]() $I':=I_{(U,u)}(t')$
is mapped to I by
$I':=I_{(U,u)}(t')$
is mapped to I by
![]() $\hat f^k$
, we get a homeomorphism
$\hat f^k$
, we get a homeomorphism
![]() $\varphi _{n,I'}:I'\to I_n':=I_{(U_n',u_n')}(t')$
by lifting
$\varphi _{n,I'}:I'\to I_n':=I_{(U_n',u_n')}(t')$
by lifting
![]() $\varphi _{n,I}$
along the maps
$\varphi _{n,I}$
along the maps
![]() $\hat f^k:I'\to I$
and
$\hat f^k:I'\to I$
and
![]() $f_n^k:I_n'\to I_n$
. Finally, define a map
$f_n^k:I_n'\to I_n$
. Finally, define a map
![]() $\varphi _n$
on
$\varphi _n$
on
![]() $\Gamma $
such that
$\Gamma $
such that
![]() ${\varphi _n}|_{I}=\varphi _{n,I}$
on each internal ray I in
${\varphi _n}|_{I}=\varphi _{n,I}$
on each internal ray I in
![]() $\Gamma $
. Then
$\Gamma $
. Then
![]() $\varphi _n$
is the desired homeomorphism from
$\varphi _n$
is the desired homeomorphism from
![]() $\Gamma $
to
$\Gamma $
to
![]() $\Gamma _n$
.
$\Gamma _n$
.
To end this section, we state a sufficient condition to guarantee that assumption (ii) in Theorem 1.1 holds. Note that for any internal ray
![]() $I\subset \Gamma $
, there exists an smallest integer
$I\subset \Gamma $
, there exists an smallest integer
![]() $k_I\ge 0$
such that
$k_I\ge 0$
such that
![]() $\hat f^{k_I}(I)$
is contained in the immediate basin of a root of
$\hat f^{k_I}(I)$
is contained in the immediate basin of a root of
![]() $\hat f$
.
$\hat f$
.
Proposition 3.9. For any internal ray
![]() $I\subset \Gamma $
, let
$I\subset \Gamma $
, let
![]() $k_I\ge 0$
be as above. Under assumption (i) in Theorem 1.1, if the perturbation of
$k_I\ge 0$
be as above. Under assumption (i) in Theorem 1.1, if the perturbation of
![]() $\hat f^{k_I}(I)$
at
$\hat f^{k_I}(I)$
at
![]() $f_n$
is landed for all large n, then assumption (ii) in Theorem 1.1 holds. In particular, under assumption (i) in Theorem 1.1, if
$f_n$
is landed for all large n, then assumption (ii) in Theorem 1.1 holds. In particular, under assumption (i) in Theorem 1.1, if
![]() $\deg f_n|_{U_n'}=\deg \hat f|_{U'}$
for all immediate basins
$\deg f_n|_{U_n'}=\deg \hat f|_{U'}$
for all immediate basins
![]() $U'\in {\mathcal U}$
, then assumption (ii) in Theorem 1.1 holds.
$U'\in {\mathcal U}$
, then assumption (ii) in Theorem 1.1 holds.
Proof. Consider an internal ray
![]() $I\subset \Gamma $
and it’s perturbation
$I\subset \Gamma $
and it’s perturbation
![]() $I_n\subset \Gamma _n$
. Let
$I_n\subset \Gamma _n$
. Let
![]() $U\in {\mathcal U}$
be the component such that
$U\in {\mathcal U}$
be the component such that
![]() $I\subset U$
, and let
$I\subset U$
, and let
![]() $U_n$
be the deformation of U at
$U_n$
be the deformation of U at
![]() $f_n$
. We show
$f_n$
. We show
![]() $I_n$
lands on
$I_n$
lands on
![]() $\partial U_n$
. If U is the immediate basin of a root of
$\partial U_n$
. If U is the immediate basin of a root of
![]() $\hat {f}$
, the conclusion follows immediately since in this case,
$\hat {f}$
, the conclusion follows immediately since in this case,
![]() $k_I=0$
.
$k_I=0$
.
Now we consider the case where U is not the immediate basin of a root of
![]() $\hat {f}$
. We set
$\hat {f}$
. We set
![]() $V=\hat f(U)$
and
$V=\hat f(U)$
and
![]() $I'=\hat f(I)$
. By an induction argument, it suffices to show
$I'=\hat f(I)$
. By an induction argument, it suffices to show
![]() $I_n$
lands on
$I_n$
lands on
![]() $\partial U_n$
under the assumption that
$\partial U_n$
under the assumption that
![]() $I^{\prime }_n$
lands on
$I^{\prime }_n$
lands on
![]() $\partial V_n$
, where
$\partial V_n$
, where
![]() $I^{\prime }_n$
is the perturbation of
$I^{\prime }_n$
is the perturbation of
![]() $I'$
and
$I'$
and
![]() $V_n$
is the deformation of V at
$V_n$
is the deformation of V at
![]() $f_n$
. Fix notation as in the proof of Proposition 3.8. Since the orbit of the landing point of the internal ray I avoids the critical points of
$f_n$
. Fix notation as in the proof of Proposition 3.8. Since the orbit of the landing point of the internal ray I avoids the critical points of
![]() $\hat f$
, we can apply a similar argument in Proposition 3.8 and obtain that
$\hat f$
, we can apply a similar argument in Proposition 3.8 and obtain that
where
![]() $L_n$
is a lift of
$L_n$
is a lift of
![]() $\psi _{(V_n,v_n)}([s^{\delta },1]e^{2\pi it'})$
based at
$\psi _{(V_n,v_n)}([s^{\delta },1]e^{2\pi it'})$
based at
![]() $\psi _{(U_n,u_n)}(se^{2\pi it})$
. Note that
$\psi _{(U_n,u_n)}(se^{2\pi it})$
. Note that
It follows that
![]() $I_n$
land on
$I_n$
land on
![]() $\partial U_n$
.
$\partial U_n$
.
If
![]() $\deg f_n|_{U^{\prime }_n}=\deg \hat f|_{U'}$
for all immediate basins
$\deg f_n|_{U^{\prime }_n}=\deg \hat f|_{U'}$
for all immediate basins
![]() $U'\in {\mathcal U}$
, since
$U'\in {\mathcal U}$
, since
![]() $f_n\xrightarrow {\deg }f$
and
$f_n\xrightarrow {\deg }f$
and
![]() $\hat f$
is post-critically finite on
$\hat f$
is post-critically finite on
![]() $U'$
, it follows that for the center
$U'$
, it follows that for the center
![]() $u^{\prime }_n$
of
$u^{\prime }_n$
of
![]() $U^{\prime }_n$
, the degrees
$U^{\prime }_n$
, the degrees
![]() $\deg _{u^{\prime }_n}f_n=\deg f_n|_{U^{\prime }_n}$
. Hence
$\deg _{u^{\prime }_n}f_n=\deg f_n|_{U^{\prime }_n}$
. Hence
![]() $u^{\prime }_n$
is the unique critical point of
$u^{\prime }_n$
is the unique critical point of
![]() $f_n$
. It follows that all internal rays in
$f_n$
. It follows that all internal rays in
![]() $U^{\prime }_n$
are landed. Thus the conclusion follows.
$U^{\prime }_n$
are landed. Thus the conclusion follows.
4 Invariant graphs for Newton maps
In this section, we introduce suitable dynamical graphs of Newton maps for later use to prove Theorem 1.3. In §4.1, we recall the Newton graphs given by Drach et al [Reference Drach, Mikukich, Rückert and Schleicher4]. In §4.2, we first state Roesch’s result on cut angles and then construct invariant graphs differing from the Newton graphs for cubic Newton maps. In §4.3, we generalize Roesch’s cut angles result to quartic Newton maps.
4.1 Newton graphs
Let
![]() $f\in \mathrm {NM}_d$
with
$f\in \mathrm {NM}_d$
with
![]() $d\ge 2$
. Recall that
$d\ge 2$
. Recall that
![]() $\Omega _{ f}$
is the union of basins of its roots. Assume that f is post-critically finite on
$\Omega _{ f}$
is the union of basins of its roots. Assume that f is post-critically finite on
![]() $\Omega _{f}$
. The dynamics of
$\Omega _{f}$
. The dynamics of
![]() $ f$
can be characterized by an invariant graph that is the so-called Newton graph. Such a graph was first constructed in [Reference Drach, Mikukich, Rückert and Schleicher4] and then applied to study the dynamics of corresponding maps, see [Reference Drach and Schleicher5, Reference Gao8, Reference Gao9, Reference Lodge, Mikulich and Schleicher14, Reference Lodge, Mikulich and Schleicher13, Reference Wang, Yin and Zeng29]. In this subsection, we state briefly the construction of Newton graphs and list some properties.
$ f$
can be characterized by an invariant graph that is the so-called Newton graph. Such a graph was first constructed in [Reference Drach, Mikukich, Rückert and Schleicher4] and then applied to study the dynamics of corresponding maps, see [Reference Drach and Schleicher5, Reference Gao8, Reference Gao9, Reference Lodge, Mikulich and Schleicher14, Reference Lodge, Mikulich and Schleicher13, Reference Wang, Yin and Zeng29]. In this subsection, we state briefly the construction of Newton graphs and list some properties.
Let r be a root of
![]() $ f$
and denote by
$ f$
and denote by
![]() $\Omega _{ f}(r)$
its immediate attracting basin. The fixed internal rays in
$\Omega _{ f}(r)$
its immediate attracting basin. The fixed internal rays in
![]() $\Omega _{ f}(r)$
land at fixed points in
$\Omega _{ f}(r)$
land at fixed points in
![]() $\partial \Omega _{ f}(r)$
. Since the only Julia fixed point of
$\partial \Omega _{ f}(r)$
. Since the only Julia fixed point of
![]() $ f$
is at
$ f$
is at
![]() $\infty $
, all fixed internal rays in
$\infty $
, all fixed internal rays in
![]() $\Omega _{ f}$
have a common landing point at
$\Omega _{ f}$
have a common landing point at
![]() $\infty $
. We denote by
$\infty $
. We denote by
![]() $\Delta _0$
the union of all fixed internal rays in
$\Delta _0$
the union of all fixed internal rays in
![]() $\Omega _{ f}$
together with
$\Omega _{ f}$
together with
![]() $\infty $
. Then
$\infty $
. Then
![]() $ f(\Delta _0)=\Delta _0$
. For any
$ f(\Delta _0)=\Delta _0$
. For any
![]() $m\geq 0$
, denote by
$m\geq 0$
, denote by
![]() $\Delta _m$
the connected component of
$\Delta _m$
the connected component of
![]() $ f^{-m}(\Delta _0)$
that contains
$ f^{-m}(\Delta _0)$
that contains
![]() $\infty $
. Following [Reference Drach, Mikukich, Rückert and Schleicher4], we call
$\infty $
. Following [Reference Drach, Mikukich, Rückert and Schleicher4], we call
![]() $\Delta _m$
the Newton graph of f at level m. The vertex set of
$\Delta _m$
the Newton graph of f at level m. The vertex set of
![]() $\Delta _n$
consists of iterated preimages of fixed points of
$\Delta _n$
consists of iterated preimages of fixed points of
![]() $ f$
contained in
$ f$
contained in
![]() $\Delta _n$
.
$\Delta _n$
.
A crucial property for Newton graphs is the following.
Lemma 4.1. [Reference Drach, Mikukich, Rückert and Schleicher4, Theorem 3.4]
There exists
![]() $M\geq 0$
such that the Newton graph
$M\geq 0$
such that the Newton graph
![]() $\Delta _M$
contains all poles of
$\Delta _M$
contains all poles of
![]() $ f$
. Hence
$ f$
. Hence
![]() $\Delta _{m+1}=f^{-1}(\Delta _m)$
and
$\Delta _{m+1}=f^{-1}(\Delta _m)$
and
![]() $\Delta _m\subseteq \Delta _{m+1}$
for any
$\Delta _m\subseteq \Delta _{m+1}$
for any
![]() $m\geq M$
.
$m\geq M$
.
The Newton graphs induce naturally a puzzle structure for
![]() $ f$
on
$ f$
on
![]() $\widehat {{\mathbb C}}$
. Let
$\widehat {{\mathbb C}}$
. Let
![]() $\Delta _{ f}$
denote the Newton graph of
$\Delta _{ f}$
denote the Newton graph of
![]() $ f$
with the least level such that
$ f$
with the least level such that
![]() $\Delta _{ f}$
contains all poles and all critical points that map to fixed points under iteration. Set
$\Delta _{ f}$
contains all poles and all critical points that map to fixed points under iteration. Set
![]() $X_0$
the complement of the union of the disks
$X_0$
the complement of the union of the disks
![]() $\{z\in U:\phi _U(z)<1/2\}$
for all connected components U of
$\{z\in U:\phi _U(z)<1/2\}$
for all connected components U of
![]() $\Omega _{ f}$
with
$\Omega _{ f}$
with
![]() $U\cap \Delta _f\not =\emptyset $
, where
$U\cap \Delta _f\not =\emptyset $
, where
![]() $\phi _U$
is the Böttcher coordinate on U. Define
$\phi _U$
is the Böttcher coordinate on U. Define
![]() $G_0:=(\Delta _f\cap X_0)\cup \partial X_0$
. Then
$G_0:=(\Delta _f\cap X_0)\cup \partial X_0$
. Then
![]() $G_0$
is a finite graph consisting of segments of internal rays and equipotential lines in
$G_0$
is a finite graph consisting of segments of internal rays and equipotential lines in
![]() $\Omega _{ f}$
. For each
$\Omega _{ f}$
. For each
![]() $m\geq 0$
, we define
$m\geq 0$
, we define
![]() $X_m:={f}^{-m}(X_0)$
and
$X_m:={f}^{-m}(X_0)$
and
![]() $G_m:={f}^{-m}(G_0)$
. Then each
$G_m:={f}^{-m}(G_0)$
. Then each
![]() $X_m$
is connected and the interior
$X_m$
is connected and the interior
![]() $\mathrm {int}(X_m)$
contains the Julia set
$\mathrm {int}(X_m)$
contains the Julia set
![]() $J_{ f}$
of
$J_{ f}$
of
![]() $ f$
. For each
$ f$
. For each
![]() $m\geq 0$
, the closures of the components of
$m\geq 0$
, the closures of the components of
![]() $X_m\setminus G_m$
are called puzzle pieces of level m. It follows that the puzzle pieces of different levels have a nested structure. For each
$X_m\setminus G_m$
are called puzzle pieces of level m. It follows that the puzzle pieces of different levels have a nested structure. For each
![]() $z\in J_{ f}$
, denote
$z\in J_{ f}$
, denote
![]() $E_m(z)$
the union of puzzle pieces of level m which contains z. Then
$E_m(z)$
the union of puzzle pieces of level m which contains z. Then
![]() $z\in \mathrm {int}(E_m(z))$
. Moreover,
$z\in \mathrm {int}(E_m(z))$
. Moreover,
![]() $E_m(z)$
are puzzle pieces for all m if and only if z is not an iterated preimage of
$E_m(z)$
are puzzle pieces for all m if and only if z is not an iterated preimage of
![]() $\infty $
.
$\infty $
.
Proposition 4.2. [Reference Drach and Schleicher5, Corollary 1.2] and [Reference Wang, Yin and Zeng29, Theorem 1.1]
If z is on the boundary of a component of
![]() $\Omega _{{f}}$
, then
$\Omega _{{f}}$
, then
In particular, the boundary of any component of basins of the roots is locally connected.
4.2 An alternative graph for cubic Newton maps
In this subsection, we focus on the case where
![]() $f\in \mathrm {NM}_3$
. Except for some special cases, we construct an invariant graph away from the unique non-fixed critical point. Our graph is based on Roesch’s work in [Reference Roesch25, §3] and differs from the Newton graphs introduced above.
$f\in \mathrm {NM}_3$
. Except for some special cases, we construct an invariant graph away from the unique non-fixed critical point. Our graph is based on Roesch’s work in [Reference Roesch25, §3] and differs from the Newton graphs introduced above.
Let
![]() $r_1,r_2$
, and
$r_1,r_2$
, and
![]() $r_3$
be the roots of f and let
$r_3$
be the roots of f and let
![]() $\Omega _1$
,
$\Omega _1$
,
![]() $\Omega _2$
, and
$\Omega _2$
, and
![]() $\Omega _3$
be the corresponding immediate basins respectively. Note that f has another critical point denoted by c. In this subsection, we always assume
$\Omega _3$
be the corresponding immediate basins respectively. Note that f has another critical point denoted by c. In this subsection, we always assume
![]() $c\not \in \Omega _1\cup \Omega _2\cup \Omega _3$
and c is not a pole, that is,
$c\not \in \Omega _1\cup \Omega _2\cup \Omega _3$
and c is not a pole, that is,
![]() $f(c)\not =\infty $
.
$f(c)\not =\infty $
.
Under the assumptions, we have that f has two distinct poles, denoted by
![]() $\xi _1$
and
$\xi _1$
and
![]() $\xi _2$
. An orientation argument implies that
$\xi _2$
. An orientation argument implies that
![]() $\partial \Omega _1$
,
$\partial \Omega _1$
,
![]() $\partial \Omega _2$
, and
$\partial \Omega _2$
, and
![]() $\partial \Omega _3$
cannot intersect at a common pole. By counting the preimages of
$\partial \Omega _3$
cannot intersect at a common pole. By counting the preimages of
![]() $\Omega _i$
basins, we have that there is a unique pole at which exactly two
$\Omega _i$
basins, we have that there is a unique pole at which exactly two
![]() $\partial \Omega _i$
basins intersect. Up to reindexing, we can assume
$\partial \Omega _i$
basins intersect. Up to reindexing, we can assume
![]() $\xi _1\in \partial \Omega _1\cap \partial \Omega _2$
. It follows that
$\xi _1\in \partial \Omega _1\cap \partial \Omega _2$
. It follows that
![]() $\xi _2\in \partial \Omega _3$
and
$\xi _2\in \partial \Omega _3$
and
![]() $\xi _2\not \in \partial \Omega _1\cup \partial \Omega _2$
.
$\xi _2\not \in \partial \Omega _1\cup \partial \Omega _2$
.
For
![]() $i=1,2$
, and
$i=1,2$
, and
![]() $3$
, denote by
$3$
, denote by
![]() $I_i(\theta )$
the internal ray in
$I_i(\theta )$
the internal ray in
![]() $\Omega _i$
of angle
$\Omega _i$
of angle
![]() $\theta \in \mathbb {R}/\mathbb {Z}$
. Following Roesch [Reference Roesch25], we say an angle
$\theta \in \mathbb {R}/\mathbb {Z}$
. Following Roesch [Reference Roesch25], we say an angle
![]() $\theta $
is a cut angle in
$\theta $
is a cut angle in
![]() $\Omega _1$
if there exists
$\Omega _1$
if there exists
![]() $\theta '\in \mathbb {R}/\mathbb {Z}$
such that
$\theta '\in \mathbb {R}/\mathbb {Z}$
such that
![]() $I_1(\theta )$
and
$I_1(\theta )$
and
![]() $I_2(\theta ')$
land at a common point. It turns out that
$I_2(\theta ')$
land at a common point. It turns out that
![]() $\theta $
is a cut angle in
$\theta $
is a cut angle in
![]() $\Omega _1$
if and only if
$\Omega _1$
if and only if
![]() $1-\theta $
is a cut angle in
$1-\theta $
is a cut angle in
![]() $\Omega _2$
. For the basin
$\Omega _2$
. For the basin
![]() $\Omega _3$
, the only cut angle is
$\Omega _3$
, the only cut angle is
![]() $0$
. Let
$0$
. Let
![]() $\Theta $
be the set of cut angles in
$\Theta $
be the set of cut angles in
![]() $\Omega _1$
. It follows immediately that
$\Omega _1$
. It follows immediately that
![]() $0,1/2\in \Theta $
. Label
$0,1/2\in \Theta $
. Label
![]() $\Omega _1$
such that
$\Omega _1$
such that
![]() $\Omega _3$
and
$\Omega _3$
and
![]() $I_{\Omega _1}(\theta )$
are in the same complementary component of the curve
$I_{\Omega _1}(\theta )$
are in the same complementary component of the curve
for any
![]() $\theta \in (0,1/2)$
, and define
$\theta \in (0,1/2)$
, and define
where
![]() $\inf $
is obtained under the order by identifying
$\inf $
is obtained under the order by identifying
![]() $\mathbb {R}/\mathbb {Z}$
with
$\mathbb {R}/\mathbb {Z}$
with
![]() $(0,1]$
. In fact, the local connectivity of
$(0,1]$
. In fact, the local connectivity of
![]() $\partial \Omega _1$
and
$\partial \Omega _1$
and
![]() $\partial \Omega _2$
implies that
$\partial \Omega _2$
implies that
![]() $\alpha \in \Theta $
.
$\alpha \in \Theta $
.
Now we summarize the properties of the cut angles for later use. We use the following notation. Let
![]() $\Omega _i^{(1)}$
be the preimage of
$\Omega _i^{(1)}$
be the preimage of
![]() $\Omega _i$
disjoint from
$\Omega _i$
disjoint from
![]() $\Omega _i$
. Then
$\Omega _i$
. Then
![]() $c\not \in \Omega _i^{(1)}$
. For
$c\not \in \Omega _i^{(1)}$
. For
![]() $j\ge 1$
, if
$j\ge 1$
, if
![]() $\Omega _i^{(j)}$
is a domain such that
$\Omega _i^{(j)}$
is a domain such that
![]() $f^j:\Omega _i^{(j)}\to \Omega _i$
is a homeomorphism, then an internal ray
$f^j:\Omega _i^{(j)}\to \Omega _i$
is a homeomorphism, then an internal ray
![]() $I_i(\theta )$
in
$I_i(\theta )$
in
![]() $\Omega _i$
deduces an internal ray
$\Omega _i$
deduces an internal ray
![]() $I_i^{(j)}(\theta )$
in
$I_i^{(j)}(\theta )$
in
![]() $\Omega _i^{(j)}$
satisfying
$\Omega _i^{(j)}$
satisfying
![]() $I_i^{(j)}(\theta )=f^{-j}(I_i(\theta ))$
.
$I_i^{(j)}(\theta )=f^{-j}(I_i(\theta ))$
.
Lemma 4.3. [Reference Roesch25, §3]
Fix the notation as above. The following statements hold.
-
(1) If the orbit of a rational angle
 $\theta $
is contained in
$\theta $
is contained in
 $[\alpha ,1]$
, then
$[\alpha ,1]$
, then
 $\theta \in \Theta $
.
$\theta \in \Theta $
. -
(2) The angle
 $0<\alpha <1/2$
. Furthermore, the periodic angles
$0<\alpha <1/2$
. Furthermore, the periodic angles
 $1-1/(2^n-1)$
belong to
$1-1/(2^n-1)$
belong to
 $\Theta $
for all large n.
$\Theta $
for all large n. -
(3) Assume
 $0<\theta <1/2$
with
$0<\theta <1/2$
with
 $2\theta \in \Theta $
. Then
$2\theta \in \Theta $
. Then
 $\theta +1/2\in \Theta $
. Furthermore, if
$\theta +1/2\in \Theta $
. Furthermore, if
 $\theta \in \Theta $
, then
$\theta \in \Theta $
, then
 $I_1^{(1)}(2\theta )$
and
$I_1^{(1)}(2\theta )$
and
 $I_2^{(1)}(1-2\theta )$
land at a common point; if
$I_2^{(1)}(1-2\theta )$
land at a common point; if
 $\theta \not \in \Theta $
, then
$\theta \not \in \Theta $
, then
 $I_1(\theta )$
and
$I_1(\theta )$
and
 $I_{2}^{(1)}(1-2\theta )$
land at a common point, as well as
$I_{2}^{(1)}(1-2\theta )$
land at a common point, as well as
 $I_2(1-\theta )$
and
$I_2(1-\theta )$
and
 $I_1^{(1)}(2\theta )$
. The two landing points are distinct.
$I_1^{(1)}(2\theta )$
. The two landing points are distinct. -
(4) The curve
 $\gamma (0,1/2)$
defined in equation (4.1) separates
$\gamma (0,1/2)$
defined in equation (4.1) separates
 $\Omega _3$
and
$\Omega _3$
and
 $\Omega _3^{(1)}$
.
$\Omega _3^{(1)}$
. -
(5) Let
 $0<\theta <1/2$
with
$0<\theta <1/2$
with
 $2\theta \in \Theta $
. If
$2\theta \in \Theta $
. If
 $\theta \not \in \Theta $
, then the curve separates c and
$\theta \not \in \Theta $
, then the curve separates c and $$ \begin{align*}I_1(1/2)\cup I_1(\theta)\cup I_2^{(1)}(1\kern1.2pt{-}\kern1.2pt2\theta)\cup I_2^{(1)}(0)\cup I_1^{(1)}(0)\cup I_1^{(1)}(2\theta)\cup I_2(1\kern1.2pt{-}\kern1.2pt\theta)\cup I_2(1/2)\end{align*} $$
$$ \begin{align*}I_1(1/2)\cup I_1(\theta)\cup I_2^{(1)}(1\kern1.2pt{-}\kern1.2pt2\theta)\cup I_2^{(1)}(0)\cup I_1^{(1)}(0)\cup I_1^{(1)}(2\theta)\cup I_2(1\kern1.2pt{-}\kern1.2pt\theta)\cup I_2(1/2)\end{align*} $$
 $\infty $
.
$\infty $
.
Figure 3 provides an example to illuminate the curves in the above lemma.

Figure 3 The dynamical plane of the Newton map for the polynomial
![]() $z^3/3-z^2/2+1$
. The curve
$z^3/3-z^2/2+1$
. The curve
![]() $\gamma (0,1/2)$
consists of the internal rays
$\gamma (0,1/2)$
consists of the internal rays
![]() $I_1(0),I_1(\tfrac 12), I_2(0)$
, and
$I_1(0),I_1(\tfrac 12), I_2(0)$
, and
![]() $I_2(\tfrac 12)$
. The angle
$I_2(\tfrac 12)$
. The angle
![]() $\theta \not \in \Theta $
but
$\theta \not \in \Theta $
but
![]() $2\theta \in \Theta $
. A curve in Lemma 4.3(5) consists of indicated internal rays except those in
$2\theta \in \Theta $
. A curve in Lemma 4.3(5) consists of indicated internal rays except those in
![]() $\gamma (0,1/2)$
. In this section, we continue to use this example in the subsequent figures.
$\gamma (0,1/2)$
. In this section, we continue to use this example in the subsequent figures.
Let
![]() $\gamma (0,1/2)$
be as in equation (4.1). Then the complement of
$\gamma (0,1/2)$
be as in equation (4.1). Then the complement of
![]() $\gamma (0,1/2)$
in
$\gamma (0,1/2)$
in
![]() $\widehat {\mathbb {C}}$
contains two components. Denote by D the one that is disjoint with
$\widehat {\mathbb {C}}$
contains two components. Denote by D the one that is disjoint with
![]() $\Omega _3$
. It follows from Lemma 4.3(4) that
$\Omega _3$
. It follows from Lemma 4.3(4) that
![]() $\Omega _3^{(1)}\subset D$
.
$\Omega _3^{(1)}\subset D$
.
By Lemma 4.3(2), we can choose a rational angle
![]() $\theta \in (0,1/2)$
satisfying:
$\theta \in (0,1/2)$
satisfying:
-
(i)
 $\theta \not \in \Theta ,$
but
$\theta \not \in \Theta ,$
but
 $2\theta \in \Theta $
;
$2\theta \in \Theta $
; -
(ii) there exists
 $k\geq 1$
such that
$k\geq 1$
such that
 $\eta :=2^k\theta \in (1/2,1)$
; and
$\eta :=2^k\theta \in (1/2,1)$
; and -
(iii) the orbit of the landing point of
 $I_1(\theta )$
avoids c and
$I_1(\theta )$
avoids c and
 $\infty $
.
$\infty $
.
Define
 $$ \begin{align*}\mathcal{L} &:= I_3(0)\cup I_3(1/2)\cup I_1(0)\cup I_1(\theta)\cup I_2(0)\cup I_2(1-\theta)\\&\quad\cup I_2^{(1)}(1-2\theta)\cup I_2^{(1)}(0)\cup I_1^{(1)}(0)\cup I_1^{(1)}(2\theta).\end{align*} $$
$$ \begin{align*}\mathcal{L} &:= I_3(0)\cup I_3(1/2)\cup I_1(0)\cup I_1(\theta)\cup I_2(0)\cup I_2(1-\theta)\\&\quad\cup I_2^{(1)}(1-2\theta)\cup I_2^{(1)}(0)\cup I_1^{(1)}(0)\cup I_1^{(1)}(2\theta).\end{align*} $$
Then Lemma 4.3(3) implies that
![]() $\mathcal {L}$
is a connected graph. Moreover,
$\mathcal {L}$
is a connected graph. Moreover,
![]() $\widehat {{\mathbb C}}\setminus \mathcal {\mathcal {L}}$
has three components. We label W the one disjoint with
$\widehat {{\mathbb C}}\setminus \mathcal {\mathcal {L}}$
has three components. We label W the one disjoint with
![]() $\Omega _3$
. In the remaining two components, we label
$\Omega _3$
. In the remaining two components, we label
![]() $W_-$
the one intersecting with
$W_-$
the one intersecting with
![]() $\Omega _1$
and label
$\Omega _1$
and label
![]() $W_+$
the one intersecting with
$W_+$
the one intersecting with
![]() $\Omega _2$
(see Figure 4). By Lemma 4.3(5), it immediately follows that
$\Omega _2$
(see Figure 4). By Lemma 4.3(5), it immediately follows that
![]() $D\cup \overline {\Omega }_3^{(1)}\subseteq W$
and
$D\cup \overline {\Omega }_3^{(1)}\subseteq W$
and
![]() $c\in W\setminus \overline {D}$
. In particular,
$c\in W\setminus \overline {D}$
. In particular,
![]() $\xi _1\in W$
. Moreover, we have
$\xi _1\in W$
. Moreover, we have
![]() $I_3(3/4)\subseteq W_-$
and
$I_3(3/4)\subseteq W_-$
and
![]() $I_3(1/4)\subseteq W_+$
.
$I_3(1/4)\subseteq W_+$
.

Figure 4 The curve
![]() $\mathcal {L}$
consists of the indicated internal rays except
$\mathcal {L}$
consists of the indicated internal rays except
![]() $I_1(1/2)$
and
$I_1(1/2)$
and
![]() $I_2(1/2)$
. The boundary of D consists of
$I_2(1/2)$
. The boundary of D consists of
![]() $I_1(0), I_1(1/2), I_2(1/2)$
, and
$I_1(0), I_1(1/2), I_2(1/2)$
, and
![]() $I_2(0)$
.
$I_2(0)$
.
Now consider the components of
![]() $f^{-1}(\Omega _1^{(1)})$
and
$f^{-1}(\Omega _1^{(1)})$
and
![]() $f^{-1}(\Omega _2^{(1)})$
. Note that
$f^{-1}(\Omega _2^{(1)})$
. Note that
![]() $f^{-1}(\Omega _2^{(1)})$
has a component whose boundary contains the landing point of
$f^{-1}(\Omega _2^{(1)})$
has a component whose boundary contains the landing point of
![]() $I_1((1+\theta )/2)$
. Since
$I_1((1+\theta )/2)$
. Since
![]() $I_1((1+\theta )/2)\subset D$
, this component is also contained in D. Hence it does not contain c since
$I_1((1+\theta )/2)\subset D$
, this component is also contained in D. Hence it does not contain c since
![]() $c\in W\setminus \overline {D}$
. Note that the landing points of
$c\in W\setminus \overline {D}$
. Note that the landing points of
![]() $I_3(1/4)$
and
$I_3(1/4)$
and
![]() $I_3(3/4)$
are contained in the boundaries of the two remaining components of
$I_3(3/4)$
are contained in the boundaries of the two remaining components of
![]() $f^{-1}(\Omega _2^{(1)})$
respectively. We denote by
$f^{-1}(\Omega _2^{(1)})$
respectively. We denote by
![]() $\Omega _2^{(2)}$
the component whose boundary contains the landing point of
$\Omega _2^{(2)}$
the component whose boundary contains the landing point of
![]() $I_3(3/4)$
. Then
$I_3(3/4)$
. Then
![]() $I_2^{(2)}(0)$
and
$I_2^{(2)}(0)$
and
![]() $I_3(3/4)$
land at a common point. Moreover,
$I_3(3/4)$
land at a common point. Moreover,
![]() $\Omega _2^{(2)}\subset W_-$
since
$\Omega _2^{(2)}\subset W_-$
since
![]() $I_3(3/4)\subseteq W_-$
. It follows that
$I_3(3/4)\subseteq W_-$
. It follows that
![]() $c\not \in \Omega _2^{(2)}$
. By Lemma 4.3(3), we have
$c\not \in \Omega _2^{(2)}$
. By Lemma 4.3(3), we have
![]() $I_1(\theta )$
and
$I_1(\theta )$
and
![]() $I_2^{(1)}(1-2\theta )$
land at a common point. It follows that
$I_2^{(1)}(1-2\theta )$
land at a common point. It follows that
![]() $I_1(\theta /2)$
and
$I_1(\theta /2)$
and
![]() $I_{2}^{(2)}(1-2\theta )$
land at a common point since
$I_{2}^{(2)}(1-2\theta )$
land at a common point since
![]() $I_1(\theta /2)\subseteq W_-$
. Similarly, denote by
$I_1(\theta /2)\subseteq W_-$
. Similarly, denote by
![]() $\Omega _1^{(2)}$
the component of
$\Omega _1^{(2)}$
the component of
![]() $f^{-1}(\Omega _1^{(1)})$
contained in
$f^{-1}(\Omega _1^{(1)})$
contained in
![]() $W_+$
. Then
$W_+$
. Then
![]() $c\not \in \Omega _1^{(2)}$
. Moreover,
$c\not \in \Omega _1^{(2)}$
. Moreover,
![]() $I_1^{(2)}(0)$
and
$I_1^{(2)}(0)$
and
![]() $I_3(1/4)$
land at a common point, as well as
$I_3(1/4)$
land at a common point, as well as
![]() $I_1^{(2)}(2\theta )$
and
$I_1^{(2)}(2\theta )$
and
![]() $I_2(1-\theta /2)$
. Define the Jordan curve
$I_2(1-\theta /2)$
. Define the Jordan curve
 $$ \begin{align} \mathcal{C}&:= I_3(1/4)\cup I_3(3/4)\cup I_2^{(2)}(0)\cup I_2^{(2)}(1-2\theta)\cup I_1(\theta/2)\cup I_1(\eta) \\ \nonumber &\cup I_2(1-\eta)\cup I_2(1-\theta/2)\cup I_1^{(2)}(2\theta)\cup I_1^{(2)}(0). \end{align} $$
$$ \begin{align} \mathcal{C}&:= I_3(1/4)\cup I_3(3/4)\cup I_2^{(2)}(0)\cup I_2^{(2)}(1-2\theta)\cup I_1(\theta/2)\cup I_1(\eta) \\ \nonumber &\cup I_2(1-\eta)\cup I_2(1-\theta/2)\cup I_1^{(2)}(2\theta)\cup I_1^{(2)}(0). \end{align} $$
See Figure 5 for an illustration for the curve
![]() $\mathcal {C}$
.
$\mathcal {C}$
.

Figure 5 The curve
![]() $\mathcal {C}$
consists of the indicated internal rays. For this
$\mathcal {C}$
consists of the indicated internal rays. For this
![]() $\theta $
, we have
$\theta $
, we have
![]() $\eta =2\theta $
.
$\eta =2\theta $
.
We show that the critical point c is not in the iterations of
![]() $\mathcal {C}$
and separated by
$\mathcal {C}$
and separated by
![]() $\mathcal {C}$
from
$\mathcal {C}$
from
![]() $\infty $
. More precisely, we have the following lemma.
$\infty $
. More precisely, we have the following lemma.
Lemma 4.4. Let
![]() $\mathcal {C}$
be as above. Then the following statements hold.
$\mathcal {C}$
be as above. Then the following statements hold.
-
(1) The orbit of any Julia point in
 $\mathcal {C}$
is disjoint with the critical points of f.
$\mathcal {C}$
is disjoint with the critical points of f. -
(2) Denote V the bounded component of
 $\widehat {\mathbb {C}}\setminus \mathcal {C}$
. Then
$\widehat {\mathbb {C}}\setminus \mathcal {C}$
. Then  $$ \begin{align*}\overline{\Omega}_1^{(1)}\cup\overline{\Omega}_2^{(1)}\cup\overline{\Omega}_3^{(1)}\cup\{\xi_1,\xi_2,c\}\subset V.\end{align*} $$
$$ \begin{align*}\overline{\Omega}_1^{(1)}\cup\overline{\Omega}_2^{(1)}\cup\overline{\Omega}_3^{(1)}\cup\{\xi_1,\xi_2,c\}\subset V.\end{align*} $$
Proof. The Julia points in
![]() $\mathcal {C}$
are the landing points of
$\mathcal {C}$
are the landing points of
![]() $I_3(1/4),I_3(3/4), I_1(\theta /2),I_1(\eta )$
, and
$I_3(1/4),I_3(3/4), I_1(\theta /2),I_1(\eta )$
, and
![]() $I_2(1-\theta /2)$
. By the choice of
$I_2(1-\theta /2)$
. By the choice of
![]() $\theta $
, the orbits of the landing points of
$\theta $
, the orbits of the landing points of
![]() $I_1(\theta /2),I_1(\eta )$
, and
$I_1(\theta /2),I_1(\eta )$
, and
![]() $I_2(1-\theta /2)$
are away from c. Since
$I_2(1-\theta /2)$
are away from c. Since
it follows that
![]() $c\not \in \partial {\Omega }_3 $
, and hence the orbits of the landing points of
$c\not \in \partial {\Omega }_3 $
, and hence the orbits of the landing points of
![]() $I_3(1/4)$
and
$I_3(1/4)$
and
![]() $I_3(3/4)$
are disjoint with c. Then statement (1) holds.
$I_3(3/4)$
are disjoint with c. Then statement (1) holds.
Statement (2) follows immediately from the construction of
![]() $\mathcal {C}$
and Lemma 4.3 (4), (5).
$\mathcal {C}$
and Lemma 4.3 (4), (5).
Since
![]() $\theta $
is rational, there is a positive integer
$\theta $
is rational, there is a positive integer
![]() $k>1$
such that the graph
$k>1$
such that the graph
 $$ \begin{align*} G:=\bigcup_{j=0}^kf^j(\mathcal{C}) \end{align*} $$
$$ \begin{align*} G:=\bigcup_{j=0}^kf^j(\mathcal{C}) \end{align*} $$
is invariant. Lemma 4.4 immediately implies that
![]() $c\not \in G$
. Moreover, obviously our graph G is distinct from the Newton graphs of f.
$c\not \in G$
. Moreover, obviously our graph G is distinct from the Newton graphs of f.
4.3 Cut angles for quartic Newton maps
In this subsection, we generalize part of results in [Reference Roesch25, §3] from the cubic case to a quartic case. Throughout this subsection, we assume that
![]() $f\in \mathrm {NM}_4$
has degree
$f\in \mathrm {NM}_4$
has degree
![]() $2$
in the immediate basin of each root.
$2$
in the immediate basin of each root.
Let
![]() $r_1,r_2,r_3$
, and
$r_1,r_2,r_3$
, and
![]() $r_4$
be the roots of f and denote by
$r_4$
be the roots of f and denote by
![]() $\Omega _1,\Omega _2,\Omega _3$
, and
$\Omega _1,\Omega _2,\Omega _3$
, and
![]() $\Omega _4$
the corresponding immediate basins. Then there exist
$\Omega _4$
the corresponding immediate basins. Then there exist
![]() $1\le i<j \le 4$
such that
$1\le i<j \le 4$
such that
![]() $\partial \Omega _i\cap \partial \Omega _j$
contains a pole. Hence the internal rays
$\partial \Omega _i\cap \partial \Omega _j$
contains a pole. Hence the internal rays
![]() $I_i(1/2)$
and
$I_i(1/2)$
and
![]() $I_j(1/2)$
land at a common point. We say that f is of separable type if there exist
$I_j(1/2)$
land at a common point. We say that f is of separable type if there exist
![]() $1\le i<j\le 4$
such that
$1\le i<j\le 4$
such that
![]() $I_i(1/2)$
and
$I_i(1/2)$
and
![]() $I_j(1/2)$
land at a common pole and each component of
$I_j(1/2)$
land at a common pole and each component of
![]() $\widehat {{\mathbb C}}\setminus \gamma (0,1/2)$
contains a pole of f, where
$\widehat {{\mathbb C}}\setminus \gamma (0,1/2)$
contains a pole of f, where
If f is not of separable type, we can choose
![]() $1\le i<j\le 4$
such that
$1\le i<j\le 4$
such that
![]() $I_i(1/2)$
and
$I_i(1/2)$
and
![]() $I_j(1/2)$
land at a common pole, but a component D of
$I_j(1/2)$
land at a common pole, but a component D of
![]() $\widehat {{\mathbb C}}\setminus \gamma (0,1/2)$
does not contain a pole of f. Relabeling the roots of f, we set
$\widehat {{\mathbb C}}\setminus \gamma (0,1/2)$
does not contain a pole of f. Relabeling the roots of f, we set
![]() $i=1$
and
$i=1$
and
![]() $j=2$
. Furthermore, we can set
$j=2$
. Furthermore, we can set
![]() $I_1(\theta )\in D$
if and only if
$I_1(\theta )\in D$
if and only if
![]() $\theta \in (1/2,1)$
. Hence
$\theta \in (1/2,1)$
. Hence
![]() $I_2(\theta ')\in D$
if and only if
$I_2(\theta ')\in D$
if and only if
![]() $\theta '\in (0,1/2)$
. We now consider the cut angles in
$\theta '\in (0,1/2)$
. We now consider the cut angles in
![]() $\Omega _1$
. An angle
$\Omega _1$
. An angle
![]() $\theta \in \mathbb {R}/\mathbb {Z}$
is a cut angle in
$\theta \in \mathbb {R}/\mathbb {Z}$
is a cut angle in
![]() $\Omega _1$
if there exists
$\Omega _1$
if there exists
![]() $\theta '\in \mathbb {R}/\mathbb {Z}$
such that
$\theta '\in \mathbb {R}/\mathbb {Z}$
such that
![]() $I_1(\theta )$
and
$I_1(\theta )$
and
![]() $I_2(\theta ')$
land at a common point. If
$I_2(\theta ')$
land at a common point. If
![]() $\theta $
is a cut angle in
$\theta $
is a cut angle in
![]() $\Omega _1$
, then the corresponding
$\Omega _1$
, then the corresponding
![]() $\theta '=1-\theta $
. Denote
$\theta '=1-\theta $
. Denote
![]() $\Theta $
the set of all cut angles in
$\Theta $
the set of all cut angles in
![]() $\Omega _1$
and set
$\Omega _1$
and set
where
![]() $\inf $
is obtained under the order by identifying
$\inf $
is obtained under the order by identifying
![]() $\mathbb {R}/\mathbb {Z}$
with
$\mathbb {R}/\mathbb {Z}$
with
![]() $(0,1]$
. Since
$(0,1]$
. Since
![]() $\widehat {{\mathbb C}}\setminus \overline {D}$
contains
$\widehat {{\mathbb C}}\setminus \overline {D}$
contains
![]() $\Omega _3\cup \Omega _4$
, it follows that
$\Omega _3\cup \Omega _4$
, it follows that
![]() $\alpha>0$
. By the local connectivity of
$\alpha>0$
. By the local connectivity of
![]() $\partial \Omega _1$
and
$\partial \Omega _1$
and
![]() $\partial \Omega _2$
, we have
$\partial \Omega _2$
, we have
![]() $\alpha \in \Theta $
and
$\alpha \in \Theta $
and
![]() $\Theta $
is a closed set in
$\Theta $
is a closed set in
![]() ${\mathbb R}/{\mathbb Z}$
.
${\mathbb R}/{\mathbb Z}$
.
Now we state some properties of the cut angles. Since we are interested in hyperbolic maps, see §5, we further assume that f is hyperbolic in the following result.
Proposition 4.5. Let f be hyperbolic and not of separable type. With the above notation, the following statements hold.
-
(1) For any
 $\theta \in \Theta $
,
$\theta \in \Theta $
,
 $(\theta +1)/2\in \Theta $
.
$(\theta +1)/2\in \Theta $
. -
(2) Let
 $\theta $
be a periodic angle. If the orbit of
$\theta $
be a periodic angle. If the orbit of
 $\theta $
belongs to
$\theta $
belongs to
 $(\alpha ,1)$
, then
$(\alpha ,1)$
, then
 $\theta \in \Theta $
.
$\theta \in \Theta $
. -
(3) The angles
 $\alpha \in (0,1/2)$
and there exist periodic angles in
$\alpha \in (0,1/2)$
and there exist periodic angles in
 $(\alpha ,1/2)\cap \Theta $
.
$(\alpha ,1/2)\cap \Theta $
.
Proof. For statement (1), since
![]() $(\theta +1)/2>1/2$
, the internal rays
$(\theta +1)/2>1/2$
, the internal rays
![]() $I_1((\theta +1)/2)\subseteq D$
. Suppose
$I_1((\theta +1)/2)\subseteq D$
. Suppose
![]() $(\theta +1)/2\not \in \Theta $
. Since
$(\theta +1)/2\not \in \Theta $
. Since
![]() $f(I_1((\theta +1)/2))=I_1(\theta )$
and
$f(I_1((\theta +1)/2))=I_1(\theta )$
and
![]() $\theta \in \Theta $
, there exists a component
$\theta \in \Theta $
, there exists a component
![]() $\Omega _2^{(1)}$
of
$\Omega _2^{(1)}$
of
![]() $f^{-1}(\Omega _2)$
disjoint with
$f^{-1}(\Omega _2)$
disjoint with
![]() $\Omega _2$
such that
$\Omega _2$
such that
![]() $\Omega _2^{(1)}$
contains the landing point of
$\Omega _2^{(1)}$
contains the landing point of
![]() $I_1((\theta +1)/2)$
. Note that f is hyperbolic and hence the landing point of
$I_1((\theta +1)/2)$
. Note that f is hyperbolic and hence the landing point of
![]() $I_2(1/2)$
is not a critical point. It follows that
$I_2(1/2)$
is not a critical point. It follows that
![]() $\overline {\Omega }_2^{(1)}\subseteq D$
. Hence D contains a pole of f. It contradicts the choice of D.
$\overline {\Omega }_2^{(1)}\subseteq D$
. Hence D contains a pole of f. It contradicts the choice of D.
To prove statement (2), let p be the period of the angle
![]() $\theta $
. Under the assumptions of f, the unique fixed angle is
$\theta $
. Under the assumptions of f, the unique fixed angle is
![]() $0$
. It follows that
$0$
. It follows that
![]() $p>1$
. Define
$p>1$
. Define
Since
![]() $\alpha \leq 1/2$
, there exists a component of
$\alpha \leq 1/2$
, there exists a component of
![]() $\widehat {{\mathbb C}}\setminus \gamma (0,\alpha )$
containing D. Denote this component by W. It follows that the only possible pole of f contained in W is the common landing point of
$\widehat {{\mathbb C}}\setminus \gamma (0,\alpha )$
containing D. Denote this component by W. It follows that the only possible pole of f contained in W is the common landing point of
![]() $I_1(1/2)$
and
$I_1(1/2)$
and
![]() $I_2(1/2)$
. Hence the only component of
$I_2(1/2)$
. Hence the only component of
![]() $f^{-1}(\Omega _1)$
(respectively
$f^{-1}(\Omega _1)$
(respectively
![]() $f^{-1}(\Omega _2)$
) intersecting with W is
$f^{-1}(\Omega _2)$
) intersecting with W is
![]() $\Omega _1$
(respectively
$\Omega _1$
(respectively
![]() $\Omega _2$
) itself.
$\Omega _2$
) itself.
For each
![]() $0\leq i\leq p$
, denote
$0\leq i\leq p$
, denote
![]() $z_i$
the landing point of
$z_i$
the landing point of
![]() $I_1(2^i\theta )$
and by
$I_1(2^i\theta )$
and by
![]() $w_i$
the landing point of
$w_i$
the landing point of
![]() $I_2(2^i(1-\theta ))=I_2(1-2^i\theta )$
. Since
$I_2(2^i(1-\theta ))=I_2(1-2^i\theta )$
. Since
![]() $\theta $
is p-periodic, the points
$\theta $
is p-periodic, the points
![]() $z_0,\ldots ,z_{p-1}$
(respectively
$z_0,\ldots ,z_{p-1}$
(respectively
![]() $w_0,\ldots ,w_{p-1}$
) are pairwise disjoint and
$w_0,\ldots ,w_{p-1}$
) are pairwise disjoint and
![]() $z_0=z_p$
(respectively
$z_0=z_p$
(respectively
![]() $w_0=w_p$
). Moreover, the assumption of
$w_0=w_p$
). Moreover, the assumption of
![]() $\theta $
implies that
$\theta $
implies that
![]() $z_0,\ldots ,z_{p-1}, w_0,\ldots ,w_{p-1}\in W$
. Suppose
$z_0,\ldots ,z_{p-1}, w_0,\ldots ,w_{p-1}\in W$
. Suppose
![]() $\theta \not \in \Theta $
. Then
$\theta \not \in \Theta $
. Then
![]() $z_0\not =w_0$
. As
$z_0\not =w_0$
. As
![]() $\Theta $
is closed, we can choose an arc
$\Theta $
is closed, we can choose an arc
![]() $\ell _0$
in
$\ell _0$
in
![]() $W\setminus \{I_1(t)\cup I_2(1-t):t\in \Theta \}$
joining the points
$W\setminus \{I_1(t)\cup I_2(1-t):t\in \Theta \}$
joining the points
![]() $z_0=z_p$
and
$z_0=z_p$
and
![]() $w_0=w_p$
such that
$w_0=w_p$
such that
![]() $\ell _0$
is disjoint with
$\ell _0$
is disjoint with
![]() $\Omega _1\cup \Omega _2$
. Let
$\Omega _1\cup \Omega _2$
. Let
![]() $\ell _1$
be the lift of
$\ell _1$
be the lift of
![]() $\ell _0$
based at
$\ell _0$
based at
![]() $z_{p-1}$
. By the choice of
$z_{p-1}$
. By the choice of
![]() $\ell _0$
, we have
$\ell _0$
, we have
and
Note that the endpoint of
![]() $\ell _1$
is on the boundary of a preimage of
$\ell _1$
is on the boundary of a preimage of
![]() $\Omega _2$
. By the previous paragraph, this preimage is
$\Omega _2$
. By the previous paragraph, this preimage is
![]() $\Omega _2$
itself. Note also that
$\Omega _2$
itself. Note also that
![]() $w_{p-1}$
is the unique preimage of
$w_{p-1}$
is the unique preimage of
![]() $w_p$
on
$w_p$
on
![]() $\partial \Omega _2$
such that
$\partial \Omega _2$
such that
![]() $w_{p-1}$
and
$w_{p-1}$
and
![]() $z_{p-1}$
are in the same component of
$z_{p-1}$
are in the same component of
![]() $W\setminus (I_1(1/2)\cup I_2(1/2))$
. Hence the endpoint of
$W\setminus (I_1(1/2)\cup I_2(1/2))$
. Hence the endpoint of
![]() $\ell _1$
is
$\ell _1$
is
![]() $w_{p-1}$
.
$w_{p-1}$
.
Inductively, for each
![]() $m\geq 1$
, we get an arc
$m\geq 1$
, we get an arc
![]() $\ell _{mp}\subseteq W$
joining
$\ell _{mp}\subseteq W$
joining
![]() $z_0$
and
$z_0$
and
![]() $w_0$
which is a lift of
$w_0$
which is a lift of
![]() $\ell _0$
by
$\ell _0$
by
![]() $f^{pm}$
. Choose
$f^{pm}$
. Choose
![]() $\ell _0$
such that it does not intersect the closure of the forward orbits of the critical points of f. Since f is hyperbolic, it is uniformly expanding near its Julia set. It follows that the length of
$\ell _0$
such that it does not intersect the closure of the forward orbits of the critical points of f. Since f is hyperbolic, it is uniformly expanding near its Julia set. It follows that the length of
![]() $\ell _{mp}$
converges to
$\ell _{mp}$
converges to
![]() $0$
as
$0$
as
![]() $m\to \infty $
. Then
$m\to \infty $
. Then
![]() $z_0=w_0$
, a contradiction. Hence
$z_0=w_0$
, a contradiction. Hence
![]() $\theta \in \Theta $
and statement (2) follows.
$\theta \in \Theta $
and statement (2) follows.
Now we prove statement
![]() $(3)$
. Note that
$(3)$
. Note that
![]() $\alpha \in (0,1/2]$
. Suppose, on the contrary, that
$\alpha \in (0,1/2]$
. Suppose, on the contrary, that
![]() $\alpha =1/2$
. According to statement (1), the angles
$\alpha =1/2$
. According to statement (1), the angles
![]() $1-1/2^n\in \Theta $
for all
$1-1/2^n\in \Theta $
for all
![]() $n\geq 1$
. Choose an angle
$n\geq 1$
. Choose an angle
![]() $\eta \in \Theta $
close to
$\eta \in \Theta $
close to
![]() $1$
and define
$1$
and define
Let
![]() $D_{\eta }$
be a component of
$D_{\eta }$
be a component of
![]() $\widehat {{\mathbb C}}\setminus \gamma (0,\eta )$
contained in D. We can choose
$\widehat {{\mathbb C}}\setminus \gamma (0,\eta )$
contained in D. We can choose
![]() $\eta $
sufficiently close to
$\eta $
sufficiently close to
![]() $1$
such that
$1$
such that
![]() $D_{\eta }$
contains no critical values of f. Since
$D_{\eta }$
contains no critical values of f. Since
![]() $\alpha =1/2$
, then
$\alpha =1/2$
, then
![]() $I_1(\eta /2)$
and
$I_1(\eta /2)$
and
![]() $I_2(1-\eta /2)$
land at distinct points. Denote by
$I_2(1-\eta /2)$
land at distinct points. Denote by
![]() $\Omega _1^{(1)}$
the component of
$\Omega _1^{(1)}$
the component of
![]() $f^{-1}(\Omega _1)$
such that
$f^{-1}(\Omega _1)$
such that
![]() $I_2(1-\eta /2)$
and
$I_2(1-\eta /2)$
and
![]() $I_1^{(1)}(\eta )$
land at a common point and denote
$I_1^{(1)}(\eta )$
land at a common point and denote
![]() $\Omega _2^{(1)}$
the component of
$\Omega _2^{(1)}$
the component of
![]() $f^{-1}(\Omega _2)$
such that
$f^{-1}(\Omega _2)$
such that
![]() $I_1(\eta /2)$
and
$I_1(\eta /2)$
and
![]() $I_2^{(1)}(1-\eta )$
land at a common point. Since f is hyperbolic, its Julia set contains no critical points. It follows that there exists a component
$I_2^{(1)}(1-\eta )$
land at a common point. Since f is hyperbolic, its Julia set contains no critical points. It follows that there exists a component
![]() $D_{\eta }'$
of
$D_{\eta }'$
of
![]() $f^{-1}(D_{\eta })$
whose boundary contains the arc
$f^{-1}(D_{\eta })$
whose boundary contains the arc
Note that the two arcs
![]() $I_1(\eta /2)\cup I_2^{(1)}(1-\eta )$
and
$I_1(\eta /2)\cup I_2^{(1)}(1-\eta )$
and
![]() $I_2(1-\eta /2)\cup I_1^{(1)}(\eta )$
are disjoint and mapped to the same arc
$I_2(1-\eta /2)\cup I_1^{(1)}(\eta )$
are disjoint and mapped to the same arc
![]() $I_1(\eta )\cup I_2(1-\eta )$
under f. Then the proper map
$I_1(\eta )\cup I_2(1-\eta )$
under f. Then the proper map
![]() $f:D_{\eta }'\to D_{\eta }$
has degree at least
$f:D_{\eta }'\to D_{\eta }$
has degree at least
![]() $2$
. It implies that
$2$
. It implies that
![]() $D_{\eta }'$
contains at least one critical point. Hence
$D_{\eta }'$
contains at least one critical point. Hence
![]() $D_{\eta }$
contains a critical value. It contradicts the choice of
$D_{\eta }$
contains a critical value. It contradicts the choice of
![]() $D_{\eta }$
.
$D_{\eta }$
.
For the second part of statement (3), let
![]() $\theta _n:=1-1/(2^n-1)$
. Then
$\theta _n:=1-1/(2^n-1)$
. Then
![]() $\theta _n$
is periodic with period n. If
$\theta _n$
is periodic with period n. If
![]() $0\le i<n-1$
, we have
$0\le i<n-1$
, we have
For
![]() $i=n-1$
, we have
$i=n-1$
, we have
 $$ \begin{align*} 2^{n-1}\theta_n=\frac{1}{2}\bigg(1-\frac{1}{2^n-1}\bigg)\in(0,1/2). \end{align*} $$
$$ \begin{align*} 2^{n-1}\theta_n=\frac{1}{2}\bigg(1-\frac{1}{2^n-1}\bigg)\in(0,1/2). \end{align*} $$
Since
![]() $\alpha <1/2$
, it follows that
$\alpha <1/2$
, it follows that
![]() $2^{n-1}\theta _n\in (\alpha ,1)$
for sufficiently large n. Then
$2^{n-1}\theta _n\in (\alpha ,1)$
for sufficiently large n. Then
![]() $\theta _n\in \Theta $
by statement (2), and hence
$\theta _n\in \Theta $
by statement (2), and hence
![]() $2^{n-1}\theta _n$
is as required.
$2^{n-1}\theta _n$
is as required.
5 The boundedness of hyperbolic components
In this section, we aim to prove Theorem 1.3. In §5.1, we classify the hyperbolic components into several types and state known boundedness results. Section 5.2 contains two key lemmas for the proof of Theorem 1.3: one concerns the orbit of a critical point and the limit of an attracting cycle; the other one concerns the combinatorial property of the limit function. Then we prove Theorem 1.3 in §5.3.
5.1 Classification of hyperbolic components and known results
Let
![]() $f\in \mathrm {NM}_4$
be the Newton map of the quartic polynomial P. Then the finite fixed points of f are the zeros of P, and the critical points of f are the zeros of P and zeros of
$f\in \mathrm {NM}_4$
be the Newton map of the quartic polynomial P. Then the finite fixed points of f are the zeros of P, and the critical points of f are the zeros of P and zeros of
![]() $P"$
. Hence zeros of P are the superattracting fixed points of f. We call any other (super)attracting cycles of f a free (super)attracting cycle. Then any free (super)attracting cycle has period at least
$P"$
. Hence zeros of P are the superattracting fixed points of f. We call any other (super)attracting cycles of f a free (super)attracting cycle. Then any free (super)attracting cycle has period at least
![]() $2$
. Moreover, we say a critical point c of f is additional if
$2$
. Moreover, we say a critical point c of f is additional if
![]() $P"(c)=0$
. Hence f has two additional critical points, counted with multiplicity. According to the orbits of the additional critical points, the hyperbolic components in the moduli space
$P"(c)=0$
. Hence f has two additional critical points, counted with multiplicity. According to the orbits of the additional critical points, the hyperbolic components in the moduli space
![]() $\mathrm {nm}_4:=\mathrm {NM}_4/\mathrm {Aut}(\mathbb {C})$
belong to the following seven types, see [Reference Nie and Pilgrim22]. The same classification is also for hyperbolic components in
$\mathrm {nm}_4:=\mathrm {NM}_4/\mathrm {Aut}(\mathbb {C})$
belong to the following seven types, see [Reference Nie and Pilgrim22]. The same classification is also for hyperbolic components in
![]() $\mathrm {NM}_4$
.
$\mathrm {NM}_4$
.
Type A. Adjacent critical points. The two additional critical points belong to the same component of the immediate basin of a free (super)attracting cycle.
Type B. Bitransitive. Each of the two additional critical points belongs to the immediate basin of a free (super)attracting period cycle, with two distinct components.
Type C. Capture. Only one additional critical point belongs to the immediate basin of a free (super)attracting cycle, but the orbit of the other additional critical point eventually lies in this immediate basin.
Type D. Disjoint (super)attracting orbits. The two additional critical points belong to the immediate basins of two distinct free (super)attracting cycles.
Type IE. Immediate escape. Some additional critical point in the immediate basin of a root.
Type FE1. One future escape. Only one additional critical point in the basin (but not immediate basin) of a root, while the other additional critical point is in the immediate basin of a free (super)attracting cycle.
Type FE2. Two future escapes. The two additional critical points belong to the basins (but not immediate basins) of one or two roots.
The above classification is an analogy of that for quadratic rational maps [Reference Milnor17] and for cubic polynomials [Reference Milnor19].
Recall that a hyperbolic component in
![]() $\mathrm {nm}_4$
is bounded if it has a compact closure in
$\mathrm {nm}_4$
is bounded if it has a compact closure in
![]() $\mathrm {nm}_4$
. Since the type-D hyperbolic components have semi-algebraic boundaries, an arithmetic argument shows that such components are bounded.
$\mathrm {nm}_4$
. Since the type-D hyperbolic components have semi-algebraic boundaries, an arithmetic argument shows that such components are bounded.
Proposition 5.1. [Reference Nie and Pilgrim22, Main Theorem]
The hyperbolic components of type D in
![]() $nm_4$
are bounded.
$nm_4$
are bounded.
In contrast, all hyperbolic components of type IE are unbounded.
Proposition 5.2. [Reference Nie and Pilgrim22, Theorem 1.4]
Let
![]() $\mathcal {H}\subset \mathrm {nm}_4$
be a hyperbolic component. If
$\mathcal {H}\subset \mathrm {nm}_4$
be a hyperbolic component. If
![]() $\mathcal {H}$
is of type IE, then
$\mathcal {H}$
is of type IE, then
![]() $\mathcal {H}$
is unbounded in
$\mathcal {H}$
is unbounded in
![]() $\mathrm {nm}_4$
.
$\mathrm {nm}_4$
.
In the remainder of this section, we give more bounded hyperbolic components in
![]() $\mathrm {nm}_4$
. In fact, we show the condition in Proposition 5.2 is also necessary.
$\mathrm {nm}_4$
. In fact, we show the condition in Proposition 5.2 is also necessary.
5.2 Key lemmas
To prove Theorem 1.3, we need two key lemmas.
Let
![]() $\{f_n\}\subset \mathrm {NM}_4$
be a sequence converging to
$\{f_n\}\subset \mathrm {NM}_4$
be a sequence converging to
![]() $f=H_f\hat f\in \overline {\mathrm {NM}}_4$
such that
$f=H_f\hat f\in \overline {\mathrm {NM}}_4$
such that
![]() $\mathrm {Hole}(f)=\{\infty \}$
and
$\mathrm {Hole}(f)=\{\infty \}$
and
![]() $\deg \hat f=3$
. Then
$\deg \hat f=3$
. Then
![]() $f_n$
has a unique additional critical point
$f_n$
has a unique additional critical point
![]() $c_n$
converging to
$c_n$
converging to
![]() $\infty $
as
$\infty $
as
![]() $n\to \infty $
. We suppose that all maps
$n\to \infty $
. We suppose that all maps
![]() $f_n$
are in a same hyperbolic component in
$f_n$
are in a same hyperbolic component in
![]() $\mathrm {NM}_4$
and assume that
$\mathrm {NM}_4$
and assume that
![]() $f_n$
has an attracting cycle
$f_n$
has an attracting cycle
![]() $\mathcal {O}_n=\{w_n^{(0)},\ldots , w_n^{(m-1)}\}$
of period
$\mathcal {O}_n=\{w_n^{(0)},\ldots , w_n^{(m-1)}\}$
of period
![]() $m\ge 2$
. Our first lemma states the orbit of
$m\ge 2$
. Our first lemma states the orbit of
![]() $c_n$
and the limit of
$c_n$
and the limit of
![]() $\mathcal {O}_n$
.
$\mathcal {O}_n$
.
Lemma 5.3. Let
![]() $f_n, f, c_n$
, and
$f_n, f, c_n$
, and
![]() $\mathcal {O}_n$
be as above. Then the following statements hold.
$\mathcal {O}_n$
be as above. Then the following statements hold.
-
(1) Given any
 $k\geq 0$
and small
$k\geq 0$
and small
 $\epsilon>0$
, the points
$\epsilon>0$
, the points
 $c_n, f_n(c_n),\ldots ,f^k_n(c_n)$
are in the
$c_n, f_n(c_n),\ldots ,f^k_n(c_n)$
are in the
 $\epsilon $
-neighborhood of
$\epsilon $
-neighborhood of
 $\infty $
for all large n.
$\infty $
for all large n. -
(2) Suppose
 $\mathcal {O}_n$
converges to
$\mathcal {O}_n$
converges to
 $\mathcal {O}$
as
$\mathcal {O}$
as
 $n\to \infty $
. Then
$n\to \infty $
. Then
 $\mathcal {O}\not =\{\infty \}$
.
$\mathcal {O}\not =\{\infty \}$
. -
(3) If
 $\infty \in \mathcal {O}$
, then
$\infty \in \mathcal {O}$
, then
 $c_n$
is not in the immediate basin of
$c_n$
is not in the immediate basin of
 $\mathcal {O}_n$
.
$\mathcal {O}_n$
.
Proof. Denote by
![]() $r_{1,n},r_{2,n},r_{3,n}$
, and
$r_{1,n},r_{2,n},r_{3,n}$
, and
![]() $r_{4,n}$
the roots of
$r_{4,n}$
the roots of
![]() $f_n$
. Since
$f_n$
. Since
![]() $\mathrm {Hole}(f)=\{\infty \}$
and
$\mathrm {Hole}(f)=\{\infty \}$
and
![]() $\deg \hat f=3$
, we may assume
$\deg \hat f=3$
, we may assume
![]() $r_{4,n}\to \infty $
, as
$r_{4,n}\to \infty $
, as
![]() $n\to \infty $
, and for
$n\to \infty $
, and for
![]() $1\le i\le 3$
, the point
$1\le i\le 3$
, the point
![]() $r_{i,n}$
is outside the
$r_{i,n}$
is outside the
![]() $\epsilon $
-neighborhood of
$\epsilon $
-neighborhood of
![]() $\infty $
for all large n. Define
$\infty $
for all large n. Define
![]() $M_n(z):=r_{4,n}z$
and let
$M_n(z):=r_{4,n}z$
and let
![]() $g_n:=M_n^{-1}\circ f_n\circ M_n$
. Then
$g_n:=M_n^{-1}\circ f_n\circ M_n$
. Then
![]() $g_n\in \mathrm {NM}_4$
with roots at
$g_n\in \mathrm {NM}_4$
with roots at
![]() $r_{1,n}/r_{4,n},r_{2,n}/r_{4,n},r_{3,n}/r_{4,n}$
, and
$r_{1,n}/r_{4,n},r_{2,n}/r_{4,n},r_{3,n}/r_{4,n}$
, and
![]() $1$
. Let
$1$
. Let
![]() $g=H_g\hat g$
be the degenerate Newton map of the polynomial
$g=H_g\hat g$
be the degenerate Newton map of the polynomial
![]() $z^3(z-1)$
. Then
$z^3(z-1)$
. Then
![]() $g_n$
converges locally uniformly to
$g_n$
converges locally uniformly to
![]() $\hat g$
away from
$\hat g$
away from
![]() $\mathrm {Hole}(g)=\{0\}$
. Note that
$\mathrm {Hole}(g)=\{0\}$
. Note that
![]() $\hat g$
has a critical point at
$\hat g$
has a critical point at
![]() $\tilde c=1/2$
and
$\tilde c=1/2$
and
![]() $\tilde {c}$
is attracted to the attracting fixed point
$\tilde {c}$
is attracted to the attracting fixed point
![]() $0$
. Given any
$0$
. Given any
![]() $k\geq 0$
, the point
$k\geq 0$
, the point
![]() $\tilde c$
is not in
$\tilde c$
is not in
![]() $\mathrm { Hole}(g^k)=\bigcup _{i=0}^{k-1}\hat g^{-i}(0)$
. It follows that there exists
$\mathrm { Hole}(g^k)=\bigcup _{i=0}^{k-1}\hat g^{-i}(0)$
. It follows that there exists
![]() $\epsilon _0=\epsilon _0(k)>0$
such that
$\epsilon _0=\epsilon _0(k)>0$
such that
![]() $|\hat g^j(\tilde c)|>\epsilon _0$
for all
$|\hat g^j(\tilde c)|>\epsilon _0$
for all
![]() $0\le j\le k$
. By Lemma 2.1, we have
$0\le j\le k$
. By Lemma 2.1, we have
![]() $|g_n^j(\tilde c_n)|>\epsilon _0$
for all large n. Note that for the maps
$|g_n^j(\tilde c_n)|>\epsilon _0$
for all large n. Note that for the maps
![]() $f_n$
, we have
$f_n$
, we have
![]() $f^j_n(c_n)=M_n(g^j_n(\tilde {c}_n))$
. It follows that
$f^j_n(c_n)=M_n(g^j_n(\tilde {c}_n))$
. It follows that
![]() $|f^j_n(c_n)|>r_{4,n}\epsilon _0$
for all
$|f^j_n(c_n)|>r_{4,n}\epsilon _0$
for all
![]() $0\le j\le k$
. Thus, statement (1) follows.
$0\le j\le k$
. Thus, statement (1) follows.
For statement (2), suppose in contrast that
![]() $\mathcal {O}=\{\infty \}$
. Then all
$\mathcal {O}=\{\infty \}$
. Then all
![]() $w_i^{(0)}$
s converge to
$w_i^{(0)}$
s converge to
![]() $\infty $
. In the following argument, we may pass to subsequences if necessary to obtain limits. Relabeling the indices, we may assume
$\infty $
. In the following argument, we may pass to subsequences if necessary to obtain limits. Relabeling the indices, we may assume
![]() $w_n^{(i)}/w_n^{(0)}$
does not converge to
$w_n^{(i)}/w_n^{(0)}$
does not converge to
![]() $0$
for all
$0$
for all
![]() $0\le i\le m-1$
. Write
$0\le i\le m-1$
. Write
![]() $L_n(z)=w_n^{(0)}z$
. Then
$L_n(z)=w_n^{(0)}z$
. Then
is an attracting cycle of
![]() $h_n:=L_n^{-1}\circ f_n\circ L_n\in \mathrm {NM}_4$
. Denote by
$h_n:=L_n^{-1}\circ f_n\circ L_n\in \mathrm {NM}_4$
. Denote by
![]() $\mathcal {O}'$
the limit of
$\mathcal {O}'$
the limit of
![]() $\mathcal {O}_n'$
. Then
$\mathcal {O}_n'$
. Then
![]() $0\not \in \mathcal {O}'$
. Assume that
$0\not \in \mathcal {O}'$
. Assume that
![]() $h_n\to h=H_h\hat h\in \overline {\mathrm {NM}}_4$
. Note that
$h_n\to h=H_h\hat h\in \overline {\mathrm {NM}}_4$
. Note that
![]() $\mathrm {Hole}(h)\subset \{0,\infty \}$
and
$\mathrm {Hole}(h)\subset \{0,\infty \}$
and
![]() $1\le \deg \hat h\le 2$
.
$1\le \deg \hat h\le 2$
.
If
![]() $\deg \hat h=1$
, then at least three roots of
$\deg \hat h=1$
, then at least three roots of
![]() $h_n$
collide to
$h_n$
collide to
![]() $0$
as
$0$
as
![]() $n\to \infty $
and the remaining root either collides to
$n\to \infty $
and the remaining root either collides to
![]() $0$
or diverges to
$0$
or diverges to
![]() $\infty $
. For otherwise,
$\infty $
. For otherwise,
![]() $\hat h$
would have degree
$\hat h$
would have degree
![]() $2$
. It follows that
$2$
. It follows that
![]() $\hat h(z)=3z/4$
or
$\hat h(z)=3z/4$
or
![]() $h(z)=2z/3$
. Thus,
$h(z)=2z/3$
. Thus,
![]() $\hat h$
has an attracting fixed point at
$\hat h$
has an attracting fixed point at
![]() $0$
and a repelling fixed point at
$0$
and a repelling fixed point at
![]() $\infty $
. Moreover,
$\infty $
. Moreover,
![]() $\mathrm {Hole}(h^j)=\mathrm {Hole}(h)\subset \{0,\infty \}$
for all
$\mathrm {Hole}(h^j)=\mathrm {Hole}(h)\subset \{0,\infty \}$
for all
![]() $j\ge 1$
. It follows that
$j\ge 1$
. It follows that
![]() $\mathcal {O}'\cap \mathrm {Hole}(h)=\emptyset $
. Then by Lemma 2.2, the set
$\mathcal {O}'\cap \mathrm {Hole}(h)=\emptyset $
. Then by Lemma 2.2, the set
![]() $\mathcal {O}'$
is a non-repelling cycle of
$\mathcal {O}'$
is a non-repelling cycle of
![]() $\hat h$
. Note
$\hat h$
. Note
![]() $1\in \mathcal {O}'$
is not a fixed point of
$1\in \mathcal {O}'$
is not a fixed point of
![]() $\hat h$
. It is a contradiction since all the periodic points of
$\hat h$
. It is a contradiction since all the periodic points of
![]() $\hat h$
are fixed points.
$\hat h$
are fixed points.
If
![]() $\deg \hat h=2$
, then
$\deg \hat h=2$
, then
![]() $\mathrm {Hole}(h)=\{0\}$
. Moreover,
$\mathrm {Hole}(h)=\{0\}$
. Moreover,
![]() $\hat h$
has an attracting fixed point at
$\hat h$
has an attracting fixed point at
![]() $0$
, a superattracting fixed point at the limit r of
$0$
, a superattracting fixed point at the limit r of
![]() $r_4^{(n)}/w_n^{(0)}$
, and a repelling fixed point at
$r_4^{(n)}/w_n^{(0)}$
, and a repelling fixed point at
![]() $\infty $
. Since
$\infty $
. Since
![]() $0\not \in \mathcal {O}'$
, then
$0\not \in \mathcal {O}'$
, then
![]() $\mathcal {O}'\cap \mathrm {Hole}(h)=\emptyset $
. By Lemma 2.2, the set
$\mathcal {O}'\cap \mathrm {Hole}(h)=\emptyset $
. By Lemma 2.2, the set
![]() $\mathcal {O}'$
is a non-repelling cycle of
$\mathcal {O}'$
is a non-repelling cycle of
![]() $\hat h$
of period at least
$\hat h$
of period at least
![]() $2$
. It follows that
$2$
. It follows that
![]() $\hat h$
has at least three non-repelling cycles: two (super)attracting fixed points
$\hat h$
has at least three non-repelling cycles: two (super)attracting fixed points
![]() $0$
and r, and one non-repelling cycle
$0$
and r, and one non-repelling cycle
![]() $\mathcal {O}'$
. It contradicts the Fatou–Shishikura inequality (see [Reference Shishikura26]) which asserts that
$\mathcal {O}'$
. It contradicts the Fatou–Shishikura inequality (see [Reference Shishikura26]) which asserts that
![]() $\hat f$
has at most two non-repelling cycles. Therefore, we have
$\hat f$
has at most two non-repelling cycles. Therefore, we have
![]() $\mathcal {O}\not =\{\infty \}$
and the conclusion follows.
$\mathcal {O}\not =\{\infty \}$
and the conclusion follows.
Now we prove statement (3). For
![]() $0\le j\le m-1$
, denote by
$0\le j\le m-1$
, denote by
![]() $U(w_n^{(j)})$
the Fatou component of
$U(w_n^{(j)})$
the Fatou component of
![]() $f_n$
containing
$f_n$
containing
![]() $w_n^{(j)}$
. Suppose in contrast that
$w_n^{(j)}$
. Suppose in contrast that
![]() $c_n\in \bigcup _{j=0}^{m-1}U(w_n^{(j)})$
. Then
$c_n\in \bigcup _{j=0}^{m-1}U(w_n^{(j)})$
. Then
![]() $c_n\in U(w_n^{(j_0)})$
for some
$c_n\in U(w_n^{(j_0)})$
for some
![]() $0\le j_0\le m-1$
. By relabeling the index, we can assume that
$0\le j_0\le m-1$
. By relabeling the index, we can assume that
![]() $j_0=0$
. If
$j_0=0$
. If
![]() $w_n^{(0)}\to \infty $
, by statement (2), there exists
$w_n^{(0)}\to \infty $
, by statement (2), there exists
![]() $1\le j\le m-1$
such that
$1\le j\le m-1$
such that
![]() $w_n^{(j)}\not \to \infty $
. It follows from Lemma 2.3 that the basin
$w_n^{(j)}\not \to \infty $
. It follows from Lemma 2.3 that the basin
![]() $U(w_n^{(j)})$
stays outside a neighborhood of
$U(w_n^{(j)})$
stays outside a neighborhood of
![]() $\infty $
for all large n. Since
$\infty $
for all large n. Since
![]() $f_n^{j}(c_n)\in U(w_n^{(j)})$
, statement (1) implies that
$f_n^{j}(c_n)\in U(w_n^{(j)})$
, statement (1) implies that
![]() $c_n\not \to \infty $
. If
$c_n\not \to \infty $
. If
![]() $w_n^{(0)}\not \to \infty $
, some
$w_n^{(0)}\not \to \infty $
, some
![]() $w_n^{(\ell )}$
with
$w_n^{(\ell )}$
with
![]() $1\le \ell \le m-1$
must converge to
$1\le \ell \le m-1$
must converge to
![]() $\infty $
since
$\infty $
since
![]() $\infty \in \mathcal {O}$
. Again by Lemma 2.3, the basin
$\infty \in \mathcal {O}$
. Again by Lemma 2.3, the basin
![]() $U(w_n^{(0)})$
stays outside a neighborhood of
$U(w_n^{(0)})$
stays outside a neighborhood of
![]() $\infty $
for all large n. Hence
$\infty $
for all large n. Hence
![]() $c_n\not \to \infty $
. It contradicts the assumption that
$c_n\not \to \infty $
. It contradicts the assumption that
![]() $c_n\to \infty $
. Hence
$c_n\to \infty $
. Hence
![]() $c_n\not \in \bigcup _{j=0}^{m-1}U(w_n^{(j)})$
.
$c_n\not \in \bigcup _{j=0}^{m-1}U(w_n^{(j)})$
.
Corollary 5.4. Let
![]() $f_n, f, c_n, \mathcal {O}_n$
, and
$f_n, f, c_n, \mathcal {O}_n$
, and
![]() $\mathcal {O}$
be as in Lemma 5.3 and let
$\mathcal {O}$
be as in Lemma 5.3 and let
![]() $\widetilde {\mathcal {H}}\subset \mathrm {NM}_4$
be the hyperbolic component containing
$\widetilde {\mathcal {H}}\subset \mathrm {NM}_4$
be the hyperbolic component containing
![]() $f_n$
s. Assume
$f_n$
s. Assume
![]() $\widetilde {\mathcal {H}}$
is of type A, B, C, or D. If
$\widetilde {\mathcal {H}}$
is of type A, B, C, or D. If
![]() $c_n$
is in the basin of
$c_n$
is in the basin of
![]() $\mathcal {O}_n$
, then
$\mathcal {O}_n$
, then
![]() $\infty \not \in \mathcal {O}$
.
$\infty \not \in \mathcal {O}$
.
Proof. If
![]() $\widetilde {\mathcal {H}}$
is of type A, B, or D, then
$\widetilde {\mathcal {H}}$
is of type A, B, or D, then
![]() $c_n$
is in the immediate basin of
$c_n$
is in the immediate basin of
![]() $\mathcal {O}_n$
. By Lemma 5.3(3), it follows that
$\mathcal {O}_n$
. By Lemma 5.3(3), it follows that
![]() $\mathcal {O}\subseteq \mathbb {C}$
. If
$\mathcal {O}\subseteq \mathbb {C}$
. If
![]() $\mathcal {H}$
is of type C, suppose
$\mathcal {H}$
is of type C, suppose
![]() $\infty \in \mathcal {O}$
. By Lemma 5.3(2), there exist periodic points
$\infty \in \mathcal {O}$
. By Lemma 5.3(2), there exist periodic points
![]() $w_n^{(i)}$
and
$w_n^{(i)}$
and
![]() $w_n^{(j)}$
in
$w_n^{(j)}$
in
![]() $\mathcal {O}_n$
such that
$\mathcal {O}_n$
such that
![]() $w_n^{(i)}\to \infty $
but
$w_n^{(i)}\to \infty $
but
![]() $w^{(j)}_n\not \to \infty $
. It follows from Lemma 2.3 that the basin
$w^{(j)}_n\not \to \infty $
. It follows from Lemma 2.3 that the basin
![]() $U(w_n^{(j)})$
stays outside a neighborhood of
$U(w_n^{(j)})$
stays outside a neighborhood of
![]() $\infty $
for all large n. Moreover, by Lemma 5.3(3), the critical point
$\infty $
for all large n. Moreover, by Lemma 5.3(3), the critical point
![]() $c_n$
is not in the immediate basin of
$c_n$
is not in the immediate basin of
![]() $\mathcal {O}_n$
. Then there exists k, independent of n, such that
$\mathcal {O}_n$
. Then there exists k, independent of n, such that
![]() $f_n^k(c_n)\in U(w_n^{(j)})$
. It contradicts Lemma 5.3(1). Hence
$f_n^k(c_n)\in U(w_n^{(j)})$
. It contradicts Lemma 5.3(1). Hence
![]() $\infty \not \in \mathcal {O}$
.
$\infty \not \in \mathcal {O}$
.
Recall from §4.3 that a quartic Newton map
![]() $f\in \mathrm {NM}_4$
is of separable type if f has two distinct immediate basins
$f\in \mathrm {NM}_4$
is of separable type if f has two distinct immediate basins
![]() $\Omega _i$
and
$\Omega _i$
and
![]() $\Omega _j$
of roots such that the corresponding internal rays
$\Omega _j$
of roots such that the corresponding internal rays
![]() $I_i(1/2)\in \Omega _i$
and
$I_i(1/2)\in \Omega _i$
and
![]() $I_j(1/2)\in \Omega _j$
land at a pole and the curve
$I_j(1/2)\in \Omega _j$
land at a pole and the curve
![]() $I_i(0)\cup I_i(1/2)\cup I_j(1/2)\cup I_j(0)$
separates the remaining poles of f. We say a hyperbolic component
$I_i(0)\cup I_i(1/2)\cup I_j(1/2)\cup I_j(0)$
separates the remaining poles of f. We say a hyperbolic component
![]() $\mathcal {H}$
of
$\mathcal {H}$
of
![]() $\mathrm {nm}_4$
is of separable type if each element in
$\mathrm {nm}_4$
is of separable type if each element in
![]() $\mathcal {H}$
is of separable type; equivalently, there is an element of separable type in
$\mathcal {H}$
is of separable type; equivalently, there is an element of separable type in
![]() $\mathcal {H}$
. Otherwise, we say
$\mathcal {H}$
. Otherwise, we say
![]() $\mathcal {H}$
is of inseparable type.
$\mathcal {H}$
is of inseparable type.
Our next key lemma asserts that a non-type-IE hyperbolic component is of inseparable type under an extra assumption on its lift.
Lemma 5.5. Let
![]() $\mathcal {H}\subset \mathrm {nm}_4$
be a non-type-IE hyperbolic component and let
$\mathcal {H}\subset \mathrm {nm}_4$
be a non-type-IE hyperbolic component and let
![]() $\widetilde {\mathcal {H}}\subset \mathrm {NM}_4$
be a lift of
$\widetilde {\mathcal {H}}\subset \mathrm {NM}_4$
be a lift of
![]() $\mathcal {H}$
. Suppose there exists a sequence
$\mathcal {H}$
. Suppose there exists a sequence
![]() $\{f_n\}\subset \widetilde {\mathcal {H}}$
such that
$\{f_n\}\subset \widetilde {\mathcal {H}}$
such that
![]() $f_n$
converges to
$f_n$
converges to
![]() $f=H_f\hat {f}\in \overline {\mathrm {NM}}_4$
with
$f=H_f\hat {f}\in \overline {\mathrm {NM}}_4$
with
![]() $\mathrm {Hole}(f)=\{\infty \}$
and
$\mathrm {Hole}(f)=\{\infty \}$
and
![]() ${\deg }(\hat {f})=3$
. Then
${\deg }(\hat {f})=3$
. Then
![]() $\mathcal {H}$
is of inseparable type. Moreover, all poles of
$\mathcal {H}$
is of inseparable type. Moreover, all poles of
![]() $\hat {f}$
are simple.
$\hat {f}$
are simple.
Proof. By the assumptions,
![]() $\hat f$
has three roots, denoted by
$\hat f$
has three roots, denoted by
![]() $r_1,r_2$
, and
$r_1,r_2$
, and
![]() $r_3$
respectively. Let
$r_3$
respectively. Let
![]() $\Omega _1,\Omega _2$
, and
$\Omega _1,\Omega _2$
, and
![]() $\Omega _3$
be the corresponding immediate basins. Moreover, since
$\Omega _3$
be the corresponding immediate basins. Moreover, since
![]() $\mathcal {H}$
is of non-type IE, the map
$\mathcal {H}$
is of non-type IE, the map
![]() $\hat f$
has a unique critical point c with
$\hat f$
has a unique critical point c with
![]() $c\not \in \bigcup _{i=1}^3\Omega _i$
. By Lemma 3.5, we have
$c\not \in \bigcup _{i=1}^3\Omega _i$
. By Lemma 3.5, we have
![]() $f_n\xrightarrow {\deg }\hat f$
on
$f_n\xrightarrow {\deg }\hat f$
on
![]() $\{\Omega _1,\Omega _2,\Omega _3\}$
. Relabeling
$\{\Omega _1,\Omega _2,\Omega _3\}$
. Relabeling
![]() $r_1$
,
$r_1$
,
![]() $r_2$
, and
$r_2$
, and
![]() $r_3$
, we may assume that there exists a pole of
$r_3$
, we may assume that there exists a pole of
![]() $\hat f$
in the intersection
$\hat f$
in the intersection
![]() $\partial \Omega _1\cap \partial \Omega _2$
. For
$\partial \Omega _1\cap \partial \Omega _2$
. For
![]() $1\le i\le 3$
, denote by
$1\le i\le 3$
, denote by
![]() $(\Omega _{i,n}, r_{i,n})$
the deformation of
$(\Omega _{i,n}, r_{i,n})$
the deformation of
![]() $(\Omega _i,r_i)$
at
$(\Omega _i,r_i)$
at
![]() $f_n$
. Then each
$f_n$
. Then each
![]() $r_{i,n}$
is a root of
$r_{i,n}$
is a root of
![]() $f_n$
and
$f_n$
and
![]() $\partial \Omega _{1,n}\cap \partial \Omega _{2,n}$
contains a pole of
$\partial \Omega _{1,n}\cap \partial \Omega _{2,n}$
contains a pole of
![]() $f_n$
. Let
$f_n$
. Let
![]() $r_{4,n}$
be the remaining root of
$r_{4,n}$
be the remaining root of
![]() $f_n$
. Then
$f_n$
. Then
![]() $r_{4,n}\to \infty $
, as
$r_{4,n}\to \infty $
, as
![]() $n\to \infty $
. Denote
$n\to \infty $
. Denote
![]() $\Omega _{4,n}$
its immediate basin.
$\Omega _{4,n}$
its immediate basin.
In contrast, we assume
![]() ${\mathcal H}$
is of separable type. Consider the internal rays in
${\mathcal H}$
is of separable type. Consider the internal rays in
![]() $\Omega _{1,n}$
and
$\Omega _{1,n}$
and
![]() $\Omega _{2,n}$
. Set
$\Omega _{2,n}$
. Set
Then each component of
![]() $\widehat {{\mathbb C}}\setminus \gamma _n(0,1/2)$
contains a pole of
$\widehat {{\mathbb C}}\setminus \gamma _n(0,1/2)$
contains a pole of
![]() $f_n$
, and hence contains
$f_n$
, and hence contains
![]() $\Omega _{3,n}$
or
$\Omega _{3,n}$
or
![]() $\Omega _{4,n}$
. We denote
$\Omega _{4,n}$
. We denote
![]() $D_n$
the one containing
$D_n$
the one containing
![]() $\Omega _{4,n}$
, and assume that
$\Omega _{4,n}$
, and assume that
![]() $I_{1,n}(\theta )\subseteq D_n$
if and only if
$I_{1,n}(\theta )\subseteq D_n$
if and only if
![]() $\theta \in (1/2,1)$
.
$\theta \in (1/2,1)$
.
Since
![]() $\Omega _{4,n}\subset D_n$
, there exists a minimal
$\Omega _{4,n}\subset D_n$
, there exists a minimal
![]() $k\geq 2$
such that the landing point
$k\geq 2$
such that the landing point
![]() $z_n$
of
$z_n$
of
![]() $I_{2,n}(1/2^k)$
is not in
$I_{2,n}(1/2^k)$
is not in
![]() $\partial \Omega _{1,n}$
. Let
$\partial \Omega _{1,n}$
. Let
![]() $\Omega _{1,n}^{(1)}$
be the component of
$\Omega _{1,n}^{(1)}$
be the component of
![]() $f_n^{-1}(\Omega _{1,n})$
such that
$f_n^{-1}(\Omega _{1,n})$
such that
![]() $z_n\in \partial \Omega _{1,n}^{(1)}$
. Then
$z_n\in \partial \Omega _{1,n}^{(1)}$
. Then
![]() $\Omega _{1,n}^{(1)}\not =\Omega _{1,n}$
and
$\Omega _{1,n}^{(1)}\not =\Omega _{1,n}$
and
![]() $\Omega _{1,n}^{(1)}\subseteq D_n$
. Note that
$\Omega _{1,n}^{(1)}\subseteq D_n$
. Note that
![]() $\Omega _{1,n}^{(1)}$
contains no critical points. For otherwise,
$\Omega _{1,n}^{(1)}$
contains no critical points. For otherwise,
![]() $\partial \Omega _{1,n}^{(1)}$
and hence
$\partial \Omega _{1,n}^{(1)}$
and hence
![]() $D_n$
would contain two poles of
$D_n$
would contain two poles of
![]() $f_n$
, which is impossible. Then
$f_n$
, which is impossible. Then
![]() $\partial \Omega _{1,n}^{(1)}$
contains a unique pole of
$\partial \Omega _{1,n}^{(1)}$
contains a unique pole of
![]() $f_n$
, which coincides with the one on
$f_n$
, which coincides with the one on
![]() $\partial \Omega _{4,n}$
. Set
$\partial \Omega _{4,n}$
. Set
![]() $I_{1,n}^{(1)}(t)$
the internal ray in
$I_{1,n}^{(1)}(t)$
the internal ray in
![]() $\Omega _{1,n}^{(1)}$
landing at
$\Omega _{1,n}^{(1)}$
landing at
![]() $z_n$
. By Proposition 3.8, the landing point
$z_n$
. By Proposition 3.8, the landing point
![]() $z_n$
of
$z_n$
of
![]() $I_{2,n}(1/2^k)$
converges to the landing point z of
$I_{2,n}(1/2^k)$
converges to the landing point z of
![]() $I_2(1/2^k)$
. Note that the pole of
$I_2(1/2^k)$
. Note that the pole of
![]() $f_n$
in
$f_n$
in
![]() $\partial \Omega _{1,n}\cap \partial \Omega _{2,n}$
(respectively
$\partial \Omega _{1,n}\cap \partial \Omega _{2,n}$
(respectively
![]() $\partial \Omega _{3,n}$
) converges to the pole of
$\partial \Omega _{3,n}$
) converges to the pole of
![]() $\hat f$
in
$\hat f$
in
![]() $\partial \Omega _1\cap \partial \Omega _2$
(respectively
$\partial \Omega _1\cap \partial \Omega _2$
(respectively
![]() $\partial \Omega _3$
). Thus, the pole of
$\partial \Omega _3$
). Thus, the pole of
![]() $f_n$
in
$f_n$
in
![]() $\partial \Omega _{4,n}\cap \partial \Omega _{1,n}^{(1)}$
converges to
$\partial \Omega _{4,n}\cap \partial \Omega _{1,n}^{(1)}$
converges to
![]() $\infty $
as
$\infty $
as
![]() $n\to \infty $
. For otherwise, these poles converge to poles of
$n\to \infty $
. For otherwise, these poles converge to poles of
![]() $\hat f$
, contradicting
$\hat f$
, contradicting
![]() $\deg \hat f =3$
. Similarly, the center of
$\deg \hat f =3$
. Similarly, the center of
![]() $\Omega _{1,n}^{(1)}$
converges to
$\Omega _{1,n}^{(1)}$
converges to
![]() $\infty $
. Then, passing to subsequences if necessary, we have that the arcs
$\infty $
. Then, passing to subsequences if necessary, we have that the arcs
![]() $I_{1,n}^{(1)}(t)$
converge to a continuum
$I_{1,n}^{(1)}(t)$
converge to a continuum
![]() $\ell $
containing
$\ell $
containing
![]() $\infty $
and
$\infty $
and
![]() ${z}$
.
${z}$
.
Recall that
![]() $\psi _{1,n}^{(1)}:\mathbb D\to \Omega _{1,n}^{(1)}$
and
$\psi _{1,n}^{(1)}:\mathbb D\to \Omega _{1,n}^{(1)}$
and
![]() $\psi _{1,n}:\mathbb D\to \Omega _{1,n}$
are the inverses of the Böttcher coordinates on
$\psi _{1,n}:\mathbb D\to \Omega _{1,n}$
are the inverses of the Böttcher coordinates on
![]() $\Omega _{1,n}^{(1)}$
and
$\Omega _{1,n}^{(1)}$
and
![]() $\Omega _{1,n}$
, respectively. Let
$\Omega _{1,n}$
, respectively. Let
![]() ${q}$
be any point in
${q}$
be any point in
![]() $\ell \setminus \{\infty \}$
. There exists
$\ell \setminus \{\infty \}$
. There exists
![]() $q_n\in I_{1,n}^{(1)}(t)$
with
$q_n\in I_{1,n}^{(1)}(t)$
with
![]() $q_n\to {q}$
. We write
$q_n\to {q}$
. We write
![]() $q_n=\psi _{1,n}^{(1)}(s_ne^{2\pi it})$
. Since
$q_n=\psi _{1,n}^{(1)}(s_ne^{2\pi it})$
. Since
![]() $q\not =\infty $
, we have
$q\not =\infty $
, we have
![]() $f_n(q_n)\to \hat {f}({q})$
. Note that
$f_n(q_n)\to \hat {f}({q})$
. Note that
Since
![]() $I_{1,n}(t)\to I_{1}(t)$
, the point
$I_{1,n}(t)\to I_{1}(t)$
, the point
![]() $\hat f({q})$
belongs to
$\hat f({q})$
belongs to
![]() $I_{1}(t)$
. We claim in fact that
$I_{1}(t)$
. We claim in fact that
![]() $\hat f({q})\in \partial \Omega _1$
. Otherwise,
$\hat f({q})\in \partial \Omega _1$
. Otherwise,
![]() ${q}$
belongs to either
${q}$
belongs to either
![]() $ \Omega _1$
or the other component
$ \Omega _1$
or the other component
![]() $\Omega _1^{(1)}$
of
$\Omega _1^{(1)}$
of
![]() $\hat {f}^{-1}( \Omega _{1})$
. Note that
$\hat {f}^{-1}( \Omega _{1})$
. Note that
![]() $\Omega _1^{(1)}\cap D_n=\emptyset $
for large n. By Lemma 2.5, we have
$\Omega _1^{(1)}\cap D_n=\emptyset $
for large n. By Lemma 2.5, we have
![]() $q_n\not \in \Omega _{1,n}^{(1)}$
. It is a contradiction. By this claim, any point in
$q_n\not \in \Omega _{1,n}^{(1)}$
. It is a contradiction. By this claim, any point in
![]() $\ell \setminus \{\infty \}$
maps under
$\ell \setminus \{\infty \}$
maps under
![]() $\hat {f}$
to the landing point of
$\hat {f}$
to the landing point of
![]() $I_1(t)$
. It is impossible. Thus,
$I_1(t)$
. It is impossible. Thus,
![]() $\mathcal {H}$
is of inseparable type.
$\mathcal {H}$
is of inseparable type.
Now we show all poles of
![]() $\hat f$
are simple. Let
$\hat f$
are simple. Let
![]() $\Theta $
be the set of angles
$\Theta $
be the set of angles
![]() $\theta $
such that
$\theta $
such that
![]() $I_{1,n}(\theta )$
and
$I_{1,n}(\theta )$
and
![]() $I_{2,n}(1-\theta )$
land at a common point. Since
$I_{2,n}(1-\theta )$
land at a common point. Since
![]() $\mathcal {H}$
is of inseparable type, by Proposition 4.5(3), there exists a periodic angle
$\mathcal {H}$
is of inseparable type, by Proposition 4.5(3), there exists a periodic angle
![]() $\theta \in \Theta \cap (0,1/2)$
. According to Proposition 3.8, the internal rays
$\theta \in \Theta \cap (0,1/2)$
. According to Proposition 3.8, the internal rays
![]() $I_{1}(\theta )$
and
$I_{1}(\theta )$
and
![]() $I_{2}(1-\theta )$
land at a common point. This implies c cannot be a pole of
$I_{2}(1-\theta )$
land at a common point. This implies c cannot be a pole of
![]() $\hat {f}$
, since otherwise c is a common point of
$\hat {f}$
, since otherwise c is a common point of
![]() $\partial \Omega _i,i=1,2,3$
, impossible.
$\partial \Omega _i,i=1,2,3$
, impossible.
5.3 Proof of Theorem 1.3
To prove Theorem 1.3, we first state the following lift result.
Lemma 5.6. For
![]() $d\ge 3$
, let
$d\ge 3$
, let
![]() $[g_n]\in \mathrm {nm}_d$
be a sequence such that
$[g_n]\in \mathrm {nm}_d$
be a sequence such that
![]() $[g_n]\to \infty $
. Then there exists a sequence
$[g_n]\to \infty $
. Then there exists a sequence
![]() $f_{n_i}\in \mathrm {NM}_d$
such that
$f_{n_i}\in \mathrm {NM}_d$
such that
![]() $[f_{n_i}]=[g_{n_i}]$
and
$[f_{n_i}]=[g_{n_i}]$
and
![]() $f_{n_i}$
converges to
$f_{n_i}$
converges to
![]() $f=H_f\hat f\in \partial \mathrm {NM}_d$
with
$f=H_f\hat f\in \partial \mathrm {NM}_d$
with
![]() $\mathrm {Hole}(f)=\{\infty \}$
and
$\mathrm {Hole}(f)=\{\infty \}$
and
![]() $\deg \hat f\ge 2$
. Moreover, if all
$\deg \hat f\ge 2$
. Moreover, if all
![]() $[g_n]$
terms are contained in a same hyperbolic component in
$[g_n]$
terms are contained in a same hyperbolic component in
![]() $\mathrm {nm}_d$
, then
$\mathrm {nm}_d$
, then
![]() $f_{n_i}$
terms are contained in the same hyperbolic component in
$f_{n_i}$
terms are contained in the same hyperbolic component in
![]() $\mathrm {NM}_d$
.
$\mathrm {NM}_d$
.
Proof. Since
![]() $[g_n]\to \infty $
, there exists a subsequence
$[g_n]\to \infty $
, there exists a subsequence
![]() $g_{n_i}$
such that
$g_{n_i}$
such that
![]() $g_{n_i}$
converges to an element in
$g_{n_i}$
converges to an element in
![]() $\partial \mathrm {NM}_d$
. We first normalize the roots of
$\partial \mathrm {NM}_d$
. We first normalize the roots of
![]() $g_{n_i}$
by affine maps to obtain a sequence
$g_{n_i}$
by affine maps to obtain a sequence
![]() $\tilde {g}_{n_i}\in \mathrm {NM}_d$
such that
$\tilde {g}_{n_i}\in \mathrm {NM}_d$
such that
![]() $0$
and
$0$
and
![]() $1$
are two roots of
$1$
are two roots of
![]() $\tilde {g}_{n_i}$
. Note
$\tilde {g}_{n_i}$
. Note
![]() $[\tilde {g}_{n_i}]=[g_{n_i}]$
. It follows that
$[\tilde {g}_{n_i}]=[g_{n_i}]$
. It follows that
![]() $[\tilde {g}_{n_i}]\to \infty $
and hence
$[\tilde {g}_{n_i}]\to \infty $
and hence
![]() $\{\tilde {g}_{n_i}\}$
contains a subsequence converging to an element in
$\{\tilde {g}_{n_i}\}$
contains a subsequence converging to an element in
![]() $\partial \mathrm {NM}_d$
. We also denote this subsequence by
$\partial \mathrm {NM}_d$
. We also denote this subsequence by
![]() $\{\tilde {g}_{n_i}\}$
. We can further assume all roots of
$\{\tilde {g}_{n_i}\}$
. We can further assume all roots of
![]() $\tilde {g}_{n_i}$
converge in
$\tilde {g}_{n_i}$
converge in
![]() $\widehat {\mathbb C}$
. Denote
$\widehat {\mathbb C}$
. Denote
![]() $r_{1,n_i},\ldots ,r_{d,n_i}$
the roots of
$r_{1,n_i},\ldots ,r_{d,n_i}$
the roots of
![]() $\tilde {g}_{n_i}$
. Choose
$\tilde {g}_{n_i}$
. Choose
![]() $1\le m_0< m_1\le d$
such that
$1\le m_0< m_1\le d$
such that
for all
![]() $1\le \ell < k\le d$
with
$1\le \ell < k\le d$
with
![]() $r_{\ell ,n_i}\not \to \infty $
and
$r_{\ell ,n_i}\not \to \infty $
and
![]() $r_{k,n_i}\not \to \infty $
, as
$r_{k,n_i}\not \to \infty $
, as
![]() $n_i\to \infty $
. Define
$n_i\to \infty $
. Define
and set
![]() $f_{n_i}:=M_{n_i}\circ \tilde g_{n_i}\circ M^{-1}_{n_i}$
. Then
$f_{n_i}:=M_{n_i}\circ \tilde g_{n_i}\circ M^{-1}_{n_i}$
. Then
![]() $f_{n_i}$
has roots at
$f_{n_i}$
has roots at
![]() $0, 1$
and no roots colliding in
$0, 1$
and no roots colliding in
![]() $\mathbb {C}$
. Then the sequence
$\mathbb {C}$
. Then the sequence
![]() $f_{n_i}$
is the desired sequence.
$f_{n_i}$
is the desired sequence.
The remaining part of the lemma follows from the connectedness of the quotient group
![]() $\mathrm {Aut}({\mathbb C})$
.
$\mathrm {Aut}({\mathbb C})$
.
Proof of Theorem 1.3
By Proposition 5.2, it suffices to show that if
![]() $\mathcal {H}\subset \mathrm {nm}_4$
is not of type IE, then
$\mathcal {H}\subset \mathrm {nm}_4$
is not of type IE, then
![]() $\mathcal {H}$
is bounded in
$\mathcal {H}$
is bounded in
![]() $\mathrm {nm}_4$
. The proof goes by contradiction.
$\mathrm {nm}_4$
. The proof goes by contradiction.
Suppose
![]() $\mathcal {H}$
is unbounded. Let
$\mathcal {H}$
is unbounded. Let
![]() $\{[f_n]\}_{n\ge 0}$
be a degenerated sequence in
$\{[f_n]\}_{n\ge 0}$
be a degenerated sequence in
![]() $\mathcal {H}$
. Passing to a subsequence, by Lemma 5.6, we can assume that all
$\mathcal {H}$
. Passing to a subsequence, by Lemma 5.6, we can assume that all
![]() $f_n$
belong to a hyperbolic component in
$f_n$
belong to a hyperbolic component in
![]() $\mathrm {NM}_4$
, and
$\mathrm {NM}_4$
, and
![]() $f_n$
converges to
$f_n$
converges to
![]() $f=H_f\hat f\in \overline {\mathrm {NM}}_4$
with
$f=H_f\hat f\in \overline {\mathrm {NM}}_4$
with
![]() $\mathrm {Hole}(f)=\{\infty \}$
and
$\mathrm {Hole}(f)=\{\infty \}$
and
![]() $\deg \hat f=2$
or
$\deg \hat f=2$
or
![]() $3$
. We deduce the contradiction case by case.
$3$
. We deduce the contradiction case by case.
Case 1:
![]() $\deg \hat f=2$
. Let
$\deg \hat f=2$
. Let
![]() $(\Omega _1,r_1)$
and
$(\Omega _1,r_1)$
and
![]() $(\Omega _2,r_2)$
be the immediate basins of roots of
$(\Omega _2,r_2)$
be the immediate basins of roots of
![]() $\hat f$
. By Lemma 3.5, we have that
$\hat f$
. By Lemma 3.5, we have that
![]() $f_n\xrightarrow {\deg }f$
on
$f_n\xrightarrow {\deg }f$
on
![]() $\{\Omega _1,\Omega _2\}$
. Denote
$\{\Omega _1,\Omega _2\}$
. Denote
![]() $(\Omega _{1,n},r_{1,n})$
and
$(\Omega _{1,n},r_{1,n})$
and
![]() $(\Omega _{2,n},r_{1,n})$
the deformations of
$(\Omega _{2,n},r_{1,n})$
the deformations of
![]() $(\Omega _1,r_1)$
and
$(\Omega _1,r_1)$
and
![]() $(\Omega _2,r_2)$
at
$(\Omega _2,r_2)$
at
![]() $f_n$
respectively. In this case, the Julia set of
$f_n$
respectively. In this case, the Julia set of
![]() $\hat f$
is
$\hat f$
is
which is a Jordan curve and contains no critical points. Given any rational angle
![]() $\theta $
, the internal rays
$\theta $
, the internal rays
![]() $I_1(\theta )$
and
$I_1(\theta )$
and
![]() $I_2(1-\theta )$
land at a common point. By Theorem 1.1, for all large n, the internal rays
$I_2(1-\theta )$
land at a common point. By Theorem 1.1, for all large n, the internal rays
![]() $I_{1,n}(\theta )$
and
$I_{1,n}(\theta )$
and
![]() $I_{2,n}(1-\theta )$
land at a common point. Since all
$I_{2,n}(1-\theta )$
land at a common point. Since all
![]() $f_n$
belong to the same hyperbolic component, we get that the internal rays
$f_n$
belong to the same hyperbolic component, we get that the internal rays
![]() $I_{1,0}(t)$
and
$I_{1,0}(t)$
and
![]() $I_{2,0}(1-t)$
of
$I_{2,0}(1-t)$
of
![]() $f_0$
land together for all
$f_0$
land together for all
![]() $t\in \mathbb Q$
. Then the boundaries
$t\in \mathbb Q$
. Then the boundaries
![]() $\partial \Omega _{1,0}$
and
$\partial \Omega _{1,0}$
and
![]() $\partial \Omega _{2,0}$
coincide. It follows that
$\partial \Omega _{2,0}$
coincide. It follows that
![]() $f_0$
is conjugate to
$f_0$
is conjugate to
![]() $z\mapsto z^2$
, which is a contradiction.
$z\mapsto z^2$
, which is a contradiction.
Case 2:
![]() $\deg \hat f=3$
. In this case,
$\deg \hat f=3$
. In this case,
![]() $\hat {f}\in \mathrm {NM}_3$
. Moreover, the unique additional critical point c of
$\hat {f}\in \mathrm {NM}_3$
. Moreover, the unique additional critical point c of
![]() $\hat f$
is not in the immediate basins of the roots of
$\hat f$
is not in the immediate basins of the roots of
![]() $\hat f$
. For otherwise,
$\hat f$
. For otherwise,
![]() $f_n$
would possess an additional critical point in the immediate basin of some root, which is a contradiction.
$f_n$
would possess an additional critical point in the immediate basin of some root, which is a contradiction.
Let
![]() $c_n$
be the additional critical point of
$c_n$
be the additional critical point of
![]() $f_n$
such that
$f_n$
such that
![]() $c_n$
converges to
$c_n$
converges to
![]() $\infty $
. Now we proceed our argument according to the type of
$\infty $
. Now we proceed our argument according to the type of
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Case 2(i):
![]() $\mathcal {H}$
is of type A,B,C, or D. Let
$\mathcal {H}$
is of type A,B,C, or D. Let
![]() $\mathcal {O}_n$
be the free (super)attracting cycle of
$\mathcal {O}_n$
be the free (super)attracting cycle of
![]() $f_n$
such that
$f_n$
such that
![]() $c_n$
is in the basin of
$c_n$
is in the basin of
![]() $\mathcal {O}_n$
. Denote by
$\mathcal {O}_n$
. Denote by
![]() $\mathcal {O}$
the limit of
$\mathcal {O}$
the limit of
![]() $\mathcal {O}_n$
. By Corollary 5.4, we have that
$\mathcal {O}_n$
. By Corollary 5.4, we have that
![]() $\mathcal {O}\subseteq {\mathbb C}$
. Then by Lemma 2.2, the set
$\mathcal {O}\subseteq {\mathbb C}$
. Then by Lemma 2.2, the set
![]() $\mathcal {O}$
is a non-repelling cycle of
$\mathcal {O}$
is a non-repelling cycle of
![]() $\hat f$
of period at least
$\hat f$
of period at least
![]() $2$
. It follows that the critical point c is not an iterated preimage of
$2$
. It follows that the critical point c is not an iterated preimage of
![]() $\infty $
under
$\infty $
under
![]() $\hat f$
. Moreover,
$\hat f$
. Moreover,
![]() $\hat f$
is post-critically finite on
$\hat f$
is post-critically finite on
![]() $\Omega _{\hat f}$
.
$\Omega _{\hat f}$
.
Consider the Newton graph
![]() $\Delta _m(\hat f)$
of
$\Delta _m(\hat f)$
of
![]() $\hat f$
at level m. Applying Proposition 4.2 to
$\hat f$
at level m. Applying Proposition 4.2 to
![]() $z=\infty $
, for a sufficiently large m, we obtain a Jordan curve
$z=\infty $
, for a sufficiently large m, we obtain a Jordan curve
![]() $\gamma \subseteq \Delta _m(\hat f)$
such that the orbit
$\gamma \subseteq \Delta _m(\hat f)$
such that the orbit
![]() $\mathcal {O}$
is contained in the bounded component of
$\mathcal {O}$
is contained in the bounded component of
![]() $\widehat {{\mathbb C}}\setminus \gamma $
. Let
$\widehat {{\mathbb C}}\setminus \gamma $
. Let
![]() ${\mathcal U}$
be the collection of components of
${\mathcal U}$
be the collection of components of
![]() $\Omega _{\hat f}$
intersecting
$\Omega _{\hat f}$
intersecting
![]() $\Delta _m(\hat f)$
. Then
$\Delta _m(\hat f)$
. Then
![]() $\hat f(U)\in {\mathcal U}$
for
$\hat f(U)\in {\mathcal U}$
for
![]() $U\in {\mathcal U}$
. By Lemma 3.5, we have that
$U\in {\mathcal U}$
. By Lemma 3.5, we have that
![]() $f_n\xrightarrow {\deg }f$
on
$f_n\xrightarrow {\deg }f$
on
![]() ${\mathcal U}$
.
${\mathcal U}$
.
Set
![]() $\delta :=d_H(\infty ,\gamma )$
. By Theorem 1.1, the curve
$\delta :=d_H(\infty ,\gamma )$
. By Theorem 1.1, the curve
![]() $\gamma $
is perturbed to a Jordan curve
$\gamma $
is perturbed to a Jordan curve
![]() $\gamma _n\subseteq \Delta _m(f_n)$
such that
$\gamma _n\subseteq \Delta _m(f_n)$
such that
![]() $\mathcal {O}_n$
is contained in the bounded component of
$\mathcal {O}_n$
is contained in the bounded component of
![]() $\widehat {{\mathbb C}}\setminus \gamma _n$
and
$\widehat {{\mathbb C}}\setminus \gamma _n$
and
![]() $d_H(\gamma _n,\gamma )<\delta /3$
for all large n. Since the immediate basin of
$d_H(\gamma _n,\gamma )<\delta /3$
for all large n. Since the immediate basin of
![]() $\mathcal {O}_n$
is disjoint with
$\mathcal {O}_n$
is disjoint with
![]() $\Delta _m(f_n)$
for all n, it is contained in the bounded component of
$\Delta _m(f_n)$
for all n, it is contained in the bounded component of
![]() $\widehat {{\mathbb C}}\setminus \gamma _n$
.
$\widehat {{\mathbb C}}\setminus \gamma _n$
.
If
![]() $\mathcal {H}$
is of type A, B, or D, then the critical point
$\mathcal {H}$
is of type A, B, or D, then the critical point
![]() $c_n$
is in the immediate basin of
$c_n$
is in the immediate basin of
![]() $\mathcal {O}_n$
. The above argument immediately implies that the distance between
$\mathcal {O}_n$
. The above argument immediately implies that the distance between
![]() $c_n$
and
$c_n$
and
![]() $\infty $
is at least
$\infty $
is at least
![]() $\delta /3$
, a contradiction to
$\delta /3$
, a contradiction to
![]() $c_n\to \infty $
.
$c_n\to \infty $
.
If
![]() $\mathcal {H}$
is of type C, since the critical point
$\mathcal {H}$
is of type C, since the critical point
![]() $c_n$
converges to
$c_n$
converges to
![]() $\infty $
, the above argument implies that
$\infty $
, the above argument implies that
![]() $c_n$
is not in the immediate basins of
$c_n$
is not in the immediate basins of
![]() $\mathcal {O}_n$
. In this case, there exists
$\mathcal {O}_n$
. In this case, there exists
![]() $k>0$
such that
$k>0$
such that
![]() $f_n^k(c_n)$
belongs to the immediate basin of
$f_n^k(c_n)$
belongs to the immediate basin of
![]() $\mathcal {O}_n$
for all n, which stays outside the
$\mathcal {O}_n$
for all n, which stays outside the
![]() $\delta /3$
neighborhood of
$\delta /3$
neighborhood of
![]() $\infty $
. It contradicts Lemma 5.3(1).
$\infty $
. It contradicts Lemma 5.3(1).
Case 2(ii):
![]() ${\mathcal H}$
is of type FE1 or FE2. First, differing from Case 2(i), the additional critical point of
${\mathcal H}$
is of type FE1 or FE2. First, differing from Case 2(i), the additional critical point of
![]() $\hat f$
may be an iterated preimage of
$\hat f$
may be an iterated preimage of
![]() $\infty $
. So the assumptions of Theorem 1.1 may fail for the Newton graphs of
$\infty $
. So the assumptions of Theorem 1.1 may fail for the Newton graphs of
![]() $\hat f$
. Alternatively, we apply Theorem 1.1 to the Jordan curve
$\hat f$
. Alternatively, we apply Theorem 1.1 to the Jordan curve
![]() ${\mathcal C}$
constructed in §4.2 in the following argument.
${\mathcal C}$
constructed in §4.2 in the following argument.
By Lemma 5.5, the additional critical point c of
![]() $\hat f$
is not a pole. We can thus use the results in §4.2. Inheriting the notation in §4.2, by Lemma 4.4, we obtain a Jordan curve
$\hat f$
is not a pole. We can thus use the results in §4.2. Inheriting the notation in §4.2, by Lemma 4.4, we obtain a Jordan curve
![]() $\mathcal {C}$
consisting of some internal rays in
$\mathcal {C}$
consisting of some internal rays in
![]() $\Omega _1, \Omega _2, \Omega _3, \Omega _1^{(2)}$
, and
$\Omega _1, \Omega _2, \Omega _3, \Omega _1^{(2)}$
, and
![]() $\Omega _2^{(2)}$
such that the orbits of the landing points of these rays are disjoint with the critical points of
$\Omega _2^{(2)}$
such that the orbits of the landing points of these rays are disjoint with the critical points of
![]() $\hat f$
and the bounded component of
$\hat f$
and the bounded component of
![]() $\widehat {{\mathbb C}}\setminus \mathcal {C}$
contains
$\widehat {{\mathbb C}}\setminus \mathcal {C}$
contains
![]() $\overline {\Omega }_1^{(1)},\overline {\Omega }_2^{(1)},\overline {\Omega }_3^{(1)},c$
, and the poles of
$\overline {\Omega }_1^{(1)},\overline {\Omega }_2^{(1)},\overline {\Omega }_3^{(1)},c$
, and the poles of
![]() $\hat f$
.
$\hat f$
.
Set
Then
![]() $\hat f(U)\in {\mathcal U}$
for
$\hat f(U)\in {\mathcal U}$
for
![]() $U\in {\mathcal U}$
. Moreover, by Lemma 3.5, we have that
$U\in {\mathcal U}$
. Moreover, by Lemma 3.5, we have that
![]() $f_n\xrightarrow {\deg }f$
on
$f_n\xrightarrow {\deg }f$
on
![]() ${\mathcal U}$
. By applying Theorem 1.1 to
${\mathcal U}$
. By applying Theorem 1.1 to
![]() $\mathcal {C}$
, for all large n, we obtain a Jordan curve
$\mathcal {C}$
, for all large n, we obtain a Jordan curve
![]() $\mathcal {C}_n$
consisting of internal rays of
$\mathcal {C}_n$
consisting of internal rays of
![]() $f_n$
in
$f_n$
in
![]() $\Omega _{1,n}\cup \Omega _{2,n}\cup \Omega _{3,n}\cup \Omega _{1,n}^{(2)}\cup \Omega _{2,n}^{(2)}$
with the same angles as those of
$\Omega _{1,n}\cup \Omega _{2,n}\cup \Omega _{3,n}\cup \Omega _{1,n}^{(2)}\cup \Omega _{2,n}^{(2)}$
with the same angles as those of
![]() $\hat f$
in
$\hat f$
in
![]() $\Omega _1\cup \Omega _2\cup \Omega _3\cup \Omega _1^{(2)}\cup \Omega _2^{(2)}$
. Then the bounded component of
$\Omega _1\cup \Omega _2\cup \Omega _3\cup \Omega _1^{(2)}\cup \Omega _2^{(2)}$
. Then the bounded component of
![]() $\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
contains
$\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
contains
![]() $\overline {\Omega }_{1,n}^{(1)}, \overline {\Omega }_{2,n}^{(1)}, \overline {\Omega }_{3,n}^{(1)}$
, two poles of
$\overline {\Omega }_{1,n}^{(1)}, \overline {\Omega }_{2,n}^{(1)}, \overline {\Omega }_{3,n}^{(1)}$
, two poles of
![]() $f_n$
, and the closures of the two preimages of
$f_n$
, and the closures of the two preimages of
![]() $\Omega _{4,n}$
disjoint with
$\Omega _{4,n}$
disjoint with
![]() $\Omega _{4,n}$
. Moreover, the unbounded component of
$\Omega _{4,n}$
. Moreover, the unbounded component of
![]() $\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
contains
$\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
contains
![]() $\overline {\Omega }_{4,n}$
.
$\overline {\Omega }_{4,n}$
.
For the additional critical point
![]() $c_n$
of
$c_n$
of
![]() $f_n$
with
$f_n$
with
![]() $c_n\to \infty $
, we claim that there exists a minimal integer
$c_n\to \infty $
, we claim that there exists a minimal integer
![]() $k\ge 1$
such that
$k\ge 1$
such that
To prove this claim, it suffices to consider the case where
![]() $f_n$
has a free (super)attracting cycle
$f_n$
has a free (super)attracting cycle
![]() $\mathcal {O}_n$
. Suppose
$\mathcal {O}_n$
. Suppose
![]() $\mathcal {O}_n$
converges to
$\mathcal {O}_n$
converges to
![]() $\mathcal {O}$
. If
$\mathcal {O}$
. If
![]() $\infty \in \mathcal {O}$
, the claim follows from Lemma 5.3(3). If
$\infty \in \mathcal {O}$
, the claim follows from Lemma 5.3(3). If
![]() $\mathcal {O}\subseteq {\mathbb C}$
, by Lemma 2.2, the set
$\mathcal {O}\subseteq {\mathbb C}$
, by Lemma 2.2, the set
![]() $\mathcal {O}$
is the non-repelling cycle of
$\mathcal {O}$
is the non-repelling cycle of
![]() $\hat f$
of period at least
$\hat f$
of period at least
![]() $2$
. It follows that
$2$
. It follows that
![]() $\hat {f}^j(c)\not =\infty $
for all
$\hat {f}^j(c)\not =\infty $
for all
![]() $j\geq 0$
. Moreover,
$j\geq 0$
. Moreover,
![]() $\hat f$
is post-critically finite in the basins of the roots. With the same argument in Case 2(i), we obtain that the immediate basin of
$\hat f$
is post-critically finite in the basins of the roots. With the same argument in Case 2(i), we obtain that the immediate basin of
![]() $\mathcal {O}_n$
is disjoint with a fixed neighborhood of
$\mathcal {O}_n$
is disjoint with a fixed neighborhood of
![]() $\infty $
. Hence the claim follows since
$\infty $
. Hence the claim follows since
![]() $c_n\to \infty $
.
$c_n\to \infty $
.
We also claim that
![]() $\partial U(f_n^i(c_n))\cap \partial \Omega _{4,n}\not =\emptyset $
for all
$\partial U(f_n^i(c_n))\cap \partial \Omega _{4,n}\not =\emptyset $
for all
![]() $0\le i\le k-1$
. By Lemma 5.3(1), for each
$0\le i\le k-1$
. By Lemma 5.3(1), for each
![]() $0\leq i\leq k-1$
and all large n, the Fatou component
$0\leq i\leq k-1$
and all large n, the Fatou component
![]() $U(f_n^i(c_n))$
containing
$U(f_n^i(c_n))$
containing
![]() $f_n^i(c_n)$
is not contained in the bounded domain of
$f_n^i(c_n)$
is not contained in the bounded domain of
![]() $\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
. Furthermore, none of these Fatou components intersect
$\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
. Furthermore, none of these Fatou components intersect
![]() $\mathcal {C}_n$
. Indeed, if
$\mathcal {C}_n$
. Indeed, if
![]() $U(f_n^i(c_n))$
intersects
$U(f_n^i(c_n))$
intersects
![]() ${\mathcal C}_n$
for some
${\mathcal C}_n$
for some
![]() $0\leq i\leq k-1$
, then
$0\leq i\leq k-1$
, then
![]() $U(f_n^i(c_n))$
coincides with either
$U(f_n^i(c_n))$
coincides with either
![]() $\Omega _{1,n}^{(2)}$
or
$\Omega _{1,n}^{(2)}$
or
![]() $\Omega _{2,n}^{(2)}$
. It then follows that
$\Omega _{2,n}^{(2)}$
. It then follows that
![]() $U(f_n^{i+1}(c_n))$
coincides with either
$U(f_n^{i+1}(c_n))$
coincides with either
![]() $\Omega _{1,n}^{(1)}$
or
$\Omega _{1,n}^{(1)}$
or
![]() $\Omega _{2,n}^{(1)}$
. Note
$\Omega _{2,n}^{(1)}$
. Note
![]() $\Omega _{1,n}^{(1)}$
and
$\Omega _{1,n}^{(1)}$
and
![]() $\Omega _{2,n}^{(1)}$
are both in the bounded component of
$\Omega _{2,n}^{(1)}$
are both in the bounded component of
![]() $\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
. It contradicts Lemma 5.3(1). Therefore, for
$\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
. It contradicts Lemma 5.3(1). Therefore, for
![]() $0\le i\le k-1$
, the component
$0\le i\le k-1$
, the component
![]() $U(f^i_n(c_n))$
is contained in the unbounded component of
$U(f^i_n(c_n))$
is contained in the unbounded component of
![]() $\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
.
$\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
.
By previous argument, the closure of any non-fixed preimage of
![]() $\Omega _{1,n}, \Omega _{2,n}, \Omega _{3,n}$
, or
$\Omega _{1,n}, \Omega _{2,n}, \Omega _{3,n}$
, or
![]() $\Omega _{4,n}$
either belongs to the bounded component of
$\Omega _{4,n}$
either belongs to the bounded component of
![]() $\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
or intersects with
$\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
or intersects with
![]() $\partial \Omega _{4,n}$
at a pole. Then
$\partial \Omega _{4,n}$
at a pole. Then
Note that
![]() $\Omega _{4,n}$
is the unique component of
$\Omega _{4,n}$
is the unique component of
![]() $f_n^{-1}(\Omega _{4,n})$
contained in the unbounded component of
$f_n^{-1}(\Omega _{4,n})$
contained in the unbounded component of
![]() $\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
. Since each
$\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
. Since each
![]() $U(f_n^i(c_n))$
is in the unbounded component of
$U(f_n^i(c_n))$
is in the unbounded component of
![]() $\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
, then for all
$\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
, then for all
![]() $0\le i\le k-1$
,
$0\le i\le k-1$
,
The claim is proved.
Moreover, we claim in fact that
![]() $k\ge 2$
. Indeed, if
$k\ge 2$
. Indeed, if
![]() $k=1$
, then the Fatou component
$k=1$
, then the Fatou component
![]() $U(c_n)$
contains two poles of
$U(c_n)$
contains two poles of
![]() $f_n$
. Note that a bounded component of
$f_n$
. Note that a bounded component of
![]() $\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
contains two poles of
$\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
contains two poles of
![]() $f_n$
and its complement contains the other pole. We then get a contradiction since
$f_n$
and its complement contains the other pole. We then get a contradiction since
![]() $U(c_n)$
is contained in the unbounded component of
$U(c_n)$
is contained in the unbounded component of
![]() $\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
.
$\widehat {{\mathbb C}}\setminus \mathcal {C}_n$
.
Note that all
![]() $f_n$
are in the same hyperbolic component, then all quantities defined for
$f_n$
are in the same hyperbolic component, then all quantities defined for
![]() $f_n$
and properties satisfied by
$f_n$
and properties satisfied by
![]() $f_n$
for n large also hold for
$f_n$
for n large also hold for
![]() $f_0$
. We deduce the contradiction by
$f_0$
. We deduce the contradiction by
![]() $f_0$
. Suppose
$f_0$
. Suppose
![]() $\partial U(f_0(c_0))$
intersects
$\partial U(f_0(c_0))$
intersects
![]() $\partial \Omega _{4,0}$
at the landing point of
$\partial \Omega _{4,0}$
at the landing point of
![]() $I_{4,0}(\theta )$
. Since
$I_{4,0}(\theta )$
. Since
![]() $U(c_0)$
contains a critical point and is contained in the unbounded component of
$U(c_0)$
contains a critical point and is contained in the unbounded component of
![]() $\widehat {{\mathbb C}}\setminus \mathcal {C}_0$
, the intersection
$\widehat {{\mathbb C}}\setminus \mathcal {C}_0$
, the intersection
![]() $\partial U(c_0)\cap \partial \Omega _{4,0}$
contains the landing points of
$\partial U(c_0)\cap \partial \Omega _{4,0}$
contains the landing points of
![]() $I_{4,0}(\theta /2)$
and
$I_{4,0}(\theta /2)$
and
![]() $I_{4,0}((1+\theta )/2)$
. We consider an arc
$I_{4,0}((1+\theta )/2)$
. We consider an arc
![]() $\gamma _1\subset \overline {U(c_0)}$
joining these two landing points and avoiding the orbits of critical points of
$\gamma _1\subset \overline {U(c_0)}$
joining these two landing points and avoiding the orbits of critical points of
![]() $f_0$
. Let
$f_0$
. Let
![]() $\gamma _2$
be the lift of
$\gamma _2$
be the lift of
![]() $\gamma _1$
based at the landing point of
$\gamma _1$
based at the landing point of
![]() $I_{4,0}(\theta /2^2)$
. Since
$I_{4,0}(\theta /2^2)$
. Since
![]() $\gamma _1$
does not intersect with
$\gamma _1$
does not intersect with
![]() $\mathcal {C}_0$
, the endpoint of
$\mathcal {C}_0$
, the endpoint of
![]() $\gamma _2$
belongs to
$\gamma _2$
belongs to
![]() $\partial \Omega _{4,0}$
. Note also that the preimages of
$\partial \Omega _{4,0}$
. Note also that the preimages of
![]() $\gamma _1(1)$
on
$\gamma _1(1)$
on
![]() $\partial \Omega _{4,0}$
are the landing points of the internal rays in
$\partial \Omega _{4,0}$
are the landing points of the internal rays in
![]() $\Omega _{4,0}$
of angles
$\Omega _{4,0}$
of angles
![]() $(1+\theta )/4$
or
$(1+\theta )/4$
or
![]() $(3+\theta )/4$
. Since
$(3+\theta )/4$
. Since
![]() $(1+\theta )/4\in (\theta /2,(1+\theta )/2)$
, it follows that the endpoint of
$(1+\theta )/4\in (\theta /2,(1+\theta )/2)$
, it follows that the endpoint of
![]() $\gamma _2$
is the landing point of
$\gamma _2$
is the landing point of
![]() $I_{4,0}((3+\theta )/4)$
.
$I_{4,0}((3+\theta )/4)$
.
Inductively, for every
![]() $m\geq 1$
, define
$m\geq 1$
, define
![]() $\gamma _{m+1}$
to be the lift of
$\gamma _{m+1}$
to be the lift of
![]() $\gamma _m$
based at the landing point of
$\gamma _m$
based at the landing point of
![]() $I_{4,0}(\theta /2^{m+1})$
. Then the endpoint of
$I_{4,0}(\theta /2^{m+1})$
. Then the endpoint of
![]() $\gamma _{m+1}$
is the landing point of
$\gamma _{m+1}$
is the landing point of
![]() $I_{4,0}(1-(1-\theta )/2^{m+1})$
. Note that for large m, each
$I_{4,0}(1-(1-\theta )/2^{m+1})$
. Note that for large m, each
![]() $\gamma _m$
is an arc joining two points of
$\gamma _m$
is an arc joining two points of
![]() $\partial \Omega _{4,0}$
in different components of
$\partial \Omega _{4,0}$
in different components of
![]() $\partial \Omega _{4,0}\setminus (I_{4,0}(0)\cup I_{4,0}(1/2))$
near
$\partial \Omega _{4,0}\setminus (I_{4,0}(0)\cup I_{4,0}(1/2))$
near
![]() $\infty $
. Moreover, the intersection of
$\infty $
. Moreover, the intersection of
![]() $\gamma _m$
and
$\gamma _m$
and
![]() $\overline {\Omega }_{1,0}\cup \overline {\Omega }_{2,0}\cup \overline {\Omega }_{3,0}\cup \overline {\Omega }_{4,0}$
is the endpoint of
$\overline {\Omega }_{1,0}\cup \overline {\Omega }_{2,0}\cup \overline {\Omega }_{3,0}\cup \overline {\Omega }_{4,0}$
is the endpoint of
![]() $\gamma _m$
. It follows that the length of
$\gamma _m$
. It follows that the length of
![]() $\gamma _m$
has a positive infinitum as
$\gamma _m$
has a positive infinitum as
![]() $m\to \infty $
. However, since
$m\to \infty $
. However, since
![]() $f_0$
is uniformly expanding near the Julia set, the length of
$f_0$
is uniformly expanding near the Julia set, the length of
![]() $\gamma _m$
decreases to
$\gamma _m$
decreases to
![]() $0$
as
$0$
as
![]() $m\to \infty $
. It is a contradiction (see Figure 6).
$m\to \infty $
. It is a contradiction (see Figure 6).

Figure 6 Sketch of the proof in Case 2(ii).
Acknowledgements
We thank Kevin Pilgrim for fruitful discussion and useful comments on an early draft. This work was discussed when Y.G. and H.N. visited the Indiana University Bloomington (IUB) in summer 2019. We are grateful to the Department of Mathematics at IUB for its hospitality. Y.G. is partially supported by NSFC grants no. 11871354, no. 12131016. We thank the referee for invaluable comments.