INTRODUCTION
A brucellosis eradication scheme commenced in Northern Ireland in 1963 and the disease was almost eradicated before recrudescence occurred in 1997 [Reference Abernethy1]. This led to a re-evaluation of the diagnostic tests through a large field trial of approximately 20 000 cattle, which were tested in parallel with six different serological tests, all of which were approved by the European Union (EU) before 2006 [Reference Abernethy2]. Bacteriological culture, the normal gold standard, was only available for a small proportion of the animals sampled in order to confirm positive results.
Tests for bovine brucellosis have been studied extensively in other countries as well, in terms of diagnostic accuracy [Reference Gall and Nielsen3] and specific aspects such as conditional dependence [Reference Mainar-Jaime4] or diagnostic equivalence [Reference Greiner, Verloo and de Massis5]. More recently, tests for brucellosis have also been evaluated using models that do not require a gold standard [Reference Muma6, Reference Sanogo7].
The latter approach uses the concept of latent class analysis (LCA) [Reference Lazarsfeld and Henry8] and addresses the problem that comparison with an imperfect gold standard invokes bias in the estimation of accuracy parameters. The principle behind this analysis is that the true disease status is latent (i.e. unknown), but can be estimated from a number of measureable items providing information about the true disease status, i.e. diagnostic test results [Reference Reboussin, Ip and Wolfson9]. The estimation of prevalence and test accuracy has become an issue of major interest over the past 20 years in both veterinary and medical disciplines [Reference Enoe, Georgiadis and Johnson10] and LCA has been recommended as the method of choice for validation of diagnostic tests in the absence of a gold standard [Reference Yang and Becker11, Reference Pepe and Janes12]. While LCA can be implemented in a frequentist framework and the model parameters can be estimated by classical inference [Reference Hui and Walter13, Reference Pouillot, Gerbier and Gardner14] it can also be implemented in a Bayesian framework where prior information about model parameters is utilized. Key assumptions of the approach, (i) different prevalences among the populations included in the model, (ii) invariance of the diagnostic performance of the tests across the populations and (iii) conditional (i.e. given the true disease status) independence of all tests, have been investigated using simulation studies [Reference Toft, Jørgensen and Højsgaard15]. However, these approaches are often limited in the level of complexity to account for the number of diagnostic tests, the number of different categories that can be observed for one test result, survey design issues (i.e. clustering of animals within herds, subgroups in the study population), and the analysis of risk factors as covariates. Features such as ability to estimate population-specific diagnostic performance and flexibility in model building implemented in the LCA procedure in SAS [Reference Collins and Lanza16] may provide new insights into the problem of diagnostic validation without a gold standard. This study describes some possibilities and limitations of employing Proc LCA in SAS [Reference Collins and Lanza16] as a LCA modelling approach for the estimation of diagnostic test accuracy. Furthermore, the application case will demonstrate the impact of sampling strategies and diagnostic test performance on prevalence estimation under natural exposure conditions.
Data from a surveillance system on bovine brucellosis gathered under natural exposure conditions in Northern Ireland serves as an exemplary dataset. Age, sex, herd type, maternal status and history of abortion are factors available from study data and known to be associated with brucellosis in cattle [Reference Stringer17, Reference Lopes, Nicolino and Haddad18]. Therefore, they are candidate predictors for the latent true infection status.
MATERIAL AND METHODS
Study population
Data were obtained from a field trial conducted in Northern Ireland between 1 January 2003 and 31 October 2004 [Reference Abernethy2]. Only results of the first test event were used in these analyses. Within the dataset, tested animals were clustered in herds.
Cattle in the study were classified by their putative exposure risk to brucellosis as described previously [Reference Abernethy2], which reflected the reason why they were tested. A ‘routine’ group comprised cattle that were tested routinely as part of the Northern Ireland surveillance system, with no anticipated increased risk of brucellosis. A ‘risk’ group was derived from animals tested due to an increased risk of exposure and subjected to more frequent testing. These herds included those contiguous to existing or previously infected herds, or with other forms of direct or indirect contact (e.g. prior movement of cattle, shared ownership or facilities). The third group (‘restricted’) consisted of cattle in herds where brucellosis had already been identified or the supervising veterinarian had reported a strong suspicion of infection [Reference Abernethy2]. As these test reasons are considered to reflect the exposure status of the cattle, they will be referred to as subgroups in the study population throughout this paper.
Diagnostic tests
The six serological tests applied to the study samples were the complement fixation test (CFT), competitive ELISA (cELISA), serum agglutination test [SAT (31 IU)], SAT with EDTA [ethylenediaminetetraacetic acid; EDTA (31 IU)] as an addition to improve specificity, indirect ELISA (iELISA) and Rose Bengal test (RBT). The screening threshold selected for the SAT and EDTA test results was 31 IU as defined by EU legislation [19]. The CFT, SAT, EDTA, iELISA and RBT are standard tests in the EU and approved for intra-community trade testing. The cELISA is a complementary test and not approved for intra-community trade testing [19, 20]. All test outcomes were recorded as dichotomous.
In the context of LCA, the indicators are the underlying observed variables from which the latent information is derived. In the study presented here, the observed classification is based on the diagnostic test results per animal. Assuming that the indicators are dichotomous (R
j
= 2; positive, negative), a response pattern Y with
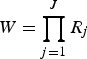 $W = \prod _{j = 1}^J R_j $
combinations of J indicators (j = 1–64) can be expected.
$W = \prod _{j = 1}^J R_j $
combinations of J indicators (j = 1–64) can be expected.
LCA modelling
According to the latent class approach, the true infection status in relation to the model parameters (prevalence, diagnostic sensitivity and specificity) is an abstract construction and not subject to a case definition fixed by the investigator (see causal graph in Fig. 1). In the context of our study data, the infection status should be interpreted as current or recent exposure to Brucella abortus. Proc LCA in SAS v. 9.3 was used for the LCA and its extension of multinomial regression was applied to assess the influence of covariates on the prevalence status (γ estimate) regardless of the number of (latent) classes of this outcome variable [Reference Lanza21–23]. Thus, a ‘class’ in this context refers to the latent, unobserved expression of the infection status being positive or negative. Furthermore, the unknown diagnostic sensitivity and specificity for all six tests was estimated (ρ estimates). Prevalence and test accuracy were estimated using maximum likelihood (ML). Structured lack of independence, caused by clustering of animals in herds, was accounted for by choosing the herd identification as the cluster variable. For models with clustering, robust standard errors (s.e.) were calculated based on Taylor linearization [Reference Lanza24].

Fig. 1. Causal diagram for conceptualization of latent class analysis with covariates for bovine Brucella abortus infection prevalence estimated using observed diagnostic test outcomes.
All models were fitted using the default maximum number of 5000 iterations and the default maximum absolute deviation of 0.000 001. In order to assess model identification, 10 sets of random starting values for the γ and ρ estimates were generated by specifying a positive integer value in the so-called SEED statement. An identical seed was used in order to make analysis exactly reproducible. Furthermore, it was ascertained if these starting values consistently converge to the same solution. Data-derived flattening priors were invoked in order to enable model identification and to stabilize the estimation of models in case of sparseness issues [Reference Collins and Lanza16, Reference Clogg25]. For the model selection, only those models were considered where a ML solution was identified with 10 randomly selected starting values and all of them were associated with the best-fit model. In those cases, all sets of starting values yielded identical results for the G 2 likelihood ratio test statistic. The seed selected for the best model fit was used for subsequent analyses (i.e. with covariates) in order to provide a standard set of starting values. When evaluating a latent class model the principles of parsimony, interpretability as well as statistical criteria were considered.
Model diagnostics
Despite the fact that the optimal number of latent classes is two (based on the biological principle of an animal either being infected or not infected), sensitivity analyses were conducted for bias or confounding, and model fit was assessed.
The optimal number of latent classes was achieved by comparing alternative models using convergence and goodness-of-fit criteria. Furthermore, G 2 statistics and their P values (significance level of 0·05) were regarded as meaningful only for models where the degrees of freedom were <60 [Reference Collins and Lanza16] and where sparseness was not an issue. P values for the G 2 statistic were derived from a comparison with a χ 2 distribution with the corresponding degrees of freedom. As G 2 statistics are only a rough method for comparing model fit, Akaike's Information Criterion (AIC) and Bayesian Information Criterion (BIC) were also considered, with the smallest values indicating the best model fit. Using these criteria, models with 1–6 latent classes were compared.
To assess the impact of conditional dependence the model selection process and the values of the test accuracy estimates were checked and the symmetry of pairwise test results was analysed using the posterior probabilities of the model to assign latent class membership (threshold ⩾70% concordant tuples) and calculate the kappa coefficient (threshold ⩾0·61).
In order to assess whether test accuracy parameters (sensitivity, specificity) were constant across the (sub-)groups of the study population, this so-called ‘measurement invariance’ was investigated by comparing a stratified, unrestricted and a stratified, restricted model. Both models were stratified by the exposure status of the animals. In the unrestricted model the test accuracy parameters were allowed to vary across groups, whereas in the restricted model the test accuracy parameters were constrained to be equal across groups. G 2 statistic model fit criteria and item-response probabilities were used to compare the model alternatives. Measurement invariance was assumed if the criteria favoured the restricted model, because this implies that the imposed restrictions are plausible. To this end, a likelihood-ratio difference test was conducted [Reference Collins and Lanza16].
Covariates
LCA covariates were also assessed as to whether and to what degree they predicted the subgroup-specific prevalences. The conceptual relationship between the latent variable and the observed indicator(s) as well as predictors is shown as a causal diagram (Fig. 1). The dichotomous candidate predictors, sex (male, female) and abortion (post-abortion, no abortion/not applicable), were derived from information about reproductive status. The herd type was classified as dairy or non-dairy; non-dairy herds consisted mainly of beef-cow herds, which are the predominant herd type in Northern Ireland, and a range of other types, including weaning, rearing and finishing herds. Non-dairy and mixed herds were combined, because the group of mixed herds was relatively small (n = 47 herds, 11·19%) and for all of these herds the type is not easily discerned. Dairy herds form a minority of herds in Northern Ireland (~15%); they are associated with increased risk of certain diseases and are readily identified by the breed of female cattle held. The age at the time of testing was available in years. In order to facilitate a basic analysis of covariates all qualitative exposure variables were dichotomized prior to analysis. Furthermore, the numeric variable age was dichotomized by the mean of its distribution in the overall study population. This was necessary, because there was no linear relationship between age and latent classification [Reference Dohoo, Martin and Stryhn26].
The study population was analysed according to the exposure risk of the herds (routine/risk/restricted), with one model per subgroup. If the pairwise cross-tabulation of covariates and a Cramer's V ⩾0·7 indicated considerable correlation between two covariates, only one of these variables was considered for multivariable modelling to avoid the effects of collinearity.
A logistic regression model was applied with two latent classes to be estimated, where non-infected cattle was the reference latent class.
A non-automated forward selection of the four covariates and their interactions was conducted comparing the model fit of two models by means of a likelihood ratio χ 2 test (significance level: P < 0·05). Interaction was considered and added to the model by calculating a product variable of the two respective covariates. Exposure variables with P⩽0·05 in the Type III test of the regression analysis were considered to significantly affect the odds of latent class membership. Only results of the final model are reported here.
RESULTS
Based on samples and information acquired for more than 1 year for 19 517 animals from 420 herds, the true prevalence of brucellosis in Northern Ireland was calculated simultaneously with test accuracy estimates for the six applied serological tests. Data of 418 further animals was not sufficiently complete for the purpose of this analysis. The observed prevalence per serological test varied between 0·61% and 3·73% (Table 1).
Table 1. Observed absolute number (n) and prevalence (%) of animals testing positive for each serological test. The study population is stratified by exposure groups, where cattle were routinely sampled, sampled due to previous risk or sampled due to known or strong suspicion of infection of the herd

CFT, Complement fixation test; IU, international units; RBT, Rose Bengal test; SAT, serum agglutination test.
The distribution of herds with regard to herd type was 28·81% (n = 121), 60·00% (n = 252) and 11·19% (n = 47) for dairy, non-dairy and mixed herds, respectively. The number of sampled animals per herd was skewed and varied between 1 and 424 [median 22, mean 46·47, interquartile range (IQR) 2·0–68·5, s.d. = 62·67]. Most (88%) of the animals were tested for the first time between December 2003 and August 2004. The age of the cattle ranged from 3 months to 19 years (median 3·5 years, mean 4·34, IQR 1·92–6·17, s.d. = 2·98). Most of the animals were female (bulls 1·77%, n = 346) and adult (heifers 27·73%, n = 5412). The percentages of tested animals belonging to the routine, risk and restricted group of herds were 26·04% (n = 5082), 32·03% (n = 6251) and 41·93% (n = 8184), respectively.
Model diagnostics
When assessing the optimal number of latent classes for the pooled sample with all exposure groups, no model fitted the data sufficiently well (G 2 P < 0·0001, see Table 2). However, AIC and BIC indicated a three-latent-class solution. As no meaningful categorization could be assigned to these three classes based on the input data, it was concluded that confounding might be an issue and stratification might improve the model fit. Stratification was conducted for the exposure status, as the most probable confounder, because it reflected on the heterogeneity of sampling schemes applied to gather study data. Stratification indicated that even fewer models converged and identified the ML solution under the given conditions. For these models, the likelihood ratio G 2 statistic could not be conducted due to the high number of degrees of freedom. Hence, the criteria for relative model fit were considered indicating that a two-latent-class solution would be favourable.
Table 2. Optimal number of latent classes for six serological tests (with a cut-off of 31 IU for SAT and EDTA) (N/W = 304·95)

AIC, Akaike's Information Criterion; BIC, Bayesian Information Criterion; d.f., degrees of freedom; G 2, likelihood ratio test statistic; LL, log likelihood; NC, model did not converge in 5000 iterations; N/W, sparseness; sample size/size of the contingency table; P G2, P value to the G 2 statistic derived from a χ 2 distribution considering the d.f., if P⩾0·05 then, by conventional criteria, this difference is considered not to be statistically significant; SAT, serum agglutination test.
* d.f. <60 allows for trust in G 2 statistic.
† Indicates certainty of class assignment to individuals in subsequent analysis.
‡ P values not reported due to the magnitude of degrees of freedom.
§ Seed selected for best-fit model: 1 444 942 552.
As the test accuracy estimates were close to 1 and the favoured model had only two latent classes, the possible impact of conditional dependence can be considered low. Additionally, in the infected group most pairwise comparisons of test results had <70% concordant tuples. In the uninfected group ⩾97% of the test results were concordant in the pairwise comparison. Kappa coefficients were >0·61 in four out of 15 test comparisons, only. As a difference between the stratified, unrestricted model and the stratified, restricted model, was identified (G 2 Δ = 129·97, d.f. = 24, P < 0·0001) and the criteria of relative model fit favoured the unrestricted model, the assumption of measurement invariance was dropped. Therefore, it can be concluded that sensitivity and specificity vary between the exposure groups in the study population. Hence, the best-fit model would account for the three exposure status subsamples, separately, and have two latent classes, each.
Latent prevalence and diagnostic test accuracy
The estimated sensitivities and specificities along with prevalences, positive and negative predictive values are summarized in Table 3. The calculated prevalence for the routinely tested animals [0·0104, 95% confidence interval (CI) 0·0078–0·0136] was lower than the prevalence of the other two subgroups [0·019 (95% CI 0·0158–0·0227), and 0·0217 (95% CI 0·0187–0·0251), for risk and restricted subgroups, respectively].
Table 3. Class membership probabilities (gamma; within-group latent prevalences) and item response probabilities (rho; latent sensitivities and specificities) for a two-latent-class model on Brucella abortus infections in Northern Ireland cattle – with the positive and negative predictive values (standard error is shown in parentheses)

CFT, Complement fixation test; IU, international units; RBT, Rose Bengal test; SAT, serum agglutination test.
For all exposure groups the EDTA (31 IU) and the SAT (31 IU) tests showed the highest sensitivities (0·84–0·93, and 0·95–0·98, respectively). The sensitivity of the tests varied among the exposure groups, where best results were achieved for cattle in the restricted subgroup. However, for the test with the highest estimated sensitivity [SAT (31 IU)], the probability of test-positive animals being true positives was 50–57% given the estimated prevalence for each of the study subgroups; whereas the highest positive predictive values could be found for the CFT and the EDTA (31 IU) tests (0·98–1·00, and 0·99–1·00, respectively). This is due to the fact that the positive predictive value is a function not only of the prevalence and the sensitivity but also of the specificity, which was lower in SAT (31 IU) than in the CFT and the EDTA (31 IU) tests.
Regardless of the exposure group the CFT, EDTA (31 IU) and the RBT tests had the highest specificities (0·9998–1·00, 0·9998–1·00, and 0·9993–0·9995, respectively). The specificity of tests varied between the exposure groups, where best results were achieved for routinely tested cattle. The negative predictive values did not vary considerably, neither among tests nor among study subgroups (0·99–1·00).
Covariates
As Cramer's V was <0·7 for all pairwise combinations of covariates in all three study subgroups, all covariates were considered appropriate for multivariable modelling. However, in the contingency tables for the association between sex and abortion as well as between age and abortion empty cells were apparent, which is plausible as bulls or maiden heifers could not have an abortion. After the forward selection process of multivariable modelling the best-fit final model identified three covariates for a latent infection with brucellosis: age, dairy status and abortion (see Table 4). Models with interaction terms either showed non-identification of the models or a worse model fit than the models without interaction.
Table 4. Predictors of latent class infection status tested against the reference latent class ‘non-infected’ identified after forward selection in the final multivariable model

CI, Confidence interval.
P, Value of the Type III beta parameter test.
Cattle aged >4·34 years were 1·41 times (restricted group) to 2·53 times (routine group) more likely to be infected than younger cattle; a finding that was statistically significant only in the risk group (P = 0·0426, see Table 4). Being kept on a dairy farm decreased the probability of being infected significantly in the routinely tested [odds ratio (OR) 0·13] and restricted (OR 0·38) groups. Cattle tested due to an abortion were significantly associated with latent class membership in all exposure groups (OR 3·3–41·3, see Table 4).
The distribution of infected and uninfected cattle over the combined covariates abortion, dairy status, sex and age was assessed. The most animals considered infected were non-dairy female cattle without abortion, irrespective of age or exposure group (routine: n = 42, 77·8%; risk: n = 77, 64·7%; restricted: n = 136, 75·6%).
DISCUSSION
The objective of this study was to estimate diagnostic accuracy in the absence of a gold standard while simultaneously calculating the true prevalence given a high number of different diagnostic tests, clustering, stratification and risk factors.
LCA modelling
Diagnostic test performance and true prevalence are best calculated using LCA. It is common knowledge that the degree to which the observed (apparent) prevalence differs from the true prevalence depends on the accuracy (sensitivity, specificity) of the diagnostic tests used. However, when calculating the true prevalence, sensitivity and specificity estimates can only be derived from previous test evaluation studies and these studies are often conducted in different populations (e.g. age structure, breed), regions or in different laboratories [Reference Greiner and Gardner27]. Therefore, all-in-one solutions like latent class models are preferable, where the true prevalence can be assessed along with test accuracy under the given field conditions [Reference Enoe, Georgiadis and Johnson10]. As the estimation of latent disease status becomes more precise the higher the number of diagnostic tests [Reference Hadgu, Dendukuri and Hilden28]; six tests, employed under field conditions in Northern Ireland, were incorporated in the study presented here.
Proc LCA is a suitable tool to conduct test accuracy estimations in the future. Although latent class modelling is a well-known method of assessing diagnostic test accuracy and true prevalence [Reference Dohoo, Martin and Stryhn26], it has rarely been conducted using Proc LCA in SAS [Reference Collins and Lanza16, Reference Koukounari29, Reference Busch30]. However, this tool provides several advantages while yielding the same point and interval estimates and model fit compared to commonly used software tools such as TAGS [Reference Pouillot, Gerbier and Gardner14]. It is not restricted to two latent classes, a maximum number of diagnostic tests or observed two-level diagnostic test results. It also includes an extension to regression modelling in order to investigate covariates and accounts for clustering of animals within herds. In other frameworks, within-herd dependencies are addressed using random effects, while Proc LCA adjusts standard errors in a pseudo-likelihood approach [Reference Lanza21]. However, one of the most interesting features is the possibility of stratifying the study population and calculating strata-specific prevalence and test accuracy estimates, which enabled the exposure status-specific estimates presented here. All options can be readily included, without the need for advanced programming skills.
Covariance cannot be directly accounted for in Proc LCA. However, for test evaluation studies it might be desirable that the covariance structure between the diagnostic test results are verifiable. Ignoring the conditional dependence between tests in such studies may yield a simplified and biased overestimation of the diagnostic accuracy parameters and true prevalence [Reference Reboussin, Ip and Wolfson9, Reference Hadgu, Dendukuri and Hilden28]. This applies especially in cases where the same biological principle is inherent in all tests as in this case, where all tests are based on detection of antibodies for the diagnosis of B. abortus infection. Therefore, conditional dependence or covariance, respectively, was taken into account [Reference Gardner31]. However, as we did not conduct a test evaluation study per se and, therefore, could not resort to the true disease status in this study [Reference Gardner31, Reference Hanson, Johnson and Gardner32], we considered external information about covariance [Reference Mainar-Jaime4] to introduce more rather than less bias due to different study conditions, i.e. target population, region [Reference Greiner and Gardner27]. Furthermore, accounting for covariance parameters of six diagnostic tests would have yielded a high total amount of parameters to be estimated in the model. Therefore, conditional dependence was assessed based on model estimates and model fit. The fact that test accuracy estimates were close to 1, the optimal latent class model corresponded with what was biologically expected (two classes) and the pairwise concordance between tests was lower than threshold, suggests that the model estimates are not relevantly biased by conditional dependence.
Stratification of the study population was deemed inevitable from a contextual and statistical point of view. As three different sampling strategies (reflecting different exposure status of cattle) were applied when gathering the study data, a pooled model seemed to be an inappropriate representative for the composition of the study population. When applying stratified modelling the violated measurement invariance [Reference Millsap and Kwok33] indicated a structured sample [Reference Collins and Lanza16], where the grouping variable is associated with the realized test accuracy and prevalence estimates. Considering the sampling strategy, it is understandable that the model estimates (prevalence, sensitivity, specificity) vary between the population subgroups. Hence, analyses had to be performed for each of the three (exposure) subgroups, separately [Reference Lanza24].
Latent prevalence and diagnostic test accuracy
Comparison of the sensitivity and specificity estimates of this study with previous publications is hindered as we did not use bacterial culture as a gold standard and calculated exposure group-specific test performances. Nevertheless, the results of this study can be considered more reliable and meaningful for brucellosis surveillance than foreign or previous estimations. Estimating test accuracy in the absence of a gold standard by means of LCA is well known [Reference Enoe, Georgiadis and Johnson10, Reference Hui and Walter13, Reference Pouillot, Gerbier and Gardner14], less expensive and faster than using culture diagnostic as the gold standard test. Nevertheless, the sensitivity and specificity estimates in this study varied (in some cases greatly) from estimates published in previous reviews of test performance [Reference Greiner, Verloo and de Massis5, Reference Gall and Nielsen34]. Furthermore, the analysis presented here was exposure group-specific; whereas calculation of diagnostic accuracy measures across all groups is biased. Nevertheless, the sensitivity and specificity estimates obtained in this study were largely in accordance with the estimates of Abernethy et al. [Reference Abernethy2], where the same data were analysed using more traditional methods. In both analyses the SAT (31 IU) yielded the best sensitivity estimates of all tests and both analytical approaches indicated that screening tests [SAT (and EDTA)] compared favourably with the other test systems with regards to sensitivity. Specificity in both analytical approaches was almost 100% for most tests (see table 7 in [Reference Abernethy2] and Table 3 of the present study). Comparing both approaches, the one presented here provides prevalence and test accuracy estimates based on all diagnostic tests together, without the need for bacterial culture or a reference panel. This is particularly important where bacteriological culture is not available. For example, in the trial that provided this dataset, only test-positive cattle were slaughtered, and a negative result was based on concordance of multiple tests in a panel. In many other studies, especially where funding is constrained, testing is restricted to few tests and often without slaughter or laboratory follow-up. Accordingly, the methods described here are less expensive (as slaughter is not a prerequisite), easier to apply and more precise. Furthermore, by considering the low prevalence in Northern Ireland when calculating predictive values, the results of our study (especially those of the sensitivity estimates) appear to be more qualified and are largely in accordance with the predictive values that can be calculated from other authors for RBT and cELISA [Reference Muma6]. As the sampling strategy of a surveillance programme influences the estimated prevalence and test performance, this should be considered in future disease control programmes. In the study presented here (latent) prevalences ranging from 1·04% to 2·17% agreed with a cohort study on risk associated with brucellosis in Northern Ireland (prevalence 1·28% [Reference Stringer17]). Furthermore, it could be shown that the more risk-based the sampling the higher the prevalence, because then the probability of finding seropositive reactors increases [Reference Hoinville35]. On the one hand, the impact a more risk-based sampling has on the prevalence is a desired effect and corresponds with requirements of the final eradication stage of brucellosis [Reference Adone and Pasquali36]. On the other hand, our results indicate that the sampling strategy not only impacts on the prevalence but also on test accuracy estimates. This applies not only on B. abortus surveillance but also to other infectious diseases and should be accounted for more thoroughly in the future when calculating the true prevalence. Therefore, we propose exposure group-specific testing strategies to optimize the diagnosis of infectious diseases within surveillance programmes.
Surveillance programmes should be adapted regarding the choice of diagnostic tests according to the intended purpose of use and the eradication stage (‘fitness for purpose’ [37]). As bovine brucellosis prevalence declines worldwide, future surveillance programmes need to contemplate the considerable reduction in positive predictive value offered by serological tests, meaning that tests adequate for an overall prevalence reduction might not be that adequate in later eradication stages (i.e. ELISA test systems). Hence, in a country with a low prevalence in the final eradication stage, it might be advisable to select a test system with a high positive predictive value from an economic point of view. This is to assure that the animals tested positively actually have the disease when being culled. On the other hand, it could have significant financial consequences missing an infected animal, which may outweigh any testing costs. Therefore, an inexpensive screening test with a low probability for animals tested negatively being diseased (i.e. high negative predictive value) might be well complemented by a follow up of animals that test positive using a test with a high positive predictive value. The importance of the negative predictive value from a disease control (and food safety) point of view has been elaborated elsewhere [20]. In this context the EDTA or CFT tests fit the requirements as they even have a high specificity under field conditions [Reference Abernethy38].
Covariates
A logistic regression model was used to predict the latent class membership (i.e. being infected). An advantage of including covariate analysis in a LCA over individual classification or scoring is that this allows uncertainty of the classification to be taken into consideration even in covariate analyses [Reference Collins and Lanza16].
The study results indicated that sex did not contribute significantly more to the prediction of the latent class membership as compared to the baseline model, which can be related to the biological assumption that the probability of being infected is not affected by sex. Previous findings of differences between sexes in Northern Ireland might reflect age differences as well as different susceptibilities due to performance stress [Reference Abernethy38]. The age-related increasing probability of infection is in agreement with the biological principle of an increasing probability of being exposed to the infectious agent the older one becomes [Reference Stringer17].
The herd type seems to impact the probability of infection in the way that cattle on dairy farms are less likely to be infected than cattle on other (or mixed) farms. This effect, being most obvious in routinely tested cattle, might be attributable to a higher level of between-herd movement [Reference Christie39] or lower herd sizes in the non-dairy and mixed farms, but should be investigated in the future in more detail.
No distinction was made between the categories ‘no abortion’ and ‘not applicable’ as one was wholly dependent on owner information for pregnancy/abortion status for older heifers or cows for tests other than those triggered by a reported abortion. This might have biased the results. Nevertheless, the impact of having an abortion on the prediction of latent class membership is obvious and can be clearly attributed to abortion being the main clinical presentation of B. abortus infection and the highly infectious nature of an abortion episode [Reference Aparicio40].
CONCLUSION
Bovine brucellosis has been controlled in Northern Ireland since 1963. After virtual eradication recrudescence occurred in 1997. Based on surveillance data this paper set out to simultaneously estimate diagnostic test accuracy parameters in the absence of a gold standard and the true prevalence, while using a high number of different diagnostic tests and accounting for aspects such as clustering, stratification and the influences of covariates.
Considering the above-mentioned prerequisites and the fact that diagnostic test performance and true prevalence are calculated most properly using LCA, Proc LCA in SAS is a suitable tool to conduct test accuracy estimations in the future.
The estimated prevalence of B. abortus in Northern Ireland was low across all exposure groups. Our estimates of risk factors adjusted for misclassification suggest that cattle from non-dairy/mixed farms and post-abortion cows are rational targets for disease control measures under the given epidemiological circumstances. Regarding the serological surveillance of B. abortus, the EDTA or CFT tests could be chosen as they have a high specificity under field conditions.
Test performances of the six investigated diagnostic tests varied depending of the sampling strategy of the surveillance system. This applies not only on B. abortus surveillance but also on other infectious diseases and should be accounted for more thoroughly in the future. Therefore, we propose exposure group-specific testing strategies to optimize the diagnosis of infectious diseases within surveillance programmes.
Furthermore, surveillance programmes should be adapted regarding the choice of diagnostic tests according to the intended purpose of use and the eradication stage. Therefore, countries, with a low prevalence in the final eradication stage, may opt for a test system with high predictive values in order to avoid costs from culling uninfected animals or from missing diseased animals.
ACKNOWLEDGEMENTS
The authors thank Dr Aaron Wagner (Methodology Center, Pennsylvania State University, USA) for his useful comments and for answering questions concerning PROC LCA in SAS; and Sonja Hartnack (Veterinary Epidemiology Group, Vetsuisse Faculty University of Zurich, Switzerland) for her support concerning the conceptional planning of analyses.
DECLARATION OF INTEREST
None.







