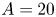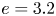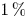1 Introduction
In recent years, the W7-X experiment has demonstrated that intricately optimised stellarators can be successfully built and operated (Pedersen et al. Reference Pedersen, König, Krychowiak, Jakubowski, Baldzuhn, Bozhenkov, Fuchert, Langenberg, Niemann and Zhang2018; Beidler et al. Reference Beidler, Smith, Alonso, Andreeva, Baldzuhn, Beurskens, Borchardt, Bozhenkov, Brunner and Damm2021). Stellarators have attractive qualities, such as little net toroidal current and capacity for steady-state operation, that make them suitable for reactors. However, unlike in tokamaks, confinement is not inherently good due to the three-dimensional geometry of the magnetic field. Stellarator magnetic fields need to be designed carefully to ensure neoclassical transport is sufficiently low. A sufficient condition for good orbit confinement in a stellarator is that of omnigenity,
where $\boldsymbol {v}_{d}$![]() is the total drift, and the integration is done over the bounce time of a trapped particle. Magnetohydrodynamic (MHD) equilibria for which trapped particle motion fulfils (1.1) have collisionless orbits that are radially confined. A subset of omnigenous magnetic fields are those that satisfy quasi-symmetry, in which the strength of the magnetic field is symmetric (axially, helically or poloidally) in magnetic coordinates. An example of omnigenous fields that are not quasi-symmetric are those called quasi-isodynamic (QI), which have poloidally closed contours of the magnetic field strength, as well as vanishing bootstrap currents at low collisionality (Helander & Nührenberg Reference Helander and Nührenberg2009; Helander Reference Helander2014). The present work concerns this class of stellarators.
is the total drift, and the integration is done over the bounce time of a trapped particle. Magnetohydrodynamic (MHD) equilibria for which trapped particle motion fulfils (1.1) have collisionless orbits that are radially confined. A subset of omnigenous magnetic fields are those that satisfy quasi-symmetry, in which the strength of the magnetic field is symmetric (axially, helically or poloidally) in magnetic coordinates. An example of omnigenous fields that are not quasi-symmetric are those called quasi-isodynamic (QI), which have poloidally closed contours of the magnetic field strength, as well as vanishing bootstrap currents at low collisionality (Helander & Nührenberg Reference Helander and Nührenberg2009; Helander Reference Helander2014). The present work concerns this class of stellarators.
Identification of good configurations, e.g. those with low neoclassical transport and easily buildable coils, is traditionally done through a two-step optimisation procedure. In the first step, a plasma boundary is deformed and the physical properties of the resulting equilibrium are assessed using various codes until the desired plasma properties have been found. Then, in a second optimisation process, coils that reproduce the desired plasma boundary are sought.Footnote 1 The equilibrium optimisation procedure requires the use of computationally expensive codes in each step and an initial plasma boundary to be prescribed (Henneberg et al. Reference Henneberg, Hudson, Pfefferlé and Helander2021b). Such optimisation procedures generally identify local minima (Henneberg, Helander & Drevlak Reference Henneberg, Helander and Drevlak2021a), and it is therefore possible that other, lower, minima may be found elsewhere in the parameter space. In addition, QI optimisation often results in highly shaped plasma boundaries. In order to generate such plasma shapes, complicated coils may be necessary, which are difficult and expensive to build. It is not clear whether this complexity is inherent to particular QI equilibria or if it may be overcome by a more exhaustive or differently initialised search of parameter space. The near-axis approach, pursued here, has the potential to do just this.
This method, first introduced by Garren & Boozer (Reference Garren and Boozer1991) and revitalised by Landreman & Sengupta (Reference Landreman and Sengupta2018) and Landreman, Sengupta & Plunk (Reference Landreman, Sengupta and Plunk2019), allows the construction of omnigenous solutions of the MHD equations at first order in the distance from the axis, using Boozer coordinates. Starting with an axis shape and a set of functions of the toroidal angle, this near-axis expansion (NAE) allows the systematic and efficient construction of plasma boundaries corresponding to omnigenous equilibria. Different procedures apply for the case of QI and for quasi-symmetry, with the latter described in Landreman et al. (Reference Landreman, Sengupta and Plunk2019) and used successfully combined with an optimisation procedure in Giuliani et al. (Reference Giuliani, Wechsung, Cerfon, Stadler and Landreman2022). The case of quasi-isodynamicity was first discussed by Plunk, Landreman & Helander (Reference Plunk, Landreman and Helander2019) and is described in greater detail in § 2.
In § 3 we derive all the constraints on the input functions for the case of a stellarator-symmetric, single-magnetic-wellFootnote 2 solution with multiple field periods. We then proceed to find expressions for the geometric functions required as input for the near-axis construction and show that, for this particular case, the number of free parameters is reduced.
Exactly omnigenous fields are necessarily non-analytic as shown by Cary & Shasharina (Reference Cary and Shasharina1997). Hence, omnigenity must necessarily be broken to achieve analytical solutions. In the NAE we do this in a controlled way, through the careful definition of one of the geometrical input functions, $\alpha (\varphi )$![]() . A new way to express this function, more smoothly than done previously by Plunk et al. (Reference Plunk, Landreman and Helander2019), is proposed in § 4.
. A new way to express this function, more smoothly than done previously by Plunk et al. (Reference Plunk, Landreman and Helander2019), is proposed in § 4.
Very recently, single-field-period QI configurations with excellent confinement properties have been found by optimising within the space of these NAE solutions in Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho and Helander2022). Configurations with more field periods have proved challenging to find, even when using the optimiser.
To investigate the causes of this difficulty, we analyse possible choices of the magnetic axis shape. In contrast to traditional optimisation, where a plasma boundary is the starting point and a magnetic axis has to be found as part of the equilibrium calculation, the NAE requires the magnetic axis shape as input. In § 5 we discuss the freedom in the shape of the axis and its mathematical description. We shed some light on the difficulties associated with finding closed curves compatible with the NAE, specifically the need to find closed curves with points of zero curvature at prescribed locations, as well as the role curvature and torsion play on the quality of the approximation. We then describe a method for generating stellarator-symmetric axis shapes with points of zero curvature and torsion at prescribed orders.
A common problem encountered when constructing NAE solutions is the tendency that the boundary cross-section becomes highly elongated. Indications that increasing elongation of the plasma boundary leads to increasingly complex coils have been found by Hudson et al. (Reference Hudson, Zhu, Pfefferlé and Gunderson2018). Another argument for reducing elongation is the fact that very elongated cross-sections result in small plasma volume, as seen from the ellipse area dependence on the elongation $e$![]() , when fixing the major axis $a$
, when fixing the major axis $a$![]() , $A={\rm \pi} a b= {\rm \pi}a^2/e$
, $A={\rm \pi} a b= {\rm \pi}a^2/e$![]() . A reduction of plasma volume results in increasing transport losses and construction costs per unit plasma volume. The relation between elongation and the relevant NAE parameters is discussed in § 5, in particular the effect of torsion on shaping.
. A reduction of plasma volume results in increasing transport losses and construction costs per unit plasma volume. The relation between elongation and the relevant NAE parameters is discussed in § 5, in particular the effect of torsion on shaping.
In § 6 we show how the NAE method can be used to construct a two-field-period solution that closely approximates omnigenity, and we discuss its geometric properties and neoclassical transport as measured by the effective ripple $\epsilon _{\mathrm {eff}}$![]() . The particular case of a family of solutions with axes of constant torsion and increasing number of field periods is analysed in § 7 to show the effect of torsion on the quality of the near-axis approximation. Finally, in § 8, a three-field-period equilibrium is constructed around an axis shape specially designed to have low torsion in order to illustrate the importance of the axis shape in controlling transport and elongation.
. The particular case of a family of solutions with axes of constant torsion and increasing number of field periods is analysed in § 7 to show the effect of torsion on the quality of the near-axis approximation. Finally, in § 8, a three-field-period equilibrium is constructed around an axis shape specially designed to have low torsion in order to illustrate the importance of the axis shape in controlling transport and elongation.
2 Near-axis expansion
The NAE, as described by Garren & Boozer (Reference Garren and Boozer1991), solves the equilibrium MHD equations by performing a first-order Taylor expansion about the magnetic axis in pseudo-Cartesian coordinates (Kuo-Petravic & Boozer Reference Kuo-Petravic and Boozer1987). When using Boozer coordinates $(\psi,\theta,\varphi )$![]() the general form of the magnetic field at first order in the distance from the axis is given by
the general form of the magnetic field at first order in the distance from the axis is given by
with the expansion parameter
being a measure of the distance from the axis. As a consequence, these solutions will only be valid in the large aspect ratio limit. The first-order correction to the magnetic field $B_{1}$![]() has the general form of an analytical function close to the axis. At this order, the solutions correspond to the vacuum case and magnetic surfaces are always guaranteed, as discussed in Jorge, Sengupta & Landreman (Reference Jorge, Sengupta and Landreman2020).
has the general form of an analytical function close to the axis. At this order, the solutions correspond to the vacuum case and magnetic surfaces are always guaranteed, as discussed in Jorge, Sengupta & Landreman (Reference Jorge, Sengupta and Landreman2020).
At first order, the spatial position is given by
where $\boldsymbol {r}_{0}$![]() describes the position of the magnetic axis, a space curve characterised by its torsion $\tau$
describes the position of the magnetic axis, a space curve characterised by its torsion $\tau$![]() and signed curvature $\kappa ^{s}$
and signed curvature $\kappa ^{s}$![]() . The signed Frenet–Serret frame, $(\boldsymbol {t}, \boldsymbol {n}^{s}, \boldsymbol {b}^{s})$
. The signed Frenet–Serret frame, $(\boldsymbol {t}, \boldsymbol {n}^{s}, \boldsymbol {b}^{s})$![]() , of this curve is used as an orthonormal basis to describe the coordinate mapping. The tangent vector $\boldsymbol {t}$
, of this curve is used as an orthonormal basis to describe the coordinate mapping. The tangent vector $\boldsymbol {t}$![]() is identical to that of the traditional Frenet–Serret apparatus, and the normal and binormal signed vectors, $\boldsymbol {n}^{s}, \boldsymbol {b}^{s}$
is identical to that of the traditional Frenet–Serret apparatus, and the normal and binormal signed vectors, $\boldsymbol {n}^{s}, \boldsymbol {b}^{s}$![]() , as well as the signed curvature change signs at points where $\kappa = 0$
, as well as the signed curvature change signs at points where $\kappa = 0$![]() .
.
When imposing the conditions for omnigenity in the NAE, as done by Plunk et al. (Reference Plunk, Landreman and Helander2019) and Plunk et al. (Reference Plunk, Landreman and Helander2021), an approximate plasma boundary corresponding to a QI magnetic equilibria can be described by
where $B_{0}$![]() is the on-axis magnetic field strength, which must vary with $\varphi$
is the on-axis magnetic field strength, which must vary with $\varphi$![]() because, as also shown by Plunk et al. (Reference Plunk, Landreman and Helander2019), at first order, constant on-axis magnetic field is incompatible with the omnigenity conditions. The functions $\alpha (\varphi )$
because, as also shown by Plunk et al. (Reference Plunk, Landreman and Helander2019), at first order, constant on-axis magnetic field is incompatible with the omnigenity conditions. The functions $\alpha (\varphi )$![]() and $d(\varphi )$
and $d(\varphi )$![]() need to be prescribed and are required to satisfy specific conditions to correspond to omnigenous solutions as will be discussed in more detail later in this work. The function $\sigma (\varphi )$
need to be prescribed and are required to satisfy specific conditions to correspond to omnigenous solutions as will be discussed in more detail later in this work. The function $\sigma (\varphi )$![]() appearing in (2.5) can be seen to relate to the elongation of the boundary cross-section.
appearing in (2.5) can be seen to relate to the elongation of the boundary cross-section.
The problem of constructing QI magnetic equilibria is then transformed into the problem of specifying an on-axis magnetic field strength $B_{0}$![]() , an axis shape, two functions $\alpha (\varphi )$
, an axis shape, two functions $\alpha (\varphi )$![]() and $d(\varphi )$
and $d(\varphi )$![]() , and solving a differential equation for the quantity $\sigma (\varphi )$
, and solving a differential equation for the quantity $\sigma (\varphi )$![]()
which must be solved self-consistently with the rotational transform on axis ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$![]() . Here $G_{0}$
. Here $G_{0}$![]() and $I_2$
and $I_2$![]() are related to the first non-zero terms of the poloidal and toroidal current functions on axis, respectively, as expanded in Garren & Boozer (Reference Garren and Boozer1991), and $\bar {d}(\varphi ) = d(\varphi ) /\kappa ^{s}(\varphi )$
are related to the first non-zero terms of the poloidal and toroidal current functions on axis, respectively, as expanded in Garren & Boozer (Reference Garren and Boozer1991), and $\bar {d}(\varphi ) = d(\varphi ) /\kappa ^{s}(\varphi )$![]() . Primes represent derivatives with respect to the toroidal angular coordinate $\varphi$
. Primes represent derivatives with respect to the toroidal angular coordinate $\varphi$![]() . In the case of stellarator symmetry, $\sigma (0) = 0$
. In the case of stellarator symmetry, $\sigma (0) = 0$![]() .
.
In order to mathematically formulate the omnigenity conditions required on $\alpha (\varphi )$![]() and $d(\varphi )$
and $d(\varphi )$![]() , a certain coordinate mapping described in Cary & Shasharina (Reference Cary and Shasharina1997) was used in Plunk et al. (Reference Plunk, Landreman and Helander2019). For each magnetic well in the on-axis magnetic field, trapping domains are delimited by the maxima defining the well. This is divided into a right-hand domain $D_{R}$
, a certain coordinate mapping described in Cary & Shasharina (Reference Cary and Shasharina1997) was used in Plunk et al. (Reference Plunk, Landreman and Helander2019). For each magnetic well in the on-axis magnetic field, trapping domains are delimited by the maxima defining the well. This is divided into a right-hand domain $D_{R}$![]() and a left-hand domain $D_{L}$
and a left-hand domain $D_{L}$![]() , depending on which side of the minimum of the well the points lie. For each point $\varphi$
, depending on which side of the minimum of the well the points lie. For each point $\varphi$![]() in a right-hand domain we identify its corresponding bounce point $\varphi _{b}(\varphi )$
in a right-hand domain we identify its corresponding bounce point $\varphi _{b}(\varphi )$![]() in the left-hand domain by the condition
in the left-hand domain by the condition
and vice versa. It is clear from this construction that
The angular distance between an arbitrary point $\varphi$![]() and its corresponding bounce point is given by
and its corresponding bounce point is given by
Plunk et al. (Reference Plunk, Landreman and Helander2019) provided a way to construct the functions $d(\varphi )$![]() and $\alpha (\varphi )$
and $\alpha (\varphi )$![]() in $D_{R}$
in $D_{R}$![]() , giving their dependency in $D_{L}$
, giving their dependency in $D_{L}$![]() , to guarantee omnigenity. This is done by equating the near-axis and the omnigenous forms of $B_{1}$
, to guarantee omnigenity. This is done by equating the near-axis and the omnigenous forms of $B_{1}$![]()
where $F_{1}(\theta,\varphi )$![]() , that comes from the expansion of the Cary–Shasharina mapping, is a small perturbation added to a zeroth-order quasi-symmetric magnetic field to satisfy omnigenity, and hence preserves the following symmetry:
, that comes from the expansion of the Cary–Shasharina mapping, is a small perturbation added to a zeroth-order quasi-symmetric magnetic field to satisfy omnigenity, and hence preserves the following symmetry:
Solving (2.10) for $F_{1}$![]() and plugging it into (2.11) we obtain the following set of conditions:
and plugging it into (2.11) we obtain the following set of conditions:
In addition, $d$![]() must vanish at all extrema of the on-axis magnetic field $B_{0}$
must vanish at all extrema of the on-axis magnetic field $B_{0}$![]() , as seen from (2.10). The curvature of the magnetic axis $\kappa ^{s}$
, as seen from (2.10). The curvature of the magnetic axis $\kappa ^{s}$![]() needs to have zeros of the same order as $d$
needs to have zeros of the same order as $d$![]() at these points for the plasma boundary to be well described, i.e. so that $X_{1}$
at these points for the plasma boundary to be well described, i.e. so that $X_{1}$![]() and $Y_{1}$
and $Y_{1}$![]() , which are proportional to $d/\kappa ^{s}$
, which are proportional to $d/\kappa ^{s}$![]() and $\kappa ^{s}/d$
and $\kappa ^{s}/d$![]() , respectively, remain non-zero and bounded.
, respectively, remain non-zero and bounded.
It is important to note that periodicity cannot be enforced if the condition (2.13) on $\alpha (\varphi )$![]() is satisfied and the rotational transform ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$
is satisfied and the rotational transform ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$![]() is irrational. We can see this from evaluating (2.13) at the maximum $\varphi = 2{\rm \pi}$
is irrational. We can see this from evaluating (2.13) at the maximum $\varphi = 2{\rm \pi}$![]() ,
,
However, continuity of $B_{1}$![]() , $X_{1}$
, $X_{1}$![]() and $Y_{1}$
and $Y_{1}$![]() requires
requires
with $M$![]() defined as the number of times the axis curvature vector $\boldsymbol {n}^{s}$
defined as the number of times the axis curvature vector $\boldsymbol {n}^{s}$![]() rotates during one toroidal transit. Thus, (2.14) is generally in conflict with (2.15) and omnigenity is only consistent with continuity for integer values of ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$
rotates during one toroidal transit. Thus, (2.14) is generally in conflict with (2.15) and omnigenity is only consistent with continuity for integer values of ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$![]() . Plunk et al. (Reference Plunk, Landreman and Helander2019) resolved this conflict by introducing small matching regions around $\varphi =0$
. Plunk et al. (Reference Plunk, Landreman and Helander2019) resolved this conflict by introducing small matching regions around $\varphi =0$![]() and $\varphi = 2{\rm \pi}$
and $\varphi = 2{\rm \pi}$![]() , where omnigenity is abandoned and $\alpha$
, where omnigenity is abandoned and $\alpha$![]() is defined to guarantee periodicity. A different approach to solving this problem, as well as the form these conditions take for a single-well, $N$
is defined to guarantee periodicity. A different approach to solving this problem, as well as the form these conditions take for a single-well, $N$![]() -field-period, stellarator-symmetric configuration is discussed in the following sections.
-field-period, stellarator-symmetric configuration is discussed in the following sections.
3 $N$ -field periods and stellarator symmetry
-field periods and stellarator symmetry
A magnetic field is said to be stellarator-symmetric if it is invariant, except for sign change, under a $180^\circ$![]() rotation (the operations $I_n$
rotation (the operations $I_n$![]() defined in the following) around a set of axes. It is conventional to take these axes to lie within the $x\unicode{x2013}y$
defined in the following) around a set of axes. It is conventional to take these axes to lie within the $x\unicode{x2013}y$![]() plane, passing through the origin, and regularly spaced in the toroidal angle. This type of symmetry was defined formally by Dewar & Hudson (Reference Dewar and Hudson1998), who introduced a symmetry operator $I_{0}$
plane, passing through the origin, and regularly spaced in the toroidal angle. This type of symmetry was defined formally by Dewar & Hudson (Reference Dewar and Hudson1998), who introduced a symmetry operator $I_{0}$![]() by
by
with $\theta$![]() and $\varphi$
and $\varphi$![]() being angular coordinates. We say that a vector $\boldsymbol {F}$
being angular coordinates. We say that a vector $\boldsymbol {F}$![]() possesses stellarator symmetry if
possesses stellarator symmetry if
where $F_{j}={\partial {\boldsymbol {x}}}/{\partial j} \boldsymbol {\cdot } \boldsymbol {F}$![]() , with $j=\{\psi,\theta,\varphi \}$
, with $j=\{\psi,\theta,\varphi \}$![]() , are the covariant components of $\boldsymbol {F}$
, are the covariant components of $\boldsymbol {F}$![]() . For the case of a scalar quantity, for instance $|F|$
. For the case of a scalar quantity, for instance $|F|$![]() , stellarator symmetry implies
, stellarator symmetry implies
If the vector field $\boldsymbol {F}$![]() possesses $N$
possesses $N$![]() -fold discrete symmetry about the $z$
-fold discrete symmetry about the $z$![]() -axis, then stellarator symmetry also exists about the cylindrical inversion symmetry operation with respect to the half-line $\{\phi = 2i{\rm \pi} /N, Z= 0\}$
-axis, then stellarator symmetry also exists about the cylindrical inversion symmetry operation with respect to the half-line $\{\phi = 2i{\rm \pi} /N, Z= 0\}$![]() , with $i= 1,2,\ldots,(N-1)$
, with $i= 1,2,\ldots,(N-1)$![]() , and with respect to the half-line in the middle of each field period $\{\phi = (2i-1){\rm \pi} /N, Z= 0\}$
, and with respect to the half-line in the middle of each field period $\{\phi = (2i-1){\rm \pi} /N, Z= 0\}$![]() , with $i= 1,2,\ldots,N$
, with $i= 1,2,\ldots,N$![]() . These symmetry operators will be referred to as $I_{2i}$
. These symmetry operators will be referred to as $I_{2i}$![]() and $I_{2i-1}$
and $I_{2i-1}$![]() , respectively.
, respectively.
Let us now consider the case of a stellarator-symmetric $N$![]() -field-period QI configuration, and focus on the case of one magnetic well per field period.Footnote 3 This symmetry is not a necessary condition but is used to reduce the complexity of the problem and is conventionally assumed in QI designs.
-field-period QI configuration, and focus on the case of one magnetic well per field period.Footnote 3 This symmetry is not a necessary condition but is used to reduce the complexity of the problem and is conventionally assumed in QI designs.
In order to be stellarator symmetric, the magnetic field strength ${B}$![]() needs to fulfil
needs to fulfil
which is obtained by invoking the symmetry operator $I_{2i-1}$![]() . The angular position of the $i$
. The angular position of the $i$![]() th minimum, $\varphi _{\mathrm {min}}^{(i)}$
th minimum, $\varphi _{\mathrm {min}}^{(i)}$![]() is located on the rotation axis, and is given by
is located on the rotation axis, and is given by
whereas the $i$![]() th maximum is
th maximum is
The trapping domain in each period is labelled with the subscript $i$![]() , shown in figure 1, and the left- and right-hand domains are defined as
, shown in figure 1, and the left- and right-hand domains are defined as

Now, (2.9), which gives the distance between bounce points, can be written as
and the bounce points can be found using
Using this new notation, we can write the symmetry operator $I_{2i-1}$![]() as
as

Figure 1. One-well magnetic field strength example, plotted over a single toroidal field period. The right- and left-hand domains, $D_{iR}$![]() and $D_{iL}$
and $D_{iL}$![]() , are indicated. The angular position of the minimum and maxima of the well are labeled by $\varphi _{\mathrm {min}}^{i}$
, are indicated. The angular position of the minimum and maxima of the well are labeled by $\varphi _{\mathrm {min}}^{i}$![]() and $\varphi _{\mathrm {max}}^{i}$
and $\varphi _{\mathrm {max}}^{i}$![]() , respectively.
, respectively.
Let us now focus on the condition for omnigenity on the function $d(\varphi )$![]() , which is shown in (2.12). We substitute $\varphi _{b}$
, which is shown in (2.12). We substitute $\varphi _{b}$![]() from expression (3.9) and note that $\varphi _{b}^{\prime }=-1$
from expression (3.9) and note that $\varphi _{b}^{\prime }=-1$![]() , to find
, to find
As a consequence, $d(\varphi )$![]() must necessarily be an odd function about $\varphi _{\mathrm {min}}^{(i)}$
must necessarily be an odd function about $\varphi _{\mathrm {min}}^{(i)}$![]() , the bottom of the well. Note that $\varphi _{b}^{\prime }(\varphi )$
, the bottom of the well. Note that $\varphi _{b}^{\prime }(\varphi )$![]() is generally negative near bounce points for $\varphi \in D_{iL}$
is generally negative near bounce points for $\varphi \in D_{iL}$![]() , even without requiring stellarator symmetry, so the order of the zeros of $d$
, even without requiring stellarator symmetry, so the order of the zeros of $d$![]() must always be odd, and therefore the same is true for those of $\kappa ^{s}$
must always be odd, and therefore the same is true for those of $\kappa ^{s}$![]() .
.
For the case of $\alpha (\varphi )$![]() , we first define a quantity $\Delta \alpha$
, we first define a quantity $\Delta \alpha$![]() in the same fashion as (2.9)
in the same fashion as (2.9)
By replacing $\alpha$![]() by expression (2.13) in the previous definition, we obtain
by expression (2.13) in the previous definition, we obtain
and using expression (3.8) we get
We see that $\alpha$![]() needs to have a part proportional to ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} \Delta \varphi (\varphi )$
needs to have a part proportional to ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} \Delta \varphi (\varphi )$![]() , to guarantee the right form of $\Delta \alpha$
, to guarantee the right form of $\Delta \alpha$![]() , and an even part $\alpha _{e}$
, and an even part $\alpha _{e}$![]() such that
such that
Accordingly, we write $\alpha$![]() as
as
In order to find $\alpha _{e}$![]() , we note that the first-order correction to the magnetic field, given in (2.1),
, we note that the first-order correction to the magnetic field, given in (2.1),
needs to possess stellarator symmetry. We know from (3.11) that $d(\varphi )$![]() is an odd function and, by construction, that $B_{0}$
is an odd function and, by construction, that $B_{0}$![]() is an even function. Therefore, $\cos {(\theta -\alpha (\varphi ))}$
is an even function. Therefore, $\cos {(\theta -\alpha (\varphi ))}$![]() must be odd under the symmetry operation defined in (3.10). In particular, this requires
must be odd under the symmetry operation defined in (3.10). In particular, this requires
at the stellarator symmetry point $(\theta _0 = 0, \varphi _{\mathrm {min}}^i)$![]() , which is valid for any integer $n_{i}$
, which is valid for any integer $n_{i}$![]() such that
such that
Evaluating (3.16) at the minimum, we find
so that $\alpha$![]() takes the form
takes the form
Now let us impose a necessary (but not sufficient) condition for periodicity of $B$![]() from one field period to the next, i.e.
from one field period to the next, i.e.
where $m$![]() is the number of times the signed curvature vector ${\boldsymbol {n}}^{s}$
is the number of times the signed curvature vector ${\boldsymbol {n}}^{s}$![]() rotates per field period. This ensures that the poloidal angle $\theta$
rotates per field period. This ensures that the poloidal angle $\theta$![]() is periodic and increases by $2{\rm \pi}$
is periodic and increases by $2{\rm \pi}$![]() after a full toroidal rotation. The addition of the term $2{\rm \pi} m$
after a full toroidal rotation. The addition of the term $2{\rm \pi} m$![]() to $\alpha$
to $\alpha$![]() compensates the poloidal rotation of the axis (measured by $m$
compensates the poloidal rotation of the axis (measured by $m$![]() ) because $\alpha$
) because $\alpha$![]() effectively behaves as a phase shift on $\theta$
effectively behaves as a phase shift on $\theta$![]() . The previous expression translates into a relation for $n_{i}$
. The previous expression translates into a relation for $n_{i}$![]()
which can also be written as
Without loss of generality we can choose $n_{1}=0$![]() , and inserting this result in (3.21) we obtain an expression for $\alpha (\varphi )$
, and inserting this result in (3.21) we obtain an expression for $\alpha (\varphi )$![]() satisfying omnigenity and $N$
satisfying omnigenity and $N$![]() -fold periodicity
-fold periodicity
The shape of the boundary must also be made periodic, which can be achieved in the same way as done in Plunk et al. (Reference Plunk, Landreman and Helander2019), by introducing so-called buffer regions around the maxima of $B_{0}$![]() . In these regions, $\alpha$
. In these regions, $\alpha$![]() is not calculated using (3.25), but is instead chosen to give a periodic plasma boundary. The function in the buffer region needs to be constructed carefully to make sure the function itself and its derivatives are continuous and smooth in order to avoid numerical difficulties in equilibrium solvers such as VMEC (Hirshman & Whitson Reference Hirshman and Whitson1983).
is not calculated using (3.25), but is instead chosen to give a periodic plasma boundary. The function in the buffer region needs to be constructed carefully to make sure the function itself and its derivatives are continuous and smooth in order to avoid numerical difficulties in equilibrium solvers such as VMEC (Hirshman & Whitson Reference Hirshman and Whitson1983).
We note that although we have some freedom in the choice of $n_{1}$![]() and, hence, in the value of $\alpha$
and, hence, in the value of $\alpha$![]() , the term entering (2.6) and defining the equilibria is $\alpha ^{\prime }(\varphi )$
, the term entering (2.6) and defining the equilibria is $\alpha ^{\prime }(\varphi )$![]() , which is independent of the choice of $n_{1}$
, which is independent of the choice of $n_{1}$![]() . The only freedom left in the choice of $\alpha (\varphi )$
. The only freedom left in the choice of $\alpha (\varphi )$![]() is on how omnigenity is broken to impose continuity of the solutions.
is on how omnigenity is broken to impose continuity of the solutions.
4 Smoother $\alpha (\varphi )$
In order to avoid the problems derived from defining $\alpha (\varphi )$![]() as a piecewise function, we propose a different approach, namely by adding an omnigenity-breaking term to (3.25) that allows periodic solutions
as a piecewise function, we propose a different approach, namely by adding an omnigenity-breaking term to (3.25) that allows periodic solutions
The last term in this expression goes to zero at the bottom of the well as long as $k\geqslant -1/2$![]() and, hence, makes the solution omnigenous for deeply trapped particles. The parameter $a$
and, hence, makes the solution omnigenous for deeply trapped particles. The parameter $a$![]() can be chosen in such a way that periodicity of $\alpha (\varphi )$
can be chosen in such a way that periodicity of $\alpha (\varphi )$![]() is guaranteed. A first requirement is continuity at $\varphi _\textrm {max}^{(i)}$
is guaranteed. A first requirement is continuity at $\varphi _\textrm {max}^{(i)}$![]() , i.e.
, i.e.
where we are considering the $i$![]() th well when approaching from the left and the well labelled $i+1$
th well when approaching from the left and the well labelled $i+1$![]() when approaching from the right. Hence, we obtain
when approaching from the right. Hence, we obtain

and when inserting the values of $\varphi _{\mathrm {max} }^{(i)}$![]() and $\varphi _{\mathrm {min} }^{(i)}$
and $\varphi _{\mathrm {min} }^{(i)}$![]()
we find an expression for $a$![]()
which finally gives us a form of $\alpha$![]() that breaks omnigenity in a smooth and controlled way
that breaks omnigenity in a smooth and controlled way

In figure 2, we can see the effect the choice of the parameter $k$![]() has over the shape of $\alpha (\varphi )$
has over the shape of $\alpha (\varphi )$![]() for an axis shape with $m=0$
for an axis shape with $m=0$![]() . It is clear that increasing $k$
. It is clear that increasing $k$![]() results in a function closer to that required for omnigenity but at the cost of a sharp behaviour around $\varphi _{\mathrm {max}}$
results in a function closer to that required for omnigenity but at the cost of a sharp behaviour around $\varphi _{\mathrm {max}}$![]() to preserve periodicity.
to preserve periodicity.

Figure 2. Behaviour of the function $\alpha (\varphi )$![]() over one period, for the case $m=0$
over one period, for the case $m=0$![]() . The dotted line shows the fully omnigenous case, which is non-continuous at $\varphi _{\mathrm {max}}$
. The dotted line shows the fully omnigenous case, which is non-continuous at $\varphi _{\mathrm {max}}$![]() . Solid lines correspond to $\alpha$
. Solid lines correspond to $\alpha$![]() given by (4.6) with values for the parameter $k$
given by (4.6) with values for the parameter $k$![]() ranging from 1 to 8.
ranging from 1 to 8.
The equilibrium constructed using this $\alpha$![]() will be approximately omnigenous as long as the last term in (3.25) is small relative to the first term, i.e.
will be approximately omnigenous as long as the last term in (3.25) is small relative to the first term, i.e.

which can be further simplified and rearranged as

The left-hand side of this expression includes $| \varphi - \varphi _{\mathrm {min}}^{(i)}|$![]() , which is always smaller than ${\rm \pi} /N$
, which is always smaller than ${\rm \pi} /N$![]() in a well. Hence, the condition for omnigenity being achieved closely everywhere in the well, i.e. also for $\varphi -\varphi _{\mathrm {min}} \approx {\rm \pi}/N$
in a well. Hence, the condition for omnigenity being achieved closely everywhere in the well, i.e. also for $\varphi -\varphi _{\mathrm {min}} \approx {\rm \pi}/N$![]() , reduces to
, reduces to
This implies $N m \sim {\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$![]() , which, as expected can only be satisfied for nearly rational ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$
, which, as expected can only be satisfied for nearly rational ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$![]() . Although a rational value of ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$
. Although a rational value of ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$![]() is inconsistent with confinement, it may be advantageous to seek nearly rational values as a strategy for finding almost omnigenous configurations. We also note that the $m=0$
is inconsistent with confinement, it may be advantageous to seek nearly rational values as a strategy for finding almost omnigenous configurations. We also note that the $m=0$![]() case, in which (4.9) is not technically satisfied, is however interesting because the limit of small ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$
case, in which (4.9) is not technically satisfied, is however interesting because the limit of small ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$![]() implies that the absolute size of $\alpha$
implies that the absolute size of $\alpha$![]() will remain small, as required for approximate omnigenity.
will remain small, as required for approximate omnigenity.
A yet smoother choice of the function $\alpha (\varphi )$![]() with continuous derivatives up to third order at $\varphi _{\mathrm {max}}$
with continuous derivatives up to third order at $\varphi _{\mathrm {max}}$![]() can be achieved by adding an extra term,
can be achieved by adding an extra term,
For the configurations shown in this work we use $\alpha (\varphi )$![]() as described in (3.25), which appears sufficiently smooth for the cases we have studied, but more details about $\alpha _{\mathrm {II}}(\varphi )$
as described in (3.25), which appears sufficiently smooth for the cases we have studied, but more details about $\alpha _{\mathrm {II}}(\varphi )$![]() are discussed in Appendix A.
are discussed in Appendix A.
5 Axis shape
The shape of the magnetic axis is perhaps the most important input for the construction of stellarator configurations since the axis properties seem to strongly affect the success of the construction, as measured by the accuracy of the approximation at finite aspect ratio.
The need to have an axis with points of zero curvature has already been discussed, but, in addition, low-curvature axes are attractive because they improve the accuracy of the near-axis approximation (indeed, the original work of Garren and Boozer defined the expansion parameter in terms of the maximum curvature of the magnetic axis), and are also associated with a low-amplitude first-order magnetic field
where the definition of $\bar {d}$![]() has been substituted in (3.17). Note that $\bar {d}$
has been substituted in (3.17). Note that $\bar {d}$![]() cannot be made too small without causing large elongation, and therefore minimising $\kappa ^s$
cannot be made too small without causing large elongation, and therefore minimising $\kappa ^s$![]() is an effective strategy for improving omnigenity at finite $\epsilon$
is an effective strategy for improving omnigenity at finite $\epsilon$![]() .
.
It is also desirable to limit axis torsion, which enters directly into (2.6) for $\sigma$![]() , as will be clear in the following discussion. At first order, the cross-sections of the plasma boundary at constant $\varphi$
, as will be clear in the following discussion. At first order, the cross-sections of the plasma boundary at constant $\varphi$![]() are elliptical, with elongation $e$
are elliptical, with elongation $e$![]() defined as the ratio between the semi-major and semi-minor axes. Landreman & Sengupta (Reference Landreman and Sengupta2018) derived an expression for elongation in terms of $X_{1}$
defined as the ratio between the semi-major and semi-minor axes. Landreman & Sengupta (Reference Landreman and Sengupta2018) derived an expression for elongation in terms of $X_{1}$![]() and $Y_{1}$
and $Y_{1}$![]() (B 4). Using (2.4) and (2.5), we obtain an expression for $e$
(B 4). Using (2.4) and (2.5), we obtain an expression for $e$![]() dependent on the input parameters of the construction, namely $\bar {d}$
dependent on the input parameters of the construction, namely $\bar {d}$![]() , $B_{0}$
, $B_{0}$![]() and $\sigma$
and $\sigma$![]() ,
,

We can simplify the previous expression by introducing
leading to
One particular interesting limit is the idealised case of constant elongation. This can be achieved by choosing $\sigma$![]() constant. Given that, due to stellarator symmetry, $\sigma (0)=0$
constant. Given that, due to stellarator symmetry, $\sigma (0)=0$![]() then $\sigma$
then $\sigma$![]() must be zero everywhere, which transforms (5.4) into
must be zero everywhere, which transforms (5.4) into
this will result in a plasma boundary with constant elongation as long as $\bar {e}$![]() is independent of the toroidal angle $\varphi$
is independent of the toroidal angle $\varphi$![]() . Finding plasma equilibria with constant elongation can be achieved by choosing $d(\varphi )$
. Finding plasma equilibria with constant elongation can be achieved by choosing $d(\varphi )$![]() appropriately so that it cancels the toroidal dependence of $\bar {e}$
appropriately so that it cancels the toroidal dependence of $\bar {e}$![]() , namely
, namely

Now, we can introduce the conditions that lead to constant elongation in (2.6)
where we have specialised to the case of vanishing current density on axis, $I=0$![]() , the standard situation for QI stellarators (Helander & Nührenberg Reference Helander and Nührenberg2009; Helander, Geiger & Maaßberg Reference Helander, Geiger and Maaßberg2011). As omnigenity requires ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} - \alpha ^\prime \approx 0$
, the standard situation for QI stellarators (Helander & Nührenberg Reference Helander and Nührenberg2009; Helander, Geiger & Maaßberg Reference Helander, Geiger and Maaßberg2011). As omnigenity requires ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} - \alpha ^\prime \approx 0$![]() (see (3.25)), (5.7) implies that $\tau \approx 0$
(see (3.25)), (5.7) implies that $\tau \approx 0$![]() is necessary for solutions with constant elongation. This shows that axes with low torsion are compatible with simple equilibrium boundary shapes.
is necessary for solutions with constant elongation. This shows that axes with low torsion are compatible with simple equilibrium boundary shapes.
The possibility of low elongation, in particular, may be unexpected, given what has been found with traditional QI optimisation, and also from considerations of basic geometry on the magnetic axis, where the identity
follows from force balance and Ampere's law, noting that $\boldsymbol {\nabla } p = 0$![]() at $\psi = 0$
at $\psi = 0$![]() , and defining $\boldsymbol {\nabla }_\perp = \boldsymbol {\nabla } - {\boldsymbol {tt}}\boldsymbol {\cdot } \boldsymbol {\nabla }$
, and defining $\boldsymbol {\nabla }_\perp = \boldsymbol {\nabla } - {\boldsymbol {tt}}\boldsymbol {\cdot } \boldsymbol {\nabla }$![]() (Landreman & Sengupta Reference Landreman and Sengupta2018). This expression seems to imply that plasma volumes that are compressed in the direction of the curvature (normal) vector, i.e. high-elongation configurations, will exhibit only weak variation of the field strength in the perpendicular direction, and therefore in $\theta$
(Landreman & Sengupta Reference Landreman and Sengupta2018). This expression seems to imply that plasma volumes that are compressed in the direction of the curvature (normal) vector, i.e. high-elongation configurations, will exhibit only weak variation of the field strength in the perpendicular direction, and therefore in $\theta$![]() . This logic, although rough, is reflected in the near-axis construction of QI configurations, where it is typical to find elongated solutions. In § 8, we show how this tendency can be overcome by choice of axis torsion.
. This logic, although rough, is reflected in the near-axis construction of QI configurations, where it is typical to find elongated solutions. In § 8, we show how this tendency can be overcome by choice of axis torsion.
5.1 Axis construction
A space curve's shape is entirely determined by its curvature $\kappa$![]() and torsion $\tau$
and torsion $\tau$![]() . From these two quantities, it is possible to calculate the tangent, normal and binormal vectors $(\boldsymbol {t}, \boldsymbol {n}, \boldsymbol {b})$
. From these two quantities, it is possible to calculate the tangent, normal and binormal vectors $(\boldsymbol {t}, \boldsymbol {n}, \boldsymbol {b})$![]() using the Frenet–Serret formulae
using the Frenet–Serret formulae

where $s$![]() is the arc length, used for parametrising the curve. Then, numerical integration of the tangent vector, $\boldsymbol {t} = \textrm {d}\boldsymbol {r}/\textrm {d}s$
is the arc length, used for parametrising the curve. Then, numerical integration of the tangent vector, $\boldsymbol {t} = \textrm {d}\boldsymbol {r}/\textrm {d}s$![]() , yields the curve described by $\boldsymbol {r}$
, yields the curve described by $\boldsymbol {r}$![]() . Unfortunately, prescribing periodic $\kappa$
. Unfortunately, prescribing periodic $\kappa$![]() and $\tau$
and $\tau$![]() is not sufficient for finding closed curves. A parameter scan is thus needed to find curves that can be used as magnetic axes. This is the approach used to find the axes curves described in § 7.
is not sufficient for finding closed curves. A parameter scan is thus needed to find curves that can be used as magnetic axes. This is the approach used to find the axes curves described in § 7.
Although a Frenet description seems optimal for controlling torsion and curvature precisely, a truncated Fourier series is advantageous for its simplicity, smoothness and the fact that such curves are automatically closed. Smoothness is especially important for obtaining solutions that remain accurate at lower aspect ratio. Note that sharp derivatives $d/d\varphi \sim 1/\epsilon$![]() invalidate the NAE, which is a limit that is especially felt at high field period number. A method for generating simple axis curves, represented by a relatively small number of Fourier coefficients, is briefly outlined here and described in greater detail in Appendix B.
invalidate the NAE, which is a limit that is especially felt at high field period number. A method for generating simple axis curves, represented by a relatively small number of Fourier coefficients, is briefly outlined here and described in greater detail in Appendix B.
We represent the magnetic axis in cylindrical coordinates as
The usual Fourier representation for a stellarator-symmetric axis is


A local form is used to establish conditions on the derivatives of these functions about a point of stellarator symmetry (also coinciding with an extrema of $B_0(\phi )$![]() ), that can be then used to generate a linear system of equations for the Fourier coefficients.
), that can be then used to generate a linear system of equations for the Fourier coefficients.
Conditions on torsion and curvature, specifically zeros of different orders, are imposed locally and converted into constraints on the derivatives of the axis components $R$![]() and $z$
and $z$![]() , and then applied to a truncated Fourier representation. This results in a set of linear conditions on the Fourier coefficients that can be solved numerically, or by computer algebra. The orders of the zeros, together with the set of Fourier coefficients, define a space that can be used for further optimisation.
, and then applied to a truncated Fourier representation. This results in a set of linear conditions on the Fourier coefficients that can be solved numerically, or by computer algebra. The orders of the zeros, together with the set of Fourier coefficients, define a space that can be used for further optimisation.
As a very simple example of curves with points of vanishing curvature at multiples of ${\rm \pi} /N$![]() , one may consider a symmetric class of curves, as in Plunk et al. (Reference Plunk, Landreman and Helander2019)
, one may consider a symmetric class of curves, as in Plunk et al. (Reference Plunk, Landreman and Helander2019)
Owing to the fact that only the even mode numbers are retained ($z_s(1) = R_c(1) = 0$![]() ), the condition for zeros of curvature at first order need only be applied at $\phi = 0$
), the condition for zeros of curvature at first order need only be applied at $\phi = 0$![]() , i.e. ${\textrm {d}^2R}/{\textrm {d}\varphi }|_{0} = R(0)$
, i.e. ${\textrm {d}^2R}/{\textrm {d}\varphi }|_{0} = R(0)$![]() , and the result is
, and the result is
which matches (8.3a) of Plunk et al. (Reference Plunk, Landreman and Helander2019) for the case $N = 1$![]() . The coefficient $Z_s(2)$
. The coefficient $Z_s(2)$![]() is free to be adjusted to satisfy other desired requirements. Note that additional Fourier modes may be retained to define a near-axis QI optimisation space, as done by Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho and Helander2022).
is free to be adjusted to satisfy other desired requirements. Note that additional Fourier modes may be retained to define a near-axis QI optimisation space, as done by Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho and Helander2022).
5.2 Controlling torsion
Noting that a curve of zero torsion lies within a plane, it would seem straightforward to realise a stellarator-symmetric axis shape of low torsion by simply reducing the magnitude of its $z$![]() component, thereby constraining the curve to lie close to the $x$
component, thereby constraining the curve to lie close to the $x$![]() –$y$
–$y$![]() plane. We can do this with the single-parameter curve defined by (5.13)–(5.14), by letting the parameter $z_s(2)$
plane. We can do this with the single-parameter curve defined by (5.13)–(5.14), by letting the parameter $z_s(2)$![]() tend to zero. Unfortunately this limit is not well-behaved, as shown in figure 3. Although torsion goes to zero almost everywhere, it tends to infinity in the neighbourhood of the zeros of curvature.
tend to zero. Unfortunately this limit is not well-behaved, as shown in figure 3. Although torsion goes to zero almost everywhere, it tends to infinity in the neighbourhood of the zeros of curvature.

Figure 3. Torsion behaviour with decreasing value of $z_{s}(2)$![]() : (a) singularity in torsion at points of stellarator symmetry as $z_{s}(2)$
: (a) singularity in torsion at points of stellarator symmetry as $z_{s}(2)$![]() approaches zero; (b) maximum torsion at different values of $z_{s}(2)$
approaches zero; (b) maximum torsion at different values of $z_{s}(2)$![]() .
.
Another approach to minimising torsion is, somewhat paradoxically, to take the limit of large $z_s(2)$![]() . Such elongated axis shapes are nearly planar around the points of zero curvature, and have their torsion peaked midway between these points. The torsion is, however, small in magnitude due to the large values of curvature around such points. As figure 4 confirms, the lowering of torsion by this method is accomplished only at the cost of raising the maximum value of curvature. Furthermore, the maximum value of torsion obtained at a fixed value of maximum curvature ($\mathrm {max}(\kappa ) = 3$
. Such elongated axis shapes are nearly planar around the points of zero curvature, and have their torsion peaked midway between these points. The torsion is, however, small in magnitude due to the large values of curvature around such points. As figure 4 confirms, the lowering of torsion by this method is accomplished only at the cost of raising the maximum value of curvature. Furthermore, the maximum value of torsion obtained at a fixed value of maximum curvature ($\mathrm {max}(\kappa ) = 3$![]() ) grows linearly with field period number, as shown in the second panel of figure 4. Requiring the maximum value of curvature to remain bounded when increasing the number of field periods results in the maximum of torsion increasing, as shown in figure 5. Finding closed curves with torsion and curvature remaining under a certain value gets more difficult when increasing the number of field periods. This might be a reason why finding good solutions with $N>1$
) grows linearly with field period number, as shown in the second panel of figure 4. Requiring the maximum value of curvature to remain bounded when increasing the number of field periods results in the maximum of torsion increasing, as shown in figure 5. Finding closed curves with torsion and curvature remaining under a certain value gets more difficult when increasing the number of field periods. This might be a reason why finding good solutions with $N>1$![]() is challenging for the optimisation procedure described in Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho and Helander2022).
is challenging for the optimisation procedure described in Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho and Helander2022).

Figure 4. (a) Maximum torsion versus maximum curvature for $N=2,4,8$![]() (blue, orange, green). Curvature and torsion are individually maximised over $\phi$
(blue, orange, green). Curvature and torsion are individually maximised over $\phi$![]() for fixed values of $z_{s}(2)$
for fixed values of $z_{s}(2)$![]() . Values used correspond to large-$z_{s}(2)$
. Values used correspond to large-$z_{s}(2)$![]() regime, $z_{s}(2)\gtrsim 0.4/N^2$
regime, $z_{s}(2)\gtrsim 0.4/N^2$![]() . (b) Maximum torsion versus $N$
. (b) Maximum torsion versus $N$![]() for $z_{s}(2)$
for $z_{s}(2)$![]() chosen such that $\mathrm {max}_{\varphi }(\kappa ) = 3$
chosen such that $\mathrm {max}_{\varphi }(\kappa ) = 3$![]() .
.

Figure 5. (a) Curvature and (b) torsion versus $\phi$![]() for different field period numbers, $N=2,4,6,8,10$
for different field period numbers, $N=2,4,6,8,10$![]() . Here $z_{s}(2)$
. Here $z_{s}(2)$![]() is chosen such that $\mathrm {max}_{\varphi }(\kappa ) = 3$
is chosen such that $\mathrm {max}_{\varphi }(\kappa ) = 3$![]() .
.
6 QI construction, two-field-period example
The construction of a two-field-period configuration is now described. The axis shape was chosen using (5.15) for the case $N=2$![]() , yielding
, yielding
The $z$![]() -coefficients were chosen to limit the curvature and torsion to tolerable levels. The normal vector $\boldsymbol {n}^{s}$
-coefficients were chosen to limit the curvature and torsion to tolerable levels. The normal vector $\boldsymbol {n}^{s}$![]() does not complete any full rotation around the axis, hence $m=0$
does not complete any full rotation around the axis, hence $m=0$![]() . This curve contains points of zero curvature as shown in figure 6. The location of these points coincide with the extrema of the on-axis magnetic field strength, which is chosen as
. This curve contains points of zero curvature as shown in figure 6. The location of these points coincide with the extrema of the on-axis magnetic field strength, which is chosen as
In general, the values of the toroidal coordinates $\varphi$![]() , the Boozer angle, and $\phi$
, the Boozer angle, and $\phi$![]() , the cylindrical angle, are not the same. However, thanks to stellarator symmetry, they coincide at the extrema points of $B_0(\varphi )$
, the cylindrical angle, are not the same. However, thanks to stellarator symmetry, they coincide at the extrema points of $B_0(\varphi )$![]() , which thus also correspond to the zeros of the axis curvature.
, which thus also correspond to the zeros of the axis curvature.
The choice of $d(\varphi )$![]() has an important effect on the elongation of the plasma boundary as can be seen from (2.4). We observed that keeping it proportional to $\kappa ^{s}(\varphi )$
has an important effect on the elongation of the plasma boundary as can be seen from (2.4). We observed that keeping it proportional to $\kappa ^{s}(\varphi )$![]() helped to reduce the elongation to manageable levels. For this example it was chosen as $d(\varphi ) = 1.03\ \kappa ^{s}$
helped to reduce the elongation to manageable levels. For this example it was chosen as $d(\varphi ) = 1.03\ \kappa ^{s}$![]() . The parameter $k$
. The parameter $k$![]() entering (4.6) controls the deviation from omnigenity and was set to $k=2$
entering (4.6) controls the deviation from omnigenity and was set to $k=2$![]() .
.
To construct numerical solutions, we first find the signed Frenet–Serret frame quantities of the axis: $\kappa ^s$![]() , $\tau$
, $\tau$![]() and $(\boldsymbol {t},\boldsymbol {n}^{\boldsymbol {s}},\boldsymbol {b}^{\boldsymbol {s}})$
and $(\boldsymbol {t},\boldsymbol {n}^{\boldsymbol {s}},\boldsymbol {b}^{\boldsymbol {s}})$![]() . Then, the relation $\varphi (\phi )$
. Then, the relation $\varphi (\phi )$![]() , as well as $G_{0}$
, as well as $G_{0}$![]() , need to be found along the axis. This is done by iteratively solving (8.1) of Plunk et al. (Reference Plunk, Landreman and Helander2019)
, need to be found along the axis. This is done by iteratively solving (8.1) of Plunk et al. (Reference Plunk, Landreman and Helander2019)
We then proceed to solve (2.6), self-consistently with ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$![]() , for one field period, i.e. in the region $\varphi \in [0,2{\rm \pi} /N]$
, for one field period, i.e. in the region $\varphi \in [0,2{\rm \pi} /N]$![]() .
.
A boundary is constructed with aspect ratio $A=10$![]() , where $A$
, where $A$![]() can be expressed in terms of the distance from the axis as
can be expressed in terms of the distance from the axis as

where $\overline {B_0}$![]() is the average value of $B_{0}$
is the average value of $B_{0}$![]() . This boundary is then used to find a fixed-boundary magnetic equilibrium with the code VMEC. The strength of the magnetic field on the boundary is shown in figure 7. The rotational transform profile obtained with VMEC is shown in figure 8 and coincides with the value calculated numerically from (2.6) ${{\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} = 0.107}$
. This boundary is then used to find a fixed-boundary magnetic equilibrium with the code VMEC. The strength of the magnetic field on the boundary is shown in figure 7. The rotational transform profile obtained with VMEC is shown in figure 8 and coincides with the value calculated numerically from (2.6) ${{\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} = 0.107}$![]() . The maximum elongation of the flux surface cross-sections (taken at $\phi =\textrm {const}.$
. The maximum elongation of the flux surface cross-sections (taken at $\phi =\textrm {const}.$![]() ), as defined by (5.4) is $e_{\mathrm {max}}=4.4$
), as defined by (5.4) is $e_{\mathrm {max}}=4.4$![]() .
.

Figure 7. Intensity of the magnetic field on the plasma boundary for a two field period, $A=10$![]() configuration: (a) side view and (b) top view.
configuration: (a) side view and (b) top view.

Figure 8. (a) Rotational transform, ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$![]() , and (b) effective ripple, $\epsilon _{\mathrm {eff}}$
, and (b) effective ripple, $\epsilon _{\mathrm {eff}}$![]() , for an $N=2$
, for an $N=2$![]() , $A=10$
, $A=10$![]() configuration.
configuration.
The effective ripple, $\epsilon _{\mathrm {eff}}$![]() , is a simple and convenient parameter that characterises low-collisionality neoclassical transport of electrons (Beidler et al. Reference Beidler, Allmaier, Isaev, Kasilov, Kernbichler, Leitold, Maaßberg, Mikkelsen, Murakami and Schmidt2011). We calculate it using the procedure described by Drevlak et al. (Reference Drevlak, Heyn, Kalyuzhnyj, Kasilov, Kernbichler, Monticello, Nemov, Nührenberg and Reiman2003) in 16 radial points, and find an $\epsilon _{\mathrm {eff}}$
, is a simple and convenient parameter that characterises low-collisionality neoclassical transport of electrons (Beidler et al. Reference Beidler, Allmaier, Isaev, Kasilov, Kernbichler, Leitold, Maaßberg, Mikkelsen, Murakami and Schmidt2011). We calculate it using the procedure described by Drevlak et al. (Reference Drevlak, Heyn, Kalyuzhnyj, Kasilov, Kernbichler, Monticello, Nemov, Nührenberg and Reiman2003) in 16 radial points, and find an $\epsilon _{\mathrm {eff}}$![]() below 1 % up to mid-radius and lower than 2 % everywhere in the plasma volume, see figure 8.
below 1 % up to mid-radius and lower than 2 % everywhere in the plasma volume, see figure 8.
The boundary shape was generated for different aspect ratios, i.e. different distances from the axis. A comparison between the contours of constant magnetic field strength obtained from the NAE (2.1) and those obtained from the VMEC calculation and transformed to boozer coordinates using BOOZ_XFORM (Sanchez et al. Reference Sanchez, Hirshman, Ware, Berry and Spong2000) is shown in figure 9. The difference between both results decreases with increasing the aspect ratio, as expected because the expansion is performed in the distance from the axis. For the largest aspect ratio, 160, the difference is almost imperceptible. The root-mean-squared difference between both magnetic fields is calculated for each aspect ratio and the results are shown in figure 10. The scaling with the aspect ratio is as expected from a first-order expansion, proportional to $1/A^2$![]() .
.

Figure 9. Contours of the magnetic field intensity on the plasma boundary, $B$![]() , are shown for increasing values of aspect ratio, starting at $A=20$
, are shown for increasing values of aspect ratio, starting at $A=20$![]() (a,b). Dotted lines are the contours obtained from the construction and solid lines from VMEC and BOOZ_XFORM. Contours on (b,d, f) correspond to the first-order correction to $B$
(a,b). Dotted lines are the contours obtained from the construction and solid lines from VMEC and BOOZ_XFORM. Contours on (b,d, f) correspond to the first-order correction to $B$![]() and (a,c,e) to the total magnetic field.
and (a,c,e) to the total magnetic field.

Figure 10. Root-mean-squared difference between the magnetic field from the construction and that calculated by VMEC, for different aspect ratios. The dashed line shows the expected scaling $\propto 1/A^{2}$![]() .
.
7 A family of constant torsion QI solutions
As illustrated by the previous example, we are capable of directly constructing QI equilibria with low electron neoclassical transport, as measured by $\epsilon _{\mathrm {eff}}$![]() , at aspect ratios comparable to existing devices. Performing an optimisation procedure in the space of QI solutions described by the NAE has led to the discovery of $N=1$
, at aspect ratios comparable to existing devices. Performing an optimisation procedure in the space of QI solutions described by the NAE has led to the discovery of $N=1$![]() configurations with excellent confinement properties as shown in Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho and Helander2022). However, finding configurations with more than one field period and good confinement has proved challenging, even when using optimisation procedures. In order to explore the role of the axis shape in causing this behaviour, we choose a family of axis shapes with $N=2,3,4$
configurations with excellent confinement properties as shown in Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho and Helander2022). However, finding configurations with more than one field period and good confinement has proved challenging, even when using optimisation procedures. In order to explore the role of the axis shape in causing this behaviour, we choose a family of axis shapes with $N=2,3,4$![]() , constant torsion and equal per-field-period maximum curvature. Constant torsion was chosen for simplicity in order to obtain smooth solutions for $\sigma$
, constant torsion and equal per-field-period maximum curvature. Constant torsion was chosen for simplicity in order to obtain smooth solutions for $\sigma$![]() from (2.6).
from (2.6).
The axis shapes chosen are closed curves with minimal bending energy and constant torsion as described in Pfefferlé et al. (Reference Pfefferlé, Gunderson, Hudson and Noakes2018). Their curvature and torsion are
where $\mathrm {sn}(a,b)$![]() is the Jacobi elliptic sine function, $L$
is the Jacobi elliptic sine function, $L$![]() the curve length, $N$
the curve length, $N$![]() the number of field periods, $p$
the number of field periods, $p$![]() a parameter yet to be chosen and $\kappa _{0}$
a parameter yet to be chosen and $\kappa _{0}$![]() the maximum curvature. Here $K(p)$
the maximum curvature. Here $K(p)$![]() is the complete elliptical integral of first kind and $X^{2}(p)= 2E(p)/K(p) -1$
is the complete elliptical integral of first kind and $X^{2}(p)= 2E(p)/K(p) -1$![]() , where $E(p) = E({\rm \pi} /2,p)$
, where $E(p) = E({\rm \pi} /2,p)$![]() is the incomplete elliptic integral of the second kind.
is the incomplete elliptic integral of the second kind.
The maximum curvature is chosen as $\kappa _0=1.6$![]() for all cases. Given a number of field periods $N$
for all cases. Given a number of field periods $N$![]() , the parameter $p$
, the parameter $p$![]() is scanned until a closed curve is found. We find $p_{2}=0.4527$
is scanned until a closed curve is found. We find $p_{2}=0.4527$![]() , $p_{3}=0.5927$
, $p_{3}=0.5927$![]() and $p_{4}=0.6580$
and $p_{4}=0.6580$![]() , for two, three and four field periods, respectively. The curvature per field period has the same maximum and similar toroidal dependence for all three cases and has zeros at multiples of ${\rm \pi} /N$
, for two, three and four field periods, respectively. The curvature per field period has the same maximum and similar toroidal dependence for all three cases and has zeros at multiples of ${\rm \pi} /N$![]() , as required by the construction. The necessary torsion for a closed curve increases with $N$
, as required by the construction. The necessary torsion for a closed curve increases with $N$![]() as seen in figure 11. The Frenet–Serret formulae (5.9) are then used to find the curve described by these values of $\kappa$
as seen in figure 11. The Frenet–Serret formulae (5.9) are then used to find the curve described by these values of $\kappa$![]() and $\tau$
and $\tau$![]() , as described in § 5. For the three curves, $m=1$
, as described in § 5. For the three curves, $m=1$![]() .
.

Figure 11. (a) Curvature, $\kappa$![]() , and torsion, $\tau$
, and torsion, $\tau$![]() , with respect to the toroidal angle $\phi$
, with respect to the toroidal angle $\phi$![]() of the magnetic axes used in the construction of the different $N$
of the magnetic axes used in the construction of the different $N$![]() field-period solutions. Here $\kappa (\varphi )$
field-period solutions. Here $\kappa (\varphi )$![]() and $\tau (\varphi )$
and $\tau (\varphi )$![]() are given by (7.2) and (7.1). The maximum curvature, $\kappa _0 = 1.6$
are given by (7.2) and (7.1). The maximum curvature, $\kappa _0 = 1.6$![]() , is the same for the three cases. (b) The $\sigma$
, is the same for the three cases. (b) The $\sigma$![]() profiles obtained by solving (2.6) for each of the curves described by $\kappa$
profiles obtained by solving (2.6) for each of the curves described by $\kappa$![]() and $\tau$
and $\tau$![]() on the left.
on the left.
Using these curves as axis shapes, three configurations were constructed following the method described in § 6. All per-period parameters and functions used in the construction are kept the same as in § 6; $d(\varphi ) = 1.03\kappa ^{s}$![]() , the parameter $k$
, the parameter $k$![]() entering (4.6) was set as $k=2$
entering (4.6) was set as $k=2$![]() , and the magnetic field on axis as
, and the magnetic field on axis as
The main differences between these configurations is the value of the torsion $\tau$![]() and the number of field periods. As we are solving (2.6) for $\sigma$
and the number of field periods. As we are solving (2.6) for $\sigma$![]() in a single period, we can compare the per-field-period solutions with respect to a scaled angular variable $\varphi /N$
in a single period, we can compare the per-field-period solutions with respect to a scaled angular variable $\varphi /N$![]() , as seen in figure 11(b). The solution for $\sigma$
, as seen in figure 11(b). The solution for $\sigma$![]() in one field period for each of these cases is very similar and only deviates in those regions where the curvature values differ, as expected. Consequently, the values found for the per-period rotational transform, ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} _{N}={\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} /N$
in one field period for each of these cases is very similar and only deviates in those regions where the curvature values differ, as expected. Consequently, the values found for the per-period rotational transform, ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} _{N}={\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} /N$![]() , are also very similar: ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} _{\mathrm {2}}= 0.4565$
, are also very similar: ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} _{\mathrm {2}}= 0.4565$![]() , ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} _{\mathrm {3}}= 0.4674$
, ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} _{\mathrm {3}}= 0.4674$![]() and ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} _{\mathrm {4}}= 0.4707$
and ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} _{\mathrm {4}}= 0.4707$![]() .
.
The resulting boundary shape is used to find the magnetic field strength on the boundary using the MHD equilibrium code VMEC and BOOZ_XFORM. The result is compared with the magnetic field from the construction (2.1), and shown for $A=40$![]() in figure 12, where it is clear that the approximation deteriorates with increasing number of field periods.
in figure 12, where it is clear that the approximation deteriorates with increasing number of field periods.

Figure 12. Contours of the magnetic field intensity on the plasma boundary, $B$![]() , are shown for increasing values of $N$
, are shown for increasing values of $N$![]() , the number of field periods, starting at (a) $N=2$
, the number of field periods, starting at (a) $N=2$![]() , (b) $N=3$
, (b) $N=3$![]() and (c) $N=4$
and (c) $N=4$![]() . Dotted lines show the contours obtained from the construction and solid lines those from the calculation with VMEC and BOOZ_XFORM. Aspect ratio was set to $A=40$
. Dotted lines show the contours obtained from the construction and solid lines those from the calculation with VMEC and BOOZ_XFORM. Aspect ratio was set to $A=40$![]() for all cases.
for all cases.
In the same manner as in the previous section, we calculate the root-mean-square difference between the intensity of $B(\theta,\varphi )$![]() in the boundary as calculated by VMEC and as expected from the construction. This calculation is done for each configuration at different aspect ratios, and is shown in figure 13. The scaling for all cases is proportional to $1/A^2$
in the boundary as calculated by VMEC and as expected from the construction. This calculation is done for each configuration at different aspect ratios, and is shown in figure 13. The scaling for all cases is proportional to $1/A^2$![]() , as expected, but the magnitude of the difference increases with the number of field periods, indicating a deterioration of the approximation with increasing $N$
, as expected, but the magnitude of the difference increases with the number of field periods, indicating a deterioration of the approximation with increasing $N$![]() . The same behaviour is observed in the effective ripple, getting significantly worse for the case with four field periods and being optimal, below $\epsilon _{\mathrm {eff}}= 8\times 10^{-3}$
. The same behaviour is observed in the effective ripple, getting significantly worse for the case with four field periods and being optimal, below $\epsilon _{\mathrm {eff}}= 8\times 10^{-3}$![]() , for two field periods, as is evident from figure 14.
, for two field periods, as is evident from figure 14.

Figure 13. Root-mean-squared difference between the magnetic field from the construction and that calculated by VMEC for configurations with $N=2,3,4$![]() and different values of $A$
and different values of $A$![]() . The dashed lines show the expected scaling $\propto 1/A^{2}$
. The dashed lines show the expected scaling $\propto 1/A^{2}$![]() .
.

Figure 14. Effective ripple, $\epsilon _{\mathrm {eff}}$![]() , profiles for configurations with $N=2,3,4$
, profiles for configurations with $N=2,3,4$![]() field periods.
field periods.
The only apparent significant differences between the solutions constructed in this section are the number of field periods and the value of the torsion. Stellarator designs constructed through conventional optimisation have $N = 4,5,6$![]() and larger, including W7-X, a QI design (very approximately) with 5 field periods. This indicates there should be no fundamental obstacle to obtaining a good approximation to QI fields at larger values of $N$
and larger, including W7-X, a QI design (very approximately) with 5 field periods. This indicates there should be no fundamental obstacle to obtaining a good approximation to QI fields at larger values of $N$![]() . Thus, with the hope to find such fields with the near-axis framework, we are further motivated to explore magnetic axes with low torsion.
. Thus, with the hope to find such fields with the near-axis framework, we are further motivated to explore magnetic axes with low torsion.
8 A three-field-period, low-torsion-axis example
Following the discussion at the beginning of § 5, and also the results of the previous section, we are motivated to consider axis curves with low torsion to both control elongation and better approximation to QI at larger $N$![]() . Using the procedure described in § 5, we therefore investigate closed curves with $N=3$
. Using the procedure described in § 5, we therefore investigate closed curves with $N=3$![]() and zeros of first order in the curvature at extrema of $B(\varphi )$
and zeros of first order in the curvature at extrema of $B(\varphi )$![]() , and zeros of torsion at second order at $\varphi _{\mathrm {min}}^{i}$
, and zeros of torsion at second order at $\varphi _{\mathrm {min}}^{i}$![]() . We choose one axis shape from this class that fulfils
. We choose one axis shape from this class that fulfils
for all toroidal points. The Fourier coefficients describing this axis are

Its curvature and torsion are shown as functions of the toroidal angle $\phi$![]() in figure 15, and $m=0$
in figure 15, and $m=0$![]() .
.

Figure 15. Curvature $\kappa$![]() (solid), torsion $\tau$
(solid), torsion $\tau$![]() (dashed) and magnetic field on-axis $B_0$
(dashed) and magnetic field on-axis $B_0$![]() (dotted) with respect to the toroidal angle $\phi$
(dotted) with respect to the toroidal angle $\phi$![]() of the magnetic axis used in the construction of an $N=3$
of the magnetic axis used in the construction of an $N=3$![]() equilibria. Curvature has zeros of first order at multiples of ${\rm \pi} /3$
equilibria. Curvature has zeros of first order at multiples of ${\rm \pi} /3$![]() , corresponding to extrema of $B_0$
, corresponding to extrema of $B_0$![]() . Torsion has a second-order zero at minima of $B_0$
. Torsion has a second-order zero at minima of $B_0$![]() , $\varphi _{\mathrm {min}}^{i}$
, $\varphi _{\mathrm {min}}^{i}$![]() .
.
Using this axis, an $N=3$![]() , QI boundary was constructed for $A=20$
, QI boundary was constructed for $A=20$![]() , with a magnetic field on-axis given by
, with a magnetic field on-axis given by
$d(\varphi ) = 1.03\kappa ^{s}$![]() and the parameter $k$
and the parameter $k$![]() entering equation (4.6) set to $2$
entering equation (4.6) set to $2$![]() . The resulting plasma boundary and the magnetic field strength on it as found by VMEC are shown in figure 16, where we can observe straight sections around $\varphi _{\mathrm {min}}$
. The resulting plasma boundary and the magnetic field strength on it as found by VMEC are shown in figure 16, where we can observe straight sections around $\varphi _{\mathrm {min}}$![]() , as a consequence of the axis choice. Figure 17 shows the contours of $|B|$
, as a consequence of the axis choice. Figure 17 shows the contours of $|B|$![]() as calculated by VMEC and from the near-axis construction in Boozer coordinates. At this aspect ratio most of the contours still close poloidally, as necessary for quasi-isodynamicity. The magnetic field contours are less straight around the point of maximum $B_{0}$
as calculated by VMEC and from the near-axis construction in Boozer coordinates. At this aspect ratio most of the contours still close poloidally, as necessary for quasi-isodynamicity. The magnetic field contours are less straight around the point of maximum $B_{0}$![]() , which is expected because this is the region where $\alpha (\varphi )$
, which is expected because this is the region where $\alpha (\varphi )$![]() deviates from a perfectly omnigenous form.
deviates from a perfectly omnigenous form.

Figure 16. Intensity of the magnetic field on the plasma boundary for a three field period, $A=20$![]() configuration: (a) side view and (b) top view.
configuration: (a) side view and (b) top view.

Figure 17. Contours of the magnetic field intensity on the boundary, for $N=3$![]() , $A=20$
, $A=20$![]() , as calculated by VMEC (solid lines) and from the near-axis construction (dotted lines).
, as calculated by VMEC (solid lines) and from the near-axis construction (dotted lines).
Zero torsion around the bottom of the magnetic well was chosen, together with $d(\varphi )$![]() , as an attempt to reduce the elongation of the plasma boundary, as described in § 5. In figure 18 we see the cross-sections of the plasma boundary for different values of toroidal angle on the left and the evolution of elongation with the toroidal angle. The maximum elongation for this configuration is $e_\mathrm {max}=3.2$
, as an attempt to reduce the elongation of the plasma boundary, as described in § 5. In figure 18 we see the cross-sections of the plasma boundary for different values of toroidal angle on the left and the evolution of elongation with the toroidal angle. The maximum elongation for this configuration is $e_\mathrm {max}=3.2$![]() , and includes regions where the elongation is nearly $e=1$
, and includes regions where the elongation is nearly $e=1$![]() , the case of a circular cross-section. We also observe that the elongation remains low around the region where torsion vanishes. These facts seem to validate our approach for controlling elongation, and demonstrate that high elongation is not a necessary sacrifice for achieving good omnigenity in QI stellarators, as might be feared from previous results, for example W7-X (Grieger et al. Reference Grieger, Lotz, Merkel, Nührenberg, Sapper, Strumberger, Wobig, Burhenn, Erckmann and Gasparino1992) with a maximum elongation around $e_{\mathrm {max}}\gtrsim 4.5$
, the case of a circular cross-section. We also observe that the elongation remains low around the region where torsion vanishes. These facts seem to validate our approach for controlling elongation, and demonstrate that high elongation is not a necessary sacrifice for achieving good omnigenity in QI stellarators, as might be feared from previous results, for example W7-X (Grieger et al. Reference Grieger, Lotz, Merkel, Nührenberg, Sapper, Strumberger, Wobig, Burhenn, Erckmann and Gasparino1992) with a maximum elongation around $e_{\mathrm {max}}\gtrsim 4.5$![]() , or the NAE configuration described by Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho and Helander2022) and QIPC (Subbotin et al. Reference Subbotin, Mikhailov, Shafranov, Isaev, Nührenberg, Nührenberg, Zille, Nemov, Kasilov and Kalyuzhnyj2006), both with maximum elongations higher than $e_{\mathrm {max}}\gtrsim 5$
, or the NAE configuration described by Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho and Helander2022) and QIPC (Subbotin et al. Reference Subbotin, Mikhailov, Shafranov, Isaev, Nührenberg, Nührenberg, Zille, Nemov, Kasilov and Kalyuzhnyj2006), both with maximum elongations higher than $e_{\mathrm {max}}\gtrsim 5$![]() .
.

Figure 18. (a) Cross sections of the plasma boundary for different values of the toroidal angle $\phi$![]() , and (b) elongation with respect to the cylindrical toroidal angle $\phi$
, and (b) elongation with respect to the cylindrical toroidal angle $\phi$![]() .
.
The rotational transform profile obtained with VMEC is shown in figure 19(a) and coincides with the value calculated numerically from (2.6), ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota} = 0.375$![]() . The effective ripple, $\epsilon _{\mathrm {eff}}$
. The effective ripple, $\epsilon _{\mathrm {eff}}$![]() , was found to be lower than 1 % throughout the plasma volume, another indication of the closeness of the solution to omnigenity. The value at different distances from the axis is shown in figure 19(b).
, was found to be lower than 1 % throughout the plasma volume, another indication of the closeness of the solution to omnigenity. The value at different distances from the axis is shown in figure 19(b).

Figure 19. (a) Rotational transform, ${\style{display: inline-block; transform: rotate(31deg)}{\raise1.5pt{\tiny{/}}}\kern-1.4pt\iota}$![]() , and (b) effective ripple $\epsilon _{\mathrm {eff}}$
, and (b) effective ripple $\epsilon _{\mathrm {eff}}$![]()
9 Conclusion
We have described in detail the NAE method to construct QI, stellarator symmetric, single-magnetic-well equilibria with $N\geqslant 1$![]() field periods, valid at first order in the distance from the magnetic axis. A new way of achieving better continuity and smoothness of these configurations, as compared with the previous method of Plunk et al. (Reference Plunk, Landreman and Helander2019), has been introduced and used to construct equilibria with $N>1$
field periods, valid at first order in the distance from the magnetic axis. A new way of achieving better continuity and smoothness of these configurations, as compared with the previous method of Plunk et al. (Reference Plunk, Landreman and Helander2019), has been introduced and used to construct equilibria with $N>1$![]() .
.
The problem of finding axis shapes compatible with the NAE is discussed, in particular the order of zeros in axis curvature, and the naturally arising increase of torsion for increasing number of field periods, which we argue is an underlying reason for the deterioration of the approximation at finite aspect ratio. A method to systematically describe and construct closed curves with zeros of curvature and torsion, at different orders, at toroidal locations of extrema of the magnetic field strength has also been presented.
We have demonstrated the validity of the NAE method, with a two-field-period example, by showing that the difference between the magnetic field as calculated by the NAE and that obtained using the equilibrium code VMEC falls with increasing aspect ratio, and scales as $1/A^2$![]() , as expected from a first-order expansion. We describe the construction of this two-field-period configuration, and find that it has good confinement, as shown by $\epsilon _{\mathrm {eff}}<2\,\%$
, as expected from a first-order expansion. We describe the construction of this two-field-period configuration, and find that it has good confinement, as shown by $\epsilon _{\mathrm {eff}}<2\,\%$![]() throughout the plasma volume at aspect ratio $A=10$
throughout the plasma volume at aspect ratio $A=10$![]() .
.
We have also constructed a family of solutions, for $N=2,3,4$![]() , having axes with constant torsion, and very similar per-field-period initial parameters. The approximate omnigenity of these solutions deteriorates if the number of field periods is increased. This example shows the importance of reducing the maximum torsion of the axis to achieve equilibria close to omnigenity at low aspect ratio.
, having axes with constant torsion, and very similar per-field-period initial parameters. The approximate omnigenity of these solutions deteriorates if the number of field periods is increased. This example shows the importance of reducing the maximum torsion of the axis to achieve equilibria close to omnigenity at low aspect ratio.
In the last section we have demonstrated how the choice of an axis with zero torsion around the point of minimum magnetic field strength and constrained maximum torsion enables us to find a three-field-period configuration with low elongation and small neoclassical transport. The effective ripple remains at under $1\,\%$![]() for an aspect ratio $A=20$
for an aspect ratio $A=20$![]() , and the maximum elongation $e_{\mathrm {max}}=3.2$
, and the maximum elongation $e_{\mathrm {max}}=3.2$![]() , demonstrating that low elongation is achievable in QI stellarators.
, demonstrating that low elongation is achievable in QI stellarators.
These configurations demonstrate that the NAE method can be used to construct magnetic equilibria with multiple field periods that maintain good confinement properties at low aspect ratios. We emphasise that these examples were all obtained without the need for numerically costly optimisation procedures.
Given the importance of the axis shape in the quality of the equilibrium, a natural next step is to reintroduce an element of optimisation, as done for the one-field-period example of Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho and Helander2022), but appropriately restricting the search space. Specifically, we can define an optimisation space according to classes of axis curves satisfying prescribed conditions on the torsion and curvature, and search this space for configurations with attractive properties. Another interesting analysis, which can be performed thanks to the speedy calculation of solutions enabled by the NAE, is to systematically and exhaustively map the space of QI solutions and its dependence on the input functions used for the construction. Such exploration might allow physical insight to be gained into the structure of the solution space and help explain certain difficulties associated with traditional optimisation techniques.
In this work, as well as in Plunk et al. (Reference Plunk, Landreman and Helander2019), the focus has been on introducing deviations to quasi-isodynamicity near the field maxima to target deeply trapped particles. Current work is being done on breaking omnigenity at other toroidal regions in order to improve confinement of different classes of trapped particles.
The only shaping of the plasma boundary that enters at first order in the NAE is the elongation of the elliptical cross-sections. Using solutions generated at higher order, together with traditional optimisation procedures also seems a promising way for obtaining configurations with better confinement properties and stronger shaping.
Acknowledgements
The authors would like to thank Matt Landreman for providing the numerical code, described in Plunk et al. (Reference Plunk, Landreman and Helander2019), which was adapted for the present study. We are grateful to Michael Drevlak for providing the code used for calculating the effective ripple and for fruitful discussions. We would also like to thank Per Helander for useful feedback during the preparation of the manuscript.
Editor Peter Catto thanks the referees for their advice in evaluating this article.
Funding
This work was partly supported by a grant from the Simons Foundation (560651, KCM).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Smoother $\alpha (\varphi )$
The behaviour of $\alpha (\varphi )$![]() around $\varphi _{\mathrm {max}}$
around $\varphi _{\mathrm {max}}$![]() , where omnigenity is broken in a controlled way, can have a detrimental effect on the smoothness of the QI solutions constructed using the NAE.
, where omnigenity is broken in a controlled way, can have a detrimental effect on the smoothness of the QI solutions constructed using the NAE.
In order to avoid this problems, a form of $\alpha$![]() with continuous derivatives up to second order is proposed
with continuous derivatives up to second order is proposed
To find the coefficients $a$![]() and $b$
and $b$![]() , we check for continuity at $\varphi _{\mathrm {max}}^{i}$
, we check for continuity at $\varphi _{\mathrm {max}}^{i}$![]()
which is equivalent to

and grouping terms we obtain
From expression (A1), we note that all even derivatives of $\alpha _{\mathrm {II}}$![]() with respect to $\varphi$
with respect to $\varphi$![]() have odd powers of $(\varphi -\varphi _{\mathrm {min}}^{i})$
have odd powers of $(\varphi -\varphi _{\mathrm {min}}^{i})$![]() , so $\textrm {d}^{2n}\alpha _{\mathrm {II}}/\textrm {d}\varphi ^{2n}$
, so $\textrm {d}^{2n}\alpha _{\mathrm {II}}/\textrm {d}\varphi ^{2n}$![]() is opposite in sign, for $n\geqslant 1$
is opposite in sign, for $n\geqslant 1$![]() , at $\varphi ^{i}_{\mathrm {max}}$
, at $\varphi ^{i}_{\mathrm {max}}$![]() when approaching from the left and from the right, hence continuity requires all even derivatives to be zero at this points. We now impose the following condition on the second derivative:
when approaching from the left and from the right, hence continuity requires all even derivatives to be zero at this points. We now impose the following condition on the second derivative:

and solve for $b$![]() ,
,
where $\nu$![]() is given by
is given by
Next, we substitute this expression for $b$![]() into (A4)
into (A4)
from where we find an expression for $a$![]()
and following the same process we obtain an expression for $b$![]()
For the case of odd derivatives of $\alpha _{\mathrm {II}}$![]() , we obtain even powers of $(\varphi -\varphi _{\mathrm {min}}^{i})$
, we obtain even powers of $(\varphi -\varphi _{\mathrm {min}}^{i})$![]() , so all odd derivatives are automatically continuous at $\varphi _{\mathrm {max}}$
, so all odd derivatives are automatically continuous at $\varphi _{\mathrm {max}}$![]() due to symmetry of the magnetic wells. As a consequence, expression (A1) with $a$
due to symmetry of the magnetic wells. As a consequence, expression (A1) with $a$![]() and $b$
and $b$![]() given by (A9) and (A10) is smooth and continuous up to third-order derivatives.
given by (A9) and (A10) is smooth and continuous up to third-order derivatives.
Appendix B. Axis shapes
We use the Fourier axis representation as described in § 5. A local form is also needed to establish conditions on the derivatives of these functions about points of stellarator symmetry (also coinciding with an extrema of $B_0(\phi )$![]() ). A Taylor expansion is used as this local form, and can be then used to generate a linear system of equations on the Fourier coefficients. These points are given at $\phi = n {\rm \pi}/N$
). A Taylor expansion is used as this local form, and can be then used to generate a linear system of equations on the Fourier coefficients. These points are given at $\phi = n {\rm \pi}/N$![]() for arbitrary integer $n$
for arbitrary integer $n$![]() , but without loss of generality we take the point to be $\phi =0$
, but without loss of generality we take the point to be $\phi =0$![]() (and perform any necessary shifts later)
(and perform any necessary shifts later)
From the stellarator-symmetric forms of $R$![]() and $z$
and $z$![]() , one significant fact should be noted: the only stellarator-symmetric planar curves are those with $z=0$
, one significant fact should be noted: the only stellarator-symmetric planar curves are those with $z=0$![]() for all $\phi$
for all $\phi$![]() (excluding the trivial ‘tilted’ one with $N=1$
(excluding the trivial ‘tilted’ one with $N=1$![]() ). As we will see, stellarator-symmetric axis curves that are consistent with omnigenity require $z\neq 0$
). As we will see, stellarator-symmetric axis curves that are consistent with omnigenity require $z\neq 0$![]() , and therefore must be non-planar, and possess finite torsion. (As experience shows, attempts to tune the axis shape for low torsion in one region, result in large torsion elsewhere.)
, and therefore must be non-planar, and possess finite torsion. (As experience shows, attempts to tune the axis shape for low torsion in one region, result in large torsion elsewhere.)
The curvature and torsion of general parameterisation of a curve are given by
where primes denote differentiation with respect to $\phi$![]() . Noting $\textrm {d}\hat {\boldsymbol {R}}/\textrm {d}\phi = \hat {\boldsymbol {\phi }}$
. Noting $\textrm {d}\hat {\boldsymbol {R}}/\textrm {d}\phi = \hat {\boldsymbol {\phi }}$![]() and $\textrm {d}\hat {\boldsymbol {\phi }} /\textrm {d}\phi = -\hat {\boldsymbol {R}}$
and $\textrm {d}\hat {\boldsymbol {\phi }} /\textrm {d}\phi = -\hat {\boldsymbol {R}}$![]() , it is straightforward to compute these derivatives. Further substituting the expansions for $R$
, it is straightforward to compute these derivatives. Further substituting the expansions for $R$![]() and $z$
and $z$![]() , (B1)–(B2), the contributions to each derivative can be collected by their order in $\phi$
, (B1)–(B2), the contributions to each derivative can be collected by their order in $\phi$![]() , the following (possibly useful) properties can be confirmed:
, the following (possibly useful) properties can be confirmed:
where the subscript $m$![]() denotes the order in $\phi$
denotes the order in $\phi$![]() .
.
We classify the zeros in curvature and torsion by the order of the first non-zero term in the power series, for example,
where it is assumed that $\phi > 0$![]() ; this is necessary to fix the sign of the coefficients noting that $\kappa > 0$
; this is necessary to fix the sign of the coefficients noting that $\kappa > 0$![]() by convention. Likewise, the first non-zero term in the power series expansion of $\tau$
by convention. Likewise, the first non-zero term in the power series expansion of $\tau$![]() determines its order:
determines its order:
We can denote the two constraints by the pair $(m, n)$![]() corresponding to the order of the curvature and torsion zeros, respectively.
corresponding to the order of the curvature and torsion zeros, respectively.
B.1 Conditions on curvature
Assuming that $\boldsymbol {x}^\prime$![]() is itself non-zero, the conditions on zeros in curvature are found by requiring
is itself non-zero, the conditions on zeros in curvature are found by requiring
at each order in $\phi$![]() . At zeroth order, $\boldsymbol {x}^{\prime \prime }$
. At zeroth order, $\boldsymbol {x}^{\prime \prime }$![]() has its only non-zero component in the $\hat {\boldsymbol {R}}$
has its only non-zero component in the $\hat {\boldsymbol {R}}$![]() direction, and the condition $\boldsymbol {x}^\prime \times \boldsymbol {x}^{\prime \prime } = 0$
direction, and the condition $\boldsymbol {x}^\prime \times \boldsymbol {x}^{\prime \prime } = 0$![]() is satisfied by $\boldsymbol {x}^{\prime \prime }\boldsymbol {\cdot }\hat {\boldsymbol {R}} = 0$
is satisfied by $\boldsymbol {x}^{\prime \prime }\boldsymbol {\cdot }\hat {\boldsymbol {R}} = 0$![]() , which results in the condition
, which results in the condition
For reference, note that the full expression for curvature is obtained from (B3) as
The curvature can be made zero to higher order by considering higher-order contributions to $\boldsymbol {x}^{\prime \prime }$![]() . At odd orders, these are contained in the $\hat {\boldsymbol {\phi }} -\hat {\boldsymbol {z}}$
. At odd orders, these are contained in the $\hat {\boldsymbol {\phi }} -\hat {\boldsymbol {z}}$![]() plane and must be made parallel to the zeroth-order contribution from $\boldsymbol {x}^\prime$
plane and must be made parallel to the zeroth-order contribution from $\boldsymbol {x}^\prime$![]() , whereas at even orders, the even-order contribution to $\boldsymbol {x}^{\prime \prime }$
, whereas at even orders, the even-order contribution to $\boldsymbol {x}^{\prime \prime }$![]() must simply be zero. Thus, conditions at arbitrary order can be obtained, and a few are listed in table 1.
must simply be zero. Thus, conditions at arbitrary order can be obtained, and a few are listed in table 1.
Table 1. Conditions for zero curvature.

As already noted, only odd-order zeros in curvature are consistent with omnigenity in the NAE. Thus, we apply these conditions only up to and including some even order. Note that planar curves (for which $z = 0$![]() ) are inconsistent with odd orders of zero in curvature, which means non-zero torsion is required for the class of configurations being considered here.
) are inconsistent with odd orders of zero in curvature, which means non-zero torsion is required for the class of configurations being considered here.
B.2 Conditions on torsion
We find curves with zero torsion to some order of accuracy in the local expansion about points of stellarator symmetry. It is assumed that the curvature is zero to some order at these points. This implies that curves of zero torsion, which are approximately planar curves, fall into one of two classes: (1) curves lying within the plane perpendicular to $\hat {\boldsymbol {x}} = \hat {\boldsymbol {R}}(0)$![]() and (2) curves lying within the plane perpendicular to a constant unit vector $\hat {\boldsymbol {n}}(t) = \cos (t)\hat {\boldsymbol {z}} + \sin (t)\hat {\boldsymbol {y}}$
and (2) curves lying within the plane perpendicular to a constant unit vector $\hat {\boldsymbol {n}}(t) = \cos (t)\hat {\boldsymbol {z}} + \sin (t)\hat {\boldsymbol {y}}$![]() , where $\hat {\boldsymbol {y}} = \hat {\boldsymbol {\phi }}(0)$
, where $\hat {\boldsymbol {y}} = \hat {\boldsymbol {\phi }}(0)$![]() , and $t$
, and $t$![]() is arbitrary.
is arbitrary.
The two classes arise in the expansion itself: let us inspect the first non-zero contribution to the numerator and denominator of the expression for the torsion (assuming a first-order zero of curvature, i.e. $R_2 = R_0$![]() )
)
which assuming $z_3 \neq 2 z_1$![]() yields a result for the torsion at $\phi = 0$
yields a result for the torsion at $\phi = 0$![]()
Thus, if the curvature is zero to first order, but not second order, we obtain a condition on the torsion being zero, $5 R_0 = R_4$![]() . The second class of curves with zero torsion is obtained by repeating this calculation assuming $z_3 = 2 z_1$
. The second class of curves with zero torsion is obtained by repeating this calculation assuming $z_3 = 2 z_1$![]() from the outset, but this is precisely the condition that curvature is zero to second order; it is also the condition that the curve lies within the described plane, and it can be derived independently by imposing the condition $\hat {\boldsymbol {n}}\boldsymbol {\cdot }\boldsymbol {x}^{\prime } = 0$
from the outset, but this is precisely the condition that curvature is zero to second order; it is also the condition that the curve lies within the described plane, and it can be derived independently by imposing the condition $\hat {\boldsymbol {n}}\boldsymbol {\cdot }\boldsymbol {x}^{\prime } = 0$![]() to first order in $\phi$
to first order in $\phi$![]() . Even-order zeros, however, are not consistent with near-axis QI configurations.
. Even-order zeros, however, are not consistent with near-axis QI configurations.
In the following we calculate the conditions for the torsion, order-by-order, assuming a number of conditions are also satisfied related to curvature. The relevant cases included in table 1 are first, third and fifth order zeros of curvature. The torsion constraints are given in tables 2, 3 and 4.
Table 2. Conditions for zero torsion, assuming first-order zero in curvature.

Table 3. Conditions for zero torsion, assuming third-order zero in curvature.

Table 4. Conditions for zero torsion, assuming third-order zero in curvature.

B.3 Truncated Fourier representations of axis curves
The tabulated constraints on the derivatives of the axis components can be applied to a truncated Fourier representation. Equations (5.11)–(5.12) are simply substituted into the constraint equations with $\phi$![]() set to a location of stellarator symmetry (for instance, at $\phi = 0, {\rm \pi}/N$
set to a location of stellarator symmetry (for instance, at $\phi = 0, {\rm \pi}/N$![]() in the first period). This results in a set of linear conditions on the Fourier coefficients that can be solved numerically, or by computer algebra.
in the first period). This results in a set of linear conditions on the Fourier coefficients that can be solved numerically, or by computer algebra.
As a very simple example, one may consider a symmetric class of curves, as in Plunk et al. (Reference Plunk, Landreman and Helander2019) and described in § 5.1.
Curve classes can, of course, also be defined without the above symmetry (retaining odd harmonics), requiring derivative constraints to be applied separately at $\phi = 0$![]() and $\phi = {\rm \pi}/N$
and $\phi = {\rm \pi}/N$![]() . For example, consider
. For example, consider
Then, applying $R_2 = R_0$![]() at both $\phi = 0$
at both $\phi = 0$![]() and $\phi = {\rm \pi}/N$
and $\phi = {\rm \pi}/N$![]() , gives
, gives
These are just the simplest cases, with only a zeroth-order condition for curvature being used. Note that different sets of derivative constraints can be applied to these two locations, to get curves with different orders of zeros in torsion and curvature at the locations of maximum and minimum magnetic field strength. The orders of the zeros, together with the set of Fourier coefficients, define a space that can be used for further optimisation.