1 Introduction
Modal logics are one of the most developed and studied families of non-classical logics, exhibiting a beautiful equilibrium between complexity and expressivity. Generalizations of the concepts of necessity and possibility offer a rich setting to model and study notions from many different areas, including provability predicates, temporal and epistemic concepts, work-flows in software applications, etc. On the other hand, many-valued logics provide a formal framework to manage gradual and resource sensitive information in a very general and adaptable way. In this work, we will focus our attention in the so-called continuous t-norm fuzzy logics, a family of many-valued logics that has received special interest due to, among other properties, their completeness with respect to algebras on the real unit interval
![]() $[0,1]$
and their ability to capture the natural order with the implication operation. Modal many-valued logics lie at the intersection of both modal and many-valued logics, extending many-valued logics with modal-like operators.
$[0,1]$
and their ability to capture the natural order with the implication operation. Modal many-valued logics lie at the intersection of both modal and many-valued logics, extending many-valued logics with modal-like operators.
This paper contributes to the problems of axiomatizability and decidability in these logics. We first show that global modal Łukasiewicz (Ł) and Product (
![]() $\varPi $
) logics are undecidable, and we later refine those results to prove that they do not belong to
$\varPi $
) logics are undecidable, and we later refine those results to prove that they do not belong to
![]() $\varSigma _1$
. Since the modal logics we investigate can be seen as fragments of the corresponding first order (F.O.) many-valued logics, our results likewise affect these fragments and the corresponding model theory [Reference Hájek and Cintula28]. On the other hand, the categorical equivalence between MV algebras (the algebraic semantics of Łukasiewicz logic) and abelian lattice-ordered groups with a strong unit [Reference Chang18, Reference Cignoli, D’Ottaviano and Mundici19] directly relate the results shown here to the theory of
$\varSigma _1$
. Since the modal logics we investigate can be seen as fragments of the corresponding first order (F.O.) many-valued logics, our results likewise affect these fragments and the corresponding model theory [Reference Hájek and Cintula28]. On the other hand, the categorical equivalence between MV algebras (the algebraic semantics of Łukasiewicz logic) and abelian lattice-ordered groups with a strong unit [Reference Chang18, Reference Cignoli, D’Ottaviano and Mundici19] directly relate the results shown here to the theory of
![]() $\ell $
-groups. Moreover, since the propositional basis of continuous logics [Reference Chang and Jerome Keisler17, Reference Ben Yaacov and Pedersen48] (namely, the logical system proposed to study the so-called continuous model theory) coincides with Łukasiewicz logic with an additional definable constant, our results also apply to modal continuous logics [Reference Baratella5, Reference Baratella6] and to fragments of F.O. continuous logics [Reference Ben Yaacov and Pedersen48, Reference Ben Yaacov and Usvyatsov49], with the natural ramifications towards continuous model theory. Lastly, the field of modal many-valued logics is intrinsically related to that of fuzzy description logics (FDL) [Reference Straccia41], which also makes the results presented in this paper applicable to certain FDLs over the standard Łukasiewicz and Product algebras (namely, over the real unit interval
$\ell $
-groups. Moreover, since the propositional basis of continuous logics [Reference Chang and Jerome Keisler17, Reference Ben Yaacov and Pedersen48] (namely, the logical system proposed to study the so-called continuous model theory) coincides with Łukasiewicz logic with an additional definable constant, our results also apply to modal continuous logics [Reference Baratella5, Reference Baratella6] and to fragments of F.O. continuous logics [Reference Ben Yaacov and Pedersen48, Reference Ben Yaacov and Usvyatsov49], with the natural ramifications towards continuous model theory. Lastly, the field of modal many-valued logics is intrinsically related to that of fuzzy description logics (FDL) [Reference Straccia41], which also makes the results presented in this paper applicable to certain FDLs over the standard Łukasiewicz and Product algebras (namely, over the real unit interval
![]() $[0,1]$
).
$[0,1]$
).
The notion of modal many-valued logic studied in this paper follows the tradition initiated by Fitting [Reference Fitting22, Reference Fitting23] and Hájek [Reference Hájek26, Reference Hájek and Harmancová29], which differs from another relevant definition of so-called modal substructural logics studied for instance in [Reference Kamide31, Reference Ono, Došen and Schroeder-Heister33, Reference Restall38]. The logics studied in this work are defined over valued Kripke models: Kripke frames
![]() enriched with a world-wise evaluationFootnote
1
of the formulas
enriched with a world-wise evaluationFootnote
1
of the formulas
![]() $e \colon W \times Fm \rightarrow \mathbf {A}$
into some algebra
$e \colon W \times Fm \rightarrow \mathbf {A}$
into some algebra
![]() $\mathbf {A}$
, and where
$\mathbf {A}$
, and where
![]() $\square , \Diamond $
are unary operators generalizing those of classical modal logic. The operators
$\square , \Diamond $
are unary operators generalizing those of classical modal logic. The operators
![]() $\square $
and
$\square $
and
![]() $\Diamond $
are not inter-definable in general [Reference Rodriguez and Vidal39] in the minimal logics, and the logics with the two modalities might not be axiomatized by the addition of the axiomatic systems of the mono-modal (i.e., with only the
$\Diamond $
are not inter-definable in general [Reference Rodriguez and Vidal39] in the minimal logics, and the logics with the two modalities might not be axiomatized by the addition of the axiomatic systems of the mono-modal (i.e., with only the
![]() $\square $
or the
$\square $
or the
![]() $\Diamond $
operator) fragments. Their respective computational behavior might also differ. The previous facts imply that each one of these fragments needs to be, in general, separately studied. On the other hand, the so-called local and global logics’ derivations arising from these models refer to the interpretation of the premises and conclusion in the derivability relation. In the former case they are considered world-wise, while in the latter the premises should hold in the whole model. These two semantics behave with respect to the F.O. semantics of the corresponding many-valued logic in the analogous way to the classical case and in Fisher–Servi Intuitionistic modal logic [Reference Fischer-Servi21].
$\Diamond $
operator) fragments. Their respective computational behavior might also differ. The previous facts imply that each one of these fragments needs to be, in general, separately studied. On the other hand, the so-called local and global logics’ derivations arising from these models refer to the interpretation of the premises and conclusion in the derivability relation. In the former case they are considered world-wise, while in the latter the premises should hold in the whole model. These two semantics behave with respect to the F.O. semantics of the corresponding many-valued logic in the analogous way to the classical case and in Fisher–Servi Intuitionistic modal logic [Reference Fischer-Servi21].
We will begin by addressing the question of the decidability of modal many-valued logics for minimal logics (namely, those that do not restrict the class of models). It is known that, in contrast to F.O. logic, which is undecidable, the minimal (classical) modal logic K is, as propositional logic, decidable. In many-valued logics, similarly, F.O. logics are in most cases undecidable, while the propositional cases are usually co-NP complete. Nevertheless, while it is known that classical F.O. logic is
![]() $\varSigma _1$
-complete, tautologies of F.O. over the standard Łukasiewicz algebra form a
$\varSigma _1$
-complete, tautologies of F.O. over the standard Łukasiewicz algebra form a
![]() $\varPi _2$
complete set [Reference Ragaz36, Reference Ragaz37], and those over the standard Product algebra are
$\varPi _2$
complete set [Reference Ragaz36, Reference Ragaz37], and those over the standard Product algebra are
![]() $\varPi _2$
-hard [Reference Hájek26]. Regarding modal many-valued logics, the known results about decidability are rather partial. Gödel modal logics do not enjoy in general the finite model property with respect to the intended semantics [Reference Caicedo and Rodriguez12]. Interestingly enough, in [Reference Balbiani, Diéguez and Fernández-Duque4, Reference Caicedo, Metcalfe, Rodríguez, Rogger, Libkin, Kohlenbach and de Queiroz10, Reference Caicedo, Metcalfe, Rodríguez and Rogger11], the decidability of the local consequence relation for the minimal mono-modal and bi-modal logics, as well as for the S4 and S5 extensions, is proven. However, regarding the ongoing work, we mention that the decidability of the global consequence over the previous classes of models is still an open problem. It is also known that the minimal local modal (standard) Łukasiewicz and Product logics are decidable [Reference Vidal42, Reference Vidal44]. On the other hand, in [Reference Vidal42], the undecidability of the local deductions over transitive models, valued respectively over the standard Łukasiewicz and Product algebras is shown. Some additional decidability results have been proven in the context of modal many-valued logics where the accessibility relation of the Kripke models is also many-valued over the corresponding algebra. These results arise indirectly from the studies over Fuzzy Description Logics, which can be roughly interpreted as a fragment of multi-modal logic with many-valued accessibility and explicit rational constants, and where additional connectives are often included. Concerning the pure Łukasiewicz and Product FDL, in [Reference Baader and Peñaloza1, Reference Baader and Peñaloza2, Reference Borgwardt, Distel and Peñaloza7, Reference Cerami and Esteva14] (see [Reference Cerami, Esteva and Garcia-Cerdaña15] for a presentation of the previous results expressed in a modal logic setting) it is proven that the r-satisfiability question (for r rational) is undecidable for the global modal Product and Łukasiewicz cases, while the local r-satisfiability problems are decidable. Nevertheless, the problems of validity and logical entailment remains open also for these modal logics with many-valued accessibility. More pertinently for the present paper, the fact that the accessibility relation is many-valued seems to be unavoidable in all the above proofs, which has shed little light on the setting based on classical Kripke frames.Footnote
2
$\varPi _2$
-hard [Reference Hájek26]. Regarding modal many-valued logics, the known results about decidability are rather partial. Gödel modal logics do not enjoy in general the finite model property with respect to the intended semantics [Reference Caicedo and Rodriguez12]. Interestingly enough, in [Reference Balbiani, Diéguez and Fernández-Duque4, Reference Caicedo, Metcalfe, Rodríguez, Rogger, Libkin, Kohlenbach and de Queiroz10, Reference Caicedo, Metcalfe, Rodríguez and Rogger11], the decidability of the local consequence relation for the minimal mono-modal and bi-modal logics, as well as for the S4 and S5 extensions, is proven. However, regarding the ongoing work, we mention that the decidability of the global consequence over the previous classes of models is still an open problem. It is also known that the minimal local modal (standard) Łukasiewicz and Product logics are decidable [Reference Vidal42, Reference Vidal44]. On the other hand, in [Reference Vidal42], the undecidability of the local deductions over transitive models, valued respectively over the standard Łukasiewicz and Product algebras is shown. Some additional decidability results have been proven in the context of modal many-valued logics where the accessibility relation of the Kripke models is also many-valued over the corresponding algebra. These results arise indirectly from the studies over Fuzzy Description Logics, which can be roughly interpreted as a fragment of multi-modal logic with many-valued accessibility and explicit rational constants, and where additional connectives are often included. Concerning the pure Łukasiewicz and Product FDL, in [Reference Baader and Peñaloza1, Reference Baader and Peñaloza2, Reference Borgwardt, Distel and Peñaloza7, Reference Cerami and Esteva14] (see [Reference Cerami, Esteva and Garcia-Cerdaña15] for a presentation of the previous results expressed in a modal logic setting) it is proven that the r-satisfiability question (for r rational) is undecidable for the global modal Product and Łukasiewicz cases, while the local r-satisfiability problems are decidable. Nevertheless, the problems of validity and logical entailment remains open also for these modal logics with many-valued accessibility. More pertinently for the present paper, the fact that the accessibility relation is many-valued seems to be unavoidable in all the above proofs, which has shed little light on the setting based on classical Kripke frames.Footnote
2
In this paper, we study the decidability of entailment from finite sets of premises in global modal logics. We show this question is undecidable for a large class of modal logics whose algebras of evaluation satisfy certain basic conditions (Theorem 3.2). This class includes the minimal (bi)modal logics over the standard Łukasiewicz and Product algebras. The main problem that remains open concerning the decidability of minimal modal logics based on continuous t-norm logics is that of the global bi-modal Gödel logic.
Since the previous undecidability results are proven using classes of finite models, it will be possible to refine them to answer open problems concerning the axiomatizability of the same logics. Let us briefly overview the known results and open questions concerning axiomatizability of the minimal modal fuzzy logics. In [Reference Caicedo and Rodriguez12, Reference Caicedo and Rodriguez13, Reference Metcalfe and Olivetti32, Reference Rodriguez and Vidal39] all the minimal modal logics associated with the standard Gödel algebra are axiomatized. This includes both local and global deductions of the two mono-modal fragments and of the bi-modal logic with both
![]() $\square $
and
$\square $
and
![]() $\Diamond $
. In [Reference Bou, Esteva, Godo and Rodríguez9], a general study is done of the logics with only
$\Diamond $
. In [Reference Bou, Esteva, Godo and Rodríguez9], a general study is done of the logics with only
![]() $\square $
arising from Kripke models valued over finite residuated lattices, including axiomatization of the local and global deductions. The axiomatic systems proposed there rely on the addition of canonical constantsFootnote
3
which among other things, make
$\square $
arising from Kripke models valued over finite residuated lattices, including axiomatization of the local and global deductions. The axiomatic systems proposed there rely on the addition of canonical constantsFootnote
3
which among other things, make
![]() $\square $
and
$\square $
and
![]() $\Diamond $
interdefinable in modal logics arising from Kripke models valued over finite algebras [Reference Vidal, Esteva and Godo47].
$\Diamond $
interdefinable in modal logics arising from Kripke models valued over finite algebras [Reference Vidal, Esteva and Godo47].
On the other hand, regarding modal Łukasiewicz (and the analogous continuous logic) and Product logics, the question of axiomatizability has not received a conclusive answer in the literature. The known results have proposed axiomatic systems that include some infinitary inference rule (i.e., with infinitely many premises), which are complete with respect to the infinitary deductions of the corresponding local or global logic. This solution is however nonconclusive, since there is no explicit axiomatization for any of the intended finitary consequence relations, and questions related to the complexity of the logics cannot be tackled as usual with an infinitary axiomatic system.Footnote
4
Regarding the (standard) Łukasiewicz case,Footnote
5
we find in [Reference Hansoul and Teheux30] an axiomatization of the infinitary local and global modal logics with an infinitary inference rule. Since the Łukasiewicz negation is involutive, in this case the
![]() $\square $
and
$\square $
and
![]() $\Diamond $
modal operators are inter-definable, and all minimal logics (in the sense of modal operators) coincide. For continuous modal logic an axiomatic system essentially equivalent to that in [Reference Hansoul and Teheux30] is proposed in [Reference Baratella5], still requiring an infinitary rule. A similar situation happens in subsequent works concerning the study of the (standard) modal Product logic [Reference Vidal, Esteva and Godo46] and other infinite linearly ordered residuated lattices [Reference Vidal43], where the proposed axiomatic systems require the extension of the logic with a dense countable set of constants, and an infinitary inference rule that quantifies over all the previous constants in the language. The cases studied in [Reference Vidal43, Reference Vidal, Esteva and Godo46] concern the logic with both
$\Diamond $
modal operators are inter-definable, and all minimal logics (in the sense of modal operators) coincide. For continuous modal logic an axiomatic system essentially equivalent to that in [Reference Hansoul and Teheux30] is proposed in [Reference Baratella5], still requiring an infinitary rule. A similar situation happens in subsequent works concerning the study of the (standard) modal Product logic [Reference Vidal, Esteva and Godo46] and other infinite linearly ordered residuated lattices [Reference Vidal43], where the proposed axiomatic systems require the extension of the logic with a dense countable set of constants, and an infinitary inference rule that quantifies over all the previous constants in the language. The cases studied in [Reference Vidal43, Reference Vidal, Esteva and Godo46] concern the logic with both
![]() $\square $
and
$\square $
and
![]() $\Diamond $
modalities, and to the best of our knowledge no works have studied the mono-modal fragments of these logics. Interestingly enough, in all the previous logics the infinitary rules are purely propositional, and result in the infinitary completeness of the corresponding propositional logic with respect to their corresponding algebraic semantics [Reference Hájek26, Reference Vidal, Bou, Esteva and Godo45].
$\Diamond $
modalities, and to the best of our knowledge no works have studied the mono-modal fragments of these logics. Interestingly enough, in all the previous logics the infinitary rules are purely propositional, and result in the infinitary completeness of the corresponding propositional logic with respect to their corresponding algebraic semantics [Reference Hájek26, Reference Vidal, Bou, Esteva and Godo45].
By proving that global modal Łukasiewicz and Product logics are not recursively enumerable we contribute to answering the previous open questions, since this implies these logics are not axiomatizable by an R.E. (finitary) axiomatization. These results can be seen in relation to the celebrated result by Scarpellini [Reference Scarpellini40] that states that the set of tautologies of the infinitely valued F.O. Łukasiewicz logic is not recursively enumerable (later refined in [Reference Ragaz36, Reference Ragaz37], proving that it is
![]() $\varPi _2$
-complete). Similarly, in [Reference Ragaz37], Ragaz also proved that the satisfiability problem for the monadic fragment of F.O. Łukasiewicz logic is
$\varPi _2$
-complete). Similarly, in [Reference Ragaz37], Ragaz also proved that the satisfiability problem for the monadic fragment of F.O. Łukasiewicz logic is
![]() $\varPi _1$
complete and undecidable in the presence of at least four symbols, and Bou showedFootnote
6
that validity in this fragment with at least two symbols is undecidable. The non-axiomatizability results for modal logics we present in this paper, when translated to F.O. Łukasiewicz and Product logics, imply that their respective two variable fragments are not recursively enumerable in the presence of at least three unary predicates and a binary one.Footnote
7
$\varPi _1$
complete and undecidable in the presence of at least four symbols, and Bou showedFootnote
6
that validity in this fragment with at least two symbols is undecidable. The non-axiomatizability results for modal logics we present in this paper, when translated to F.O. Łukasiewicz and Product logics, imply that their respective two variable fragments are not recursively enumerable in the presence of at least three unary predicates and a binary one.Footnote
7
In the last section of this paper, we study the relation between the local and the global modal deductions, particularly motivated by the peculiarities intrinsic to the Łukasiewicz case: while the local deduction (and so, the set of tautologies) is decidable (
![]() $\varDelta _1$
), the global deduction is not recursively enumerable (
$\varDelta _1$
), the global deduction is not recursively enumerable (
![]() $\varSigma _1$
). We will see that, as a consequence, the global deduction cannot be axiomatized by the local one extended with the usual necessitation rule (
$\varSigma _1$
). We will see that, as a consequence, the global deduction cannot be axiomatized by the local one extended with the usual necessitation rule (
![]() $\varphi \vdash \square \varphi $
). This contrasts with all other known cases in the literature and allows us to answer negatively this open question, raised in [Reference Bou, Esteva, Godo and Rodríguez9].
$\varphi \vdash \square \varphi $
). This contrasts with all other known cases in the literature and allows us to answer negatively this open question, raised in [Reference Bou, Esteva, Godo and Rodríguez9].
The paper is organized as follows. We start in Section 2 by introducing some necessary preliminaries. In Section 3 we study the decidability of a large family of residuated lattice-based global modal logics, and prove they are undecidable by reducing the Post Correspondence Problem to them. This includes the standard Łukasiewicz and Product cases. In Section 4 we obtain negative results concerning the axiomatization (in the usual finitary way) of some of the above logics, namely that the (finitary) global modal standard Łukasiewicz and Product logics are not recursively enumerable. We conclude the paper in Section 5 by showing that a global modal logic might fail to be axiomatized by an axiomatization of its corresponding logic plus the necessitation rule (which holds true for all logics from Section 3).
2 Preliminaries
In this work, a logic is identified with a consequence relation [Reference Font24], as opposed to only a set of formulas. While the second approach is more common in the literature of modal logics [Reference Chagrov and Zakharyaschev16], we opt for the former definition because the differences between local and global modal logics are lost if only the tautologies of the logic are considered. Observe that the lack of the Deduction Theorem in the global logic makes the implication and the logical consequence not interchangeable.
Given a set of variables
![]() $\mathcal {V}$
and an algebraic language
$\mathcal {V}$
and an algebraic language
![]() $\mathtt {L}$
, the set
$\mathtt {L}$
, the set
![]() $Fm^{\mathtt {L}}(\mathcal {V})$
is the set of formulas built from
$Fm^{\mathtt {L}}(\mathcal {V})$
is the set of formulas built from
![]() $\mathcal {V}$
using the symbols from
$\mathcal {V}$
using the symbols from
![]() $\mathtt {L}$
. Unless stated otherwise,
$\mathtt {L}$
. Unless stated otherwise,
![]() $\mathcal {V}$
is a fixed denumerable set, and it will be omitted in the notation of the set of formulas, and if the language is clear from the context we will omit it as well. A rule in
$\mathcal {V}$
is a fixed denumerable set, and it will be omitted in the notation of the set of formulas, and if the language is clear from the context we will omit it as well. A rule in
![]() $Fm$
is a pair
$Fm$
is a pair
![]() . We say a rule is finitary whenever
. We say a rule is finitary whenever
![]() $\varGamma $
is a finite set. A logic
$\varGamma $
is a finite set. A logic
![]() $\mathcal {L}$
over
$\mathcal {L}$
over
![]() $Fm$
is a consequence relation on
$Fm$
is a consequence relation on
![]() $Fm$
, that is, a set of rules such that
$Fm$
, that is, a set of rules such that
-
(1)
 $\mathcal {L}$
is reflexive, i.e., for every
$\mathcal {L}$
is reflexive, i.e., for every
 $\varGamma \subseteq Fm$
and every
$\varGamma \subseteq Fm$
and every
 $\gamma \in \varGamma $
,
$\gamma \in \varGamma $
,
 ,
, -
(2)
 $\mathcal {L}$
satisfies cut, i.e., if
$\mathcal {L}$
satisfies cut, i.e., if
 for all
for all
 $\phi \in \Phi $
, and
$\phi \in \Phi $
, and
 then
then
 ,
, -
(3)
 $\mathcal {L}$
is substitution invariant, i.e., for each substitution
$\mathcal {L}$
is substitution invariant, i.e., for each substitution
 $\sigma $
, if
$\sigma $
, if
 then
then
 .
.
Whenever
![]() we will write
we will write
![]() $\varGamma \vdash _{\mathcal {L}} \varphi $
. Given a set of rules R, we will write
$\varGamma \vdash _{\mathcal {L}} \varphi $
. Given a set of rules R, we will write
![]() $R^l$
to denote the minimal logic containing the rules in R. We say that a set of rules R axiomatizes a logic
$R^l$
to denote the minimal logic containing the rules in R. We say that a set of rules R axiomatizes a logic
![]() $\mathcal {L}$
whenever
$\mathcal {L}$
whenever
![]() $R^l = \mathcal {L}$
. Observe that in this sense, every logic is axiomatized at least by itself.
$R^l = \mathcal {L}$
. Observe that in this sense, every logic is axiomatized at least by itself.
With computational questions in mind, we will be focused on logics determined by finitary rules. A logic
![]() $\mathcal {L}$
is finitary whenever
$\mathcal {L}$
is finitary whenever
![]() $\varGamma \vdash _{\mathcal {L}} \varphi $
if and only if
$\varGamma \vdash _{\mathcal {L}} \varphi $
if and only if
![]() $\varGamma _0 \vdash _{\mathcal {L}} \varphi $
for some finite
$\varGamma _0 \vdash _{\mathcal {L}} \varphi $
for some finite
![]() $\varGamma _0 \subseteq _\omega \varGamma $
.Footnote
8
For convenience, we will denote by
$\varGamma _0 \subseteq _\omega \varGamma $
.Footnote
8
For convenience, we will denote by
![]() $\mathcal {L}^{fin}$
the set of finitary consequences of
$\mathcal {L}^{fin}$
the set of finitary consequences of
![]() $\mathcal {L}$
, namely
$\mathcal {L}$
, namely
![]() .
.
As it is most usual, in this work we do not consider infinite inputs for the computability questions. We say that a logic
![]() $\mathcal {L}$
is decidable, recursive, or recursively enumerable, respectively, if this is the case for the set
$\mathcal {L}$
is decidable, recursive, or recursively enumerable, respectively, if this is the case for the set
![]() $\mathcal {L}^{fin}$
.
$\mathcal {L}^{fin}$
.
When R is a set of finitary rules, the logic
![]() $R^l$
can be equivalently characterized through the usual notion of finite proofFootnote
9
in R. Given a finite set of formulas
$R^l$
can be equivalently characterized through the usual notion of finite proofFootnote
9
in R. Given a finite set of formulas
![]() $\varGamma \cup \{\varphi \}$
, a proof or derivation of
$\varGamma \cup \{\varphi \}$
, a proof or derivation of
![]() $\varphi $
from
$\varphi $
from
![]() $\varGamma $
in R is a finite list of formulas
$\varGamma $
in R is a finite list of formulas
![]() such that
such that
![]() $\psi _n = \varphi $
and for each
$\psi _n = \varphi $
and for each
![]() $\psi _i$
in the list, either
$\psi _i$
in the list, either
![]() $\psi _i \in \varGamma $
or there is a rule
$\psi _i \in \varGamma $
or there is a rule
![]() $\varSigma \vdash \phi $
in R and a substitution
$\varSigma \vdash \phi $
in R and a substitution
![]() $\sigma $
such that
$\sigma $
such that
![]() $\sigma (\phi ) = \psi _i$
and
$\sigma (\phi ) = \psi _i$
and
![]() $\sigma [\varSigma ]$
(possibly empty) is a subset of
$\sigma [\varSigma ]$
(possibly empty) is a subset of
![]() (or empty if
(or empty if
![]() $i = 1$
). It is well known that
$i = 1$
). It is well known that
![]() .
.
We will say that a logic is axiomatizable whenever it can be axiomatized using a recursive set of finitary rules. It is clear that an axiomatizable logic is finitary and R.E. On the other hand, a finitary R.E. logic with a definable idempotent n-ary operation for every n is always axiomatizable. This fact is a natural generalization of Craig’s Theorem, and it can be checked in a similar way. For the interested reader we provide the details in Section 7.
In the rest of the paper we will work with logics having such an idempotent operation (which will be simply
![]() $\wedge $
). Thereby we will resort without further notice to the following observation.
$\wedge $
). Thereby we will resort without further notice to the following observation.
Observation. A finitary logic is recursively enumerable if and only if it is axiomatizable.
Modal many-valued logics arise from Kripke structures evaluated over certain algebras, putting together relational and algebraic semantics in a way adapted to model different reasoning notions. In the next section, the general algebraic setting of these semantics will be the one of
![]() $FL_{ew}$
-algebras, the corresponding algebraic semantics of the Full Lambek Calculus with exchange and weakening. This will offer a very general approach to the topic while relying on well-known algebraic structures. We will later focus on modal expansions of MV and product algebras, particular classes of
$FL_{ew}$
-algebras, the corresponding algebraic semantics of the Full Lambek Calculus with exchange and weakening. This will offer a very general approach to the topic while relying on well-known algebraic structures. We will later focus on modal expansions of MV and product algebras, particular classes of
![]() $FL_{ew}$
-algebras.
$FL_{ew}$
-algebras.
Definition 2.1. An
![]() $\mathbf {FL_{ew}}$
-algebra is a structure
$\mathbf {FL_{ew}}$
-algebra is a structure
![]() such that
such that
-
•
 is a bounded lattice,
is a bounded lattice, -
•
 is a commutative monoid,
is a commutative monoid, -
•
 if and only if
if and only if
 for all
for all
 $a,b,c\in A$
.
$a,b,c\in A$
.
We will usually write
![]() $ab$
instead of
$ab$
instead of
![]() $a \cdot b$
, and abbreviate
$a \cdot b$
, and abbreviate
![]() $\overbrace {x \cdot x \cdots x}^{n}$
by
$\overbrace {x \cdot x \cdots x}^{n}$
by
![]() $x^n$
for
$x^n$
for
![]() $n \geqslant 1$
. Moreover, as usual, we will define
$n \geqslant 1$
. Moreover, as usual, we will define
![]() $\neg a$
to stand for
$\neg a$
to stand for
![]() $a \rightarrow \overline {0}$
. A chain is a linearly ordered
$a \rightarrow \overline {0}$
. A chain is a linearly ordered
![]() $\mathbf {FL_{ew}}$
-algebra.
$\mathbf {FL_{ew}}$
-algebra.
In the setting of the previous definition, we will denote by
![]() $\mathbf {Fm}'$
the algebra of formulas built over a countable set of variables
$\mathbf {Fm}'$
the algebra of formulas built over a countable set of variables
![]() $\mathcal {V}$
using the language corresponding to the above class of algebras (i.e.,
$\mathcal {V}$
using the language corresponding to the above class of algebras (i.e.,
). We will refer to the bottom and top elements of the algebra,
![]() $\overline {0}$
and
$\overline {0}$
and
![]() $\overline {1}$
, simply by
$\overline {1}$
, simply by
![]() $0$
and
$0$
and
![]() $1$
. Moreover, we will again write
$1$
. Moreover, we will again write
![]() $\varphi \psi $
instead of
$\varphi \psi $
instead of
![]() $\varphi \cdot \psi $
and
$\varphi \cdot \psi $
and
![]() $\varphi ^n$
for the product of
$\varphi ^n$
for the product of
![]() $\varphi $
with itself n times (for
$\varphi $
with itself n times (for
![]() $n \geqslant 1$
), and we let, as usual
$n \geqslant 1$
), and we let, as usual
For a set of formulas
![]() $\varGamma \cup \{\varphi \}$
and a class of
$\varGamma \cup \{\varphi \}$
and a class of
![]() $\mathbf {FL_{ew}}$
-algebras
$\mathbf {FL_{ew}}$
-algebras
![]() $\mathbb {A}$
, we write
$\mathbb {A}$
, we write
![]() $\varGamma \models _{\mathbb {A}} \varphi $
if and only if, for each
$\varGamma \models _{\mathbb {A}} \varphi $
if and only if, for each
![]() $\mathbf {A} \in \mathbb {A}$
and each
$\mathbf {A} \in \mathbb {A}$
and each
![]() $h \in Hom(\mathbf {Fm}',\mathbf {A})$
, if
$h \in Hom(\mathbf {Fm}',\mathbf {A})$
, if
![]() $h(\gamma ) = 1$
for each
$h(\gamma ) = 1$
for each
![]() $\gamma \in \varGamma $
, then
$\gamma \in \varGamma $
, then
![]() $h(\varphi ) = 1$
too. We will write
$h(\varphi ) = 1$
too. We will write
![]() $\models _{\mathbf {A}}$
instead of
$\models _{\mathbf {A}}$
instead of
![]() $\models _{\{\mathbf {A}\}}$
. As expected,
$\models _{\{\mathbf {A}\}}$
. As expected,
![]() $\models _{\mathbb {A}}$
is a logic, and by convenience we will write
$\models _{\mathbb {A}}$
is a logic, and by convenience we will write
![]() $\models _{\mathbb {A}}$
instead of
$\models _{\mathbb {A}}$
instead of
![]() $\vdash _{\models _{\mathbb {A}}}$
.
$\vdash _{\models _{\mathbb {A}}}$
.
![]() $\mathbb {FL}_{ew}$
, the class of
$\mathbb {FL}_{ew}$
, the class of
![]() $\mathbf {FL_{ew}}$
-algebras, is a variety studied in depth, see for instance [Reference Galatos, Jipsen, Kowalski and Ono25, Reference Ono34].
$\mathbf {FL_{ew}}$
-algebras, is a variety studied in depth, see for instance [Reference Galatos, Jipsen, Kowalski and Ono25, Reference Ono34].
Let us introduce some examples of well-known subvarieties of
![]() $\mathbb {FL}_{ew}$
. Heyting Algebras, the algebraic counterpart of Intuitionistic logic, are
$\mathbb {FL}_{ew}$
. Heyting Algebras, the algebraic counterpart of Intuitionistic logic, are
![]() $\mathbf {FL_{ew}}$
-algebras where
$\mathbf {FL_{ew}}$
-algebras where
![]() $\wedge = \cdot $
. The variety of Gödel algebras,
$\wedge = \cdot $
. The variety of Gödel algebras,
![]() $\mathbb {G}$
, (corresponding to intermediate Gödel–Dummett logic
$\mathbb {G}$
, (corresponding to intermediate Gödel–Dummett logic
![]() $\mathcal {G}$
) is that of semilinear Heyting algebras, i.e., those satisfying
$\mathcal {G}$
) is that of semilinear Heyting algebras, i.e., those satisfying
![]() $(a \rightarrow b) \vee (b \rightarrow a)=1$
for all
$(a \rightarrow b) \vee (b \rightarrow a)=1$
for all
![]() $a,b$
in the algebra. BL algebras, the algebraic counterpart of Hájek Basic Logic
$a,b$
in the algebra. BL algebras, the algebraic counterpart of Hájek Basic Logic
![]() $\mathcal {BL}$
, are semilinear
$\mathcal {BL}$
, are semilinear
![]() $\mathbf {FL_{ew}}$
algebras where
$\mathbf {FL_{ew}}$
algebras where
![]() $a \cdot (a \rightarrow b) = a \wedge b$
for every
$a \cdot (a \rightarrow b) = a \wedge b$
for every
![]() $a, b$
in the algebra. The variety of MV algebras
$a, b$
in the algebra. The variety of MV algebras
![]() $\mathbb {MV}$
, algebraic counterpart of Łukasiewicz logic
$\mathbb {MV}$
, algebraic counterpart of Łukasiewicz logic
![]() , is formed by the involutive BL algebras (i.e., satisfying
, is formed by the involutive BL algebras (i.e., satisfying
![]() ), and that of Product algebras
), and that of Product algebras
![]() $\mathbb {P}$
(corresponding to Product Logic
$\mathbb {P}$
(corresponding to Product Logic
![]() $\varPi $
), is formed by those BL algebras satisfying
$\varPi $
), is formed by those BL algebras satisfying
![]() and
and
![]() .
.
Particular algebras in the previous classes are the so-called standard ones, whose universe is the standard unit real interval
![]() $[0,1]$
and the order (affecting the lattice
$[0,1]$
and the order (affecting the lattice
![]() $\wedge , \vee $
operations) is the standard one. Let us introduce explicitly the operations, which we will denote, for convenience, with the subscripts G,
$\wedge , \vee $
operations) is the standard one. Let us introduce explicitly the operations, which we will denote, for convenience, with the subscripts G,
![]() and
and
![]() $\varPi $
(for Gödel, Łukasiewicz, and Product logics, respectively).
$\varPi $
(for Gödel, Łukasiewicz, and Product logics, respectively).
-
•
 $[0,1]_G$
, the standard Gödel algebra, defines
$[0,1]_G$
, the standard Gödel algebra, defines 
-
•
 , the standard MV algebra, defines
, the standard MV algebra, defines 
-
•
 $\bf {MV_n}$
, the n-valued MV algebra is the subalgebra of
$\bf {MV_n}$
, the n-valued MV algebra is the subalgebra of
 with universe
with universe
 .
. -
•
 $[0,1]_\varPi $
, the standard Product (
$[0,1]_\varPi $
, the standard Product (
 $\varPi $
) algebra, defines with
$\varPi $
) algebra, defines with
 $\times $
being the usual product between real numbers.
$\times $
being the usual product between real numbers.
It is known that the standard Gödel, MV, and Product algebras generate their corresponding varieties. They do so also as quasi-varieties, which implies the completeness of the logics (understood as consequence relations) with respect to the logical matrices over the respective standard algebra. In the case of Gödel, it is also the case that the variety is generated as a generalized quasi-variety, while this fails for MV and Product algebras. The first claim amounts to saying that for each set of formulas
![]() $\varGamma \cup \{ \varphi \}$
, it holds that
$\varGamma \cup \{ \varphi \}$
, it holds that
![]() $\varGamma \vdash _{\mathcal {G}} \varphi $
if and only if
$\varGamma \vdash _{\mathcal {G}} \varphi $
if and only if
![]() $\varGamma \models _{[0,1]_G} \varphi $
(and if and only if
$\varGamma \models _{[0,1]_G} \varphi $
(and if and only if
![]() $\varGamma \models _{\mathbb {G}} \varphi $
). For a finite set of formulas
$\varGamma \models _{\mathbb {G}} \varphi $
). For a finite set of formulas
![]() $\varGamma \cup \{\varphi \}$
it holds that
$\varGamma \cup \{\varphi \}$
it holds that
![]() if and only if
if and only if
![]() (if and only if
(if and only if
![]() $\varGamma \models _{\mathbb {MV}} \varphi $
); and
$\varGamma \models _{\mathbb {MV}} \varphi $
); and
![]() $\varGamma \vdash _{\varPi } \varphi $
if and only if
$\varGamma \vdash _{\varPi } \varphi $
if and only if
![]() $\varGamma \models _{[0,1]_{\varPi }} \varphi $
(if and only if
$\varGamma \models _{[0,1]_{\varPi }} \varphi $
(if and only if
![]() $\varGamma \models _{\mathbb {P}} \varphi $
). The last conditions might fail for infinite
$\varGamma \models _{\mathbb {P}} \varphi $
). The last conditions might fail for infinite
![]() $\varGamma $
.
$\varGamma $
.
Let us introduce some other families of
![]() $\mathbf {FL_{ew}}$
-algebras that will be of use later on.
$\mathbf {FL_{ew}}$
-algebras that will be of use later on.
Definition 2.2. Let
![]() $\mathbf {A}$
be an
$\mathbf {A}$
be an
![]() $\mathbf {FL_{ew}}$
-algebra.
$\mathbf {FL_{ew}}$
-algebra.
-
•
 $\mathbf {A}$
is n-contractive whenever
$\mathbf {A}$
is n-contractive whenever
 $a^{n+1} = a^n$
for all
$a^{n+1} = a^n$
for all
 $a \in A$
.
$a \in A$
. -
•
 $\mathbf {A}$
is weakly saturated if for any two elements
$\mathbf {A}$
is weakly saturated if for any two elements
 $a,b \in A$
, if
$a,b \in A$
, if
 for all
for all
 $n \in \mathbb {N}$
then
$n \in \mathbb {N}$
then
 $ab = a$
.
$ab = a$
.
Observe that if
![]() $\mathbf {A}$
is n-contractive, the element
$\mathbf {A}$
is n-contractive, the element
![]() $a^n$
is idempotent (namely
$a^n$
is idempotent (namely
![]() ${a^n\cdot a^n = a^n}$
) for every
${a^n\cdot a^n = a^n}$
) for every
![]() $a \in A$
. Simple examples of these algebras include Heyting algebras (
$a \in A$
. Simple examples of these algebras include Heyting algebras (
![]() $1$
-contractive), or
$1$
-contractive), or
![]() $MV_n$
algebras (
$MV_n$
algebras (
![]() $(n-1)$
-contractive). On the other hand, the standard MV-algebra and product algebra are not n-contractive for any n. Regarding weakly saturation, observe that if the element
$(n-1)$
-contractive). On the other hand, the standard MV-algebra and product algebra are not n-contractive for any n. Regarding weakly saturation, observe that if the element
![]() $\inf \{b^n\colon n \in \mathbb {N}\}$
exists in a weakly saturated algebra, then it is an idempotent element. Examples of weakly saturated algebras are the standard MV-algebra, the standard product algebra, as well as the algebras belonging to the generalised quasi-varieties generated by them.
$\inf \{b^n\colon n \in \mathbb {N}\}$
exists in a weakly saturated algebra, then it is an idempotent element. Examples of weakly saturated algebras are the standard MV-algebra, the standard product algebra, as well as the algebras belonging to the generalised quasi-varieties generated by them.
The algebra of modal formulas
![]() $\mathbf {Fm}$
is built in the same way as
$\mathbf {Fm}$
is built in the same way as
![]() $\mathbf {Fm'}$
, expanding the language of
$\mathbf {Fm'}$
, expanding the language of
![]() $\mathbf {FL_{ew}}$
-algebras with two unary operators
$\mathbf {FL_{ew}}$
-algebras with two unary operators
![]() $\square $
and
$\square $
and
![]() $\Diamond $
. While it is clear how to lift an evaluation from the set of propositional variables
$\Diamond $
. While it is clear how to lift an evaluation from the set of propositional variables
![]() $\mathcal {V}$
into an
$\mathcal {V}$
into an
![]() $FL_{ew}$
-algebra to
$FL_{ew}$
-algebra to
![]() $\mathbf {Fm'}$
, the semantic definition of the modal operators depends on the relational structure in the following way.
$\mathbf {Fm'}$
, the semantic definition of the modal operators depends on the relational structure in the following way.
Definition 2.3. Let
![]() $\mathbf {A}$
be an
$\mathbf {A}$
be an
![]() $\mathbf {FL_{ew}}$
-algebra. An
$\mathbf {FL_{ew}}$
-algebra. An
![]() $\mathbf {A}$
-Kripke model is a structure
$\mathbf {A}$
-Kripke model is a structure
such that
-
•
 is a Kripke frame. That is to say, W is a non-empty set of so-called worlds and
is a Kripke frame. That is to say, W is a non-empty set of so-called worlds and
 $R\subseteq W \times W$
is a binary relation over W, called an accessibility relation. We will often write
$R\subseteq W \times W$
is a binary relation over W, called an accessibility relation. We will often write
 $Rvw$
instead of
$Rvw$
instead of
 ;
; -
• e is a map from
 $W \times \mathcal {V}$
to A.
$W \times \mathcal {V}$
to A.
The evaluation e of an
![]() $\mathbf {A}$
-Kripke model
$\mathbf {A}$
-Kripke model
is uniquely extended to a map from
![]() $W \times Fm$
to A by letting
$W \times Fm$
to A by letting

A model
![]() is safe whenever the values of
is safe whenever the values of
![]() $e(v, \square \varphi )$
and
$e(v, \square \varphi )$
and
![]() $e(v, \Diamond \varphi )$
are defined for every formula
$e(v, \Diamond \varphi )$
are defined for every formula
![]() $\varphi $
at each world
$\varphi $
at each world
![]() $v \in W$
. The class of
$v \in W$
. The class of
![]() $\mathbf {FL_{ew}}$
-Kripke models is the (set) union of all safe
$\mathbf {FL_{ew}}$
-Kripke models is the (set) union of all safe
![]() $\mathbf {A}$
-Kripke models, for
$\mathbf {A}$
-Kripke models, for
![]() $\mathbf {A} \in \mathbf {FL_{ew}}$
.
$\mathbf {A} \in \mathbf {FL_{ew}}$
.
We call a model
![]() $\mathfrak {M}$
directed whenever there is some world
$\mathfrak {M}$
directed whenever there is some world
![]() $u \in W$
in it such that, for each
$u \in W$
in it such that, for each
![]() $v \in W$
, there is some path from u to v
Footnote
10
in
$v \in W$
, there is some path from u to v
Footnote
10
in
![]() $\mathfrak {M}$
.
$\mathfrak {M}$
.
Regarding notation, given a class of models
![]() $\mathbb {C}$
, we denote by
$\mathbb {C}$
, we denote by
![]() $\omega \mathbb {C}$
the class of finite models in
$\omega \mathbb {C}$
the class of finite models in
![]() $\mathbb {C}$
(namely, the models
$\mathbb {C}$
(namely, the models
![]() Footnote
11
). On the other hand, for a class of algebras
Footnote
11
). On the other hand, for a class of algebras
![]() $\mathbb {A}$
(or a single algebra
$\mathbb {A}$
(or a single algebra
![]() $\mathbf {A}$
) we write
$\mathbf {A}$
) we write
![]() $K{\mathbb {A}}$
(
$K{\mathbb {A}}$
(
![]() $K{\mathbf {A}}$
) to denote the class of safe Kripke models over the algebras in the class (or over the single algebra specified). Finally, in order to lighten the reading, we will let
$K{\mathbf {A}}$
) to denote the class of safe Kripke models over the algebras in the class (or over the single algebra specified). Finally, in order to lighten the reading, we will let
![]() and
and
![]() $K{\varPi }$
to denote respectively
$K{\varPi }$
to denote respectively
![]() and
and
![]() $K{[0,1]_\varPi }$
.
$K{[0,1]_\varPi }$
.
Towards the definition of modal logics over
![]() $\mathbf {FL_{ew}}$
-algebras relying on the notion of
$\mathbf {FL_{ew}}$
-algebras relying on the notion of
![]() $\mathbf {FL_{ew}}$
-Kripke models, it is natural to use the notion of truth world-wise being
$\mathbf {FL_{ew}}$
-Kripke models, it is natural to use the notion of truth world-wise being
![]() $\{1\}$
(in order to obtain, world-wise, the propositional
$\{1\}$
(in order to obtain, world-wise, the propositional
![]() $\mathbb {FL}_{ew}$
logic). With this in mind, for each
$\mathbb {FL}_{ew}$
logic). With this in mind, for each
![]() $\mathbf {A}$
-Kripke model
$\mathbf {A}$
-Kripke model
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $v \in W$
we say that
$v \in W$
we say that
![]() $\mathfrak {M}$
satisfies a formula
$\mathfrak {M}$
satisfies a formula
![]() $\varphi $
in v, and write
$\varphi $
in v, and write
![]() $\mathfrak {M},v \models \varphi $
whenever
$\mathfrak {M},v \models \varphi $
whenever
![]() $e(v, \varphi ) = 1$
. Similarly, we simply say that
$e(v, \varphi ) = 1$
. Similarly, we simply say that
![]() $\mathfrak {M}$
satisfies a formula
$\mathfrak {M}$
satisfies a formula
![]() $\varphi $
, and write
$\varphi $
, and write
![]() $\mathfrak {M} \models \varphi $
whenever for all
$\mathfrak {M} \models \varphi $
whenever for all
![]() $v \in W \mathfrak {M},v \models \varphi $
. The same definitions apply to sets of formulas.
$v \in W \mathfrak {M},v \models \varphi $
. The same definitions apply to sets of formulas.
As in the classical case, the previous definition of satisfiability gives rise to two different logics: the local logic and the global one. In this work we will focus on the study of the global logic, but in Section 5 we will point out some results involving the local modal logic as well.
Definition 2.4. Let
![]() $\varGamma \cup \{ \varphi \} \subseteq _{\omega } Fm$
, and
$\varGamma \cup \{ \varphi \} \subseteq _{\omega } Fm$
, and
![]() $\mathbb {C}$
be a class of safe
$\mathbb {C}$
be a class of safe
![]() $\mathbf {FL_{ew}}$
-Kripke models.
$\mathbf {FL_{ew}}$
-Kripke models.
-
•
 $\varphi $
globally follows from
$\varphi $
globally follows from
 $\varGamma $
in
$\varGamma $
in
 $\mathbb {C}$
, and we write
$\mathbb {C}$
, and we write
 $\varGamma \vdash _{\mathbb {C}} \varphi $
, whenever for every
$\varGamma \vdash _{\mathbb {C}} \varphi $
, whenever for every
 $\mathfrak {M} \in \mathbb {C}$
,
$\mathfrak {M} \in \mathbb {C}$
,  $$ \begin{align*}\mathfrak{M} \models \varGamma \text{ implies }\mathfrak{M} \models \varphi.\end{align*} $$
$$ \begin{align*}\mathfrak{M} \models \varGamma \text{ implies }\mathfrak{M} \models \varphi.\end{align*} $$
-
•
 $\varphi $
locally follows from
$\varphi $
locally follows from
 $\varGamma $
in
$\varGamma $
in
 $\mathbb {C}$
, and we write
$\mathbb {C}$
, and we write
 $\varGamma \vdash ^l_{\mathbb {C}} \varphi $
, whenever for every
$\varGamma \vdash ^l_{\mathbb {C}} \varphi $
, whenever for every
 $\mathfrak {M} \in \mathbb {C}$
and every
$\mathfrak {M} \in \mathbb {C}$
and every
 $v \in W$
,
$v \in W$
,  $$ \begin{align*}\mathfrak{M}, v \models \varGamma \text{ implies }\mathfrak{M}, v \models \varphi.\end{align*} $$
$$ \begin{align*}\mathfrak{M}, v \models \varGamma \text{ implies }\mathfrak{M}, v \models \varphi.\end{align*} $$
If
![]() $\mathbb {C}$
is clear from the context, we will simply write
$\mathbb {C}$
is clear from the context, we will simply write
![]() $\vdash $
and
$\vdash $
and
![]() $\vdash ^l$
instead.
$\vdash ^l$
instead.
For arbitrary
![]() $\varGamma \cup \{ \varphi \} \subseteq Fm$
, we let
$\varGamma \cup \{ \varphi \} \subseteq Fm$
, we let
![]() $ \varGamma \vdash _{\mathbb {C}} \varphi \text { whenever there is } \varGamma _0 \subseteq _\omega \varGamma \text { such that} \varGamma _0 \vdash _{\mathbb {C}} \varphi $
, and the analogous for the local logic.
$ \varGamma \vdash _{\mathbb {C}} \varphi \text { whenever there is } \varGamma _0 \subseteq _\omega \varGamma \text { such that} \varGamma _0 \vdash _{\mathbb {C}} \varphi $
, and the analogous for the local logic.
For a single Kripke model
![]() $\mathfrak {M}$
, we write
$\mathfrak {M}$
, we write
![]() $\varGamma \vdash _{\mathfrak {M}} \varphi $
instead of
$\varGamma \vdash _{\mathfrak {M}} \varphi $
instead of
![]() $\varGamma \vdash _{\{\mathfrak {M}\}} \varphi $
. In a similar way, for a model
$\varGamma \vdash _{\{\mathfrak {M}\}} \varphi $
. In a similar way, for a model
![]() $\mathfrak {M}$
and a world
$\mathfrak {M}$
and a world
![]() $u \in W$
we write
$u \in W$
we write
![]() to denote that
to denote that
![]() $\mathfrak {M} \models \varGamma $
and
$\mathfrak {M} \models \varGamma $
and
![]() $\mathfrak {M},u \not \models \varphi $
(namely,
$\mathfrak {M},u \not \models \varphi $
(namely,
![]() $\varphi $
does not follow globally from
$\varphi $
does not follow globally from
![]() $\varGamma $
in
$\varGamma $
in
![]() $\mathfrak {M}$
, and world u witnesses this fact). In a more general setting, fixing a Kripke frame
$\mathfrak {M}$
, and world u witnesses this fact). In a more general setting, fixing a Kripke frame
![]() $\mathfrak {F}$
and an algebra
$\mathfrak {F}$
and an algebra
![]() $\mathbf {A}$
, we write
$\mathbf {A}$
, we write
![]() $\varGamma \vdash _{\mathfrak {F}_{\mathbf {A}}} \varphi $
whenever
$\varGamma \vdash _{\mathfrak {F}_{\mathbf {A}}} \varphi $
whenever
![]() $\varGamma \vdash _{\mathfrak {M}} \varphi $
for every safe
$\varGamma \vdash _{\mathfrak {M}} \varphi $
for every safe
![]() $\mathbf {A}$
-Kripke model
$\mathbf {A}$
-Kripke model
![]() $\mathfrak {M}$
with underlying Kripke frame
$\mathfrak {M}$
with underlying Kripke frame
![]() $\mathfrak {F}$
. Analogously, for a class of frames
$\mathfrak {F}$
. Analogously, for a class of frames
![]() $\mathbb {F}$
and a class of algebras
$\mathbb {F}$
and a class of algebras
![]() $\mathbb {C}$
, we write
$\mathbb {C}$
, we write
![]() $\varGamma \vdash _{\mathbb {F}_{\mathbb {C}}} \varphi $
whenever
$\varGamma \vdash _{\mathbb {F}_{\mathbb {C}}} \varphi $
whenever
![]() $\varGamma \vdash _{\mathfrak {F}_{\mathbf {A}}} \varphi $
for each
$\varGamma \vdash _{\mathfrak {F}_{\mathbf {A}}} \varphi $
for each
![]() $\mathfrak {F} \in \mathbb {F}$
and each
$\mathfrak {F} \in \mathbb {F}$
and each
![]() $\mathbf {A} \in \mathbb {C}$
.
$\mathbf {A} \in \mathbb {C}$
.
Tautologies (formulas following from
![]() $\emptyset $
) of
$\emptyset $
) of
![]() $ \vdash ^l_{\mathbb {C}}$
and
$ \vdash ^l_{\mathbb {C}}$
and
![]() $\vdash _{\mathbb {C}}$
coincide, and
$\vdash _{\mathbb {C}}$
coincide, and
![]() $\vdash ^l_{\mathbb {C}}$
is strictly weaker than
$\vdash ^l_{\mathbb {C}}$
is strictly weaker than
![]() $\vdash _{\mathbb {C}}$
, a trivial separating case being the usual necessitation rule
$\vdash _{\mathbb {C}}$
, a trivial separating case being the usual necessitation rule
![]() $\varphi \vdash \square \varphi $
(valid in the global case and not in the local one). Observe that
$\varphi \vdash \square \varphi $
(valid in the global case and not in the local one). Observe that
![]() $ \vdash ^l_{\mathbb {C}}$
and
$ \vdash ^l_{\mathbb {C}}$
and
![]() $\vdash _{\mathbb {C}}$
are, by their definition, determined by the safe directed models generated from the models in
$\vdash _{\mathbb {C}}$
are, by their definition, determined by the safe directed models generated from the models in
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
Also, the unraveling and filtrationFootnote
12
techniques can be applied to an arbitrary directed model, obtaining a directed tree that, from the logical point of view, behaves in its root as the original model (i.e., satisfies exactly the same global and local derivations). Even if the resulting tree might be infinite, all worlds in the tree are, by construction, at a finite distance from the root. Thus,
![]() $\vdash _{K\mathbb {C}} {{\kern-2pt}={\kern-2pt}} \vdash_{K\mathbb {C}^T}$
, for
$\vdash _{K\mathbb {C}} {{\kern-2pt}={\kern-2pt}} \vdash_{K\mathbb {C}^T}$
, for
![]() $K\mathbb {C}^T$
being the class of safe directed trees generated by models in
$K\mathbb {C}^T$
being the class of safe directed trees generated by models in
![]() $\ K\mathbb {C}$
.
$\ K\mathbb {C}$
.
Some useful notions concerning Kripke models are the following ones.
Definition 2.5. Given a Kripke model
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $w \in W$
, we let the height of w,
$w \in W$
, we let the height of w,
![]() $\mathbf {\mathtt {h}}(w)$
be the element in
$\mathbf {\mathtt {h}}(w)$
be the element in
![]() $\mathbb {N}\cup \{\infty \}$
Footnote
13
given by
$\mathbb {N}\cup \{\infty \}$
Footnote
13
given by
Observe that if there exists some cycle in the model, all worlds involved in that cycle (and every predecessor of each world in that cycle in the model) have infinite height.
Definition 2.6. Let
![]() $\varphi $
be a formula of
$\varphi $
be a formula of
![]() $Fm$
. We let the subformulas of
$Fm$
. We let the subformulas of
![]() $\varphi $
be the set inductively defined by
$\varphi $
be the set inductively defined by

We let the propositional subformulas of
![]() $\varphi $
be the set inductively defined by
$\varphi $
be the set inductively defined by

For
![]() $\varGamma $
a set of formulas we let
$\varGamma $
a set of formulas we let
Let us finish the preliminaries by stating a well-known undecidable problem, that will be used in the next sections to show undecidability of some of the modal logics introduced above. Recall that given two numbers
![]() $\mathtt { x}, \mathtt { y}$
in base
$\mathtt { x}, \mathtt { y}$
in base
![]() $s \in \mathbb {N}$
, their concatenation
$s \in \mathbb {N}$
, their concatenation
![]() $\mathtt { x_\smile y}$
is given by
$\mathtt { x_\smile y}$
is given by
![]() $\mathtt { x}s^{\parallel \mathtt { y} \parallel } + \mathtt { y}$
, where
$\mathtt { x}s^{\parallel \mathtt { y} \parallel } + \mathtt { y}$
, where
![]() $\parallel \mathtt {y}\parallel $
is the number of digits of
$\parallel \mathtt {y}\parallel $
is the number of digits of
![]() $\mathtt { y}$
in base s.
$\mathtt { y}$
in base s.
Definition 2.7 (Post Correspondence Problem (PCP)).
An instance P of the PCP consists of a list
![]() of pairs of numbers in some base
of pairs of numbers in some base
![]() $s \geqslant 2$
. A solution for P is a sequence of indexes
$s \geqslant 2$
. A solution for P is a sequence of indexes
![]() with
with
![]() such that
such that
The decision problem for PCP is, given a PCP instance, to decide whether such a solution exists or not. This question is undecidable [Reference Post35].
3 Undecidability of global modal logics
In this section, unless stated otherwise, we let
![]() $\mathbb {A}$
be a class of weakly saturated
$\mathbb {A}$
be a class of weakly saturated
![]() $\mathbf {FL_{ew}}$
chains such that for every
$\mathbf {FL_{ew}}$
chains such that for every
![]() $n \in \mathbb {N}$
there is some
$n \in \mathbb {N}$
there is some
![]() $\mathbf {A}_n \in \mathbb {A}$
such that
$\mathbf {A}_n \in \mathbb {A}$
such that
![]() $\mathbf {A}_n$
is non n-contractive. That is to say, there is some
$\mathbf {A}_n$
is non n-contractive. That is to say, there is some
![]() $a \in A_n$
such that
$a \in A_n$
such that
![]() $a^{n+1} < a^n.$
$a^{n+1} < a^n.$
Examples of such classes of algebras are
![]() and
and
![]() $\{[0,1]_{\varPi }\}$
. Natural examples of classes of algebras not satisfying the above conditions are
$\{[0,1]_{\varPi }\}$
. Natural examples of classes of algebras not satisfying the above conditions are
![]() $\{[0,1]_G\}$
and the variety generated by it, and the varieties of MV and product algebras (since these are not classes of weakly saturated chains).
$\{[0,1]_G\}$
and the variety generated by it, and the varieties of MV and product algebras (since these are not classes of weakly saturated chains).
Let the class of frames
![]() $\mathbb {L}$
be the isomorphic copies of the frames in the set
$\mathbb {L}$
be the isomorphic copies of the frames in the set
Namely,
![]() $\mathbb {L}$
is given by the frames whose structure is isomorphic to the one depicted in Figure 1, for any
$\mathbb {L}$
is given by the frames whose structure is isomorphic to the one depicted in Figure 1, for any
![]() $k \in \mathbb {N}$
.
$k \in \mathbb {N}$
.

Figure 1 Structure of the frames in
![]() $\mathbb {L}$
.
$\mathbb {L}$
.
Theorem 3.1. For any class of frames
![]() $\mathbb {F}$
such that
$\mathbb {F}$
such that
![]() $\mathbb {L} \subseteq \mathbb {F}$
the logic
$\mathbb {L} \subseteq \mathbb {F}$
the logic
![]() $\vdash _{\mathbb {F}_{\mathbb {A}}}$
is undecidable. In particular, the logics
$\vdash _{\mathbb {F}_{\mathbb {A}}}$
is undecidable. In particular, the logics
![]() $\vdash _{K{\mathbb {A}}}$
and
$\vdash _{K{\mathbb {A}}}$
and
![]() $\vdash _{\omega K{\mathbb {A}}}$
are undecidable.
$\vdash _{\omega K{\mathbb {A}}}$
are undecidable.
More precisely, the three-variable fragments of the previous logics are undecidable.
The previous theorem follows as a direct consequence of the next result.
Theorem 3.2. Let P be an instance of the Post Correspondence Problem. Then we can recursively define a set
![]() $\varGamma _P \cup \{\varphi _P\} \subseteq _{\omega } Fm$
in three variables from P for which the following are equivalent:
$\varGamma _P \cup \{\varphi _P\} \subseteq _{\omega } Fm$
in three variables from P for which the following are equivalent:
-
(1) P is satisfiable.
-
(2)
 $\varGamma _P \not \vdash _{K{\mathbb {A}}} \varphi _P$
.
$\varGamma _P \not \vdash _{K{\mathbb {A}}} \varphi _P$
. -
(3)
 $\varGamma _P \not \vdash _{\omega K{\mathbb {A}}} \varphi _P$
.
$\varGamma _P \not \vdash _{\omega K{\mathbb {A}}} \varphi _P$
. -
(4)
 $\varGamma _P \not \vdash _{\mathbb {L}_{\mathbb {A}}} \varphi _P$
.
$\varGamma _P \not \vdash _{\mathbb {L}_{\mathbb {A}}} \varphi _P$
.
Trivially,
![]() $(4) \Rightarrow (3)$
and
$(4) \Rightarrow (3)$
and
![]() $(3) \Rightarrow (2)$
for any
$(3) \Rightarrow (2)$
for any
![]() $\varGamma _P \cup \{\varphi _P\} \subseteq _{\omega } Fm$
. In what remains of this section we will first show that
$\varGamma _P \cup \{\varphi _P\} \subseteq _{\omega } Fm$
. In what remains of this section we will first show that
![]() $(1) \Rightarrow (4)$
, and afterwards, that both
$(1) \Rightarrow (4)$
, and afterwards, that both
![]() $(2) \Rightarrow (4)$
and
$(2) \Rightarrow (4)$
and
![]() $(4) \Rightarrow (1)$
. To this aim, let us begin by explicitly defining a suitable set of formulas
$(4) \Rightarrow (1)$
. To this aim, let us begin by explicitly defining a suitable set of formulas
![]() $\varGamma _P \cup \{\varphi _P\}$
.
$\varGamma _P \cup \{\varphi _P\}$
.
For
![]() list of pairs of numbers in base s, we let
list of pairs of numbers in base s, we let
![]() $\varGamma _P$
be the set with formulas in variables
$\varGamma _P$
be the set with formulas in variables
![]() $\mathcal {V} = \{x, y, z\}$
:
$\mathcal {V} = \{x, y, z\}$
:
-
(1)
 for each
for each
 $p \in \mathcal {V}$
.
$p \in \mathcal {V}$
. -
(2)
 .
. -
(3)
 .
.
Finally, let
![]()
Roughly speaking, variables x and y will store information on the concatenation of the corresponding elements of the PCP, while z will have a technical role.
Given a solution of P, it is not hard to construct a finite model globally satisfying
![]() $\varGamma _P$
and not
$\varGamma _P$
and not
![]() $\varphi _P$
.
$\varphi _P$
.
Proof. (Of Theorem 3.2,
![]() $(1) \Rightarrow (4)$
).
$(1) \Rightarrow (4)$
).
Let
![]() be a solution for P, so
be a solution for P, so
![]() $\mathtt { x_{i_1}} {_\smile } \dots {_\smile } \mathtt { x_{i_k}} = \mathtt { y_{i_1}} {_\smile } \dots {_\smile } \mathtt { y_{i_k}} = r$
for some
$\mathtt { x_{i_1}} {_\smile } \dots {_\smile } \mathtt { x_{i_k}} = \mathtt { y_{i_1}} {_\smile } \dots {_\smile } \mathtt { y_{i_k}} = r$
for some
![]() $r \in \mathbb {N}$
. Pick some non r-contractive algebra
$r \in \mathbb {N}$
. Pick some non r-contractive algebra
![]() $\mathbf {A} \in \mathbb {A}$
and
$\mathbf {A} \in \mathbb {A}$
and
![]() $a \in A$
such that
$a \in A$
such that
![]() $a^{r+1} < a^r$
, and define a finite
$a^{r+1} < a^r$
, and define a finite
![]() $\mathbf {A}$
-Kripke model
$\mathbf {A}$
-Kripke model
![]() $\mathfrak {M}$
as follows:
$\mathfrak {M}$
as follows:
-
•
 .
. -
•
 .
. -
• For each
 let
let-
–
 $\ e(v_j, z) = a$
,
$\ e(v_j, z) = a$
, -
–
 $\ e(v_j, x) = a^{{\mathtt {x_{i_1}}}{_\smile } \dots {_\smile } {\mathtt {x_{i_j}} }}$
,
$\ e(v_j, x) = a^{{\mathtt {x_{i_1}}}{_\smile } \dots {_\smile } {\mathtt {x_{i_j}} }}$
, -
–
 $\ e(v_j, y) = a^{\mathtt { y_{i_1}} {_\smile } \dots {_\smile } \mathtt { y_{i_j}}}$
.
$\ e(v_j, y) = a^{\mathtt { y_{i_1}} {_\smile } \dots {_\smile } \mathtt { y_{i_j}}}$
.
-
The formula
![]() $\neg \square 0$
is evaluated to
$\neg \square 0$
is evaluated to
![]() $0$
in
$0$
in
![]() $v_1$
, and to
$v_1$
, and to
![]() $1$
in all other worlds of the model. Thus, since z is evaluated to the same value in all worlds of the model, and each world has exactly one successor except for
$1$
in all other worlds of the model. Thus, since z is evaluated to the same value in all worlds of the model, and each world has exactly one successor except for
![]() $v_1$
(which has none), clearly the family of formulas in
$v_1$
(which has none), clearly the family of formulas in
![]() $(1)$
and in
$(1)$
and in
![]() $(2)$
from
$(2)$
from
![]() $\varGamma _P$
are satisfied in all worlds of the model.
$\varGamma _P$
are satisfied in all worlds of the model.
To check that formula
![]() $(3)$
from
$(3)$
from
![]() $\varGamma _P$
is satisfied in all worlds of the model we reason by induction on the height of the world (Definition 2.5). For
$\varGamma _P$
is satisfied in all worlds of the model we reason by induction on the height of the world (Definition 2.5). For
![]() $v_1$
(with height equal to
$v_1$
(with height equal to
![]() $0$
), given that it does not have any successors, it is clear that
$0$
), given that it does not have any successors, it is clear that

For all other
![]() $v_r$
with
$v_r$
with
![]() $r>1$
, recall that its only successor is
$r>1$
, recall that its only successor is
![]() $v_{r-1}$
. Applying the definition of concatenation, and the fact that for every
$v_{r-1}$
. Applying the definition of concatenation, and the fact that for every
![]() $\mathbf {A} \in \mathbb {A}$
and each
$\mathbf {A} \in \mathbb {A}$
and each
![]() $a \in A$
and
$a \in A$
and
![]() $n,m\in \mathbb {N}$
, trivially
$n,m\in \mathbb {N}$
, trivially
![]() $a^n a^m = a^{n+m}$
and
$a^n a^m = a^{n+m}$
and
![]() $(a^n)^m = a^{nm}$
, we can prove that
$(a^n)^m = a^{nm}$
, we can prove that

With the above, we have proven that
![]() $\mathfrak {M} \models \varGamma _P$
.
$\mathfrak {M} \models \varGamma _P$
.
On the other hand, since
![]() $i_1, \dots , i_k$
was a solution for P,
$i_1, \dots , i_k$
was a solution for P,
![]() $e(v_k, x) = e(v_k, y)$
. Moreover,
$e(v_k, x) = e(v_k, y)$
. Moreover,
![]() $e(v_k, z) = a < 1$
, and
$e(v_k, z) = a < 1$
, and
![]() $e(v_k, xz) = a^{r+1} < a^r = e(v_k, x)$
, so
$e(v_k, xz) = a^{r+1} < a^r = e(v_k, x)$
, so
![]() $e(v_k, xz \rightarrow x) < 1$
. This implies that
$e(v_k, xz \rightarrow x) < 1$
. This implies that
![]() , proving that
, proving that
![]() $\varGamma _P \not \vdash _{\omega K{\mathbb {A}}} \varphi _P$
.⊣
$\varGamma _P \not \vdash _{\omega K{\mathbb {A}}} \varphi _P$
.⊣
In order to prove the other implications of Theorem 3.2, let us first show some technical characteristics of the models satisfying
![]() $\varGamma _P$
and not
$\varGamma _P$
and not
![]() $\varphi _P$
.
$\varphi _P$
.
A first easy observation is that in every model satisfying
![]() $\varGamma _P$
, the variable z takes the same value in all connected worlds of the model. Relying on the completeness with respect to trees, we can prove that, in these models, z is evaluated to the same value in the whole model.
$\varGamma _P$
, the variable z takes the same value in all connected worlds of the model. Relying on the completeness with respect to trees, we can prove that, in these models, z is evaluated to the same value in the whole model.
Lemma 3.3. Let
![]() $\mathbf {A} \in \mathbb {A}$
, and
$\mathbf {A} \in \mathbb {A}$
, and
![]() $\mathfrak {M} \in K\mathbf {A}^T$
with root u be such that
$\mathfrak {M} \in K\mathbf {A}^T$
with root u be such that
![]() . Then there is
. Then there is
![]() $\alpha _z \in A$
such that, for each world v in the model,
$\alpha _z \in A$
such that, for each world v in the model,
![]() $e(v,z) = \alpha _z$
.
$e(v,z) = \alpha _z$
.
Proof. Let
![]() $\alpha _z = e(u, z)$
. It is easy to prove the lemma by induction on the distance of v from u, which is always finite because
$\alpha _z = e(u, z)$
. It is easy to prove the lemma by induction on the distance of v from u, which is always finite because
![]() $K\mathbf {A}^T$
is a class of directed trees.
$K\mathbf {A}^T$
is a class of directed trees.
If
![]() $v = u$
then the claim follows trivially. Otherwise, assume that there are
$v = u$
then the claim follows trivially. Otherwise, assume that there are
![]() with
with
![]() $w_0 = u, w_{k+1} = v$
and such that
$w_0 = u, w_{k+1} = v$
and such that
![]() $R w_i w_{i+1}$
for all
$R w_i w_{i+1}$
for all
![]() . Since
. Since
![]() $e(w_k, (1)) = e(w_k, (2)) = 1 $
and
$e(w_k, (1)) = e(w_k, (2)) = 1 $
and
![]() $R w_kw_{k+1}$
, then we know
$R w_kw_{k+1}$
, then we know
From the first equality we get that
![]() $e(v_1, z) = e(v_2,z)$
for all
$e(v_1, z) = e(v_2,z)$
for all
![]() $v_1,v_2\in W$
such that
$v_1,v_2\in W$
such that
![]() $R w_k v_1$
and
$R w_k v_1$
and
![]() $R w_k v_2$
. In particular, this yields that
$R w_k v_2$
. In particular, this yields that
![]() $e(w_k, \square z) = e(w_{k+1}, z)$
. Together with the second equality, it follows that
$e(w_k, \square z) = e(w_{k+1}, z)$
. Together with the second equality, it follows that
![]() $e(w_k, z) = e(w_{k+1}, z) = e(v,z)$
. Applying the Induction Hypothesis, we conclude
$e(w_k, z) = e(w_{k+1}, z) = e(v,z)$
. Applying the Induction Hypothesis, we conclude
![]() $e(u, z) = e(w_k, z) = e(v, z)$
.⊣
$e(u, z) = e(w_k, z) = e(v, z)$
.⊣
The fact that algebras in
![]() $\mathbb {A}$
are linearly ordered and weakly saturated allows us to also prove that such models can be assumed to have finite height.
$\mathbb {A}$
are linearly ordered and weakly saturated allows us to also prove that such models can be assumed to have finite height.
Lemma 3.4. Let
![]() $\mathbf {A} \in \mathbb {A}$
, and
$\mathbf {A} \in \mathbb {A}$
, and
![]() $\mathfrak {M} \in K\mathbf {A}^T$
with root u be such that
$\mathfrak {M} \in K\mathbf {A}^T$
with root u be such that
![]() . Then u has finite height.
. Then u has finite height.
Proof. From Lemma 3.3 we know that in each world v of
![]() $\mathfrak {M}$
it holds that
$\mathfrak {M}$
it holds that
![]() $e(u, z) = e(v, z) = \alpha _z$
. Moreover, from
$e(u, z) = e(v, z) = \alpha _z$
. Moreover, from
![]() $(3)$
in
$(3)$
in
![]() $\varGamma _P$
it follows that
$\varGamma _P$
it follows that
If u was of infinite height, by weak saturation of
![]() $\mathbf {A}$
, it would follow that
$\mathbf {A}$
, it would follow that
![]() $e(u,x) e(u,z) = e(u,x)$
. However, since
$e(u,x) e(u,z) = e(u,x)$
. However, since
![]() $e(u, \varphi _P) <1$
, necessarily
$e(u, \varphi _P) <1$
, necessarily
![]() $e(u, xz) < e(u, x)$
, and thus u must be of finite height.⊣
$e(u, xz) < e(u, x)$
, and thus u must be of finite height.⊣
As a corollary, we get that the values of x and y at each world are powers of
![]() $\alpha _z$
.
$\alpha _z$
.
Corollary 3.5. Let
![]() $\mathbf {A} \in \mathbb {A}$
, and
$\mathbf {A} \in \mathbb {A}$
, and
![]() $\mathfrak {M} \in K\mathbf {A}^T$
with root
$\mathfrak {M} \in K\mathbf {A}^T$
with root
![]() $u \in W$
be such that
$u \in W$
be such that
![]() . Then for each
. Then for each
![]() $v \in W$
there are
$v \in W$
there are
![]() $a_v, b_v \in \mathbb {N}$
such that
$a_v, b_v \in \mathbb {N}$
such that
Moreover, if
![]() $\mathbf {\mathtt {h}}(v) < \mathbf {\mathtt {h}}(w)$
then
$\mathbf {\mathtt {h}}(v) < \mathbf {\mathtt {h}}(w)$
then
![]() $a_v < a_w$
and
$a_v < a_w$
and
![]() $b_v < b_w$
.
$b_v < b_w$
.
Proof. The first part easily follows by induction on the height of the model, from the previous lemma and formulas
![]() $(1)$
and
$(1)$
and
![]() $(3)$
in
$(3)$
in
![]() $\varGamma _P$
. The second claim is immediate for the case when
$\varGamma _P$
. The second claim is immediate for the case when
![]() $Rvw$
, since from
$Rvw$
, since from
![]() $(3)$
implies that
$(3)$
implies that
![]() (and the same for variable y). For arbitrary
(and the same for variable y). For arbitrary
![]() $\mathbf {\mathtt {h}}(v) < \mathbf {\mathtt {h}}(w)$
, this process is iterated.⊣
$\mathbf {\mathtt {h}}(v) < \mathbf {\mathtt {h}}(w)$
, this process is iterated.⊣
Another corollary can be proven after observing the way in which the implication behaves between powers of the same element in
![]() $FL_{ew}$
chains.
$FL_{ew}$
chains.
Lemma 3.6. Let
![]() $\mathbf {A} \in \mathbb {A}$
. For every
$\mathbf {A} \in \mathbb {A}$
. For every
![]() $m> n \in \mathbb {N}$
and every
$m> n \in \mathbb {N}$
and every
![]() $a \in A$
such that
$a \in A$
such that
![]() $a^{m+1} < a^m$
, it holds that
$a^{m+1} < a^m$
, it holds that
![]() .
.
Proof. If
![]() $n+1 < m$
(i.e.,
$n+1 < m$
(i.e.,
![]() $m = n+1+k$
for some
$m = n+1+k$
for some
![]() $k \geqslant 1$
), we know that
$k \geqslant 1$
), we know that
![]() $a^{n+1}> a^m$
: otherwise
$a^{n+1}> a^m$
: otherwise
![]() $a^m = a^{n+1+k} = a^{n+1}$
implying that
$a^m = a^{n+1+k} = a^{n+1}$
implying that
![]() $a^{m+1} = a^{n+2} = a^{n+1} = a^m$
too, which contradicts the assumptions. Thus,
$a^{m+1} = a^{n+2} = a^{n+1} = a^m$
too, which contradicts the assumptions. Thus,
![]() $a^{n+1} \rightarrow a^m < 1$
. By residuation, this is equivalent to
$a^{n+1} \rightarrow a^m < 1$
. By residuation, this is equivalent to
![]() $a \rightarrow (a^n \rightarrow a^m) < 1$
, which implies
$a \rightarrow (a^n \rightarrow a^m) < 1$
, which implies
![]() $a> a^n \rightarrow a^m$
. In particular, the latter is also greater or equal than
$a> a^n \rightarrow a^m$
. In particular, the latter is also greater or equal than
![]() $( a^n \rightarrow a^m)^2$
.
$( a^n \rightarrow a^m)^2$
.
Otherwise, necessarily
![]() $n+1 = m$
. Let
$n+1 = m$
. Let
![]() $a^n \rightarrow a^{n+1} = b$
for some
$a^n \rightarrow a^{n+1} = b$
for some
![]() $b \in A$
. By residuation,
$b \in A$
. By residuation,
![]() , and so,
, and so,
![]() . Again by residuation, it follows that
. Again by residuation, it follows that
![]() . This is now an implication falling in the previous case (with
. This is now an implication falling in the previous case (with
![]() $n+1 < m' = n+2$
). Thus, we know that
$n+1 < m' = n+2$
). Thus, we know that
![]() $a^n \rightarrow a^{n+2} < a$
. We conclude that
$a^n \rightarrow a^{n+2} < a$
. We conclude that
![]() .⊣
.⊣
Corollary 3.7. Let
![]() $\mathbf {A} \in \mathbb {A}$
, and
$\mathbf {A} \in \mathbb {A}$
, and
![]() $\mathfrak {M} \in K\mathbf {A}^T$
with root
$\mathfrak {M} \in K\mathbf {A}^T$
with root
![]() $u \in W$
be such that
$u \in W$
be such that
![]() . Then
. Then
![]() $e(u, x) = e(u,y)$
.
$e(u, x) = e(u,y)$
.
Proof. Corollary 3.5 implies
![]() for some
for some
![]() $a,b \in \mathbb {N}$
. From the previous lemma we get that either
$a,b \in \mathbb {N}$
. From the previous lemma we get that either
![]() or
or
![]() . Since the second condition implies
. Since the second condition implies
![]() $e(u, \varphi _P) = 1$
, and this is false, necessarily
$e(u, \varphi _P) = 1$
, and this is false, necessarily
![]() $e(u, x) = e(u, y)$
.⊣
$e(u, x) = e(u, y)$
.⊣
We can now prove that if
![]() $\varGamma _P \not \vdash _{K{\mathbb {A}}} \varphi _P$
then this happens in a model whose frame belongs to the class
$\varGamma _P \not \vdash _{K{\mathbb {A}}} \varphi _P$
then this happens in a model whose frame belongs to the class
![]() $\mathbb {L}$
, introduced at the beginning of this section (Figure 1).
$\mathbb {L}$
, introduced at the beginning of this section (Figure 1).
Lemma 3.8.
Proof. Left-to-right direction is immediate since
![]() $\mathbb {L}_{\mathbb {A}} \subseteq K{\mathbb {A}}$
. Concerning the right-to-left direction, assume
$\mathbb {L}_{\mathbb {A}} \subseteq K{\mathbb {A}}$
. Concerning the right-to-left direction, assume
![]() $\varGamma _P \not \vdash _{K{\mathbb {A}}} \varphi _P$
. We know then there is a model
$\varGamma _P \not \vdash _{K{\mathbb {A}}} \varphi _P$
. We know then there is a model
![]() $\mathfrak {M} \in K{\mathbb {A}}^T$
and
$\mathfrak {M} \in K{\mathbb {A}}^T$
and
![]() $u \in W$
such that
$u \in W$
such that
![]() .
.
We let the submodel
![]() of
of
![]() $\mathfrak {M}$
be defined with universe
$\mathfrak {M}$
be defined with universe
![]() $\{v_i\colon i \in \mathbb {N}, v_i \in W\}$
such that
$\{v_i\colon i \in \mathbb {N}, v_i \in W\}$
such that
![]() and for each
and for each
![]() $i \in \mathbb {N}$
, either
$i \in \mathbb {N}$
, either
![]() $Rv_iv_{i+1}$
or
$Rv_iv_{i+1}$
or
![]() $v_i$
has no successors in
$v_i$
has no successors in
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $v_{i+1} = v_i$
. Namely, the universe of
$v_{i+1} = v_i$
. Namely, the universe of
![]() is any chain of worlds from
is any chain of worlds from
![]() $\mathfrak {M}$
beginning by u and ending in a world with no successors.
$\mathfrak {M}$
beginning by u and ending in a world with no successors.
Define the model
![]() by restricting to
by restricting to
![]() the accessibility relation and the evaluation from
the accessibility relation and the evaluation from
![]() $\mathfrak {M}$
. From Lemma 3.4 we know u has finite height in the original model, and so also
$\mathfrak {M}$
. From Lemma 3.4 we know u has finite height in the original model, and so also
![]() is finite (since by definition, for any
is finite (since by definition, for any
![]() $j> \mathbf {\mathtt {h}}(w)$
,
$j> \mathbf {\mathtt {h}}(w)$
,
![]() $v_j = v_{\mathbf {\mathtt {h}}(w)}$
). Henceforth, by construction, its underlying frame is isomorphic to the frame from
$v_j = v_{\mathbf {\mathtt {h}}(w)}$
). Henceforth, by construction, its underlying frame is isomorphic to the frame from
![]() $\mathbb {L}$
with universe
$\mathbb {L}$
with universe
![]() . Namely,
. Namely,
![]() .
.
It remains to prove that, for every
![]() $\psi \in SFm(\varGamma _P\cup \{\varphi _P\})$
and each
$\psi \in SFm(\varGamma _P\cup \{\varphi _P\})$
and each
![]() , it holds that
, it holds that
![]() . It is clear that restricting to a submodel does not change the value of propositional variables at each world, i.e., for every
. It is clear that restricting to a submodel does not change the value of propositional variables at each world, i.e., for every
![]() $p \in \mathcal {V}$
(and thus, also for every propositional formula) and any
$p \in \mathcal {V}$
(and thus, also for every propositional formula) and any
![]() it holds that
it holds that
![]() . For other formulas, we prove the analogous claim by induction on the formula and on the height of v in
. For other formulas, we prove the analogous claim by induction on the formula and on the height of v in
![]() .
.
The case for
![]() $\mathbf {\mathtt {h}}(v)= 0 $
(i.e., there are no successors) is trivial to check, since by construction, v does not have successors in
$\mathbf {\mathtt {h}}(v)= 0 $
(i.e., there are no successors) is trivial to check, since by construction, v does not have successors in
![]() $\mathfrak {M}$
either. Thus, all formulas beginning with a modality contained in
$\mathfrak {M}$
either. Thus, all formulas beginning with a modality contained in
![]() $\textit {SFm}(\varGamma _P \cup \{\varphi _P\})$
are evaluated (both in
$\textit {SFm}(\varGamma _P \cup \{\varphi _P\})$
are evaluated (both in
![]() $\mathfrak {M}$
and in
$\mathfrak {M}$
and in
![]() ) to either
) to either
![]() $\overline {1}$
(
$\overline {1}$
(
![]() $\square $
) or
$\square $
) or
![]() $\overline {0}$
(
$\overline {0}$
(
![]() $\Diamond $
). Since the values of the propositional variables are not modified by taking submodels, this concludes the proof of the step.
$\Diamond $
). Since the values of the propositional variables are not modified by taking submodels, this concludes the proof of the step.
Regarding the case for
![]() $\mathbf {\mathtt {h}}(v) = n+1$
in
$\mathbf {\mathtt {h}}(v) = n+1$
in
![]() , observe that v has successors both in
, observe that v has successors both in
![]() $\mathfrak {\mathfrak {M}}$
and
$\mathfrak {\mathfrak {M}}$
and
![]() , so
, so
![]() . On the other hand,
. On the other hand,
![]() $e(v, \square p) = e(v, \Diamond p)$
for all
$e(v, \square p) = e(v, \Diamond p)$
for all
![]() $p \in \mathcal {V}$
(from formulas in
$p \in \mathcal {V}$
(from formulas in
![]() $(1)$
), and so, in all successors of v in
$(1)$
), and so, in all successors of v in
![]() $\mathfrak {M}$
, each variable p takes the same value, say
$\mathfrak {M}$
, each variable p takes the same value, say
![]() $\alpha _p$
. Then, in particular, in the world w chosen as the only successor of v in the construction of
$\alpha _p$
. Then, in particular, in the world w chosen as the only successor of v in the construction of
![]() , it also holds that
, it also holds that
![]() . Since by construction of
. Since by construction of
![]() the world v has as only successor w, it holds that
the world v has as only successor w, it holds that
![]() . Then,
. Then,
![]() .
.
The only formulas beginning with a modality appearing in
![]() $\textit {SFm}(\varGamma _P \cup \{\varphi _P\})$
are of the form
$\textit {SFm}(\varGamma _P \cup \{\varphi _P\})$
are of the form
![]() $\square \overline {0}$
,
$\square \overline {0}$
,
![]() $\square p$
and
$\square p$
and
![]() $\Diamond p$
for
$\Diamond p$
for
![]() $p \in \mathcal {V}$
. Since the evaluation of all these formulas and of the propositional variables from
$p \in \mathcal {V}$
. Since the evaluation of all these formulas and of the propositional variables from
![]() $\mathcal {V}$
in the world v coincides in
$\mathcal {V}$
in the world v coincides in
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() we conclude that the evaluation in v of formulas built from these ones using propositional connectives is also preserved from
we conclude that the evaluation in v of formulas built from these ones using propositional connectives is also preserved from
![]() $\mathfrak {M}$
to
$\mathfrak {M}$
to
![]() .⊣
.⊣
At this point, it is possible to obtain a useful characterization of x and y in terms of
![]() $\alpha _z$
at each world of a model with a frame isomorphic to one in
$\alpha _z$
at each world of a model with a frame isomorphic to one in
![]() $\mathbb {L}$
that satisfies
$\mathbb {L}$
that satisfies
![]() $\varGamma _P$
and not
$\varGamma _P$
and not
![]() $\varphi _P$
in its root. For convenience, in the next result we will invert the labeling of the worlds in the frames isomorphic to those in
$\varphi _P$
in its root. For convenience, in the next result we will invert the labeling of the worlds in the frames isomorphic to those in
![]() $\mathbb {L}$
, namely resorting to frames with structure
$\mathbb {L}$
, namely resorting to frames with structure
![]() (trivially isomorphic to
(trivially isomorphic to
![]() ).
).
Lemma 3.9. Let
![]() be an
be an
![]() $\mathbb {A}$
-Kripke model such that
$\mathbb {A}$
-Kripke model such that
![]() . Then there exist
. Then there exist
![]() with
with
![]() for each
for each
![]() , such that for each
, such that for each
![]() ,
,
Moreover, for each
![]() ,
,
Proof. We will prove the first claim of the lemma by induction on j. The details are only given for the x case, the other one is proven in the same way.
For
![]() $j = 1$
,
$j = 1$
,
![]() $u_1$
does not have successors. From formula
$u_1$
does not have successors. From formula
![]() $(3)$
in
$(3)$
in
![]() $\varGamma _P$
(relying on the fact that the algebras in
$\varGamma _P$
(relying on the fact that the algebras in
![]() $\mathbb {A}$
are chains) and Lemma 3.3 it follows that there is
$\mathbb {A}$
are chains) and Lemma 3.3 it follows that there is
![]() for which
for which
For
![]() $j = r+1$
, observe the only successor of
$j = r+1$
, observe the only successor of
![]() $u_j$
in
$u_j$
in
![]() $\mathfrak {M}$
is
$\mathfrak {M}$
is
![]() $u_r$
. Then, from
$u_r$
. Then, from
![]() $(3)$
and Lemma 3.3 it follows that there is
$(3)$
and Lemma 3.3 it follows that there is
![]() for which
for which
By the Induction Hypothesis, the above value is equal to
![]() $ (\alpha _z^{{\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_r}}}})^{s^{\parallel \mathtt { x_{i_j}}\parallel }} \alpha _z^{\mathtt { x_{i_j}}}$
, and through simple properties of the monoidal operation, to
$ (\alpha _z^{{\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_r}}}})^{s^{\parallel \mathtt { x_{i_j}}\parallel }} \alpha _z^{\mathtt { x_{i_j}}}$
, and through simple properties of the monoidal operation, to
![]() $ (\alpha _z^{{\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_r}}}})^{s^{\parallel \mathtt { x_{i_j}}\parallel } + \mathtt { x_{i_j}}}$
as well. This value, by definition of the concatenation of numbers in base s, is exactly
$ (\alpha _z^{{\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_r}}}})^{s^{\parallel \mathtt { x_{i_j}}\parallel } + \mathtt { x_{i_j}}}$
as well. This value, by definition of the concatenation of numbers in base s, is exactly
![]() $\alpha _z^{{\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}}}}$
, concluding the proof of the first claim.
$\alpha _z^{{\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}}}}$
, concluding the proof of the first claim.
Concerning the second claim, assume towards a contradiction that there is
![]() such that
such that
![]() $\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}} \neq \mathtt { y_{i_1}}{_\smile } \dots {_\smile } \mathtt { y_{i_j}}$
and
$\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}} \neq \mathtt { y_{i_1}}{_\smile } \dots {_\smile } \mathtt { y_{i_j}}$
and
![]() $e(u_j, x) = \alpha _z^{\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}}} = \alpha _z^{\mathtt { y_{i_1}}{_\smile } \dots {_\smile } \mathtt { y_{i_j}}} = e(u_j,y)$
. If
$e(u_j, x) = \alpha _z^{\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}}} = \alpha _z^{\mathtt { y_{i_1}}{_\smile } \dots {_\smile } \mathtt { y_{i_j}}} = e(u_j,y)$
. If
![]() $\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}} < \mathtt { y_{i_1}}{_\smile } \dots {_\smile } \mathtt { y_{i_j}}$
, it follows that
$\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}} < \mathtt { y_{i_1}}{_\smile } \dots {_\smile } \mathtt { y_{i_j}}$
, it follows that
![]() $\alpha _z^{\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}}} \alpha _z^n = \alpha _z^{\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}}} $
for every
$\alpha _z^{\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}}} \alpha _z^n = \alpha _z^{\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}}} $
for every
![]() $n \geqslant 0$
. Thus, in particular, from Corollary 3.5
$n \geqslant 0$
. Thus, in particular, from Corollary 3.5
![]() $e(u_k, x) = e(u_j, x)$
, and also
$e(u_k, x) = e(u_j, x)$
, and also
![]() $e(u_k, x) \alpha _z = e(u_k, x) = e(u_j, x)$
. However,
$e(u_k, x) \alpha _z = e(u_k, x) = e(u_j, x)$
. However,
![]() $\mathfrak {M}, u_k \not \models \varphi _P$
implies that
$\mathfrak {M}, u_k \not \models \varphi _P$
implies that
![]() $e(u_k, x) \alpha _z < e(u_k,x)$
, reaching a contradiction.
$e(u_k, x) \alpha _z < e(u_k,x)$
, reaching a contradiction.
The proof is analogous if
![]() $\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}}> \mathtt { y_{i_1}}{_\smile } \dots {_\smile } \mathtt { y_{i_j}}$
.⊣
$\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_j}}> \mathtt { y_{i_1}}{_\smile } \dots {_\smile } \mathtt { y_{i_j}}$
.⊣
All the previous technical lemmas lead to a simple proof of Theorem 3.2.
Proof. (Of Theorem 3.2,
![]() $(2) \Rightarrow (3) \Rightarrow (1)$
).
$(2) \Rightarrow (3) \Rightarrow (1)$
).
Assume condition
![]() $\mathit {(2)}$
of the lemma, i.e.,
$\mathit {(2)}$
of the lemma, i.e.,
![]() $\varGamma _P \not \vdash _{K{\mathbb {A}}} \varphi _P$
. Lemma 3.8 implies there is a model
$\varGamma _P \not \vdash _{K{\mathbb {A}}} \varphi _P$
. Lemma 3.8 implies there is a model
![]() and
and
![]() $u \in W$
such that
$u \in W$
such that
![]() . Since all models in
. Since all models in
![]() are finite, this proves point
are finite, this proves point
![]() $(3)$
. From here, from Corollary 3.7 we know that
$(3)$
. From here, from Corollary 3.7 we know that
![]() $e(u, x) = e(u, y)$
. Then, by Lemma 3.9, it follows that there exist indexes
$e(u, x) = e(u, y)$
. Then, by Lemma 3.9, it follows that there exist indexes
![]() in
in
![]() for which
for which
![]() $\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_k}}= \mathtt { y_{i_1}}{_\smile } \dots {_\smile } \mathtt { y_{i_k}}$
. This is a solution for the Post Correspondence Instance
$\mathtt { x_{i_1}}{_\smile } \dots {_\smile } \mathtt { x_{i_k}}= \mathtt { y_{i_1}}{_\smile } \dots {_\smile } \mathtt { y_{i_k}}$
. This is a solution for the Post Correspondence Instance
![]() $(P)$
, concluding the proof of
$(P)$
, concluding the proof of
![]() $(3) \Rightarrow (1)$
⊣
$(3) \Rightarrow (1)$
⊣
Let us conclude this section by pointing out that the undecidability results in [Reference Vidal42], affecting the local deduction over transitive models evaluated over classes of algebras like
![]() $\mathbb {A}$
, are immediately translatable to the global logic. Consider the class of frames
$\mathbb {A}$
, are immediately translatable to the global logic. Consider the class of frames
![]() $\mathbb {L}^4$
given by isomorphic copies of the frames in the set
$\mathbb {L}^4$
given by isomorphic copies of the frames in the set
where
![]() $<$
is the usual strict order relation in
$<$
is the usual strict order relation in
![]() $\mathbb {N}$
restricted in each case to the corresponding universe.
$\mathbb {N}$
restricted in each case to the corresponding universe.
Corollary 3.10 (Of Theorem 3.1 from [Reference Vidal42]).
For any class of transitive frames
![]() $\mathbb {T}$
containing an isomorphic copy of
$\mathbb {T}$
containing an isomorphic copy of
![]() $\mathbb {L}^4$
, the logic
$\mathbb {L}^4$
, the logic
![]() $\vdash _{\mathbb {T}_{\mathbb {A}}}$
is undecidable. In particular, the logic
$\vdash _{\mathbb {T}_{\mathbb {A}}}$
is undecidable. In particular, the logic
![]() $\vdash _{K4\mathbb {A}}$
is undecidable, for
$\vdash _{K4\mathbb {A}}$
is undecidable, for
![]() $K4\mathbb {A}$
being all safe transitive Kripke models evaluated over the algebras in
$K4\mathbb {A}$
being all safe transitive Kripke models evaluated over the algebras in
![]() $\mathbb {A}$
.
$\mathbb {A}$
.
More precisely, the three-variable fragments of the previous logics are undecidable.
Proof. It is straightforward, since for any finite
![]() $\varGamma \cup \{\varphi \} \subseteq Fm$
and any class of transitive models
$\varGamma \cup \{\varphi \} \subseteq Fm$
and any class of transitive models
![]() $\mathbb {C}$
, it is routine to check that
$\mathbb {C}$
, it is routine to check that
⊣
4 Non axiomatizability of modal Łukasiewicz and product logics
The undecidability of the previous family of modal logics over finite models raises the question of their axiomatizability. In particular, it was an open problem how to axiomatize the finitary standard modal Łukasiewicz logic [Reference Diaconescu, Metcalfe and Schnuriger20, Reference Hansoul and Teheux30] and standard modal Product logic [Reference Vidal, Esteva and Godo46]. None of the minimal modal logics over the previous standard algebras has been axiomatized in the literature, including the logics arising from crisp-accessibility frames (nor those from many-valued frames) with either one or both modal operators. In the previous references, infinitary axiomatic systems complete with respect to related (but different) deductive systems have been proposed. For instance, their corresponding infinitary companions (have been axiomatized in some cases, over extended languages).
We close this open problem for the standard Łukasiewicz and Product logics with a negative answer: these logics are in fact not axiomatizable, since their respective sets of valid consequences are not recursively enumerable. We will devote this section to prove the previous claims. For that, three properties turn out to be crucial: undecidability of the global consequence over finite models of the class, decidability of the propositional logic, and completeness of the global consequence with respect to certain well-behaved models (in these cases, in terms of witnessing conditions). We will prove this negative result for the modal expansion of the standard Łukasiewicz logic. Then, the analogous result will follow for the Product logic, relying on the known isomorphism between the standard MV-algebra and a certain Product algebra.
The first one of the above properties was proven in Section 3. Let us show how decidability of the underlying propositional logic
![]() $\models _{\mathbb {A}}$
implies that the set
$\models _{\mathbb {A}}$
implies that the set
![]() is R.E., which will allow us to conclude there is no possible axiomatization for the logics of finite models over those classes of algebras.
is R.E., which will allow us to conclude there is no possible axiomatization for the logics of finite models over those classes of algebras.
We first see that the global consequence relation over a finite frame is decidable as long as the underlying propositional consequence relation is decidable too.
Lemma 4.1. Let
![]() $\mathfrak {F}$
be a finite frame, and
$\mathfrak {F}$
be a finite frame, and
![]() $\mathbb {A}$
a class of residuated lattices for which
$\mathbb {A}$
a class of residuated lattices for which
![]() $ \models _{\mathbb {A}}$
is decidable. Then
$ \models _{\mathbb {A}}$
is decidable. Then
![]() $\vdash _{\mathfrak {F}_{\mathbb {A}}}$
is decidable.
$\vdash _{\mathfrak {F}_{\mathbb {A}}}$
is decidable.
Proof. Let
a Kripke frame,
![]() $v \in W$
a world in the frame,
$v \in W$
a world in the frame,
![]() $\psi $
a modal formula with variables in a finite set
$\psi $
a modal formula with variables in a finite set
![]() $\mathcal {V}$
, and x not in
$\mathcal {V}$
, and x not in
![]() $\mathcal {V}$
. Consider the extended set of propositional variables
$\mathcal {V}$
. Consider the extended set of propositional variables
We recursively define the non-modal formula
over
![]() $\mathcal {V}^*$
as follows:
$\mathcal {V}^*$
as follows:

Then, for
![]() $\varSigma $
a set of formulas we let
$\varSigma $
a set of formulas we let
, where set of original variables is
. Moreover, consider the formulasFootnote 14
From those, define the set of formulas
We will now prove that
which implies the lemma.
To prove the right-to-left direction, assume
![]() $\varGamma \not \vdash _{\mathfrak {F}_{\mathbb {A}}} \varphi $
. Then there is
$\varGamma \not \vdash _{\mathfrak {F}_{\mathbb {A}}} \varphi $
. Then there is
![]() $\mathbf {A} \in \mathbb {A}$
, and an
$\mathbf {A} \in \mathbb {A}$
, and an
![]() $\mathbf {A}$
-Kripke model over
$\mathbf {A}$
-Kripke model over
![]() $\mathfrak {F}$
in which
$\mathfrak {F}$
in which
![]() $e(v, \varGamma ) \subseteq \{1\}$
for all v and
$e(v, \varGamma ) \subseteq \{1\}$
for all v and
![]() $e(v_0, \varphi ) < 1$
for some
$e(v_0, \varphi ) < 1$
for some
![]() $v_0 \in W$
. Consider then the mapping
$v_0 \in W$
. Consider then the mapping
![]() $h \colon \mathcal {V}^* \rightarrow A$
defined by
$h \colon \mathcal {V}^* \rightarrow A$
defined by
![]() $h(p^v) = e(v, p)$
,
$h(p^v) = e(v, p)$
,
![]() $h(x_{\square \psi }^v) = e(v, \square \psi )$
and
$h(x_{\square \psi }^v) = e(v, \square \psi )$
and
![]() $h(x_{\Diamond \psi }^v) = e(v, \Diamond \psi )$
. It is easy to see that the extension of this mapping to a homomorphism into
$h(x_{\Diamond \psi }^v) = e(v, \Diamond \psi )$
. It is easy to see that the extension of this mapping to a homomorphism into
![]() $\mathbf {A}$
satisfies
$\mathbf {A}$
satisfies
![]() for every
for every
![]() $\psi \in SFm(\varGamma , \varphi )$
. Thus, it satisfies the premises in the derivation at the right side, since
$\psi \in SFm(\varGamma , \varphi )$
. Thus, it satisfies the premises in the derivation at the right side, since
![]() $e(v, \varGamma ) \subseteq \{1\}$
for all v and by the semantical definition of
$e(v, \varGamma ) \subseteq \{1\}$
for all v and by the semantical definition of
![]() $\square $
and
$\square $
and
![]() $\Diamond $
in the model. On the other hand, it does not satisfy the consequence, since
$\Diamond $
in the model. On the other hand, it does not satisfy the consequence, since
![]() $e(v_0, \varphi ) < 1$
.
$e(v_0, \varphi ) < 1$
.
Conversely, given a propositional homomorphism h over some algebra
![]() $\mathbf {A} \in \mathbb {A}$
satisfying
$\mathbf {A} \in \mathbb {A}$
satisfying
and not satisfying
, we can consider the
![]() $\mathbf {A}$
-Kripke model over
$\mathbf {A}$
-Kripke model over
![]() $\mathfrak {F}$
that lets
$\mathfrak {F}$
that lets
![]() $e(v, p) = h(p^v)$
. Since
$e(v, p) = h(p^v)$
. Since
![]() $h(\varDelta ^v(\varGamma , \varphi )) = \{1\}$
, then
$h(\varDelta ^v(\varGamma , \varphi )) = \{1\}$
, then
for every
![]() $\psi \in SFm(\varGamma , \varphi )$
, concluding the proof.⊣
$\psi \in SFm(\varGamma , \varphi )$
, concluding the proof.⊣
Corollary 4.2. Let
![]() $\mathbb {A}$
be a class of residuated lattices for which
$\mathbb {A}$
be a class of residuated lattices for which
![]() $\models _{\mathbb {A}}$
is decidable, and
$\models _{\mathbb {A}}$
is decidable, and
![]() $j \in \mathbb {N}$
. Then the problem of determining whether a formula
$j \in \mathbb {N}$
. Then the problem of determining whether a formula
![]() $\varphi $
follows globally from a finite set of formulas
$\varphi $
follows globally from a finite set of formulas
![]() $\varGamma $
in all
$\varGamma $
in all
![]() $\mathbb {A}$
-models of cardinality j (denoted by
$\mathbb {A}$
-models of cardinality j (denoted by
![]() $\vdash _{jK{\mathbb {A}}}$
) is decidable.
$\vdash _{jK{\mathbb {A}}}$
) is decidable.
Proof. There is a finite number of frames of cardinality j, and so, for each one, we can run the decision procedure from the above lemma.⊣
Exhibiting a recursive procedure enumerating the elements not belonging to
![]() $\vdash _{\omega K{\mathbb {A}}}$
is now easy.
$\vdash _{\omega K{\mathbb {A}}}$
is now easy.
Lemma 4.3. Let
![]() $\mathbb {A}$
be a class of residuated lattices for which
$\mathbb {A}$
be a class of residuated lattices for which
![]() $\models _{\mathbb {A}}$
is decidable. Then the set
$\models _{\mathbb {A}}$
is decidable. Then the set
![]() is recursively enumerable.
is recursively enumerable.
Proof. Let us enumerate all pairs
![]() , and initialize P as the empty set. Now, for each
, and initialize P as the empty set. Now, for each
![]() $i \in \mathbb {N}$
, store
$i \in \mathbb {N}$
, store
![]() in P. Then check, for each
in P. Then check, for each
![]() and for each
and for each
![]() , whether
, whether
![]() $\varGamma \vdash _{jK{\mathbb {A}}} \varphi $
. This is a finite amount (since P is always finite) of decidable operations (from Corollary 4.2), thus a decidable operation. Whenever the answer is negative, return that pair and continue.
$\varGamma \vdash _{jK{\mathbb {A}}} \varphi $
. This is a finite amount (since P is always finite) of decidable operations (from Corollary 4.2), thus a decidable operation. Whenever the answer is negative, return that pair and continue.
To see that the previous procedure enumerates exactly
![]() , pick an arbitrary
, pick an arbitrary
![]() (according to the initial enumeration).
(according to the initial enumeration).
First suppose that
![]() $\varGamma \not \vdash _{\omega K{\mathbb {A}}} \varphi $
, and that this happens in some
$\varGamma \not \vdash _{\omega K{\mathbb {A}}} \varphi $
, and that this happens in some
![]() $\mathbf {A}$
-model of cardinality j for some
$\mathbf {A}$
-model of cardinality j for some
![]() $\mathbf {A}\in \mathbb {A}$
. Then, at step
$\mathbf {A}\in \mathbb {A}$
. Then, at step
![]() $\max \{i, j\}$
it is checked whether
$\max \{i, j\}$
it is checked whether
![]() $\varGamma _i \vdash _{jK{\mathbb {A}}} \varphi _i$
. By assumption we know this condition does not hold, so the answer is negative and the pair
$\varGamma _i \vdash _{jK{\mathbb {A}}} \varphi _i$
. By assumption we know this condition does not hold, so the answer is negative and the pair
![]() is returned.
is returned.
On the other hand, suppose
![]() $\varGamma _i \vdash _{\omega K{\mathbb {A}}} \varphi _i$
. For every
$\varGamma _i \vdash _{\omega K{\mathbb {A}}} \varphi _i$
. For every
![]() $j < i$
, the above procedure cannot output
$j < i$
, the above procedure cannot output
![]() since this has not been stored in P yet. On the other hand, for every
since this has not been stored in P yet. On the other hand, for every
![]() $j \geqslant i$
, we know that the procedure to decide whether
$j \geqslant i$
, we know that the procedure to decide whether
![]() $\varGamma _i \vdash _{jK{\mathbb {A}}} \varphi _i\rangle $
answers positively, and then the pair is never returned.⊣
$\varGamma _i \vdash _{jK{\mathbb {A}}} \varphi _i\rangle $
answers positively, and then the pair is never returned.⊣
The previous lemma implies that, for every class of algebras
![]() $\mathbb {C}$
satisfying the premises of Theorem 3.1 for which
$\mathbb {C}$
satisfying the premises of Theorem 3.1 for which
![]() $\models _{\mathbb {C}}$
is decidable, the logic
$\models _{\mathbb {C}}$
is decidable, the logic
![]() $\vdash _{\omega K{\mathbb {C}}}$
is not recursively enumerable. Otherwise, since the previous lemma proves that
$\vdash _{\omega K{\mathbb {C}}}$
is not recursively enumerable. Otherwise, since the previous lemma proves that
![]() is recursively enumerable, the logic
is recursively enumerable, the logic
![]() $\vdash _{\omega K{\mathbb {C}}}$
would be decidable, contradicting Theorem 3.1. Since
$\vdash _{\omega K{\mathbb {C}}}$
would be decidable, contradicting Theorem 3.1. Since
![]() and
and
![]() $\varPi $
are decidable logics [Reference Hájek26], their standard completeness implies that
$\varPi $
are decidable logics [Reference Hájek26], their standard completeness implies that
![]() and
and
![]() $\models _{[0,1]_\varPi }$
are decidable too, leading to the following corollary.
$\models _{[0,1]_\varPi }$
are decidable too, leading to the following corollary.
Corollary 4.4. The logics
![]() and
and
![]() $\vdash _{\omega K{\varPi }}$
are not axiomatizable.
$\vdash _{\omega K{\varPi }}$
are not axiomatizable.
However, since it is not a general fact that the logics
![]() $\vdash _{K{\mathbb {C}}}$
are complete with respect to finite models, the lack of axiomatization of the previous logics does still not close the problems mentioned in the beginning of this section.
$\vdash _{K{\mathbb {C}}}$
are complete with respect to finite models, the lack of axiomatization of the previous logics does still not close the problems mentioned in the beginning of this section.
4.1 Modal Łukasiewicz logic is not axiomatizable
We can show that, even if the global modal Łukasiewicz logic might not enjoy the finite model property, if the global modal (standard) Łukasiewicz logic
![]() is R.E. then
is R.E. then
![]() (the analogous logic over finite models) would be R.E. too. Since we saw before the latter does not hold, we will conclude that
(the analogous logic over finite models) would be R.E. too. Since we saw before the latter does not hold, we will conclude that
![]() is not R.E. and so, not axiomatizable.
is not R.E. and so, not axiomatizable.
Lemma 3 from [Reference Hájek27] allows us to prove completeness of
![]() with respect to witnessed models, in a similar way to how it is done for tautologies of fuzzy description logic (FDL) over Łukasiewicz logic in the same publication. We do not introduce details of F.O. (standard) Łukasiewicz logic here, we refer the interested reader to, e.g., [Reference Hájek26]. Just recall that:
with respect to witnessed models, in a similar way to how it is done for tautologies of fuzzy description logic (FDL) over Łukasiewicz logic in the same publication. We do not introduce details of F.O. (standard) Łukasiewicz logic here, we refer the interested reader to, e.g., [Reference Hájek26]. Just recall that:
-
• A standard Łukasiewicz F.O. model is a structure
 where W is a non-empty set and for each
where W is a non-empty set and for each
 $i \in I$
and
$i \in I$
and
 $ar(i)$
the arity of
$ar(i)$
the arity of
 $P_i$
,
$P_i$
,
 $P_i \colon W^{ar(i)} \rightarrow [0,1]$
.
$P_i \colon W^{ar(i)} \rightarrow [0,1]$
. -
• An evaluation in an (F.O.) model is a mapping
 $v \colon \mathcal {V} \mapsto W$
. Moreover, we write
$v \colon \mathcal {V} \mapsto W$
. Moreover, we write
 $v[x \mapsto m]$
to denote the evaluation v where the mapping of the variable x is overwritten and x is mapped to m (and simply
$v[x \mapsto m]$
to denote the evaluation v where the mapping of the variable x is overwritten and x is mapped to m (and simply
 $[x \mapsto m]$
denotes that the evaluation of x is m and the other variables are irrelevant).
$[x \mapsto m]$
denotes that the evaluation of x is m and the other variables are irrelevant). -
• The value of a formula
 $\varphi $
in an (F.O.) model
$\varphi $
in an (F.O.) model
 $\mathfrak {M}$
under an evaluation v, denoted by
$\mathfrak {M}$
under an evaluation v, denoted by
 $\|\varphi \|_{\mathfrak {M}, v}$
is inductively defined by
$\|\varphi \|_{\mathfrak {M}, v}$
is inductively defined by-
–
 .
. -
–
 $\ \|\varphi _1 \star \varphi _2\|_{\mathfrak {M}, v} = \|\varphi _1\|_{\mathfrak {M}, v} \star \|\varphi _2\|_{\mathfrak {M}, v}$
for
$\ \|\varphi _1 \star \varphi _2\|_{\mathfrak {M}, v} = \|\varphi _1\|_{\mathfrak {M}, v} \star \|\varphi _2\|_{\mathfrak {M}, v}$
for
 $\star $
propositional (Ł) operation.
$\star $
propositional (Ł) operation. -
–
 $\ \|\forall x \varphi (x)\|_{\mathfrak {M}, v} = \bigwedge _{m \in W} \|\varphi \|_{\mathfrak {M}, v[x \mapsto m]}$
.
$\ \|\forall x \varphi (x)\|_{\mathfrak {M}, v} = \bigwedge _{m \in W} \|\varphi \|_{\mathfrak {M}, v[x \mapsto m]}$
. -
–
 $\ \|\exists x \varphi (x)\|_{\mathfrak {M}, v} = \bigvee _{m \in W} \|\varphi \|_{\mathfrak {M}, v[x \mapsto m]}$
.
$\ \|\exists x \varphi (x)\|_{\mathfrak {M}, v} = \bigvee _{m \in W} \|\varphi \|_{\mathfrak {M}, v[x \mapsto m]}$
.
-
Observe that the value of a sentence (i.e., closed formula, without free variables)
![]() $\varphi $
in a model is constant under any evaluation, so we can simply write
$\varphi $
in a model is constant under any evaluation, so we can simply write
![]() $\|\varphi \|_{\mathfrak {M}}$
to denote its value in a model. Moreover, we say that a model
$\|\varphi \|_{\mathfrak {M}}$
to denote its value in a model. Moreover, we say that a model
![]() $\mathfrak {M}$
is witnessed whenever for every sentence
$\mathfrak {M}$
is witnessed whenever for every sentence
![]() $Qx \varphi (x)$
for
$Qx \varphi (x)$
for
![]() $Q \in \{\forall , \exists \}$
there is some
$Q \in \{\forall , \exists \}$
there is some
![]() $m \in W$
such that
$m \in W$
such that
The consequence relation over standard Łukasiewicz F.O. models,
![]() , is defined for sentences by letting
, is defined for sentences by letting
![]() whenever for every standard Łukasiewicz F.O. model
whenever for every standard Łukasiewicz F.O. model
![]() $\mathfrak {M}$
, if
$\mathfrak {M}$
, if
![]() $\|\varGamma \|_{\mathfrak {M}} \subseteq \{1\}$
then
$\|\varGamma \|_{\mathfrak {M}} \subseteq \{1\}$
then
![]() $\|\varphi \|_{\mathfrak {M}} = 1$
.
$\|\varphi \|_{\mathfrak {M}} = 1$
.
Lemma 4.5 [Reference Hájek27, Lemma 3].
Let
![]() $\mathfrak {M}$
be a standard Łukasiewicz F.O. model. Then there is a (standard Łukasiewicz F.O.) witnessed model
$\mathfrak {M}$
be a standard Łukasiewicz F.O. model. Then there is a (standard Łukasiewicz F.O.) witnessed model
![]() $\mathfrak {M}'$
such that
$\mathfrak {M}'$
such that
![]() $\mathfrak {M}$
is a submodel of
$\mathfrak {M}$
is a submodel of
![]() $\mathfrak {M}'$
and for every sentence
$\mathfrak {M}'$
and for every sentence
![]() $\alpha $
it holds that
$\alpha $
it holds that
From here, we can easily prove completeness of
![]() with respect to witnessed Kripke models, i.e., those for which, for every modal formula
with respect to witnessed Kripke models, i.e., those for which, for every modal formula
![]() $\triangledown \varphi $
(with
$\triangledown \varphi $
(with
![]() $\triangledown \in \{\square , \Diamond \}$
) and every world v there is some world w such that
$\triangledown \in \{\square , \Diamond \}$
) and every world v there is some world w such that
![]() $Rvw$
and
$Rvw$
and
Lemma 4.6. If
![]() there is a witnessed standard Łukasiewicz Kripke model
there is a witnessed standard Łukasiewicz Kripke model
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $v \in W$
such that
$v \in W$
such that
![]() .
.
Proof. We can use the usual translation from modal to F.O. logics in order to move from a Kripke model to a suitable F.O. model. For a modal formula
![]() $\varphi $
consider the F.O. language
$\varphi $
consider the F.O. language
![]() $\{R/2, \{P_p/1\colon p\text { variable in }\varphi \}\}$
. For an arbitrary natural number
$\{R/2, \{P_p/1\colon p\text { variable in }\varphi \}\}$
. For an arbitrary natural number
![]() $i \in \mathbb {N}$
, let us define the translation
$i \in \mathbb {N}$
, let us define the translation
![]() recursively by letting:
recursively by letting:
-
•
 ,
, -
•
 for a propositional connective
for a propositional connective
 $\star $
,
$\star $
, -
•
 ,
, -
•
 .
.
It is a simple exercise to check that

If
![]() there is some F.O. model satisfying the premises of the right side of the above consequence and not
there is some F.O. model satisfying the premises of the right side of the above consequence and not
![]() . From the previous lemma we know there is a witnessed (F.O.) model
. From the previous lemma we know there is a witnessed (F.O.) model
![]() $\mathfrak {M}$
in which the same conditions hold. Then, there is some m in the universe for which
$\mathfrak {M}$
in which the same conditions hold. Then, there is some m in the universe for which
![]() . At this point, it is only necessary to build a witnessed Kripke model
. At this point, it is only necessary to build a witnessed Kripke model
![]() from
from
![]() $\mathfrak {M}$
that is a global model for
$\mathfrak {M}$
that is a global model for
![]() $\varGamma $
but does not satisfy
$\varGamma $
but does not satisfy
![]() $\varphi $
at some world. In order to do that, let the universe of the Kripke model be the same universe of
$\varphi $
at some world. In order to do that, let the universe of the Kripke model be the same universe of
![]() $\mathfrak {M}$
, and let the accessibility relation be given by the interpretation of the binary predicate R in
$\mathfrak {M}$
, and let the accessibility relation be given by the interpretation of the binary predicate R in
![]() $\mathfrak {M}$
. Observe that, since
$\mathfrak {M}$
. Observe that, since
![]() $\forall x\forall y (R(x,y) \vee \neg R(x,y))$
is true in the model, necessarily
$\forall x\forall y (R(x,y) \vee \neg R(x,y))$
is true in the model, necessarily
![]() $R(x,y) \in \{0,1\}$
, and thus the resulting model will be crisp. Finally, let
$R(x,y) \in \{0,1\}$
, and thus the resulting model will be crisp. Finally, let
![]() $e(v, p) = \|P_p(v)\|_{\mathfrak {M}}$
for each variable p and each world
$e(v, p) = \|P_p(v)\|_{\mathfrak {M}}$
for each variable p and each world
![]() $v \in W$
.
$v \in W$
.
By induction on the complexity of the formula it is routine to check that for every
![]() $\psi \in SFm(\varGamma , \varphi )$
and every
$\psi \in SFm(\varGamma , \varphi )$
and every
![]() $v \in W$
,
$v \in W$
,
![]() . Moreover, since the F.O. model is witnessed, the Kripke model is witnessed too.
. Moreover, since the F.O. model is witnessed, the Kripke model is witnessed too.
![]() is a global model of
is a global model of
![]() $\varGamma $
, while
$\varGamma $
, while
![]() , concluding the proof of the lemma.⊣
, concluding the proof of the lemma.⊣
We can use the non-idempotency of the Łukasiewicz t-norm to recursively reduce the global consequence relation over finite models to the unrestricted global consequence relation.
Lemma 4.7. Let
![]() $\varGamma \cup \{\varphi \} \subseteq _{\omega } Fm$
and
$\varGamma \cup \{\varphi \} \subseteq _{\omega } Fm$
and
![]() $p,q \not \in \mathcal {V}(\varGamma , \varphi )$
. Define
$p,q \not \in \mathcal {V}(\varGamma , \varphi )$
. Define
-
•
 ,
, -
•
 ,
, -
•
 .
.
Then
Proof.
![]() $\Rightarrow $
: Assume
$\Rightarrow $
: Assume
![]() by Lemma 4.6, there is a witnessed standard Łukasiewicz Kripke model
by Lemma 4.6, there is a witnessed standard Łukasiewicz Kripke model
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $v \in W$
such that
$v \in W$
such that
![]() $\mathfrak {M} \models \varGamma , \varXi (p), \xi (p,q)$
l (i.e.,
$\mathfrak {M} \models \varGamma , \varXi (p), \xi (p,q)$
l (i.e.,
![]() $e(u, \varGamma , \varXi (p) \cup \xi (p,q)) \subseteq \{1\}$
for all u) and
$e(u, \varGamma , \varXi (p) \cup \xi (p,q)) \subseteq \{1\}$
for all u) and
![]() $e(v, \varphi \vee \psi (p,q)) < 1$
. We can assume that
$e(v, \varphi \vee \psi (p,q)) < 1$
. We can assume that
![]() $\mathfrak {M}$
is the unraveled tree generated from v. We will now prove that we can define a finite model equivalent to this one for what concerns the formulas in
$\mathfrak {M}$
is the unraveled tree generated from v. We will now prove that we can define a finite model equivalent to this one for what concerns the formulas in
![]() $F = \textit {SFm}(\varGamma \cup \varXi (p) \cup \{\xi (p,q)\} \cup \{\varphi \vee \psi (p,q)\})$
.
$F = \textit {SFm}(\varGamma \cup \varXi (p) \cup \{\xi (p,q)\} \cup \{\varphi \vee \psi (p,q)\})$
.
First, since
![]() $e(u, \varXi (p)) \subseteq \{1\}$
for each
$e(u, \varXi (p)) \subseteq \{1\}$
for each
![]() $u \in W$
, it follows that there is
$u \in W$
, it follows that there is
![]() $a \in [0,1]$
such that for all
$a \in [0,1]$
such that for all
![]() $u \in W$
,
$u \in W$
,
![]() $e(u, p) = a$
, as it was proven in Lemma 3.3. Moreover, from
$e(u, p) = a$
, as it was proven in Lemma 3.3. Moreover, from
![]() $e(v, p \vee \neg p) < 1$
we have that
$e(v, p \vee \neg p) < 1$
we have that
![]() $a \in (0,1)$
.
$a \in (0,1)$
.
On the other hand, from
![]() $e(u, \xi (p,q)) =1$
for each
$e(u, \xi (p,q)) =1$
for each
![]() $u \in W$
we get that
$u \in W$
we get that
![]() $e(u, q) = e(u, \square q) a$
. Thus, for each world
$e(u, q) = e(u, \square q) a$
. Thus, for each world
![]() $u \in W$
we have that
$u \in W$
we have that
![]() for all
for all
![]() . In particular, if there was any
. In particular, if there was any
![]() $u \in W$
with
$u \in W$
with
![]() $\mathbf {\mathtt {h}}(u) = \infty $
, v would also have infinite height, and so
$\mathbf {\mathtt {h}}(u) = \infty $
, v would also have infinite height, and so
![]() for all
for all
![]() $n\in \mathbb {N}$
. Since
$n\in \mathbb {N}$
. Since
![]() $a \in (0,1)$
, by the definition of the product in the standard MV algebra, the previous family of inequalities would imply that
$a \in (0,1)$
, by the definition of the product in the standard MV algebra, the previous family of inequalities would imply that
![]() $e(v, q) = 0$
. Then it would holds that
$e(v, q) = 0$
. Then it would holds that
![]() $e(v, \neg q) = 1$
, which is not possible since by the assumption
$e(v, \neg q) = 1$
, which is not possible since by the assumption
![]() $e(v, \varphi \vee \psi (p,q)) < 1$
. Thus, v—and so, all worlds of the model—must have finite height.
$e(v, \varphi \vee \psi (p,q)) < 1$
. Thus, v—and so, all worlds of the model—must have finite height.
We can apply now a filtration-like transformation to
![]() $\mathfrak {M}$
with respect to the set of formulas F in order to obtain a finite directed model. To do this, let us denote by
$\mathfrak {M}$
with respect to the set of formulas F in order to obtain a finite directed model. To do this, let us denote by
![]() $wit(u, \triangledown \chi )$
an arbitrary witnessing world for the modal formula
$wit(u, \triangledown \chi )$
an arbitrary witnessing world for the modal formula
![]() $\triangledown \chi $
at world u (i.e., such that
$\triangledown \chi $
at world u (i.e., such that
![]() $e(u, \triangledown \chi ) = e(wit(u, \triangledown \chi ), \chi )$
. Then define the universe
$e(u, \triangledown \chi ) = e(wit(u, \triangledown \chi ), \chi )$
. Then define the universe
with

Observe that if there is some
![]() $i \in \mathbb {N}$
for which the worlds in
$i \in \mathbb {N}$
for which the worlds in
![]() $W_i$
do not have successors,
$W_i$
do not have successors,
![]() $W_j = \emptyset $
for any
$W_j = \emptyset $
for any
![]() $j> i$
.
$j> i$
.
We proved above that all worlds in
![]() $\mathfrak {M}$
have finite height. Further, F is a finite set of formulas. Henceforth, the model
$\mathfrak {M}$
have finite height. Further, F is a finite set of formulas. Henceforth, the model
![]() $\mathfrak {M}'$
resulting from restring
$\mathfrak {M}'$
resulting from restring
![]() $\mathfrak {M}$
to the universe
$\mathfrak {M}$
to the universe
![]() $W'$
is a finite directed model with root v. Moreover, it is such that
$W'$
is a finite directed model with root v. Moreover, it is such that
![]() $e'(w, \varGamma , \varXi (p), \xi (p,q)) \subseteq \{1\}$
for each world
$e'(w, \varGamma , \varXi (p), \xi (p,q)) \subseteq \{1\}$
for each world
![]() $w \in W'$
, and
$w \in W'$
, and
![]() $e'(v, \varphi \vee \psi (p,q)) < 1$
. In particular,
$e'(v, \varphi \vee \psi (p,q)) < 1$
. In particular,
![]() $e(w, \varGamma ) \subseteq \{1\}$
at each world w, and
$e(w, \varGamma ) \subseteq \{1\}$
at each world w, and
![]() $e(v, \varphi ) < 1$
.
$e(v, \varphi ) < 1$
.
![]() : Assume
: Assume
![]() , so there is a finite model
, so there is a finite model
![]() $\mathfrak {M}$
and a world
$\mathfrak {M}$
and a world
![]() $v \in W$
such that
$v \in W$
such that
![]() . Let
. Let
![]() $\mathfrak {M}'$
be the model with universe equal to that of
$\mathfrak {M}'$
be the model with universe equal to that of
![]() $\mathfrak {M}$
, such that
$\mathfrak {M}$
, such that
![]() $e'(u,x) = e(u,x)$
for all
$e'(u,x) = e(u,x)$
for all
![]() $x \in \mathcal {V}(\varGamma , \varphi )$
and each
$x \in \mathcal {V}(\varGamma , \varphi )$
and each
![]() $u \in W$
, and where the values of variables
$u \in W$
, and where the values of variables
![]() $p,q$
are defined as follows. Pick an arbitrary element
$p,q$
are defined as follows. Pick an arbitrary element
![]() $a \in \big(\frac {\mathbf {\mathtt {h}}{v}}{\mathbf {\mathtt {h}}{v}+1}, 1\big)$
and let, for each
$a \in \big(\frac {\mathbf {\mathtt {h}}{v}}{\mathbf {\mathtt {h}}{v}+1}, 1\big)$
and let, for each
![]() $u \in W$
,
$u \in W$
,
-
•
 $e(u, p) = a$
,
$e(u, p) = a$
, -
•
 $e(u, q) = e(u, \square q) a$
(observe this is well defined since all worlds have finite height, so we can define q inductively from the worlds with height
$e(u, q) = e(u, \square q) a$
(observe this is well defined since all worlds have finite height, so we can define q inductively from the worlds with height
 $0$
).
$0$
).
This evaluation satisfies, in all worlds of the model, all formulas from
![]() $\varXi (p)$
and
$\varXi (p)$
and
![]() $\xi (p,q)$
, and it forces
$\xi (p,q)$
, and it forces
![]() $e(v, p) \not \in \{0,1\}$
and
$e(v, p) \not \in \{0,1\}$
and
![]() $e(v, q) \not \in \{0,1\}$
. Moreover, it satisfies the formulas from
$e(v, q) \not \in \{0,1\}$
. Moreover, it satisfies the formulas from
![]() $\varGamma $
, and
$\varGamma $
, and
![]() $e(v, \varphi ) <1$
, since the evaluation of all the variables appearing in
$e(v, \varphi ) <1$
, since the evaluation of all the variables appearing in
![]() $\varGamma $
and
$\varGamma $
and
![]() $\varphi $
has been preserved. Thus,
$\varphi $
has been preserved. Thus,
![]() either.⊣
either.⊣
The fact that the (finitary) Łukasiewicz global modal logic is not axiomatizable follows as a consequence of previous reduction (which is recursive) and the undecidability of
![]() .
.
Theorem 4.8.
![]() is not axiomatizable.
is not axiomatizable.
Proof. Assume
![]() is axiomatizable, and so, recursively enumerable. We can prove that then
is axiomatizable, and so, recursively enumerable. We can prove that then
![]() is recursively enumerable too, contradicting Corollary 4.4. For that, take a recursive enumeration of all pairs
is recursively enumerable too, contradicting Corollary 4.4. For that, take a recursive enumeration of all pairs
![]() such that
such that
![]() . For each pair, let
. For each pair, let
![]() $\mathcal {V} = \mathcal {V}ars(\varGamma , \varphi )$
, and check whether there are some
$\mathcal {V} = \mathcal {V}ars(\varGamma , \varphi )$
, and check whether there are some
![]() $p,q \in \mathcal {V}$
for which
$p,q \in \mathcal {V}$
for which
![]() $\varGamma = \varGamma _0(\mathcal {V}\setminus \{p,q\}) \cup \varXi (p) \cup \{\xi (p,q)\}$
and
$\varGamma = \varGamma _0(\mathcal {V}\setminus \{p,q\}) \cup \varXi (p) \cup \{\xi (p,q)\}$
and
![]() $\varphi = \varphi _0(\mathcal {V}\setminus \{p,q\}) \vee \psi (p,q)$
for some
$\varphi = \varphi _0(\mathcal {V}\setminus \{p,q\}) \vee \psi (p,q)$
for some
![]() $\varGamma _0, \varphi _0$
. This is a decidable procedure because
$\varGamma _0, \varphi _0$
. This is a decidable procedure because
![]() $\varGamma $
is a finite set and the translations
$\varGamma $
is a finite set and the translations
![]() $\varGamma _0$
and
$\varGamma _0$
and
![]() $\varphi _0$
are recursive. If that is the case, output
$\varphi _0$
are recursive. If that is the case, output
![]() , and don’t output anything otherwise. Lemma 4.7 implies that this procedure enumerates
, and don’t output anything otherwise. Lemma 4.7 implies that this procedure enumerates
![]() .
.
However, Corollary 4.4 states that
![]() is not R.E., a contradiction.⊣
is not R.E., a contradiction.⊣
4.2 Modal product logic is not axiomatizable either
In [Reference Baaz, Hájek, Krajíček and Švejda3], the authors observe, roughly speaking, that the standard MV algebra is isomorphic to the standard product algebra restricted to
![]() $[a,1]$
for arbitrary fixed
$[a,1]$
for arbitrary fixed
![]() $0 < a < 1$
. Relying on the isomorphism there provided, they also show that the tautologies of standard Łukasiewicz propositional and F.O. logicsFootnote
15
can be recursively reduced to those of the respective (standard) Product logic. In [Reference Hájek26, Lemmas 4.1.14 and 6.3.5] these results are formulated regarding the corresponding logical deduction relations.
$0 < a < 1$
. Relying on the isomorphism there provided, they also show that the tautologies of standard Łukasiewicz propositional and F.O. logicsFootnote
15
can be recursively reduced to those of the respective (standard) Product logic. In [Reference Hájek26, Lemmas 4.1.14 and 6.3.5] these results are formulated regarding the corresponding logical deduction relations.
We can use a similar argument, slightly modifying the reduction so it works in the modal case.Footnote 16
Given a finite set of variables
![]() $\mathcal {V}$
, let x be a propositional variable not in
$\mathcal {V}$
, let x be a propositional variable not in
![]() $\mathcal {V}$
. For each formula
$\mathcal {V}$
. For each formula
![]() $\varphi $
of
$\varphi $
of
in variables
![]() $\mathcal {V}$
, define its translation
$\mathcal {V}$
, define its translation
![]() $\varphi ^x$
as follows:
$\varphi ^x$
as follows:

Further, let
![]() .
.
In the spirit of Lemmas 2 and 3 from [Reference Baaz, Hájek, Krajíček and Švejda3] it is possible to prove the following result. The proof is very similar to the one in the previous reference, but for the sake of completeness we provide the details in Section 7.
Lemma 4.9. For every
![]() $x \not \in \mathcal {V}ar(\varGamma \cup \{\varphi \})$
, it holds that
$x \not \in \mathcal {V}ar(\varGamma \cup \{\varphi \})$
, it holds that
![]() if and only if
if and only if
![]() $\varGamma ^x, \varTheta ^x \vdash _{K\varPi } \varphi ^x$
.
$\varGamma ^x, \varTheta ^x \vdash _{K\varPi } \varphi ^x$
.
Since the reduction is recursive, together with Theorem 4.8, the following is immediate.
Corollary 4.10.
![]() $\vdash _{K\varPi }$
is not axiomatizable.
$\vdash _{K\varPi }$
is not axiomatizable.
We have proven that
![]() and
and
![]() $\vdash _{K\varPi }$
are not in
$\vdash _{K\varPi }$
are not in
![]() $\varSigma _1$
from the Arithmetical Hierarchy. We leave open the question of whether they are
$\varSigma _1$
from the Arithmetical Hierarchy. We leave open the question of whether they are
![]() $\varPi _2$
-complete, as it is the case for the tautologies of their F.O. versions, or whether they belong to some other level of the hierarchy. The proofs of Ragaz in [Reference Ragaz36, Reference Ragaz37] heavily rely on the expressive power of F.O. logic, and also in proving the result directly for tautologies of the logic. In the present work, the results affect the logic itself, since for instance, the tautologies of
$\varPi _2$
-complete, as it is the case for the tautologies of their F.O. versions, or whether they belong to some other level of the hierarchy. The proofs of Ragaz in [Reference Ragaz36, Reference Ragaz37] heavily rely on the expressive power of F.O. logic, and also in proving the result directly for tautologies of the logic. In the present work, the results affect the logic itself, since for instance, the tautologies of
![]() are decidable: they coincide with those of
are decidable: they coincide with those of
![]() and this logic is decidable [Reference Vidal42, Corollary 4.5].
and this logic is decidable [Reference Vidal42, Corollary 4.5].
5 The necessitation rule
Recall that in (classical) modal logic, the global deduction is axiomatized as the local one plus the (unrestricted) necessitation rule
![]() $N_\square \colon x \vdash \square x$
. It was asked in [Reference Bou, Esteva, Godo and Rodríguez9] whether this was the case in general, or whether at least, this condition held for modal expansions of fuzzy logics. This was the case in the modal logics known up to now (e.g., in modal Gödel logics, and in the infinitary modal Łukasiewicz and Product logics studied in the literature). The question remained open in full generality over modal many-valued logics. We can give a negative answer to the problem, first by a simple counter-example over the modal expansions of Łukasiewicz logic (using the non-axiomatizability of
$N_\square \colon x \vdash \square x$
. It was asked in [Reference Bou, Esteva, Godo and Rodríguez9] whether this was the case in general, or whether at least, this condition held for modal expansions of fuzzy logics. This was the case in the modal logics known up to now (e.g., in modal Gödel logics, and in the infinitary modal Łukasiewicz and Product logics studied in the literature). The question remained open in full generality over modal many-valued logics. We can give a negative answer to the problem, first by a simple counter-example over the modal expansions of Łukasiewicz logic (using the non-axiomatizability of
![]() proven in Theorem 4.8) and later proving that this is a more general fact.
proven in Theorem 4.8) and later proving that this is a more general fact.
First, it is possible to see that the local deduction is decidable using the version of Lemma 4.6 referring to the local logic. A detailed proof of the decidability of
![]() can be found in [Reference Vidal42, Corollary 4.5]. Thus,
can be found in [Reference Vidal42, Corollary 4.5]. Thus,
![]() has a recursive axiomatization (for instance, built by enumerating all possible pairs
has a recursive axiomatization (for instance, built by enumerating all possible pairs
![]() with
with
![]() $\varGamma \cup \{ \varphi \} \subseteq _{\omega } Fm$
, and then returning the pairs for which
$\varGamma \cup \{ \varphi \} \subseteq _{\omega } Fm$
, and then returning the pairs for which
![]() ). On the other hand, if the global consequence were to coincide with the local one plus the
). On the other hand, if the global consequence were to coincide with the local one plus the
![]() $N_\square $
rule, the logic axiomatized by adding to the previous system the
$N_\square $
rule, the logic axiomatized by adding to the previous system the
![]() $N_\square $
rule should produce a recursive axiomatization of
$N_\square $
rule should produce a recursive axiomatization of
![]() , contradicting Theorem 4.8.
, contradicting Theorem 4.8.
As we said, it is possible to widen the scope of the previous result, and produce a constructive proof serving all modal logics built over classes of algebras like the ones in Theorem 3.1. This can be done following an approach different from the previous direct one working for the Łukasiewicz case, and instead providing a derivation that is valid in the global modal logics and not in the local ones extended by the necessitation rule.
For simplicity, let us fix a class of algebras
![]() $\mathbb {A}$
like the one from Section 3, and let
$\mathbb {A}$
like the one from Section 3, and let
![]() $\vdash $
and
$\vdash $
and
![]() $\vdash ^l$
denote
$\vdash ^l$
denote
![]() $\vdash _{K_{\mathbb {A}}}$
and
$\vdash _{K_{\mathbb {A}}}$
and
![]() $\vdash ^l_{K_{\mathbb {A}}}$
respectively. Further, let
$\vdash ^l_{K_{\mathbb {A}}}$
respectively. Further, let
![]() $\vdash ^l_{N_\square }$
denote the logic
$\vdash ^l_{N_\square }$
denote the logic
![]() $\vdash ^l$
plus the necessitation rule
$\vdash ^l$
plus the necessitation rule
![]() $x \vdash \square x$
. A natural way to understand this extension is by considering the (possibly non recursive) list of finite derivations valid in
$x \vdash \square x$
. A natural way to understand this extension is by considering the (possibly non recursive) list of finite derivations valid in
![]() $\vdash ^l_{K_{\mathbb {A}}}$
and add to this set the rule schemata
$\vdash ^l_{K_{\mathbb {A}}}$
and add to this set the rule schemata
![]() $N_\square $
. Let us call this set R. The minimal logic containing R, namely
$N_\square $
. Let us call this set R. The minimal logic containing R, namely
![]() $R^l$
, is the logic
$R^l$
, is the logic
![]() $\vdash ^l_{N_\square }$
. Since all rules in R have finitely many premises, the resulting logic is finitary.
$\vdash ^l_{N_\square }$
. Since all rules in R have finitely many premises, the resulting logic is finitary.
Considering R as a (possibly non recursive) axiomatization for
![]() $\vdash ^l_{N_\square }$
, all derivations valid in
$\vdash ^l_{N_\square }$
, all derivations valid in
![]() $\vdash ^l$
have a proof in the extended system of length
$\vdash ^l$
have a proof in the extended system of length
![]() $0$
. Thus, the length of the proofs in the extended system only reflects the applications of the necessitation rule. Since by definition
$0$
. Thus, the length of the proofs in the extended system only reflects the applications of the necessitation rule. Since by definition
![]() $\vdash ^l$
is a finitary logic, only finitely many applications of the rule are used at each specific derivation. This means that a proof of
$\vdash ^l$
is a finitary logic, only finitely many applications of the rule are used at each specific derivation. This means that a proof of
![]() $\varphi $
from a finite set of premises
$\varphi $
from a finite set of premises
![]() $\varGamma $
in this axiomatic system is given simply as a finite list of pairs
$\varGamma $
in this axiomatic system is given simply as a finite list of pairs
![]() such that
such that
-
•
 $\varGamma _0 = \varGamma $
and
$\varGamma _0 = \varGamma $
and
 $\varphi _N = \varphi $
,
$\varphi _N = \varphi $
, -
• For each
 ,
,
 $\varGamma _i \vdash ^l \varphi _i$
,
$\varGamma _i \vdash ^l \varphi _i$
, -
•
 $\varGamma _{i+1} = \varGamma _i \cup \{\square \varphi _i\}$
.
$\varGamma _{i+1} = \varGamma _i \cup \{\square \varphi _i\}$
.
From here, it is quite simple to prove the following characterization of
![]() $\vdash ^l_{N_\square }$
.
$\vdash ^l_{N_\square }$
.
Lemma 5.1.
Proof. The right-to-left direction is immediate. For the other direction, if
![]() ${\varGamma \vdash ^l_{N_\square } \varphi}$
, since the logic is finitary,
${\varGamma \vdash ^l_{N_\square } \varphi}$
, since the logic is finitary,
![]() $\varphi $
can be proven from
$\varphi $
can be proven from
![]() $\varGamma $
by using the
$\varGamma $
by using the
![]() $N_\square $
rule a finite number of times, say n. It can be easily proven by induction in n
Footnote
17
that
$N_\square $
rule a finite number of times, say n. It can be easily proven by induction in n
Footnote
17
that
![]() if and only if
if and only if
![]() $\varSigma \vdash ^l_{n \cdot N_\square } \chi $
, where
$\varSigma \vdash ^l_{n \cdot N_\square } \chi $
, where
![]() $n\cdot N_\square $
stands for using the
$n\cdot N_\square $
stands for using the
![]() $N_\square $
rule up to n times. This concludes the proof.⊣
$N_\square $
rule up to n times. This concludes the proof.⊣
We can then produce a set of formulas that yields a valid derivation in the global logics, but it does not in the corresponding local logics plus necessitation.
Theorem 5.2.
![]() $\vdash $
does not coincide with
$\vdash $
does not coincide with
![]() $\vdash ^l_{N_\square }$
.
$\vdash ^l_{N_\square }$
.
Proof. We claim that both
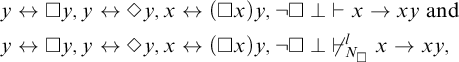
which proves the theorem.
Regarding the first claim, consider an arbitrary Kripke model satisfying globally the set of premises. In particular, from
![]() $\neg \square \perp $
we get that each world in the model has a successor, and so, has infinite height in the sense of Definition 2.5. Moreover, the value of y is constant inside each connected part of the model, as in Lemma 3.3. Consider each connected submodel
$\neg \square \perp $
we get that each world in the model has a successor, and so, has infinite height in the sense of Definition 2.5. Moreover, the value of y is constant inside each connected part of the model, as in Lemma 3.3. Consider each connected submodel
![]() $\mathfrak {M}$
, and let
$\mathfrak {M}$
, and let
![]() $\alpha $
be the value of y in it. Then, at each point of the model,
$\alpha $
be the value of y in it. Then, at each point of the model,
![]() for all
for all
![]() $i\in \mathbb {N}$
. Then, since the algebras in the class are weakly saturated, we get that
$i\in \mathbb {N}$
. Then, since the algebras in the class are weakly saturated, we get that
![]() $e(u,x) \alpha = e(u,x)$
, proving the formula in the right side.
$e(u,x) \alpha = e(u,x)$
, proving the formula in the right side.
In order to prove the second claim, let us denote by
![]() $\varSigma $
the set of premises. From the previous lemma we have that our claim holds if and only if
$\varSigma $
the set of premises. From the previous lemma we have that our claim holds if and only if
Since
![]() $\vdash ^l$
is finitary by definition, this holds if and only if
$\vdash ^l$
is finitary by definition, this holds if and only if
![]() for all
for all
![]() $N \in \mathbb {N}$
. We can produce a counter-model for each
$N \in \mathbb {N}$
. We can produce a counter-model for each
![]() $N \in \mathbb {N}$
.
$N \in \mathbb {N}$
.
Indeed, consider a model with universe
, and the accessibility relation given by
. Regarding the evaluation, pick an arbitrary
![]() $\mathbf {A} \in \mathbb {A}$
that is not
$\mathbf {A} \in \mathbb {A}$
that is not
![]() $(N+1)$
-contractive, and pick
$(N+1)$
-contractive, and pick
![]() $a \in \mathbf {A}$
such that
$a \in \mathbf {A}$
such that
![]() $a^{N+2} < a^{N+1}$
. Then let
$a^{N+2} < a^{N+1}$
. Then let
It is routine to check that this evaluation satisfies
![]() at the world
at the world
![]() $0$
, i.e.,
$0$
, i.e.,
![]() $e(0, \square ^i\varSigma ) = 1$
for all
$e(0, \square ^i\varSigma ) = 1$
for all
![]() . On the other hand, observe that
. On the other hand, observe that
![]() $e(0, x) = a^{N+1}$
. Due to the way we chose a it holds that
$e(0, x) = a^{N+1}$
. Due to the way we chose a it holds that
![]() $e(0, x y) = a^{N+2} < a^{N+1} = e(0,x)$
, thus falsifying the consequence.⊣
$e(0, x y) = a^{N+2} < a^{N+1} = e(0,x)$
, thus falsifying the consequence.⊣
6 Acknowledgments
I am thankful to the anonymous referee for many useful and detailed contributions. This project has received funding from the following sources: the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 101027914 and the Grant No. CZ.02.2.69/0.0/0.0/17050/0008361 of the Operational programme Research, Development, Education of the Ministry of Education, Youth and Sport of the Czech Republic. I also wish to thank Lluís Godo, Gavin St. John, and Tommaso Moraschini for their useful help.
7 Appendix
7.1 Craig’s Theorem
It is easy to see that a finitary R.E. logic with a definable idempotent n-ary operation for every n is always axiomatizable. This can be checked as it is done in Craig’s Theorem for classical logic.
Indeed, let
![]() $\star _n$
be an idempotent n-ary operation (i.e., such that
$\star _n$
be an idempotent n-ary operation (i.e., such that
and
), as for instance, the classical conjunction
![]() $\wedge $
in classical logic. For convenience, denote
$\wedge $
in classical logic. For convenience, denote
by
![]() $\star _n(\varphi )$
. Consider a recursive enumeration of the finitary derivations of the logic, i.e.,
$\star _n(\varphi )$
. Consider a recursive enumeration of the finitary derivations of the logic, i.e.,
(which exists because the logic is R.E), and take the axiomatization given by the set of rules
This is a recursive set: for a finitary rule
, it is first possible to decide whether there is some
(where
![]() $symb(\chi )$
denotes the number of symbols appearing in
$symb(\chi )$
denotes the number of symbols appearing in
![]() $\chi $
) such that
$\chi $
) such that
![]() $\chi $
is of the form
$\chi $
is of the form
![]() $\star _j(\varphi _j)$
and
$\star _j(\varphi _j)$
and
![]() $\varSigma = \varGamma _j$
. If this is the case,
$\varSigma = \varGamma _j$
. If this is the case,
belongs to R. Otherwise, it is possible to decide whether
![]() $\varSigma $
is a singleton
$\varSigma $
is a singleton
![]() $\{\psi \}$
and, in this case, whether there is some
$\{\psi \}$
and, in this case, whether there is some
such that
![]() $\psi $
is of the form
$\psi $
is of the form
![]() $\star _j(\varphi _j)$
and
$\star _j(\varphi _j)$
and
![]() $\chi $
is exactly
$\chi $
is exactly
![]() $\varphi _j$
. If the answer to both questions is yes,
$\varphi _j$
. If the answer to both questions is yes,
belongs to R. Otherwise, the rule does not belong to R.
Further, it is clear that
![]() $\mathcal {L}\subseteq R^l$
. On the other hand, since the rules in R are finitary, it is easy to see (by means of the characterization of
$\mathcal {L}\subseteq R^l$
. On the other hand, since the rules in R are finitary, it is easy to see (by means of the characterization of
![]() $R^l$
as the proofs in R) that
$R^l$
as the proofs in R) that
![]() $R^l \subseteq \mathcal {L}$
too.
$R^l \subseteq \mathcal {L}$
too.
7.2 Proof of Lemma 4.9
The proof of Lemma 4.9 detailed below draws inspiration from the results in [Reference Baaz, Hájek, Krajíček and Švejda3], and relies in the same isomorphic mappings introduced there. However, the approach and details are slightly different here, since we formulate alternative intermediate results, and we propose a more explicit proof using basic arithmetics.
Proof of Lemma 4.9.
(For every
![]() $x \not \in \mathcal {V}ar(\varGamma \cup \{\varphi \})$
, it holds that
$x \not \in \mathcal {V}ar(\varGamma \cup \{\varphi \})$
, it holds that
![]() if and only if
if and only if
![]() $\varGamma ^x, \varTheta ^x \vdash _{K\varPi } \varphi ^x$
.)
$\varGamma ^x, \varTheta ^x \vdash _{K\varPi } \varphi ^x$
.)
: Assume
. Then there is some standard Łukasiewicz Kripke model
![]() $\mathfrak {M}$
such that
$\mathfrak {M}$
such that
![]() $\mathfrak {M} \models \varGamma $
but
$\mathfrak {M} \models \varGamma $
but
![]() $\mathfrak {M},v \not \models \varphi $
for some v in the model. Chose an arbitrary
$\mathfrak {M},v \not \models \varphi $
for some v in the model. Chose an arbitrary
![]() $a \in (0,1)$
, and let us define a standard product model
$a \in (0,1)$
, and let us define a standard product model
![]() $\mathfrak {M}'$
by letting the universe and accessibility relations be those of
$\mathfrak {M}'$
by letting the universe and accessibility relations be those of
![]() $\mathfrak {M}$
, and further, for each
$\mathfrak {M}$
, and further, for each
![]() $w \in W$
, letFootnote
18
$w \in W$
, letFootnote
18
Claim 1. For every formula
![]() $\psi $
in variables from
$\psi $
in variables from
![]() $\mathcal {V}ar(\varGamma \cup \{\varphi \})$
, and for each
$\mathcal {V}ar(\varGamma \cup \{\varphi \})$
, and for each
![]() $w \in W$
, it holds that
$w \in W$
, it holds that
The conclusion easily follows, as we proceed to explain. Indeed, Claim 1 implies that
![]() $e'(w, \gamma ^x) = a^{1-e(w, \gamma )} = a^0 = 1$
for each
$e'(w, \gamma ^x) = a^{1-e(w, \gamma )} = a^0 = 1$
for each
![]() $\gamma \in \varGamma $
and
$\gamma \in \varGamma $
and
![]() $w \in W$
. It is also clear that
$w \in W$
. It is also clear that
![]() $e'(w, \varTheta ^x) = 1$
, since x is evaluated to the same element
$e'(w, \varTheta ^x) = 1$
, since x is evaluated to the same element
![]() $a> 0$
in all worlds of
$a> 0$
in all worlds of
![]() $\mathfrak {M}'$
. On the other hand,
$\mathfrak {M}'$
. On the other hand,
![]() $e'(v, \varphi ^x) = a^{1-e(v, \varphi )} <1$
, since
$e'(v, \varphi ^x) = a^{1-e(v, \varphi )} <1$
, since
![]() $e(v, \varphi ) <1$
. Thereby,
$e(v, \varphi ) <1$
. Thereby,
![]() $\mathfrak {M}' \models \varGamma ^x, \varTheta ^x$
and
$\mathfrak {M}' \models \varGamma ^x, \varTheta ^x$
and
![]() $\mathfrak {M}',v \not \models \varphi ^x$
, and so,
$\mathfrak {M}',v \not \models \varphi ^x$
, and so,
![]() $\varGamma ^x, \varTheta ^x \not \vdash _{K\varPi } \varphi ^x$
. Then, it only remains to prove the claim.
$\varGamma ^x, \varTheta ^x \not \vdash _{K\varPi } \varphi ^x$
. Then, it only remains to prove the claim.
Proof of Claim 1. It can be proven by induction on the complexity of the formula.
-
• For variables it is straightforward from the definition, since
 $e'(w,q^x) = e'(w,q \vee x) = a \vee a^{1-e(w,q)}$
, and
$e'(w,q^x) = e'(w,q \vee x) = a \vee a^{1-e(w,q)}$
, and
 for every
for every
 $q \in [0,1]$
.
$q \in [0,1]$
. -
• For
 $\psi = \psi _1 \cdot \psi _2$
, we have the following chain of equalities:
$\psi = \psi _1 \cdot \psi _2$
, we have the following chain of equalities: 
-
• For
 $\psi = \psi _1 \rightarrow \psi _2$
, we have the following chain of equalities:
$\psi = \psi _1 \rightarrow \psi _2$
, we have the following chain of equalities: 
-
• For
 $\psi = \square \psi _1$
, we know that On the one hand, since
$\psi = \square \psi _1$
, we know that On the one hand, since $$ \begin{align*} e'(w, (\square \psi_1)^x) & = e'(w, \square \psi_1^x) = \bigwedge_{Rwu} e'(u, \psi_1^x) \overset{I.H}{=} \bigwedge_{Rwu} a^{1-e(u, \psi_1)}. \end{align*} $$
$$ \begin{align*} e'(w, (\square \psi_1)^x) & = e'(w, \square \psi_1^x) = \bigwedge_{Rwu} e'(u, \psi_1^x) \overset{I.H}{=} \bigwedge_{Rwu} a^{1-e(u, \psi_1)}. \end{align*} $$
 for each u with
for each u with
 $Rwu$
, it holds that
$Rwu$
, it holds that
 .
.
On the other hand,
This concludes the proof of the claim.⊣
![]() $\Rightarrow $
: It is proven similarly, using the corresponding inverse of the isomorphism from [Reference Baaz, Hájek, Krajíček and Švejda3]. Assume there is a standard product model
$\Rightarrow $
: It is proven similarly, using the corresponding inverse of the isomorphism from [Reference Baaz, Hájek, Krajíček and Švejda3]. Assume there is a standard product model
![]() $\mathfrak {P}$
such that
$\mathfrak {P}$
such that
![]() $\mathfrak {P} \models \varGamma ^x, \varTheta ^x$
and
$\mathfrak {P} \models \varGamma ^x, \varTheta ^x$
and
![]() $\mathfrak {P},v \not \models \varphi ^x$
for some v in the model. As proven in Lemma 3.3, there is some element a such that
$\mathfrak {P},v \not \models \varphi ^x$
for some v in the model. As proven in Lemma 3.3, there is some element a such that
![]() $e(w,x) = a$
for all w in the universe of the model. Moreover, since
$e(w,x) = a$
for all w in the universe of the model. Moreover, since
![]() $e(v, \neg \neg x) = 1$
, necessarily
$e(v, \neg \neg x) = 1$
, necessarily
![]() $a> 0$
.
$a> 0$
.
Observe first that if
![]() $a = 1$
then
$a = 1$
then
![]() $e(w,\psi ^x) = 1$
for every
$e(w,\psi ^x) = 1$
for every
![]() $\psi $
with variables in
$\psi $
with variables in
![]() $\mathcal {V}ar(\varGamma \cup \{\varphi \})$
and each w in the universe. This observation is immediate by induction on the complexity of the formula. Since this would contradict the fact that
$\mathcal {V}ar(\varGamma \cup \{\varphi \})$
and each w in the universe. This observation is immediate by induction on the complexity of the formula. Since this would contradict the fact that
![]() $e(v, \varphi ^x) < 1$
, necessarily
$e(v, \varphi ^x) < 1$
, necessarily
![]() $a < 1$
.
$a < 1$
.
Let us define a standard Łukasiewicz model
![]() $\mathfrak {P}'$
as the model whose universe and accessibility relation are those of
$\mathfrak {P}'$
as the model whose universe and accessibility relation are those of
![]() $\mathfrak {P}$
and for each variable q and each world w let
$\mathfrak {P}$
and for each variable q and each world w let
![]() .
.
Claim 2. For every formula
![]() $\psi $
in variables from
$\psi $
in variables from
![]() $\mathcal {V}ar(\varGamma \cup \{\varphi \})$
and for each
$\mathcal {V}ar(\varGamma \cup \{\varphi \})$
and for each
![]() $w \in W$
it holds that
$w \in W$
it holds that
As in the previous case, the conclusion easily follows. Indeed, If Claim 2 holds,
![]() $e'(w, \gamma ) = 1-log_a e(w, \gamma ^x) = 1 - log_a 1 = 1$
for each
$e'(w, \gamma ) = 1-log_a e(w, \gamma ^x) = 1 - log_a 1 = 1$
for each
![]() $\gamma \in \varGamma $
and
$\gamma \in \varGamma $
and
![]() $w \in W$
, and
$w \in W$
, and
![]() $e'(v, \varphi ) = 1-log_a e(v, \varphi ^x) = 1 - log_a \alpha $
for some
$e'(v, \varphi ) = 1-log_a e(v, \varphi ^x) = 1 - log_a \alpha $
for some
![]() . Since the logarithm in base a of elements in that interval is a value in
. Since the logarithm in base a of elements in that interval is a value in
![]() $(0,1]$
, necessarily
$(0,1]$
, necessarily
![]() $e'(v, \varphi ) < 1$
, concluding the proof of the lemma. Then, it only remains to prove the claim.
$e'(v, \varphi ) < 1$
, concluding the proof of the lemma. Then, it only remains to prove the claim.
Proof of Claim 2. We will prove it by induction on the complexity of the formula. Observe a consequence of Claim 2 is that
![]() $e(w, \psi ^x) \geqslant a$
for all
$e(w, \psi ^x) \geqslant a$
for all
![]() $\psi $
and w as before.Footnote
19
We will (inductively) use this property in the modal step, and refer to it by
$\psi $
and w as before.Footnote
19
We will (inductively) use this property in the modal step, and refer to it by
![]() $I.H'$
.
$I.H'$
.
-
• For variables it is immediate, since
 $e'(w, q) = 1-log_a a \vee e(w, q) = 1-log_a e(w, q^x)$
.
$e'(w, q) = 1-log_a a \vee e(w, q) = 1-log_a e(w, q^x)$
. -
• For
 $\psi = \psi _1 \cdot \psi _2$
, we have the following chain of equalities:
$\psi = \psi _1 \cdot \psi _2$
, we have the following chain of equalities:
 .
.Now, if
 $0 < e(w, \psi _1^x \cdot \psi _2^x) < a$
, it holds that
$0 < e(w, \psi _1^x \cdot \psi _2^x) < a$
, it holds that
 $ log_a(e(w, \psi _1^x \cdot \psi _2^x))> 1$
, and thus,
$ log_a(e(w, \psi _1^x \cdot \psi _2^x))> 1$
, and thus,
 $max\{0, 1 - log_a(e(w, \psi _1^x \cdot \psi _2^x))\} = 0 = 1 - log_a(e(w, \psi _1^x \cdot \psi _2^x)\vee a)$
. It follows that
$max\{0, 1 - log_a(e(w, \psi _1^x \cdot \psi _2^x))\} = 0 = 1 - log_a(e(w, \psi _1^x \cdot \psi _2^x)\vee a)$
. It follows that  $$ \begin{align*}max\{0, 1 - log_a(e(w, \psi_1^x \cdot \psi_2^x))\} & = 1-log_a(e(w, \psi_1^x \cdot \psi_2^x)\vee a) \\[3pt] & = 1 - log_a e(w, (\psi_1 \cdot \psi_2)^x).\end{align*} $$
$$ \begin{align*}max\{0, 1 - log_a(e(w, \psi_1^x \cdot \psi_2^x))\} & = 1-log_a(e(w, \psi_1^x \cdot \psi_2^x)\vee a) \\[3pt] & = 1 - log_a e(w, (\psi_1 \cdot \psi_2)^x).\end{align*} $$
-
• For
 $\psi = \psi _1 \rightarrow \psi _2$
, we have the following chain of equalities:
$\psi = \psi _1 \rightarrow \psi _2$
, we have the following chain of equalities:  $$ \begin{align*} & e'(w, \psi_1 \rightarrow \psi_2) = min\{1, 1 e'(w, \psi_1) + e'(w, \psi_2)\}\\[3pt] & \overset{I.H} = min\{1, 1 - (1-log_a e(w, \psi_1^x)) + 1- log_a e(w, \psi_2^x)\}\\[3pt] &= min\{1, 1 - (log_a e(w, \psi_2^x) - log_a e(w, \psi_1^x))\}\\[3pt] &= min\{1, 1 - log_a e(w, \psi_2^x)/e(w, \psi_1^x)\} \\[3pt] &= 1-log_a(min\{1, e(w, \psi_2^x)/e(w, \psi_1^x)\})\\[3pt] &= 1 - log_a e(w, \psi_1^x \rightarrow \psi_2^x)\\[3pt] &= 1 - log_a e(w, (\psi_1 \rightarrow \psi_2)^x). \end{align*} $$
$$ \begin{align*} & e'(w, \psi_1 \rightarrow \psi_2) = min\{1, 1 e'(w, \psi_1) + e'(w, \psi_2)\}\\[3pt] & \overset{I.H} = min\{1, 1 - (1-log_a e(w, \psi_1^x)) + 1- log_a e(w, \psi_2^x)\}\\[3pt] &= min\{1, 1 - (log_a e(w, \psi_2^x) - log_a e(w, \psi_1^x))\}\\[3pt] &= min\{1, 1 - log_a e(w, \psi_2^x)/e(w, \psi_1^x)\} \\[3pt] &= 1-log_a(min\{1, e(w, \psi_2^x)/e(w, \psi_1^x)\})\\[3pt] &= 1 - log_a e(w, \psi_1^x \rightarrow \psi_2^x)\\[3pt] &= 1 - log_a e(w, (\psi_1 \rightarrow \psi_2)^x). \end{align*} $$
-
• For
 $\psi = \square \psi _1$
, we have that
$\psi = \square \psi _1$
, we have that
 $e'(w, \square \psi _1) = \bigwedge _{Rwv}e'(v,\psi _1) \overset {I.H}{=} \bigwedge _{Rwv} (1-log_a e(v, \psi _1^x)) = 1 - \bigvee _{Rwv}log_a e(v, \psi _1^x)$
. Now, by
$e'(w, \square \psi _1) = \bigwedge _{Rwv}e'(v,\psi _1) \overset {I.H}{=} \bigwedge _{Rwv} (1-log_a e(v, \psi _1^x)) = 1 - \bigvee _{Rwv}log_a e(v, \psi _1^x)$
. Now, by
 $I.H'$
, we know that
$I.H'$
, we know that
 $e(v, \psi _1^x) \geqslant a$
for all v in the model, so in particular
$e(v, \psi _1^x) \geqslant a$
for all v in the model, so in particular
 $\bigwedge _{Rwv} e(v, \psi _1^x) \in [a,1]$
. Since the function
$\bigwedge _{Rwv} e(v, \psi _1^x) \in [a,1]$
. Since the function
 $log_a()$
is continuous and decreasing in
$log_a()$
is continuous and decreasing in
 $[a, 1]$
, it follows that
$[a, 1]$
, it follows that
 $1 - \bigvee _{Rwv}log_a e(v, \psi _1^x) = 1 - log_a \bigwedge _{Rwv} e(v, \psi _1^x) = 1 - log_a e(w, \square \psi _1^x) = 1 - log_a e(w, (\square \psi _1)^x)$
.⊣
$1 - \bigvee _{Rwv}log_a e(v, \psi _1^x) = 1 - log_a \bigwedge _{Rwv} e(v, \psi _1^x) = 1 - log_a e(w, \square \psi _1^x) = 1 - log_a e(w, (\square \psi _1)^x)$
.⊣















