Impact of DEM Resolution

Following the experiment suggested by Reference PaulPaul (2008), we resampled the 90 m SRTM C-band DEM to 40 m, resampled it back to 90 m and subtracted it from the original (90 m) DEM. Elevation changes were averaged in 100 m altitude bins, and a bias with altitude similar to Reference PaulPaul (2008) was found on and off glaciers, with higher values off glaciers (not shown here). Reference PaulPaul (2008) suggested that terrain slope determines the amplitude of the elevation differences and that plan curvature (the second derivative of the topography) determines the sign of this difference. Here we build on these previous findings but show that terrain maximum curvature can be used to correct those elevation biases (Fig. 1a and b). The curvature used in this study is computed with a 5 × 5 kernel size (in this regard, it is only a local derivative of the slope) and defined as the maximum curvature in any plane intersecting the surface (Reference WoodWood, 1996). The computation was done with the IDL/ENVI (Research Systems Inc., Boulder, CO) software, but is also implanted in the open-source GRASS GIS software.

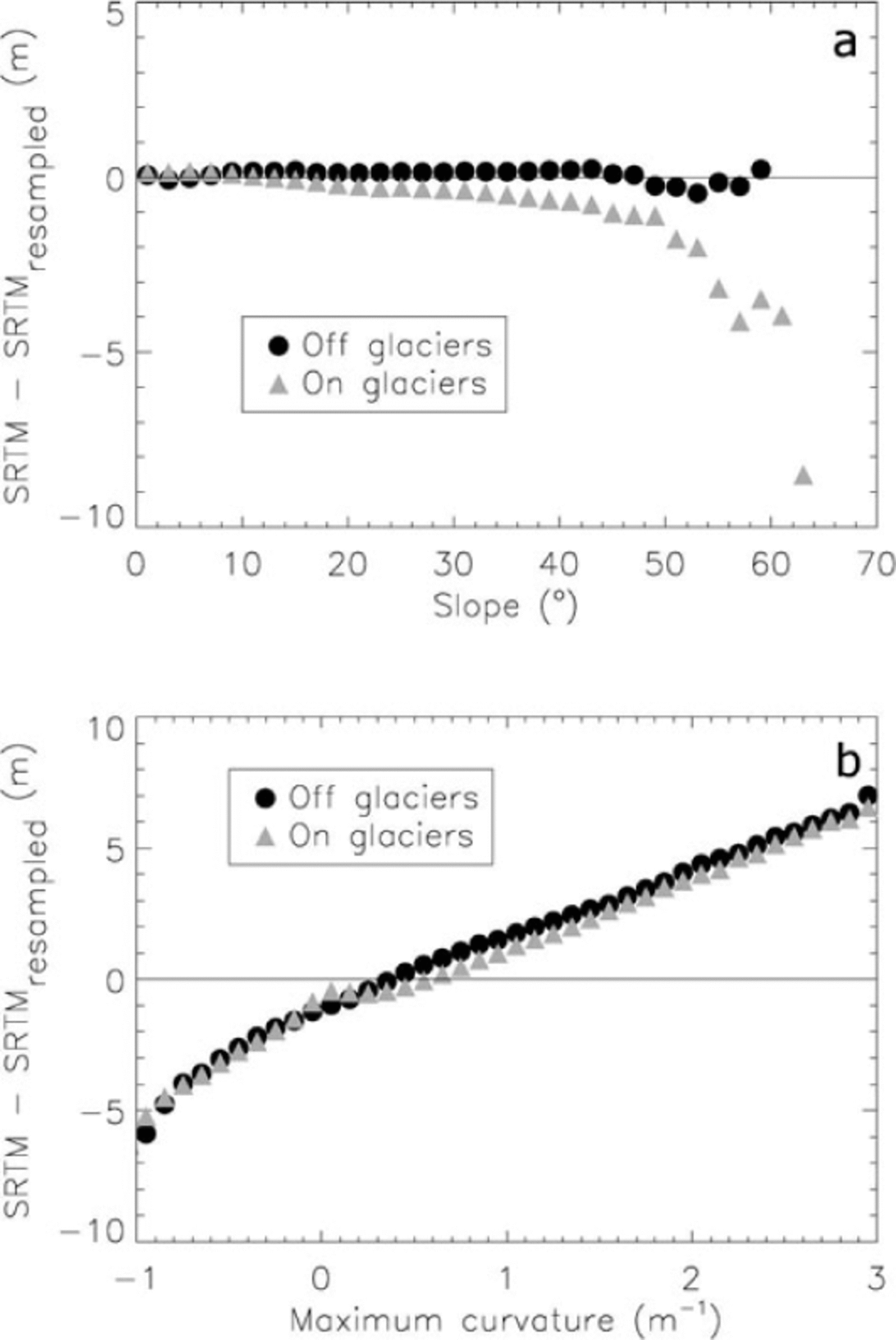
Fig. 1. Relation between terrain slope (a) and maximum curvature (b) and the elevation differences computed from the original 90m C-band SRTM and the one resampled from 40 m. Grey triangles represent glacier pixels, black circles non-glacier pixels.

The link between the maximum curvature and the elevation bias can be qualitatively illustrated if we consider how slopes are represented by low- and high-resolution DEMs. A slope that is constant over numerous continuous coarse pixels (i.e. low curvature values in the direction of the slope) will be equally represented by the low- and high- resolution DEMs. By contrast, a slope that is constant only over a few high-resolution pixels (i.e. high curvature values in the direction of the slope) will be better estimated by the high-resolution than by the coarser DEM (Reference Kervyn, Ernst, Goossens and JacobsKervyn and others, 2008).

The relation between elevation differences and the terrain maximum curvature from our experiment (Fig. 1b) is similar over and outside glaciers, a key condition for using it confidently to correct the elevation differences on glaciers. Conversely, elevation differences as a function of altitude (not shown here) or as a function of slope (Fig. 1a) differ strongly on and off glaciers, because of different curvature distributions. We also tested other definitions of curvature for correcting this bias, which revealed that the plan curvature also has a clear relationship with the elevation difference, but does not fully compensate the bias, as the maximum curvature does (squares in Fig. 2).

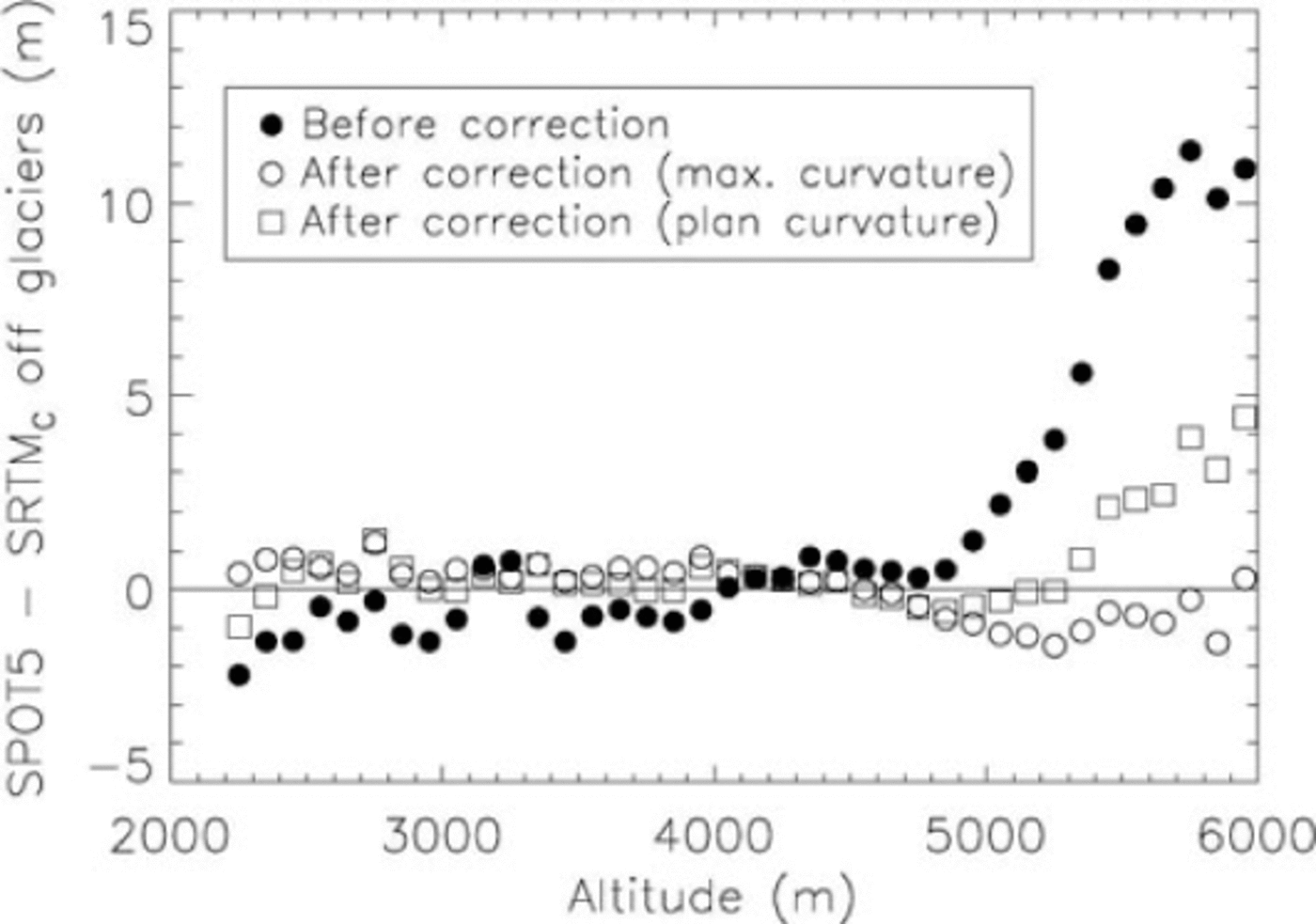
Fig. 2. Elevation differences off glaciers between SPOT5 and SRTM C-band DEMs as a function of altitude. Filled circles represent raw elevation differences, open circles elevation differences after correction based on terrain maximum curvature, and squares those after a correction based on terrain plan curvature.

This bias due to DEMs of different resolutions can thus be corrected on and off glaciers, based on the maximum curvature of each pixel (taken from the high-resolution DEM) and using the relation between elevation differences and maximum curvature established off glaciers. As the curvature varies within a glacier, the correction will introduce local modifications of elevation changes. How this correction will influence the individual glacier (or glacier- complex) mass balance will depend on the curvature distribution, which varies from one glacier to another.

This validity of the curvature correction has been tested in a real case study involving a SPOT5 DEM from December 2008 and the SRTM C-band DEM from February 2000 over Karakoram. The raw elevation differences (SPOT5-SRTM_C-band) off glaciers exhibit a positive elevation bias above 5000 m that reaches 11 m at 6000 m (black circles in Fig. 2). The relation between maximum curvature and the elevation differences has been computed on ice- free terrain and used to correct the elevation bias. The SPOT5-SRTM_C-band differences after correction show that the elevation bias has been properly removed (open circles in Fig. 2). A correction based on plan curvature has also been tested (squares in Fig. 2). Part of the bias is corrected, but the adjustment is not as good, with a 5 m bias remaining at 6000 m.

Accounting for Radar Penetration

Another factor that can affect the glacier elevation changes computed with at least one radar DEM (e.g. SRTM C-band) is the penetration of the radar signal into snow and/or ice. Comparison of the SRTM X-band (9.7GHz) and C-band (5.7GHz) DEMs allows us to quantify this penetration, as it is much smaller in the X-band than in the C-band. These two DEMs were acquired simultaneously, so no ‘glaciological’ elevation change is expected. However, the coverage of the SRTM X-band DEM is not continuous. The swath width is narrower (~50 km), and the resulting DEM is available only along selected strips.

The C-band DEM has been resampled to 30 m and subtracted from the X-band DEM. First, because of the difference in the original resolution of the DEMs, a correction according to the terrain maximum curvature was applied using the above-described method. Then, in addition to the glacier inventory, we identified the snow- covered areas (both on and off glaciers) on a Landsat image from 24 February 2000, a few days after the acquisition of both SRTM DEMs. The SRTM_X-band-SRTM_C-band differences as a function of altitude (Fig. 3) show no significant bias over debris-covered parts of glaciers or bare ice-free terrain, confirming the efficiency of the curvature correction.

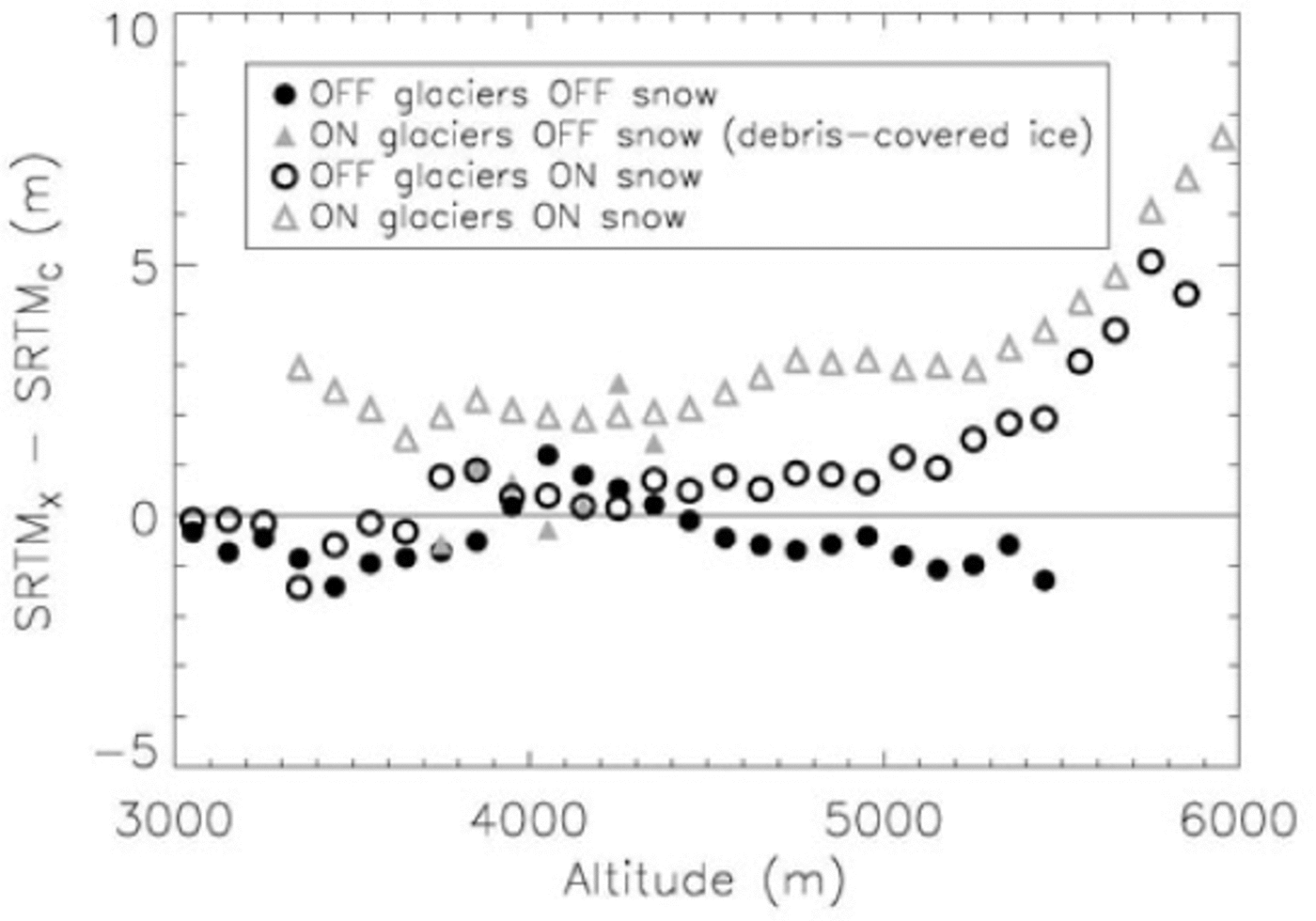
Fig. 3. Elevation differences between SRTM_X-band and SRTM_C-band as a function of altitude.

The snow-covered ice-free terrain exhibits a strong bias with altitude above 5000 m that reaches ~5 m at 6000 m. The bias on snow-covered glacier parts is similar but is ~2m higher at all altitudes. We interpret the bias above 5000 m as a differential penetration in snow between C-band and X-band radar. The 2 m systematic bias on snow-covered glaciers is attributed to the differential penetration in ice, C-band having a larger penetration than X-band. Little is known about the absolute value of X-band penetration into snow and glacier ice, but it decreases as temperature and water content rise (Reference Ulaby, Moore and FungUlaby and others, 1986; Reference SurdykSurdyk, 2002). In Antarctica, Reference Davis and PoznyakDavis and Poznyak (1993) measured penetration depths at 10GHz from 2.1 to 4.7 m, and Reference SurdykSurdyk (2002) reported a 4m penetration depth at 10.7GHz at -8°C. However, ice and snow conditions in winter in Karakoram are not identical to those in Antarctica: temperature is probably higher, snow is wetter and ice is dirtier (presence of debris), so penetration depth in the X-band should be less than the values found in the literature. As a first approximation, we assume no penetration of the X-band signal and consider that the SRTM_X-band-SRTM_C-band value corresponds to the C-band penetration. Clearly, this hypothesis requires further validation, especially by the German Aerospace Center (DLR) TanDEM-X mission, which will release high- resolution DEMs from X-band radar data.

Comparing C-band and X-band DEMs makes it possible to better take into account and correct for SRTM penetration into snow and ice. We stress that the amplitude of penetration will likely be peculiar to each region as snowfall seasonality and snowpack characteristics were different among glacierized areas in February 2000, when the SRTM was flown. One limitation of the methodology proposed to account for C-band penetration is the limited coverage of the X-band DEM, restricted to some stripes.

Conclusion

We have analyzed, and proposed corrections for, two issues that can lead to altitude-dependent bias between DEMs and, thus, erroneous measurements of glacier elevation and volume changes. The first issue concerns the comparison of DEMs with different original resolutions. Building on previous findings (Reference PaulPaul, 2008), we found that these biases are directly explained by variations in terrain maximum curvature and that, importantly, the relationship is unchanged on and off glaciers. Thus, the relationship between elevation differences and maximum curvature can be established off glaciers and applied to the ice-covered areas. The second issue is related to the penetration of the radar signal into ice and snow, a penetration that can reach several meters in the case of the SRTM C-band DEM. We have shown that analyzing the elevation differences between the two SRTM DEMs (30 m X-band and 90 m C-band acquired simultaneously in February 2000) can provide a first-order estimate of C-band penetration. A 3m average penetration of the SRTM C-band signal was found for Karakoram but must be recalculated for each ice-covered region.

It is known that DEMs should be corrected prior to comparison, but we stress here that the elevation differences on the ice-free terrain cannot readily be used to correct the ice/snow elevation changes. Together with other processing steps (Reference Nuth and KääbNuth and Kääb, 2011), particular attention should be paid to the two additional corrections proposed in this correspondence when the forthcoming 30m global Tan- DEM-X DEM is compared to the SRTM 90 m C-band DEM or any other earlier DEMs acquired with different resolution and/or in a different wavelength of the electromagnetic spectrum. In addition, we recommend investigation of the potentially strong impact of such corrections on previously published mass-balance estimates (Reference Surazakov and AizenSurazakov and Aizen, 2006; Reference Berthier, Arnaud, Kumar, Ahmad, Wagnon and ChevallierBerthier and others, 2007; Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007; Reference Möller, Schneider and KilianMöller and others, 2007; Reference Schiefer, Menounos and WheateSchiefer and others, 2007; Reference PaulPaul and Haeberli, 2008).