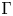1. Introduction
In this paper, we study the effective behaviour of scale-dependent integral functionals with possibly degenerate integrands. Functionals of this kind typically model the energy of a heterogeneous material whose physical properties (elastic, thermal, electrical, etc.) may both deteriorate and vary significantly from point to point, on a mesoscopic scale.
The energy functionals we consider are of the form
where $A\subset \mathbb {R}^{n}$![]() is an open, bounded, Lipschitz set, $k\in \mathbb {N}$
is an open, bounded, Lipschitz set, $k\in \mathbb {N}$![]() is a parameter related to some material property (e.g. the size of the microstructure) and $u \colon A \to \mathbb {R}^{m}$
is a parameter related to some material property (e.g. the size of the microstructure) and $u \colon A \to \mathbb {R}^{m}$![]() represents a physical variable (e.g. the elastic deformation of the body).
represents a physical variable (e.g. the elastic deformation of the body).
The degeneracy of the integrands $f_k \colon \mathbb {R}^{n} \times \mathbb {R}^{m\times n} \to [0,\,+\infty )$![]() is expressed in terms of growth and coercivity conditions which can depend both on the parameter $k$
is expressed in terms of growth and coercivity conditions which can depend both on the parameter $k$![]() and on the spatial variable $x$
and on the spatial variable $x$![]() . These are given by introducing weight functions $\lambda _k\colon \mathbb {R}^{n} \to [0,\,+\infty )$
. These are given by introducing weight functions $\lambda _k\colon \mathbb {R}^{n} \to [0,\,+\infty )$![]() which modulate the typical superlinear growth in the gradient variable. That is, for every $x\in \mathbb {R}^{n}$
which modulate the typical superlinear growth in the gradient variable. That is, for every $x\in \mathbb {R}^{n}$![]() , $\xi \in \mathbb {R}^{m\times n}$
, $\xi \in \mathbb {R}^{m\times n}$![]() , and $k\in \mathbb {N}$
, and $k\in \mathbb {N}$![]() the integrands $f_k$
the integrands $f_k$![]() satisfy
satisfy
where $p>1$![]() , and $0<\alpha \leq \beta <+\infty$
, and $0<\alpha \leq \beta <+\infty$![]() .
.
If the weight functions $\lambda _k$![]() are bounded in $L^{\infty }$
are bounded in $L^{\infty }$![]() uniformly in $k$
uniformly in $k$![]() , then (1.2) reduces to the standard growth and coercivity of order $p>1$
, then (1.2) reduces to the standard growth and coercivity of order $p>1$![]() . In this case, the limit behaviour of $F_k$
. In this case, the limit behaviour of $F_k$![]() is well understood and can be described using the language of $\Gamma$
is well understood and can be described using the language of $\Gamma$![]() -convergence. Namely, if $k\to \infty$
-convergence. Namely, if $k\to \infty$![]() , the functionals $F_k$
, the functionals $F_k$![]() $\Gamma$
$\Gamma$![]() -converge (up to subsequences), on $W^{1,p}(A;\mathbb {R}^{m})$
-converge (up to subsequences), on $W^{1,p}(A;\mathbb {R}^{m})$![]() , to an integral functional of the form
, to an integral functional of the form
with $f_0$![]() satisfying the same (nondegenerate) growth conditions satisfied by $f_k$
satisfying the same (nondegenerate) growth conditions satisfied by $f_k$![]() (see [Reference Buttazzo and Dal Maso9]). Moreover, if $\varepsilon _k \to 0^{+}$
(see [Reference Buttazzo and Dal Maso9]). Moreover, if $\varepsilon _k \to 0^{+}$![]() and $f_k(x,\,\xi )=f(x/{\varepsilon _k},\,\xi )$
and $f_k(x,\,\xi )=f(x/{\varepsilon _k},\,\xi )$![]() for some nondegenerate $f$
for some nondegenerate $f$![]() , then the limit integrand $f_0$
, then the limit integrand $f_0$![]() is $x$
is $x$![]() -independent and subsequence-independent both in the periodic [Reference Braides6, Reference Müller30] and in the stationary random case [Reference Dal Maso and Modica15, Reference Dal Maso and Modica16, Reference Messaoudi and Michaille28], and given by a so-called homogenization formula. As a result, in this case, the whole sequence $(F_k)$
-independent and subsequence-independent both in the periodic [Reference Braides6, Reference Müller30] and in the stationary random case [Reference Dal Maso and Modica15, Reference Dal Maso and Modica16, Reference Messaoudi and Michaille28], and given by a so-called homogenization formula. As a result, in this case, the whole sequence $(F_k)$![]() $\Gamma$
$\Gamma$![]() -converges to $F$
-converges to $F$![]() .
.
In this paper, we consider sequences of weight functions $(\lambda _k)$![]() which are not bounded in general. Specifically, for every $k\in \mathbb {N}$
which are not bounded in general. Specifically, for every $k\in \mathbb {N}$![]() we assume that
we assume that
moreover, we additionally require the existence of a constant $K\geq 1$![]() such that for every $k\in \mathbb {N}$
such that for every $k\in \mathbb {N}$![]() there holds
there holds
for every cube $Q \subset \mathbb {R}^{n}$![]() . The uniform integrability condition (1.5) is known as Muckenhoupt condition and the functions satisfying it are referred to as Muckenhoupt $A_p(K)$
. The uniform integrability condition (1.5) is known as Muckenhoupt condition and the functions satisfying it are referred to as Muckenhoupt $A_p(K)$![]() -weights [Reference Muckenhoupt29].
-weights [Reference Muckenhoupt29].
In this case, the growth conditions (1.2) satisfied by $f_k$![]() naturally set the problem in the parameter-dependent weighted Sobolev space $W^{1,p}_{\lambda _k}(A;\mathbb {R}^{m})$
naturally set the problem in the parameter-dependent weighted Sobolev space $W^{1,p}_{\lambda _k}(A;\mathbb {R}^{m})$![]() where, for a given $A_p(K)$
where, for a given $A_p(K)$![]() -weight $\lambda$
-weight $\lambda$![]() we have
we have
The limit behaviour of functionals $F_k$![]() with integrands satisfying (1.2) was studied for the first time in [Reference Carbone and Sbordone10], in the convex, scalar case and under the sole integrability condition (1.4). Assuming that $\lambda _k$
with integrands satisfying (1.2) was studied for the first time in [Reference Carbone and Sbordone10], in the convex, scalar case and under the sole integrability condition (1.4). Assuming that $\lambda _k$![]() converges weakly to some $\lambda _\infty$
converges weakly to some $\lambda _\infty$![]() in $L^{1}$
in $L^{1}$![]() , in [Reference Carbone and Sbordone10] the authors proved a $\Gamma$
, in [Reference Carbone and Sbordone10] the authors proved a $\Gamma$![]() -convergence and integral representation result for the $\Gamma$
-convergence and integral representation result for the $\Gamma$![]() -limit of $F_k$
-limit of $F_k$![]() , on the space of Lipschitz functions. The latter, though, in general is smaller than the domain of the $\Gamma$
, on the space of Lipschitz functions. The latter, though, in general is smaller than the domain of the $\Gamma$![]() -limit. Moreover, in the setting considered in [Reference Carbone and Sbordone10] the functionals $F_k$
-limit. Moreover, in the setting considered in [Reference Carbone and Sbordone10] the functionals $F_k$![]() are not equi-coercive and therefore a convergence result for the associated minimization problems cannot be derived from the $\Gamma$
are not equi-coercive and therefore a convergence result for the associated minimization problems cannot be derived from the $\Gamma$![]() -convergence analysis.
-convergence analysis.
In order to extend the $\Gamma$![]() -convergence result in [Reference Carbone and Sbordone10] to the domain of the $\Gamma$
-convergence result in [Reference Carbone and Sbordone10] to the domain of the $\Gamma$![]() -limit and to gain compactness, in [Reference De Arcangelis17] the Muckenhoupt condition (1.5) was also required together with the additional bound
-limit and to gain compactness, in [Reference De Arcangelis17] the Muckenhoupt condition (1.5) was also required together with the additional bound
where $0< c_1\leq c_2<+\infty$![]() and $Q_0\subset \mathbb {R}^{n}$
and $Q_0\subset \mathbb {R}^{n}$![]() is a given cube. The Muckenhoupt condition (1.5) guarantees the continuous embedding of $W^{1,p}_{\lambda _k}(A)$
is a given cube. The Muckenhoupt condition (1.5) guarantees the continuous embedding of $W^{1,p}_{\lambda _k}(A)$![]() in the Sobolev space $W^{1,1+\delta }(A)$
in the Sobolev space $W^{1,1+\delta }(A)$![]() , for some $\delta >0$
, for some $\delta >0$![]() . Then, a combination of (1.5) and (1.6) ensures that sequences with equi-bounded energy are bounded in $W^{1,1+\delta }(A)$
. Then, a combination of (1.5) and (1.6) ensures that sequences with equi-bounded energy are bounded in $W^{1,1+\delta }(A)$![]() , and hence precompact in $L^{1}(A)$
, and hence precompact in $L^{1}(A)$![]() (whenever $A\subset Q_0$
(whenever $A\subset Q_0$![]() ). Therefore, in the setting considered in [Reference De Arcangelis17] the equi-coerciveness of the functionals $F_k$
). Therefore, in the setting considered in [Reference De Arcangelis17] the equi-coerciveness of the functionals $F_k$![]() can be recovered. Moreover, again thanks to (1.5)–(1.6) a lower bound on the $\Gamma$
can be recovered. Moreover, again thanks to (1.5)–(1.6) a lower bound on the $\Gamma$![]() -limit can be established, which shows that its domain is the weighted Sobolev space $W^{1,p}_{\lambda _\infty }(A)$
-limit can be established, which shows that its domain is the weighted Sobolev space $W^{1,p}_{\lambda _\infty }(A)$![]() , where $\lambda _\infty$
, where $\lambda _\infty$![]() belongs to a Muckenhoupt class and is the weak $L^{1}$
belongs to a Muckenhoupt class and is the weak $L^{1}$![]() -limit of (a subsequence of) $\lambda _k$
-limit of (a subsequence of) $\lambda _k$![]() .
.
Besides the contributions [Reference Carbone and Sbordone10, Reference De Arcangelis17], $\Gamma$![]() -convergence and relaxation results for functionals of type (1.1)–(1.2) defined on weighted Sobolev spaces were also established in [Reference Baldi and Tesi3, Reference Chiadó Piat and Serra Cassano11, Reference De Arcangelis and Serra Cassano18, Reference De Arcangelis and Serra Cassano19, Reference Engström, Persson, Piatnitski and Wall21, Reference Franchi and Tesi22, Reference Neukamm, Schäffner and Schlömerkemper31] without departing, though, from the convex/monotone operator, scalar setting, with the only exception of [Reference Neukamm, Schäffner and Schlömerkemper31]. More specifically, in [Reference Neukamm, Schäffner and Schlömerkemper31] the authors proved a stochastic homogenization result for a sequence of discrete nonconvex, vectorial energy functionals with degenerate integrands. Under suitable assumptions on the random weights, which are weaker than (1.5) in the scalar case but not really comparable to (1.5) in the vectorial case, the authors showed that in the stationary ergodic case the energies homogenize to a nondegenerate deterministic integral functional. We observe that the case of homogenization is somehow special since in this case the limit functional is always nondegenerate and thus defined on the space $W^{1,p}$
-convergence and relaxation results for functionals of type (1.1)–(1.2) defined on weighted Sobolev spaces were also established in [Reference Baldi and Tesi3, Reference Chiadó Piat and Serra Cassano11, Reference De Arcangelis and Serra Cassano18, Reference De Arcangelis and Serra Cassano19, Reference Engström, Persson, Piatnitski and Wall21, Reference Franchi and Tesi22, Reference Neukamm, Schäffner and Schlömerkemper31] without departing, though, from the convex/monotone operator, scalar setting, with the only exception of [Reference Neukamm, Schäffner and Schlömerkemper31]. More specifically, in [Reference Neukamm, Schäffner and Schlömerkemper31] the authors proved a stochastic homogenization result for a sequence of discrete nonconvex, vectorial energy functionals with degenerate integrands. Under suitable assumptions on the random weights, which are weaker than (1.5) in the scalar case but not really comparable to (1.5) in the vectorial case, the authors showed that in the stationary ergodic case the energies homogenize to a nondegenerate deterministic integral functional. We observe that the case of homogenization is somehow special since in this case the limit functional is always nondegenerate and thus defined on the space $W^{1,p}$![]() .
.
In the present paper, we extend the analysis in [Reference De Arcangelis17] to the nonconvex, vectorial setting, without assuming any periodicity or stationarity of the integrands $f_k$![]() . Namely, we assume that $f_k$
. Namely, we assume that $f_k$![]() satisfies (1.2), together with some mild continuity condition in $\xi$
satisfies (1.2), together with some mild continuity condition in $\xi$![]() (cf. (3.3)), and that the weight functions $\lambda _k$
(cf. (3.3)), and that the weight functions $\lambda _k$![]() are as in (1.4)–(1.6). Under these assumptions we show the existence of a subsequence $(k_h)$
are as in (1.4)–(1.6). Under these assumptions we show the existence of a subsequence $(k_h)$![]() , a limit Muckenhoupt weight $\lambda _\infty$
, a limit Muckenhoupt weight $\lambda _\infty$![]() , with $\lambda _{k_h} \rightharpoonup \lambda _\infty$
, with $\lambda _{k_h} \rightharpoonup \lambda _\infty$![]() in $L^{1}(Q_0)$
in $L^{1}(Q_0)$![]() , and a degenerate integrand $f_\infty$
, and a degenerate integrand $f_\infty$![]() satisfying
satisfying
a.e. in $Q_0$![]() and for every $\xi \in \mathbb {R}^{m\times n}$
and for every $\xi \in \mathbb {R}^{m\times n}$![]() , such that the functionals $F_{k_h}$
, such that the functionals $F_{k_h}$![]() $\Gamma$
$\Gamma$![]() -converge, with respect to the strong $L^{1}(A;\mathbb {R}^{m})$
-converge, with respect to the strong $L^{1}(A;\mathbb {R}^{m})$![]() -convergence, to the integral functional
-convergence, to the integral functional
We also show that the $\Gamma$![]() -convergence holds true, with the same subsequence $(k_h)$
-convergence holds true, with the same subsequence $(k_h)$![]() , for every open, bounded, Lipschitz set $A\subset \mathbb {R}^{n}$
, for every open, bounded, Lipschitz set $A\subset \mathbb {R}^{n}$![]() , with $A\subset \subset Q_0$
, with $A\subset \subset Q_0$![]() . Moreover, we derive an asymptotic formula for the limit integrand $f_\infty$
. Moreover, we derive an asymptotic formula for the limit integrand $f_\infty$![]() which can be expressed as a (double) limit of sequences of scaled minimization problems as follows:
which can be expressed as a (double) limit of sequences of scaled minimization problems as follows:

where $Q_\rho (x)\subset \mathbb {R}^{n}$![]() denotes the cube centred in $x$
denotes the cube centred in $x$![]() with side-length $\rho >0$
with side-length $\rho >0$![]() , and
, and
The proof of this result is carried out in a number of intermediate steps. Namely, we first prove the $\Gamma$![]() -convergence and integral representation result on the space $W^{1,\infty }(A;\mathbb {R}^{m}) \subsetneq W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$
-convergence and integral representation result on the space $W^{1,\infty }(A;\mathbb {R}^{m}) \subsetneq W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() . To do so, we use the localization method of $\Gamma$
. To do so, we use the localization method of $\Gamma$![]() -convergence and adapt the approach in [Reference Braides and Defranceschi7, Reference Dal Maso14] to our setting to get an integral representation result for functionals with degenerate integrands. We remark here that the most delicate part in the implementation of the localization method is the proof of the subadditivity of the $\Gamma$
-convergence and adapt the approach in [Reference Braides and Defranceschi7, Reference Dal Maso14] to our setting to get an integral representation result for functionals with degenerate integrands. We remark here that the most delicate part in the implementation of the localization method is the proof of the subadditivity of the $\Gamma$![]() -limit, which requires to combine a fundamental estimate for the functionals $F_k$
-limit, which requires to combine a fundamental estimate for the functionals $F_k$![]() together with an ad hoc vectorial truncation argument, in the same spirit as, e.g. [Reference Braides, Defranceschi and Vitali8, lemma 3.5]. We then extend the $\Gamma$
together with an ad hoc vectorial truncation argument, in the same spirit as, e.g. [Reference Braides, Defranceschi and Vitali8, lemma 3.5]. We then extend the $\Gamma$![]() -convergence and integral representation result to the limit weighted Sobolev space $W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$
-convergence and integral representation result to the limit weighted Sobolev space $W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() . The latter coincides with the domain of $F_\infty$
. The latter coincides with the domain of $F_\infty$![]() , thanks to (1.7); hence we get a complete description of the $\Gamma$
, thanks to (1.7); hence we get a complete description of the $\Gamma$![]() -limit of $F_{k_h}$
-limit of $F_{k_h}$![]() . The passage from $W^{1,\infty }(A;\mathbb {R}^{m})$
. The passage from $W^{1,\infty }(A;\mathbb {R}^{m})$![]() to $W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$
to $W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() is performed by resorting to classical approximation argument (see [Reference Acerbi and Fusco1, theorem II.4]) which exploits the property of the maximal function in relation to the Muckenhoupt weights. More precisely, we can adapt [Reference De Arcangelis17, theorem 3.1] to the vectorial setting to show that in the liminf inequality, we can replace a sequence $(u_k)$
is performed by resorting to classical approximation argument (see [Reference Acerbi and Fusco1, theorem II.4]) which exploits the property of the maximal function in relation to the Muckenhoupt weights. More precisely, we can adapt [Reference De Arcangelis17, theorem 3.1] to the vectorial setting to show that in the liminf inequality, we can replace a sequence $(u_k)$![]() , with $u_k \to u$
, with $u_k \to u$![]() in $L^{1}(A;\mathbb {R}^{m})$
in $L^{1}(A;\mathbb {R}^{m})$![]() and equi-bounded $W^{1,p}_{\lambda _k}(A;\mathbb {R}^{m})$
and equi-bounded $W^{1,p}_{\lambda _k}(A;\mathbb {R}^{m})$![]() -norm, with a sequence of Lipschitz functions converging to a $W^{1,\infty }(A;\mathbb {R}^{m})$
-norm, with a sequence of Lipschitz functions converging to a $W^{1,\infty }(A;\mathbb {R}^{m})$![]() -function which differs from $u$
-function which differs from $u$![]() on a set with vanishing measure. Eventually, the asymptotic formula for $f_\infty$
on a set with vanishing measure. Eventually, the asymptotic formula for $f_\infty$![]() is obtained by combining a convergence result for minimization problems with prescribed Dirichlet conditions together with a derivation formula for $f_\infty$
is obtained by combining a convergence result for minimization problems with prescribed Dirichlet conditions together with a derivation formula for $f_\infty$![]() which is obtained by extending to the weighted Sobolev setting the method developed in [Reference Bouchitté, Fonseca and Mascarenhas4, Reference Bouchitté, Fonseca, Leoni and Mascarenhas5].
which is obtained by extending to the weighted Sobolev setting the method developed in [Reference Bouchitté, Fonseca and Mascarenhas4, Reference Bouchitté, Fonseca, Leoni and Mascarenhas5].
Finally, the general $\Gamma$![]() -convergence analysis is complemented by an application to the case of stationary random weights and integrands, thus generalizing the classical stochastic homogenization result in [Reference Dal Maso and Modica15, Reference Dal Maso and Modica16, Reference Messaoudi and Michaille28] to the degenerate setting.
-convergence analysis is complemented by an application to the case of stationary random weights and integrands, thus generalizing the classical stochastic homogenization result in [Reference Dal Maso and Modica15, Reference Dal Maso and Modica16, Reference Messaoudi and Michaille28] to the degenerate setting.
That is, we specialize our general result to the choice
where $\omega$![]() belongs to the sample space of a given probability space $(\Omega,\, \mathcal {F},\, P)$
belongs to the sample space of a given probability space $(\Omega,\, \mathcal {F},\, P)$![]() , $\lambda$
, $\lambda$![]() is a random Muckenhoupt weight (cf. assumption 8.5), and $f$
is a random Muckenhoupt weight (cf. assumption 8.5), and $f$![]() is a degenerate stationary random integrand (cf. definition 8.7). Then, following the same approach as in [Reference Dal Maso and Modica16], we combine the deterministic analysis and the subadditive ergodic theorem [Reference Akcoglu and Krengel2, theorem 2.9] to show that, almost surely, the random functionals
is a degenerate stationary random integrand (cf. definition 8.7). Then, following the same approach as in [Reference Dal Maso and Modica16], we combine the deterministic analysis and the subadditive ergodic theorem [Reference Akcoglu and Krengel2, theorem 2.9] to show that, almost surely, the random functionals
$\Gamma$![]() -converge to a nondegenerate (spatially) homogeneous random functional
-converge to a nondegenerate (spatially) homogeneous random functional
where $f_{\rm hom}$![]() satisfies standard growth conditions of order $p>1$
satisfies standard growth conditions of order $p>1$![]() with random coefficients (cf. (8.10)) and is given by the following asymptotic cell formula
with random coefficients (cf. (8.10)) and is given by the following asymptotic cell formula

If, moreover, $\lambda$![]() and $f$
and $f$![]() are ergodic, we show that $f_{\rm hom}$
are ergodic, we show that $f_{\rm hom}$![]() is deterministic and given by the expected value of the right hand side of (1.9). Furthermore, in the ergodic case $f_{\rm hom}$
is deterministic and given by the expected value of the right hand side of (1.9). Furthermore, in the ergodic case $f_{\rm hom}$![]() satisfies the following deterministic growth and coercivity conditions of order $p>1$
satisfies the following deterministic growth and coercivity conditions of order $p>1$![]() :
:
for every $\xi \in \mathbb {R}^{m \times n}$![]() .
.
Outline of the paper. The paper is organized as follows. In § 2 we recall the notions of Muckenhoupt classes and weights and of weighted Sobolev spaces. Moreover, we recall here some well-known related results which will be used throughout. In § 3 we introduce the functionals we study and state the main result of this paper, theorem 3.2. The proof of theorem 3.2 is then carried out in § 4–7. Namely, in § 4 we prove a $\Gamma$![]() -convergence and integral representation result in the space $W^{1,\infty }$
-convergence and integral representation result in the space $W^{1,\infty }$![]() , theorem 4.1. In § 5 we establish theorem 5.2 which extends the results in theorem 4.1 to the weighted Sobolev space $W^{1,p}_{\lambda _\infty }$
, theorem 4.1. In § 5 we establish theorem 5.2 which extends the results in theorem 4.1 to the weighted Sobolev space $W^{1,p}_{\lambda _\infty }$![]() , also showing that the latter coincides with the domain of the $\Gamma$
, also showing that the latter coincides with the domain of the $\Gamma$![]() -limit. On account of theorem 5.2, in § 6 we prove that in this setting $\Gamma$
-limit. On account of theorem 5.2, in § 6 we prove that in this setting $\Gamma$![]() -convergence is stable under the addition of Dirichlet boundary conditions and we derive a convergence result for the associated minimization problems. In § 7 we prove a derivation formula for the integrand of the $\Gamma$
-convergence is stable under the addition of Dirichlet boundary conditions and we derive a convergence result for the associated minimization problems. In § 7 we prove a derivation formula for the integrand of the $\Gamma$![]() -limit, theorem 7.1 (see also corollary 7.2). Eventually, in § 8 we prove a stochastic homogenization result for stationary random weights and integrands, theorem 8.12.
-limit, theorem 7.1 (see also corollary 7.2). Eventually, in § 8 we prove a stochastic homogenization result for stationary random weights and integrands, theorem 8.12.
2. Preliminaries
In this section, we collect some useful definitions and preliminary results which will be used throughout.
2.1 Muckenhoupt classes
We start by recalling the definition of the so-called Muckenhoupt classes. An introduction to the theory of Muckenhoupt classes can be found in [Reference Garcia-Cuerva and Rubio de Francia24].
Definition 2.1 Let $p>1$![]() and $K\geq 1$
and $K\geq 1$![]() . The Muckenhoupt class $A_p(K)$
. The Muckenhoupt class $A_p(K)$![]() is defined as the collection of all nonnegative functions $\lambda \colon \mathbb {R}^{n} \to [0,\,+\infty )$
is defined as the collection of all nonnegative functions $\lambda \colon \mathbb {R}^{n} \to [0,\,+\infty )$![]() , with $\lambda,\,\lambda ^{-1/(p-1)}\in L^{1}_{\rm loc}(\mathbb {R}^{n})$
, with $\lambda,\,\lambda ^{-1/(p-1)}\in L^{1}_{\rm loc}(\mathbb {R}^{n})$![]() , such that
, such that

for every cube $Q \subset \mathbb {R}^{n}$![]() with faces parallel to the coordinate hyperplanes.
with faces parallel to the coordinate hyperplanes.
Moreover, we set $A_p:=\bigcup _{K\geq 1}A_p(K)$![]() .
.
The elements of the class $A_p$![]() (resp. $A_p(K)$
(resp. $A_p(K)$![]() ) are usually referred to as $A_p$
) are usually referred to as $A_p$![]() -weights (resp. $A_p(K)$
-weights (resp. $A_p(K)$![]() -weights). Simple examples of $A_p$
-weights). Simple examples of $A_p$![]() -weights are radially symmetric functions of the type
-weights are radially symmetric functions of the type
Further examples can be found, e.g. in [Reference Heinonen, Kilpeläinen and Martio25].
We recall the following ‘reverse Hölder inequality’ which holds for functions in $A_p$![]() and whose proof can be found in [Reference Coifman and Fefferman13, theorem IV].
and whose proof can be found in [Reference Coifman and Fefferman13, theorem IV].
Theorem 2.2 Let $p>1$![]() and $K\geq 1$
and $K\geq 1$![]() . Then there exist an exponent $\sigma =\sigma (K,\,p,\,n)>0$
. Then there exist an exponent $\sigma =\sigma (K,\,p,\,n)>0$![]() and a constant $c=c(K,\,p,\,n)>0$
and a constant $c=c(K,\,p,\,n)>0$![]() such that
such that
for every cube $Q$![]() and for every $\lambda \in A_p(K)$
and for every $\lambda \in A_p(K)$![]() .
.
Remark 2.3 We observe that since $\lambda ^{-1/(p-1)}\in A_{p'}(K)$![]() with $p':=p/(p-1)$
with $p':=p/(p-1)$![]() , then inequality (2.2) can be obtained by applying (2.1) to the weight $\lambda ^{-1/(p-1)}$
, then inequality (2.2) can be obtained by applying (2.1) to the weight $\lambda ^{-1/(p-1)}$![]() .
.
In this paper, we will deal with sequences of $A_p(K)$![]() -weights. The following result is a consequence of theorem 2.2 and its proof can be found in [Reference De Arcangelis17, proposition 4.1].
-weights. The following result is a consequence of theorem 2.2 and its proof can be found in [Reference De Arcangelis17, proposition 4.1].
Proposition 2.4 Let $K\geq 1,$![]() $p>1,$
$p>1,$![]() and let $(\lambda _k)$
and let $(\lambda _k)$![]() be a sequence of functions in $A_p(K)$
be a sequence of functions in $A_p(K)$![]() . Let $Q_0 \subset \mathbb {R}^{n}$
. Let $Q_0 \subset \mathbb {R}^{n}$![]() be a cube and assume that there exist two constants $c_1,\, c_2$
be a cube and assume that there exist two constants $c_1,\, c_2$![]() with $0< c_1\leq c_2$
with $0< c_1\leq c_2$![]() such that
such that
for every $k\in \mathbb {N}$![]() . Then there exist a subsequence $(\lambda _{k_h}) \subset (\lambda _k),$
. Then there exist a subsequence $(\lambda _{k_h}) \subset (\lambda _k),$![]() a constant $c_3=c_3(n),$
a constant $c_3=c_3(n),$![]() depending only on $n$
depending only on $n$![]() , and functions $\lambda _\infty$
, and functions $\lambda _\infty$![]() and $\tilde {\lambda }_\infty$
and $\tilde {\lambda }_\infty$![]() in $A_p(c_3^{p}K)$
in $A_p(c_3^{p}K)$![]() such that
such that
and
for some $\sigma >0$![]() . Moreover, there holds
. Moreover, there holds
a.e. in $Q_0$![]() .
.
If (2.3) is replaced by the stronger condition
then (2.4) and (2.5) holds true for every cube $Q\subset \mathbb {R}^{n},$![]() (2.6) holds a.e. in $\mathbb {R}^{n},$
(2.6) holds a.e. in $\mathbb {R}^{n},$![]() and $\lambda _\infty \in A_p(K)$
and $\lambda _\infty \in A_p(K)$![]() .
.
The equi-integrability estimate below is another immediate consequence of theorem 2.2.
Proposition 2.5 Let $p>1,$![]() $K\geq 1,$
$K\geq 1,$![]() and let $(\lambda _k)$
and let $(\lambda _k)$![]() be a sequence of functions in $A_p(K)$
be a sequence of functions in $A_p(K)$![]() satisfying (2.3). Then there exist $\sigma =\sigma (K,\,p,\,n)>0$
satisfying (2.3). Then there exist $\sigma =\sigma (K,\,p,\,n)>0$![]() and $c=c(K,\,p,\,n)>0$
and $c=c(K,\,p,\,n)>0$![]() such that
such that

for every measurable set $E\subset Q_0$![]() and every $k\in \mathbb {N}$
and every $k\in \mathbb {N}$![]() .
.
Proof. Let $\sigma >0$![]() and $c>0$
and $c>0$![]() be the constants given by theorem 2.2. By (2.1) and (2.3) we get
be the constants given by theorem 2.2. By (2.1) and (2.3) we get

for every $k\in \mathbb {N}$![]() . Therefore, the Hölder inequality easily gives
. Therefore, the Hölder inequality easily gives

2.2 Weighted Sobolev spaces
In this short subsection, we recall the definition and the basic properties of weighted Sobolev spaces. For a comprehensive treatment of this subject we refer the reader to the monographs [Reference Heinonen, Kilpeläinen and Martio25, Reference Turesson34]. For further relevant results concerning weighted Sobolev spaces, we will provide a precise reference to the literature whenever these results are used in the paper.
Let $p>1$![]() , let $\lambda \in A_p$
, let $\lambda \in A_p$![]() . In all that follows $A\subset \mathbb {R}^{n}$
. In all that follows $A\subset \mathbb {R}^{n}$![]() denotes an open and bounded set with Lipschitz boundary. Let $m\in \mathbb {N},\, m\geq 1$
denotes an open and bounded set with Lipschitz boundary. Let $m\in \mathbb {N},\, m\geq 1$![]() ; we define the weighted Lebesgue space
; we define the weighted Lebesgue space
we recall that $L^{p}_\lambda (A;\mathbb {R}^{m})$![]() equipped with the norm
equipped with the norm

is a reflexive Banach space. Moreover, we define the weighted Sobolev space $W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() as
as
the latter is also a reflexive Banach space when endowed with the norm

We recall that the embedding of $W^{1,p}_{\lambda }(A;\mathbb {R}^{m})$![]() in $L^{p}_{\lambda }(A;\mathbb {R}^{m})$
in $L^{p}_{\lambda }(A;\mathbb {R}^{m})$![]() is compact (see, e.g. [Reference Fröhlich23, lemma 1]). Furthermore, we have the following continuous embeddings:
is compact (see, e.g. [Reference Fröhlich23, lemma 1]). Furthermore, we have the following continuous embeddings:

for some $\delta >0$![]() .
.
Throughout the paper, we will also use the fact that $C^{\infty }(\overline A;\mathbb {R}^{m})$![]() is dense in $W^{1,p}_\lambda (A;\mathbb {R}^{m})$
is dense in $W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() (see, e.g. [Reference Turesson34, corollary 2.1.6]).
(see, e.g. [Reference Turesson34, corollary 2.1.6]).
The following characterization of $W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() will be useful for our purposes.
will be useful for our purposes.
Proposition 2.6 Let $p>1,$![]() $\lambda \in A_p,$
$\lambda \in A_p,$![]() and let $A \subset \mathbb {R}^{n}$
and let $A \subset \mathbb {R}^{n}$![]() be open, bounded, and with Lipschitz boundary. Define
be open, bounded, and with Lipschitz boundary. Define
then $\widehat W^{1,p}_\lambda (A;\mathbb {R}^{m})=W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() .
.
Proof. The inclusion $W^{1,p}_\lambda (A;\mathbb {R}^{m}) \subset \widehat W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() is obvious, therefore we only need to show that
is obvious, therefore we only need to show that
To prove (2.7) we will establish the following Poincaré-type inequality: there exists $C>0$![]() such that
such that
for every $u\in C^{\infty }(\overline A;\mathbb {R}^{m})$![]() .
.
We will obtain (2.8) arguing by contradiction. Were (2.8) false, then for every $j\in \mathbb {N}$![]() there would exist $u_j \in C^{\infty }(\overline A;\mathbb {R}^{m})$
there would exist $u_j \in C^{\infty }(\overline A;\mathbb {R}^{m})$![]() such that
such that
Define the renormalized functions $v_j \in C^{\infty }(\overline A;\mathbb {R}^{m})$![]() as
as
Then,
for every $j\in \mathbb {N}$![]() . Hence, in particular, the sequence $(v_j)$
. Hence, in particular, the sequence $(v_j)$![]() is bounded in $W^{1,p}_\lambda (A;\mathbb {R}^{m})$
is bounded in $W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() . Therefore, by the compact embedding of $W^{1,p}_\lambda (A;\mathbb {R}^{m})$
. Therefore, by the compact embedding of $W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() in $L^{p}_\lambda (A;\mathbb {R}^{m})$
in $L^{p}_\lambda (A;\mathbb {R}^{m})$![]() , up to subsequences (not relabelled), $v_j \to v$
, up to subsequences (not relabelled), $v_j \to v$![]() in $L^{p}_\lambda (A;\mathbb {R}^{m})$
in $L^{p}_\lambda (A;\mathbb {R}^{m})$![]() , for some $v\in L^{p}_\lambda (A;\mathbb {R}^{m})$
, for some $v\in L^{p}_\lambda (A;\mathbb {R}^{m})$![]() . Moreover, since the embedding of $L^{p}_\lambda (A;\mathbb {R}^{m})$
. Moreover, since the embedding of $L^{p}_\lambda (A;\mathbb {R}^{m})$![]() in $L^{1}(A;\mathbb {R}^{m})$
in $L^{1}(A;\mathbb {R}^{m})$![]() is continuous, we also have $v_j \to v$
is continuous, we also have $v_j \to v$![]() in $L^{1}(A;\mathbb {R}^{m})$
in $L^{1}(A;\mathbb {R}^{m})$![]() . Therefore, (2.9) entails both $\|v\|_{L^{p}_\lambda (A;\mathbb {R}^{m})}= 1$
. Therefore, (2.9) entails both $\|v\|_{L^{p}_\lambda (A;\mathbb {R}^{m})}= 1$![]() and $v=0$
and $v=0$![]() a.e. in $A$
a.e. in $A$![]() and hence a contradiction.
and hence a contradiction.
Now let $u\in \widehat W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() ; by [Reference Chiadó Piat and Serra Cassano11, proposition 3.5] (see also [Reference Chua12, theorem 6.1]) there exists $(u_j) \subset C^{\infty }(\overline A;\mathbb {R}^{m})$
; by [Reference Chiadó Piat and Serra Cassano11, proposition 3.5] (see also [Reference Chua12, theorem 6.1]) there exists $(u_j) \subset C^{\infty }(\overline A;\mathbb {R}^{m})$![]() such that
such that
Moreover, in view of (2.8) the sequence $(u_j)$![]() is bounded in $W^{1,p}_\lambda (A;\mathbb {R}^{m})$
is bounded in $W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() , therefore again appealing to the compact embedding of $W^{1,p}_\lambda (A;\mathbb {R}^{m})$
, therefore again appealing to the compact embedding of $W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() in $L^{p}_\lambda (A;\mathbb {R}^{m})$
in $L^{p}_\lambda (A;\mathbb {R}^{m})$![]() we deduce that $u_j \to u$
we deduce that $u_j \to u$![]() in $L^{p}_\lambda (A;\mathbb {R}^{m})$
in $L^{p}_\lambda (A;\mathbb {R}^{m})$![]() and hence $u\in W^{1,p}_\lambda (A;\mathbb {R}^{m})$
and hence $u\in W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() , as desired.
, as desired.
Remark 2.7 We note that by the density of $C^{\infty }(\overline A;\mathbb {R}^{m})$![]() in $W^{1,p}_\lambda (A;\mathbb {R}^{m})$
in $W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() inequality (2.8) actually holds in the whole space $W^{1,p}_\lambda (A;\mathbb {R}^{m})$
inequality (2.8) actually holds in the whole space $W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() . That is, there exists a constant $C>0$
. That is, there exists a constant $C>0$![]() such that
such that
for every $u \in W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() .
.
Finally, in this paper, we will also consider the space
We recall that $W^{1,p}_{0,\lambda }(A;\mathbb {R}^{m})$![]() agrees with the closure of $C_0^{\infty }(A;\mathbb {R}^{m})$
agrees with the closure of $C_0^{\infty }(A;\mathbb {R}^{m})$![]() in $W^{1,p}_\lambda (A;\mathbb {R}^{m})$
in $W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() (see, e.g. [Reference Serra Cassano32, theorem 1.4] or [Reference De Arcangelis17, proposition 2.1]).
(see, e.g. [Reference Serra Cassano32, theorem 1.4] or [Reference De Arcangelis17, proposition 2.1]).
2.3 Maximal function and measure theory
In this subsection, we recall the definition of maximal function and some of its properties which are useful for our purposes. Moreover, for the readers’ convenience we also recall some classical result in measure theory which we are going to employ in the paper.
For the theory of maximal functions we refer to [Reference Stein33].
Let $u\in L^{1}_{\rm loc}(\mathbb {R}^{n})$![]() , then the Hardy maximal function of $u$
, then the Hardy maximal function of $u$![]() at $x$
at $x$![]() is defined as
is defined as
where $Q_r(x)$![]() is the cube centred at $x$
is the cube centred at $x$![]() , with side length $r$
, with side length $r$![]() and faces parallel to the coordinate planes. The following property will be useful for our purposes: there exists a constant $\tilde {c}=\tilde {c}(n)>0$
and faces parallel to the coordinate planes. The following property will be useful for our purposes: there exists a constant $\tilde {c}=\tilde {c}(n)>0$![]() depending only on $n$
depending only on $n$![]() such that
such that
for every $u\in L^{1}(\mathbb {R}^{n})$![]() and every $l>0$
and every $l>0$![]() .
.
The following result is proven in [Reference Muckenhoupt29, theorem 9].
Theorem 2.8 Let $p>1,$![]() $K\geq 1,$
$K\geq 1,$![]() and let $\lambda \in A_p(K)$
and let $\lambda \in A_p(K)$![]() . Then there exists a constant $c_4=c_4(K,\,p,\,n)>0$
. Then there exists a constant $c_4=c_4(K,\,p,\,n)>0$![]() such that
such that
for every $u\in L^{1}_{\rm loc}(\mathbb {R}^{n})$![]() .
.
We observe that theorem 2.8 in particular implies that if $u\in L^{p}_\lambda (\mathbb {R}^{n})$![]() then $Mu \in L^{p}_\lambda (\mathbb {R}^{n})$
then $Mu \in L^{p}_\lambda (\mathbb {R}^{n})$![]() .
.
For the following lemma we refer to [Reference Acerbi and Fusco1, lemma I.11].
Lemma 2.9 Let $u\in C_0^{\infty }(\mathbb {R}^{n})$![]() and let $l>0$
and let $l>0$![]() . Set
. Set
Then $u$![]() is Lipschitz continuous in $H^{l}$
is Lipschitz continuous in $H^{l}$![]() ; i.e. there exists a constant $c_5=c_5(n)>0$
; i.e. there exists a constant $c_5=c_5(n)>0$![]() such that
such that
for every $x,\,y\in H^{l}$![]() .
.
We recall the following result which can be found in [Reference Eisen20].
Lemma 2.10 Let $G\subset \mathbb {R}^{n}$![]() be measurable with $|G|<+\infty$
be measurable with $|G|<+\infty$![]() . Let $(E_h)$
. Let $(E_h)$![]() be a sequence of measurable subsets of $G$
be a sequence of measurable subsets of $G$![]() such that $|E_h|\geq \tau$
such that $|E_h|\geq \tau$![]() for every $h\in \mathbb {N}$
for every $h\in \mathbb {N}$![]() and for some $\tau >0$
and for some $\tau >0$![]() . Then there exists a subsequence $(E_{h_j}) \subset (E_h)$
. Then there exists a subsequence $(E_{h_j}) \subset (E_h)$![]() such that $\bigcap _{j\in \mathbb {N}}E_{h_j}\neq \emptyset$
such that $\bigcap _{j\in \mathbb {N}}E_{h_j}\neq \emptyset$![]() .
.
Eventually, we state the following technical lemma whose proof can be found in [Reference Acerbi and Fusco1, lemma I.7].
Lemma 2.11 Let $(\phi _h)$![]() be a bounded sequence in $L^{1}(\mathbb {R}^{n})$
be a bounded sequence in $L^{1}(\mathbb {R}^{n})$![]() . Then for every $\tau >0$
. Then for every $\tau >0$![]() there exist a measurable set $E_\tau$
there exist a measurable set $E_\tau$![]() with $|E_\tau |<\tau,$
with $|E_\tau |<\tau,$![]() $\delta _\tau >0,$
$\delta _\tau >0,$![]() and a sequence $(h_j^{\tau })$
and a sequence $(h_j^{\tau })$![]() such that for every $j\in \mathbb {N}$
such that for every $j\in \mathbb {N}$![]()
for every measurable set $B$![]() such that $B\cap E_\tau =\emptyset$
such that $B\cap E_\tau =\emptyset$![]() and $|B|<\delta _\tau$
and $|B|<\delta _\tau$![]() .
.
3. Setting of the problem and statement of the main result
In this section, we introduce the functionals we are going to study and state the main result of the paper.
Assumption 3.1 (Admissible weights)
Let $p>1,$![]() $K\geq 1,$
$K\geq 1,$![]() and let $A_p(K)$
and let $A_p(K)$![]() denote the Muckenhoupt class as in definition 2.1. A sequence of measurable weight functions $\lambda _k \colon \mathbb {R}^{n} \to [0,\,+\infty )$
denote the Muckenhoupt class as in definition 2.1. A sequence of measurable weight functions $\lambda _k \colon \mathbb {R}^{n} \to [0,\,+\infty )$![]() is admissible if:
is admissible if:
• $\lambda _k \in A_p(K),$
 for every $k\in \mathbb {N};$
for every $k\in \mathbb {N};$
• there exists a cube $Q_0 \subset \mathbb {R}^{n}$
 such that for every $k\in \mathbb {N}$
such that for every $k\in \mathbb {N}$ there holds
(3.1)\begin{equation} c_1\leq {- \hskip-1.05em \int}_{Q_0}\lambda_k\,{\rm d}x \leq c_2, \end{equation}for some constants $0< c_1\leq c_2<+\infty$
there holds
(3.1)\begin{equation} c_1\leq {- \hskip-1.05em \int}_{Q_0}\lambda_k\,{\rm d}x \leq c_2, \end{equation}for some constants $0< c_1\leq c_2<+\infty$
 .
.
Let $(\lambda _k)$![]() be a sequence of weights satisfying assumption 3.1; in this paper, we consider Borel integrands $f_k:\mathbb {R}^{n} \times \mathbb {R}^{m\times n}\to [0,\,+\infty )$
be a sequence of weights satisfying assumption 3.1; in this paper, we consider Borel integrands $f_k:\mathbb {R}^{n} \times \mathbb {R}^{m\times n}\to [0,\,+\infty )$![]() satisfying the two following conditions:
satisfying the two following conditions:
(1) (degenerate growth conditions) there exist two constants $0<\alpha \leq \beta <+\infty$
 such that for almost every $x\in \mathbb {R}^{n}$
such that for almost every $x\in \mathbb {R}^{n}$ (3.2)\begin{equation} \alpha\lambda_k(x)(|\xi|^{p}-1)\leq f_k(x,\xi)\leq\beta\lambda_k(x)(|\xi|^{p}+1), \end{equation}for every $\xi \in \mathbb {R}^{m\times n}$
(3.2)\begin{equation} \alpha\lambda_k(x)(|\xi|^{p}-1)\leq f_k(x,\xi)\leq\beta\lambda_k(x)(|\xi|^{p}+1), \end{equation}for every $\xi \in \mathbb {R}^{m\times n}$
 and every $k\in \mathbb {N}$
and every $k\in \mathbb {N}$ ;
;(2) (continuity in $\xi$
 ) there exists $L>0$
) there exists $L>0$ such that for almost every $x\in \mathbb {R}^{n}$
such that for almost every $x\in \mathbb {R}^{n}$ (3.3)\begin{equation} |f_k(x,\xi_1)-f_k(x,\xi_2)|\leq L\lambda_k(x)(|\xi_1|^{p-1}+|\xi_2|^{p-1}+1)|\xi_1-\xi_2|, \end{equation}for every $\xi _1,\,\xi _2\in \mathbb {R}^{m\times n}$
(3.3)\begin{equation} |f_k(x,\xi_1)-f_k(x,\xi_2)|\leq L\lambda_k(x)(|\xi_1|^{p-1}+|\xi_2|^{p-1}+1)|\xi_1-\xi_2|, \end{equation}for every $\xi _1,\,\xi _2\in \mathbb {R}^{m\times n}$
 , and every $k\in \mathbb {N}$
, and every $k\in \mathbb {N}$ .
.
Let $\mathcal {A}(Q_0)$![]() denote the collection of all open subsets of $Q_0$
denote the collection of all open subsets of $Q_0$![]() with Lipschitz boundary. We consider the sequence of localized integral functionals $F_k:W^{1,1}(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0)\longrightarrow [0,\,+\infty )$
with Lipschitz boundary. We consider the sequence of localized integral functionals $F_k:W^{1,1}(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0)\longrightarrow [0,\,+\infty )$![]() defined as
defined as

We endow $W^{1,1}(Q_0;\mathbb {R}^{m})$![]() with the strong $L^{1}(Q_0;\mathbb {R}^{m})$
with the strong $L^{1}(Q_0;\mathbb {R}^{m})$![]() -topology. If not otherwise specified, throughout the paper the $\Gamma$
-topology. If not otherwise specified, throughout the paper the $\Gamma$![]() -limits will all be computed with respect to this topology.
-limits will all be computed with respect to this topology.
The following theorem is the main result of this paper.
Theorem 3.2 Let $F_k$![]() be the functionals defined in (3.4). Then there exists a subsequence $(F_{k_h})$
be the functionals defined in (3.4). Then there exists a subsequence $(F_{k_h})$![]() such that for every $A\in \mathcal {A}(Q_0),$
such that for every $A\in \mathcal {A}(Q_0),$![]() $A\subset \subset Q_0,$
$A\subset \subset Q_0,$![]() the functionals $F_{k_h}(\cdot,\, A)$
the functionals $F_{k_h}(\cdot,\, A)$![]() $\Gamma$
$\Gamma$![]() -converge to the functional $F_\infty (\cdot,\, A)$
-converge to the functional $F_\infty (\cdot,\, A)$![]() with $F_{\infty }:W^{1,1}(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0)\longrightarrow [0,\,+\infty ]$
with $F_{\infty }:W^{1,1}(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0)\longrightarrow [0,\,+\infty ]$![]() given by
given by

where, for some $c_3=c_3(n)>0,$![]() $\lambda _\infty$
$\lambda _\infty$![]() belongs to $A_p(c_3^{p} K)$
belongs to $A_p(c_3^{p} K)$![]() and satisfies
and satisfies
The integrand $f_\infty \colon Q_0 \times \mathbb {R}^{m\times n} \to [0,\,+\infty )$![]() is a Borel function and for a.e. $x\in Q_0$
is a Borel function and for a.e. $x\in Q_0$![]() and every $\xi \in \mathbb {R}^{m\times n}$
and every $\xi \in \mathbb {R}^{m\times n}$![]() is given by the following asymptotic formula
is given by the following asymptotic formula
where, for every $A\in \mathcal {A}(Q_0),$![]()
with $u_\xi (x):=\xi x$![]() .
.
Moreover, $f_\infty$![]() satisfies the following properties for almost every $x\in Q_0$
satisfies the following properties for almost every $x\in Q_0$![]() :
:
(i) for every $\xi \in \mathbb {R}^{m\times n}$
 (3.6)\begin{equation} \alpha\lambda_\infty(x)\left(\frac{1}{K}|\xi|^{p}-1\right)\leq f_\infty(x,\xi)\leq\beta\lambda_\infty(x)(|\xi|^{p}+1); \end{equation}
(3.6)\begin{equation} \alpha\lambda_\infty(x)\left(\frac{1}{K}|\xi|^{p}-1\right)\leq f_\infty(x,\xi)\leq\beta\lambda_\infty(x)(|\xi|^{p}+1); \end{equation}
(ii) for every $\xi _1,\,\xi _2\in \mathbb {R}^{m\times n}$
 (3.7)\begin{equation} |f_\infty(x,\xi_1)-f_\infty(x,\xi_2)|\leq L'\lambda_\infty(x)(|\xi_1|^{p-1}+|\xi_2|^{p-1}+1)|\xi_1-\xi_2|, \end{equation}for some $L'>0$
(3.7)\begin{equation} |f_\infty(x,\xi_1)-f_\infty(x,\xi_2)|\leq L'\lambda_\infty(x)(|\xi_1|^{p-1}+|\xi_2|^{p-1}+1)|\xi_1-\xi_2|, \end{equation}for some $L'>0$
 .
.
Remark 3.3 We observe that if we replace (3.1) with the following stronger condition:
then theorem 3.2 holds true without the restriction $A\subset \subset Q_0$![]() . Specifically, if (3.8) holds, then if we define the functionals $F_k$
. Specifically, if (3.8) holds, then if we define the functionals $F_k$![]() on $W^{1,1}_{\rm loc}(\mathbb {R}^{n};\mathbb {R}^{m})\times \mathcal {A}_0$
on $W^{1,1}_{\rm loc}(\mathbb {R}^{n};\mathbb {R}^{m})\times \mathcal {A}_0$![]() , where $\mathcal {A}_0$
, where $\mathcal {A}_0$![]() is the collection of open, bounded, and Lipschitz subsets of $\mathbb {R}^{n}$
is the collection of open, bounded, and Lipschitz subsets of $\mathbb {R}^{n}$![]() , thanks to a diagonal argument, it can be shown that the functionals $F_{k_h}(\cdot,\,A)$
, thanks to a diagonal argument, it can be shown that the functionals $F_{k_h}(\cdot,\,A)$![]() $\Gamma$
$\Gamma$![]() -converge with respect to the $L^{1}_{\rm loc}(\mathbb {R}^{n};\mathbb {R}^{m})$
-converge with respect to the $L^{1}_{\rm loc}(\mathbb {R}^{n};\mathbb {R}^{m})$![]() -convergence to $F_{\infty }(\cdot,\,A)$
-convergence to $F_{\infty }(\cdot,\,A)$![]() , for every $A \in \mathcal {A}_0$
, for every $A \in \mathcal {A}_0$![]() ; moreover, $\lambda _\infty \in A_p(K)$
; moreover, $\lambda _\infty \in A_p(K)$![]() (cf. proposition 2.4) and $f_\infty$
(cf. proposition 2.4) and $f_\infty$![]() is defined through (3.5) for a.e. $x\in \mathbb {R}^{n}$
is defined through (3.5) for a.e. $x\in \mathbb {R}^{n}$![]() .
.
We note that (3.8) holds true in the case of admissible periodic or stationary weights (cf. § 8 and remark 8.11).
The proof of theorem 3.2 will be broken up in several intermediate results and it will be carried out in § 4–7. Namely, in § 4 we prove that (up to subsequences) the functionals $F_k$![]() $\Gamma$
$\Gamma$![]() -converge to the integral functional $F_{\infty }$
-converge to the integral functional $F_{\infty }$![]() on the space $W^{1,\infty }(Q_0;\mathbb {R}^{m})$
on the space $W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() . Moreover, in this section we also prove that the limit integrand $f_\infty$
. Moreover, in this section we also prove that the limit integrand $f_\infty$![]() satisfies the desired growth conditions as well as the continuity property. By means of an approximation argument, in § 5 we extend the $\Gamma$
satisfies the desired growth conditions as well as the continuity property. By means of an approximation argument, in § 5 we extend the $\Gamma$![]() -convergence result established in § 4 to the whole $W^{1,1}(Q_0;\mathbb {R}^{m})$
-convergence result established in § 4 to the whole $W^{1,1}(Q_0;\mathbb {R}^{m})$![]() , also showing that the domain of $F_\infty$
, also showing that the domain of $F_\infty$![]() coincides with the ‘limit’ weighted Sobolev space $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$
coincides with the ‘limit’ weighted Sobolev space $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() . Eventually, by combining the analysis in § 6 and § 7, we derive the asymptotic formula (3.5) for $f_\infty$
. Eventually, by combining the analysis in § 6 and § 7, we derive the asymptotic formula (3.5) for $f_\infty$![]() .
.
4. $\Gamma$ -convergence and integral representation in $W^{1,\infty }$
-convergence and integral representation in $W^{1,\infty }$
In this section, we show that on $W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() the sequence $(F_k)$
the sequence $(F_k)$![]() $\Gamma$
$\Gamma$![]() -converges (up to subsequences) to a limit functional which can be represented in an integral form.
-converges (up to subsequences) to a limit functional which can be represented in an integral form.
The following theorem is the main result of the present section.
Theorem 4.1 ($\Gamma$ -convergence in $W^{1,\infty }$
-convergence in $W^{1,\infty }$ )
)
Let $F_k$![]() be the functionals defined in ( 3.4). Then there exists a subsequence $(F_{k_h})$
be the functionals defined in ( 3.4). Then there exists a subsequence $(F_{k_h})$![]() such that for every $A\in \mathcal {A}(Q_0)$
such that for every $A\in \mathcal {A}(Q_0)$![]() the functionals $F_{k_h}(\cdot,\, A)$
the functionals $F_{k_h}(\cdot,\, A)$![]() $\Gamma$
$\Gamma$![]() -converge on $W^{1,\infty }(A;\mathbb {R}^{m})$
-converge on $W^{1,\infty }(A;\mathbb {R}^{m})$![]() to the functional $F(\cdot,\, A)$
to the functional $F(\cdot,\, A)$![]() with $F:W^{1,\infty }(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0)\longrightarrow [0,\,+\infty )$
with $F:W^{1,\infty }(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0)\longrightarrow [0,\,+\infty )$![]() given by
given by
for some Borel function $f_\infty :Q_0\times \mathbb {R}^{m\times n}\to [0,\,+\infty )$![]() . Moreover, the function $f_\infty$
. Moreover, the function $f_\infty$![]() satisfies the following properties for almost every $x\in Q_0:$
satisfies the following properties for almost every $x\in Q_0:$![]()
(i) for every $\xi \in \mathbb {R}^{m\times n}$
 (4.2)\begin{equation} \alpha\lambda_\infty(x)\left(\frac{1}{K}|\xi|^{p}-1\right)\leq f_\infty(x,\xi)\leq\beta\lambda_\infty(x)(|\xi|^{p}+1), \end{equation}where $\lambda _\infty \in A_p(c_3^{p} K),$
(4.2)\begin{equation} \alpha\lambda_\infty(x)\left(\frac{1}{K}|\xi|^{p}-1\right)\leq f_\infty(x,\xi)\leq\beta\lambda_\infty(x)(|\xi|^{p}+1), \end{equation}where $\lambda _\infty \in A_p(c_3^{p} K),$
 for some $c_3=c_3(n)>0$
for some $c_3=c_3(n)>0$ , and $\lambda _{k_h} \rightharpoonup \lambda _{\infty }$
, and $\lambda _{k_h} \rightharpoonup \lambda _{\infty }$ in $L^{1}(Q_0);$
in $L^{1}(Q_0);$
(ii) for every $\xi _1,\,\xi _2\in \mathbb {R}^{m\times n}$
 (4.3)\begin{equation} |f_\infty(x,\xi_1)-f_\infty(x,\xi_2)|\leq L'\lambda_\infty(x)(|\xi_1|^{p-1}+|\xi_2|^{p-1}+1)|\xi_1-\xi_2|, \end{equation}for some $L'>0$
(4.3)\begin{equation} |f_\infty(x,\xi_1)-f_\infty(x,\xi_2)|\leq L'\lambda_\infty(x)(|\xi_1|^{p-1}+|\xi_2|^{p-1}+1)|\xi_1-\xi_2|, \end{equation}for some $L'>0$
 .
.
The proof of theorem 4.1 will be achieved in a number of intermediate steps by means of the so-called localization method of $\Gamma$![]() -convergence (see, e.g.[Reference Braides and Defranceschi7, chapters 9–11] or [Reference Dal Maso14, chapters 16–19]).
-convergence (see, e.g.[Reference Braides and Defranceschi7, chapters 9–11] or [Reference Dal Maso14, chapters 16–19]).
To this end, we consider the localized $\Gamma$![]() -liminf and the $\Gamma$
-liminf and the $\Gamma$![]() -limsup of $F_k$
-limsup of $F_k$![]() ; i.e. we consider the functionals $F',\,F'' \colon W^{1,1}(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0) \longrightarrow [0,\,+\infty ]$
; i.e. we consider the functionals $F',\,F'' \colon W^{1,1}(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0) \longrightarrow [0,\,+\infty ]$![]() defined as
defined as
for $u\in W^{1,1}(Q_0;\mathbb {R}^{m})$![]() and $A\in \mathcal {A}(Q_0)$
and $A\in \mathcal {A}(Q_0)$![]() . Then, the aim of this section is to show that, up to subsequences, for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$
. Then, the aim of this section is to show that, up to subsequences, for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and $A\in \mathcal {A}(Q_0)$
and $A\in \mathcal {A}(Q_0)$![]() we have
we have
where $F$![]() is as in (4.1).
is as in (4.1).
Remark 4.2 We observe that $F'$![]() and $F''$
and $F''$![]() are lower semicontinuous with respect to the strong topology of $L^{1}(Q_0;\mathbb {R}^{m})$
are lower semicontinuous with respect to the strong topology of $L^{1}(Q_0;\mathbb {R}^{m})$![]() [Reference Dal Maso14, proposition 6.8]. They also inherit some of the properties of the functionals $F_k$
[Reference Dal Maso14, proposition 6.8]. They also inherit some of the properties of the functionals $F_k$![]() . Namely, as set functions they are both increasing [Reference Dal Maso14, proposition 6.7], moreover, $F'$
. Namely, as set functions they are both increasing [Reference Dal Maso14, proposition 6.7], moreover, $F'$![]() is superadditive on pairwise-disjoint sets [Reference Dal Maso14, proposition 16.12]; while as functionals they are both local [Reference Dal Maso14, proposition 16.15].
is superadditive on pairwise-disjoint sets [Reference Dal Maso14, proposition 16.12]; while as functionals they are both local [Reference Dal Maso14, proposition 16.15].
Thanks to assumption 3.1 we can invoke proposition 2.4 to deduce the existence of $\lambda _\infty \in A_p(c_3^{p} K)$![]() such that $\lambda _k \rightharpoonup \lambda _\infty$
such that $\lambda _k \rightharpoonup \lambda _\infty$![]() in $L^{1+\sigma }(Q_0)$
in $L^{1+\sigma }(Q_0)$![]() .
.
Then in the following lemma we show that the domain of $F''$![]() (and hence also the domain of $F'$
(and hence also the domain of $F'$![]() ) contains the space $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$
) contains the space $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() .
.
Lemma 4.3 Up to subsequences, there holds
for every $u\in W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() and $A\in \mathcal {A}(Q_0)$
and $A\in \mathcal {A}(Q_0)$![]() .
.
Proof. Let $(\lambda _{k_h})\subset (\lambda _{k})$![]() be the subsequence whose existence is established by proposition 2.4. Hence, in particular, $\lambda _{k_h} \rightharpoonup \lambda _\infty$
be the subsequence whose existence is established by proposition 2.4. Hence, in particular, $\lambda _{k_h} \rightharpoonup \lambda _\infty$![]() weakly in $L^{1}(Q_0)$
weakly in $L^{1}(Q_0)$![]() and $\lambda _\infty \in A_p(c_3^{p}K)$
and $\lambda _\infty \in A_p(c_3^{p}K)$![]() , for some $c_3=c_3(n)>0$
, for some $c_3=c_3(n)>0$![]() .
.
Let $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and let $A\in \mathcal {A}(Q_0)$
and let $A\in \mathcal {A}(Q_0)$![]() . Therefore, if $F''$
. Therefore, if $F''$![]() is as in (4.5) with $k$
is as in (4.5) with $k$![]() replaced by $k_h$
replaced by $k_h$![]() , by (3.2) we readily get
, by (3.2) we readily get

hence (4.6) is proven for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() .
.
Now let $u \in W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() ; then there exists $(u_j)\subset C^{\infty }(\overline Q_0;\mathbb {R}^{m}) \subset W^{1,\infty }(Q_0;\mathbb {R}^{m})$
; then there exists $(u_j)\subset C^{\infty }(\overline Q_0;\mathbb {R}^{m}) \subset W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() such that $u_j \to u$
such that $u_j \to u$![]() in $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$
in $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() . Hence, thanks to (4.7), to the fact that $u_j \to u$
. Hence, thanks to (4.7), to the fact that $u_j \to u$![]() in $L^{1}(Q_0;\mathbb {R}^{m})$
in $L^{1}(Q_0;\mathbb {R}^{m})$![]() , and to the lower semicontinuity of $F''$
, and to the lower semicontinuity of $F''$![]() with respect to the strong $L^{1}(Q_0;\mathbb {R}^{m})$
with respect to the strong $L^{1}(Q_0;\mathbb {R}^{m})$![]() -convergence, we obtain
-convergence, we obtain

and thus the claim.
The following lemma shows that $F_k$![]() (almost) decreases by smooth truncations.
(almost) decreases by smooth truncations.
Lemma 4.4 Let $F_k$![]() be the functionals defined in (3.4). Let $A\in \mathcal {A}(Q_0)$
be the functionals defined in (3.4). Let $A\in \mathcal {A}(Q_0)$![]() and let $(u_k) \subset W^{1,1}(Q_0;\mathbb {R}^{m})$
and let $(u_k) \subset W^{1,1}(Q_0;\mathbb {R}^{m})$![]() be such that
be such that
Then for every $\eta >0$![]() , $M>0$
, $M>0$![]() and for every $k\in \mathbb {N}$
and for every $k\in \mathbb {N}$![]() there exists a Lipschitz function $\varphi _k:\mathbb {R}^{m}\to \mathbb {R}^{m}$
there exists a Lipschitz function $\varphi _k:\mathbb {R}^{m}\to \mathbb {R}^{m}$![]() with Lipschitz constant less than or equal to $1$
with Lipschitz constant less than or equal to $1$![]() satisfying
satisfying

for suitable constants $a_k,\,b_k>0$![]() with $M \leq a_k< b_k,$
with $M \leq a_k< b_k,$![]() such that
such that
for every $k\in \mathbb {N}$![]() . Moreover, the function $\varphi _k$
. Moreover, the function $\varphi _k$![]() can be chosen in a finite family independent of $k$
can be chosen in a finite family independent of $k$![]() .
.
Proof. The proof of this lemma is classical and follows the line of, e.g. [Reference Braides, Defranceschi and Vitali8, lemma 3.5] with minor modifications. However, since we work in a different functional setting, we repeat the proof here for the readers’ convenience.
Let $\eta >0$![]() and $M>0$
and $M>0$![]() be fixed. Let $(a_j)$
be fixed. Let $(a_j)$![]() be a strictly increasing sequence of positive real numbers such that for every $j\in \mathbb {N}$
be a strictly increasing sequence of positive real numbers such that for every $j\in \mathbb {N}$![]() there exists a Lipschitz function $\varphi _j:\mathbb {R}^{m}\to \mathbb {R}^{m}$
there exists a Lipschitz function $\varphi _j:\mathbb {R}^{m}\to \mathbb {R}^{m}$![]() with Lipschitz constant less than or equal to $1$
with Lipschitz constant less than or equal to $1$![]() satisfying
satisfying

For every $k\in \mathbb {N}$![]() and every $j\in \mathbb {N}$
and every $j\in \mathbb {N}$![]() set $w_k^{j}:=\varphi _j(u_k)$
set $w_k^{j}:=\varphi _j(u_k)$![]() . We have
. We have

where to establish the last inequality we have used the nonnegativity of $f_k$![]() , (3.2), and the fact that $\varphi _j$
, (3.2), and the fact that $\varphi _j$![]() has Lipschitz constant less than or equal to $1$
has Lipschitz constant less than or equal to $1$![]() .
.
Let $N\in \mathbb {N}$![]() be arbitrary; we now want to estimate $1/N\sum _{j=1}^{N} F_k(w_k^{j},\,A)$
be arbitrary; we now want to estimate $1/N\sum _{j=1}^{N} F_k(w_k^{j},\,A)$![]() , for every $k\in \mathbb {N}$
, for every $k\in \mathbb {N}$![]() . To this end we start noticing that $(\{a_j<|u_k|\leq a_{j+1}\})_{j\in \mathbb {N}}$
. To this end we start noticing that $(\{a_j<|u_k|\leq a_{j+1}\})_{j\in \mathbb {N}}$![]() is a family of pairwise-disjoint sets. Therefore, we get
is a family of pairwise-disjoint sets. Therefore, we get

In view of (3.1) and (4.8) we can find a constant $C>0$![]() such that
such that
for every $k\in \mathbb {N}$![]() . Moreover, thanks to proposition 2.5 there exist $c,\,\sigma >0$
. Moreover, thanks to proposition 2.5 there exist $c,\,\sigma >0$![]() such that
such that
for every $k\in \mathbb {N}$![]() and every $j\in {1,\,\ldots,\, N}$
and every $j\in {1,\,\ldots,\, N}$![]() .
.
Therefore, we define the sequence $(a_j)$![]() recursively by imposing the following condition on $a_1$
recursively by imposing the following condition on $a_1$![]() :
:
which is clearly possible thanks to the boundedness of $(u_k)$![]() in $L^{1}(A;\mathbb {R}^{m})$
in $L^{1}(A;\mathbb {R}^{m})$![]() . Eventually, by choosing $N\in \mathbb {N}$
. Eventually, by choosing $N\in \mathbb {N}$![]() in a way such that $C/N\leq \eta /2$
in a way such that $C/N\leq \eta /2$![]() , gathering (4.9)–(4.12) we obtain
, gathering (4.9)–(4.12) we obtain

Therefore, for every $k\in \mathbb {N}$![]() we can find $j(k)\in \{1,\,\ldots,\,N\}$
we can find $j(k)\in \{1,\,\ldots,\,N\}$![]() such that
such that
hence the proof is accomplished by setting $\varphi _k:=\varphi _{j(k)}$![]() . Finally, we note that $N$
. Finally, we note that $N$![]() is independent of $k$
is independent of $k$![]() .
.
We now use lemma 4.4 to show that if $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() then for every $A \in \mathcal {A}(Q_0)$
then for every $A \in \mathcal {A}(Q_0)$![]() the value of the $\Gamma$
the value of the $\Gamma$![]() -limsup $F''(u,\,A)$
-limsup $F''(u,\,A)$![]() can be recovered along a sequence $(w_k)$
can be recovered along a sequence $(w_k)$![]() which is bounded in $L^{\infty }(Q_0;\mathbb {R}^{m})$
which is bounded in $L^{\infty }(Q_0;\mathbb {R}^{m})$![]() and such that $u_k \to u$
and such that $u_k \to u$![]() in $L^{q}(Q_0;\mathbb {R}^{m})$
in $L^{q}(Q_0;\mathbb {R}^{m})$![]() , for every $1\leq q<+\infty$
, for every $1\leq q<+\infty$![]() .
.
Proposition 4.5 Let $F_k$![]() be the functionals defined in (3.4) and let $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$
be the functionals defined in (3.4) and let $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() . Then there exists a sequence $(w_k)\subset W^{1,1}(Q_0;\mathbb {R}^{m})$
. Then there exists a sequence $(w_k)\subset W^{1,1}(Q_0;\mathbb {R}^{m})$![]() satisfying the following properties:
satisfying the following properties:
(i) $\sup _{k}\|u_k\|_{L^{\infty }(Q_0;\mathbb {R}^{m})}<+\infty ;$

(ii) $w_k\to u$
 in $L^{q}(Q_0;\mathbb {R}^{m})$
in $L^{q}(Q_0;\mathbb {R}^{m})$ for every $1\leq q<+\infty ;$
for every $1\leq q<+\infty ;$
(iii) $\limsup _{k\to \infty }F_k(w_k,\,A)= F''(u,\,A),$
 for every $A\in \mathcal {A}(Q_0)$
for every $A\in \mathcal {A}(Q_0)$ .
.
Proof. Let $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() ; by [Reference Dal Maso14, proposition 8.1] there exists $(u_k)\subset W^{1,1}(Q_0;\mathbb {R}^{m})$
; by [Reference Dal Maso14, proposition 8.1] there exists $(u_k)\subset W^{1,1}(Q_0;\mathbb {R}^{m})$![]() such that $u_k\to u$
such that $u_k\to u$![]() in $L^{1}(Q_0;\mathbb {R}^{m})$
in $L^{1}(Q_0;\mathbb {R}^{m})$![]() and
and
where the last inequality follows by lemma 4.3.
Let $\eta >0$![]() be fixed: by applying lemma 4.4 to the sequence $(u_k)$
be fixed: by applying lemma 4.4 to the sequence $(u_k)$![]() with $M:=\|u\|_{L^{\infty }(Q_0;\mathbb {R}^{m})}$
with $M:=\|u\|_{L^{\infty }(Q_0;\mathbb {R}^{m})}$![]() we obtain a sequence $(w_k)\subset W^{1,1}(Q_0;\mathbb {R}^{m}) \cap L^{\infty } (Q_0;\mathbb {R}^{m})$
we obtain a sequence $(w_k)\subset W^{1,1}(Q_0;\mathbb {R}^{m}) \cap L^{\infty } (Q_0;\mathbb {R}^{m})$![]() which is bounded in $L^{\infty }(Q_0;\mathbb {R}^{m})$
which is bounded in $L^{\infty }(Q_0;\mathbb {R}^{m})$![]() , such that $w_k\to u$
, such that $w_k\to u$![]() in $L^{q}(Q_0;\mathbb {R}^{m})$
in $L^{q}(Q_0;\mathbb {R}^{m})$![]() for every $1\leq q<+\infty$
for every $1\leq q<+\infty$![]() and
and
for every $A \in \mathcal {A}(Q_0)$![]() . Then, taking the $\limsup$
. Then, taking the $\limsup$![]() as $k\to \infty$
as $k\to \infty$![]() in (4.14) and appealing to (4.13) we obtain
in (4.14) and appealing to (4.13) we obtain
Eventually, the claim follows by the definition of $F''$![]() and the arbitrariness of $\eta$
and the arbitrariness of $\eta$![]() .
.
The following proposition shows that the functionals $F_k$![]() satisfy the fundamental estimate, uniformly in $k$
satisfy the fundamental estimate, uniformly in $k$![]() .
.
Proposition 4.6 (Fundamental estimate)
Let $F_k$![]() be the functionals defined in (3.4) and let $A\in \mathcal {A}(Q_0)$
be the functionals defined in (3.4) and let $A\in \mathcal {A}(Q_0)$![]() . For every $\eta >0$
. For every $\eta >0$![]() and for every $A',\,A'',\,B\in \mathcal {A}(Q_0)$
and for every $A',\,A'',\,B\in \mathcal {A}(Q_0)$![]() with $A'\subset \subset A''\subset \subset A$
with $A'\subset \subset A''\subset \subset A$![]() there exists a constant $M_\eta >0$
there exists a constant $M_\eta >0$![]() with the following property: for every $k\in \mathbb {N}$
with the following property: for every $k\in \mathbb {N}$![]() and for every $u,\,\tilde {u}\in W^{1,p}_{\lambda _k}(A;\mathbb {R}^{m})$
and for every $u,\,\tilde {u}\in W^{1,p}_{\lambda _k}(A;\mathbb {R}^{m})$![]() there exists a function $\varphi \in C_0^{\infty }(A'')$
there exists a function $\varphi \in C_0^{\infty }(A'')$![]() with $\varphi =1$
with $\varphi =1$![]() in a neighbourhood of $\overline {A'}$
in a neighbourhood of $\overline {A'}$![]() and $0\leq \varphi \leq 1$
and $0\leq \varphi \leq 1$![]() such that
such that

where $S:=B\cap (A''\setminus A')$![]() .
.
Proof. Let $\eta >0$![]() , $A$
, $A$![]() , $A'$
, $A'$![]() , $A''$
, $A''$![]() , $B$
, $B$![]() and $S$
and $S$![]() be as in the statement. We start observing that by (3.1) there exists a constant $C>0$
be as in the statement. We start observing that by (3.1) there exists a constant $C>0$![]() such that
such that
for every $k\in \mathbb {N}$![]() . Let $N\in \mathbb {N}$
. Let $N\in \mathbb {N}$![]() be such that
be such that
Let $A_1,\,\ldots,\,A_{N+1}$![]() be $N+1$
be $N+1$![]() open sets satisfying $A'\subset \subset A_1\subset \subset \cdots \subset \subset A_{N+1}\subset \subset A''$
open sets satisfying $A'\subset \subset A_1\subset \subset \cdots \subset \subset A_{N+1}\subset \subset A''$![]() , and for $i=1,\,\ldots,\,N$
, and for $i=1,\,\ldots,\,N$![]() consider the function $\varphi _i\in C_0^{\infty }(A)$
consider the function $\varphi _i\in C_0^{\infty }(A)$![]() such that $\mathop{}\!\mathrm{supp} \,\varphi _i\subset A_{i+1}$
such that $\mathop{}\!\mathrm{supp} \,\varphi _i\subset A_{i+1}$![]() and $\varphi _i=1$
and $\varphi _i=1$![]() on a neighbourhood of $\overline {A_i}$
on a neighbourhood of $\overline {A_i}$![]() . Finally, define
. Finally, define
For every $k\in \mathbb {N}$![]() and for $i=1,\,\ldots,\,N$
and for $i=1,\,\ldots,\,N$![]() we have
we have

where $F^{*}_k$![]() denotes the extension of $F_k$
denotes the extension of $F_k$![]() to the Borel subsets of $Q_0$
to the Borel subsets of $Q_0$![]() .
.
Denote by $I_{k,i}$![]() the last term in (4.17). For every $k\in \mathbb {N}$
the last term in (4.17). For every $k\in \mathbb {N}$![]() and for $i=1,\,\ldots,\,N$
and for $i=1,\,\ldots,\,N$![]() , using (3.2) we obtain
, using (3.2) we obtain

where $S_i:=B\cap (A_{i+1}\setminus \overline {A_i})$![]() . Therefore, by the growth condition from below (3.2) on $f_k$
. Therefore, by the growth condition from below (3.2) on $f_k$![]() we get
we get
for every $k\in \mathbb {N}$![]() and for $i=1,\,\ldots,\,N$
and for $i=1,\,\ldots,\,N$![]() . Hence, there exists $i_0\in \{1,\,\ldots,\,N\}$
. Hence, there exists $i_0\in \{1,\,\ldots,\,N\}$![]() such that
such that

for every $k\in \mathbb {N}$![]() ; thus by (4.15) we get
; thus by (4.15) we get
Eventually, in view of (4.16) and (4.17) the proof is accomplished choosing $\varphi :=\varphi _{i_0}$![]() .
.
With the help of propositions 4.5 and 4.6 we can deduce the following result which will eventually lead to the inner regularity and subadditivity of the set function $F''(u,\,\cdot )$![]() , for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$
, for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() .
.
Lemma 4.7 Let $F''$![]() be as in (4.5). Let $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$
be as in (4.5). Let $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and let $A',\,A'',\,B\in \mathcal {A}(Q_0)$
and let $A',\,A'',\,B\in \mathcal {A}(Q_0)$![]() be such that $A'\subset \subset A''\subset \subset A;$
be such that $A'\subset \subset A''\subset \subset A;$![]() then
then
Proof. Let $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() ; by proposition 4.5 there exist $(u_k)\subset W^{1,p}_{\lambda _k}(A'';\mathbb {R}^{m})$
; by proposition 4.5 there exist $(u_k)\subset W^{1,p}_{\lambda _k}(A'';\mathbb {R}^{m})$![]() and $(\tilde {u}_k) \subset W^{1,p}_{\lambda _k}(B;\mathbb {R}^{m})$
and $(\tilde {u}_k) \subset W^{1,p}_{\lambda _k}(B;\mathbb {R}^{m})$![]() which are bounded in $L^{\infty }(Q_0;\mathbb {R}^{m})$
which are bounded in $L^{\infty }(Q_0;\mathbb {R}^{m})$![]() , converge to $u$
, converge to $u$![]() in $L^{q}(Q_0;\mathbb {R}^{m})$
in $L^{q}(Q_0;\mathbb {R}^{m})$![]() for every $q\geq 1$
for every $q\geq 1$![]() , and satisfy
, and satisfy
Let $\eta >0$![]() be fixed; then, in view of proposition 4.6 we can find a constant $M_\eta >0$
be fixed; then, in view of proposition 4.6 we can find a constant $M_\eta >0$![]() and a sequence $(\varphi _k)$
and a sequence $(\varphi _k)$![]() of cut-off functions between $A'$
of cut-off functions between $A'$![]() and $A''$
and $A''$![]() such that
such that

where $S=B\cap (A''\setminus A')$![]() . Since the sequence $\varphi _k u_k+(1-\varphi _k)\tilde {u}_k$
. Since the sequence $\varphi _k u_k+(1-\varphi _k)\tilde {u}_k$![]() converges to $u$
converges to $u$![]() in $L^{1}(Q_0;\mathbb {R}^{m})$
in $L^{1}(Q_0;\mathbb {R}^{m})$![]() , by (4.19) we obtain
, by (4.19) we obtain

Now let $\sigma >0$![]() be the exponent as in theorem 2.2, using the Hölder inequality and recalling (3.1) we get
be the exponent as in theorem 2.2, using the Hölder inequality and recalling (3.1) we get

Therefore, since $\|u_k-\tilde u_k\|_{L^{q}(Q_0;\mathbb {R}^{m})}\to 0$![]() for every $q\geq 1$
for every $q\geq 1$![]() , we immediately obtain
, we immediately obtain
Hence, (4.18) follows by the arbitrariness of $\eta >0$![]() .
.
The proof of the following proposition is classical, for this reason we only sketch it here, while we refer the reader to the monographs [Reference Braides and Defranceschi7, Reference Dal Maso14] for further details.
Proposition 4.8 ($\Gamma$ -convergence and measure property of the $\Gamma$
-convergence and measure property of the $\Gamma$ -limit)
-limit)
Let $F_k$![]() be the functionals defined in ( 3.4). Then there exist a subsequence $(k_h)$
be the functionals defined in ( 3.4). Then there exist a subsequence $(k_h)$![]() and a functional $F\colon W^{1,\infty }(Q_0;\mathbb {R}^{m}) \times \mathcal {A}(Q_0) \longrightarrow [0,\,+\infty )$
and a functional $F\colon W^{1,\infty }(Q_0;\mathbb {R}^{m}) \times \mathcal {A}(Q_0) \longrightarrow [0,\,+\infty )$![]() such that for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$
such that for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and every $A\in \mathcal {A}(Q_0)$
and every $A\in \mathcal {A}(Q_0)$![]()
where $F'$![]() and $F''$
and $F''$![]() are as in (4.4) and (4.5), respectively, with $k$
are as in (4.4) and (4.5), respectively, with $k$![]() replaced by $k_h$
replaced by $k_h$![]() .
.
Moreover, for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() the set function $F(u,\,\cdot )$
the set function $F(u,\,\cdot )$![]() is the restriction to $\mathcal {A}(Q_0)$
is the restriction to $\mathcal {A}(Q_0)$![]() of a Radon measure on $Q_0$
of a Radon measure on $Q_0$![]() .
.
Proof. Let $(k_h)$![]() be the subsequence whose existence is established by proposition 2.4. Thanks to the compactness of $\Gamma$
be the subsequence whose existence is established by proposition 2.4. Thanks to the compactness of $\Gamma$![]() -convergence [Reference Dal Maso14, theorem 8.5], a standard diagonal argument gives the existence of a further subsequence (not relabelled), such that the corresponding functionals $F'$
-convergence [Reference Dal Maso14, theorem 8.5], a standard diagonal argument gives the existence of a further subsequence (not relabelled), such that the corresponding functionals $F'$![]() and $F''$
and $F''$![]() satisfy
satisfy
for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and for every $A\in \mathcal {A}(Q_0)$
and for every $A\in \mathcal {A}(Q_0)$![]() . We note that the set function $F(u,\,\cdot )$
. We note that the set function $F(u,\,\cdot )$![]() is inner regular by definition.
is inner regular by definition.
Moreover, by virtue of lemma 4.7 we can reason as in [Reference Dal Maso14, proposition 18.4] to deduce that $F(u,\,\cdot )$![]() is subadditive.
is subadditive.
We now prove that (4.20), which will ensure that $F$![]() is the $\Gamma$
is the $\Gamma$![]() -limit of $F_k$
-limit of $F_k$![]() on $W^{1,\infty }(Q_0;\mathbb {R}^{m})$
on $W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() .
.
Since by definition of $F$![]() we have $F\leq F'\leq F''$
we have $F\leq F'\leq F''$![]() , to get (4.20) it suffices to show that
, to get (4.20) it suffices to show that
for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and $A \in \mathcal {A}(Q_0)$
and $A \in \mathcal {A}(Q_0)$![]() .
.
To prove (4.21) we consider the localized functional $H:W^{1,\infty }(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0)\longrightarrow [0,\,+\infty )$![]() defined as
defined as
Therefore, by lemma 4.3 we immediately obtain that $F''(u,\,A)\leq H(u,\,A)$![]() , for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$
, for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and $A \in \mathcal {A}(Q_0)$
and $A \in \mathcal {A}(Q_0)$![]() . For every fixed $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$
. For every fixed $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() the set function $H(u,\,\cdot )$
the set function $H(u,\,\cdot )$![]() defines a Radon measure on $Q_0$
defines a Radon measure on $Q_0$![]() , hence for every $\eta >0$
, hence for every $\eta >0$![]() fixed there exists a compact set $K_\eta \subset A$
fixed there exists a compact set $K_\eta \subset A$![]() such that $H(u,\,A\setminus K_\eta )<\eta$
such that $H(u,\,A\setminus K_\eta )<\eta$![]() . Let now $A',\,A''\in \mathcal {A}(Q_0)$
. Let now $A',\,A''\in \mathcal {A}(Q_0)$![]() be such that $K_\eta \subset A'\subset \subset A''\subset \subset A$
be such that $K_\eta \subset A'\subset \subset A''\subset \subset A$![]() and let $B=A\setminus K_\eta$
and let $B=A\setminus K_\eta$![]() . By (4.18) we have
. By (4.18) we have
Then by definition of $F$![]() we readily obtain
we readily obtain
thus (4.21) follows by the arbitrariness of $\eta >0$![]() .
.
Finally, the inner regularity and subadditivity of $F(u,\,\cdot )$![]() together with remark 4.2 allow us to apply the De Giorgi–Letta measure criterion (see, e.g.[Reference Dal Maso14, theorem 14.23]) to deduce that $F(u,\,\cdot )$
together with remark 4.2 allow us to apply the De Giorgi–Letta measure criterion (see, e.g.[Reference Dal Maso14, theorem 14.23]) to deduce that $F(u,\,\cdot )$![]() is the restriction to $\mathcal {A}(Q_0)$
is the restriction to $\mathcal {A}(Q_0)$![]() of a Radon measure on $Q_0$
of a Radon measure on $Q_0$![]() , and thus to conclude.
, and thus to conclude.
Remark 4.9 We observe that for every $A\in \mathcal {A}(Q_0)$![]() the functional $F(\cdot,\,A)$
the functional $F(\cdot,\,A)$![]() is invariant under translations in $u$
is invariant under translations in $u$![]() . Indeed, for given $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$
. Indeed, for given $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and $A\in \mathcal {A}(Q_0)$
and $A\in \mathcal {A}(Q_0)$![]() let $(u_k)\subset W^{1,1}(Q_0;\mathbb {R}^{m})$
let $(u_k)\subset W^{1,1}(Q_0;\mathbb {R}^{m})$![]() be such that $u_k\to u$
be such that $u_k\to u$![]() in $L^{1}(Q_0;\mathbb {R}^{m})$
in $L^{1}(Q_0;\mathbb {R}^{m})$![]() and $\lim _{k\to \infty }F_k(u_k,\,A)=F(u,\,A)$
and $\lim _{k\to \infty }F_k(u_k,\,A)=F(u,\,A)$![]() . Let now $s\in \mathbb {R}^{m}$
. Let now $s\in \mathbb {R}^{m}$![]() , then clearly $(u_k+s)$
, then clearly $(u_k+s)$![]() converges to $u+s$
converges to $u+s$![]() in $L^{1}(Q_0;\mathbb {R}^{m})$
in $L^{1}(Q_0;\mathbb {R}^{m})$![]() and by (4.20)
and by (4.20)
since $F_k$![]() is invariant under translations in $u$
is invariant under translations in $u$![]() . On the other hand, the argument above also gives
. On the other hand, the argument above also gives
and thus the claim.
Theorem 4.10 (Integral representation)
Let $F_k$![]() be the functionals defined in (3.4). Then there exist a subsequence $(F_{k_h})$
be the functionals defined in (3.4). Then there exist a subsequence $(F_{k_h})$![]() and a Borel function $f_\infty :Q_0\times \mathbb {R}^{m\times n}\to [0,\,+\infty ),$
and a Borel function $f_\infty :Q_0\times \mathbb {R}^{m\times n}\to [0,\,+\infty ),$![]() satisfying (4.2) and (4.3), such that for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$
satisfying (4.2) and (4.3), such that for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and every $A\in \mathcal {A}(Q_0)$
and every $A\in \mathcal {A}(Q_0)$![]() there holds
there holds
where $F:W^{1,\infty }(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0)\longrightarrow [0,\,+\infty )$![]() is given by
is given by
Proof. Proposition 4.8 ensures the existence of a subsequence $(F_{k_h})$![]() of $(F_k)$
of $(F_k)$![]() such that $F_{k_h}(u,\,A)$
such that $F_{k_h}(u,\,A)$![]() $\Gamma$
$\Gamma$![]() -converges to a functional $F(u,\,A)$
-converges to a functional $F(u,\,A)$![]() for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$
for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and every $A\in \mathcal {A}(Q_0)$
and every $A\in \mathcal {A}(Q_0)$![]() . Then, it remains to prove that the functional $F$
. Then, it remains to prove that the functional $F$![]() admits an integral representation as in (4.22).
admits an integral representation as in (4.22).
We will break up the proof of the integral representation into a number of steps.
Step 1. Definition of $f_\infty$![]() . Let $\xi \in \mathbb {R}^{m\times n}$
. Let $\xi \in \mathbb {R}^{m\times n}$![]() be fixed and set $u_\xi (x):=\xi x$
be fixed and set $u_\xi (x):=\xi x$![]() . By the measure property of $F$
. By the measure property of $F$![]() established in proposition 4.8, the set function $F(u_\xi,\,\cdot )$
established in proposition 4.8, the set function $F(u_\xi,\,\cdot )$![]() can be extended to a Radon measure on $Q_0$
can be extended to a Radon measure on $Q_0$![]() . Moreover, thanks to lemma 4.3, $F(u_\xi,\,\cdot )$
. Moreover, thanks to lemma 4.3, $F(u_\xi,\,\cdot )$![]() is absolutely continuous with respect to the Lebesgue measure. For every $x\in Q_0$
is absolutely continuous with respect to the Lebesgue measure. For every $x\in Q_0$![]() define
define
where $Q_\rho (x)$![]() is the cube centred at $x$
is the cube centred at $x$![]() , with side length $\rho >0$
, with side length $\rho >0$![]() , and faces parallel to the coordinate planes. Then, $f_\infty$
, and faces parallel to the coordinate planes. Then, $f_\infty$![]() is a Borel function and the Lebesgue differentiation theorem guarantees that
is a Borel function and the Lebesgue differentiation theorem guarantees that
for every $A\in \mathcal {A}(Q_0)$![]() .
.
We now show that $f_\infty$![]() satisfies the growth and coercivity conditions as in (4.2). To this end, we start observing that the growth condition from above readily follows from lemma 4.3. In fact, choosing in (4.6) $u=u_\xi$
satisfies the growth and coercivity conditions as in (4.2). To this end, we start observing that the growth condition from above readily follows from lemma 4.3. In fact, choosing in (4.6) $u=u_\xi$![]() , $A=Q_\rho (x)$
, $A=Q_\rho (x)$![]() , with $x$
, with $x$![]() Lebesgue point for $\lambda _\infty$
Lebesgue point for $\lambda _\infty$![]() , the estimate from above in (4.2) follows by dividing both sides of (4.6) by $|Q_\rho (x)|$
, the estimate from above in (4.2) follows by dividing both sides of (4.6) by $|Q_\rho (x)|$![]() , and eventually passing to the limit as $\rho \to 0^{+}$
, and eventually passing to the limit as $\rho \to 0^{+}$![]() .
.
To derive the growth condition from below on $f_\infty$![]() let $u\in W^{1,1}(Q_0;\mathbb {R}^{m})$
let $u\in W^{1,1}(Q_0;\mathbb {R}^{m})$![]() and $A\in \mathcal {A}(Q_0)$
and $A\in \mathcal {A}(Q_0)$![]() be fixed. By the Hölder inequality and by the growth condition from below in (3.2) we get
be fixed. By the Hölder inequality and by the growth condition from below in (3.2) we get

therefore the following lower bound
for every $k\in \mathbb {N}$![]() . Now let $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$
. Now let $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and let $(u_h)\subset W^{1,1}(Q_0;\mathbb {R}^{m})$
and let $(u_h)\subset W^{1,1}(Q_0;\mathbb {R}^{m})$![]() be such that
be such that
Hence, by the lower semicontinuity of $u\mapsto \int _A|\nabla u|\,{\rm d}x$![]() with respect to the $L^{1}(Q_0;\mathbb {R}^{m})$
with respect to the $L^{1}(Q_0;\mathbb {R}^{m})$![]() -topology and by proposition 2.4, evaluating (4.23) in $(u_h)$
-topology and by proposition 2.4, evaluating (4.23) in $(u_h)$![]() and passing to the limit as $h\to \infty$
and passing to the limit as $h\to \infty$![]() we find
we find
for every $u\in W^{1,\infty }(A;\mathbb {R}^{m})$![]() and every $A\in \mathcal {A}(Q_0)$
and every $A\in \mathcal {A}(Q_0)$![]() . Now let $x\in Q_0$
. Now let $x\in Q_0$![]() be a Lebesgue point for $\lambda _\infty$
be a Lebesgue point for $\lambda _\infty$![]() and $\tilde \lambda _\infty$
and $\tilde \lambda _\infty$![]() and choose in (4.24) $u=u_\xi$
and choose in (4.24) $u=u_\xi$![]() and $A=Q_\rho (x)$
and $A=Q_\rho (x)$![]() ; then, dividing both sides of (4.24) by $|Q_\rho (x)|$
; then, dividing both sides of (4.24) by $|Q_\rho (x)|$![]() and passing to the limit as $\rho \to 0^{+}$
and passing to the limit as $\rho \to 0^{+}$![]() give
give
for a.e. $x\in Q_0$![]() and every $\xi \in \mathbb {R}^{m\times n}$
and every $\xi \in \mathbb {R}^{m\times n}$![]() . Eventually, (2.6) entails the desired bound from below.
. Eventually, (2.6) entails the desired bound from below.
Step 2. Integral representation on piecewise affine functions. Let $A\in \mathcal {A}(Q_0)$![]() and $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$
and $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() be piecewise affine on $A$
be piecewise affine on $A$![]() ; i.e. there exists a finite family of pairwise disjoint open sets $A_j$
; i.e. there exists a finite family of pairwise disjoint open sets $A_j$![]() such that $|A\setminus \bigcup _{j=1}^{N}A_j|=0$
such that $|A\setminus \bigcup _{j=1}^{N}A_j|=0$![]() and
and

for every $x\in A$![]() with $\xi ^{j}\in \mathbb {R}^{m\times n}$
with $\xi ^{j}\in \mathbb {R}^{m\times n}$![]() , $z_j\in \mathbb {R}^{m}$
, $z_j\in \mathbb {R}^{m}$![]() for $j=1,\,\ldots,\,N$
for $j=1,\,\ldots,\,N$![]() . By remark 4.9 and step 1, taking into account the locality of $F$
. By remark 4.9 and step 1, taking into account the locality of $F$![]() , we have
, we have

that is, the integral representation (4.22) on piecewise affine functions.
Step 3. Convexity properties of $f_\infty$![]() . For every $A\in \mathcal {A}(Q_0)$
. For every $A\in \mathcal {A}(Q_0)$![]() the functional $F(\cdot,\,A)$
the functional $F(\cdot,\,A)$![]() is lower semicontinuous on $W^{1,\infty }(Q_0;\mathbb {R}^{m})$
is lower semicontinuous on $W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() with respect to the strong convergence of $L^{1}(Q_0;\mathbb {R}^{m})$
with respect to the strong convergence of $L^{1}(Q_0;\mathbb {R}^{m})$![]() , thus, in particular, it is lower semicontinuous with respect to the weak$^{*}$
, thus, in particular, it is lower semicontinuous with respect to the weak$^{*}$![]() $W^{1,\infty }(Q_0;\mathbb {R}^{m})$
$W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() -convergence. Therefore, the function $\xi \to f_\infty (x,\,\xi )$
-convergence. Therefore, the function $\xi \to f_\infty (x,\,\xi )$![]() is $W^{1,\infty }$
is $W^{1,\infty }$![]() -quasiconvex (and rank-$1$
-quasiconvex (and rank-$1$![]() -convex) for a.e. $x\in Q_0$
-convex) for a.e. $x\in Q_0$![]() (see, e.g. [Reference Braides and Defranceschi7, proposition 4.3, corollary 4.12]). Then, it is easy to check that the growth condition (4.2) together with the convexity property of $f_\infty (x,\,\cdot )$
(see, e.g. [Reference Braides and Defranceschi7, proposition 4.3, corollary 4.12]). Then, it is easy to check that the growth condition (4.2) together with the convexity property of $f_\infty (x,\,\cdot )$![]() yield the local Lipschitz continuity in (4.3) (see, e.g. [Reference Braides and Defranceschi7, remark 4.13]).
yield the local Lipschitz continuity in (4.3) (see, e.g. [Reference Braides and Defranceschi7, remark 4.13]).
Step 4. Integral representation. For $u\in W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() consider the functional
consider the functional
We observe that the local Lipschitz condition (4.3) satisfied by $f_\infty$![]() ensures that, for every $A\in \mathcal {A}(Q_0)$
ensures that, for every $A\in \mathcal {A}(Q_0)$![]() , the functional (4.26) is continuous with respect to the strong $W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$
, the functional (4.26) is continuous with respect to the strong $W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() -convergence. Indeed, using Hölder's inequality we easily get
-convergence. Indeed, using Hölder's inequality we easily get

for every $u_1,\,u_2\in W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() . Moreover, arguing as in the proof of lemma 4.7 we can deduce that (4.26) is also continuous with respect to the strong convergence of $W^{1,q}(Q_0;\mathbb {R}^{m})$
. Moreover, arguing as in the proof of lemma 4.7 we can deduce that (4.26) is also continuous with respect to the strong convergence of $W^{1,q}(Q_0;\mathbb {R}^{m})$![]() , for $q\geq p(1+\sigma )/\sigma$
, for $q\geq p(1+\sigma )/\sigma$![]() .
.
Let $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and $A\in \mathcal {A}(Q_0)$
and $A\in \mathcal {A}(Q_0)$![]() be given; then there exists a sequence $(u_j)\subset W^{1,q}(Q_0;\mathbb {R}^{m})$
be given; then there exists a sequence $(u_j)\subset W^{1,q}(Q_0;\mathbb {R}^{m})$![]() strongly converging to $u$
strongly converging to $u$![]() in $W^{1,q}(Q_0;\mathbb {R}^{m})$
in $W^{1,q}(Q_0;\mathbb {R}^{m})$![]() for any $q\in [1,\,\infty )$
for any $q\in [1,\,\infty )$![]() such that its restrictions to $A$
such that its restrictions to $A$![]() are piecewise affine. Since $F$
are piecewise affine. Since $F$![]() is lower semicontinuous with respect to the strong topology of $L^{1}(Q_0;\mathbb {R}^{m})$
is lower semicontinuous with respect to the strong topology of $L^{1}(Q_0;\mathbb {R}^{m})$![]() , appealing to step 2 and to the continuity of (4.26) we then obtain
, appealing to step 2 and to the continuity of (4.26) we then obtain
Hence, to represent $F$![]() in an integral form it only remains to prove the opposite inequality. To this end fix $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$
in an integral form it only remains to prove the opposite inequality. To this end fix $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and consider the functional $\widetilde F:W^{1,\infty }(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0)\longrightarrow [0,\,+\infty )$
and consider the functional $\widetilde F:W^{1,\infty }(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0)\longrightarrow [0,\,+\infty )$![]() defined as
defined as
We observe that $\widetilde F$![]() satisfies the same properties as $F$
satisfies the same properties as $F$![]() , hence there exists a Carathéodory function $h_\infty :Q_0\times \mathbb {R}^{m\times n}\to [0,\,+\infty )$
, hence there exists a Carathéodory function $h_\infty :Q_0\times \mathbb {R}^{m\times n}\to [0,\,+\infty )$![]() such that
such that
for every $v \in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and every $A\in \mathcal {A}(Q_0)$
and every $A\in \mathcal {A}(Q_0)$![]() . Note that the equality holds whenever $v$
. Note that the equality holds whenever $v$![]() is piecewise affine on $A$
is piecewise affine on $A$![]() .
.
Let $(u_j)$![]() be the sequence of piecewise affine functions considered above. Then
be the sequence of piecewise affine functions considered above. Then

hence the equality in (4.22) holds for every $u\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() and every $A\in \mathcal {A}(Q_0)$
and every $A\in \mathcal {A}(Q_0)$![]() .
.
Remark 4.11 From (4.25) it can be seen that actually $f_{\infty }$![]() satisfies the growth conditions
satisfies the growth conditions
for a.e. $x\in Q_0$![]() and every $\xi \in \mathbb {R}^{m\times n}$
and every $\xi \in \mathbb {R}^{m\times n}$![]() , which then reduce to those established in [Reference Braides6, Reference Buttazzo and Dal Maso9, Reference Müller30] when $\lambda _k \equiv 1$
, which then reduce to those established in [Reference Braides6, Reference Buttazzo and Dal Maso9, Reference Müller30] when $\lambda _k \equiv 1$![]() .
.
5. $\Gamma$ -convergence and integral representation in $W^{1,p}_{\lambda _\infty }$
-convergence and integral representation in $W^{1,p}_{\lambda _\infty }$
Consider now the integral functional $F_\infty \colon W^{1,1}(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0) \longrightarrow [0,\,+\infty ]$![]() defined as
defined as

with $f_\infty$![]() as in theorem 4.10.
as in theorem 4.10.
The purpose of this section is to show that (up to subsequences) there holds
for every $u \in W^{1,1}(Q_0;\mathbb {R}^{m})$![]() and every $A \in \mathcal {A}(Q_0)$
and every $A \in \mathcal {A}(Q_0)$![]() , where $F'$
, where $F'$![]() and $F''$
and $F''$![]() are as in (4.4) and (4.5), respectively. In other words we will show that, up to subsequences, the functionals $F_k$
are as in (4.4) and (4.5), respectively. In other words we will show that, up to subsequences, the functionals $F_k$![]() defined in (3.4) $\Gamma$
defined in (3.4) $\Gamma$![]() -converge on the whole space $W^{1,1}(Q_0;\mathbb {R}^{m})$
-converge on the whole space $W^{1,1}(Q_0;\mathbb {R}^{m})$![]() to the functional $F_\infty$
to the functional $F_\infty$![]() , whose domain is the (limit) weighted Sobolev space $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$
, whose domain is the (limit) weighted Sobolev space $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() .
.
To do so, we will make use of the following approximation result whose proof follows the line of that of [Reference Acerbi and Fusco1, theorem II.4] (see also [Reference De Arcangelis17, theorem 3.1]).
Theorem 5.1 Let $F_k$![]() be the functionals defined in ( 3.4). Let $A\subset \subset Q_0$
be the functionals defined in ( 3.4). Let $A\subset \subset Q_0$![]() be open and with Lipschitz boundary, let $u\in W^{1,1}(Q_0;\mathbb {R}^{m})$
be open and with Lipschitz boundary, let $u\in W^{1,1}(Q_0;\mathbb {R}^{m})$![]() and let $(u_k)\subset W^{1,p}_{\lambda _k}(A;\mathbb {R}^{m})$
and let $(u_k)\subset W^{1,p}_{\lambda _k}(A;\mathbb {R}^{m})$![]() be such that
be such that
Then, for every $\tau >0$![]() there exist: $\beta _\tau >0$
there exist: $\beta _\tau >0$![]() with $\beta _\tau \to 0$
with $\beta _\tau \to 0$![]() as $\tau \to 0^{+},$
as $\tau \to 0^{+},$![]() $L_\tau >0$
$L_\tau >0$![]() with $L_\tau \to +\infty$
with $L_\tau \to +\infty$![]() as $\tau \to 0^{+},$
as $\tau \to 0^{+},$![]() a sequence $(v_k^{\tau })$
a sequence $(v_k^{\tau })$![]() and a function $v^{\tau }$
and a function $v^{\tau }$![]() in $W^{1,\infty }(\mathbb {R}^{n};\mathbb {R}^{m})$
in $W^{1,\infty }(\mathbb {R}^{n};\mathbb {R}^{m})$![]() with Lipschitz constant $c(n)L_\tau,$
with Lipschitz constant $c(n)L_\tau,$![]() for some $c(n)>0$
for some $c(n)>0$![]() depending only on $n,$
depending only on $n,$![]() such that:
such that:
(1) $v_k^{\tau }\to v^{\tau }$
 in $L^{\infty }(Q_0;\mathbb {R}^{m})$
in $L^{\infty }(Q_0;\mathbb {R}^{m})$ as $k\to \infty ;$
as $k\to \infty ;$
(2) $|\{x\in A\colon v^{\tau }(x)\neq u(x)\}|\leq (m+1)\tau ;$

(3) the following estimate holds for every $\tau >0$
 :
(5.4)\begin{equation} \liminf_{k \to \infty}\int_Af_k(x,\nabla u_k)\,{\rm d}x\geq\liminf_{k \to \infty}\int_{A_\tau} f_k(x,\nabla v_k^{\tau})\,{\rm d}x-\beta_\tau, \end{equation}for some open set $A_\tau \subset A$
:
(5.4)\begin{equation} \liminf_{k \to \infty}\int_Af_k(x,\nabla u_k)\,{\rm d}x\geq\liminf_{k \to \infty}\int_{A_\tau} f_k(x,\nabla v_k^{\tau})\,{\rm d}x-\beta_\tau, \end{equation}for some open set $A_\tau \subset A$
 with $|A\setminus A_\tau |<\tau$
with $|A\setminus A_\tau |<\tau$ .
.
Proof. Without loss of generality, we can assume that liminf in the left-hand side of (5.4) is actually a limit. Moreover, we can also assume that $(u_k) \subset C_0^{\infty }(\mathbb {R}^{n};\mathbb {R}^{m})$![]() , ${\rm supp}(u_k) \subset \subset Q_0$
, ${\rm supp}(u_k) \subset \subset Q_0$![]() , and
, and
Indeed, thanks to (2.10) from (5.3) we have
then, since $A \subset \subset Q_0$![]() , the extension result [Reference Turesson34, theorem 2.1.13] allows us to replace $(u_k)$
, the extension result [Reference Turesson34, theorem 2.1.13] allows us to replace $(u_k)$![]() with a sequence of functions in $W^{1,p}_{\lambda _k}(\mathbb {R}^{n};\mathbb {R}^{m})$
with a sequence of functions in $W^{1,p}_{\lambda _k}(\mathbb {R}^{n};\mathbb {R}^{m})$![]() , whose support is compactly contained in $Q_0$
, whose support is compactly contained in $Q_0$![]() , and such that (5.5) holds. Moreover, since for fixed $k$
, and such that (5.5) holds. Moreover, since for fixed $k$![]() the space $C_0^{\infty }(\mathbb {R}^{n};\mathbb {R}^{m})$
the space $C_0^{\infty }(\mathbb {R}^{n};\mathbb {R}^{m})$![]() is dense in $W^{1,p}_{\lambda _k}(\mathbb {R}^{n};\mathbb {R}^{m})$
is dense in $W^{1,p}_{\lambda _k}(\mathbb {R}^{n};\mathbb {R}^{m})$![]() (see, e.g. [Reference Turesson34, corollary 2.1.6]), a diagonal argument provides us with a sequence $(w_k)\subset C_0^{\infty }(\mathbb {R}^{n};\mathbb {R}^{m})$
(see, e.g. [Reference Turesson34, corollary 2.1.6]), a diagonal argument provides us with a sequence $(w_k)\subset C_0^{\infty }(\mathbb {R}^{n};\mathbb {R}^{m})$![]() , with ${\rm supp} (w_k) \subset \subset Q_0$
, with ${\rm supp} (w_k) \subset \subset Q_0$![]() , such that
, such that
Then, we readily get
and by the compact embedding of $W^{1,p}_{\lambda _k}(Q_0;\mathbb {R}^{m})$![]() in $L^{1}(Q_0;\mathbb {R}^{m})$
in $L^{1}(Q_0;\mathbb {R}^{m})$![]() , (5.6) also implies that $w_k \to u$
, (5.6) also implies that $w_k \to u$![]() in $L^{1}(A;\mathbb {R}^{m})$
in $L^{1}(A;\mathbb {R}^{m})$![]() .
.
Furthermore, we observe that $u_k$![]() and $w_k$
and $w_k$![]() are close in energy so that once we establish the estimate (5.4) along $(w_k)$
are close in energy so that once we establish the estimate (5.4) along $(w_k)$![]() , the same estimate will hold true along $(u_k)$
, the same estimate will hold true along $(u_k)$![]() . In fact, (3.3) gives
. In fact, (3.3) gives

hence gathering (5.6)–(5.8) yields
for some constant $C>0$![]() .
.
Therefore, in all that follows, with a little abuse of notation, $(u_k)$![]() denotes a sequence in $C_0^{\infty }(\mathbb {R}^{n};\mathbb {R}^{m})$
denotes a sequence in $C_0^{\infty }(\mathbb {R}^{n};\mathbb {R}^{m})$![]() , with ${\rm supp}(u_k) \subset \subset Q_0$
, with ${\rm supp}(u_k) \subset \subset Q_0$![]() , and such that (5.5) holds.
, and such that (5.5) holds.
For $k\in \mathbb {N}$![]() and $i \in \{1,\,\ldots,\,m\}$
and $i \in \{1,\,\ldots,\,m\}$![]() , let $u_k^{(i)}$
, let $u_k^{(i)}$![]() denote the $i$
denote the $i$![]() -th component of the vector-valued function $u_k$
-th component of the vector-valued function $u_k$![]() . By applying theorem 2.8 to $|\nabla u_k^{(i)}|\in L^{1}(\mathbb {R}^{n})$
. By applying theorem 2.8 to $|\nabla u_k^{(i)}|\in L^{1}(\mathbb {R}^{n})$![]() we deduce
we deduce
for every $k\in \mathbb {N}$![]() , every $i=1,\,\ldots,\,m$
, every $i=1,\,\ldots,\,m$![]() , and for some $c_4>0$
, and for some $c_4>0$![]() . Hence, by combining (5.5) and (5.9) it follows that the sequence $(\lambda _k(M|\nabla u_h^{(i)}|)^{p})$
. Hence, by combining (5.5) and (5.9) it follows that the sequence $(\lambda _k(M|\nabla u_h^{(i)}|)^{p})$![]() is bounded in $L^{1}(\mathbb {R}^{n})$
is bounded in $L^{1}(\mathbb {R}^{n})$![]() , for every $i=1,\,\ldots,\,m$
, for every $i=1,\,\ldots,\,m$![]() . Let now $\tau >0$
. Let now $\tau >0$![]() , then lemma 2.11 ensures the existence of a measurable set $E_\tau$
, then lemma 2.11 ensures the existence of a measurable set $E_\tau$![]() , with
, with
of a constant $\delta _\tau >0$![]() , and a subsequence $(k_j^{\tau })$
, and a subsequence $(k_j^{\tau })$![]() such that
such that
for every $j \in \mathbb {N}$![]() , every $i=1,\,\ldots,\, m$
, every $i=1,\,\ldots,\, m$![]() , and for every measurable set $B$
, and for every measurable set $B$![]() with $B\cap E_\tau =\emptyset$
with $B\cap E_\tau =\emptyset$![]() and $|B|<\delta _\tau$
and $|B|<\delta _\tau$![]() .
.
To simplify the notation we drop the dependence of the sequence on $j$![]() and $\tau$
and $\tau$![]() , thus we write
, thus we write
for every $k\in \mathbb {N}$![]() , every $i=1,\,\ldots,\, m$
, every $i=1,\,\ldots,\, m$![]() , and every measurable $B$
, and every measurable $B$![]() with $B\cap E_\tau =\emptyset$
with $B\cap E_\tau =\emptyset$![]() and $|B|<\delta _\tau$
and $|B|<\delta _\tau$![]() .
.
By the Hölder inequality we deduce

hence by (3.1), (5.5) and (5.12), since $\lambda _k$![]() belongs to $A_p(K)$
belongs to $A_p(K)$![]() we get
we get
for every $k \in \mathbb {N}$![]() , $i=1,\,\ldots,\,m$
, $i=1,\,\ldots,\,m$![]() , and some $C>0$
, and some $C>0$![]() . In its turn (5.13) together with (2.11) provide us with a constant $L_\tau \geq (\tilde c/\tau )(CK/c_1)^{1/p}$
. In its turn (5.13) together with (2.11) provide us with a constant $L_\tau \geq (\tilde c/\tau )(CK/c_1)^{1/p}$![]() such that for every $k\in \mathbb {N}$
such that for every $k\in \mathbb {N}$![]() , and $i=1,\,\ldots,\,m$
, and $i=1,\,\ldots,\,m$![]()
For $k\in \mathbb {N}$![]() , and $i=1,\,\ldots,\,m$
, and $i=1,\,\ldots,\,m$![]() define the sets
define the sets

Then lemma 2.9 yields
for every $k\in \mathbb {N}$![]() , $i=1,\,\ldots,\,m$
, $i=1,\,\ldots,\,m$![]() , and every $x,\, y \in H_k^{\tau }$
, and every $x,\, y \in H_k^{\tau }$![]() . Namely, the functions $u_k^{(i)}$
. Namely, the functions $u_k^{(i)}$![]() are Lipschitz continuous on $H_k^{\tau }$
are Lipschitz continuous on $H_k^{\tau }$![]() with Lipschitz constant $c_5(n)L_\tau$
with Lipschitz constant $c_5(n)L_\tau$![]() , for every $k\in \mathbb {N}$
, for every $k\in \mathbb {N}$![]() and every $i=1,\,\ldots,\,m$
and every $i=1,\,\ldots,\,m$![]() .
.
Appealing to McShane's theorem [Reference McShane27] we can extend $u_k^{(i)}$![]() from $H_k^{\tau } \cap Q_0$
from $H_k^{\tau } \cap Q_0$![]() to $\mathbb {R}^{n}$
to $\mathbb {R}^{n}$![]() keeping the same Lipschitz constant $c_5(n)L_\tau$
keeping the same Lipschitz constant $c_5(n)L_\tau$![]() . We denote this extension with $v_k^{\tau,(i)}$
. We denote this extension with $v_k^{\tau,(i)}$![]() and note that we can assume that $v_k^{\tau,(i)}(x)=0$
and note that we can assume that $v_k^{\tau,(i)}(x)=0$![]() if $\mathop{}\!\mathrm{dist} (x,\,Q_0)>1$
if $\mathop{}\!\mathrm{dist} (x,\,Q_0)>1$![]() . We then have
. We then have
and
Now, let $x'\in \mathbb {R}^{n}$![]() be such that $\mathop{}\!\mathrm{dist} (x',\,Q_0)>1$
be such that $\mathop{}\!\mathrm{dist} (x',\,Q_0)>1$![]() , then
, then
for every $x\in Q_0$![]() . Hence, gathering (5.15) and (5.16) entails
. Hence, gathering (5.15) and (5.16) entails
for every $i=1,\,\ldots,\, m$![]() , and every $\tau >0$
, and every $\tau >0$![]() . Therefore, up to subsequences (not relabelled), for every $\tau >0$
. Therefore, up to subsequences (not relabelled), for every $\tau >0$![]() fixed, we get that in particular
fixed, we get that in particular
as $k \to \infty$![]() , with
, with
for every $i=1,\,\ldots,\,m$![]() . Finally, set
. Finally, set
Now, define the set $B_\tau :=\{x\in A\colon v^{\tau }(x)\neq u(x)\}$![]() , then it must hold
, then it must hold
To prove (5.17) we start observing that there exists a subsequence $(k_j)$![]() such that if
such that if
then $|A\setminus E|=0$![]() ; hence, as a consequence, $|B_\tau \cap E|=|B_\tau |$
; hence, as a consequence, $|B_\tau \cap E|=|B_\tau |$![]() . Moreover, since $v_k^{\tau }\to v^{\tau }$
. Moreover, since $v_k^{\tau }\to v^{\tau }$![]() in $L^{\infty }(A;\mathbb {R}^{m})$
in $L^{\infty }(A;\mathbb {R}^{m})$![]() as $k\to \infty$
as $k\to \infty$![]() we have that
we have that
for every $x\in A$![]() and hence, in particular, for every $x\in B_\tau$
and hence, in particular, for every $x\in B_\tau$![]() .
.
Assume by contradiction that $|B_\tau |>(m+1)\tau$![]() , then by (5.14) we obtain
, then by (5.14) we obtain
for every $j\in \mathbb {N}$![]() . Therefore, by (5.19) and lemma 2.10 there exists $(k_{j_h})\subset (k_j)$
. Therefore, by (5.19) and lemma 2.10 there exists $(k_{j_h})\subset (k_j)$![]() such that
such that
Thus, if $x$![]() belongs to the set above by (5.18) we get
belongs to the set above by (5.18) we get
which is a contradiction in view of the definition of $B_\tau$![]() . Therefore, (5.17) holds.
. Therefore, (5.17) holds.
To conclude, it only remains to prove the energy estimate (5.4). Let $E_\tau$![]() be as in (5.10); by the nonnegativity of $f_k$
be as in (5.10); by the nonnegativity of $f_k$![]() we have
we have

By (5.14) we get
hence invoking (3.2), (5.15), (5.14), (5.11), (2.3), proposition 2.5 and (5.21) we obtain

where $\alpha _\tau :=\beta cc_2|Q_0|({m\tau }/{|Q_0|})^{\sigma /(1+\sigma )}$![]() ; thus $\alpha _\tau \to 0$
; thus $\alpha _\tau \to 0$![]() , as $\tau \to 0^{+}$
, as $\tau \to 0^{+}$![]() .
.
Now let $A_\tau \subset A$![]() be an open set containing $A\setminus E_\tau$
be an open set containing $A\setminus E_\tau$![]() and such that
and such that

We note that this choice is always possible thanks to the growth conditions satisfied by $f_k$![]() (3.2), to (5.15), and in view of proposition 2.5. Indeed, we have
(3.2), to (5.15), and in view of proposition 2.5. Indeed, we have

moreover, $|A\setminus A_\tau |\leq |E_\tau |<\tau$![]() .
.
Eventually, by combining (5.20), (5.22) and (5.23) we deduce
and hence the claim follows with $\beta _\tau :=\alpha _\tau +\tau (\beta m^{p-1}c_5(n)^{p}+1)$![]() .
.
We are now in a position to show that, up to subsequences, the functionals $F_k$![]() $\Gamma$
$\Gamma$![]() -converge to $F_\infty$
-converge to $F_\infty$![]() .
.
Theorem 5.2 Let $F_k$![]() and $F_\infty$
and $F_\infty$![]() be the functionals defined in (3.4) and (5.1), respectively. Then there exists a subsequence $(k_h)$
be the functionals defined in (3.4) and (5.1), respectively. Then there exists a subsequence $(k_h)$![]() such that for every $u\in W^{1,1}(Q_0;\mathbb {R}^{m})$
such that for every $u\in W^{1,1}(Q_0;\mathbb {R}^{m})$![]() and for every $A\in \mathcal {A}(Q_0)$
and for every $A\in \mathcal {A}(Q_0)$![]() with $A \subset \subset Q_0$
with $A \subset \subset Q_0$![]() there holds
there holds
where $F'$![]() and $F''$
and $F''$![]() are, respectively, as in (4.4) and (4.5) with $k$
are, respectively, as in (4.4) and (4.5) with $k$![]() replaced by $k_h$
replaced by $k_h$![]() .
.
Proof. In all that follows $(k_h)$![]() denotes the subsequence provided by theorem 4.10.
denotes the subsequence provided by theorem 4.10.
We divide the proof into two main steps.
Step 1: Lower bound. In this step, we prove that
for every $u\in W^{1,1}(Q_0;\mathbb {R}^{m})$![]() and every $A\in \mathcal {A}(Q_0)$
and every $A\in \mathcal {A}(Q_0)$![]() with $A \subset \subset Q_0$
with $A \subset \subset Q_0$![]() .
.
To this end, let $u\in W^{1,1}(Q_0;\mathbb {R}^{m})$![]() and $A\in \mathcal {A}(Q_0)$
and $A\in \mathcal {A}(Q_0)$![]() , $A \subset \subset Q_0$
, $A \subset \subset Q_0$![]() be fixed.
be fixed.
Substep 1.1: $u \in W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() . By [Reference Dal Maso14, proposition 8.1] there exists $(u_h)\subset W^{1,1}(Q_0;\mathbb {R}^{m})$
. By [Reference Dal Maso14, proposition 8.1] there exists $(u_h)\subset W^{1,1}(Q_0;\mathbb {R}^{m})$![]() with $u_h\to u$
with $u_h\to u$![]() in $L^{1}(Q_0;\mathbb {R}^{m})$
in $L^{1}(Q_0;\mathbb {R}^{m})$![]() such that
such that
We observe that lemma 4.3 guarantees that $F'(u,\,A)<+\infty$![]() ; therefore, $(u_h)\subset W^{1,p}_{\lambda _h}(A;\mathbb {R}^{m})$
; therefore, $(u_h)\subset W^{1,p}_{\lambda _h}(A;\mathbb {R}^{m})$![]() and (up to possibly passing to a subsequence) by (3.2) we get
and (up to possibly passing to a subsequence) by (3.2) we get
Now let $\tau >0$![]() be fixed and arbitrary; theorem 5.1 provides us with $(\beta _\tau )$
be fixed and arbitrary; theorem 5.1 provides us with $(\beta _\tau )$![]() , infinitesimal as $\tau \to 0^{+}$
, infinitesimal as $\tau \to 0^{+}$![]() , $A_\tau \subset A$
, $A_\tau \subset A$![]() , with $|A\setminus A_\tau |<\tau$
, with $|A\setminus A_\tau |<\tau$![]() , and $(v_h^{\tau })$
, and $(v_h^{\tau })$![]() , $v^{\tau }$
, $v^{\tau }$![]() in $W^{1,\infty }(\mathbb {R}^{n};\mathbb {R}^{m})$
in $W^{1,\infty }(\mathbb {R}^{n};\mathbb {R}^{m})$![]() , such that $v_h^{\tau }\to v^{\tau }$
, such that $v_h^{\tau }\to v^{\tau }$![]() in $L^{1}(Q_0;\mathbb {R}^{m})$
in $L^{1}(Q_0;\mathbb {R}^{m})$![]() , as $h\to \infty$
, as $h\to \infty$![]() . Moreover, by (5.26) and (5.4) we obtain
. Moreover, by (5.26) and (5.4) we obtain

where the last inequality follows by theorem 4.10, since $v^{\tau }\in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() .
.
Now let $B_\tau :=\{x\in A\colon v^{\tau }(x)\neq u(x)\}$![]() be as in the proof of theorem 5.1 and recall that
be as in the proof of theorem 5.1 and recall that
By (5.27) and the nonnegativity of $f_\infty$![]() we have
we have
for every $\tau >0$![]() . Now, since $|A\setminus A_\tau |<\tau$
. Now, since $|A\setminus A_\tau |<\tau$![]() , using (5.28) we get
, using (5.28) we get
thus, thanks to (4.2) and (5.30), we can pass to the limit as $\tau \to 0^{+}$![]() in (5.29) and obtain
in (5.29) and obtain
hence the lower bound for $u\in W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() .
.
Substep 1.2: $u \notin W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() . In this case, from (5.1) we have $F_\infty (u,\,A)=+\infty$
. In this case, from (5.1) we have $F_\infty (u,\,A)=+\infty$![]() , hence to conclude we need to show that $F'(u,\,A)=+\infty$
, hence to conclude we need to show that $F'(u,\,A)=+\infty$![]() . Assume by contradiction that
. Assume by contradiction that
If this is the case, we may argue exactly as in substep 1.1 and get
By the Fatou lemma, (4.2) and proposition 2.6 this yields $u\in W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() and hence a contradiction.
and hence a contradiction.
Step 2. Upper bound. In this step, we prove that
for every $u\in W^{1,1}(Q_0;\mathbb {R}^{m})$![]() and every $A\in \mathcal {A}(Q_0)$
and every $A\in \mathcal {A}(Q_0)$![]() with $A \subset \subset Q_0$
with $A \subset \subset Q_0$![]() .
.
To this end, let $u\in W^{1,1}(Q_0;\mathbb {R}^{m})$![]() and $A\in \mathcal {A}(Q_0)$
and $A\in \mathcal {A}(Q_0)$![]() , $A \subset \subset Q_0$
, $A \subset \subset Q_0$![]() be fixed. We start observing that by the definition of $F_\infty$
be fixed. We start observing that by the definition of $F_\infty$![]() , if $u\notin W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$
, if $u\notin W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() then there is nothing to prove. Therefore, we only consider the case $u \in W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$
then there is nothing to prove. Therefore, we only consider the case $u \in W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() .
.
Since $A$![]() is Lipschitz, by [Reference Turesson34, theorem 2.1.13] we can find a function $\tilde u \in W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$
is Lipschitz, by [Reference Turesson34, theorem 2.1.13] we can find a function $\tilde u \in W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() with $u=\tilde u$
with $u=\tilde u$![]() a.e. in $A$
a.e. in $A$![]() . Then, by density (see, e.g. [Reference Turesson34, corollary 2.1.6]) there exists $(u_j)\subset W^{1,\infty }(Q_0;\mathbb {R}^{m})$
. Then, by density (see, e.g. [Reference Turesson34, corollary 2.1.6]) there exists $(u_j)\subset W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() such that $u_j\to \tilde u$
such that $u_j\to \tilde u$![]() in $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$
in $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() . Then, by the locality of $F''$
. Then, by the locality of $F''$![]() and $F_\infty$
and $F_\infty$![]() , the continuity of $F_\infty$
, the continuity of $F_\infty$![]() in $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$
in $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() , and the $L^{1}(Q_0;\mathbb {R}^{m})$
, and the $L^{1}(Q_0;\mathbb {R}^{m})$![]() -lower semicontinuity of $F''$
-lower semicontinuity of $F''$![]() , invoking theorem 4.10 we deduce
, invoking theorem 4.10 we deduce
thus the upper bound.
6. Convergence of minimization problems
In this section, we modify the domain of the functionals $F_k$![]() by prescribing boundary conditions of Dirichlet type. We then study the $\Gamma$
by prescribing boundary conditions of Dirichlet type. We then study the $\Gamma$![]() -convergence of the corresponding functionals and prove a convergence result for the associated minimization problems.
-convergence of the corresponding functionals and prove a convergence result for the associated minimization problems.
We start by proving a preliminary energy bound.
Proposition 6.1 Let $F_k$![]() be the functionals defined in (3.4). Then there exist an exponent $\delta >0$
be the functionals defined in (3.4). Then there exist an exponent $\delta >0$![]() and a constant $C>0$
and a constant $C>0$![]() such that
such that
for every $A\in \mathcal {A}(Q_0),$![]() every $u\in W^{1,p}_{\lambda _k}(A;\mathbb {R}^{m}),$
every $u\in W^{1,p}_{\lambda _k}(A;\mathbb {R}^{m}),$![]() and every $k\in \mathbb {N}$
and every $k\in \mathbb {N}$![]() .
.
Proof. By theorem 2.2 we can deduce the existence of an exponent $\sigma >0$![]() and a constant $c>0$
and a constant $c>0$![]() such that
such that
for every cube $Q$![]() and for every $k\in \mathbb {N}$
and for every $k\in \mathbb {N}$![]() .
.
Now, let $A\in \mathcal {A}(Q_0)$![]() and $u\in W^{1,p}_{\lambda _k}(A;\mathbb {R}^{m})$
and $u\in W^{1,p}_{\lambda _k}(A;\mathbb {R}^{m})$![]() be arbitrary, and let $\delta >0$
be arbitrary, and let $\delta >0$![]() to be chosen later. By the Hölder inequality we have
to be chosen later. By the Hölder inequality we have

For $\delta :=(p-1)\sigma /(p+\sigma )$![]() it is immediate to check that
it is immediate to check that
hence by (6.2) we readily get

Moreover, since $\lambda _k$![]() belongs to $A_p(K)$
belongs to $A_p(K)$![]() , by (3.1) we also deduce that
, by (3.1) we also deduce that

and therefore

Eventually, gathering (3.1), (3.2) and (6.3) gives

for every $k\in \mathbb {N}$![]() . Hence, (6.1) immediately follows by choosing $C:=\max \{C_1,\, C_2\}$
. Hence, (6.1) immediately follows by choosing $C:=\max \{C_1,\, C_2\}$![]() with
with
Let $F_k$![]() be functionals defined in (3.4). We consider $F_k^{\psi }:W^{1,1}(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0)\longrightarrow [0,\,+\infty ]$
be functionals defined in (3.4). We consider $F_k^{\psi }:W^{1,1}(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0)\longrightarrow [0,\,+\infty ]$![]() given by
given by
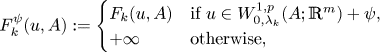
with $\psi \in W^{1,\infty }(Q_0;\mathbb {R}^{m})$![]() .
.
We are now in a position to prove a $\Gamma$![]() -convergence result for the functionals $F_k^{\psi }$
-convergence result for the functionals $F_k^{\psi }$![]() .
.
Theorem 6.2 ($\Gamma$ -convergence with boundary data)
-convergence with boundary data)
Let $F_k^{\psi }$![]() be the functionals defined in (6.4). Then there exists a subsequence $(k_h)$
be the functionals defined in (6.4). Then there exists a subsequence $(k_h)$![]() such that for every $A\in \mathcal {A}(Q_0),$
such that for every $A\in \mathcal {A}(Q_0),$![]() $A\subset \subset Q_0$
$A\subset \subset Q_0$![]()
where $F_\infty ^{\psi }: W^{1,1}(Q_0;\mathbb {R}^{m})\times \mathcal {A}(Q_0)\longrightarrow [0,\,+\infty ]$![]() is given by
is given by

with $F_\infty$![]() as in (5.1).
as in (5.1).
Proof. Let $u\in W^{1,1}(Q_0;\mathbb {R}^{m})$![]() and $A\in \mathcal {A} (Q_0)$
and $A\in \mathcal {A} (Q_0)$![]() , with $A\subset \subset Q_0$
, with $A\subset \subset Q_0$![]() be fixed and let $(k_h)$
be fixed and let $(k_h)$![]() be the subsequence whose existence is guaranteed by theorem 5.2.
be the subsequence whose existence is guaranteed by theorem 5.2.
We divide the proof into two main steps.
Step 1: Lower bound. Let $(u_h)\subset W^{1,1}(Q_0;\mathbb {R}^{m})$![]() be such that $u_h\to u$
be such that $u_h\to u$![]() in $L^{1}(Q_0;\mathbb {R}^{m})$
in $L^{1}(Q_0;\mathbb {R}^{m})$![]() . In this step, we want to show that
. In this step, we want to show that
We note that we can always assume that
otherwise there is nothing to prove. Moreover, without loss of generality, we may also assume that the liminf in (6.7) is actually a limit. Then, by the definition of $F_{k_h}^{\psi }$![]() we have that $(u_h) \subset W^{1,p}_{0,\lambda _{k_h}}(A;\mathbb {R}^{m})+\psi$
we have that $(u_h) \subset W^{1,p}_{0,\lambda _{k_h}}(A;\mathbb {R}^{m})+\psi$![]() ; while by theorem 5.2 we get that $u\in W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$
; while by theorem 5.2 we get that $u\in W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() and
and
Since $W^{1,p}_{0,\lambda _\infty }(A;\mathbb {R}^{m})= W^{1,1}_{0}(A;\mathbb {R}^{m}) \cap W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() , to conclude it is enough to show that $u$
, to conclude it is enough to show that $u$![]() belongs to $W^{1,1}_{0}(A;\mathbb {R}^{m})+\psi$
belongs to $W^{1,1}_{0}(A;\mathbb {R}^{m})+\psi$![]() .
.
To this end, we start observing that thanks to (6.7), proposition 6.1 yields the existence of an exponent $\delta >0$![]() and of a constant $C>0$
and of a constant $C>0$![]() such that
such that
for every $h\in \mathbb {N}$![]() . Then, by Poincaré's inequality the sequence $(u_h)$
. Then, by Poincaré's inequality the sequence $(u_h)$![]() is bounded in $W^{1,1+\delta }(A;\mathbb {R}^{m})$
is bounded in $W^{1,1+\delta }(A;\mathbb {R}^{m})$![]() . This readily implies that, up to subsequences, $u_h\rightharpoonup u$
. This readily implies that, up to subsequences, $u_h\rightharpoonup u$![]() in $W^{1,1+\delta }(A;\mathbb {R}^{m})$
in $W^{1,1+\delta }(A;\mathbb {R}^{m})$![]() . Since $(u_h)\subset W^{1,1+\delta }_0(A;\mathbb {R}^{m})+\psi$
. Since $(u_h)\subset W^{1,1+\delta }_0(A;\mathbb {R}^{m})+\psi$![]() and this space is weakly closed, we immediately get $u\in W^{1,1+\delta }_0(A;\mathbb {R}^{m})+\psi$
and this space is weakly closed, we immediately get $u\in W^{1,1+\delta }_0(A;\mathbb {R}^{m})+\psi$![]() , and therefore the claim.
, and therefore the claim.
Step 2: Upper bound. We start by considering the case $u \in C^{\infty }_0(A;\mathbb {R}^{m})+\psi$![]() .
.
By proposition 4.5 and theorem 5.2 there exists a sequence $(u_h)\subset W^{1,p}_{\lambda _{k_h}}(A;\mathbb {R}^{m})$![]() such that $u_h\to u$
such that $u_h\to u$![]() in $L^{q}(Q_0;\mathbb {R}^{m})$
in $L^{q}(Q_0;\mathbb {R}^{m})$![]() for every $1\leq q<+\infty$
for every $1\leq q<+\infty$![]() and
and
Starting from $u_h$![]() we now want to construct a recovery sequence which also satisfies the boundary condition. To this purpose, let $\eta >0$
we now want to construct a recovery sequence which also satisfies the boundary condition. To this purpose, let $\eta >0$![]() be fixed. By the equi-integrability of the sequence $(\lambda _{k_h})$
be fixed. By the equi-integrability of the sequence $(\lambda _{k_h})$![]() (cf. proposition 2.5) there exists a compact set $K_\eta \subset A$
(cf. proposition 2.5) there exists a compact set $K_\eta \subset A$![]() such that
such that
for every $h\in \mathbb {N}$![]() .
.
Choose $A',\,A''\in \mathcal {A}(Q_0)$![]() such that $K_\eta \subset A'\subset \subset A''\subset \subset A$
such that $K_\eta \subset A'\subset \subset A''\subset \subset A$![]() . Then, proposition 4.6 ensures the existence of a positive constant $M_\eta$
. Then, proposition 4.6 ensures the existence of a positive constant $M_\eta$![]() and a sequence $(\varphi _h)$
and a sequence $(\varphi _h)$![]() of cut-off functions between $A'$
of cut-off functions between $A'$![]() and $A''$
and $A''$![]() such that
such that

Set $w_h:=\varphi _hu_h+(1-\varphi _h)u$![]() ; then by definition $(w_h)\subset W^{1,p}_{0,\lambda _{k_h}}(A;\mathbb {R}^{m})+\psi$
; then by definition $(w_h)\subset W^{1,p}_{0,\lambda _{k_h}}(A;\mathbb {R}^{m})+\psi$![]() and $w_h\to u$
and $w_h\to u$![]() in $L^{q}(Q_0;\mathbb {R}^{m})$
in $L^{q}(Q_0;\mathbb {R}^{m})$![]() for every $1\leq q<+\infty$
for every $1\leq q<+\infty$![]() . Moreover, by (6.10) and (3.2) we get
. Moreover, by (6.10) and (3.2) we get

Hence, by (6.8), (6.9) and (6.11) we have

Therefore, by the arbitrariness of $\eta >0$![]() we conclude that
we conclude that
for every $u\in C_0^{\infty }(A;\mathbb {R}^{m})+\psi$![]() .
.
Now, let $u\in W^{1,p}_{0,\lambda _\infty }(A;\mathbb {R}^{m})+\psi$![]() . We extend $u$
. We extend $u$![]() to $\psi$
to $\psi$![]() outside $A$
outside $A$![]() ; we clearly have that the extended function (still denoted by $u$
; we clearly have that the extended function (still denoted by $u$![]() ) belongs to $W^{1,p}_{0,\lambda _\infty }(Q_0;\mathbb {R}^{m})+\psi$
) belongs to $W^{1,p}_{0,\lambda _\infty }(Q_0;\mathbb {R}^{m})+\psi$![]() . Now, let $(u_j)\subset C_0^{\infty }(Q_0;\mathbb {R}^{m})$
. Now, let $(u_j)\subset C_0^{\infty }(Q_0;\mathbb {R}^{m})$![]() be such that $u_j\to u$
be such that $u_j\to u$![]() in $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$
in $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() , hence, in particular, $u_j\to u$
, hence, in particular, $u_j\to u$![]() strongly in $L^{1}(Q_0;\mathbb {R}^{m})$
strongly in $L^{1}(Q_0;\mathbb {R}^{m})$![]() . By the $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$
. By the $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() -continuity of $F_\infty ^{\psi }$
-continuity of $F_\infty ^{\psi }$![]() , by (6.12), and by the lower semicontinuity of the $\Gamma$
, by (6.12), and by the lower semicontinuity of the $\Gamma$![]() -limsup with respect to the strong topology of $L^{1}(Q_0;\mathbb {R}^{m})$
-limsup with respect to the strong topology of $L^{1}(Q_0;\mathbb {R}^{m})$![]() we get
we get
for every $u\in W^{1,p}_{0,\lambda _\infty }(A;\mathbb {R}^{m})+\psi$![]() , and therefore the upper bound.
, and therefore the upper bound.
The following result shows that the functionals $F^{\psi }_k$![]() are equi-coercive with respect to the strong $L^{1}(Q_0;\mathbb {R}^{m})$
are equi-coercive with respect to the strong $L^{1}(Q_0;\mathbb {R}^{m})$![]() -topology.
-topology.
Proposition 6.3 (Equi-coerciveness)
Let $F_k^{\psi }$![]() be functionals defined in ( 6.4) , let $A\in \mathcal {A}(Q_0),$
be functionals defined in ( 6.4) , let $A\in \mathcal {A}(Q_0),$![]() $A \subset \subset Q_0$
$A \subset \subset Q_0$![]() , and let $(u_k)\subset W^{1,1}(A;\mathbb {R}^{m})$
, and let $(u_k)\subset W^{1,1}(A;\mathbb {R}^{m})$![]() be such that
be such that
Then there exist a subsequence $(u_{k_h})\subset (u_k)$![]() and an exponent $\delta >0$
and an exponent $\delta >0$![]() such that
such that
with $u\in W^{1,p}_{0,\lambda _\infty }(A;\mathbb {R}^{m})+\psi$![]() . Moreover, if we extend $u_{k_h}$
. Moreover, if we extend $u_{k_h}$![]() and $u$
and $u$![]() to $Q_0$
to $Q_0$![]() by setting $u_{k_h}:=\psi$
by setting $u_{k_h}:=\psi$![]() and $u:=\psi$
and $u:=\psi$![]() in $Q_0 \setminus A,$
in $Q_0 \setminus A,$![]() respectively, then $u_{k_h}\to u$
respectively, then $u_{k_h}\to u$![]() in $L^{1}(Q_0;\mathbb {R}^{m})$
in $L^{1}(Q_0;\mathbb {R}^{m})$![]() .
.
Proof. By (6.13) and by (6.4) we have $u_k \in W^{1,p}_{0,\lambda _k}(A;\mathbb {R}^{m})+\psi$![]() , for every $k\in \mathbb {N}$
, for every $k\in \mathbb {N}$![]() . Then, arguing exactly as in the proof of theorem 6.2 we may deduce the existence of a subsequence $(u_{k_h})\subset (u_k)$
. Then, arguing exactly as in the proof of theorem 6.2 we may deduce the existence of a subsequence $(u_{k_h})\subset (u_k)$![]() which weakly converges in $W^{1,1+\delta }(A;\mathbb {R}^{m})$
which weakly converges in $W^{1,1+\delta }(A;\mathbb {R}^{m})$![]() to a function $u\in W_0^{1,1}(A;\mathbb {R}^{m})+\psi$
to a function $u\in W_0^{1,1}(A;\mathbb {R}^{m})+\psi$![]() . Furthermore, by the compact embedding of $W^{1,1+\delta }(A;\mathbb {R}^{m})$
. Furthermore, by the compact embedding of $W^{1,1+\delta }(A;\mathbb {R}^{m})$![]() in $L^{1,1+\delta }(A;\mathbb {R}^{m})$
in $L^{1,1+\delta }(A;\mathbb {R}^{m})$![]() we have that, in particular, $u_{k_h}\to u$
we have that, in particular, $u_{k_h}\to u$![]() in $L^{1}(A;\mathbb {R}^{m})$
in $L^{1}(A;\mathbb {R}^{m})$![]() . Now, extend $u_{k_h}$
. Now, extend $u_{k_h}$![]() and $u$
and $u$![]() by setting $u_{k_h}:=\psi$
by setting $u_{k_h}:=\psi$![]() , $u:=\psi$
, $u:=\psi$![]() in $Q_0 \setminus A$
in $Q_0 \setminus A$![]() . Then, clearly $u_{k_h}\to u$
. Then, clearly $u_{k_h}\to u$![]() in $L^{1}(Q_0;\mathbb {R}^{m})$
in $L^{1}(Q_0;\mathbb {R}^{m})$![]() . Hence, by theorem 6.2 and by (6.13) there holds
. Hence, by theorem 6.2 and by (6.13) there holds
thus by (6.5) we get $u\in W^{1,p}_{0,\lambda _\infty }(A;\mathbb {R}^{m})+\psi$![]() .
.
Thanks to the fundamental property of $\Gamma$![]() -convergence, by combining theorem 6.2 and proposition 6.3 we obtain the following convergence result for the associated minimization problems.
-convergence, by combining theorem 6.2 and proposition 6.3 we obtain the following convergence result for the associated minimization problems.
Theorem 6.4 Let $A\subset \mathcal {A}(Q_0)$![]() with $A\subset \subset Q_0$
with $A\subset \subset Q_0$![]() . Let $f_k$
. Let $f_k$![]() be functions satisfying (3.2) and (3.3) and set
be functions satisfying (3.2) and (3.3) and set
Let $(u_k) \subset W^{1,p}_{0,\lambda _{k}}(A;\mathbb {R}^{m})+\psi$![]() be such that
be such that
Then, up to subsequences (not relabelled), $u_k\to u_\infty$![]() in $L^{1}(A;\mathbb {R}^{m})$
in $L^{1}(A;\mathbb {R}^{m})$![]() with $u_\infty$
with $u_\infty$![]() solution to
solution to
Moreover, we have $M_k \to M_\infty,$![]() as $k\to +\infty$
as $k\to +\infty$![]() .
.
7. Asymptotic formula for $f_\infty$
In this section, we derive an asymptotic formula for the integrand of the $\Gamma$![]() -limit, $f_\infty$
-limit, $f_\infty$![]() . This formula will be particularly useful when proving the homogenization result in § 8.
. This formula will be particularly useful when proving the homogenization result in § 8.
In all that follows $F_\infty \colon W^{1,1}(Q_0;\mathbb {R}^{m}) \times \mathcal {A}(Q_0) \longrightarrow [0,\,+\infty ]$![]() denotes the $\Gamma$
denotes the $\Gamma$![]() -limit of $(F_{k_h})$
-limit of $(F_{k_h})$![]() where $(k_h)$
where $(k_h)$![]() as in theorem 5.2. That is, $F_\infty$
as in theorem 5.2. That is, $F_\infty$![]() coincides with the integral functional
coincides with the integral functional
for every $u\in W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() , where for a.e. $x\in Q_0$
, where for a.e. $x\in Q_0$![]() and for every $\xi \in \mathbb {R}^{m\times n}$
and for every $\xi \in \mathbb {R}^{m\times n}$![]()
moreover, $f_\infty$![]() satisfies (4.2) and (4.3) (cf. theorem 4.1). We also recall that, being $F_\infty$
satisfies (4.2) and (4.3) (cf. theorem 4.1). We also recall that, being $F_\infty$![]() a $\Gamma$
a $\Gamma$![]() -limit, it is lower semicontinuous with respect to the strong $L^{1}(Q_0;\mathbb {R}^{m})$
-limit, it is lower semicontinuous with respect to the strong $L^{1}(Q_0;\mathbb {R}^{m})$![]() -convergence.
-convergence.
The following theorem is the main result of this section.
Theorem 7.1 For almost every $x\in Q_0$![]() and every $\xi \in \mathbb {R}^{m\times n}$
and every $\xi \in \mathbb {R}^{m\times n}$![]() there holds
there holds
where, for every $A\in \mathcal {A}(Q_0)$![]() ,
,
The proof of theorem 7.1 will be achieved by combining lemmas 7.3–7.5 below, by following the same strategy as in [Reference Bouchitté, Fonseca and Mascarenhas4, § 3] (see also [Reference Bouchitté, Fonseca, Leoni and Mascarenhas5, § 2.2]).
As an immediate corollary of theorems 6.4 and 7.1 we also obtain the following asymptotic formula for $f_\infty$![]() .
.
Corollary 7.2 (Asymptotic formula for $f_{\infty }$ )
)
For almost every $x\in Q_0$![]() and every $\xi \in \mathbb {R}^{m\times n}$
and every $\xi \in \mathbb {R}^{m\times n}$![]() there holds
there holds
where, for every $A\in \mathcal {A}(Q_0),$![]()
We now turn to the proof of theorem 7.1; to this end, we need to introduce the following notation. Set $\mathcal {A}^{*}:=\{Q_\rho (x)\colon x\in Q_0,\,\ \rho >0\}$![]() and let $\delta >0$
and let $\delta >0$![]() . For $A\in \mathcal {A}(Q_0)$
. For $A\in \mathcal {A}(Q_0)$![]() define
define

We note that $m_{F_\infty }^{\delta }$![]() is decreasing in $\delta$
is decreasing in $\delta$![]() ; hence for every $A\in \mathcal {A}(Q_0)$
; hence for every $A\in \mathcal {A}(Q_0)$![]() we can consider
we can consider
We start by proving the following technical lemma which is an adaptation from [Reference Bouchitté, Fonseca and Mascarenhas4, lemma 3.3] to the setting of weighted Sobolev spaces.
Lemma 7.3 Let $A\in \mathcal {A}(Q_0),$![]() $A\subset \subset Q_0;$
$A\subset \subset Q_0;$![]() there holds
there holds
Proof. We observe that the inequality
is an immediate consequence of the definition of $m_{F_\infty }^{*}$![]() . Indeed, let $\delta >0$
. Indeed, let $\delta >0$![]() be fixed and let $(Q_i)$
be fixed and let $(Q_i)$![]() be an admissible sequence in the sense of the definition of $m_{F_\infty }^{\delta }(u_\xi,\,A)$
be an admissible sequence in the sense of the definition of $m_{F_\infty }^{\delta }(u_\xi,\,A)$![]() , then
, then

thus (7.5) follows by taking the limit as $\delta \to 0^{+}$![]() .
.
We now prove the converse inequality; i.e.
To this end, let $\delta >0$![]() be fixed and let $(Q_i^{\delta })$
be fixed and let $(Q_i^{\delta })$![]() be an admissible sequence in the definition of $m_{F_\infty }^{\delta }(u_\xi,\,A)$
be an admissible sequence in the definition of $m_{F_\infty }^{\delta }(u_\xi,\,A)$![]() such that
such that
By definition of $m_{F_\infty }$![]() , for every $i\in \mathbb {N}$
, for every $i\in \mathbb {N}$![]() we can choose $v_i^{\delta }\in W^{1,p}_{0,\lambda _\infty }(Q_i^{\delta };\mathbb {R}^{m})+u_\xi$
we can choose $v_i^{\delta }\in W^{1,p}_{0,\lambda _\infty }(Q_i^{\delta };\mathbb {R}^{m})+u_\xi$![]() such that
such that
Set

we claim that $v^{\delta }\in W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() . To prove the claim define
. To prove the claim define

clearly $v^{\delta,N}\in W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() and $v^{\delta,N} \to v^{\delta }$
and $v^{\delta,N} \to v^{\delta }$![]() a.e. in $Q_0$
a.e. in $Q_0$![]() , as $N\to \infty$
, as $N\to \infty$![]() . Since $v_i^{\delta }\in W^{1,p}_{0,\lambda _\infty }(Q_i^{\delta };\mathbb {R}^{m})+u_\xi$
. Since $v_i^{\delta }\in W^{1,p}_{0,\lambda _\infty }(Q_i^{\delta };\mathbb {R}^{m})+u_\xi$![]() for every $i=1,\,\ldots,\, N$
for every $i=1,\,\ldots,\, N$![]() , by the Poincaré inequality in weighted Sobolev spaces (see, e.g. [Reference Fröhlich23, corollary 1]) we have
, by the Poincaré inequality in weighted Sobolev spaces (see, e.g. [Reference Fröhlich23, corollary 1]) we have

for some $C(\delta,\,p)>0$![]() . By (4.2), (7.7) and (7.8) we get
. By (4.2), (7.7) and (7.8) we get

Hence, for $\delta >0$![]() fixed, the sequence $(v^{\delta,N})$
fixed, the sequence $(v^{\delta,N})$![]() is bounded in $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$
is bounded in $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() , uniformly in $N$
, uniformly in $N$![]() . Then, by [Reference Heinonen, Kilpeläinen and Martio25, theorem 1.32] $v^{\delta }$
. Then, by [Reference Heinonen, Kilpeläinen and Martio25, theorem 1.32] $v^{\delta }$![]() belongs to $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$
belongs to $W^{1,p}_{\lambda _\infty }(Q_0;\mathbb {R}^{m})$![]() and the claim is proven. Moreover, we have
and the claim is proven. Moreover, we have
indeed, by (4.2)
since $\lambda _\infty \in L^{1}(Q_0)$![]() and $|A\setminus \cup _{i=1}^{\infty } Q_i^{\delta }|=0$
and $|A\setminus \cup _{i=1}^{\infty } Q_i^{\delta }|=0$![]() . By combining (7.7)–(7.9) we deduce that
. By combining (7.7)–(7.9) we deduce that

We now claim that $v^{\delta }\to u_\xi$![]() in $L^{1}(Q_0;\mathbb {R}^{m})$
in $L^{1}(Q_0;\mathbb {R}^{m})$![]() . If so, by virtue of the lower semicontinuity of $F_\infty$
. If so, by virtue of the lower semicontinuity of $F_\infty$![]() with respect to the strong $L^{1}(Q_0;\mathbb {R}^{m})$
with respect to the strong $L^{1}(Q_0;\mathbb {R}^{m})$![]() -convergence, passing to the limit as $\delta \to 0^{+}$
-convergence, passing to the limit as $\delta \to 0^{+}$![]() in (7.10) would give
in (7.10) would give
and therefore (7.6). Hence, to conclude the proof it only remains to show that $v^{\delta }\to u_\xi$![]() in $L^{1}(Q_0;\mathbb {R}^{m})$
in $L^{1}(Q_0;\mathbb {R}^{m})$![]() . Since, in particular, $v_i^{\delta }\in W^{1,1}_0(Q_i^{\delta };\mathbb {R}^{m})+u_\xi$
. Since, in particular, $v_i^{\delta }\in W^{1,1}_0(Q_i^{\delta };\mathbb {R}^{m})+u_\xi$![]() , by the Poincaré inequality in $W^{1,1}(Q_i;\mathbb {R}^{m})$
, by the Poincaré inequality in $W^{1,1}(Q_i;\mathbb {R}^{m})$![]() there exists a constant $C>0$
there exists a constant $C>0$![]() such that
such that

Moreover, arguing similarly as above, by (4.2), (7.7) and (7.8) we deduce

Therefore, gathering (7.4), (7.11) and (7.12) gives the desired convergence and completes the proof.
We also need the following lemma.
Lemma 7.4 Let $A\in \mathcal {A}(Q_0),$![]() $\delta >0$
$\delta >0$![]() and define $A_\delta :=\{x\in A\colon \mathop{}\!\mathrm{dist} (x,\,\partial A)>\delta \}$
and define $A_\delta :=\{x\in A\colon \mathop{}\!\mathrm{dist} (x,\,\partial A)>\delta \}$![]() . Then
. Then
Proof. Let $\delta,\,\eta >0$![]() . By the definition of $m_{F_\infty }$
. By the definition of $m_{F_\infty }$![]() , we can choose $v\in W^{1,p}_{0,\lambda _\infty }(A_\delta ;\mathbb {R}^{m})+u_\xi$
, we can choose $v\in W^{1,p}_{0,\lambda _\infty }(A_\delta ;\mathbb {R}^{m})+u_\xi$![]() such that
such that
Set

clearly $w\in W^{1,p}_{0,\lambda _\infty }(A;\mathbb {R}^{m})+u_\xi$![]() . Using (4.2) and (7.13) we have
. Using (4.2) and (7.13) we have

Letting $\eta \to 0^{+}$![]() we conclude that
we conclude that
and therefore
since $\lambda _\infty \in L^{1}(A)$![]() .
.
Conversely, let $\eta >0$![]() and choose $v\in W^{1,p}_{0,\lambda _\infty }(A;\mathbb {R}^{m})+u_\xi$
and choose $v\in W^{1,p}_{0,\lambda _\infty }(A;\mathbb {R}^{m})+u_\xi$![]() such that
such that
Let $(v_j)\subset C_0^{\infty }(A;\mathbb {R}^{m})+u_\xi$![]() be such that $v_j\to v$
be such that $v_j\to v$![]() in $W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$
in $W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() . We can find $\delta _0>0$
. We can find $\delta _0>0$![]() small enough so that $(v_j)\subset C_0^{\infty }(A_\delta ;\mathbb {R}^{m})+u_\xi$
small enough so that $(v_j)\subset C_0^{\infty }(A_\delta ;\mathbb {R}^{m})+u_\xi$![]() for every $0<\delta <\delta _0$
for every $0<\delta <\delta _0$![]() , hence
, hence
for every $j\in \mathbb {N}$![]() . By the continuity of $F_\infty (\cdot,\,A)$
. By the continuity of $F_\infty (\cdot,\,A)$![]() with respect to the strong convergence of $W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$
with respect to the strong convergence of $W^{1,p}_{\lambda _\infty }(A;\mathbb {R}^{m})$![]() , (7.14) and (7.15) we deduce that
, (7.14) and (7.15) we deduce that
Letting first $\delta \to 0^{+}$![]() and then $\eta \to 0^{+}$
and then $\eta \to 0^{+}$![]() we eventually get
we eventually get
Eventually, we are in a position to prove the following lemma which, in its turn, yields the desired derivation formula (7.2) (cf. (7.1)).
Lemma 7.5 For a.e. $x\in Q_0$![]() there holds
there holds
Proof. The proof follows arguing exactly as in [Reference Bouchitté, Fonseca and Mascarenhas4, lemma 3.5], now using lemmas 7.3 and 7.4.
8. Stochastic homogenization
In this last section, we illustrate an application of the $\Gamma$![]() -convergence result theorem 3.2 to the case of stochastic homogenization.
-convergence result theorem 3.2 to the case of stochastic homogenization.
We start by recalling some basic notions and results from ergodic theory.
8.1 Ergodic theory
Let $d\geq 1$![]() be an integer; in all that follows $\mathcal {B}^{d}$
be an integer; in all that follows $\mathcal {B}^{d}$![]() denotes the Borel $\sigma$
denotes the Borel $\sigma$![]() -algebra of $\mathbb {R}^{d}$
-algebra of $\mathbb {R}^{d}$![]() ; if $d=1$
; if $d=1$![]() we set $\mathcal {B}:= \mathcal {B}^{1}$
we set $\mathcal {B}:= \mathcal {B}^{1}$![]() .
.
Let $(\Omega,\,\mathcal {F},\,P)$![]() be a probability space and let $\tau =(\tau _y)_{y\in \mathbb {R}^{n}}$
be a probability space and let $\tau =(\tau _y)_{y\in \mathbb {R}^{n}}$![]() denote a group of $P$
denote a group of $P$![]() -preserving transformations on $(\Omega,\,\mathcal {F},\,P)$
-preserving transformations on $(\Omega,\,\mathcal {F},\,P)$![]() ; i.e. $\tau$
; i.e. $\tau$![]() is a family of measurable mappings $\tau _y:\Omega \to \Omega$
is a family of measurable mappings $\tau _y:\Omega \to \Omega$![]() satisfying the following properties:
satisfying the following properties:
• $\tau _y\tau _{y'}=\tau _{y+y'}$
 , $\tau _y^{-1}=\tau _{-y}$
, $\tau _y^{-1}=\tau _{-y}$ , for every $y,\,y'\in \mathbb {R}^{n}$
, for every $y,\,y'\in \mathbb {R}^{n}$ ;
;• the map $\tau _y$
 preserves the probability measure $P$
preserves the probability measure $P$ ; i.e. $P(\tau _yE)=P(E)$
; i.e. $P(\tau _yE)=P(E)$ , for every $y\in \mathbb {R}^{n}$
, for every $y\in \mathbb {R}^{n}$ and every $E\in \mathcal {F}$
and every $E\in \mathcal {F}$ ;
;• for any measurable function $\varphi$
 on $\Omega$
on $\Omega$ , the function $\phi (\omega,\, x):=\varphi (\tau _y\omega )$
, the function $\phi (\omega,\, x):=\varphi (\tau _y\omega )$ is $\mathcal {F}\otimes \mathcal {B}^{n}$
is $\mathcal {F}\otimes \mathcal {B}^{n}$ -measurable on $\Omega \times \mathbb {R}^{n}$
-measurable on $\Omega \times \mathbb {R}^{n}$ .
.
If in addition every $\tau$![]() -invariant set $E\in \mathcal {F}$
-invariant set $E\in \mathcal {F}$![]() has either probabilty $0$
has either probabilty $0$![]() or $1$
or $1$![]() , then $\tau$
, then $\tau$![]() is called ergodic.
is called ergodic.
We also need to recall the notion of subadditive process. In what follows $\mathcal {A}_0$![]() denotes the family of all open, bounded subsets of $\mathbb {R}^{n}$
denotes the family of all open, bounded subsets of $\mathbb {R}^{n}$![]() with Lipschitz boundary.
with Lipschitz boundary.
Definition 8.1 (Subadditive process)
Let $\tau =(\tau _y)_{y\in \mathbb {R}^{n}}$![]() be a group of $P$
be a group of $P$![]() -preserving transformations on $(\Omega,\,\mathcal {F},\,P)$
-preserving transformations on $(\Omega,\,\mathcal {F},\,P)$![]() . A subadditive process is a function $\mu :\Omega \times \mathcal {A}_0\rightarrow [0,\,+\infty )$
. A subadditive process is a function $\mu :\Omega \times \mathcal {A}_0\rightarrow [0,\,+\infty )$![]() satisfying the following properties:
satisfying the following properties:
(1) for every $A\in \mathcal {A}_0$
 , $\mu (\cdot,\,A)$
, $\mu (\cdot,\,A)$ is $\mathcal {F}$
is $\mathcal {F}$ -measurable;
-measurable;(2) for every $\omega \in \Omega$
 , $A\in \mathcal {A}_0$
, $A\in \mathcal {A}_0$ , and $y\in \mathbb {R}^{n}$
, and $y\in \mathbb {R}^{n}$ \[ \mu(\omega,A+y)=\mu(\tau_y\omega,A); \]
\[ \mu(\omega,A+y)=\mu(\tau_y\omega,A); \]
(3) for every $\omega \in \Omega$
 , for every $A\in \mathcal {A}_0$
, for every $A\in \mathcal {A}_0$ , and for every finite family $(A_i)_{i\in I}\subset \mathcal {A}_0$
, and for every finite family $(A_i)_{i\in I}\subset \mathcal {A}_0$ of pairwise disjoint sets such that $A_i\subset A$
of pairwise disjoint sets such that $A_i\subset A$ for every $i\in I$
for every $i\in I$ and $|A\setminus \cup _{i\in I}A_i|=0$
and $|A\setminus \cup _{i\in I}A_i|=0$ , there holds
\[ \mu(\omega,A)\leq\sum_{i\in I}\mu(\omega,A_i); \]
, there holds
\[ \mu(\omega,A)\leq\sum_{i\in I}\mu(\omega,A_i); \]
(4) there exists a constant $c>0$
 such that for every $A\in \mathcal {A}_0$
such that for every $A\in \mathcal {A}_0$ \[ 0\leq\int_{\Omega}\mu(\omega,A)\,{\rm d}P\leq c|A|. \]
\[ 0\leq\int_{\Omega}\mu(\omega,A)\,{\rm d}P\leq c|A|. \]
Moreover, if $\tau :=(\tau _y)_{y\in \mathbb {R}^{n}}$![]() is ergodic then $\mu$
is ergodic then $\mu$![]() is called a subadditive ergodic process.
is called a subadditive ergodic process.
We now state a version of the subadditive ergodic theorem, originally proven by Akcoglu and Krengel [Reference Akcoglu and Krengel2], which is suitable for our purposes (see [Reference Licht and Michaille26, theorem 4.3]).
Theorem 8.2 Let $\mu :\Omega \times \mathcal {A}_0\rightarrow [0,\,+\infty )$![]() be a subadditive process. Then there exist a $\mathcal {F}$
be a subadditive process. Then there exist a $\mathcal {F}$![]() -measurable function $\phi :\Omega \rightarrow [0,\,+\infty )$
-measurable function $\phi :\Omega \rightarrow [0,\,+\infty )$![]() and a set $\Omega '\in \mathcal {F}$
and a set $\Omega '\in \mathcal {F}$![]() with $P(\Omega ')=1$
with $P(\Omega ')=1$![]() such that
such that
for every $\omega \in \Omega '$![]() and for every cube $Q$
and for every cube $Q$![]() in $\mathbb {R}^{n}$
in $\mathbb {R}^{n}$![]() with faces parallel to the coordinate planes.
with faces parallel to the coordinate planes.
If in addition $\mu$![]() is ergodic, then $\phi$
is ergodic, then $\phi$![]() is constant.
is constant.
For later use we also recall the Birkhoff ergodic theorem. To this end, we preliminarily need to fix some notation. Let $\varphi$![]() be a measurable function on $(\Omega,\,\mathcal {F},\,P)$
be a measurable function on $(\Omega,\,\mathcal {F},\,P)$![]() ; we denote with $\mathbb {E}[\varphi ]$
; we denote with $\mathbb {E}[\varphi ]$![]() the expected value of $\varphi$
the expected value of $\varphi$![]() ; i.e.
; i.e.
For every $\varphi \in L^{1}(\Omega )$![]() and for every $\sigma$
and for every $\sigma$![]() -algebra $\mathcal {F}'\subset \mathcal {F}$
-algebra $\mathcal {F}'\subset \mathcal {F}$![]() , we denote with $\mathbb {E}[\varphi |\mathcal {F}']$
, we denote with $\mathbb {E}[\varphi |\mathcal {F}']$![]() the conditional expectation of $\varphi$
the conditional expectation of $\varphi$![]() with respect to $\mathcal {F}'$
with respect to $\mathcal {F}'$![]() . We recall that $\mathbb {E}[\varphi |\mathcal {F}']$
. We recall that $\mathbb {E}[\varphi |\mathcal {F}']$![]() is the unique $L^{1}(\Omega )$
is the unique $L^{1}(\Omega )$![]() -function satisfying
-function satisfying
for every $E\in \mathcal {F}'$![]() .
.
We now state the following version of the Birkhoff ergodic theorem which is convenient for our purposes.
Theorem 8.3 (Birkhoff's ergodic theorem)
Let $\varphi \in L^{1}(\Omega ),$![]() let $\tau =(\tau _y)_{y\in \mathbb {R}^{n}}$
let $\tau =(\tau _y)_{y\in \mathbb {R}^{n}}$![]() be a group of $P$
be a group of $P$![]() -preserving transformations on $(\Omega,\,\mathcal {F},\,P),$
-preserving transformations on $(\Omega,\,\mathcal {F},\,P),$![]() and let $\mathcal {F}_\tau$
and let $\mathcal {F}_\tau$![]() denote the $\sigma$
denote the $\sigma$![]() -algebra of $\tau$
-algebra of $\tau$![]() -invariants sets. Then there exists a set $\widetilde {\Omega }\in \mathcal {F}$
-invariants sets. Then there exists a set $\widetilde {\Omega }\in \mathcal {F}$![]() with $P(\widetilde {\Omega })=1$
with $P(\widetilde {\Omega })=1$![]() such that
such that
for every $\omega \in \widetilde {\Omega }$![]() and for every measurable bounded set $B\subset \mathbb {R}^{n}$
and for every measurable bounded set $B\subset \mathbb {R}^{n}$![]() with $|B|>0$
with $|B|>0$![]() .
.
Remark 8.4 We note that if $\tau$![]() is ergodic, then $\mathcal {F}_\tau$
is ergodic, then $\mathcal {F}_\tau$![]() reduces to the trivial $\sigma$
reduces to the trivial $\sigma$![]() -algebra, therefore (8.1) becomes
-algebra, therefore (8.1) becomes
8.2 Setting of the problem and main results
In this section, we introduce the random integral functionals we are going to analyse. To this end, we preliminarily need to define the class of admissible random weights.
Assumption 8.5 (Admissible random weights)
Let $\tau =(\tau _y)_{y\in \mathbb {R}^{n}}$![]() be a group of $P$
be a group of $P$![]() -preserving transformations on $(\Omega,\,\mathcal {F},\, P)$
-preserving transformations on $(\Omega,\,\mathcal {F},\, P)$![]() . A function $\lambda :\Omega \times \mathbb {R}^{n}\rightarrow [0,\,+\infty )$
. A function $\lambda :\Omega \times \mathbb {R}^{n}\rightarrow [0,\,+\infty )$![]() is an admissible weight if:
is an admissible weight if:
• $\lambda$
 is $\mathcal {F}\otimes \mathcal {B}^{n}$
is $\mathcal {F}\otimes \mathcal {B}^{n}$ -measurable;
-measurable;• $\lambda$
 is stationary; i.e. $\lambda (\omega,\,x+y)=\lambda (\tau _y\omega,\,x)$
is stationary; i.e. $\lambda (\omega,\,x+y)=\lambda (\tau _y\omega,\,x)$ , for every $\omega \in \Omega$
, for every $\omega \in \Omega$ , $x,\,y \in \mathbb {R}^{n}$
, $x,\,y \in \mathbb {R}^{n}$ ;
;• $\lambda (\omega,\,\cdot )\in A_p(K)$
 , for every $\omega \in \Omega$
, for every $\omega \in \Omega$ ;
;• $\lambda (\cdot,\, 0)>0$
 in $\Omega$
in $\Omega$ ;
;• $\lambda (\cdot,\,0),\, \lambda (\cdot,\,0)^{-1/(p-1)}\in L^{1}(\Omega )$
 .
.
Remark 8.6 We note that $\lambda =\lambda (\omega,\,x)$![]() is $\tau$
is $\tau$![]() -stationary if and only if for every $\omega \in \Omega$
-stationary if and only if for every $\omega \in \Omega$![]() and every $x\in \mathbb {R}^{n}$
and every $x\in \mathbb {R}^{n}$![]() there holds
there holds
with $\hat \lambda (\omega ):=\lambda (\omega,\,0)$![]() .
.
Since by assumption $\lambda (\omega,\,0)>0$![]() for every $\omega \in \Omega$
for every $\omega \in \Omega$![]() , we then have $\mathbb {E}[\hat \lambda |\mathcal {F}'](\omega )>0$
, we then have $\mathbb {E}[\hat \lambda |\mathcal {F}'](\omega )>0$![]() , for every $\mathcal {F}' \subset \mathcal {F}$
, for every $\mathcal {F}' \subset \mathcal {F}$![]() . Moreover, we also observe that if we assume $\hat {\lambda },\,\hat {\lambda }^{-1/(p-1)}\in L^{1}(\Omega )$
. Moreover, we also observe that if we assume $\hat {\lambda },\,\hat {\lambda }^{-1/(p-1)}\in L^{1}(\Omega )$![]() , then the Fubini theorem yields $\lambda (\omega,\,\cdot ),\,\lambda ^{-1/(p-1)}(\omega,\,\cdot )\in L^{1}_{\rm loc}(\mathbb {R}^{n})$
, then the Fubini theorem yields $\lambda (\omega,\,\cdot ),\,\lambda ^{-1/(p-1)}(\omega,\,\cdot )\in L^{1}_{\rm loc}(\mathbb {R}^{n})$![]() , for every $\omega \in \Omega$
, for every $\omega \in \Omega$![]() . However, in order to apply theorem 3.2 we need the stronger condition $\lambda (\omega,\,\cdot ) \in A_p(K)$
. However, in order to apply theorem 3.2 we need the stronger condition $\lambda (\omega,\,\cdot ) \in A_p(K)$![]() , for every $\omega \in \Omega$
, for every $\omega \in \Omega$![]() .
.
Below we introduce the notion of stationary random integrand.
Definition 8.7 (Stationary random integrand)
Let $\tau =(\tau _y)_{y\in \mathbb {R}^{n}}$![]() be a group of $P$
be a group of $P$![]() -preserving transformations on $(\Omega,\,\mathcal {F},\, P)$
-preserving transformations on $(\Omega,\,\mathcal {F},\, P)$![]() and let $\lambda \colon \Omega \times \mathbb {R}^{n}\rightarrow [0,\,+\infty )$
and let $\lambda \colon \Omega \times \mathbb {R}^{n}\rightarrow [0,\,+\infty )$![]() satisfy assumption 8.5.
satisfy assumption 8.5.
${\rm (i)}$![]() We say that $f:\Omega \times \mathbb {R}^{n}\times \mathbb {R}^{m\times n}\rightarrow [0,\,+\infty )$
We say that $f:\Omega \times \mathbb {R}^{n}\times \mathbb {R}^{m\times n}\rightarrow [0,\,+\infty )$![]() is a random integrand if:
is a random integrand if:
• $f$
 is $(\mathcal {F}\otimes \mathcal {B}^{n}\otimes \mathcal {B}^{m\times n},\,\mathcal {B})$
is $(\mathcal {F}\otimes \mathcal {B}^{n}\otimes \mathcal {B}^{m\times n},\,\mathcal {B})$ -measurable;
-measurable;• for every $\omega \in \Omega$
 and for every $x\in \mathbb {R}^{n}$
and for every $x\in \mathbb {R}^{n}$ , the two following conditions hold:
(8.4)\begin{equation} \alpha \lambda (\omega, x)(|\xi|^{p}-1) \leq f(\omega,x,\xi)\leq \beta \lambda (\omega, x)(|\xi|^{p}+1), \end{equation}for every $\xi \in \mathbb {R}^{m\times n}$
, the two following conditions hold:
(8.4)\begin{equation} \alpha \lambda (\omega, x)(|\xi|^{p}-1) \leq f(\omega,x,\xi)\leq \beta \lambda (\omega, x)(|\xi|^{p}+1), \end{equation}for every $\xi \in \mathbb {R}^{m\times n}$
 and for some $0<\alpha \leq \beta <+\infty$
and for some $0<\alpha \leq \beta <+\infty$ , and
(8.5)\begin{equation} |f(\omega,x,\xi_1)-f(\omega, x,\xi_2)|\leq L\lambda(\omega, x)(|\xi_1|^{p-1}+|\xi_2|^{p-1}+1)|\xi_1-\xi_2|, \end{equation}for every $\xi _1,\,\xi _2 \in \mathbb {R}^{m\times n}$
, and
(8.5)\begin{equation} |f(\omega,x,\xi_1)-f(\omega, x,\xi_2)|\leq L\lambda(\omega, x)(|\xi_1|^{p-1}+|\xi_2|^{p-1}+1)|\xi_1-\xi_2|, \end{equation}for every $\xi _1,\,\xi _2 \in \mathbb {R}^{m\times n}$
 and for some $L>0$
and for some $L>0$ .
.
${\rm (ii)}$![]() We say that a random integrand $f$
We say that a random integrand $f$![]() is stationary if for every $\omega \in \Omega$
is stationary if for every $\omega \in \Omega$![]() , for every $x,\,y\in \mathbb {R}^{n}$
, for every $x,\,y\in \mathbb {R}^{n}$![]() and every $\xi \in \mathbb {R}^{m\times n}$
and every $\xi \in \mathbb {R}^{m\times n}$![]() it holds:
it holds:
• $f(\omega,\,x+y,\,\xi )=f(\tau _y\omega,\,x,\,\xi )$
 .
.
${\rm (iii)}$![]() We say that a stationary random integrand $f$
We say that a stationary random integrand $f$![]() is ergodic if $\tau =(\tau _y)_{y\in \mathbb {R}^{n}}$
is ergodic if $\tau =(\tau _y)_{y\in \mathbb {R}^{n}}$![]() is ergodic.
is ergodic.
Let $f$![]() be a stationary random integrand in the sense of definition 8.7. Let $\omega \in \Omega$
be a stationary random integrand in the sense of definition 8.7. Let $\omega \in \Omega$![]() be fixed and consider the integral functional $F(\omega ):W^{1,1}_{\rm loc}(\mathbb {R}^{n};\mathbb {R}^{m})\times \mathcal {A}_0\longrightarrow [0,\,+\infty ]$
be fixed and consider the integral functional $F(\omega ):W^{1,1}_{\rm loc}(\mathbb {R}^{n};\mathbb {R}^{m})\times \mathcal {A}_0\longrightarrow [0,\,+\infty ]$![]() defined as
defined as

Moreover, for every $\omega \in \Omega$![]() , $A \in \mathcal {A}_0$
, $A \in \mathcal {A}_0$![]() , and $\xi \in \mathbb {R}^{m\times n}$
, and $\xi \in \mathbb {R}^{m\times n}$![]() set
set

The following proposition shows that for every fixed $\xi \in \mathbb {R}^{m\times n}$![]() , the minimization problem in (8.7) defines a subadditive process.
, the minimization problem in (8.7) defines a subadditive process.
Proposition 8.8 Let $f$![]() be a stationary random integrand; let $F(\omega )$
be a stationary random integrand; let $F(\omega )$![]() and $m_{F(\omega )}$
and $m_{F(\omega )}$![]() be as in (8.6) and (8.7), respectively. Then for every $\xi \in \mathbb {R}^{m\times n}$
be as in (8.6) and (8.7), respectively. Then for every $\xi \in \mathbb {R}^{m\times n}$![]() the function
the function
defines a subadditive process on $(\Omega,\,\mathcal {F},\,P)$![]() .
.
Moreover, for every $\xi \in \mathbb {R}^{m\times n}$![]() and $A\in \mathcal {A}_0$
and $A\in \mathcal {A}_0$![]()
where $\hat {\lambda }$![]() is as in (8.3).
is as in (8.3).
Proof. Let $\xi \in \mathbb {R}^{m\times n}$![]() and $A\in \mathcal {A}_0$
and $A\in \mathcal {A}_0$![]() be fixed. We first show that $\omega \mapsto m_{F(\omega )}(u_\xi,\,A)$
be fixed. We first show that $\omega \mapsto m_{F(\omega )}(u_\xi,\,A)$![]() is $\mathcal {F}$
is $\mathcal {F}$![]() -measurable. To this end fix $u\in W^{1,p}_\lambda (A;\mathbb {R}^{m})$
-measurable. To this end fix $u\in W^{1,p}_\lambda (A;\mathbb {R}^{m})$![]() , then the function $(\omega,\,x)\mapsto f(\omega,\,x,\,\nabla u+\xi )$
, then the function $(\omega,\,x)\mapsto f(\omega,\,x,\,\nabla u+\xi )$![]() is $\mathcal {F}\otimes \mathcal {L}^{n}$
is $\mathcal {F}\otimes \mathcal {L}^{n}$![]() -measurable, hence by Fubini's theorem
-measurable, hence by Fubini's theorem
is $\mathcal {F}$![]() -measurable. Observe now that $W^{1,p}_{0,\lambda }(A;\mathbb {R}^{m})$
-measurable. Observe now that $W^{1,p}_{0,\lambda }(A;\mathbb {R}^{m})$![]() endowed with the norm $\|\nabla \cdot \|_{L^{p}_\lambda (A;\mathbb {R}^{m\times n})}$
endowed with the norm $\|\nabla \cdot \|_{L^{p}_\lambda (A;\mathbb {R}^{m\times n})}$![]() is a separable Banach space and that, by virtue of (8.5), the map $u\mapsto F(\omega )(u+u_\xi,\,A)$
is a separable Banach space and that, by virtue of (8.5), the map $u\mapsto F(\omega )(u+u_\xi,\,A)$![]() is continuous with respect to the same norm. Then there exists a countable dense set $D\subset W^{1,p}_{0,\lambda }(A;\mathbb {R}^{m})$
is continuous with respect to the same norm. Then there exists a countable dense set $D\subset W^{1,p}_{0,\lambda }(A;\mathbb {R}^{m})$![]() such that
such that
hence the map $\omega \mapsto m_{F(\omega )}(u_\xi,\,A)$![]() is $\mathcal {F}$
is $\mathcal {F}$![]() -measurable.
-measurable.
We now show that for every fixed $\xi \in \mathbb {R}^{m\times n}$![]() there holds
there holds
for every $\omega \in \Omega$![]() , $A\in \mathcal {A}_0$
, $A\in \mathcal {A}_0$![]() and $y\in \mathbb {R}^{n}$
and $y\in \mathbb {R}^{n}$![]() . Indeed, a change of variables and the stationarity of $f$
. Indeed, a change of variables and the stationarity of $f$![]() yield
yield

Let $\xi \in \mathbb {R}^{m\times n}$![]() and $\omega \in \Omega$
and $\omega \in \Omega$![]() be fixed. We now prove that the function $A\mapsto m_{F(\omega )}(u_\xi,\,A)$
be fixed. We now prove that the function $A\mapsto m_{F(\omega )}(u_\xi,\,A)$![]() is subadditive in the sense of definition 8.1. To this end, let $A\in \mathcal {A}_0$
is subadditive in the sense of definition 8.1. To this end, let $A\in \mathcal {A}_0$![]() and let $(A_i)_{i\in I}$
and let $(A_i)_{i\in I}$![]() be a finite family of pairwise disjoint sets in $\mathcal {A}_0$
be a finite family of pairwise disjoint sets in $\mathcal {A}_0$![]() such that $A_i\subset A$
such that $A_i\subset A$![]() , for every $i\in I$
, for every $i\in I$![]() , and $|A\setminus \cup _{i\in I}A_i|=0$
, and $|A\setminus \cup _{i\in I}A_i|=0$![]() . Let $\eta >0$
. Let $\eta >0$![]() and choose $u_i\in W^{1,p}_{0,\lambda }(A_i,\,\mathbb {R}^{m})$
and choose $u_i\in W^{1,p}_{0,\lambda }(A_i,\,\mathbb {R}^{m})$![]() such that $F(\omega )(u_i+u_\xi,\,A_i)\leq m_{F(\omega )}(u_\xi,\,A_i)+\eta$
such that $F(\omega )(u_i+u_\xi,\,A_i)\leq m_{F(\omega )}(u_\xi,\,A_i)+\eta$![]() . Define $u\in W^{1,p}_{0,\lambda }(A;\mathbb {R}^{m})$
. Define $u\in W^{1,p}_{0,\lambda }(A;\mathbb {R}^{m})$![]() by setting $u:=\sum _{i\in I}u_i \chi _{A_i}$
by setting $u:=\sum _{i\in I}u_i \chi _{A_i}$![]() . Then by the locality of $F(\omega )$
. Then by the locality of $F(\omega )$![]() we have
we have
which proves the subadditivity thanks to the arbitrariness of $\eta >0$![]() .
.
Finally, by definition of $m_F(u_\xi,\,A)$![]() , choosing $u=0$
, choosing $u=0$![]() , by (8.4) we have
, by (8.4) we have
for every $\xi \in \mathbb {R}^{m\times n}$![]() , every $\omega \in \Omega$
, every $\omega \in \Omega$![]() , and every $A\in \mathcal {A}_0$
, and every $A\in \mathcal {A}_0$![]() . Therefore, integrating on $\Omega$
. Therefore, integrating on $\Omega$![]() both sides of (8.9) and using the stationarity of $\lambda$
both sides of (8.9) and using the stationarity of $\lambda$![]() we get
we get
where to establish the last equality we have used the Tonelli theorem together with a change of variables in $\omega$![]() . Eventually, we deduce both (8.8) and that $(\omega,\,A)\mapsto m_{F(\omega )}(u_\xi,\,A)$
. Eventually, we deduce both (8.8) and that $(\omega,\,A)\mapsto m_{F(\omega )}(u_\xi,\,A)$![]() is a subadditive process.
is a subadditive process.
By combining proposition 8.8 together with the subadditive ergodic theorem 8.2 we are now able to establish the existence of the homogenization formula which will eventually define the integrand of the $\Gamma$![]() -limit (cf. theorem 8.12 below).
-limit (cf. theorem 8.12 below).
Proposition 8.9 Let $f$![]() be a stationary random integrand. Then there exist a set $\Omega '\in \mathcal {F}$
be a stationary random integrand. Then there exist a set $\Omega '\in \mathcal {F}$![]() with $P(\Omega ')=1$
with $P(\Omega ')=1$![]() and a $\mathcal {F}\otimes \mathcal {B}^{m\times n}$
and a $\mathcal {F}\otimes \mathcal {B}^{m\times n}$![]() -measurable function $f_{\rm hom}:\Omega \times \mathbb {R}^{m\times n}\rightarrow [0,\,+\infty )$
-measurable function $f_{\rm hom}:\Omega \times \mathbb {R}^{m\times n}\rightarrow [0,\,+\infty )$![]() such that for every $\omega \in \Omega ',$
such that for every $\omega \in \Omega ',$![]() $\xi \in \mathbb {R}^{m\times n},$
$\xi \in \mathbb {R}^{m\times n},$![]() and every cube $Q$
and every cube $Q$![]() in $\mathbb {R}^{n}$
in $\mathbb {R}^{n}$![]() there holds
there holds
Moreover, for every $\omega \in \Omega ',$![]() $f_{\rm hom}$
$f_{\rm hom}$![]() satisfies the following conditions:
satisfies the following conditions:
for every $\xi,\,\xi _1,\,\xi _2\in \mathbb {R}^{m\times n}$![]() and for some $L'>0$
and for some $L'>0$![]() , where $\hat {\lambda }$
, where $\hat {\lambda }$![]() is as in (8.3).
is as in (8.3).
If in addition $f$![]() is ergodic, then $f_{\rm hom}$
is ergodic, then $f_{\rm hom}$![]() does not depend on $\omega$
does not depend on $\omega$![]() and
and
for every $\xi \in \mathbb {R}^{m\times n}$![]() . Moreover, in this case (8.10) and (8.11) become, respectively,
. Moreover, in this case (8.10) and (8.11) become, respectively,
and
for every $\xi,\,\xi _1,\,\xi _2\in \mathbb {R}^{m\times n}$![]() .
.
Proof. Let $\xi \in \mathbb {R}^{m\times n}$![]() be fixed; theorem 8.2 and proposition 8.8 ensure the existence of a set $\Omega ^{\xi }\in \mathcal {F}$
be fixed; theorem 8.2 and proposition 8.8 ensure the existence of a set $\Omega ^{\xi }\in \mathcal {F}$![]() with $P(\Omega ^{\xi })=1$
with $P(\Omega ^{\xi })=1$![]() and of a $\mathcal {F}$
and of a $\mathcal {F}$![]() -measurable function $\phi ^{\xi }:\Omega \longrightarrow [0,\,+\infty )$
-measurable function $\phi ^{\xi }:\Omega \longrightarrow [0,\,+\infty )$![]() such that
such that
for every $\omega \in \Omega ^{\xi }$![]() and for every cube $Q$
and for every cube $Q$![]() in $\mathbb {R}^{n}$
in $\mathbb {R}^{n}$![]() .
.
Now, let $t>0$![]() and denote with $Q_t=Q_t(0)$
and denote with $Q_t=Q_t(0)$![]() the cube centred at the origin and with side length $t$
the cube centred at the origin and with side length $t$![]() . Let $f_{\rm hom}:\Omega \times \mathbb {R}^{m\times n}\rightarrow [0,\,+\infty )$
. Let $f_{\rm hom}:\Omega \times \mathbb {R}^{m\times n}\rightarrow [0,\,+\infty )$![]() be the function defined as
be the function defined as
Let $\omega \in \Omega$![]() and $A\in \mathcal {A}_0$
and $A\in \mathcal {A}_0$![]() be fixed; we start by showing that the function
be fixed; we start by showing that the function
is locally Lipschitz continuous. To this end, let $\xi _1,\,\xi _2\in \mathbb {R}^{m\times n}$![]() , let $\eta >0$
, let $\eta >0$![]() be arbitrary, and let $u\in W^{1,p}_{0,\lambda }(A;\mathbb {R}^{m})$
be arbitrary, and let $u\in W^{1,p}_{0,\lambda }(A;\mathbb {R}^{m})$![]() be such that
be such that
Then, appealing to (8.5) and to the Hölder inequality we deduce

where $C(p)>0$![]() depends only on $p$
depends only on $p$![]() . By using (8.4) (see also (8.9)) we get
. By using (8.4) (see also (8.9)) we get

Therefore, plugging (8.17) into (8.16) gives

where $C>0$![]() depends on $p,\,\alpha,\, \beta$
depends on $p,\,\alpha,\, \beta$![]() . Hence, by the arbitrariness of $\eta >0$
. Hence, by the arbitrariness of $\eta >0$![]() we get
we get
Thus, the claim simply follows by interchanging the role of $\xi _1$![]() and $\xi _2$
and $\xi _2$![]() .
.
Now, choose $A=tQ$![]() in (8.18) with $Q$
in (8.18) with $Q$![]() cube of $\mathbb {R}^{n}$
cube of $\mathbb {R}^{n}$![]() and $t>0$
and $t>0$![]() . By the stationarity of $\lambda$
. By the stationarity of $\lambda$![]() and a change of variables we obtain
and a change of variables we obtain

and, as above, the other inequality follows by exchanging the role of $\xi _1$![]() and $\xi _2$
and $\xi _2$![]() . Therefore, taking the $\limsup$
. Therefore, taking the $\limsup$![]() as $t\to \infty$
as $t\to \infty$![]() and invoking theorem 8.3, we deduce the existence of a set $\widetilde {\Omega }\in \mathcal {F}$
and invoking theorem 8.3, we deduce the existence of a set $\widetilde {\Omega }\in \mathcal {F}$![]() with $P(\widetilde {\Omega })=1$
with $P(\widetilde {\Omega })=1$![]() such that
such that

for every $\omega \in \widetilde {\Omega }$![]() . We also observe that choosing in (8.19) $Q=Q_1(0)$
. We also observe that choosing in (8.19) $Q=Q_1(0)$![]() , it is immediate to check that $f_{\rm hom}(\omega,\,\cdot )$
, it is immediate to check that $f_{\rm hom}(\omega,\,\cdot )$![]() satisfies the local Lipschitz condition (8.20), for every $\omega \in \widetilde {\Omega }$
satisfies the local Lipschitz condition (8.20), for every $\omega \in \widetilde {\Omega }$![]() .
.
Set $\Omega ':=(\cap _{\xi \in \mathbb {Q}^{m\times n}}\Omega ^{\xi })\cap \widetilde {\Omega }$![]() , clearly $P(\Omega ')=1$
, clearly $P(\Omega ')=1$![]() and (8.15) holds true for every fixed $\xi \in \mathbb {Q}^{m\times n}$
and (8.15) holds true for every fixed $\xi \in \mathbb {Q}^{m\times n}$![]() and every $\omega \in \Omega '$
and every $\omega \in \Omega '$![]() . Let now $\xi \in \mathbb {R}^{m\times n}$
. Let now $\xi \in \mathbb {R}^{m\times n}$![]() be fixed and let $(\xi _j)\subset \mathbb {Q}^{m\times n}$
be fixed and let $(\xi _j)\subset \mathbb {Q}^{m\times n}$![]() be such that $\xi _j\to \xi$
be such that $\xi _j\to \xi$![]() , as $j\to \infty$
, as $j\to \infty$![]() . For $\omega \in \Omega '$
. For $\omega \in \Omega '$![]() we have
we have

Then, view of (8.11), (8.15), and (8.20) we get that for every $j\in \mathbb {N}$![]() there holds
there holds

Thus, by letting $j\to \infty$![]() we obtain
we obtain
for every $\omega \in \Omega '$![]() and every $\xi \in \mathbb {R}^{m\times n}$
and every $\xi \in \mathbb {R}^{m\times n}$![]() , as desired.
, as desired.
Then, it only remains to show that $f_{\rm hom}(\omega,\,\cdot )$![]() satisfies the growth condition (8.10) for every $\omega \in \Omega '$
satisfies the growth condition (8.10) for every $\omega \in \Omega '$![]() . The growth condition from above readily follows from
. The growth condition from above readily follows from
passing to the limit as $t \to \infty$![]() , and using theorem 8.3.
, and using theorem 8.3.
We now establish the growth condition from below. To this end let $u\in W^{1,p}_{0,\lambda }(tQ;\mathbb {R}^{m})$![]() be arbitrary; then Hölder's inequality and (8.4) give
be arbitrary; then Hölder's inequality and (8.4) give

Dividing both sides by $|tQ|^{p}$![]() and taking the infimum over $W^{1,p}_{0,\lambda }(tQ;\mathbb {R}^{m})$
and taking the infimum over $W^{1,p}_{0,\lambda }(tQ;\mathbb {R}^{m})$![]() we get
we get

then, recalling that $\lambda (\omega,\,\cdot ) \in A_p(K)$![]() we find
we find
Therefore, passing to the limit as $t\to \infty$![]() and using again the Birkhoff ergodic theorem we finally obtain the growth conditions from below in (8.10).
and using again the Birkhoff ergodic theorem we finally obtain the growth conditions from below in (8.10).
We note that the $\mathcal {F}\otimes \mathcal {B}^{m\times n}$![]() -measurability of $f_{\rm hom}$
-measurability of $f_{\rm hom}$![]() follows from the $\mathcal {F}$
follows from the $\mathcal {F}$![]() -measurability of $\omega \mapsto f_{\rm hom}(\omega,\,\xi )$
-measurability of $\omega \mapsto f_{\rm hom}(\omega,\,\xi )$![]() and the continuity of $\xi \mapsto f_{\rm hom}(\omega,\,\xi )$
and the continuity of $\xi \mapsto f_{\rm hom}(\omega,\,\xi )$![]() .
.
If $f$![]() is ergodic, then theorem 8.2 ensures that $f_{\rm hom}$
is ergodic, then theorem 8.2 ensures that $f_{\rm hom}$![]() does not depend on $\omega$
does not depend on $\omega$![]() . Moreover, by (8.21) and the Birkhoff ergodic theorem we can invoke a generalized version of the dominated convergence theorem to deduce (8.12). Eventually, (8.13) and (8.14) follow, respectively, by integrating (8.10) and (8.11) on $\Omega$
. Moreover, by (8.21) and the Birkhoff ergodic theorem we can invoke a generalized version of the dominated convergence theorem to deduce (8.12). Eventually, (8.13) and (8.14) follow, respectively, by integrating (8.10) and (8.11) on $\Omega$![]() and using the definition of conditional expectation.
and using the definition of conditional expectation.
Remark 8.10 From the proof of proposition 8.9 it can be actually seen that in the ergodic case $f_{\rm hom}$![]() satisfies the standard growth conditions
satisfies the standard growth conditions
for every $\xi \in \mathbb {R}^{m \times n}$![]() (and similarly in the general stationary case), which then reduce to those established in [Reference Dal Maso and Modica15, Reference Dal Maso and Modica16, Reference Messaoudi and Michaille28] when $\lambda \equiv 1$
(and similarly in the general stationary case), which then reduce to those established in [Reference Dal Maso and Modica15, Reference Dal Maso and Modica16, Reference Messaoudi and Michaille28] when $\lambda \equiv 1$![]() .
.
Now, let $(\varepsilon _k) \searrow 0$![]() be a vanishing sequence of strictly positive real numbers and let $f$
be a vanishing sequence of strictly positive real numbers and let $f$![]() be a stationary random integrand. For $\omega \in \Omega$
be a stationary random integrand. For $\omega \in \Omega$![]() let $F_k(\omega ):W^{1,1}_{\rm loc}(\mathbb {R}^{n};\mathbb {R}^{m})\times \mathcal {A}_0\longrightarrow [0,\,+\infty ]$
let $F_k(\omega ):W^{1,1}_{\rm loc}(\mathbb {R}^{n};\mathbb {R}^{m})\times \mathcal {A}_0\longrightarrow [0,\,+\infty ]$![]() be the functionals defined as
be the functionals defined as

where for every $\omega \in \Omega$![]() and $x\in \mathbb {R}^{n}$
and $x\in \mathbb {R}^{n}$![]() we set
we set
with $\lambda$![]() satisfying assumption 8.5.
satisfying assumption 8.5.
Remark 8.11 If $\lambda _k$![]() is as in (8.23) then by assumption 8.5 and the Birkhoff ergodic theorem there exists $\Omega '\in \mathcal {F}$
is as in (8.23) then by assumption 8.5 and the Birkhoff ergodic theorem there exists $\Omega '\in \mathcal {F}$![]() with $P(\Omega ')=1$
with $P(\Omega ')=1$![]() such that (3.8) holds true for every $\omega \in \Omega '$
such that (3.8) holds true for every $\omega \in \Omega '$![]() .
.
The following homogenization theorem is the main result of this section.
Theorem 8.12 (Stochastic homogenization)
Let $f$![]() be a stationary random integrand and let $F_k(\omega )$
be a stationary random integrand and let $F_k(\omega )$![]() be as in (8.22). Then there exists $\Omega '\in \mathcal {F}$
be as in (8.22). Then there exists $\Omega '\in \mathcal {F}$![]() with $P(\Omega ')=1$
with $P(\Omega ')=1$![]() such that for every $\omega \in \Omega '$
such that for every $\omega \in \Omega '$![]() and every $A\in \mathcal {A}_0$
and every $A\in \mathcal {A}_0$![]()
where $F_{\rm hom}(\omega ):W^{1,1}_{\rm loc}(\mathbb {R}^{n};\mathbb {R}^{m})\times \mathcal {A}_0\longrightarrow [0,\,+\infty ]$![]() is the random functional defined as
is the random functional defined as

with $f_{\rm hom}$![]() as in proposition 8.9.
as in proposition 8.9.
If in addition $f$![]() is ergodic, then $F_{\rm \hom }$
is ergodic, then $F_{\rm \hom }$![]() is deterministic with integrand given by
is deterministic with integrand given by

for every $\xi \in \mathbb {R}^{m\times n}$![]() .
.
Proof. Let $\Omega '\in \mathcal {F}$![]() be the measurable set whose existence is ensured by proposition 8.9. In all that follows we fix $\omega$
be the measurable set whose existence is ensured by proposition 8.9. In all that follows we fix $\omega$![]() in $\Omega '$
in $\Omega '$![]() .
.
In view of remark 8.11, theorem 3.2 provides us with a subsequence $(k_h)$![]() such that for every $A\in \mathcal {A}_0$
such that for every $A\in \mathcal {A}_0$![]() the functionals $F_{k_h}(\omega )(\cdot,\,A)$
the functionals $F_{k_h}(\omega )(\cdot,\,A)$![]() $\Gamma$
$\Gamma$![]() -converge to the integral functional $F_\infty (\omega )(\cdot,\,A)$
-converge to the integral functional $F_\infty (\omega )(\cdot,\,A)$![]() with respect to the strong $L^{1}_{\rm loc}(\mathbb {R}^{n};\mathbb {R}^{m})$
with respect to the strong $L^{1}_{\rm loc}(\mathbb {R}^{n};\mathbb {R}^{m})$![]() -convergence, where $F_\infty (\omega ):W^{1,1}_{\rm loc}(\mathbb {R}^{n};\mathbb {R}^{m})\times \mathcal {A}_0\longrightarrow [0,\,+\infty ]$
-convergence, where $F_\infty (\omega ):W^{1,1}_{\rm loc}(\mathbb {R}^{n};\mathbb {R}^{m})\times \mathcal {A}_0\longrightarrow [0,\,+\infty ]$![]() is given by
is given by

we note that $f_\infty$![]() is nondegenerate since, by assumption, $\mathbb {E}[\hat \lambda |\mathcal {F}_\tau ](\omega )>0$
is nondegenerate since, by assumption, $\mathbb {E}[\hat \lambda |\mathcal {F}_\tau ](\omega )>0$![]() . Moreover, again invoking theorem 3.2, we have
. Moreover, again invoking theorem 3.2, we have
for a.e. $x\in \mathbb {R}^{n}$![]() and for every $\xi \in \mathbb {R}^{m\times n}$
and for every $\xi \in \mathbb {R}^{m\times n}$![]() . Hence, from (8.25) by a change of variables we immediately get
. Hence, from (8.25) by a change of variables we immediately get

where (8.26) follows by proposition 8.9 by setting $t:=\rho /\varepsilon _{k_h} \to \infty$![]() , as $h\to \infty$
, as $h\to \infty$![]() .
.
As a consequence, we deduce that $f_\infty$![]() is independent of the subsequence $(k_h)$
is independent of the subsequence $(k_h)$![]() and hence the Urysohn property of $\Gamma$
and hence the Urysohn property of $\Gamma$![]() -convergence (see [Reference Dal Maso14, proposition 8.3]) allows us to conclude that the whole sequence $(F_k(\omega ))$
-convergence (see [Reference Dal Maso14, proposition 8.3]) allows us to conclude that the whole sequence $(F_k(\omega ))$![]() $\Gamma$
$\Gamma$![]() -converges to $F_{\rm hom}(\omega )$
-converges to $F_{\rm hom}(\omega )$![]() , for every $\omega \in \Omega '$
, for every $\omega \in \Omega '$![]() .
.
Eventually, in the ergodic case the claim readily follows from the corresponding statement in proposition 8.9.
Acknowledgements
This study was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under the Germany Excellence Strategy EXC 2044-390685587 Mathematics Münster: Dynamics–Geometry–Structure.