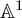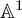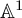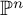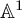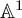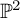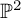1 Introduction
Let C be a smooth projective curve of genus
![]() $g $
over a field k. Fix a line bundle
$g $
over a field k. Fix a line bundle
![]() $\mathcal {L} \in \mathrm {Pic}(C)$
. Consider the following moduli stack
$\mathcal {L} \in \mathrm {Pic}(C)$
. Consider the following moduli stack
![]() $Bun_{n,\mathcal {L}}$
.
$Bun_{n,\mathcal {L}}$
.
![]() $ Bun_{n,\mathcal {L}} (Y)$
= { category of rank
$ Bun_{n,\mathcal {L}} (Y)$
= { category of rank
![]() $n $
vector bundles on
$n $
vector bundles on
![]() $C \times Y$
, such that for any object
$C \times Y$
, such that for any object
![]() $\mathcal {V}$
,
$\mathcal {V}$
,
![]() $\mathrm {det}\mathcal {V} \cong p^\ast (\mathcal {L}),$
where
$\mathrm {det}\mathcal {V} \cong p^\ast (\mathcal {L}),$
where
![]() $p: C \times Y \rightarrow C \} $
$p: C \times Y \rightarrow C \} $
This is a smooth algebraic stack [Reference Alper, Belmans, Bragg, Liang and Tajakka1, Prop 1.3]. Any stack can be regarded as a simplicial sheaf via the nerve construction (see [Reference Hollander6]) and thus it defines an object in the
![]() ${\mathbb A}^1$
-homotopy category. Therefore, it makes sense to talk about
${\mathbb A}^1$
-homotopy category. Therefore, it makes sense to talk about
![]() ${\mathbb A}^1$
-connectedness of
${\mathbb A}^1$
-connectedness of
![]() $Bun_{n,\mathcal {L}}$
. Following is the main theorem of this note:
$Bun_{n,\mathcal {L}}$
. Following is the main theorem of this note:
Theorem 1.1.
![]() $Bun_{n,\mathcal {L}}$
is
$Bun_{n,\mathcal {L}}$
is
![]() ${\mathbb A}^1$
-connected for any curve C over an infinite field k and
${\mathbb A}^1$
-connected for any curve C over an infinite field k and
![]() $\mathcal {L} \in \mathrm {Pic}(C)$
.
$\mathcal {L} \in \mathrm {Pic}(C)$
.
The proof of Theorem 1.1 relies on finding an explicit
![]() ${\mathbb A}^1$
-concordance (see [Reference Asok, Kebekus and Wendt2, Definition 5.1] or Definition 2.1) between a vector bundle
${\mathbb A}^1$
-concordance (see [Reference Asok, Kebekus and Wendt2, Definition 5.1] or Definition 2.1) between a vector bundle
![]() $\mathcal {E}$
of rank n and determinant
$\mathcal {E}$
of rank n and determinant
![]() $\mathcal {L}$
to the vector bundle
$\mathcal {L}$
to the vector bundle
![]() $\mathcal {O}_C^{n-1} \oplus \mathcal {L}$
. This is achieved by induction on n. In the course of this proof, we also achieve the classification of vector bundles of a given rank on the curve C up to
$\mathcal {O}_C^{n-1} \oplus \mathcal {L}$
. This is achieved by induction on n. In the course of this proof, we also achieve the classification of vector bundles of a given rank on the curve C up to
![]() ${\mathbb A}^1$
-concordance (Theorem 2.5). Once the question of
${\mathbb A}^1$
-concordance (Theorem 2.5). Once the question of
![]() ${\mathbb A}^1$
-connectedness of
${\mathbb A}^1$
-connectedness of
![]() $ Bun_{n,\mathcal {L}} $
is settled, it is natural to wonder the same about its open substack
$ Bun_{n,\mathcal {L}} $
is settled, it is natural to wonder the same about its open substack
![]() $ Bun_{n,\mathcal {L}} ^s$
, the moduli of stable vector bundles for a curve of genus greater than 1. Assuming that n and degree of
$ Bun_{n,\mathcal {L}} ^s$
, the moduli of stable vector bundles for a curve of genus greater than 1. Assuming that n and degree of
![]() $\mathcal {L}$
are co-prime, k algebraically closed, the coarse moduli space is known to be rational ([Reference King and Schofield8, Theorem 1.2]) and one may be tempted to conclude that
$\mathcal {L}$
are co-prime, k algebraically closed, the coarse moduli space is known to be rational ([Reference King and Schofield8, Theorem 1.2]) and one may be tempted to conclude that
![]() ${\mathbb A}^1$
-connectedness of an algebraic stack is dictated by that of its coarse moduli space (if it exists). However, in Example 2.9, we show that this simply is not the case. We give an example of “stacky”
${\mathbb A}^1$
-connectedness of an algebraic stack is dictated by that of its coarse moduli space (if it exists). However, in Example 2.9, we show that this simply is not the case. We give an example of “stacky”
![]() ${\mathbb P}^1$
, an orbifold with
${\mathbb P}^1$
, an orbifold with
![]() ${\mathbb P}^1$
as a coarse moduli space, which is not
${\mathbb P}^1$
as a coarse moduli space, which is not
![]() ${\mathbb A}^1$
-connected. It should also be noted that the
${\mathbb A}^1$
-connected. It should also be noted that the
![]() ${\mathbb A}^1$
-connectedness is not preserved under rationality of a morphism of schemes as illustrated by
${\mathbb A}^1$
-connectedness is not preserved under rationality of a morphism of schemes as illustrated by
![]() $\mathbb {G}_m \hookrightarrow {\mathbb A}^1$
.
$\mathbb {G}_m \hookrightarrow {\mathbb A}^1$
.
Related to
![]() ${\mathbb A}^1$
-concordance is the notion of an
${\mathbb A}^1$
-concordance is the notion of an
![]() ${\mathbb A}^1$
-h-cobordism ([Reference Asok and Morel3, Definition 3.1.1] or Definition 3.1). Furthermore, projectivizations of two
${\mathbb A}^1$
-h-cobordism ([Reference Asok and Morel3, Definition 3.1.1] or Definition 3.1). Furthermore, projectivizations of two
![]() ${\mathbb A}^1$
-concordant vector bundles are
${\mathbb A}^1$
-concordant vector bundles are
![]() ${\mathbb A}^1$
-h-cobordant. As an application of
${\mathbb A}^1$
-h-cobordant. As an application of
![]() ${\mathbb A}^1$
-connectedness of
${\mathbb A}^1$
-connectedness of
![]() $ Bun_{n,\mathcal {L}} $
, we obtain the following theorem which classifies
$ Bun_{n,\mathcal {L}} $
, we obtain the following theorem which classifies
![]() ${\mathbb P}^n$
-bundles over any curve of genus g up to
${\mathbb P}^n$
-bundles over any curve of genus g up to
![]() ${\mathbb A}^1$
-weak equivalence. This extends the result on classification of
${\mathbb A}^1$
-weak equivalence. This extends the result on classification of
![]() ${\mathbb P}^n$
-bundles over
${\mathbb P}^n$
-bundles over
![]() ${\mathbb P}^1$
given in [Reference Asok and Morel3].
${\mathbb P}^1$
given in [Reference Asok and Morel3].
Theorem 1.2. Let
![]() $X={\mathbb P}_{C}(\mathcal {E})$
and
$X={\mathbb P}_{C}(\mathcal {E})$
and
![]() $Y={\mathbb P}_{C}(\mathcal {F})$
be
$Y={\mathbb P}_{C}(\mathcal {F})$
be
![]() ${\mathbb P}^n$
-bundles over C, where C lies over an infinite field. Then the following are equivalent:
${\mathbb P}^n$
-bundles over C, where C lies over an infinite field. Then the following are equivalent:
-
(1) X and Y are
 ${\mathbb A}^1$
- weakly equivalent.
${\mathbb A}^1$
- weakly equivalent. -
(2) X and Y are
 ${\mathbb A}^1$
-h-cobordant.
${\mathbb A}^1$
-h-cobordant. -
(3)
 $\mathrm {det}(\mathcal {E}) \otimes \mathrm {det}(\mathcal {F})^{-1} = \mathcal {L}^{\otimes n+1}$
, for some
$\mathrm {det}(\mathcal {E}) \otimes \mathrm {det}(\mathcal {F})^{-1} = \mathcal {L}^{\otimes n+1}$
, for some
 $\mathcal {L} \in \mathrm {Pic} (C)$
.
$\mathcal {L} \in \mathrm {Pic} (C)$
.
In another application of our theorem, we answer a question raised in [Reference Asok, Kebekus and Wendt2]: whether a variety which is
![]() ${\mathbb A}^1$
-h-cobordant to a
${\mathbb A}^1$
-h-cobordant to a
![]() ${\mathbb P}^1$
-bundle over
${\mathbb P}^1$
-bundle over
![]() ${\mathbb P}^2$
has a structure of
${\mathbb P}^2$
has a structure of
![]() ${\mathbb P}^1$
-bundle over
${\mathbb P}^1$
-bundle over
![]() ${\mathbb P}^2$
. The answer is no and we prove in the following theorem that the suggested example in op. cit. indeed works.
${\mathbb P}^2$
. The answer is no and we prove in the following theorem that the suggested example in op. cit. indeed works.
Theorem 1.3. Let
![]() $ X:={\mathbb P}_{{\mathbb P}^1}(\mathcal {E})$
, where
$ X:={\mathbb P}_{{\mathbb P}^1}(\mathcal {E})$
, where
![]() $ \mathcal {E} := \mathcal {O} \oplus \mathcal {O}(-1) \oplus \mathcal {O}(1)$
on
$ \mathcal {E} := \mathcal {O} \oplus \mathcal {O}(-1) \oplus \mathcal {O}(1)$
on
![]() ${\mathbb P}^1_k$
(where k is an infinite field). Then X is
${\mathbb P}^1_k$
(where k is an infinite field). Then X is
![]() ${\mathbb A}^1$
-h-cobordant to
${\mathbb A}^1$
-h-cobordant to
![]() ${\mathbb P}^1_k \times {\mathbb P}^2_k$
but doesn’t have the structure of a
${\mathbb P}^1_k \times {\mathbb P}^2_k$
but doesn’t have the structure of a
![]() ${\mathbb P}^1_k$
-bundle over
${\mathbb P}^1_k$
-bundle over
![]() ${\mathbb P}^2_k$
.
${\mathbb P}^2_k$
.
2 Classification of vector bundles on a curve up to
 ${\mathbb A}^1$
-concordance
${\mathbb A}^1$
-concordance
In this section, we classify vector bundles on a curve up to
![]() ${\mathbb A}^1$
-concordance (Theorem 2.5) and obtain the proof of Theorem 1.1 as a consequence of that. Recall the following definition from [Reference Asok, Kebekus and Wendt2].
${\mathbb A}^1$
-concordance (Theorem 2.5) and obtain the proof of Theorem 1.1 as a consequence of that. Recall the following definition from [Reference Asok, Kebekus and Wendt2].
Definition 2.1. [Reference Asok, Kebekus and Wendt2, Definition 5.1]
Let X be a scheme over a field k. Then two given vector bundles
![]() $\mathcal {E}_0$
and
$\mathcal {E}_0$
and
![]() $\mathcal {E}_1$
on X are said to be directly
$\mathcal {E}_1$
on X are said to be directly
![]() ${\mathbb A}^1$
-concordant if there exists a vector bundle
${\mathbb A}^1$
-concordant if there exists a vector bundle
![]() $\mathcal {E}$
on
$\mathcal {E}$
on
![]() $X \times {\mathbb A}^1$
such that
$X \times {\mathbb A}^1$
such that
![]() $i_0^{\ast }\mathcal {E} \cong \mathcal {E}_0$
and
$i_0^{\ast }\mathcal {E} \cong \mathcal {E}_0$
and
![]() $i_1^{\ast }\mathcal {E} \cong \mathcal {E}_1$
, where
$i_1^{\ast }\mathcal {E} \cong \mathcal {E}_1$
, where
![]() $i_k: X \times \{k\} \hookrightarrow X \times {\mathbb A}^1$
, for
$i_k: X \times \{k\} \hookrightarrow X \times {\mathbb A}^1$
, for
![]() $k=0,1$
.
$k=0,1$
.
![]() $\mathcal {E}_0$
and
$\mathcal {E}_0$
and
![]() $\mathcal {E}_1$
on X are
$\mathcal {E}_1$
on X are
![]() ${\mathbb A}^1$
-concordant if they are equivalent under the equivalence relation generated by direct
${\mathbb A}^1$
-concordant if they are equivalent under the equivalence relation generated by direct
![]() ${\mathbb A}^1$
-concordance.
${\mathbb A}^1$
-concordance.
Lemma 2.2. Let
![]() $\mathcal {E}_0$
and
$\mathcal {E}_0$
and
![]() $\mathcal {E}_1$
be
$\mathcal {E}_1$
be
![]() ${\mathbb A}^1$
-concordant vector bundles on a normal variety X, and let
${\mathbb A}^1$
-concordant vector bundles on a normal variety X, and let
![]() $\mathcal {V}$
be a vector bundle on
$\mathcal {V}$
be a vector bundle on
![]() $X\times {\mathbb A}^1$
. Then
$X\times {\mathbb A}^1$
. Then
![]() $(i_0^{\ast }(\mathcal {V}) \otimes \mathcal {L}) \oplus \mathcal {E}_0$
and
$(i_0^{\ast }(\mathcal {V}) \otimes \mathcal {L}) \oplus \mathcal {E}_0$
and
![]() $(i_1^{\ast }(\mathcal {V}) \otimes \mathcal {L}) \oplus \mathcal {E}_1$
are
$(i_1^{\ast }(\mathcal {V}) \otimes \mathcal {L}) \oplus \mathcal {E}_1$
are
![]() ${\mathbb A}^1$
-concordant, for any
${\mathbb A}^1$
-concordant, for any
![]() $\mathcal {L} \in \mathrm {Pic} (X)$
.
$\mathcal {L} \in \mathrm {Pic} (X)$
.
Proof. It is enough to prove the lemma in the case when
![]() $\mathcal {E}_0$
and
$\mathcal {E}_0$
and
![]() $\mathcal {E}_1$
are directly
$\mathcal {E}_1$
are directly
![]() ${\mathbb A}^1$
-concordant. Let the direct
${\mathbb A}^1$
-concordant. Let the direct
![]() ${\mathbb A}^1$
-concordance be given by a vector bundle
${\mathbb A}^1$
-concordance be given by a vector bundle
![]() $\mathcal {E}$
on
$\mathcal {E}$
on
![]() $X \times {\mathbb A}^1$
. Note that
$X \times {\mathbb A}^1$
. Note that
![]() $p^{\ast } : \mathrm {Pic} (X) \rightarrow \mathrm {Pic} (X \times {\mathbb A}^1)$
(where
$p^{\ast } : \mathrm {Pic} (X) \rightarrow \mathrm {Pic} (X \times {\mathbb A}^1)$
(where
![]() $p: X \times {\mathbb A}^1 \rightarrow X$
) is an isomorphism (see [Reference Hartshorne5, II, Prop. 6.6]) with the inverse given by
$p: X \times {\mathbb A}^1 \rightarrow X$
) is an isomorphism (see [Reference Hartshorne5, II, Prop. 6.6]) with the inverse given by
![]() $i_0^{\ast } = i_1^{\ast }$
. Then the lemma immediately follows from the definition by considering the vector bundle
$i_0^{\ast } = i_1^{\ast }$
. Then the lemma immediately follows from the definition by considering the vector bundle
![]() $(\mathcal {V} \otimes p^{\ast }\mathcal {L}) \oplus \mathcal {E}$
and the fact that the pullback functor commutes with the direct sums.
$(\mathcal {V} \otimes p^{\ast }\mathcal {L}) \oplus \mathcal {E}$
and the fact that the pullback functor commutes with the direct sums.
In light of the previous lemma, the following corollary is rather obvious, but we state it nevertheless, keeping in mind its direct application in the proof of Theorem 1.1.
Corollary 2.3. Let
![]() $\mathcal {E}_0$
and
$\mathcal {E}_0$
and
![]() $\mathcal {E}_1$
be
$\mathcal {E}_1$
be
![]() ${\mathbb A}^1$
-concordant vector bundles on a normal variety X Then the following statements hold:
${\mathbb A}^1$
-concordant vector bundles on a normal variety X Then the following statements hold:
-
(1)
 $\mathcal {O}_X^n \oplus \mathcal {E}_0$
and
$\mathcal {O}_X^n \oplus \mathcal {E}_0$
and
 $\mathcal {O}_X^n \oplus \mathcal {E}_1$
are
$\mathcal {O}_X^n \oplus \mathcal {E}_1$
are
 ${\mathbb A}^1$
-concordant for any
${\mathbb A}^1$
-concordant for any
 $n \geq 0$
.
$n \geq 0$
. -
(2)
 $\mathcal {O}_X(m) \oplus \mathcal {E}_0$
and
$\mathcal {O}_X(m) \oplus \mathcal {E}_0$
and
 $\mathcal {O}_X(m) \oplus \mathcal {E}_1$
are
$\mathcal {O}_X(m) \oplus \mathcal {E}_1$
are
 ${\mathbb A}^1$
-concordant for any m.
${\mathbb A}^1$
-concordant for any m.
Proof. For the first statement, take
![]() $\mathcal {V} = \mathcal {O}_{X \times {\mathbb A}^1}^n$
, keeping the notation of the previous lemma in mind.
$\mathcal {V} = \mathcal {O}_{X \times {\mathbb A}^1}^n$
, keeping the notation of the previous lemma in mind.
For the second statement, take
![]() $\mathcal {V} = \mathcal {O}_{X \times {\mathbb A}^1}$
and
$\mathcal {V} = \mathcal {O}_{X \times {\mathbb A}^1}$
and
![]() $\mathcal {L} = p^{\ast } \mathcal {O}_X(m)$
.
$\mathcal {L} = p^{\ast } \mathcal {O}_X(m)$
.
2.1
 ${\mathbb A}^1$
-concordance via Ext classes
${\mathbb A}^1$
-concordance via Ext classes
Now we look at a way of constructing
![]() ${\mathbb A}^1$
-concordance between vector bundles.
${\mathbb A}^1$
-concordance between vector bundles.
Proposition 2.4. Let
![]() $0 \rightarrow \mathcal {E}_0 \rightarrow \mathcal {E} \rightarrow \mathcal {E}_1 \rightarrow 0$
be any short exact sequence of vector bundles on a projective scheme X over a field k. Then
$0 \rightarrow \mathcal {E}_0 \rightarrow \mathcal {E} \rightarrow \mathcal {E}_1 \rightarrow 0$
be any short exact sequence of vector bundles on a projective scheme X over a field k. Then
![]() $\mathcal {E}$
is directly
$\mathcal {E}$
is directly
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {E}_0 \oplus \mathcal {E}_1$
.
$\mathcal {E}_0 \oplus \mathcal {E}_1$
.
Proof. Consider
![]() $\mathcal {E}$
as an element in
$\mathcal {E}$
as an element in
![]() $\mathrm {Ext}^1(\mathcal {E}_1, \mathcal {E}_0)$
. If
$\mathrm {Ext}^1(\mathcal {E}_1, \mathcal {E}_0)$
. If
![]() $\mathcal {E}$
is trivial, then our claim is obvious, so assume to the contrary. Consider the moduli functor
$\mathcal {E}$
is trivial, then our claim is obvious, so assume to the contrary. Consider the moduli functor
![]() $\boldsymbol {\mathrm {Ext}^1}(\mathcal {E}_1, \mathcal {E}_0)$
given by
$\boldsymbol {\mathrm {Ext}^1}(\mathcal {E}_1, \mathcal {E}_0)$
given by
![]() $Y \mapsto \mathrm {Ext}^1(p^{\ast }\mathcal {E}_1, p^{\ast }\mathcal {E}_0)$
, where
$Y \mapsto \mathrm {Ext}^1(p^{\ast }\mathcal {E}_1, p^{\ast }\mathcal {E}_0)$
, where
![]() $p: X \times Y \rightarrow X$
. It is well-known ([Reference Lange7, Proposition 3.1]) that this functor is representable by
$p: X \times Y \rightarrow X$
. It is well-known ([Reference Lange7, Proposition 3.1]) that this functor is representable by
![]() ${\mathbb A}^n_k$
, where
${\mathbb A}^n_k$
, where
![]() $n= \mathrm {dim}(\mathrm {Ext}^1(\mathcal {E}_1, \mathcal {E}_0))$
as a vector space over k and
$n= \mathrm {dim}(\mathrm {Ext}^1(\mathcal {E}_1, \mathcal {E}_0))$
as a vector space over k and
![]() $n>0$
by the assumption that
$n>0$
by the assumption that
![]() $\mathcal {E}$
is nontrivial. Therefore, by representability, there is a universal class
$\mathcal {E}$
is nontrivial. Therefore, by representability, there is a universal class
![]() $\mathcal {V}$
(of vector bundle) on
$\mathcal {V}$
(of vector bundle) on
![]() $X \times {\mathbb A}^n_k$
whose pullback to
$X \times {\mathbb A}^n_k$
whose pullback to
![]() $X\times {t_i} \hookrightarrow X \times {\mathbb A}^n_k$
,
$X\times {t_i} \hookrightarrow X \times {\mathbb A}^n_k$
,
![]() $i=0,1$
is
$i=0,1$
is
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\mathcal {E}_0 \oplus \mathcal {E}_1$
respectively for some k-rational points
$\mathcal {E}_0 \oplus \mathcal {E}_1$
respectively for some k-rational points
![]() $t_i \in {\mathbb A}^n_k$
. For any two given k-rational points in
$t_i \in {\mathbb A}^n_k$
. For any two given k-rational points in
![]() ${\mathbb A}^n_k$
(in our case
${\mathbb A}^n_k$
(in our case
![]() $t_0$
and
$t_0$
and
![]() $t_1$
), there is a closed embedding
$t_1$
), there is a closed embedding
![]() $i:{\mathbb A}^1_k \hookrightarrow {\mathbb A}^n_k$
such that the composition
$i:{\mathbb A}^1_k \hookrightarrow {\mathbb A}^n_k$
such that the composition
![]() $\mathrm {Spec \,} k \xrightarrow {0} {\mathbb A}^1_k \xrightarrow {i}{\mathbb A}^n_k$
is
$\mathrm {Spec \,} k \xrightarrow {0} {\mathbb A}^1_k \xrightarrow {i}{\mathbb A}^n_k$
is
![]() $t_0$
and the composition
$t_0$
and the composition
![]() $\mathrm {Spec \,} k \xrightarrow {1} {\mathbb A}^1_k\xrightarrow {i} {\mathbb A}^n_k$
is
$\mathrm {Spec \,} k \xrightarrow {1} {\mathbb A}^1_k\xrightarrow {i} {\mathbb A}^n_k$
is
![]() $t_1$
. Now consider the pullback of the universal class,
$t_1$
. Now consider the pullback of the universal class,
![]() $(id_X \times i)^{\ast }\mathcal {V}$
, via the map
$(id_X \times i)^{\ast }\mathcal {V}$
, via the map
![]() $id_X \times i : X \times {\mathbb A}^1_k \to X \times {\mathbb A}^n_k$
. By construction, the vector bundle
$id_X \times i : X \times {\mathbb A}^1_k \to X \times {\mathbb A}^n_k$
. By construction, the vector bundle
![]() $(id_X \times i)^{\ast }\mathcal {V}$
on
$(id_X \times i)^{\ast }\mathcal {V}$
on
![]() $X \times {\mathbb A}^1_k$
gives a direct
$X \times {\mathbb A}^1_k$
gives a direct
![]() ${\mathbb A}^1$
-concordance between
${\mathbb A}^1$
-concordance between
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\mathcal {E}_0 \oplus \mathcal {E}_1$
$\mathcal {E}_0 \oplus \mathcal {E}_1$
2.2 Classification result and proof of Theorem 1.1
Theorem 2.5. Let
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\mathcal {F}$
be rank n vector bundles on the curve C. Then the following hold:
$\mathcal {F}$
be rank n vector bundles on the curve C. Then the following hold:
-
(1)
 $\mathcal {E}$
is
$\mathcal {E}$
is
 ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
 $\mathcal {O}_C^{n-1} \oplus \det (\mathcal {E})$
.
$\mathcal {O}_C^{n-1} \oplus \det (\mathcal {E})$
. -
(2)
 $\mathcal {E}$
is
$\mathcal {E}$
is
 ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
 $\mathcal {F}$
iff
$\mathcal {F}$
iff
 $\det (\mathcal {E}) \cong \det (\mathcal {F})$
.
$\det (\mathcal {E}) \cong \det (\mathcal {F})$
.
Proof. We first prove (1) for the case when
![]() $n = 2$
. For the general case we will use induction.
$n = 2$
. For the general case we will use induction.
Case 1:
![]() $n=2$
. First, assume
$n=2$
. First, assume
![]() $\mathcal {E}$
is globally generated and denote
$\mathcal {E}$
is globally generated and denote
![]() $\det (\mathcal {E})$
by
$\det (\mathcal {E})$
by
![]() $\mathcal {L}$
. Then, by [Reference Hartshorne5, II, Exercise 8.2], we have the following short exact sequence
$\mathcal {L}$
. Then, by [Reference Hartshorne5, II, Exercise 8.2], we have the following short exact sequence
where
![]() $\mathcal {E}'$
is a line bundle. By the Whitney sum formula of Chern classes ([Reference Eisenbud and Harris4, Theorem 5.3(c)])
$\mathcal {E}'$
is a line bundle. By the Whitney sum formula of Chern classes ([Reference Eisenbud and Harris4, Theorem 5.3(c)])
Therefore, by Proposition 2.4,
![]() $\mathcal {E}$
is directly
$\mathcal {E}$
is directly
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {O}_C \oplus \mathcal {L}$
. For a general
$\mathcal {O}_C \oplus \mathcal {L}$
. For a general
![]() $\mathcal {E}$
, choose
$\mathcal {E}$
, choose
![]() $m>>0$
such that
$m>>0$
such that
![]() $\mathcal {E}(m)$
,
$\mathcal {E}(m)$
,
![]() $\mathcal {L}(m)$
are globally generated. Then again, by applying [Reference Hartshorne5, II, Exercise 8.2], we get a short exact sequence for
$\mathcal {L}(m)$
are globally generated. Then again, by applying [Reference Hartshorne5, II, Exercise 8.2], we get a short exact sequence for
![]() $\mathcal {E}(m)$
which we tensor by
$\mathcal {E}(m)$
which we tensor by
![]() $\mathcal {O}(-m) $
to obtain the following short exact sequence.
$\mathcal {O}(-m) $
to obtain the following short exact sequence.
This proves
![]() $\mathcal {E}$
is directly
$\mathcal {E}$
is directly
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {O}_C(-m) \oplus \mathcal {L}(m)$
. As the final step, we now prove that
$\mathcal {O}_C(-m) \oplus \mathcal {L}(m)$
. As the final step, we now prove that
![]() $\mathcal {O}_C(-m) \oplus \mathcal {L}(m)$
is directly
$\mathcal {O}_C(-m) \oplus \mathcal {L}(m)$
is directly
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {O}_C \oplus \mathcal {L}$
. Note that m is chosen such that
$\mathcal {O}_C \oplus \mathcal {L}$
. Note that m is chosen such that
![]() $\mathcal {L}(m)$
is globally generated, therefore
$\mathcal {L}(m)$
is globally generated, therefore
![]() $\mathcal {O}_C(m) \oplus \mathcal {L}(m)$
is globally generated. Hence, we have a short exact sequence which shows
$\mathcal {O}_C(m) \oplus \mathcal {L}(m)$
is globally generated. Hence, we have a short exact sequence which shows
![]() $\mathcal {O}_C(-m) \oplus \mathcal {L}(m)$
is directly
$\mathcal {O}_C(-m) \oplus \mathcal {L}(m)$
is directly
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {O}_C \oplus \mathcal {L}$
.
$\mathcal {O}_C \oplus \mathcal {L}$
.
Therefore,
![]() $\mathcal {E}$
is
$\mathcal {E}$
is
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {O}_C\oplus \mathcal {L}$
.
$\mathcal {O}_C\oplus \mathcal {L}$
.
Case 2: Now we handle the general case. So assume
![]() $n>2$
and choose m such that
$n>2$
and choose m such that
![]() $\mathcal {E}(m)$
and
$\mathcal {E}(m)$
and
![]() $\mathcal {L}(m)$
are globally generated. Then we have a short exact sequence giving a direct
$\mathcal {L}(m)$
are globally generated. Then we have a short exact sequence giving a direct
![]() ${\mathbb A}^1$
-concordance between
${\mathbb A}^1$
-concordance between
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\mathcal {O}_C(-m) \oplus \mathcal {E}'$
, where
$\mathcal {O}_C(-m) \oplus \mathcal {E}'$
, where
![]() $\mathcal {E}'$
is a vector bundle of rank
$\mathcal {E}'$
is a vector bundle of rank
![]() $n-1$
with determinant
$n-1$
with determinant
![]() $\mathcal {L}(m)$
. By induction,
$\mathcal {L}(m)$
. By induction,
![]() $\mathcal {E}'$
is
$\mathcal {E}'$
is
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {O}_C^{n-2} \oplus \mathcal {L}(m)$
. Therefore, by the second statement of Corollary 2.3, we have an
$\mathcal {O}_C^{n-2} \oplus \mathcal {L}(m)$
. Therefore, by the second statement of Corollary 2.3, we have an
![]() ${\mathbb A}^1$
-concordance between
${\mathbb A}^1$
-concordance between
![]() $\mathcal {O}_C(-m)\oplus \mathcal {O}_C^{n-2} \oplus \mathcal {L}(m)$
and
$\mathcal {O}_C(-m)\oplus \mathcal {O}_C^{n-2} \oplus \mathcal {L}(m)$
and
![]() $\mathcal {O}_C(-m) \oplus \mathcal {E}'$
. Hence,
$\mathcal {O}_C(-m) \oplus \mathcal {E}'$
. Hence,
![]() $\mathcal {E}$
is
$\mathcal {E}$
is
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {O}(-m)\oplus \mathcal {O}_C^{n-2} \oplus \mathcal {L}(m)$
. Now by the short exact sequence 2.3,
$\mathcal {O}(-m)\oplus \mathcal {O}_C^{n-2} \oplus \mathcal {L}(m)$
. Now by the short exact sequence 2.3,
![]() $\mathcal {O}_C\oplus \mathcal {L}$
is directly
$\mathcal {O}_C\oplus \mathcal {L}$
is directly
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {O}_C(-m) \oplus \mathcal {L}(m)$
, which implies, by the first statement of Corollary 2.3, that
$\mathcal {O}_C(-m) \oplus \mathcal {L}(m)$
, which implies, by the first statement of Corollary 2.3, that
![]() $\mathcal {O}(-m)\oplus \mathcal {O}_C^{n-2} \oplus \mathcal {L}(m)$
is directly
$\mathcal {O}(-m)\oplus \mathcal {O}_C^{n-2} \oplus \mathcal {L}(m)$
is directly
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {O}_C^{n-1} \oplus \mathcal {L}$
, thus finishing the proof of (1).
$\mathcal {O}_C^{n-1} \oplus \mathcal {L}$
, thus finishing the proof of (1).
For proving (2), we first observe that if
![]() $\det (\mathcal {E}) \cong \det (\mathcal {F})$
, then (1) implies that
$\det (\mathcal {E}) \cong \det (\mathcal {F})$
, then (1) implies that
![]() $\mathcal {E}$
is
$\mathcal {E}$
is
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {F}$
. Hence, it remains to show that if
$\mathcal {F}$
. Hence, it remains to show that if
![]() $\mathcal {E}$
is directly
$\mathcal {E}$
is directly
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {F}$
, then
$\mathcal {F}$
, then
![]() $\mathrm {det}(\mathcal {E})\cong \mathrm {det}(\mathcal {F})$
.
$\mathrm {det}(\mathcal {E})\cong \mathrm {det}(\mathcal {F})$
.
So assume that
![]() $\mathcal {E}$
is directly
$\mathcal {E}$
is directly
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {F}$
, which by definition gives us a vector bundle
$\mathcal {F}$
, which by definition gives us a vector bundle
![]() $\mathcal {E}'$
on
$\mathcal {E}'$
on
![]() $C \times {\mathbb A}^1$
such that
$C \times {\mathbb A}^1$
such that
![]() $i_0^{\ast }\mathcal {E}' \cong \mathcal {E}$
and
$i_0^{\ast }\mathcal {E}' \cong \mathcal {E}$
and
![]() $i_1^{\ast }\mathcal {E}' \cong \mathcal {F}$
. We have
$i_1^{\ast }\mathcal {E}' \cong \mathcal {F}$
. We have
![]() $ c_1(\mathrm {det}\mathcal {E}) = c_1(i_{0}^{\ast }\mathcal {E}') = i_0^{\ast }(c_1(\mathcal {E}'))$
, where the first equality follows from the isomorphism
$ c_1(\mathrm {det}\mathcal {E}) = c_1(i_{0}^{\ast }\mathcal {E}') = i_0^{\ast }(c_1(\mathcal {E}'))$
, where the first equality follows from the isomorphism
![]() $i_0^{\ast }\mathcal {E}' \cong \mathcal {E}$
and the fact that for any vector bundle
$i_0^{\ast }\mathcal {E}' \cong \mathcal {E}$
and the fact that for any vector bundle
![]() $\mathcal {V}$
,
$\mathcal {V}$
,
![]() $c_1(\mathcal {V})=c_1(\mathrm {det}\mathcal {V})$
, while the second equality is the functoriality of Chern classes ([Reference Eisenbud and Harris4, Theorem 5.3(d)]). Similarly, we have
$c_1(\mathcal {V})=c_1(\mathrm {det}\mathcal {V})$
, while the second equality is the functoriality of Chern classes ([Reference Eisenbud and Harris4, Theorem 5.3(d)]). Similarly, we have
![]() $ c_1(\mathrm {det}\mathcal {F}) = c_1(i_{1}^{\ast }\mathcal {E}') = i_1^{\ast }(c_1(\mathcal {E}'))$
. Moreover,
$ c_1(\mathrm {det}\mathcal {F}) = c_1(i_{1}^{\ast }\mathcal {E}') = i_1^{\ast }(c_1(\mathcal {E}'))$
. Moreover,
![]() $(i_{0})^{\ast } = (i_{1})^{\ast }: \mathrm { CH}^1(C \times {\mathbb A}^1) \to \mathrm {CH}^1(C) $
, which implies
$(i_{0})^{\ast } = (i_{1})^{\ast }: \mathrm { CH}^1(C \times {\mathbb A}^1) \to \mathrm {CH}^1(C) $
, which implies
![]() $c_1(\mathrm {det}\mathcal {E})=c_1(\mathrm {det}\mathcal {F})$
Therefore,
$c_1(\mathrm {det}\mathcal {E})=c_1(\mathrm {det}\mathcal {F})$
Therefore,
![]() $\mathrm {det}(\mathcal {E}) \cong \mathrm {det}(\mathcal {F})$
.
$\mathrm {det}(\mathcal {E}) \cong \mathrm {det}(\mathcal {F})$
.
Before we proceed with the proof of Theorem 1.1, we recall some standard definitions.
Definition 2.6. Let
![]() $\mathcal {X}$
be a simplicial sheaf and U a scheme. Then x and y in
$\mathcal {X}$
be a simplicial sheaf and U a scheme. Then x and y in
![]() $\mathcal {X}(U)$
are said to be naively
$\mathcal {X}(U)$
are said to be naively
![]() ${\mathbb A}^1$
-homotopic if there exists
${\mathbb A}^1$
-homotopic if there exists
![]() $f: {\mathbb A}^1_U \rightarrow \mathcal {X}$
such that
$f: {\mathbb A}^1_U \rightarrow \mathcal {X}$
such that
![]() $f_0 = x$
and
$f_0 = x$
and
![]() $f_1 =y$
, where
$f_1 =y$
, where
![]() $f_i $
is the composition
$f_i $
is the composition
![]() $ U \xrightarrow {i} {\mathbb A}^1_U \xrightarrow {f} \mathcal {X}$
, for
$ U \xrightarrow {i} {\mathbb A}^1_U \xrightarrow {f} \mathcal {X}$
, for
![]() $i=0,1$
.
$i=0,1$
.
Definition 2.7. For a given simplicial sheaf
![]() $\mathcal {X}$
, we define
$\mathcal {X}$
, we define
![]() $\mathcal {S}(\mathcal {X})$
to be the Nisnevich sheafification of the presheaf
$\mathcal {S}(\mathcal {X})$
to be the Nisnevich sheafification of the presheaf
![]() $U \mapsto \mathcal {X}(U)/\sim $
, where
$U \mapsto \mathcal {X}(U)/\sim $
, where
![]() $\sim $
is the equivalence relation generated by naive
$\sim $
is the equivalence relation generated by naive
![]() ${\mathbb A}^1$
-homotopies.
${\mathbb A}^1$
-homotopies.
The following standard lemma will be required in our proof. It is essentially [Reference Morel and Voevodsky11, Section 2, Corollary 3.22] combined with [Reference Morel9, Lemma 6.1.3.],
Lemma 2.8. A simplicial sheaf
![]() $\mathcal {X}$
is
$\mathcal {X}$
is
![]() ${\mathbb A}^1$
-connected if
${\mathbb A}^1$
-connected if
![]() $\mathcal {S}(\mathcal {X})(F) = \ast $
for every finitely generated field extension F over k.
$\mathcal {S}(\mathcal {X})(F) = \ast $
for every finitely generated field extension F over k.
Now we have all the ingredients in place to prove Theorem 1.1.
Proof of Theorem 1.1
We regard
![]() $Bun_{n,\mathcal {L}}$
as a simplicial sheaf. By definition, any two F-valued points of
$Bun_{n,\mathcal {L}}$
as a simplicial sheaf. By definition, any two F-valued points of
![]() $Bun_{n,\mathcal {L}}$
are two rank n (with determinant condition) vector bundles, say
$Bun_{n,\mathcal {L}}$
are two rank n (with determinant condition) vector bundles, say
![]() $\mathcal {E}_0$
and
$\mathcal {E}_0$
and
![]() $\mathcal {E}_1$
on C. A morphism
$\mathcal {E}_1$
on C. A morphism
![]() ${\mathbb A}^1_F \rightarrow Bun_{n,\mathcal {L}}$
is a vector bundle
${\mathbb A}^1_F \rightarrow Bun_{n,\mathcal {L}}$
is a vector bundle
![]() $\mathcal {E}$
on
$\mathcal {E}$
on
![]() $C \times {\mathbb A}^1$
. Then
$C \times {\mathbb A}^1$
. Then
![]() $\mathcal {E}_0$
and
$\mathcal {E}_0$
and
![]() $\mathcal {E}_1$
are naively
$\mathcal {E}_1$
are naively
![]() ${\mathbb A}^1$
-homotopic if and only if they are
${\mathbb A}^1$
-homotopic if and only if they are
![]() ${\mathbb A}^1$
-concordant. By Theorem 2.5, both
${\mathbb A}^1$
-concordant. By Theorem 2.5, both
![]() $\mathcal {E}_0$
and
$\mathcal {E}_0$
and
![]() $\mathcal {E}_1$
are
$\mathcal {E}_1$
are
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {O}_C^{n-1} \oplus \mathcal {L}$
. Hence, they are
$\mathcal {O}_C^{n-1} \oplus \mathcal {L}$
. Hence, they are
![]() ${\mathbb A}^1$
-concordant to each other. Therefore, by Lemma 2.8,
${\mathbb A}^1$
-concordant to each other. Therefore, by Lemma 2.8,
![]() $Bun_{n,\mathcal {L}}$
is
$Bun_{n,\mathcal {L}}$
is
![]() ${\mathbb A}^1$
-connected.
${\mathbb A}^1$
-connected.
Motivated by the question of
![]() ${\mathbb A}^1$
-connectedness of moduli stack of stable vector bundles, we observe in the example below that there does not seem to be an immediate way of concluding
${\mathbb A}^1$
-connectedness of moduli stack of stable vector bundles, we observe in the example below that there does not seem to be an immediate way of concluding
![]() ${\mathbb A}^1$
-connectedness of a stack by looking at its coarse moduli space.
${\mathbb A}^1$
-connectedness of a stack by looking at its coarse moduli space.
Example 2.9. Let C be a curve of genus
![]() $2$
over a field with characteristics not equal to
$2$
over a field with characteristics not equal to
![]() $2$
. In particular, it is a hyperelliptic curve (See [Reference Hartshorne5, IV, Exercise 1.7(a)]). Therefore, there is a finite morphism
$2$
. In particular, it is a hyperelliptic curve (See [Reference Hartshorne5, IV, Exercise 1.7(a)]). Therefore, there is a finite morphism
![]() $f: C \rightarrow {\mathbb P}^1$
of degree
$f: C \rightarrow {\mathbb P}^1$
of degree
![]() $2$
, and we have an action of the finite group
$2$
, and we have an action of the finite group
![]() $G:={\mathbb Z}/2{\mathbb Z}$
on C. By [Reference Hartshorne5, IV, Exercise 2.2(a)], such a morphism is unramified at all but 6 points (denoted as closed subscheme
$G:={\mathbb Z}/2{\mathbb Z}$
on C. By [Reference Hartshorne5, IV, Exercise 2.2(a)], such a morphism is unramified at all but 6 points (denoted as closed subscheme
![]() $Z'$
) of C. So the action of G is free on
$Z'$
) of C. So the action of G is free on
![]() $C \setminus Z'$
. Let Z denote the closed subset in
$C \setminus Z'$
. Let Z denote the closed subset in
![]() ${\mathbb P}^1$
corresponding to the 6 branched points. The quotient stack
${\mathbb P}^1$
corresponding to the 6 branched points. The quotient stack
![]() $\big [C/G\big ]$
has coarse moduli space
$\big [C/G\big ]$
has coarse moduli space
![]() ${\mathbb P}^1$
, and the morphism
${\mathbb P}^1$
, and the morphism
![]() $\pi : \big [C/G\big ] \rightarrow {\mathbb P}^1$
gives an isomorphism of an open subscheme of
$\pi : \big [C/G\big ] \rightarrow {\mathbb P}^1$
gives an isomorphism of an open subscheme of
![]() $\big [C/G\big ] $
with
$\big [C/G\big ] $
with
![]() ${\mathbb P}^1 \setminus Z$
. See [Reference Olsson12, Example 8.1.12] for more details on quotient stacks.
${\mathbb P}^1 \setminus Z$
. See [Reference Olsson12, Example 8.1.12] for more details on quotient stacks.
Let
![]() $E(G)$
denote the simplicially contractible, simplicial sheaf with
$E(G)$
denote the simplicially contractible, simplicial sheaf with
![]() $E(G)_n = G^{n+1}$
(See [Reference Morel and Voevodsky11, Example 1.11, page 128]). The morphism
$E(G)_n = G^{n+1}$
(See [Reference Morel and Voevodsky11, Example 1.11, page 128]). The morphism
![]() $C \to \big [C/G\big ] $
is a G-torsor. Moreover, G acts freely on the space
$C \to \big [C/G\big ] $
is a G-torsor. Moreover, G acts freely on the space
![]() $E(G) \times C$
and
$E(G) \times C$
and
![]() $(E(G) \times C)/G \simeq \big [C/G\big ] $
.
$(E(G) \times C)/G \simeq \big [C/G\big ] $
.
![]() $\pi _0^{{\mathbb A}^1}(G) \cong {\mathbb Z}/2{\mathbb Z}$
, being a finite abelian group, is a strictly
$\pi _0^{{\mathbb A}^1}(G) \cong {\mathbb Z}/2{\mathbb Z}$
, being a finite abelian group, is a strictly
![]() ${\mathbb A}^1$
-invariant sheaf. So all the hypotheses of the statement of [Reference Morel10, Theorem 6.50] are satisfied, as a consequence of which we obtain the following long exact sequence of
${\mathbb A}^1$
-invariant sheaf. So all the hypotheses of the statement of [Reference Morel10, Theorem 6.50] are satisfied, as a consequence of which we obtain the following long exact sequence of
![]() ${\mathbb A}^1$
-homotopy groups/pointed sets, where
${\mathbb A}^1$
-homotopy groups/pointed sets, where
![]() $\ast $
is a chosen basepoint.
$\ast $
is a chosen basepoint.
But on the account of
![]() $E(G)$
being simplicially contractible and C being
$E(G)$
being simplicially contractible and C being
![]() ${\mathbb A}^1$
-rigid (as all curves of genus
${\mathbb A}^1$
-rigid (as all curves of genus
![]() $g> 0$
are),
$g> 0$
are),
![]() $\pi _0^{{\mathbb A}^1}(E(G) \times C) \cong \pi _0^{{\mathbb A}^1}(C) \cong C $
. So by long exact sequence,
$\pi _0^{{\mathbb A}^1}(E(G) \times C) \cong \pi _0^{{\mathbb A}^1}(C) \cong C $
. So by long exact sequence,
![]() $\big [C/G\big ]$
being
$\big [C/G\big ]$
being
![]() ${\mathbb A}^1$
-connected would imply surjection of finite group
${\mathbb A}^1$
-connected would imply surjection of finite group
![]() ${\mathbb Z}/2{\mathbb Z}$
on
${\mathbb Z}/2{\mathbb Z}$
on
![]() $C \cong \pi _0^{{\mathbb A}^1}(C)$
, which cannot happen.
$C \cong \pi _0^{{\mathbb A}^1}(C)$
, which cannot happen.
Remark 2.10. By definition, any hyperelliptic curve of genus g admits a finite map of degree
![]() $2$
to
$2$
to
![]() ${\mathbb P}^1$
. By Hurwitz’s theorem, such a morphism has
${\mathbb P}^1$
. By Hurwitz’s theorem, such a morphism has
![]() $2g+2$
ramified points. Therefore, Example 2.9 can be generalised to an hyperelliptic curve of any genus (which is necessarily greater than 1).
$2g+2$
ramified points. Therefore, Example 2.9 can be generalised to an hyperelliptic curve of any genus (which is necessarily greater than 1).
3 Applications
As applications of the results in the previous section, we give a proof of Theorem 1.2 and Theorem 1.3. We first recall the following definition from [Reference Asok and Morel3].
Definition 3.1. [Reference Asok and Morel3, Definition 3.1.1]
Let
![]() $X_0$
and
$X_0$
and
![]() $X_1 $
be smooth and proper varieties over k. They are directly
$X_1 $
be smooth and proper varieties over k. They are directly
![]() ${\mathbb A}^1$
-h- cobordant if there exists a smooth scheme X with
${\mathbb A}^1$
-h- cobordant if there exists a smooth scheme X with
![]() $f: X \rightarrow {\mathbb A}^1$
a proper surjective morphism such that
$f: X \rightarrow {\mathbb A}^1$
a proper surjective morphism such that
-
(1) the fibers of f over
 $0$
and
$0$
and
 $1$
are
$1$
are
 $X_0$
and
$X_0$
and
 $X_1$
respectively
$X_1$
respectively -
(2) the natural maps
 $X_i \hookrightarrow X$
for
$X_i \hookrightarrow X$
for
 $i=0,1$
are
$i=0,1$
are
 ${\mathbb A}^1$
-weak equivalences.
${\mathbb A}^1$
-weak equivalences.
![]() $X_0$
and
$X_0$
and
![]() $X_1 $
are
$X_1 $
are
![]() ${\mathbb A}^1$
-h-cobordant if they are equivalent under the equivalence relation generated by direct
${\mathbb A}^1$
-h-cobordant if they are equivalent under the equivalence relation generated by direct
![]() ${\mathbb A}^1$
-h-cobordance.
${\mathbb A}^1$
-h-cobordance.
While
![]() ${\mathbb A}^1$
-concordance is a relation between vector bundles,
${\mathbb A}^1$
-concordance is a relation between vector bundles,
![]() ${\mathbb A}^1$
-h-cobordism a relation between proper schemes. Note that by [Reference Asok, Kebekus and Wendt2, Lemma 6.4], projectivizations of
${\mathbb A}^1$
-h-cobordism a relation between proper schemes. Note that by [Reference Asok, Kebekus and Wendt2, Lemma 6.4], projectivizations of
![]() ${\mathbb A}^1$
-concordant vector bundles are
${\mathbb A}^1$
-concordant vector bundles are
![]() ${\mathbb A}^1$
-h-cobordant.
${\mathbb A}^1$
-h-cobordant.
Recall that, given a locally free sheaf
![]() $\mathcal {E}$
of rank
$\mathcal {E}$
of rank
![]() $n+1$
on a scheme X, the associated
$n+1$
on a scheme X, the associated
![]() ${\mathbb P}^n$
-bundle, denoted
${\mathbb P}^n$
-bundle, denoted
![]() ${\mathbb P}_X(\mathcal {E})$
, is the scheme
${\mathbb P}_X(\mathcal {E})$
, is the scheme
![]() $\mathbf {{Proj}}_X(\mathrm {Sym}(\mathcal {E}))$
. Here,
$\mathbf {{Proj}}_X(\mathrm {Sym}(\mathcal {E}))$
. Here,
![]() $\mathbf {{Proj}}$
is the relative proj construction and
$\mathbf {{Proj}}$
is the relative proj construction and
![]() $\mathrm {Sym}(\mathcal {E})$
is the symmetric algebra of
$\mathrm {Sym}(\mathcal {E})$
is the symmetric algebra of
![]() $\mathcal {E}$
as an
$\mathcal {E}$
as an
![]() $\mathcal {O}_X$
-module. See [Reference Hartshorne5, II, page 162] for more details.
$\mathcal {O}_X$
-module. See [Reference Hartshorne5, II, page 162] for more details.
We now paraphrase the classification of
![]() ${\mathbb P}^n$
-bundles on
${\mathbb P}^n$
-bundles on
![]() ${\mathbb P}^1$
up to
${\mathbb P}^1$
up to
![]() ${\mathbb A}^1$
-weak equivalence proved in [Reference Asok and Morel3] to highlight that Theorem 1.2 is its direct generalisation to an arbitrary smooth projective curve.
${\mathbb A}^1$
-weak equivalence proved in [Reference Asok and Morel3] to highlight that Theorem 1.2 is its direct generalisation to an arbitrary smooth projective curve.
Proposition 3.2. [Reference Asok and Morel3, Proposition 3.2.10]
Let
![]() $X := {\mathbb P} (\mathcal {O}_{{\mathbb P}^1}^{n} \oplus \mathcal {O}_{{\mathbb P}^1}(a))$
and
$X := {\mathbb P} (\mathcal {O}_{{\mathbb P}^1}^{n} \oplus \mathcal {O}_{{\mathbb P}^1}(a))$
and
![]() $Y := {\mathbb P} (\mathcal {O}_{{\mathbb P}^1}^{n} \oplus \mathcal {O}_{{\mathbb P}^1}(b))$
be two
$Y := {\mathbb P} (\mathcal {O}_{{\mathbb P}^1}^{n} \oplus \mathcal {O}_{{\mathbb P}^1}(b))$
be two
![]() ${\mathbb P}^n$
-bundles over
${\mathbb P}^n$
-bundles over
![]() ${\mathbb P}^1$
. Then the following statements are equivalent:
${\mathbb P}^1$
. Then the following statements are equivalent:
-
(1) X and Y are
 ${\mathbb A}^1$
- weakly equivalent.
${\mathbb A}^1$
- weakly equivalent. -
(2) X and Y are
 ${\mathbb A}^1$
-h-cobordant.
${\mathbb A}^1$
-h-cobordant. -
(3)
 $n+1$
divides
$n+1$
divides
 $a-b$
.
$a-b$
.
Note that in case of
![]() $ C ={\mathbb P}^1$
, the condition
$ C ={\mathbb P}^1$
, the condition
![]() $\mathrm {det}(\mathcal {E}) \otimes \mathrm {det}(\mathcal {F})^{-1} = \mathcal {L}^{\otimes n+1}$
in Theorem 1.2 exactly translates to the fact that
$\mathrm {det}(\mathcal {E}) \otimes \mathrm {det}(\mathcal {F})^{-1} = \mathcal {L}^{\otimes n+1}$
in Theorem 1.2 exactly translates to the fact that
![]() $n+1$
divides
$n+1$
divides
![]() $a-b$
as stated in the Proposition 3.2. This is due to
$a-b$
as stated in the Proposition 3.2. This is due to
![]() $\mathrm {Pic}({\mathbb P}^1)$
being isomorphic to
$\mathrm {Pic}({\mathbb P}^1)$
being isomorphic to
![]() ${\mathbb Z}$
. For a general curve, Picard group is much more complicated and humongous (think of the Jacobian variety of a curve), so one doesn’t get any further simplification. We now prove Theorem 1.2, which is an extension of the previous proposition.
${\mathbb Z}$
. For a general curve, Picard group is much more complicated and humongous (think of the Jacobian variety of a curve), so one doesn’t get any further simplification. We now prove Theorem 1.2, which is an extension of the previous proposition.
Proof of Theorem 1.2
(3)
![]() $\implies $
(2): By Theorem 2.5,
$\implies $
(2): By Theorem 2.5,
![]() $\mathcal {E}$
is
$\mathcal {E}$
is
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {O}_C^{n} \oplus \mathcal {L}_1$
, where
$\mathcal {O}_C^{n} \oplus \mathcal {L}_1$
, where
![]() $\mathcal {L}_1 = \mathrm {det}(\mathcal {E})$
and
$\mathcal {L}_1 = \mathrm {det}(\mathcal {E})$
and
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() ${\mathbb A}^1$
-concordant to
${\mathbb A}^1$
-concordant to
![]() $\mathcal {O}_C^{n} \oplus \mathcal {L}_2$
, where
$\mathcal {O}_C^{n} \oplus \mathcal {L}_2$
, where
![]() $\mathcal {L}_2 = \mathrm {det}(\mathcal {F})$
. Hence, X and
$\mathcal {L}_2 = \mathrm {det}(\mathcal {F})$
. Hence, X and
![]() ${\mathbb P}_C(\mathcal {O}_C^{n} \oplus \mathcal {L}_1)$
are
${\mathbb P}_C(\mathcal {O}_C^{n} \oplus \mathcal {L}_1)$
are
![]() ${\mathbb A}^1$
-h-cobordant. In the exact same manner, Y and
${\mathbb A}^1$
-h-cobordant. In the exact same manner, Y and
![]() ${\mathbb P}_C(\mathcal {O}_C^{n} \oplus \mathcal {L}_2)$
are
${\mathbb P}_C(\mathcal {O}_C^{n} \oplus \mathcal {L}_2)$
are
![]() ${\mathbb A}^1$
-h-cobordant. Suppose
${\mathbb A}^1$
-h-cobordant. Suppose
![]() $\mathcal {L}_1 \otimes \mathcal {L}_2 ^{-1} = \mathcal {L}^{\otimes n+1}$
. That implies
$\mathcal {L}_1 \otimes \mathcal {L}_2 ^{-1} = \mathcal {L}^{\otimes n+1}$
. That implies
![]() $\mathcal {L}_1 = \mathcal {L}^{\otimes n+1} \otimes \mathcal {L}_2$
for some
$\mathcal {L}_1 = \mathcal {L}^{\otimes n+1} \otimes \mathcal {L}_2$
for some
![]() $\mathcal {L} \in \mathrm {Pic}(C)$
. Let
$\mathcal {L} \in \mathrm {Pic}(C)$
. Let
![]() $\mathcal {E}' = (\mathcal {O}_C ^n\oplus \mathcal {L}_2) \otimes \mathcal {L} $
. Then
$\mathcal {E}' = (\mathcal {O}_C ^n\oplus \mathcal {L}_2) \otimes \mathcal {L} $
. Then
![]() $\mathrm {det}(\mathcal {E}') = \mathcal {L}_1$
. Therefore,
$\mathrm {det}(\mathcal {E}') = \mathcal {L}_1$
. Therefore,
![]() ${\mathbb P}(\mathcal {E}')$
is
${\mathbb P}(\mathcal {E}')$
is
![]() ${\mathbb A}^1$
-h-cobordant to
${\mathbb A}^1$
-h-cobordant to
![]() ${\mathbb P}(\mathcal {O}_C^n \oplus \mathcal {L}_1)$
. Furthermore,
${\mathbb P}(\mathcal {O}_C^n \oplus \mathcal {L}_1)$
. Furthermore,
![]() ${\mathbb P}(\mathcal {E}')$
is isomorphic (as a scheme) to
${\mathbb P}(\mathcal {E}')$
is isomorphic (as a scheme) to
![]() ${\mathbb P}(\mathcal {O}_C^n \oplus \mathcal {L}_2)$
by the general fact that tensoring a vector bundle by a line bundle gives an isomorphism of projectivization of the two vector bundles. This proves X and Y are
${\mathbb P}(\mathcal {O}_C^n \oplus \mathcal {L}_2)$
by the general fact that tensoring a vector bundle by a line bundle gives an isomorphism of projectivization of the two vector bundles. This proves X and Y are
![]() ${\mathbb A}^1$
-h-cobordant.
${\mathbb A}^1$
-h-cobordant.
(2)
![]() $\implies $
(1): this is immediate from the definition of
$\implies $
(1): this is immediate from the definition of
![]() ${\mathbb A}^1$
-h-cobordism.
${\mathbb A}^1$
-h-cobordism.
(1)
![]() $\implies $
(3):
$\implies $
(3):
![]() ${\mathbb A}^1$
-invariance of the Chow rings implies that it is enough to show that the Chow rings of
${\mathbb A}^1$
-invariance of the Chow rings implies that it is enough to show that the Chow rings of
![]() ${\mathbb P}(\mathcal {O}_C^{n}\oplus \mathcal {L}_1)$
and
${\mathbb P}(\mathcal {O}_C^{n}\oplus \mathcal {L}_1)$
and
![]() ${\mathbb P}(\mathcal {O}_C^{n}\oplus \mathcal {L}_2)$
are not isomorphic if
${\mathbb P}(\mathcal {O}_C^{n}\oplus \mathcal {L}_2)$
are not isomorphic if
![]() $\mathcal {L}_1 \otimes \mathcal {L}_2^{-1} \neq \mathcal {L}^{\otimes n+1}$
for any
$\mathcal {L}_1 \otimes \mathcal {L}_2^{-1} \neq \mathcal {L}^{\otimes n+1}$
for any
![]() $\mathcal {L} \in \mathrm {Pic} (C)$
. The Chow ring of C – which is simply
$\mathcal {L} \in \mathrm {Pic} (C)$
. The Chow ring of C – which is simply
![]() ${\mathbb Z} \oplus \mathrm {Pic}(C)$
, with product of any two line bundles under the ring structure being zero – is denoted R. For simplicity of notation, we will denote
${\mathbb Z} \oplus \mathrm {Pic}(C)$
, with product of any two line bundles under the ring structure being zero – is denoted R. For simplicity of notation, we will denote
![]() $\mathcal {O}_C^n \oplus \mathcal {L}_i$
,
$\mathcal {O}_C^n \oplus \mathcal {L}_i$
,
![]() $i=1,2$
by
$i=1,2$
by
![]() $\mathcal {E}_i$
. Then by the projective bundle formula for the Chow rings [Reference Eisenbud and Harris4, Theorem 9.6], the Chow ring of
$\mathcal {E}_i$
. Then by the projective bundle formula for the Chow rings [Reference Eisenbud and Harris4, Theorem 9.6], the Chow ring of
![]() ${\mathbb P}(\mathcal {E}_1)$
is
${\mathbb P}(\mathcal {E}_1)$
is
![]() $ R_1 := R[\zeta ]/(\zeta ^{n+1} + c_1(\mathcal {E}_1)\zeta ^{n})$
. But
$ R_1 := R[\zeta ]/(\zeta ^{n+1} + c_1(\mathcal {E}_1)\zeta ^{n})$
. But
![]() $c_1(\mathcal {E}_1) = c_1(\mathcal {L}_1)$
. In the ring
$c_1(\mathcal {E}_1) = c_1(\mathcal {L}_1)$
. In the ring
![]() $R_1$
,
$R_1$
,
![]() $\zeta $
as well as any element
$\zeta $
as well as any element
![]() $x \in \mathrm {Pic}(C)$
has grading
$x \in \mathrm {Pic}(C)$
has grading
![]() $1$
with
$1$
with
![]() $xy=0$
for
$xy=0$
for
![]() $x,y \in \mathrm {Pic}(C)$
. Let’s assume we have a graded ring isomorphism
$x,y \in \mathrm {Pic}(C)$
. Let’s assume we have a graded ring isomorphism
![]() $\phi $
between
$\phi $
between
![]() $R_1$
and
$R_1$
and
![]() $R _2 := R[\sigma ]/(\sigma ^{n+1} + c_1(\mathcal {L}_2)\sigma ^{n})$
. Then such an isomorphism has to respect the grading and hence
$R _2 := R[\sigma ]/(\sigma ^{n+1} + c_1(\mathcal {L}_2)\sigma ^{n})$
. Then such an isomorphism has to respect the grading and hence
![]() $\phi (\zeta ) = x + a\sigma $
, where
$\phi (\zeta ) = x + a\sigma $
, where
![]() $x \in \mathrm {Pic}(C)$
and
$x \in \mathrm {Pic}(C)$
and
![]() $a \in {\mathbb Z}$
. Similarly,
$a \in {\mathbb Z}$
. Similarly,
![]() $\phi ^{-1}(\sigma ) = y + b\zeta $
, where
$\phi ^{-1}(\sigma ) = y + b\zeta $
, where
![]() $b \in {\mathbb Z}$
and
$b \in {\mathbb Z}$
and
![]() $y \in \mathrm {Pic}(C)$
. We first prove that
$y \in \mathrm {Pic}(C)$
. We first prove that
![]() $ a = \pm 1$
. The condition
$ a = \pm 1$
. The condition
![]() $\phi ^{-1}\circ \phi (\zeta ) = \zeta $
implies that
$\phi ^{-1}\circ \phi (\zeta ) = \zeta $
implies that
![]() $x + ay + ab\zeta = \zeta $
. Hence,
$x + ay + ab\zeta = \zeta $
. Hence,
![]() $ab =1$
, so
$ab =1$
, so
![]() $a = \pm 1$
.
$a = \pm 1$
.
By the graded ring structure of
![]() $R_1$
, as discussed before,
$R_1$
, as discussed before,
![]() $x^i =0$
for any
$x^i =0$
for any
![]() $i>1$
. Moreover,
$i>1$
. Moreover,
![]() $\phi (\zeta ^{n+1} + c_1(\mathcal {L}_1)\zeta ^{n})$
has to be divisible by
$\phi (\zeta ^{n+1} + c_1(\mathcal {L}_1)\zeta ^{n})$
has to be divisible by
![]() $\sigma ^{n+1} + c_1(\mathcal {L}_2)\sigma ^{n}$
in
$\sigma ^{n+1} + c_1(\mathcal {L}_2)\sigma ^{n}$
in
![]() $R_2$
. First assume
$R_2$
. First assume
![]() $a=1$
. Proof for the case
$a=1$
. Proof for the case
![]() $a=-1$
is similar. We expand
$a=-1$
is similar. We expand
![]() $\phi (\zeta ^{n+1} + c_1(\mathcal {L}_1)\zeta ^{n})$
as
$\phi (\zeta ^{n+1} + c_1(\mathcal {L}_1)\zeta ^{n})$
as
![]() $\sigma ^{n+1} + \sigma ^n((n+1)x + c_1(\mathcal {L}_1))$
and this expression is divisible by
$\sigma ^{n+1} + \sigma ^n((n+1)x + c_1(\mathcal {L}_1))$
and this expression is divisible by
![]() $\sigma ^{n+1} + c_1(\mathcal {L}_2)\sigma ^{n}$
. Comparing coefficients, we conclude that
$\sigma ^{n+1} + c_1(\mathcal {L}_2)\sigma ^{n}$
. Comparing coefficients, we conclude that
![]() $c_1(\mathcal {L}_1) - c_1(\mathcal {L}_2) = (n+1)x$
. This implies that
$c_1(\mathcal {L}_1) - c_1(\mathcal {L}_2) = (n+1)x$
. This implies that
![]() $\mathcal {L}_1 \otimes \mathcal {L}_2^{-1} = \mathcal {L}^{\otimes n+1}$
, where
$\mathcal {L}_1 \otimes \mathcal {L}_2^{-1} = \mathcal {L}^{\otimes n+1}$
, where
![]() $c_1(\mathcal {L}) = x$
.
$c_1(\mathcal {L}) = x$
.
Now, we answer a question raised in [Reference Asok, Kebekus and Wendt2] negatively.
Question 3.3. [Reference Asok, Kebekus and Wendt2, Question 6.9.1]
If X is any smooth projective variety that is
![]() ${\mathbb A}^1$
-h-cobordant to a
${\mathbb A}^1$
-h-cobordant to a
![]() ${\mathbb P}^1$
-bundle over
${\mathbb P}^1$
-bundle over
![]() ${\mathbb P}^2$
, does X have the structure of a
${\mathbb P}^2$
, does X have the structure of a
![]() ${\mathbb P}^1$
-bundle over
${\mathbb P}^1$
-bundle over
![]() ${\mathbb P}^2$
?
${\mathbb P}^2$
?
The authors further add the answer is possibly no, and nontrivial rank three vector bundles over
![]() ${\mathbb P}^1$
deformable to the trivial one are the likely counterexamples. We now prove Theorem 1.3 which shows that the example alluded to above is indeed a correct counterexample.
${\mathbb P}^1$
deformable to the trivial one are the likely counterexamples. We now prove Theorem 1.3 which shows that the example alluded to above is indeed a correct counterexample.
Proof of Theorem 1.3
By Theorem 2.5,
![]() $ X:={\mathbb P}(\mathcal {E}) \xrightarrow {\pi } {\mathbb P}^1$
is
$ X:={\mathbb P}(\mathcal {E}) \xrightarrow {\pi } {\mathbb P}^1$
is
![]() ${\mathbb A}^1$
-h-cobordant to the trivial
${\mathbb A}^1$
-h-cobordant to the trivial
![]() ${\mathbb P}^2$
- bundle on
${\mathbb P}^2$
- bundle on
![]() ${\mathbb P}^1$
, namely,
${\mathbb P}^1$
, namely,
![]() ${\mathbb P}^1 \times {\mathbb P}^2$
. However, X and
${\mathbb P}^1 \times {\mathbb P}^2$
. However, X and
![]() ${\mathbb P}^1 \times {\mathbb P}^2$
are not isomorphic as schemes. By [Reference Hartshorne5, II, Exercise 7.9(b)], an isomorphism would imply that for some line bundle on
${\mathbb P}^1 \times {\mathbb P}^2$
are not isomorphic as schemes. By [Reference Hartshorne5, II, Exercise 7.9(b)], an isomorphism would imply that for some line bundle on
![]() ${\mathbb P}^1$
, say
${\mathbb P}^1$
, say
![]() $\mathcal {O}(a)$
where
$\mathcal {O}(a)$
where
![]() $a \in {\mathbb Z}$
,
$a \in {\mathbb Z}$
,
![]() $\mathcal {O}(a) \otimes \mathcal {E} \simeq \mathcal {O}(a) \oplus \mathcal {O}(a-1) \oplus \mathcal {O}(a+1)\simeq \mathcal {O}^{\oplus 3}$
is an isomorphism of vector bundles on
$\mathcal {O}(a) \otimes \mathcal {E} \simeq \mathcal {O}(a) \oplus \mathcal {O}(a-1) \oplus \mathcal {O}(a+1)\simeq \mathcal {O}^{\oplus 3}$
is an isomorphism of vector bundles on
![]() ${\mathbb P}^1$
, which cannot happen.
${\mathbb P}^1$
, which cannot happen.
Now suppose
![]() $ X \xrightarrow {\theta } {\mathbb P}_{{\mathbb P}^2}(\mathcal {E}') := Y \xrightarrow {\phi } {\mathbb P}^2$
, with
$ X \xrightarrow {\theta } {\mathbb P}_{{\mathbb P}^2}(\mathcal {E}') := Y \xrightarrow {\phi } {\mathbb P}^2$
, with
![]() $\theta $
an isomorphism of schemes, for some rank
$\theta $
an isomorphism of schemes, for some rank
![]() $2$
vector bundle
$2$
vector bundle
![]() $\mathcal {E}'$
on
$\mathcal {E}'$
on
![]() ${\mathbb P}^2$
. We thus have the following diagram
${\mathbb P}^2$
. We thus have the following diagram

Without loss of generality we can assume (by twisting
![]() $\mathcal {E}'$
with a suitable line bundle in
$\mathcal {E}'$
with a suitable line bundle in
![]() $\mathrm {Pic}({\mathbb P}^2) $
as
$\mathrm {Pic}({\mathbb P}^2) $
as
![]() $c_1(\mathcal {E}' \otimes \mathcal {L}) = c_1(\mathcal {E}') + 2c_1(\mathcal {L})$
),
$c_1(\mathcal {E}' \otimes \mathcal {L}) = c_1(\mathcal {E}') + 2c_1(\mathcal {L})$
),
![]() $c_1(\mathcal {E}') \in \{0,1\}$
. Since Y is
$c_1(\mathcal {E}') \in \{0,1\}$
. Since Y is
![]() ${\mathbb A}^1$
-weakly equivalent to the trivial bundle on
${\mathbb A}^1$
-weakly equivalent to the trivial bundle on
![]() ${\mathbb P}^2$
, their Chow rings are isomorphic. By [Reference Asok, Kebekus and Wendt2, Lemma 4.5], we have
${\mathbb P}^2$
, their Chow rings are isomorphic. By [Reference Asok, Kebekus and Wendt2, Lemma 4.5], we have
![]() $c_1(\mathcal {E}')^2 - 4c_2(\mathcal {E}') = 0$
. So
$c_1(\mathcal {E}')^2 - 4c_2(\mathcal {E}') = 0$
. So
![]() $c_1(\mathcal {E}') = 0 = c_2(\mathcal {E}')$
. It thus suffices to show that
$c_1(\mathcal {E}') = 0 = c_2(\mathcal {E}')$
. It thus suffices to show that
![]() $\mathcal {E}'$
splits as a direct sum of line bundles as this will prove that
$\mathcal {E}'$
splits as a direct sum of line bundles as this will prove that
![]() $\mathcal {E}' \simeq \mathcal {O}_{{\mathbb P}^2} \oplus \mathcal {O}_{{\mathbb P}^2} $
. By the assumption that
$\mathcal {E}' \simeq \mathcal {O}_{{\mathbb P}^2} \oplus \mathcal {O}_{{\mathbb P}^2} $
. By the assumption that
![]() $X \simeq Y$
, this will imply that X is isomorphic to
$X \simeq Y$
, this will imply that X is isomorphic to
![]() ${\mathbb P}^2 \times {\mathbb P}^1$
, which from the discussion in the first paragraph of this proof cannot happen.
${\mathbb P}^2 \times {\mathbb P}^1$
, which from the discussion in the first paragraph of this proof cannot happen.
We will prove that
![]() $\phi $
has a section. Such a section will give the following short exact sequence.
$\phi $
has a section. Such a section will give the following short exact sequence.
As both Chern classes of
![]() $\mathcal {E}'$
vanish, by the Whitney sum formula of Chern classes, both
$\mathcal {E}'$
vanish, by the Whitney sum formula of Chern classes, both
![]() $\mathcal {L}_1$
and
$\mathcal {L}_1$
and
![]() $\mathcal {L}_2$
will be trivial. Therefore such a short exact sequence has to be a split one. This will prove
$\mathcal {L}_2$
will be trivial. Therefore such a short exact sequence has to be a split one. This will prove
![]() $\mathcal {E}' \simeq \mathcal {O}_{{\mathbb P}^2} \oplus \mathcal {O}_{{\mathbb P}^2}$
.
$\mathcal {E}' \simeq \mathcal {O}_{{\mathbb P}^2} \oplus \mathcal {O}_{{\mathbb P}^2}$
.
Define
![]() $F \hookrightarrow Y$
to be
$F \hookrightarrow Y$
to be
![]() $\theta \circ \pi ^{-1}(z)$
for a point
$\theta \circ \pi ^{-1}(z)$
for a point
![]() $ z \in {\mathbb P}^1$
. By construction,
$ z \in {\mathbb P}^1$
. By construction,
![]() $F \simeq {\mathbb P}^2$
. We claim
$F \simeq {\mathbb P}^2$
. We claim
![]() $\phi $
maps F isomorphically onto
$\phi $
maps F isomorphically onto
![]() ${\mathbb P}^2$
. First we claim that
${\mathbb P}^2$
. First we claim that
![]() $\phi _{|F}$
is surjective. If not, then
$\phi _{|F}$
is surjective. If not, then
![]() $Z:=\phi (F)$
is either a point or an irreducible curve (not necessarily smooth) in
$Z:=\phi (F)$
is either a point or an irreducible curve (not necessarily smooth) in
![]() ${\mathbb P}^2$
. Since
${\mathbb P}^2$
. Since
![]() $\phi : Y \to {\mathbb P}^2$
is a
$\phi : Y \to {\mathbb P}^2$
is a
![]() ${\mathbb P}^1$
-bundle map, the fiber of
${\mathbb P}^1$
-bundle map, the fiber of
![]() $\phi $
over each point of
$\phi $
over each point of
![]() ${\mathbb P}^2$
is
${\mathbb P}^2$
is
![]() ${\mathbb P}^1$
. Therefore, Z cannot be a point. So assume Z is an irreducible curve in
${\mathbb P}^1$
. Therefore, Z cannot be a point. So assume Z is an irreducible curve in
![]() ${\mathbb P}^2$
. Consider smooth points
${\mathbb P}^2$
. Consider smooth points
![]() $z_1 \neq z_2 \in Z$
. Then using flatness of
$z_1 \neq z_2 \in Z$
. Then using flatness of
![]() $\phi $
, we have
$\phi $
, we have
![]() $\phi ^{-1}(z_i) \simeq {\mathbb P}^1 \subset F$
for
$\phi ^{-1}(z_i) \simeq {\mathbb P}^1 \subset F$
for
![]() $i=1,2$
. However, any two lines in
$i=1,2$
. However, any two lines in
![]() ${\mathbb P}^2$
intersect, so
${\mathbb P}^2$
intersect, so
![]() $\phi ^{-1}(z_1)$
and
$\phi ^{-1}(z_1)$
and
![]() $\phi ^{-1}(z_i)$
intersect in F(which is isomorphic to
$\phi ^{-1}(z_i)$
intersect in F(which is isomorphic to
![]() ${\mathbb P}^2$
). This contradicts our assumption that
${\mathbb P}^2$
). This contradicts our assumption that
![]() $z_1 \neq z_2$
. This establishes the surjectivity of
$z_1 \neq z_2$
. This establishes the surjectivity of
![]() $\phi _{|F}$
. We also conclude
$\phi _{|F}$
. We also conclude
![]() $\phi |_{F}$
is a degree d morphism to
$\phi |_{F}$
is a degree d morphism to
![]() ${\mathbb P}^2$
with
${\mathbb P}^2$
with
![]() $d\geq 1$
.
$d\geq 1$
.
We now show that
![]() $d=1$
. This is achieved by comparing the graded ring isomorphism induced on the Chow rings of X and Y. The Chow ring of X is
$d=1$
. This is achieved by comparing the graded ring isomorphism induced on the Chow rings of X and Y. The Chow ring of X is
![]() $ R _1 := {\mathbb Z}[x,y]/(x^2,y^3)$
, where
$ R _1 := {\mathbb Z}[x,y]/(x^2,y^3)$
, where
-
(i) x is the divisor
 ${\mathbb P}^2$
as a fiber over a point of
${\mathbb P}^2$
as a fiber over a point of
 ${\mathbb P}^1$
${\mathbb P}^1$
-
(ii) y corresponds to a divisor
 $D'$
, such that the pushforward
$D'$
, such that the pushforward
 $\pi _{\ast }(\mathcal {O}_X(D'))$
to
$\pi _{\ast }(\mathcal {O}_X(D'))$
to
 ${\mathbb P}^1$
is the vector bundle
${\mathbb P}^1$
is the vector bundle
 $\mathcal {E}$
.
$\mathcal {E}$
.
Similarly, the Chow ring of Y is
![]() $ R_2:= {\mathbb Z}[s,t]/(s^2,t^3)$
where
$ R_2:= {\mathbb Z}[s,t]/(s^2,t^3)$
where
-
(i) t corresponds to fiber of
 ${\mathbb P}^1$
(as a degree
${\mathbb P}^1$
(as a degree
 $1$
curve in
$1$
curve in
 ${\mathbb P}^2$
) via
${\mathbb P}^2$
) via
 $\phi $
$\phi $
-
(ii) s corresponds to a divisor D, such that the pushforward
 $\phi _{\ast }(\mathcal {O}_Y(D))$
to
$\phi _{\ast }(\mathcal {O}_Y(D))$
to
 ${\mathbb P}^2$
is the rank two vector bundle
${\mathbb P}^2$
is the rank two vector bundle
 $\mathcal {E}'$
.
$\mathcal {E}'$
.
Let
![]() $\psi : R_1 \to R_2$
be an isomorphism of graded rings. Then
$\psi : R_1 \to R_2$
be an isomorphism of graded rings. Then
![]() $\psi (x) = as + bt$
, where
$\psi (x) = as + bt$
, where
![]() $a,b \in {\mathbb Z}$
. We have the condition that
$a,b \in {\mathbb Z}$
. We have the condition that
![]() $\psi (x^2) = \psi (x)^2 = a^2s^2 + 2abst + b^2t^2$
lies in the ideal generated by
$\psi (x^2) = \psi (x)^2 = a^2s^2 + 2abst + b^2t^2$
lies in the ideal generated by
![]() $s^2$
and
$s^2$
and
![]() $t^3$
. This implies
$t^3$
. This implies
![]() $b=0$
. Morever,
$b=0$
. Morever,
![]() $\psi ^{-1}\circ \psi (x) = x$
. Therefore,
$\psi ^{-1}\circ \psi (x) = x$
. Therefore,
![]() $a = \pm 1$
. In a similar fashion, one proves that any isomorphism between
$a = \pm 1$
. In a similar fashion, one proves that any isomorphism between
![]() $R_1$
and
$R_1$
and
![]() $R_2$
sends y to
$R_2$
sends y to
![]() $\pm t$
. Therefore, we conclude that the graded ring isomorphism between
$\pm t$
. Therefore, we conclude that the graded ring isomorphism between
![]() $R_1$
and
$R_1$
and
![]() $R_2$
is given by
$R_2$
is given by
![]() $x \mapsto \pm s$
and
$x \mapsto \pm s$
and
![]() $y \mapsto \pm t$
. This implies s is equivalent (in the Chow ring) to the class of
$y \mapsto \pm t$
. This implies s is equivalent (in the Chow ring) to the class of
![]() $F \simeq {\mathbb P}^2$
. Grauert’s theorem ([Reference Hartshorne5, III, Corollary 12.9]) implies that the intersection multiplicity of divisor D corresponding to s (see the description of
$F \simeq {\mathbb P}^2$
. Grauert’s theorem ([Reference Hartshorne5, III, Corollary 12.9]) implies that the intersection multiplicity of divisor D corresponding to s (see the description of
![]() $R_2$
above) with any fiber of the map
$R_2$
above) with any fiber of the map
![]() $\phi $
is
$\phi $
is
![]() $1$
. As s and F are equivalent in the Chow ring, the same holds for F. This cannot happen unless
$1$
. As s and F are equivalent in the Chow ring, the same holds for F. This cannot happen unless
![]() $d=1$
because if not, one can consider a point
$d=1$
because if not, one can consider a point
![]() $z'$
in
$z'$
in
![]() ${\mathbb P}^2$
such that the set
${\mathbb P}^2$
such that the set
![]() $\phi |_{{\mathbb P}^2}^{-1}(z') $
has more than one point. This will force
$\phi |_{{\mathbb P}^2}^{-1}(z') $
has more than one point. This will force
![]() $\phi ^{-1}(z') = {\mathbb P}^1$
to intersect
$\phi ^{-1}(z') = {\mathbb P}^1$
to intersect
![]() ${\mathbb P}^2$
in more than one point, meaning an intersection multiplicity of greater than
${\mathbb P}^2$
in more than one point, meaning an intersection multiplicity of greater than
![]() $1$
which, as we just proved, cannot happen. This proves
$1$
which, as we just proved, cannot happen. This proves
![]() $\phi |_{F}$
is an isomorphism onto
$\phi |_{F}$
is an isomorphism onto
![]() ${\mathbb P}^2$
and hence establishes the existence of a section of
${\mathbb P}^2$
and hence establishes the existence of a section of
![]() $\phi $
. Via the short exact sequence 3.1, this proves that
$\phi $
. Via the short exact sequence 3.1, this proves that
![]() $\mathcal {E}'$
is a trivial rank 2 vector bundle on
$\mathcal {E}'$
is a trivial rank 2 vector bundle on
![]() ${\mathbb P}^2$
, and thereby finishes the proof.
${\mathbb P}^2$
, and thereby finishes the proof.
Acknowledgments
We thank the anonymous referees for their careful reading, comments and corrections. In particular, Remark 2.10 is the result of a question by one of the referees. The second-named author was supported by SFB 1085 Higher Invariants, University of Regensburg, NBHM fellowship of the Department of Atomic Energy, Govt. of India and Fulbright-Nehru Doctoral Research fellowship during this work and thanks the Department of Math, University of Southern California for the hospitality.
Competing Interests
None.