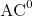1 Introduction
Description logics (DLs) (Baader et al. 2007) are a well-known and widely used family of knowledge representation formalisms that, thanks to their clear syntax and formal semantics, have been used to represent and deal with the knowledge of various representation domains. Among the many members of this family, a subfamily of languages with a limited expressivity, known as the DL-Lite family (Calvanese et al. Reference Calvanese, De Giacomo, Lembo, Lenzerini and Rosati2007), has a prominent role. In fact, simplifying a bit, DL-Lite was originally designed with the goal of including background knowledge within the task of answering queries and avoiding the need for an explicit enumeration of all the facts that are implicitly implied by the domain knowledge.
Consider for example a touristic scenario, which includes information about museums, monuments, restaurants, and pubs. Knowing that museums and monuments are touristic attractions and that restaurants and pubs are eateries, one can immediately deduce that the modern art museum and the peace monument are touristic attractions, and that the Irish pub is an eatery, without having to make this knowledge explicit. A user may thus ask for example, a tourist attraction that contains an eatery. Using classical query answering techniques (Ortiz and Šimkus Reference Ortiz and Šimkus2012), all attractions that satisfy this requirement can be efficiently retrieved.
Being based on classical logic, DLs in general and DL-Lite in particular are unable to handle imprecise or vague knowledge effectively. In our touristic scenario, for instance, we may want to extend the knowledge with some additional properties of the objects of interest. For example, a tourist in a hurry may want to visit the popular attractions first; a backpacker on a budget may be more interested in finding cheap eateries. Note that cheap and popular are two vague notions that do not allow for any precise definition. In a simplistic scenario, cheapness may be defined in terms of the mean cost for a meal, but even then, it is impossible to specify a precise price-point where an eatery stops being cheap; moreover, this is also a subjective notion. The case of popularity is even worse, as there is no obvious proxy for it.
To solve this issue, fuzzy extensions of DLs have been widely studied; see for example Borgwardt (Reference Borgwardt2014), Borgwardt and Peñaloza (Reference Borgwardt and Peñaloza2017), Bobillo et al. (Reference Bobillo, Cerami, Esteva, García-Cerdaña, Peñaloza, Straccia, Cintula, Fermüller and Noguera2015), Lukasiewicz and Straccia (Reference Lukasiewicz and Straccia2008) and Cerami (Reference Cerami2012) and references therein. In essence, fuzzy logic (Hájek Reference Hájek1998) extends classical logic by allowing truth degrees in the interval [0,1] for the propositions that contain fuzzy (or vague) predicates. One can thus say, for example, that the modern art museum is popular to a degree of
![]() $0.8$
meaning, intuitively, that it is popular, but more popular attractions may exist.
$0.8$
meaning, intuitively, that it is popular, but more popular attractions may exist.
Interestingly, although fuzzy DLs and their reasoning services have been widely studied, the task of answering queries based on fuzzy ontologies has been mostly ignored. Most of the earlier work from this point of view was carried out by Straccia and Pan. Specifically, Straccia (Reference Straccia2006) studied the problem of computing the answers with highest degree on a query w.r.t. some background knowledge. This was followed by Pan et al. (Reference Pan, Stamou, Stoilos and Thomas2007), who considered more complex queries to be answered. While from some perspective these works seem to cover the whole area of query answering, they were based on the so-called Zadeh semantics, which does not have adequate properties from a mathematical logic point of view (Hájek Reference Hájek1998). Another limitation of all these approaches is that they allowed only the facts in the ontology to be graded, but restricted the terminological knowledge to be crisp (i.e. hold fully). Other work considering query answering in fuzzy DLs includes (Straccia Reference Straccia2012), where the k answers with the highest degree are retrieved. This latter work is closer to our approach but has several limitations. Perhaps the most obvious is that its semantics follows a closed-world assumption, even in the case of background knowledge. In addition, background knowledge is interpreted as a rule, where the degrees of the body of an axiom define the degree of the head, but knowledge about the head cannot be used to infer knowledge about the body. We, in change, use the open world assumption, as typical in knowledge representation, and use the logical interpretation of axioms.
Later on, Turhan and Mailis studied the problem of query answering w.r.t. background knowledge from the point of view of fuzzy logic (Hájek Reference Hájek1998), where the semantics are based on the properties of continuous triangular norms (Klement et al. Reference Klement, Mesiar and Pap2000). They developed a technique for computing the satisfaction degrees of conjunctive queries when the semantics were based on the Gödel t-norm (Mailis and Turhan Reference Mailis and Turhan2014). This technique, which is based on the construction of a classical query, was later implemented and shown to be effective by Mailis et al. (Reference Mailis, Turhan, Zenker, Calvanese and Konev2015). However, it still suffered from two main drawbacks: (i) it was only capable to handle the idempotent (Gödel) t-norm, and (ii) terminological knowledge had to still be precise, allowing no graded axioms. The latter condition is essential for the correctness of their approach: their reduction is unable to keep track of the degrees used by the terminological axioms, as this would require an unbounded memory use.
In this paper, we study the problem of query answering w.r.t. DL-Lite ontologies, filling out the gaps left by the existing work. To be more explicit, our work is the first to consider adequate semantics from the mathematical fuzzy logic point of view, alongside graded axioms stating vague knowledge beyond just vague data. We start by considering the kind of conjunctive queries studied by Turhan and Mailis, but allowing the association of numeric degrees also in the TBox. Interestingly, although this is a generalization of the previously studied setting, we are able to develop a much simpler method, which does not rely on rewriting, but rather on a reduction to a classical query answering scenario. The method is based on the idea of cut ontologies, where all knowledge holding to a low degree is ignored. Hence, we obtain a more robust and easier to maintain approach than previous work. Still considering the Gödel t-norm, we considered the case of threshold queries, also left open in previous work, in which every conjunct in a query is assigned a different degree. In this case, a direct reduction to classical query answering does not work, but we were able to adapt the classical rewriting methods to handle the degrees effectively.
The final part of the paper considers other t-norms as the underlying semantics for the fuzzy constructors. In this case, we show through several examples that conjunctive queries cannot be easily handled, but we identify some special cases where queries can be effectively answered. On the other hand, we show that we can still apply the rewriting technique to answer threshold queries, even for non-idempotent t-norms. This is a surprising result because in the idempotent scenario threshold queries are a generalization of conjunctive queries.
Some of the results in this paper were previously published (Pasi and Peñaloza Reference Pasi and Peñaloza2020). In addition to full proofs, deeper explanations, and examples, here we extend that previous work by handling threshold queries, including the full rewriting technique from Section 5. We also provide better results for non-idempotent t-norms, and highlight some of the problems of combining conjunctions and non-idempotent t-norms in the appendix.
2 Preliminaries
We briefly introduce the syntax and semantics of fuzzy
![]() $\text{DL-Lite}_{R}$
and other related notions that will be important for this paper. Let
$\text{DL-Lite}_{R}$
and other related notions that will be important for this paper. Let
![]() ${N_C}$
,
${N_C}$
,
![]() ${N_R}$
, and
${N_R}$
, and
![]() ${N_I}$
be three mutually disjoint sets whose elements are called concept names, role names, and individual names, respectively. The sets of
${N_I}$
be three mutually disjoint sets whose elements are called concept names, role names, and individual names, respectively. The sets of
![]() $\text{DL-Lite}_{R}$
concepts and roles are built through the grammar rules:
$\text{DL-Lite}_{R}$
concepts and roles are built through the grammar rules:
where
![]() $A\in{N_C}$
and
$A\in{N_C}$
and
![]() $P\in{N_R}$
. Concepts of the form B and roles of the form Q are called basic, and all others are called general.
$P\in{N_R}$
. Concepts of the form B and roles of the form Q are called basic, and all others are called general.
Definition 1
(ontology) A fuzzy
![]() $\text{DL-Lite}_{R}$
TBox is a finite set of fuzzy axioms of the form
$\text{DL-Lite}_{R}$
TBox is a finite set of fuzzy axioms of the form
![]() $\left<B\sqsubseteq C,d\right>$
and
$\left<B\sqsubseteq C,d\right>$
and
![]() $\left<Q\sqsubseteq R,d\right>$
, where d is a number in [0,1]. An axiom is positive if it does not have negation on its right-hand side and negative otherwise. A fuzzy
$\left<Q\sqsubseteq R,d\right>$
, where d is a number in [0,1]. An axiom is positive if it does not have negation on its right-hand side and negative otherwise. A fuzzy
![]() $\text{DL-Lite}_{R}$
ABox is a finite set of fuzzy assertions of the form
$\text{DL-Lite}_{R}$
ABox is a finite set of fuzzy assertions of the form
![]() $\left<B(a),d\right>$
and
$\left<B(a),d\right>$
and
![]() $\left<P(a,b),d\right>$
, where
$\left<P(a,b),d\right>$
, where
![]() $a,b\in{N_I}$
. A fuzzy
$a,b\in{N_I}$
. A fuzzy
![]() $\text{DL-Lite}_{R}$
ontology is a pair of the form
$\text{DL-Lite}_{R}$
ontology is a pair of the form
![]() ${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
where
${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
where
![]() ${\mathcal{T}}$
is a TBox and
${\mathcal{T}}$
is a TBox and
![]() ${\mathcal{A}}$
is an ABox.
${\mathcal{A}}$
is an ABox.
Note that negations can never occur on the left-hand side of an axiom. In the remainder of this paper, we will mostly exclude the qualifiers “fuzzy,” and “DL-Lite” and simply refer to axioms, ontologies, etc.
The semantics of fuzzy
![]() $\text{DL-Lite}_{R}$
is based on fuzzy interpretations, which provide a membership degree or for objects belonging to the different concept and role names. Formally, following the basics of classical description logics, concept names are interpreted as fuzzy unary relations, and role names are interpreted as fuzzy binary relations. To fully define this semantics in the presence of other constructors according to fuzzy logic, we need the notion of a triangular norm (or t-norm for short).
$\text{DL-Lite}_{R}$
is based on fuzzy interpretations, which provide a membership degree or for objects belonging to the different concept and role names. Formally, following the basics of classical description logics, concept names are interpreted as fuzzy unary relations, and role names are interpreted as fuzzy binary relations. To fully define this semantics in the presence of other constructors according to fuzzy logic, we need the notion of a triangular norm (or t-norm for short).
Definition 2
(t-norm) A t-norm
![]() $\otimes$
is a binary operator over the real interval [0,1] that is commutative, associative, monotonic, and has 1 as the neutral element; that is,
$\otimes$
is a binary operator over the real interval [0,1] that is commutative, associative, monotonic, and has 1 as the neutral element; that is,
![]() $1\otimes x=x$
for all
$1\otimes x=x$
for all
![]() $x\in[0,1]$
(Klement et al. 2000).
$x\in[0,1]$
(Klement et al. 2000).
Triangular norms are used to generalize the logical conjunction to handle truth degrees that take values from the interval [0,1]. Every continuous t-norm defines a unique residuum
![]() $\Rightarrow$
where
$\Rightarrow$
where
![]() $f\otimes d\le e$
iff
$f\otimes d\le e$
iff
![]() $f\le d\Rightarrow e$
. The residuum interprets implications. With the help of this operation, it is also possible to interpret other logical operators such as negation (
$f\le d\Rightarrow e$
. The residuum interprets implications. With the help of this operation, it is also possible to interpret other logical operators such as negation (
![]() $\ominus d:=d\Rightarrow 0$
). The three basic continuous t-norms are the Gödel, Łukasiewicz, and product t-norms, which are defined, with their residua and negations in Table 1. These t-norms are the “fundamental” ones in the sense that every other continuous t-norm is isomorphic to the ordinal sum of copies of them (Hájek Reference Hájek1998; Mostert and Shields Reference Mostert and Shields1957). Hence, as usual, we focus our study on these three t-norms.
$\ominus d:=d\Rightarrow 0$
). The three basic continuous t-norms are the Gödel, Łukasiewicz, and product t-norms, which are defined, with their residua and negations in Table 1. These t-norms are the “fundamental” ones in the sense that every other continuous t-norm is isomorphic to the ordinal sum of copies of them (Hájek Reference Hájek1998; Mostert and Shields Reference Mostert and Shields1957). Hence, as usual, we focus our study on these three t-norms.
Table 1. The three fundamental continuous t-norms and related operations

Note that the residuum always satisfies that
![]() $d\Rightarrow e=1$
iff
$d\Rightarrow e=1$
iff
![]() $d\le e$
, and that in the Gödel and product t-norms the negation is annihilating in the sense that it maps to 0 any positive value, while the negation of 0 is 1. In particular, this means that the negation is not involutive; that is,
$d\le e$
, and that in the Gödel and product t-norms the negation is annihilating in the sense that it maps to 0 any positive value, while the negation of 0 is 1. In particular, this means that the negation is not involutive; that is,
![]() $\ominus\ominus d\not=d$
in general. In contrast, the negation operator for the Łukasiewicz t-norm is involutive. In addition, the Łukasiewicz t-norm is the only t-norm (up to isomorphism) with the property that for every
$\ominus\ominus d\not=d$
in general. In contrast, the negation operator for the Łukasiewicz t-norm is involutive. In addition, the Łukasiewicz t-norm is the only t-norm (up to isomorphism) with the property that for every
![]() $x\in (0,1)$
there exists a
$x\in (0,1)$
there exists a
![]() $y\in (0,1)$
such that
$y\in (0,1)$
such that
![]() $x\otimes y=0$
. Specifically, this y is
$x\otimes y=0$
. Specifically, this y is
![]() $1-x$
. In other words, the Łukasiewicz t-norm is nilpotent. From now on, unless specified explicitly otherwise, we assume that we have an arbitrary, but fixed, t-norm
$1-x$
. In other words, the Łukasiewicz t-norm is nilpotent. From now on, unless specified explicitly otherwise, we assume that we have an arbitrary, but fixed, t-norm
![]() $\otimes$
which underlies the operators used. When the t-norm becomes relevant in the following sections, we will often use G,
$\otimes$
which underlies the operators used. When the t-norm becomes relevant in the following sections, we will often use G,
![]() $\Pi$
, and Ł as prefixes to express that the underlying t-norm is Gödel, product, or Łukasiewicz, respectively, as usual in the literature.
$\Pi$
, and Ł as prefixes to express that the underlying t-norm is Gödel, product, or Łukasiewicz, respectively, as usual in the literature.
We can now formally define the semantics of the logic. An interpretation is a pair
![]() ${\mathcal{I}}=(\Delta^{\mathcal{I}},\cdot^{\mathcal{I}})$
, where
${\mathcal{I}}=(\Delta^{\mathcal{I}},\cdot^{\mathcal{I}})$
, where
![]() $\Delta^{\mathcal{I}}$
is a non-empty set called the domain, and
$\Delta^{\mathcal{I}}$
is a non-empty set called the domain, and
![]() $\cdot^{\mathcal{I}}$
is the interpretation function which maps: (i) every individual name
$\cdot^{\mathcal{I}}$
is the interpretation function which maps: (i) every individual name
![]() $a\in{N_I}$
to an element
$a\in{N_I}$
to an element
![]() $a^{\mathcal{I}}\in\Delta^{\mathcal{I}}$
; (ii) every concept name
$a^{\mathcal{I}}\in\Delta^{\mathcal{I}}$
; (ii) every concept name
![]() $A\in{N_C}$
to a function
$A\in{N_C}$
to a function
![]() $A^{\mathcal{I}}:\Delta^{\mathcal{I}}\to[0,1]$
; and (iii) every role name
$A^{\mathcal{I}}:\Delta^{\mathcal{I}}\to[0,1]$
; and (iii) every role name
![]() $P\in{N_R}$
to a function
$P\in{N_R}$
to a function
![]() $P^{\mathcal{I}}:\Delta^{\mathcal{I}}\times\Delta^{\mathcal{I}}\to[0,1]$
. That is, concept names are interpreted as fuzzy unary relations and role names are interpreted as fuzzy binary relations over
$P^{\mathcal{I}}:\Delta^{\mathcal{I}}\times\Delta^{\mathcal{I}}\to[0,1]$
. That is, concept names are interpreted as fuzzy unary relations and role names are interpreted as fuzzy binary relations over
![]() $\Delta^{\mathcal{I}}$
. The interpretation function is extended to other constructors with the help of the t-norm operators as follows. For every
$\Delta^{\mathcal{I}}$
. The interpretation function is extended to other constructors with the help of the t-norm operators as follows. For every
![]() $\delta,\eta\in\Delta^{\mathcal{I}}$
,
$\delta,\eta\in\Delta^{\mathcal{I}}$
,
 \begin{align*}(\exists Q)^{\mathcal{I}}(\delta) := {} & \sup_{\delta'\in\Delta^{\mathcal{I}}}Q^{\mathcal{I}}(\delta,\delta') &(\neg B)^{\mathcal{I}}(\delta) := & \ominus B^{\mathcal{I}}(\delta) &(\top)^{\mathcal{I}}(\delta) := & 1 \\(P^-)^{\mathcal{I}}(\delta,\eta) := {} & P^{\mathcal{I}}(\eta,\delta) &(\neg Q)^{\mathcal{I}}(\delta,\eta) := & \ominus Q^{\mathcal{I}}(\delta,\eta). &\end{align*}
\begin{align*}(\exists Q)^{\mathcal{I}}(\delta) := {} & \sup_{\delta'\in\Delta^{\mathcal{I}}}Q^{\mathcal{I}}(\delta,\delta') &(\neg B)^{\mathcal{I}}(\delta) := & \ominus B^{\mathcal{I}}(\delta) &(\top)^{\mathcal{I}}(\delta) := & 1 \\(P^-)^{\mathcal{I}}(\delta,\eta) := {} & P^{\mathcal{I}}(\eta,\delta) &(\neg Q)^{\mathcal{I}}(\delta,\eta) := & \ominus Q^{\mathcal{I}}(\delta,\eta). &\end{align*}
The interpretation
![]() ${\mathcal{I}}$
satisfies the axiom
${\mathcal{I}}$
satisfies the axiom
-
 $\left<B\sqsubseteq C,d\right>$
iff
$\left<B\sqsubseteq C,d\right>$
iff
 $B^{\mathcal{I}}(\delta)\Rightarrow C^{\mathcal{I}}(\delta)\ge d$
holds for every
$B^{\mathcal{I}}(\delta)\Rightarrow C^{\mathcal{I}}(\delta)\ge d$
holds for every
 $\delta\in\Delta^{\mathcal{I}}$
; and
$\delta\in\Delta^{\mathcal{I}}$
; and -
 $\left<Q\sqsubseteq R,d\right>$
iff
$\left<Q\sqsubseteq R,d\right>$
iff
 $Q^{\mathcal{I}}(\delta,\eta)\Rightarrow R^{\mathcal{I}}(\delta,\eta)\ge d$
holds for every
$Q^{\mathcal{I}}(\delta,\eta)\Rightarrow R^{\mathcal{I}}(\delta,\eta)\ge d$
holds for every
 $\delta,\eta\in\Delta^{\mathcal{I}}$
$\delta,\eta\in\Delta^{\mathcal{I}}$
It is a model of the TBox
![]() ${\mathcal{T}}$
if it satisfies all axioms in
${\mathcal{T}}$
if it satisfies all axioms in
![]() ${\mathcal{T}}$
.
${\mathcal{T}}$
.
![]() ${\mathcal{I}}$
satisfies the assertion
${\mathcal{I}}$
satisfies the assertion
-
 $\left<B(a),d\right>$
iff
$\left<B(a),d\right>$
iff
 $B^{\mathcal{I}}(a^{\mathcal{I}})\ge d$
;
$B^{\mathcal{I}}(a^{\mathcal{I}})\ge d$
; -
 $\left<P(a,b),d\right>$
iff
$\left<P(a,b),d\right>$
iff
 $P^{\mathcal{I}}(a^{\mathcal{I}},b^{\mathcal{I}})\ge d$
.
$P^{\mathcal{I}}(a^{\mathcal{I}},b^{\mathcal{I}})\ge d$
.
It is a model of the ABox
![]() ${\mathcal{A}}$
if it satisfies all axioms in
${\mathcal{A}}$
if it satisfies all axioms in
![]() $ {\mathcal{A}}$
, and it is a model of the ontology
$ {\mathcal{A}}$
, and it is a model of the ontology
![]() ${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
if it is a model of
${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
if it is a model of
![]() ${\mathcal{T}}$
and of
${\mathcal{T}}$
and of
![]() ${\mathcal{A}}$
.
${\mathcal{A}}$
.
We note that the classical notion of
![]() $\text{DL-Lite}_{R}$
(Calvanese et al. Reference Calvanese, De Giacomo, Lembo, Lenzerini and Rosati2007) is a special case of fuzzy
$\text{DL-Lite}_{R}$
(Calvanese et al. Reference Calvanese, De Giacomo, Lembo, Lenzerini and Rosati2007) is a special case of fuzzy
![]() $\text{DL-Lite}_{R}$
, where all the axioms and assertions hold with degree 1. In that case, it suffices to consider interpretations which map all elements to
$\text{DL-Lite}_{R}$
, where all the axioms and assertions hold with degree 1. In that case, it suffices to consider interpretations which map all elements to
![]() $\{0,1\}$
representing the classical truth values. When speaking of classical ontologies, we remove the degree and assume it implicitly to be 1.
$\{0,1\}$
representing the classical truth values. When speaking of classical ontologies, we remove the degree and assume it implicitly to be 1.
Example 3 Consider an ontology
![]() ${\mathcal{O}_\textsf{exa}}=({\mathcal{T}_\textsf{exa}},{\mathcal{A}_\textsf{exa}})$
representing some knowledge about a touristic location. The TBox
${\mathcal{O}_\textsf{exa}}=({\mathcal{T}_\textsf{exa}},{\mathcal{A}_\textsf{exa}})$
representing some knowledge about a touristic location. The TBox
 \begin{align*}{\mathcal{T}_\textsf{exa}} =\{ & {\left<{\textsf{Monument} \sqsubseteq \textsf{TouristAttraction}}\right>}, \quad {\left<{\textsf{Museum} \sqsubseteq \textsf{TouristAttraction}}\right>}, \\ & {\left<{\textsf{Pub} \sqsubseteq \textsf{Eatery}}\right>}, \quad {\left<{\textsf{Restaurant} \sqsubseteq \textsf{Eatery}}\right>}, \quad {\left<{\textsf{locIn}\sqsubseteq \textsf{Near}}\right>}\\ & {\left<{\textsf{Museum} \sqsubseteq \textsf{Popular}},[0.6]\right>}, \quad {\left<{\exists \textsf{locIn}\sqsubseteq \neg \textsf{Cheap}},[0.5]\right>} & \}\end{align*}
\begin{align*}{\mathcal{T}_\textsf{exa}} =\{ & {\left<{\textsf{Monument} \sqsubseteq \textsf{TouristAttraction}}\right>}, \quad {\left<{\textsf{Museum} \sqsubseteq \textsf{TouristAttraction}}\right>}, \\ & {\left<{\textsf{Pub} \sqsubseteq \textsf{Eatery}}\right>}, \quad {\left<{\textsf{Restaurant} \sqsubseteq \textsf{Eatery}}\right>}, \quad {\left<{\textsf{locIn}\sqsubseteq \textsf{Near}}\right>}\\ & {\left<{\textsf{Museum} \sqsubseteq \textsf{Popular}},[0.6]\right>}, \quad {\left<{\exists \textsf{locIn}\sqsubseteq \neg \textsf{Cheap}},[0.5]\right>} & \}\end{align*}
defines some notions about eateries and tourist attractions, including some vague notions in the last two axioms. For example, it expresses that museums are popular (with a degree at least 0.6), and that services located at some attraction are not cheap (with degree at least 0.5). The ABox
 \begin{align*}{\mathcal{A}_\textsf{exa}} = \{ & {\left<{\textsf{Monument}(\textsf{peace})}\right>}, \quad {\left<{\textsf{Monument}(\textsf{love})}\right>}, \\ & {\left<{\textsf{Museum}(\textsf{modernArt})}\right>}, \quad {\left<{\textsf{Museum}(\textsf{contArt})}\right>}, \quad {\left<{\textsf{Museum}(\textsf{comic})}\right>}, \\ & {\left<{\textsf{Restaurant}(\textsf{sioux})}\right>}, \quad {\left<{\textsf{Restaurant}(\textsf{gamberone})}\right>}, \\ & {\left<{\textsf{Pub}(\textsf{irish})}\right>}, \quad {\left<{\textsf{locIn}(\textsf{sioux},\textsf{modernArt})}\right>}, \\ & {\left<{\textsf{Popular}(\textsf{comic})},[0.8]\right>}, \quad {\left<{\textsf{Cheap}(\textsf{irish})},[0.6]\right>}, \quad {\left<{\textsf{near}(\textsf{irish},\textsf{comic})},[0.7]\right>} & \}\end{align*}
\begin{align*}{\mathcal{A}_\textsf{exa}} = \{ & {\left<{\textsf{Monument}(\textsf{peace})}\right>}, \quad {\left<{\textsf{Monument}(\textsf{love})}\right>}, \\ & {\left<{\textsf{Museum}(\textsf{modernArt})}\right>}, \quad {\left<{\textsf{Museum}(\textsf{contArt})}\right>}, \quad {\left<{\textsf{Museum}(\textsf{comic})}\right>}, \\ & {\left<{\textsf{Restaurant}(\textsf{sioux})}\right>}, \quad {\left<{\textsf{Restaurant}(\textsf{gamberone})}\right>}, \\ & {\left<{\textsf{Pub}(\textsf{irish})}\right>}, \quad {\left<{\textsf{locIn}(\textsf{sioux},\textsf{modernArt})}\right>}, \\ & {\left<{\textsf{Popular}(\textsf{comic})},[0.8]\right>}, \quad {\left<{\textsf{Cheap}(\textsf{irish})},[0.6]\right>}, \quad {\left<{\textsf{near}(\textsf{irish},\textsf{comic})},[0.7]\right>} & \}\end{align*}
provides information about the specific attractions and services provided at the location. From this information, we can deduce, for example, that the modernArt museum is a TouristAttraction, and is Popular to a degree at least
![]() $0.6$
. Under the Gödel t-norm, a possible model of
$0.6$
. Under the Gödel t-norm, a possible model of
![]() ${\mathcal{O}_\textsf{exa}}$
is depicted graphically in Figure 1, where any assertion not depicted is considered to hold to degree 0. For example, the model from Figure 1 interprets the irish pub as being Cheap to degree 0.7, which satisfies the constraint in the ABox requiring this degree to be at least 0.6. In addition, the peace monument is Popular to degree 0.3, even though there is no explicit requirement for this in
${\mathcal{O}_\textsf{exa}}$
is depicted graphically in Figure 1, where any assertion not depicted is considered to hold to degree 0. For example, the model from Figure 1 interprets the irish pub as being Cheap to degree 0.7, which satisfies the constraint in the ABox requiring this degree to be at least 0.6. In addition, the peace monument is Popular to degree 0.3, even though there is no explicit requirement for this in
![]() ${\mathcal{O}_\textsf{exa}}$
. Note that under this semantics, any model
${\mathcal{O}_\textsf{exa}}$
. Note that under this semantics, any model
![]() ${\mathcal{I}}$
of
${\mathcal{I}}$
of
![]() ${\mathcal{O}_\textsf{exa}}$
should necessarily satisfy that
${\mathcal{O}_\textsf{exa}}$
should necessarily satisfy that
![]() $\textsf{Cheap}^{\mathcal{I}}(\textsf{sioux}^{\mathcal{I}})=0$
; this is in fact the case in the model from Figure 1. Hence, adding any assertion of the form
$\textsf{Cheap}^{\mathcal{I}}(\textsf{sioux}^{\mathcal{I}})=0$
; this is in fact the case in the model from Figure 1. Hence, adding any assertion of the form
![]() ${\left<{\textsf{Cheap}(\textsf{sioux})},[d]\right>}$
with
${\left<{\textsf{Cheap}(\textsf{sioux})},[d]\right>}$
with
![]() $d>0$
to this ontology would make it inconsistent.
$d>0$
to this ontology would make it inconsistent.

Figure 1. A model for the ontology
![]() ${\mathcal{O}_\textsf{exa}}$
from Example 3. Individual names are abbreviated to avoid cluttering, and start with a lower-case letter as customary in DLs. The shape and border of the nodes represent the crisp concepts, while vague concepts are associated to a degree.
${\mathcal{O}_\textsf{exa}}$
from Example 3. Individual names are abbreviated to avoid cluttering, and start with a lower-case letter as customary in DLs. The shape and border of the nodes represent the crisp concepts, while vague concepts are associated to a degree.
For this paper, we are interested in answering two kinds of queries. The first kind are conjunctive queries, which consider whether a combination of facts can be derived from the knowledge in an ontology. In the fuzzy setting, the degree of such derivation must also be taken into account.
Let
![]() ${N_V}$
be a set of variables, which is disjoint from
${N_V}$
be a set of variables, which is disjoint from
![]() ${N_I}$
,
${N_I}$
,
![]() ${N_C}$
, and
${N_C}$
, and
![]() ${N_R}$
. A term is an element of
${N_R}$
. A term is an element of
![]() ${N_V}\cup{N_I}$
; that is, an individual name or a variable. An atom is an expression of the form C(t) (concept atom) or
${N_V}\cup{N_I}$
; that is, an individual name or a variable. An atom is an expression of the form C(t) (concept atom) or
![]() $P(t_1,t_2)$
(role atom). Henceforth,
$P(t_1,t_2)$
(role atom). Henceforth,
![]() ${\mathbf{x}}$
and
${\mathbf{x}}$
and
![]() ${\mathbf{y}}$
denote tuples of variables.
${\mathbf{y}}$
denote tuples of variables.
Definition 4
(conjunctive query) A conjunctive query (CQ) is a first-order formula of the form
![]() $\exists {\mathbf{y}}.\phi({\mathbf{x}},{\mathbf{y}})$
where
$\exists {\mathbf{y}}.\phi({\mathbf{x}},{\mathbf{y}})$
where
![]() $\phi$
is a conjunction of atoms which only use the variables from
$\phi$
is a conjunction of atoms which only use the variables from
![]() ${\mathbf{x}}$
and
${\mathbf{x}}$
and
![]() ${\mathbf{y}}$
. The variables
${\mathbf{y}}$
. The variables
![]() ${\mathbf{y}}$
are called existential variables, and those in
${\mathbf{y}}$
are called existential variables, and those in
![]() ${\mathbf{x}}$
are answer variables. A union of conjunctive queries (UCQ) is a finite set of CQs that use the same answer variables. Henceforth,
${\mathbf{x}}$
are answer variables. A union of conjunctive queries (UCQ) is a finite set of CQs that use the same answer variables. Henceforth,
![]() ${\mathsf{At}}(\phi)$
denotes the set of all atoms appearing in
${\mathsf{At}}(\phi)$
denotes the set of all atoms appearing in
![]() $\phi$
.
$\phi$
.
As in the classical setting, an answer to a conjunctive query, or a union of conjunctive queries, is only considered when it is provided by every model of the ontology. This is usually known as a certain answer.
Given the CQ
![]() $q({\mathbf{x}})=\exists {\mathbf{y}}.\phi({\mathbf{x}},{\mathbf{y}})$
, the interpretation
$q({\mathbf{x}})=\exists {\mathbf{y}}.\phi({\mathbf{x}},{\mathbf{y}})$
, the interpretation
![]() ${\mathcal{I}}$
, and a tuple of individuals
${\mathcal{I}}$
, and a tuple of individuals
![]() ${\mathbf{a}}$
of the same length as
${\mathbf{a}}$
of the same length as
![]() ${\mathbf{x}}$
, a match is a mapping
${\mathbf{x}}$
, a match is a mapping
![]() $\pi$
which assigns to each
$\pi$
which assigns to each
![]() $a\in{N_I}$
the value
$a\in{N_I}$
the value
![]() $a^{\mathcal{I}}$
; to each variable in
$a^{\mathcal{I}}$
; to each variable in
![]() ${\mathbf{x}}$
the corresponding element of
${\mathbf{x}}$
the corresponding element of
![]() ${\mathbf{a}}^{\mathcal{I}}$
; and to each variable in
${\mathbf{a}}^{\mathcal{I}}$
; and to each variable in
![]() ${\mathbf{y}}$
an element
${\mathbf{y}}$
an element
![]() $\delta\in\Delta^{\mathcal{I}}$
. We extend the match
$\delta\in\Delta^{\mathcal{I}}$
. We extend the match
![]() $\pi$
to apply to assertions as follows:
$\pi$
to apply to assertions as follows:
![]() $\pi(B(t))=B(\pi(t))$
and
$\pi(B(t))=B(\pi(t))$
and
![]() $\pi(P(t_1,t_2))=P(\pi(t_1),\pi(t_2))$
. The degree of the CQ
$\pi(P(t_1,t_2))=P(\pi(t_1),\pi(t_2))$
. The degree of the CQ
![]() $q({\mathbf{x}})$
w.r.t. the match
$q({\mathbf{x}})$
w.r.t. the match
![]() $\pi$
is
$\pi$
is
That is, a match maps all the variables in the query to elements of the interpretation domain, where the tuple
![]() ${\mathbf{a}}$
is used to identify the mapping of the answer variables. The satisfaction or matching degree of the query is the (fuzzy) conjunction – that is, the t-norm – of the satisfaction or matching degrees of the atoms under this mapping. From now on,
${\mathbf{a}}$
is used to identify the mapping of the answer variables. The satisfaction or matching degree of the query is the (fuzzy) conjunction – that is, the t-norm – of the satisfaction or matching degrees of the atoms under this mapping. From now on,
![]() $\Pi({\mathcal{I}})$
denotes the set of all matches of
$\Pi({\mathcal{I}})$
denotes the set of all matches of
![]() $q({\mathbf{x}})$
w.r.t. the interpretation
$q({\mathbf{x}})$
w.r.t. the interpretation
![]() ${\mathcal{I}}$
. An important difference between classical query answering and our setting is that the fuzzy semantics provides a degree to every possible atom. Hence, in reality
${\mathcal{I}}$
. An important difference between classical query answering and our setting is that the fuzzy semantics provides a degree to every possible atom. Hence, in reality
![]() $\Pi({\mathcal{I}})$
is always defined by the set of all tuples of individuals with length
$\Pi({\mathcal{I}})$
is always defined by the set of all tuples of individuals with length
![]() $|{\mathbf{x}}|$
. However, the degree of these matches varies and may often be zero. For example, for the model
$|{\mathbf{x}}|$
. However, the degree of these matches varies and may often be zero. For example, for the model
![]() ${\mathcal{I}}$
in Figure 1 and the query
${\mathcal{I}}$
in Figure 1 and the query
![]() $q(x)=\textsf{Popular}(x)$
, the set of all matches
$q(x)=\textsf{Popular}(x)$
, the set of all matches
![]() $\Pi({\mathcal{I}})$
assigns to the variable x any of the constants
$\Pi({\mathcal{I}})$
assigns to the variable x any of the constants
![]() $\{\textsf{mA},\textsf{cA},\textsf{c},\textsf{p},\textsf{l},\textsf{s},\textsf{i},\textsf{g}\}$
to degrees
$\{\textsf{mA},\textsf{cA},\textsf{c},\textsf{p},\textsf{l},\textsf{s},\textsf{i},\textsf{g}\}$
to degrees
![]() $0.7,0.6,0.9,0.3,0,0,0$
, and 0, respectively. When answering a query, one is often interested in the matches that hold to at least some degree d, as defined next.
$0.7,0.6,0.9,0.3,0,0,0$
, and 0, respectively. When answering a query, one is often interested in the matches that hold to at least some degree d, as defined next.
Definition 5
(degree queries) A tuple of individuals
![]() ${\mathbf{a}}$
is an answer of the conjunctive query
${\mathbf{a}}$
is an answer of the conjunctive query
![]() $q({\mathbf{x}})$
to degree d w.r.t. the interpretation
$q({\mathbf{x}})$
to degree d w.r.t. the interpretation
![]() ${\mathcal{I}}$
(denoted by
${\mathcal{I}}$
(denoted by
![]() ${\mathcal{I}}\models q({\mathbf{a}})\ge d$
) iff
${\mathcal{I}}\models q({\mathbf{a}})\ge d$
) iff
![]() $q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}}):=\sup_{\pi\in\Pi({\mathcal{I}})}q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}},\pi({\mathbf{y}}))\ge d$
. It is a certain answer (or answer for short) of
$q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}}):=\sup_{\pi\in\Pi({\mathcal{I}})}q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}},\pi({\mathbf{y}}))\ge d$
. It is a certain answer (or answer for short) of
![]() $q({\mathbf{x}})$
over the ontology
$q({\mathbf{x}})$
over the ontology
![]() ${\mathcal{O}}$
to degree d (denoted by
${\mathcal{O}}$
to degree d (denoted by
![]() ${\mathcal{O}}\models q({\mathbf{a}})\ge d$
) iff
${\mathcal{O}}\models q({\mathbf{a}})\ge d$
) iff
![]() ${\mathcal{I}}\models q({\mathbf{a}})\ge d$
holds for every model
${\mathcal{I}}\models q({\mathbf{a}})\ge d$
holds for every model
![]() ${\mathcal{I}}$
of
${\mathcal{I}}$
of
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
The crisp set of certain answers of the query
![]() $q({\mathbf{x}})$
w.r.t.
$q({\mathbf{x}})$
w.r.t.
![]() ${\mathcal{O}}$
and their degree is denoted by
${\mathcal{O}}$
and their degree is denoted by
![]() ${\mathsf{ans}}(q({\mathbf{x}}),{\mathcal{O}})$
; that is,
${\mathsf{ans}}(q({\mathbf{x}}),{\mathcal{O}})$
; that is,
It is important to keep in mind that the atoms in a CQ are not graded, but simply try to match with elements in the domain as both concept and roles are interpreted as fuzzy relations (unary and binary, respectively). The use of the truth degrees in the ontology becomes relevant in the degree of the answers found. Moreover, recall that every tuple of individuals of length
![]() $|{\mathbf{x}}|$
belongs to
$|{\mathbf{x}}|$
belongs to
![]() ${\mathsf{ans}}(q({\mathbf{x}}),{\mathcal{O}})$
, but with different associated degrees.
${\mathsf{ans}}(q({\mathbf{x}}),{\mathcal{O}})$
, but with different associated degrees.
Returning to our example, while all individuals belong to the set
![]() ${\mathsf{ans}}(q(x))$
, for the query
${\mathsf{ans}}(q(x))$
, for the query
![]() $q(x)=\textsf{Popular}(x)$
to some degree, the certain answers for q(x) w.r.t.
$q(x)=\textsf{Popular}(x)$
to some degree, the certain answers for q(x) w.r.t.
![]() ${\mathcal{O}_\textsf{exa}}$
to degree at least 0.6 are only modernArt, contArt, and comic. The latter one is the only answer to degree at least 0.8.
${\mathcal{O}_\textsf{exa}}$
to degree at least 0.6 are only modernArt, contArt, and comic. The latter one is the only answer to degree at least 0.8.
The second kind of query we are interested in generalizes that of degree queries, when considering the Gödel semantics, by allowing a degree threshold for each of the atoms in the conjunction, rather than for the overall conjunction. We formally define this class next.
Definition 6
(threshold queries) A threshold atom is an expression of the form
![]() $\alpha\ge d$
, where
$\alpha\ge d$
, where
![]() $\alpha$
is an atom and
$\alpha$
is an atom and
![]() $d\in[0,1]$
. A threshold query (TQ) is a first-order formula of the form
$d\in[0,1]$
. A threshold query (TQ) is a first-order formula of the form
![]() $\exists {\mathbf{y}}.\phi({\mathbf{x}},{\mathbf{y}})$
where
$\exists {\mathbf{y}}.\phi({\mathbf{x}},{\mathbf{y}})$
where
![]() $\phi$
is a conjunction of threshold atoms using only the variables from
$\phi$
is a conjunction of threshold atoms using only the variables from
![]() ${\mathbf{x}}$
and
${\mathbf{x}}$
and
![]() ${\mathbf{y}}$
.
${\mathbf{y}}$
.
The notion of a match and an answer to a threshold query are analogous to those of degree queries, with the proviso that the degree bounds apply at the level of atoms, and not at the level of queries.
Definition 7
(TQ answer) Given an interpretation
![]() ${\mathcal{I}}$
and a tuple of individuals
${\mathcal{I}}$
and a tuple of individuals
![]() ${\mathbf{a}}$
, the match
${\mathbf{a}}$
, the match
![]() $\pi$
satisfies the threshold atom
$\pi$
satisfies the threshold atom
![]() $\alpha\ge d$
(denoted by
$\alpha\ge d$
(denoted by
![]() $\pi\models\alpha\ge d$
) iff
$\pi\models\alpha\ge d$
) iff
![]() $\alpha^{\mathcal{I}}\ge d$
. It satisfies the threshold query
$\alpha^{\mathcal{I}}\ge d$
. It satisfies the threshold query
![]() $q({\mathbf{x}})=\exists {\mathbf{y}}.\phi({\mathbf{x}},{\mathbf{y}})$
(
$q({\mathbf{x}})=\exists {\mathbf{y}}.\phi({\mathbf{x}},{\mathbf{y}})$
(
![]() $\pi\models q({\mathbf{a}})$
) iff
$\pi\models q({\mathbf{a}})$
) iff
![]() $\pi\models \alpha\ge d$
holds for every threshold atom in q.
$\pi\models \alpha\ge d$
holds for every threshold atom in q.
A tuple of individuals
![]() ${\mathbf{a}}$
is an answer to the TQ
${\mathbf{a}}$
is an answer to the TQ
![]() $q({\mathbf{x}})$
w.r.t. the interpretation
$q({\mathbf{x}})$
w.r.t. the interpretation
![]() ${\mathcal{I}}$
(
${\mathcal{I}}$
(
![]() ${\mathcal{I}}\models q({\mathbf{a}})$
) iff there is a match
${\mathcal{I}}\models q({\mathbf{a}})$
) iff there is a match
![]() $\pi$
w.r.t.
$\pi$
w.r.t.
![]() ${\mathbf{a}}$
and
${\mathbf{a}}$
and
![]() ${\mathcal{I}}$
such that
${\mathcal{I}}$
such that
![]() $\pi\models q({\mathbf{a}})$
. It is a certain answer of
$\pi\models q({\mathbf{a}})$
. It is a certain answer of
![]() $q({\mathbf{x}})$
over the ontology
$q({\mathbf{x}})$
over the ontology
![]() ${\mathcal{O}}$
iff for every model
${\mathcal{O}}$
iff for every model
![]() ${\mathcal{I}}$
of
${\mathcal{I}}$
of
![]() ${\mathcal{O}}$
it holds that
${\mathcal{O}}$
it holds that
![]() ${\mathcal{I}}\models q({\mathbf{a}})$
.
${\mathcal{I}}\models q({\mathbf{a}})$
.
Note that, differently from conjunctive queries, but in an analogous manner to degree queries, the answers to a threshold query are not graded. Indeed, a tuple
![]() ${\mathbf{a}}$
may or may not be an answer, and we are interested in finding those tuples which satisfy the degrees at each of the threshold atoms. In a sense, threshold queries provide a more fine-grained structure to deal with the properties of interest within a query in relation to degree queries. Indeed, in a degree query, one can only provide an overall degree which should be obtained after the degrees of all the atoms are conjoined via the t-norm. In particular, for non-idempotent t-norms and large queries, this conjunction will tend to be smaller and smaller, and the degrees of the independent atoms have the same influence overall. Even when considering the idempotent Gödel t-norm, a degree query
${\mathbf{a}}$
may or may not be an answer, and we are interested in finding those tuples which satisfy the degrees at each of the threshold atoms. In a sense, threshold queries provide a more fine-grained structure to deal with the properties of interest within a query in relation to degree queries. Indeed, in a degree query, one can only provide an overall degree which should be obtained after the degrees of all the atoms are conjoined via the t-norm. In particular, for non-idempotent t-norms and large queries, this conjunction will tend to be smaller and smaller, and the degrees of the independent atoms have the same influence overall. Even when considering the idempotent Gödel t-norm, a degree query
![]() $q({\mathbf{x}})\ge d$
only expresses that all the atoms in q should hold to degree at least d (recall that the Gödel t-norm refers to the minimum operator), but it is not possible to express that some atoms should hold with a higher degree. A threshold query, on the other hand, is capable of requiring different degrees for each of the atoms.
$q({\mathbf{x}})\ge d$
only expresses that all the atoms in q should hold to degree at least d (recall that the Gödel t-norm refers to the minimum operator), but it is not possible to express that some atoms should hold with a higher degree. A threshold query, on the other hand, is capable of requiring different degrees for each of the atoms.
Example 8 Suppose, in our running example, that we are interested in finding a cheap eatery that is nearby a popular tourist attraction, and that we are using the Gödel semantics. This basic query could be expressed as Footnote 1
Since this query considers vague concepts and roles, we want to find answers that satisfy it to at least some degree. For the degree query
![]() $q(x)\ge 0.6$
, the only possible answer is the irish pub.
$q(x)\ge 0.6$
, the only possible answer is the irish pub.
Suppose now that for us it is more important that the eatery is cheap than the popularity of the tourist attraction. For example, even though we are content with the tourist attraction being popular to only degree 0.6, the eatery should be cheap to a degree at least 0.8. This can be expressed through the threshold query
In this case, the TQ has no answers w.r.t. the ontology
![]() ${\mathcal{O}}$
. However, any answer to q’ would also be an answer to
${\mathcal{O}}$
. However, any answer to q’ would also be an answer to
![]() $q(x)\ge 0.6$
, as overall they define the same minimum over all the degrees of interest. Note that this last claim only holds for the case of the Gödel semantics. Indeed, as we will see later in this paper, for other semantics degree queries are not properly special cases of TQs.
$q(x)\ge 0.6$
, as overall they define the same minimum over all the degrees of interest. Note that this last claim only holds for the case of the Gödel semantics. Indeed, as we will see later in this paper, for other semantics degree queries are not properly special cases of TQs.
A class of conjunctive queries of special significance is that where the tuple of answer variables
![]() ${\mathbf{x}}$
is empty. This means that the answer tuple of individuals provided as an answer must also be empty. In the classical setting, these are called Boolean queries, because they can only return a Boolean value: true if there is a match for the existential variables in every model, and false otherwise. In the fuzzy setting, the set of answers to such a query will only contain one element ((),d). Thus, in that case, we are only interested in finding the degree d, and call those queries fuzzy queries. This degree is the tightest value for which we can find a satisfying matching. Formally, the ontology
${\mathbf{x}}$
is empty. This means that the answer tuple of individuals provided as an answer must also be empty. In the classical setting, these are called Boolean queries, because they can only return a Boolean value: true if there is a match for the existential variables in every model, and false otherwise. In the fuzzy setting, the set of answers to such a query will only contain one element ((),d). Thus, in that case, we are only interested in finding the degree d, and call those queries fuzzy queries. This degree is the tightest value for which we can find a satisfying matching. Formally, the ontology
![]() ${\mathcal{O}}$
entails the fuzzy query q() to degree d iff
${\mathcal{O}}$
entails the fuzzy query q() to degree d iff
![]() ${\mathcal{O}}\models q()\ge d$
and
${\mathcal{O}}\models q()\ge d$
and
![]() ${\mathcal{O}}\not\models q()\ge d'$
for all
${\mathcal{O}}\not\models q()\ge d'$
for all
![]() $d'>d$
. Fuzzy queries allow us to find the degree of a specific answer
$d'>d$
. Fuzzy queries allow us to find the degree of a specific answer
![]() ${\mathbf{a}}$
without having to compute
${\mathbf{a}}$
without having to compute
![]() ${\mathsf{ans}}(q({\mathbf{x}}),{\mathcal{O}})$
: simply compute the degree of the fuzzy query
${\mathsf{ans}}(q({\mathbf{x}}),{\mathcal{O}})$
: simply compute the degree of the fuzzy query
![]() $q({\mathbf{a}})$
.
$q({\mathbf{a}})$
.
In the case of threshold queries, we can also consider the special case where the answer tuple
![]() ${\mathbf{x}}$
is empty. In that case, as in the classical case, the only possible answer is the empty tuple (if there is a match which satisfies the query) or no answer if no such match exists. For that reason, in the case of threshold queries without answer variables we preserve the classical terminology and call them Boolean (threshold) queries.
${\mathbf{x}}$
is empty. In that case, as in the classical case, the only possible answer is the empty tuple (if there is a match which satisfies the query) or no answer if no such match exists. For that reason, in the case of threshold queries without answer variables we preserve the classical terminology and call them Boolean (threshold) queries.
As it is typically done for query answering in description logics, we consider two measures of complexity: data complexity, where only the size of the ABox (and the candidate answer, if any) is considered as part of the input, and combined complexity in which the size of the whole ontology (including the TBox) is taken into account.
Footnote 2
For data complexity, it is relevant to consider sub-linear complexity classes. In particular, we consider
![]() ${AC}^{0}$
and
${AC}^{0}$
and
![]() ${\rm L{\small OG} S{\small PACE}}$
. For the full formal definitions, we refer the interested reader to Papadimitriou (Reference Papadimitriou1994) and Boppana and Sipser (Reference Boppana and Sipser1990). Here we only mention briefly that evaluation of FO-queries over a database is in
${\rm L{\small OG} S{\small PACE}}$
. For the full formal definitions, we refer the interested reader to Papadimitriou (Reference Papadimitriou1994) and Boppana and Sipser (Reference Boppana and Sipser1990). Here we only mention briefly that evaluation of FO-queries over a database is in
![]() ${AC}^{0}$
on the size of the database (Abiteboul et al. Reference Abiteboul, Hull and Vianu1994) and
${AC}^{0}$
on the size of the database (Abiteboul et al. Reference Abiteboul, Hull and Vianu1994) and
![]() ${AC}^{0}$
is strictly contained in
${AC}^{0}$
is strictly contained in
![]() ${\rm L{\small OG} S{\small PACE}}$
(Furst et al. Reference Furst, Saxe and Sipser1984). In classical
${\rm L{\small OG} S{\small PACE}}$
(Furst et al. Reference Furst, Saxe and Sipser1984). In classical
![]() $\text{DL-Lite}_{R}$
, query answering w.r.t. an ontology is reduced to the standard problem of query answering over a database through a process known as query rewriting, and thus is in
$\text{DL-Lite}_{R}$
, query answering w.r.t. an ontology is reduced to the standard problem of query answering over a database through a process known as query rewriting, and thus is in
![]() ${AC}^{0}$
w.r.t. data complexity. The main idea is to include in the query all the information that is required by the TBox, in such a way that only assertions from the ABox need to be considered. In our running example, note that there is no assertion in the ABox
${AC}^{0}$
w.r.t. data complexity. The main idea is to include in the query all the information that is required by the TBox, in such a way that only assertions from the ABox need to be considered. In our running example, note that there is no assertion in the ABox
![]() ${\mathcal{A}_\textsf{exa}}$
which explicitly mentions a tourist attraction. We only know that the two monuments and the three museums are tourist attractions thanks to the TBox. In this case, the query rewriting approach would take the query
${\mathcal{A}_\textsf{exa}}$
which explicitly mentions a tourist attraction. We only know that the two monuments and the three museums are tourist attractions thanks to the TBox. In this case, the query rewriting approach would take the query
![]() $q(x)=\textsf{TouristAttraction}(x)$
and transform it into the UCQ
$q(x)=\textsf{TouristAttraction}(x)$
and transform it into the UCQ
looking “backwards” over the axioms in the TBox. The answers of this UCQ over the ABox alone are exactly those of the original query over the whole ontology.
As seen in this simple example, there are many possible choices to create the matches that comply with the TBox. Hence, this method results in a UCQ even if the original query is a simple CQ. At this point, the ABox is treated as a database, which suffices to find all the certain answers. Similarly, a special UCQ can be used to verify that the ontology is consistent; that is, whether it is possible to build a model for this ontology. For the full details on how these query rewritings work in classical
![]() $\text{DL-Lite}_{R}$
, see the work by (Artale et al. Reference Artale, Calvanese, Kontchakov and Zakharyaschev2009). In terms of combined complexity, consistency can be decided in polynomial time; in fact, it is
$\text{DL-Lite}_{R}$
, see the work by (Artale et al. Reference Artale, Calvanese, Kontchakov and Zakharyaschev2009). In terms of combined complexity, consistency can be decided in polynomial time; in fact, it is
![]() ${\rm N \rm L{\small OG} S{\small PACE}}$
-complete (Artale et al. Reference Artale, Calvanese, Kontchakov and Zakharyaschev2009).
${\rm N \rm L{\small OG} S{\small PACE}}$
-complete (Artale et al. Reference Artale, Calvanese, Kontchakov and Zakharyaschev2009).
3 The canonical interpretation
A very useful tool for developing techniques for answering queries in
![]() $\text{DL-Lite}_{R}$
is the canonical interpretation. We first show that the same idea can be extended (with the necessary modifications) to fuzzy ontologies, independently of the t-norm underlying its semantics.
$\text{DL-Lite}_{R}$
is the canonical interpretation. We first show that the same idea can be extended (with the necessary modifications) to fuzzy ontologies, independently of the t-norm underlying its semantics.
Let
![]() ${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
be a
${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
be a
![]() $\text{DL-Lite}_{R}$
ontology and assume w.l.o.g. that there are no axioms of the form
$\text{DL-Lite}_{R}$
ontology and assume w.l.o.g. that there are no axioms of the form
![]() $\left<\exists Q_1\sqsubseteq\exists Q_2,d\right>\in{\mathcal{T}}$
; any such axiom can be substituted by the two axioms
$\left<\exists Q_1\sqsubseteq\exists Q_2,d\right>\in{\mathcal{T}}$
; any such axiom can be substituted by the two axioms
![]() $\left<\exists Q_1\sqsubseteq A,1\right>,\left<A\sqsubseteq \exists Q_2,d\right>$
where A is a new concept name not appearing in
$\left<\exists Q_1\sqsubseteq A,1\right>,\left<A\sqsubseteq \exists Q_2,d\right>$
where A is a new concept name not appearing in
![]() ${\mathcal{T}}$
. The canonical interpretation of
${\mathcal{T}}$
. The canonical interpretation of
![]() ${\mathcal{O}}$
is the interpretation
${\mathcal{O}}$
is the interpretation
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})=(\Delta^{{\mathcal{I}_\mathsf{can}}},\cdot^{{\mathcal{I}_\mathsf{can}}})$
over the domain
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})=(\Delta^{{\mathcal{I}_\mathsf{can}}},\cdot^{{\mathcal{I}_\mathsf{can}}})$
over the domain
![]() $\Delta^{{\mathcal{I}_\mathsf{can}}}:={N_I}\cup{N_N}$
– where
$\Delta^{{\mathcal{I}_\mathsf{can}}}:={N_I}\cup{N_N}$
– where
![]() ${N_N}$
is a countable set of constants – obtained through the following (infinite) process. Starting from the empty interpretation which sets
${N_N}$
is a countable set of constants – obtained through the following (infinite) process. Starting from the empty interpretation which sets
![]() $A^{{\mathcal{I}_\mathsf{can}}}(\delta)=0$
and
$A^{{\mathcal{I}_\mathsf{can}}}(\delta)=0$
and
![]() $P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)=0$
for every
$P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)=0$
for every
![]() $A\in{N_C}, P\in{N_R}$
and
$A\in{N_C}, P\in{N_R}$
and
![]() $\delta,\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
, exhaustively apply the following rules:
$\delta,\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
, exhaustively apply the following rules:
-
R1. if
 $\left<A(a),d\right>\in{\mathcal{A}}$
and
$\left<A(a),d\right>\in{\mathcal{A}}$
and
 $A^{{\mathcal{I}_\mathsf{can}}}(a)< d$
, then update the value
$A^{{\mathcal{I}_\mathsf{can}}}(a)< d$
, then update the value
 $A^{{\mathcal{I}_\mathsf{can}}}(a):=d$
;
$A^{{\mathcal{I}_\mathsf{can}}}(a):=d$
; -
R2. if
 $\left<P(a,b),d\right>\in{\mathcal{A}}$
and
$\left<P(a,b),d\right>\in{\mathcal{A}}$
and
 $P^{{\mathcal{I}_\mathsf{can}}}(a,b)< d$
, then update the value
$P^{{\mathcal{I}_\mathsf{can}}}(a,b)< d$
, then update the value
 $P^{{\mathcal{I}_\mathsf{can}}}(a,b):=d$
;
$P^{{\mathcal{I}_\mathsf{can}}}(a,b):=d$
; -
R3. if
 $\left<A_1\sqsubseteq A_2,d\right>\in{\mathcal{T}}$
and
$\left<A_1\sqsubseteq A_2,d\right>\in{\mathcal{T}}$
and
 $A_2^{{\mathcal{I}_\mathsf{can}}}(\delta)< A_1^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
, then update
$A_2^{{\mathcal{I}_\mathsf{can}}}(\delta)< A_1^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
, then update
 $A_2^{{\mathcal{I}_\mathsf{can}}}(\delta):=A_1^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
;
$A_2^{{\mathcal{I}_\mathsf{can}}}(\delta):=A_1^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
; -
R4. if
 $\left<A\sqsubseteq \exists P,d\right>\in{\mathcal{T}}$
and for every
$\left<A\sqsubseteq \exists P,d\right>\in{\mathcal{T}}$
and for every
 $\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
,
$\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
,
 $P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)<A^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
holds, then select a fresh element
$P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)<A^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
holds, then select a fresh element
 $\eta_0$
such that
$\eta_0$
such that
 $P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta_0)=0$
and update the value
$P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta_0)=0$
and update the value
 $P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta_0):=A^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
;
$P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta_0):=A^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
; -
R5. if
 $\left<A\sqsubseteq \exists P^-,d\right>\in{\mathcal{T}}$
and for every
$\left<A\sqsubseteq \exists P^-,d\right>\in{\mathcal{T}}$
and for every
 $\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
$\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
 $P^{{\mathcal{I}_\mathsf{can}}}(\eta,\delta)<A^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
holds, then select a fresh element
$P^{{\mathcal{I}_\mathsf{can}}}(\eta,\delta)<A^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
holds, then select a fresh element
 $\eta_0$
such that
$\eta_0$
such that
 $P^{{\mathcal{I}_\mathsf{can}}}(\eta_0,\delta)=0$
and update the value
$P^{{\mathcal{I}_\mathsf{can}}}(\eta_0,\delta)=0$
and update the value
 $P^{{\mathcal{I}_\mathsf{can}}}(\eta_0,\delta):=A^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
;
$P^{{\mathcal{I}_\mathsf{can}}}(\eta_0,\delta):=A^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
; -
R6. if
 $\left<\exists P\sqsubseteq A,d\right>\in {\mathcal{T}}$
and
$\left<\exists P\sqsubseteq A,d\right>\in {\mathcal{T}}$
and
 $\exists\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
such that
$\exists\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
such that
 $A^{{\mathcal{I}_\mathsf{can}}}(\delta)<P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d$
, then update
$A^{{\mathcal{I}_\mathsf{can}}}(\delta)<P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d$
, then update
 $A^{{\mathcal{I}_\mathsf{can}}}(\delta):=P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d$
;
$A^{{\mathcal{I}_\mathsf{can}}}(\delta):=P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d$
; -
R7. if
 $\left<\exists P^-\sqsubseteq A,d\right>\in {\mathcal{T}}$
and
$\left<\exists P^-\sqsubseteq A,d\right>\in {\mathcal{T}}$
and
 $\exists\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
such that
$\exists\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
such that
 $A^{{\mathcal{I}_\mathsf{can}}}(\delta)<P^{{\mathcal{I}_\mathsf{can}}}(\eta,\delta)\otimes d$
, then update
$A^{{\mathcal{I}_\mathsf{can}}}(\delta)<P^{{\mathcal{I}_\mathsf{can}}}(\eta,\delta)\otimes d$
, then update
 $A^{{\mathcal{I}_\mathsf{can}}}(\delta):=P^{{\mathcal{I}_\mathsf{can}}}(\eta,\delta)\otimes d$
;
$A^{{\mathcal{I}_\mathsf{can}}}(\delta):=P^{{\mathcal{I}_\mathsf{can}}}(\eta,\delta)\otimes d$
; -
R8. if
 $\left<Q_1\sqsubseteq Q_2,d\right>\in{\mathcal{T}}$
and
$\left<Q_1\sqsubseteq Q_2,d\right>\in{\mathcal{T}}$
and
 $Q_2^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)<Q_1^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d$
, then update
$Q_2^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)<Q_1^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d$
, then update
 $Q_2^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)$
to the value
$Q_2^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)$
to the value
 $Q_1^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d$
.
$Q_1^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d$
.
where the rules are applied in a fair manner; that is, an applicable rule is eventually triggered. The process of rule application is a monotone non-decreasing function, and as such has a least fixpoint, which is the canonical interpretation
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
.
Footnote 3
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
.
Footnote 3
Intuitively,
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
should be a minimal model of
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
should be a minimal model of
![]() ${\mathcal{O}}$
, which describes the necessary conditions of all other models of
${\mathcal{O}}$
, which describes the necessary conditions of all other models of
![]() ${\mathcal{O}}$
. Indeed, the first two rules ensure that the conditions imposed by the ABox are satisfied, by setting the degrees of the unary and binary relations to the smallest required value. The remaining rules guarantee that all elements of the domain satisfy the positive axioms from the TBox, and each rule is as weak as possible in satisfying these constraints. The canonical interpretation of the ontology
${\mathcal{O}}$
. Indeed, the first two rules ensure that the conditions imposed by the ABox are satisfied, by setting the degrees of the unary and binary relations to the smallest required value. The remaining rules guarantee that all elements of the domain satisfy the positive axioms from the TBox, and each rule is as weak as possible in satisfying these constraints. The canonical interpretation of the ontology
![]() ${\mathcal{O}_\textsf{exa}}$
from Example 3 is depicted in Figure 2. Note that in general it provides a lower membership degree of each individual to every concept when compared to the model from Figure 1. This intuition justifies the name of canonical interpretation. As in the classical case,
${\mathcal{O}_\textsf{exa}}$
from Example 3 is depicted in Figure 2. Note that in general it provides a lower membership degree of each individual to every concept when compared to the model from Figure 1. This intuition justifies the name of canonical interpretation. As in the classical case,
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
can be homomorphically embedded in every model of
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
can be homomorphically embedded in every model of
![]() ${\mathcal{O}}$
, and hence be used as a representative of them all. We show a similar result with the difference that in this case, the homomorphism needs to take into account the truth degrees from the interpretation function as well.
Footnote 4
This is described in the following proposition.
${\mathcal{O}}$
, and hence be used as a representative of them all. We show a similar result with the difference that in this case, the homomorphism needs to take into account the truth degrees from the interpretation function as well.
Footnote 4
This is described in the following proposition.

Figure 2. The canonical interpretation for the ontology
![]() ${\mathcal{O}_\textsf{exa}}$
from our running example.
${\mathcal{O}_\textsf{exa}}$
from our running example.
Proposition 9 Let
![]() ${\mathcal{O}}$
be a consistent fuzzy DL-Lite ontology,
${\mathcal{O}}$
be a consistent fuzzy DL-Lite ontology,
![]() ${\mathcal{I}}=(\Delta^{\mathcal{I}},\cdot^{\mathcal{I}})$
be a model of
${\mathcal{I}}=(\Delta^{\mathcal{I}},\cdot^{\mathcal{I}})$
be a model of
![]() ${\mathcal{O}}$
, and
${\mathcal{O}}$
, and
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})=(\Delta^{{\mathcal{I}_\mathsf{can}}},\cdot^{{\mathcal{I}_\mathsf{can}}})$
its canonical interpretation. There is a function
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})=(\Delta^{{\mathcal{I}_\mathsf{can}}},\cdot^{{\mathcal{I}_\mathsf{can}}})$
its canonical interpretation. There is a function
![]() $\psi$
from
$\psi$
from
![]() $\Delta^{{\mathcal{I}_\mathsf{can}}}$
to
$\Delta^{{\mathcal{I}_\mathsf{can}}}$
to
![]() $\Delta^{\mathcal{I}}$
such that:
$\Delta^{\mathcal{I}}$
such that:
-
1. for each
 $A\in{N_C}$
and
$A\in{N_C}$
and
 $\delta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
,
$\delta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
,
 $A^{{\mathcal{I}_\mathsf{can}}}(\delta)\le A^{\mathcal{I}}(\psi(\delta))$
; and
$A^{{\mathcal{I}_\mathsf{can}}}(\delta)\le A^{\mathcal{I}}(\psi(\delta))$
; and -
2. for each
 $P\in{N_R}$
and
$P\in{N_R}$
and
 $\delta,\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
,
$\delta,\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
,
 $P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\le P^{\mathcal{I}}(\psi(\delta),\psi(\eta))$
.
$P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\le P^{\mathcal{I}}(\psi(\delta),\psi(\eta))$
.
Proof. Let
![]() ${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
. We construct the function
${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
. We construct the function
![]() $\psi$
recursively through the rule applications that define
$\psi$
recursively through the rule applications that define
![]() $A^{{\mathcal{I}_\mathsf{can}}}$
, and show that the two properties from the proposition are invariant w.r.t. the rule applications. We define first
$A^{{\mathcal{I}_\mathsf{can}}}$
, and show that the two properties from the proposition are invariant w.r.t. the rule applications. We define first
![]() $\psi(a)=a^{\mathcal{I}}$
for all
$\psi(a)=a^{\mathcal{I}}$
for all
![]() $a\in {N_I}$
. Recall that initially,
$a\in {N_I}$
. Recall that initially,
![]() $A^{{\mathcal{I}_\mathsf{can}}}(\delta)=P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)=0$
for all
$A^{{\mathcal{I}_\mathsf{can}}}(\delta)=P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)=0$
for all
![]() $A\in {N_C}, P\in{N_R}, \delta,\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
. Hence, the properties hold trivially in this case.
$A\in {N_C}, P\in{N_R}, \delta,\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
. Hence, the properties hold trivially in this case.
Assume now that the properties hold before a rule application; we show that they also hold afterwards by a case analysis over the rule used:
-
R1. if
 $\left<A(a),d\right>\in{\mathcal{A}}$
, since
$\left<A(a),d\right>\in{\mathcal{A}}$
, since
 ${\mathcal{I}}$
is a model of this axiom, it follows that
${\mathcal{I}}$
is a model of this axiom, it follows that
 $A^{\mathcal{I}}(a^{\mathcal{I}})\ge d$
. The rule application sets
$A^{\mathcal{I}}(a^{\mathcal{I}})\ge d$
. The rule application sets
 $A^{{\mathcal{I}_\mathsf{can}}}(a)=d$
and hence
$A^{{\mathcal{I}_\mathsf{can}}}(a)=d$
and hence
 $A^{{\mathcal{I}_\mathsf{can}}}(a)\le A^{\mathcal{I}}(\psi(a))=A^{\mathcal{I}}(a^{\mathcal{I}})$
.
$A^{{\mathcal{I}_\mathsf{can}}}(a)\le A^{\mathcal{I}}(\psi(a))=A^{\mathcal{I}}(a^{\mathcal{I}})$
. -
R2. if
 $\left<P(a,b),d\right>\in{\mathcal{A}}$
, the rule application sets
$\left<P(a,b),d\right>\in{\mathcal{A}}$
, the rule application sets
 $P^{{\mathcal{I}_\mathsf{can}}}(a,b)=d$
. Since
$P^{{\mathcal{I}_\mathsf{can}}}(a,b)=d$
. Since
 ${\mathcal{I}}$
satisfies this axiom, it follows that
${\mathcal{I}}$
satisfies this axiom, it follows that
 $P^{\mathcal{I}}(\psi(a),\psi(b))=P^{\mathcal{I}}(a^{\mathcal{I}},b^{\mathcal{I}})\ge d=P^{{\mathcal{I}_\mathsf{can}}}(a,b)$
.
$P^{\mathcal{I}}(\psi(a),\psi(b))=P^{\mathcal{I}}(a^{\mathcal{I}},b^{\mathcal{I}})\ge d=P^{{\mathcal{I}_\mathsf{can}}}(a,b)$
. -
R3. if
 $\left<A_1\sqsubseteq A_2,d\right>\in{\mathcal{T}}$
, the rule application over a given
$\left<A_1\sqsubseteq A_2,d\right>\in{\mathcal{T}}$
, the rule application over a given
 $\delta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
updates
$\delta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
updates
 $A_2^{{\mathcal{I}_\mathsf{can}}}(\delta)$
to
$A_2^{{\mathcal{I}_\mathsf{can}}}(\delta)$
to
 $A_1^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
. Since
$A_1^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
. Since
 ${\mathcal{I}}$
satisfies this axiom, by the induction hypothesis and monotonicity of
${\mathcal{I}}$
satisfies this axiom, by the induction hypothesis and monotonicity of
 $\otimes$
we know that
$\otimes$
we know that
 $A_2^{\mathcal{I}}(\psi(\delta))\ge A_1^{\mathcal{I}}(\psi(\delta))\otimes d\ge A_1^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d =A_2^{{\mathcal{I}_\mathsf{can}}}(\delta)$
.
$A_2^{\mathcal{I}}(\psi(\delta))\ge A_1^{\mathcal{I}}(\psi(\delta))\otimes d\ge A_1^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d =A_2^{{\mathcal{I}_\mathsf{can}}}(\delta)$
. -
R4. if
 $\left<A\sqsubseteq \exists P,d\right>\in{\mathcal{T}}$
, let
$\left<A\sqsubseteq \exists P,d\right>\in{\mathcal{T}}$
, let
 $\delta$
be the element over which the rule is applicable, and
$\delta$
be the element over which the rule is applicable, and
 $\eta_0$
the fresh element selected by the rule application. Since
$\eta_0$
the fresh element selected by the rule application. Since
 ${\mathcal{I}}$
is a model, we know that there exists an element
${\mathcal{I}}$
is a model, we know that there exists an element
 $\kappa\in\Delta^{\mathcal{I}}$
such that
$\kappa\in\Delta^{\mathcal{I}}$
such that
 $P^{\mathcal{I}}(\psi(\delta),\kappa)\ge A^{\mathcal{I}}(\psi(\delta))\otimes d$
. We thus define
$P^{\mathcal{I}}(\psi(\delta),\kappa)\ge A^{\mathcal{I}}(\psi(\delta))\otimes d$
. We thus define
 $\psi(\eta_0):=\kappa$
. By the induction hypothesis and monotonicity of
$\psi(\eta_0):=\kappa$
. By the induction hypothesis and monotonicity of
 $\otimes$
we get
$\otimes$
we get
 $P^{\mathcal{I}}(\psi(\delta),\psi(\eta_0))P^{\mathcal{I}}(\psi(\delta),\kappa)\ge A^{\mathcal{I}}(\psi(\delta))\otimes d\ge A^{{\mathcal{I}_\mathsf{can}}}(\psi(\delta))\otimes d= P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta_0)$
.
$P^{\mathcal{I}}(\psi(\delta),\psi(\eta_0))P^{\mathcal{I}}(\psi(\delta),\kappa)\ge A^{\mathcal{I}}(\psi(\delta))\otimes d\ge A^{{\mathcal{I}_\mathsf{can}}}(\psi(\delta))\otimes d= P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta_0)$
. -
R5. if
 $\left<A\sqsubseteq \exists P^-,d\right>\in{\mathcal{T}}$
, let
$\left<A\sqsubseteq \exists P^-,d\right>\in{\mathcal{T}}$
, let
 $\delta$
be the element over which the rule is applicable, and
$\delta$
be the element over which the rule is applicable, and
 $\eta_0$
the fresh element selected by the rule application. Since
$\eta_0$
the fresh element selected by the rule application. Since
 ${\mathcal{I}}$
is a model, we know that there exists an element
${\mathcal{I}}$
is a model, we know that there exists an element
 $\kappa\in\Delta^{\mathcal{I}}$
such that
$\kappa\in\Delta^{\mathcal{I}}$
such that
 $P^{\mathcal{I}}(\kappa,\psi(\delta))\ge A^{\mathcal{I}}(\psi(\delta))\otimes d$
. We thus define
$P^{\mathcal{I}}(\kappa,\psi(\delta))\ge A^{\mathcal{I}}(\psi(\delta))\otimes d$
. We thus define
 $\psi(\eta_0):=\kappa$
. By the induction hypothesis and monotonicity of
$\psi(\eta_0):=\kappa$
. By the induction hypothesis and monotonicity of
 $\otimes$
we get
$\otimes$
we get
 $P^{\mathcal{I}}(\psi(\eta_0),\psi(\delta))P^{\mathcal{I}}(\kappa,\psi(\delta))\ge A^{\mathcal{I}}(\psi(\delta))\otimes d\ge A^{{\mathcal{I}_\mathsf{can}}}(\psi(\delta))\otimes d= P^{{\mathcal{I}_\mathsf{can}}}(\eta_0,\delta)$
.
$P^{\mathcal{I}}(\psi(\eta_0),\psi(\delta))P^{\mathcal{I}}(\kappa,\psi(\delta))\ge A^{\mathcal{I}}(\psi(\delta))\otimes d\ge A^{{\mathcal{I}_\mathsf{can}}}(\psi(\delta))\otimes d= P^{{\mathcal{I}_\mathsf{can}}}(\eta_0,\delta)$
. -
R6. if
 $\left<\exists P\sqsubseteq A,d\right>\in{\mathcal{T}}$
, then for the chosen
$\left<\exists P\sqsubseteq A,d\right>\in{\mathcal{T}}$
, then for the chosen
 $\delta,\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
we have by the induction hypothesis that
$\delta,\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
we have by the induction hypothesis that
 $A^{{\mathcal{I}_\mathsf{can}}}(\delta)=P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d\le P^{\mathcal{I}}(\psi(\delta),\psi(\eta))\otimes d \le A^{\mathcal{I}}(\psi(\delta))$
.
$A^{{\mathcal{I}_\mathsf{can}}}(\delta)=P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d\le P^{\mathcal{I}}(\psi(\delta),\psi(\eta))\otimes d \le A^{\mathcal{I}}(\psi(\delta))$
. -
R7. if
 $\left<\exists P\sqsubseteq A,d\right>\in{\mathcal{T}}$
, then for the chosen
$\left<\exists P\sqsubseteq A,d\right>\in{\mathcal{T}}$
, then for the chosen
 $\delta,\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
we have by the induction hypothesis that
$\delta,\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
we have by the induction hypothesis that
 $A^{{\mathcal{I}_\mathsf{can}}}(\delta)=P^{{\mathcal{I}_\mathsf{can}}}(\eta,\delta)\otimes d\le P^{\mathcal{I}}(\psi(\eta),\psi(\delta))\otimes d \le A^{\mathcal{I}}(\psi(\delta))$
.
$A^{{\mathcal{I}_\mathsf{can}}}(\delta)=P^{{\mathcal{I}_\mathsf{can}}}(\eta,\delta)\otimes d\le P^{\mathcal{I}}(\psi(\eta),\psi(\delta))\otimes d \le A^{\mathcal{I}}(\psi(\delta))$
. -
R8. if
 $\left<Q_1\sqsubseteq Q_2,d\right>\in{\mathcal{T}}$
, the rule application over given
$\left<Q_1\sqsubseteq Q_2,d\right>\in{\mathcal{T}}$
, the rule application over given
 $\delta,\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
updates
$\delta,\eta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
updates
 $Q_2^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)$
to
$Q_2^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)$
to
 $Q_1^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d$
. Since
$Q_1^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d$
. Since
 ${\mathcal{I}}$
satisfies this axiom, by the induction hypothesis and monotonicity of
${\mathcal{I}}$
satisfies this axiom, by the induction hypothesis and monotonicity of
 $\otimes$
we know that
$\otimes$
we know that  \begin{equation*}Q_2^{\mathcal{I}}(\psi(\delta),\psi(\eta))\ge Q_1^{\mathcal{I}}(\psi(\delta),\psi(\eta))\otimes d\ge Q_1^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d =Q_2^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta).\end{equation*}
\begin{equation*}Q_2^{\mathcal{I}}(\psi(\delta),\psi(\eta))\ge Q_1^{\mathcal{I}}(\psi(\delta),\psi(\eta))\otimes d\ge Q_1^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\otimes d =Q_2^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta).\end{equation*}
Hence, the result holds after the fair application of all possible rules.
Importantly, note that the construction of
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
does not take the negations into account; for example, the axiom
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
does not take the negations into account; for example, the axiom
![]() ${\left<{\exists\textsf{locIn}\sqsubseteq \neg\textsf{Cheap}},[0.5]\right>}$
is never used during this construction. The effect of this is that
${\left<{\exists\textsf{locIn}\sqsubseteq \neg\textsf{Cheap}},[0.5]\right>}$
is never used during this construction. The effect of this is that
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
might not be a model of
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
might not be a model of
![]() ${\mathcal{O}}$
at all.
${\mathcal{O}}$
at all.
Example 10 Consider the fuzzy
![]() $\text{DL-Lite}_{R}$
ontology
$\text{DL-Lite}_{R}$
ontology
![]() ${\mathcal{O}_\textsf{exa}}=({\mathcal{T}_0},{\mathcal{A}_0})$
where
${\mathcal{O}_\textsf{exa}}=({\mathcal{T}_0},{\mathcal{A}_0})$
where
Under the Gödel semantics, by application of the first rule, the canonical interpretation maps
![]() $A_1^{{\mathcal{I}_\mathsf{can}}}(a)=A_2^{{\mathcal{I}_\mathsf{can}}}(a)=0.5$
. However, this violates the axiom in
$A_1^{{\mathcal{I}_\mathsf{can}}}(a)=A_2^{{\mathcal{I}_\mathsf{can}}}(a)=0.5$
. However, this violates the axiom in
![]() ${\mathcal{T}_0}$
, which requires that
${\mathcal{T}_0}$
, which requires that
![]() $A_1^{{\mathcal{I}_\mathsf{can}}}(a)\Rightarrow\ominus A_2^{{\mathcal{I}_\mathsf{can}}}(a)=1$
. That is, it requires that
$A_1^{{\mathcal{I}_\mathsf{can}}}(a)\Rightarrow\ominus A_2^{{\mathcal{I}_\mathsf{can}}}(a)=1$
. That is, it requires that
![]() $A_1^{{\mathcal{I}_\mathsf{can}}}(a)<\ominus A_2^{{\mathcal{I}_\mathsf{can}}}(a)$
, which is only possible when
$A_1^{{\mathcal{I}_\mathsf{can}}}(a)<\ominus A_2^{{\mathcal{I}_\mathsf{can}}}(a)$
, which is only possible when
![]() $A_1^{{\mathcal{I}_\mathsf{can}}}(a)=0$
or
$A_1^{{\mathcal{I}_\mathsf{can}}}(a)=0$
or
![]() $A_2^{{\mathcal{I}_\mathsf{can}}}(a)=0$
. Note that a similar phenomenon could be observed also in the TBox
$A_2^{{\mathcal{I}_\mathsf{can}}}(a)=0$
. Note that a similar phenomenon could be observed also in the TBox
![]() ${\mathcal{T}_\textsf{exa}}$
of our running example, which contains an axiom with a negated concept.
${\mathcal{T}_\textsf{exa}}$
of our running example, which contains an axiom with a negated concept.
The issue is that the negative axioms may introduce inconsistencies, by enforcing upper bounds in the degrees used, which are not verified by the canonical interpretation; recall, in fact, that the previously described construction monotonically increases the degrees to satisfy the minimal requirements, but never verifies whether these degrees affect some upper bound. On the other hand, we can prove that, as long as there is a model,
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is one.
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is one.
Proposition 11
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is a model of
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is a model of
![]() ${\mathcal{O}}$
iff
${\mathcal{O}}$
iff
![]() ${\mathcal{O}}$
is consistent.
${\mathcal{O}}$
is consistent.
Proof. The only if direction is trivial, hence we focus on showing that if
![]() ${\mathcal{O}}$
is consistent, then
${\mathcal{O}}$
is consistent, then
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is a model of
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is a model of
![]() ${\mathcal{O}}$
. Note first that, by construction,
${\mathcal{O}}$
. Note first that, by construction,
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
satisfies all positive axioms. Otherwise, a rule would trigger, and since the construction applies all rules fairly until exhaustion, no rule is applicable in the resulting interpretation
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
satisfies all positive axioms. Otherwise, a rule would trigger, and since the construction applies all rules fairly until exhaustion, no rule is applicable in the resulting interpretation
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
. Hence, if
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
. Hence, if
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is not a model of
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is not a model of
![]() ${\mathcal{O}}$
, there must exist a negative axiom of the form (i)
${\mathcal{O}}$
, there must exist a negative axiom of the form (i)
![]() $\left<B\sqsubseteq \neg C,d\right>$
or (ii)
$\left<B\sqsubseteq \neg C,d\right>$
or (ii)
![]() $\left<Q\sqsubseteq \neg R,d\right>$
that is not satisfied by the canonical interpretation. We consider the case (i); the other case can be treated analogously.
$\left<Q\sqsubseteq \neg R,d\right>$
that is not satisfied by the canonical interpretation. We consider the case (i); the other case can be treated analogously.
If
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})\not\models\left<B\sqsubseteq \neg C,d\right>$
, then there must exist an element
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})\not\models\left<B\sqsubseteq \neg C,d\right>$
, then there must exist an element
![]() $\delta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
such that
$\delta\in\Delta^{{\mathcal{I}_\mathsf{can}}}$
such that
![]() $B^{{\mathcal{I}_\mathsf{can}}}(\delta)\Rightarrow (\neg C)^{{\mathcal{I}_\mathsf{can}}}(\delta)<d$
or, equivalently,
$B^{{\mathcal{I}_\mathsf{can}}}(\delta)\Rightarrow (\neg C)^{{\mathcal{I}_\mathsf{can}}}(\delta)<d$
or, equivalently,
![]() $\ominus C^{{\mathcal{I}_\mathsf{can}}}(\delta)< B^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
. Since
$\ominus C^{{\mathcal{I}_\mathsf{can}}}(\delta)< B^{{\mathcal{I}_\mathsf{can}}}(\delta)\otimes d$
. Since
![]() ${\mathcal{O}}$
is consistent, there must exist a model
${\mathcal{O}}$
is consistent, there must exist a model
![]() ${\mathcal{I}}=(\Delta^{\mathcal{I}},\cdot^{\mathcal{I}})$
of
${\mathcal{I}}=(\Delta^{\mathcal{I}},\cdot^{\mathcal{I}})$
of
![]() ${\mathcal{O}}$
. By Proposition 9, there exists a function
${\mathcal{O}}$
. By Proposition 9, there exists a function
![]() $\psi:\Delta^{{\mathcal{I}_\mathsf{can}}}\to \Delta^{\mathcal{I}}$
such that, in particular,
$\psi:\Delta^{{\mathcal{I}_\mathsf{can}}}\to \Delta^{\mathcal{I}}$
such that, in particular,
![]() $B^{{\mathcal{I}_\mathsf{can}}}(\delta)<B^{\mathcal{I}}(\psi(\delta))$
and
$B^{{\mathcal{I}_\mathsf{can}}}(\delta)<B^{\mathcal{I}}(\psi(\delta))$
and
![]() $C^{{\mathcal{I}_\mathsf{can}}}(\delta)<C^{\mathcal{I}}(\psi(\delta))$
. By antitonicity of
$C^{{\mathcal{I}_\mathsf{can}}}(\delta)<C^{\mathcal{I}}(\psi(\delta))$
. By antitonicity of
![]() $\ominus$
, the latter means that
$\ominus$
, the latter means that
![]() $\ominus C^{\mathcal{I}}(\psi(\delta))\le \ominus C^{{\mathcal{I}_\mathsf{can}}}(\delta)$
and hence
$\ominus C^{\mathcal{I}}(\psi(\delta))\le \ominus C^{{\mathcal{I}_\mathsf{can}}}(\delta)$
and hence
But this means that
![]() ${\mathcal{I}}\not\models \left<B\sqsubseteq \neg C,d\right>$
, which contradicts the assumption that
${\mathcal{I}}\not\models \left<B\sqsubseteq \neg C,d\right>$
, which contradicts the assumption that
![]() ${\mathcal{I}}$
was a model of
${\mathcal{I}}$
was a model of
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
It can be seen that the ontology
![]() ${\mathcal{O}_0}$
from Example 10 is inconsistent under the Gödel semantics. On the other hand, under the Łukasiewicz semantics,
${\mathcal{O}_0}$
from Example 10 is inconsistent under the Gödel semantics. On the other hand, under the Łukasiewicz semantics,
![]() ${\mathcal{O}_0}$
is in fact consistent which, by this proposition, means that
${\mathcal{O}_0}$
is in fact consistent which, by this proposition, means that
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is a model of this ontology. This is easily confirmed by recalling that the Łukasiewicz negation is involutive; that is
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is a model of this ontology. This is easily confirmed by recalling that the Łukasiewicz negation is involutive; that is
![]() $\ominus d=1-d$
. In the case of the example, we have
$\ominus d=1-d$
. In the case of the example, we have
![]() $\ominus 0.5=0.5$
; the axiom
$\ominus 0.5=0.5$
; the axiom
![]() ${\left<{A_1\sqsubseteq \neg A_2}\right>}$
is satisfied because
${\left<{A_1\sqsubseteq \neg A_2}\right>}$
is satisfied because
![]() $0.5 = A_1^{{\mathcal{I}_\mathsf{can}}}(a) \le (\neg A_2)^{{\mathcal{I}_\mathsf{can}}}(a)=0.5$
.
$0.5 = A_1^{{\mathcal{I}_\mathsf{can}}}(a) \le (\neg A_2)^{{\mathcal{I}_\mathsf{can}}}(a)=0.5$
.
The consequence of the last two propositions is that
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is complete for existential positive queries, and in particular for conjunctive queries and threshold queries.
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is complete for existential positive queries, and in particular for conjunctive queries and threshold queries.
Corollary 12 If
![]() ${\mathcal{O}}$
is a consistent fuzzy
${\mathcal{O}}$
is a consistent fuzzy
![]() $\text{DL-Lite}_{R}$
ontology, then
$\text{DL-Lite}_{R}$
ontology, then
-
1. for every CQ
 $q({\mathbf{x}})$
, answer tuple
$q({\mathbf{x}})$
, answer tuple
 ${\mathbf{a}}$
, and
${\mathbf{a}}$
, and
 $d\in[0,1]$
it holds that
$d\in[0,1]$
it holds that
 ${\mathcal{O}}\models q({\mathbf{a}})\ge d$
iff
${\mathcal{O}}\models q({\mathbf{a}})\ge d$
iff
 ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})\models q({\mathbf{a}})\ge d$
;
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})\models q({\mathbf{a}})\ge d$
; -
2. for every TQ
 $q({\mathbf{x}})$
and answer tuple
$q({\mathbf{x}})$
and answer tuple
 ${\mathbf{a}}$
,
${\mathbf{a}}$
,
 ${\mathcal{O}}\models q({\mathbf{a}})$
iff
${\mathcal{O}}\models q({\mathbf{a}})$
iff
 ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})\models q({\mathbf{a}})$
.
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})\models q({\mathbf{a}})$
.
Proof. Proposition 11 states that
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is a model; hence anything that does not follow from it cannot be an answer. On the other hand, Proposition 9 states that the degree of every atom in any model is at least the degree given by
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is a model; hence anything that does not follow from it cannot be an answer. On the other hand, Proposition 9 states that the degree of every atom in any model is at least the degree given by
![]() ${{\mathcal{I}_\mathsf{can}}}$
, and hence if a tuple is an answer in
${{\mathcal{I}_\mathsf{can}}}$
, and hence if a tuple is an answer in
![]() ${{\mathcal{I}_\mathsf{can}}}$
, it is also an answer in every other model.
${{\mathcal{I}_\mathsf{can}}}$
, it is also an answer in every other model.
A short note on the canonical interpretation
Before delving deeper into the process of answering queries (the main contribution of this paper), it is worth considering the canonical interpretation in more detail, starting with the definite article used in its naming. Indeed, although we always speak about the canonical interpretation, the actual structure produced is not necessarily unique, and depends on the order in which rules are chosen to apply, specially in relation to rules R4 and R5, which introduce new relevant elements. This is highlighted in the following example.
Example 13 Consider an ontology containing the axioms
After applying the rule R1 over the ABox axioms, we have an interpretation where
![]() $A^{{\mathcal{I}_\mathsf{can}}}(a)=B^{{\mathcal{I}_\mathsf{can}}}(a)=1$
. At this point, rule R4 is applicable for any of the two axioms in
$A^{{\mathcal{I}_\mathsf{can}}}(a)=B^{{\mathcal{I}_\mathsf{can}}}(a)=1$
. At this point, rule R4 is applicable for any of the two axioms in
![]() ${\mathcal{T}}$
. If we first apply it to the first axiom, we select a fresh element, for example,
${\mathcal{T}}$
. If we first apply it to the first axiom, we select a fresh element, for example,
![]() $\eta_0$
and set
$\eta_0$
and set
![]() $R(a,\eta_0)=0.3$
; at this point, the rule is still applicable to the second axiom. This application requires selecting a new fresh element (now
$R(a,\eta_0)=0.3$
; at this point, the rule is still applicable to the second axiom. This application requires selecting a new fresh element (now
![]() $\eta_1$
) and set
$\eta_1$
) and set
![]() $R(a,\eta_1)=0.5$
. At this point, no rules are applicable and we have a canonical interpretation.
$R(a,\eta_1)=0.5$
. At this point, no rules are applicable and we have a canonical interpretation.
If instead we chose first to apply the rule on the second axiom, we would choose a fresh element (say,
![]() $\eta_2$
) and set
$\eta_2$
) and set
![]() $R(a,\eta_2)=0.5$
. This application immediately disallows the application of the rule to the first axiom, and hence the process stops.
$R(a,\eta_2)=0.5$
. This application immediately disallows the application of the rule to the first axiom, and hence the process stops.
Note that the two interpretations built in this example are not equivalent (see Figure 3). However, they are homomorphic in the sense specified by Proposition 9. This is not a coincidence. In fact, note that the proofs of Propositions 9 and 11 do not depend on the order of rule applications, but only on the fact that these rules were exhaustively (and fairly) applied. If the ontology is consistent, by the latter proposition the interpretation obtained is a model, regardless of the order chosen, and by the former proposition, it is homomorphic to all the interpretations which can be derived following different application orderings. In other words, the canonical interpretation is unique up to homomorphism. In the following, we disregard this issue and consider an arbitrary, but fixed, canonical interpretation as unique.

Figure 3. Two canonical interpretation constructions from the ontology in Example 13. From the empty interpretation (a), R1 is applied to each assertion to reach (c). One can either apply R4 to
![]() $\left<A\sqsubseteq \exists R, 0.3 \right>$
and go through the upper branch (d) to build the interpretation (e); or to
$\left<A\sqsubseteq \exists R, 0.3 \right>$
and go through the upper branch (d) to build the interpretation (e); or to
![]() $\left<B\sqsubseteq \exists R, 0.5 \right>$
and obtain (f) directly.
$\left<B\sqsubseteq \exists R, 0.5 \right>$
and obtain (f) directly.
We now return to the issue of answering queries. Corollary 12 states that these queries can be answered through the canonical interpretation. Obviously, such an approach is impractical; in fact, impossible, because it is an infinite model constructed through an infinitary process. Additionally, we still have the burden to prove that the ontology is consistent, which is a prerequisite for the use of Corollary 12 to answer queries. Fortunately, for the Gödel and product t-norms, we can resort to existing results from the literature for this latter task.
Definition 14
(classical version) Let
![]() ${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
be a fuzzy DL-Lite ontology. The classical version
${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
be a fuzzy DL-Lite ontology. The classical version
![]() $\widehat{\mathcal{O}}$
of
$\widehat{\mathcal{O}}$
of
![]() ${\mathcal{O}}$
is defined by
${\mathcal{O}}$
is defined by
![]() $\widehat{\mathcal{O}}:=(\widehat{\mathcal{T}},\widehat{\mathcal{A}})$
, where
$\widehat{\mathcal{O}}:=(\widehat{\mathcal{T}},\widehat{\mathcal{A}})$
, where
 \begin{align*}\widehat{\mathcal{T}}:={} & \{ B\sqsubseteq C \mid \left<B\sqsubseteq C,d\right>\in{\mathcal{T}}, d>0\} \cup \{ Q\sqsubseteq R \mid \left<Q\sqsubseteq R,d\right>\in{\mathcal{T}}, d>0\}, \\\widehat{\mathcal{A}}:={} & \{ B(a) \mid \left<B(a),d\right>\in{\mathcal{T}}, d>0\} \cup \{ P(a,b) \mid \left<P(a,b),d\right>\in{\mathcal{T}}, d>0\}.\end{align*}
\begin{align*}\widehat{\mathcal{T}}:={} & \{ B\sqsubseteq C \mid \left<B\sqsubseteq C,d\right>\in{\mathcal{T}}, d>0\} \cup \{ Q\sqsubseteq R \mid \left<Q\sqsubseteq R,d\right>\in{\mathcal{T}}, d>0\}, \\\widehat{\mathcal{A}}:={} & \{ B(a) \mid \left<B(a),d\right>\in{\mathcal{T}}, d>0\} \cup \{ P(a,b) \mid \left<P(a,b),d\right>\in{\mathcal{T}}, d>0\}.\end{align*}
That is,
![]() $\widehat{\mathcal{O}}$
contains all the axioms and assertions from
$\widehat{\mathcal{O}}$
contains all the axioms and assertions from
![]() ${\mathcal{O}}$
which hold with a positive degree – note that any fuzzy axiom or assertion with degree 0 could be removed w.l.o.g. anyway. The following result is a direct consequence of work on more expressive fuzzy DLs (Borgwardt et al. Reference Borgwardt, Cerami and Peñaloza2015).
${\mathcal{O}}$
which hold with a positive degree – note that any fuzzy axiom or assertion with degree 0 could be removed w.l.o.g. anyway. The following result is a direct consequence of work on more expressive fuzzy DLs (Borgwardt et al. Reference Borgwardt, Cerami and Peñaloza2015).
Proposition 15 Let
![]() ${\mathcal{O}}$
be a G-
${\mathcal{O}}$
be a G-
![]() $\text{DL-Lite}_{R}$
or
$\text{DL-Lite}_{R}$
or
![]() $\Pi-\text{DL-Lite}_{R}$
ontology. Then
$\Pi-\text{DL-Lite}_{R}$
ontology. Then
![]() ${\mathcal{O}}$
is consistent iff
${\mathcal{O}}$
is consistent iff
![]() $\widehat{\mathcal{O}}$
is consistent.
$\widehat{\mathcal{O}}$
is consistent.
In those cases, consistency checking can be reduced to the classical case, without the need to modify the query or the basic formulation of the ontology. For the ontology
![]() ${\mathcal{O}_0}$
in Example 10, we have
${\mathcal{O}_0}$
in Example 10, we have
![]() $\widehat{\mathcal{O}_0}=(\{A_1\sqsubseteq \neg A_2\},\{A_1(a),A_2(a)\})$
, which is inconsistent in the classical case, thus showing (through Proposition 15) that it is inconsistent under the Gödel and product t-norm semantics. We note that the example also shows that Proposition 15 does not hold for the Łukasiewicz t-norm, since we have established that
$\widehat{\mathcal{O}_0}=(\{A_1\sqsubseteq \neg A_2\},\{A_1(a),A_2(a)\})$
, which is inconsistent in the classical case, thus showing (through Proposition 15) that it is inconsistent under the Gödel and product t-norm semantics. We note that the example also shows that Proposition 15 does not hold for the Łukasiewicz t-norm, since we have established that
![]() ${\mathcal{O}_0}$
is consistent under this semantics, although its classical version remains inconsistent under classical interpretations.
${\mathcal{O}_0}$
is consistent under this semantics, although its classical version remains inconsistent under classical interpretations.
A particular consequence of Proposition 15 is that deciding consistency of G-
![]() $\text{DL-Lite}_{R}$
and
$\text{DL-Lite}_{R}$
and
![]() $\Pi-\text{DL-Lite}_{R}$
ontologies is in
$\Pi-\text{DL-Lite}_{R}$
ontologies is in
![]() ${AC}^{0}$
w.r.t. data complexity, and
${AC}^{0}$
w.r.t. data complexity, and
![]() ${\rm N \rm L{\small OG} S{\small PACE}}$
-complete w.r.t. combined complexity, where the
${\rm N \rm L{\small OG} S{\small PACE}}$
-complete w.r.t. combined complexity, where the
![]() ${\rm N \rm L{\small OG} S{\small PACE}}$
lower bound comes from known results in classical
${\rm N \rm L{\small OG} S{\small PACE}}$
lower bound comes from known results in classical
![]() $\text{DL-Lite}_{R}$
(Artale et al. Reference Artale, Calvanese, Kontchakov and Zakharyaschev2009). Thus adding truth degrees does not affect the complexity of this basic reasoning task. We now turn our attention to the task of query answering with the different semantics, starting with the idempotent case of the Gödel t-norm. We consider first the case of conjunctive queries, which allows for a simple solution, and then study threshold queries for which a rewriting technique is needed.
$\text{DL-Lite}_{R}$
(Artale et al. Reference Artale, Calvanese, Kontchakov and Zakharyaschev2009). Thus adding truth degrees does not affect the complexity of this basic reasoning task. We now turn our attention to the task of query answering with the different semantics, starting with the idempotent case of the Gödel t-norm. We consider first the case of conjunctive queries, which allows for a simple solution, and then study threshold queries for which a rewriting technique is needed.
Before studying how to answer queries over fuzzy
![]() $\text{DL-Lite}_{R}$
ontologies and its complexity, we note that in the case that an ontology is classical – that is, it uses only degree 1 in all its axioms – its canonical interpretation constructed as described in this section is equivalent to the classical canonical interpretation proposed by Calvanese et al. (Reference Calvanese, De Giacomo, Lembo, Lenzerini and Rosati2007). This fact will be used in the following sections.
$\text{DL-Lite}_{R}$
ontologies and its complexity, we note that in the case that an ontology is classical – that is, it uses only degree 1 in all its axioms – its canonical interpretation constructed as described in this section is equivalent to the classical canonical interpretation proposed by Calvanese et al. (Reference Calvanese, De Giacomo, Lembo, Lenzerini and Rosati2007). This fact will be used in the following sections.
4 Answering conjunctive queries over Gödel ontologies
For this and the following section, we are always considering the Gödel t-norm as the underlying operator for interpreting all fuzzy statements, and in particular the conjunctive queries.
The Gödel semantics are very limited in their expressivity. On the one hand, we have seen that
![]() $\ominus d\in\{0,1\}$
for all
$\ominus d\in\{0,1\}$
for all
![]() $d\in[0,1]$
. This means that whenever we have an axiom of the form
$d\in[0,1]$
. This means that whenever we have an axiom of the form
![]() $\left<B\sqsubseteq \neg B',d\right>$
or
$\left<B\sqsubseteq \neg B',d\right>$
or
![]() $\left<Q\sqsubseteq \neg Q',d\right>$
with
$\left<Q\sqsubseteq \neg Q',d\right>$
with
![]() $d>0$
, we are in fact saying that for every element
$d>0$
, we are in fact saying that for every element
![]() $\delta\in\Delta^{\mathcal{I}}$
, if
$\delta\in\Delta^{\mathcal{I}}$
, if
![]() $B^{\mathcal{I}}(\delta)>0$
, then
$B^{\mathcal{I}}(\delta)>0$
, then
![]() $B'^{\mathcal{I}}(\delta)=0$
– because in this case
$B'^{\mathcal{I}}(\delta)=0$
– because in this case
![]() $\ominus B'^{\mathcal{I}}(\delta)=1$
, which is the only possible way of satisfying the axiom. A similar argument holds for role axioms. Thus, for this section we can assume w.l.o.g. that all negative axioms hold with degree 1; that is, they are of the form
$\ominus B'^{\mathcal{I}}(\delta)=1$
, which is the only possible way of satisfying the axiom. A similar argument holds for role axioms. Thus, for this section we can assume w.l.o.g. that all negative axioms hold with degree 1; that is, they are of the form
![]() ${\left<{B\sqsubseteq \neg B'}\right>}$
or
${\left<{B\sqsubseteq \neg B'}\right>}$
or
![]() ${\left<{Q\sqsubseteq \neg Q'}\right>}$
. On the other hand, a positive axiom of the form
${\left<{Q\sqsubseteq \neg Q'}\right>}$
. On the other hand, a positive axiom of the form
![]() $\left<B\sqsubseteq B',d\right>$
requires that for every
$\left<B\sqsubseteq B',d\right>$
requires that for every
![]() $\delta\in\Delta^{\mathcal{I}}$
,
$\delta\in\Delta^{\mathcal{I}}$
,
![]() $B'^{\mathcal{I}}(\delta)\ge \min\{B^{\mathcal{I}}(\delta),d\}$
. That is, the only way to guarantee that an atom gets a high degree is to use axioms with a high degree. We use these facts to reduce reasoning tasks in this setting to the classical
$B'^{\mathcal{I}}(\delta)\ge \min\{B^{\mathcal{I}}(\delta),d\}$
. That is, the only way to guarantee that an atom gets a high degree is to use axioms with a high degree. We use these facts to reduce reasoning tasks in this setting to the classical
![]() $\text{DL-Lite}_{R}$
scenario.
$\text{DL-Lite}_{R}$
scenario.
Consider a consistent G-
![]() $\text{DL-Lite}_{R}$
ontology
$\text{DL-Lite}_{R}$
ontology
![]() ${\mathcal{O}}$
. We can decide a lower bound for the degree of a CQ simply by querying a cut of
${\mathcal{O}}$
. We can decide a lower bound for the degree of a CQ simply by querying a cut of
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
Definition 16
(cut ontology) Given a value
![]() $\theta\in(0,1]$
, the
$\theta\in(0,1]$
, the
![]() $\theta$
-cut of the ontology
$\theta$
-cut of the ontology
![]() ${\mathcal{O}}$
is defined as the subontology
${\mathcal{O}}$
is defined as the subontology
![]() ${\mathcal{O}}_{\ge \theta}:=({\mathcal{T}}_{\ge \theta},{\mathcal{A}}_{\ge \theta})$
where
${\mathcal{O}}_{\ge \theta}:=({\mathcal{T}}_{\ge \theta},{\mathcal{A}}_{\ge \theta})$
where
That is,
![]() ${\mathcal{O}}_{\ge \theta}$
is the subontology containing only the axioms and assertions that hold to degree at least
${\mathcal{O}}_{\ge \theta}$
is the subontology containing only the axioms and assertions that hold to degree at least
![]() $\theta$
. To show that
$\theta$
. To show that
![]() $\theta$
-cuts suffice for answering queries, we use the canonical interpretation.
$\theta$
-cuts suffice for answering queries, we use the canonical interpretation.
Note that including new axioms or assertions to an ontology would result in an update of the canonical interpretation which only increases the degree of some of the elements of the domain. More precisely, if
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is the canonical interpretation of
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
is the canonical interpretation of
![]() ${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
, then the canonical interpretation of
${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
, then the canonical interpretation of
![]() ${\mathcal{O}}'=({\mathcal{T}}\cup\{\left<B\sqsubseteq C,d\right>\},{\mathcal{A}})$
is the result of applying the construction rules starting from
${\mathcal{O}}'=({\mathcal{T}}\cup\{\left<B\sqsubseteq C,d\right>\},{\mathcal{A}})$
is the result of applying the construction rules starting from
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
. This holds because the resulting canonical interpretation is not dependent on the order in which rules are applied (and hence axioms taken into account) as long as this is done fairly.
Footnote 5
Since
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
. This holds because the resulting canonical interpretation is not dependent on the order in which rules are applied (and hence axioms taken into account) as long as this is done fairly.
Footnote 5
Since
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
has already applied all the rules on axioms of
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
has already applied all the rules on axioms of
![]() ${\mathcal{O}}$
exhaustively, the only remaining rule applications will be based on the new axiom
${\mathcal{O}}$
exhaustively, the only remaining rule applications will be based on the new axiom
![]() $\left<B\sqsubseteq C,d\right>$
and new applications over
$\left<B\sqsubseteq C,d\right>$
and new applications over
![]() ${\mathcal{T}}$
arising from it. Under the Gödel semantics, all the updates increase the interpretation function up to the value d; that is, if
${\mathcal{T}}$
arising from it. Under the Gödel semantics, all the updates increase the interpretation function up to the value d; that is, if
![]() $\cdot^{{\mathcal{I}'_\mathsf{can}}}$
is the interpretation function of
$\cdot^{{\mathcal{I}'_\mathsf{can}}}$
is the interpretation function of
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}}')$
, the difference between
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}}')$
, the difference between
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
and
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
and
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}}')$
is that there exist some elements such that
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}}')$
is that there exist some elements such that
![]() $A^{{\mathcal{I}_\mathsf{can}}}(\delta)<A^{{\mathcal{I}'_\mathsf{can}}}(\delta)=d$
, and similarly for roles there exist some pairs
$A^{{\mathcal{I}_\mathsf{can}}}(\delta)<A^{{\mathcal{I}'_\mathsf{can}}}(\delta)=d$
, and similarly for roles there exist some pairs
![]() $\delta,\eta$
such that
$\delta,\eta$
such that
![]() $P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)<P^{{\mathcal{I}'_\mathsf{can}}}(\delta,\eta)=d$
. For all others, the degrees remain unchanged. Moreover, if
$P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)<P^{{\mathcal{I}'_\mathsf{can}}}(\delta,\eta)=d$
. For all others, the degrees remain unchanged. Moreover, if
![]() $d_0$
is the smallest degree appearing in the ontology
$d_0$
is the smallest degree appearing in the ontology
![]() ${\mathcal{O}}$
, then its canonical interpretation uses only truth degrees in
${\mathcal{O}}$
, then its canonical interpretation uses only truth degrees in
![]() $\{0\}\cup[d_0,1]$
; that is, no truth degree in
$\{0\}\cup[d_0,1]$
; that is, no truth degree in
![]() $(0,d_0)$
appears in
$(0,d_0)$
appears in
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
. With these insights we are ready to produce our first results. Recall, once again, that for the rest of this section, we always consider that the semantics is based on the Gödel t-norm; that is, we have a G-
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
. With these insights we are ready to produce our first results. Recall, once again, that for the rest of this section, we always consider that the semantics is based on the Gödel t-norm; that is, we have a G-
![]() $\text{DL-Lite}_{R}$
ontology.
$\text{DL-Lite}_{R}$
ontology.
Lemma 17 Let
![]() ${\mathcal{O}}$
be a consistent G-
${\mathcal{O}}$
be a consistent G-
![]() $\text{DL-Lite}_{R}$
ontology,
$\text{DL-Lite}_{R}$
ontology,
![]() $q({\mathbf{x}})$
a query,
$q({\mathbf{x}})$
a query,
![]() ${\mathbf{a}}$
a tuple of individuals, and
${\mathbf{a}}$
a tuple of individuals, and
![]() $\theta\in(0,1]$
. Then
$\theta\in(0,1]$
. Then
![]() ${\mathcal{O}}\models q({\mathbf{a}})\ge \theta$
iff
${\mathcal{O}}\models q({\mathbf{a}})\ge \theta$
iff
![]() ${\mathcal{O}}_{\ge \theta}\models q({\mathbf{a}})\ge \theta$
.
${\mathcal{O}}_{\ge \theta}\models q({\mathbf{a}})\ge \theta$
.
Proof. Since
![]() ${\mathcal{O}}_{\ge \theta}\subseteq {\mathcal{O}}$
, every model of
${\mathcal{O}}_{\ge \theta}\subseteq {\mathcal{O}}$
, every model of
![]() ${\mathcal{O}}$
is also a model of
${\mathcal{O}}$
is also a model of
![]() ${\mathcal{O}}_{\ge \theta}$
. Hence, if
${\mathcal{O}}_{\ge \theta}$
. Hence, if
![]() ${\mathcal{O}}_{\ge \theta}\models q({\mathbf{a}})\ge \theta$
, then
${\mathcal{O}}_{\ge \theta}\models q({\mathbf{a}})\ge \theta$
, then
![]() ${\mathcal{O}}\models q({\mathbf{a}})\ge \theta$
.
${\mathcal{O}}\models q({\mathbf{a}})\ge \theta$
.
For the converse, assume that
![]() ${\mathcal{O}}_{\ge \theta}\not\models q({\mathbf{a}})\ge \theta$
. By Corollary 12, this means that
${\mathcal{O}}_{\ge \theta}\not\models q({\mathbf{a}})\ge \theta$
. By Corollary 12, this means that
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}}_{\ge \theta})\not\models q({\mathbf{a}})\ge \theta$
. That is,
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}}_{\ge \theta})\not\models q({\mathbf{a}})\ge \theta$
. That is,
![]() $q^{{\mathcal{I}_\mathsf{can}}}({\mathbf{a}}^{{\mathcal{I}_\mathsf{can}}})< \theta$
. Let
$q^{{\mathcal{I}_\mathsf{can}}}({\mathbf{a}}^{{\mathcal{I}_\mathsf{can}}})< \theta$
. Let
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})=(\Delta^{{\mathcal{I}'_\mathsf{can}}},\cdot^{{\mathcal{I}'_\mathsf{can}}})$
be the canonical interpretation of
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})=(\Delta^{{\mathcal{I}'_\mathsf{can}}},\cdot^{{\mathcal{I}'_\mathsf{can}}})$
be the canonical interpretation of
![]() ${\mathcal{O}}$
. Recall that the difference between
${\mathcal{O}}$
. Recall that the difference between
![]() ${\mathcal{O}}$
and
${\mathcal{O}}$
and
![]() ${\mathcal{O}}_{\ge \theta}$
is that the former has some additional axioms with degrees smaller than
${\mathcal{O}}_{\ge \theta}$
is that the former has some additional axioms with degrees smaller than
![]() $\theta$
. As argued before, this means that the difference between
$\theta$
. As argued before, this means that the difference between
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
and
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
and
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}}_{\ge \theta})$
are just some degrees, which are all smaller than
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}}_{\ge \theta})$
are just some degrees, which are all smaller than
![]() $\theta$
; that is, for every
$\theta$
; that is, for every
![]() $A\in{N_C}$
,
$A\in{N_C}$
,
![]() $P\in{N_R}$
, and
$P\in{N_R}$
, and
![]() $\delta,\eta\in\Delta^{{\mathcal{I}'_\mathsf{can}}}$
, if
$\delta,\eta\in\Delta^{{\mathcal{I}'_\mathsf{can}}}$
, if
![]() $A^{{\mathcal{I}'_\mathsf{can}}}(\delta)\ge \theta$
, then
$A^{{\mathcal{I}'_\mathsf{can}}}(\delta)\ge \theta$
, then
![]() $A^{{\mathcal{I}_\mathsf{can}}}(\delta)\ge \theta$
and if
$A^{{\mathcal{I}_\mathsf{can}}}(\delta)\ge \theta$
and if
![]() $P^{{\mathcal{I}'_\mathsf{can}}}(\delta,\eta)\ge \theta$
, then
$P^{{\mathcal{I}'_\mathsf{can}}}(\delta,\eta)\ge \theta$
, then
![]() $P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\ge \theta$
. By assumption, this means that
$P^{{\mathcal{I}_\mathsf{can}}}(\delta,\eta)\ge \theta$
. By assumption, this means that
![]() $q^{{\mathcal{I}'_\mathsf{can}}}({\mathbf{a}}^{{\mathcal{I}'_\mathsf{can}}})<\theta$
, and hence
$q^{{\mathcal{I}'_\mathsf{can}}}({\mathbf{a}}^{{\mathcal{I}'_\mathsf{can}}})<\theta$
, and hence
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})\not\models q({\mathbf{a}})\ge \theta$
. Thus,
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})\not\models q({\mathbf{a}})\ge \theta$
. Thus,
![]() ${\mathcal{O}}\not\models q({\mathbf{a}})\ge \theta$
.
${\mathcal{O}}\not\models q({\mathbf{a}})\ge \theta$
.
What this lemma states is that in order to find a lower bound for the degree of a query, one can ignore all the axioms and assertions that provide a smaller degree than the bound we are interested in. However, one still needs to answer a query for a fuzzy ontology (
![]() ${\mathcal{O}}_{\ge \theta}$
is still fuzzy), for which we still do not have any effective method. The following lemma solves this issue, considering the classical version of this ontology.
${\mathcal{O}}_{\ge \theta}$
is still fuzzy), for which we still do not have any effective method. The following lemma solves this issue, considering the classical version of this ontology.
Lemma 18 Let
![]() ${\mathcal{O}}$
be a consistent G-
${\mathcal{O}}$
be a consistent G-
![]() $\text{DL-Lite}_{R}$
ontology such that
$\text{DL-Lite}_{R}$
ontology such that
![]() ${\mathcal{O}}_{\ge \theta}={\mathcal{O}}$
for some
${\mathcal{O}}_{\ge \theta}={\mathcal{O}}$
for some
![]() $\theta>0$
. Then,
$\theta>0$
. Then,
![]() ${\mathcal{O}}\models q({\mathbf{a}})\ge \theta$
iff
${\mathcal{O}}\models q({\mathbf{a}})\ge \theta$
iff
![]() $\widehat{\mathcal{O}}\models q({\mathbf{a}})$
.
$\widehat{\mathcal{O}}\models q({\mathbf{a}})$
.
Proof. Every model of
![]() $\widehat{\mathcal{O}}$
is also a model of
$\widehat{\mathcal{O}}$
is also a model of
![]() ${\mathcal{O}}$
, with the additional property that the interpretation function maps all elements to
${\mathcal{O}}$
, with the additional property that the interpretation function maps all elements to
![]() $\{0,1\}$
. If
$\{0,1\}$
. If
![]() ${\mathcal{O}}\models q({\mathbf{a}})\ge \theta>0$
, then for every model
${\mathcal{O}}\models q({\mathbf{a}})\ge \theta>0$
, then for every model
![]() ${\mathcal{I}}$
of
${\mathcal{I}}$
of
![]() $\widehat{\mathcal{O}}$
it holds that
$\widehat{\mathcal{O}}$
it holds that
![]() $q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}})\ge \theta>0$
, and thus
$q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}})\ge \theta>0$
, and thus
![]() $q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}})=1$
, which means that
$q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}})=1$
, which means that
![]() $\widehat{\mathcal{O}}\models q({\mathbf{a}})$
.
$\widehat{\mathcal{O}}\models q({\mathbf{a}})$
.
Conversely, if
![]() $\widehat{\mathcal{O}}\models q({\mathbf{a}})$
, the canonical interpretation
$\widehat{\mathcal{O}}\models q({\mathbf{a}})$
, the canonical interpretation
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
must be such that
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
must be such that
![]() $q^{{\mathcal{I}_\mathsf{can}}}({\mathbf{a}}^{{\mathcal{I}_\mathsf{can}}})>0$
; but as argued before, since
$q^{{\mathcal{I}_\mathsf{can}}}({\mathbf{a}}^{{\mathcal{I}_\mathsf{can}}})>0$
; but as argued before, since
![]() ${\mathcal{O}}$
only has axioms and assertions with degrees
${\mathcal{O}}$
only has axioms and assertions with degrees
![]() $\ge \theta$
, it must be the case that all degrees of
$\ge \theta$
, it must be the case that all degrees of
![]() ${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
are in
${{\mathcal{I}_\mathsf{can}}}({\mathcal{O}})$
are in
![]() $\{0\}\cup[\theta,1]$
, and hence
$\{0\}\cup[\theta,1]$
, and hence
![]() $q^{{\mathcal{I}_\mathsf{can}}}({\mathbf{a}}^{{\mathcal{I}_\mathsf{can}}})\ge \theta$
. This implies, by Corollary 12 that
$q^{{\mathcal{I}_\mathsf{can}}}({\mathbf{a}}^{{\mathcal{I}_\mathsf{can}}})\ge \theta$
. This implies, by Corollary 12 that
![]() ${\mathcal{O}}\models q({\mathbf{a}})\ge \theta$
.
${\mathcal{O}}\models q({\mathbf{a}})\ge \theta$
.
Note that the condition of this lemma, which requires that
![]() ${\mathcal{O}}_{\ge \theta}={\mathcal{O}}$
, is only stating that all the degrees in the ontology
${\mathcal{O}}_{\ge \theta}={\mathcal{O}}$
, is only stating that all the degrees in the ontology
![]() ${\mathcal{O}}$
are at least
${\mathcal{O}}$
are at least
![]() $\theta$
. That condition is immediately satisfied by a cut ontology, and hence the lemma can be applied directly to it.
$\theta$
. That condition is immediately satisfied by a cut ontology, and hence the lemma can be applied directly to it.
Lemmas 17 and 18 together provide a method for reducing answering degree queries over G-
![]() $\text{DL-Lite}_{R}$
ontologies to query answering in classical
$\text{DL-Lite}_{R}$
ontologies to query answering in classical
![]() $\text{DL-Lite}_{R}$
.
$\text{DL-Lite}_{R}$
.
Theorem 19 If
![]() ${\mathcal{O}}$
is a consistent G-
${\mathcal{O}}$
is a consistent G-
![]() $\text{DL-Lite}_{R}$
ontology and
$\text{DL-Lite}_{R}$
ontology and
![]() $\theta>0$
, then it holds that
$\theta>0$
, then it holds that
![]() ${\mathcal{O}}\models q({\mathbf{a}})\ge \theta$
iff
${\mathcal{O}}\models q({\mathbf{a}})\ge \theta$
iff
![]() $\widehat{\mathcal{O}}_{\ge \theta}\models q({\mathbf{a}})$
.
$\widehat{\mathcal{O}}_{\ge \theta}\models q({\mathbf{a}})$
.
This means that we can use a standard ontology-based query answering system to answer fuzzy queries in
![]() $\text{DL-Lite}_{R}$
as well. Note that the approach proposed by Theorem 19 can only decide whether the degree of an answer to a query is at least
$\text{DL-Lite}_{R}$
as well. Note that the approach proposed by Theorem 19 can only decide whether the degree of an answer to a query is at least
![]() $\theta$
, but it needs the value
$\theta$
, but it needs the value
![]() $\theta\in (0,1]$
as a parameter. If, instead, we are interested in computing the degree of an answer, or
$\theta\in (0,1]$
as a parameter. If, instead, we are interested in computing the degree of an answer, or
![]() ${\mathsf{ans}}(q({\mathbf{x}}),{\mathcal{O}})$
, we can still use a classical query answering method as an underlying black box aid as described next.
${\mathsf{ans}}(q({\mathbf{x}}),{\mathcal{O}})$
, we can still use a classical query answering method as an underlying black box aid as described next.
Since the TBox
![]() ${\mathcal{T}}$
and the ABox
${\mathcal{T}}$
and the ABox
![]() ${\mathcal{A}}$
which compose the ontology
${\mathcal{A}}$
which compose the ontology
![]() ${\mathcal{O}}$
are both finite, the set
${\mathcal{O}}$
are both finite, the set
![]() ${\mathcal{D}}:=\{d\mid \left<\alpha,d\right>\in{\mathcal{T}}\cup{\mathcal{A}}\}$
of degrees appearing in the ontology is also finite; in fact, its size is bounded by the size of
${\mathcal{D}}:=\{d\mid \left<\alpha,d\right>\in{\mathcal{T}}\cup{\mathcal{A}}\}$
of degrees appearing in the ontology is also finite; in fact, its size is bounded by the size of
![]() ${\mathcal{O}}$
. Hence, we can assume that
${\mathcal{O}}$
. Hence, we can assume that
![]() ${\mathcal{D}}$
is of the form
${\mathcal{D}}$
is of the form
![]() ${\mathcal{D}}=\{d_0,d_1,\ldots,d_n,d_{n+1}\}$
where
${\mathcal{D}}=\{d_0,d_1,\ldots,d_n,d_{n+1}\}$
where
![]() $d_0\ge 0,d_{n+1}=1$
and for all
$d_0\ge 0,d_{n+1}=1$
and for all
![]() $i,0\le i\le n$
,
$i,0\le i\le n$
,
![]() $d_{i}<d_{i+1}$
. In order to find the degree of an answer
$d_{i}<d_{i+1}$
. In order to find the degree of an answer
![]() ${\mathbf{a}}$
to a query q, we proceed as follows: starting from
${\mathbf{a}}$
to a query q, we proceed as follows: starting from
![]() $i:=n+1$
, we iteratively ask the query
$i:=n+1$
, we iteratively ask the query
![]() ${\mathcal{O}}_{\ge d_i}\models q({\mathbf{a}})$
and decrease i until the query is answered affirmatively, or i becomes 0 (see Algorithm 1).
${\mathcal{O}}_{\ge d_i}\models q({\mathbf{a}})$
and decrease i until the query is answered affirmatively, or i becomes 0 (see Algorithm 1).

In the former case,
![]() $d_i$
is the degree for
$d_i$
is the degree for
![]() $q({\mathbf{a}})$
; in the latter, the degree is 0 – that is,
$q({\mathbf{a}})$
; in the latter, the degree is 0 – that is,
![]() ${\mathbf{a}}$
is not an answer of q.
Footnote 6
${\mathbf{a}}$
is not an answer of q.
Footnote 6
During the execution of this algorithm, each classical query needed at line 3 can be executed in
![]() ${AC}^{0}$
(and in particular in
${AC}^{0}$
(and in particular in
![]() ${\rm L{\small OG} S{\small PACE}}$
) in the size of the data; that is, the ABox as shown in Artale et al. (Reference Artale, Calvanese, Kontchakov and Zakharyaschev2009). The iterations in the loop do not affect the overall space used, as one can simply produce a new query every time and clean up the previous information. Overall, this means that the degree of an answer can be computed in
${\rm L{\small OG} S{\small PACE}}$
) in the size of the data; that is, the ABox as shown in Artale et al. (Reference Artale, Calvanese, Kontchakov and Zakharyaschev2009). The iterations in the loop do not affect the overall space used, as one can simply produce a new query every time and clean up the previous information. Overall, this means that the degree of an answer can be computed in
![]() ${\rm L{\small OG} S{\small PACE}}$
in data complexity, using a classical query answering engine.
${\rm L{\small OG} S{\small PACE}}$
in data complexity, using a classical query answering engine.
Corollary 20 The degree of an answer
![]() ${\mathbf{a}}$
to a query q w.r.t. the G-
${\mathbf{a}}$
to a query q w.r.t. the G-
![]() $\text{DL-Lite}_{R}$
ontology
$\text{DL-Lite}_{R}$
ontology
![]() ${\mathcal{O}}$
is computable in logarithmic space w.r.t. the size of the ABox (i.e. in data complexity).
${\mathcal{O}}$
is computable in logarithmic space w.r.t. the size of the ABox (i.e. in data complexity).
We will later see that this upper bound can indeed be reduced to
![]() ${AC}^{0}$
by seeing a degree query as a special case of a threshold query. However, the method that provides a tight complexity bound requires a new implementation of the rewriting approach, with all its associated optimizations, in contrast to the method from Algorithm 2, which can simply call any existing classical tool; for example, De Giacomo et al. (Reference De Giacomo, Lembo, Lenzerini, Poggi, Rosati, Ruzzi and Savo2012) and Calvanese et al. (Reference Calvanese, Cogrel, Kalayci, Komla-Ebri, Kontchakov, Lanti, Rezk, Rodriguez-Muro and Xiao2015).
${AC}^{0}$
by seeing a degree query as a special case of a threshold query. However, the method that provides a tight complexity bound requires a new implementation of the rewriting approach, with all its associated optimizations, in contrast to the method from Algorithm 2, which can simply call any existing classical tool; for example, De Giacomo et al. (Reference De Giacomo, Lembo, Lenzerini, Poggi, Rosati, Ruzzi and Savo2012) and Calvanese et al. (Reference Calvanese, Cogrel, Kalayci, Komla-Ebri, Kontchakov, Lanti, Rezk, Rodriguez-Muro and Xiao2015).
Computing the whole set of pairs
![]() ${\mathsf{ans}}(q({\mathbf{x}}),{\mathcal{O}})$
is a more complex task. Although we can follow an approach similar to Algorithm 1, where the answers to
${\mathsf{ans}}(q({\mathbf{x}}),{\mathcal{O}})$
is a more complex task. Although we can follow an approach similar to Algorithm 1, where the answers to
![]() $q({\mathbf{x}})$
are computed for each ontology
$q({\mathbf{x}})$
are computed for each ontology
![]() $\widehat{\mathcal{O}}_{\ge d_i}$
, in order to assign the appropriate degree to each answer, we need to either keep track of all the answers found so far, or add a negated query which excludes the answers with a higher degree. In both cases, we require a different approach and a potential larger use of memory. On the other hand, the whole set of answers
$\widehat{\mathcal{O}}_{\ge d_i}$
, in order to assign the appropriate degree to each answer, we need to either keep track of all the answers found so far, or add a negated query which excludes the answers with a higher degree. In both cases, we require a different approach and a potential larger use of memory. On the other hand, the whole set of answers
![]() ${\mathsf{ans}}(q({\mathbf{x}}),{\mathcal{O}})$
will usually contain many answers that hold with a very low degree, which may not be of much interest to the user making the query. When dealing with degrees, a more meaningful task is to find the k answers with the highest degree, for some natural number k; that is, the top-k answers of q.
${\mathsf{ans}}(q({\mathbf{x}}),{\mathcal{O}})$
will usually contain many answers that hold with a very low degree, which may not be of much interest to the user making the query. When dealing with degrees, a more meaningful task is to find the k answers with the highest degree, for some natural number k; that is, the top-k answers of q.
Algorithm 2 once again suggests a way to compute the top-k answers. As in the algorithm, one starts with the highest possible degree, and expands the classical ontology by including the axioms and assertions with a lower degree. The difference is that one stops now when the query returns at least k tuples as answers. At that point, the tuples found are those with the highest degree for the query. As before, each of these queries can be answered in
![]() ${AC}^{0}$
in data complexity, which yields a
${AC}^{0}$
in data complexity, which yields a
![]() ${\rm L{\small OG} S{\small PACE}}$
upper bound for answering top-k queries in data complexity.
${\rm L{\small OG} S{\small PACE}}$
upper bound for answering top-k queries in data complexity.
Corollary 21 Top-k queries over consistent G-
![]() $\text{DL-Lite}_{R}$
ontologies can be answered in logarithmic space w.r.t. the size of the ABox.
$\text{DL-Lite}_{R}$
ontologies can be answered in logarithmic space w.r.t. the size of the ABox.
5 Threshold queries over Gödel semantics
We now turn our attention to the case of threshold queries, but keeping the assumption of the Gödel semantics in place. The first thing to notice when considering threshold queries is that the simple approach developed in the previous section, where one calls a classical query answering engine over a cut subontology, cannot work. Indeed, as each atom needs to be satisfied potentially to a different degree, there is no one cut that can suffice to answer them all. Indeed, we have already seen a TQ in Example 8 which has no answers even though the natural cut ontology provides one answer.
When considering Boolean threshold queries, it may be tempting to simply try to verify each threshold atom separately through a cut ontology. However, such an approach is not sound due to the existentially quantified variables which need to be associated to a (potentially anonymous) individual. This problem is not new, as it arises already for conjunctive queries over classical databases.
To answer these queries, we will adapt the query rewriting technique from the classical setting. The underlying idea is essentially the same, as described previously in this paper, where an atom B(x) may be substituted by an atom C(x) if the TBox contains the axiom
![]() $C\sqsubseteq B$
. However, one has to be careful with the degrees used. In fact, some axioms may not be applied during the rewriting, if their degree is not large enough.
$C\sqsubseteq B$
. However, one has to be careful with the degrees used. In fact, some axioms may not be applied during the rewriting, if their degree is not large enough.
Example 22 Consider once again the TBox
![]() ${\mathcal{T}_\textsf{exa}}$
from Example 3, and suppose that we are interested in finding all popular attractions, up to a given degree
${\mathcal{T}_\textsf{exa}}$
from Example 3, and suppose that we are interested in finding all popular attractions, up to a given degree
![]() $d\in[0,1]$
; that is, we have the query
$d\in[0,1]$
; that is, we have the query
![]() $q(x)=\textsf{Popular}(x)\ge d$
. The TBox contains the axiom
$q(x)=\textsf{Popular}(x)\ge d$
. The TBox contains the axiom
![]() ${\left<{\textsf{Museum}\sqsubseteq \textsf{Popular}},[0.6]\right>}$
. This means that answers to q(x) w.r.t. this TBox should also include the answers to
${\left<{\textsf{Museum}\sqsubseteq \textsf{Popular}},[0.6]\right>}$
. This means that answers to q(x) w.r.t. this TBox should also include the answers to
![]() $\textsf{Museum}(x)$
, but this depends on the value of d, as we explain next.
$\textsf{Museum}(x)$
, but this depends on the value of d, as we explain next.
Suppose that
![]() $d>0.6$
; for example, if we have
$d>0.6$
; for example, if we have
![]() $q(x)=\textsf{Popular}(x)\ge 0.7$
. For an individual a and any model
$q(x)=\textsf{Popular}(x)\ge 0.7$
. For an individual a and any model
![]() ${\mathcal{I}}$
of the ontology, we have no guarantee that
${\mathcal{I}}$
of the ontology, we have no guarantee that
![]() $\textsf{Popular}^{\mathcal{I}}(a^{\mathcal{I}})\ge 0.7$
regardless of the degree of
$\textsf{Popular}^{\mathcal{I}}(a^{\mathcal{I}})\ge 0.7$
regardless of the degree of
![]() $\textsf{Museum}^{\mathcal{I}}(a^{\mathcal{I}})$
. Indeed, even if
$\textsf{Museum}^{\mathcal{I}}(a^{\mathcal{I}})$
. Indeed, even if
![]() $\textsf{Museum}^{\mathcal{I}}(a^{\mathcal{I}})=1$
, the only thing that can be guaranteed is that the degree of a belonging to Popular is at least
$\textsf{Museum}^{\mathcal{I}}(a^{\mathcal{I}})=1$
, the only thing that can be guaranteed is that the degree of a belonging to Popular is at least
![]() $0.6$
, which does not suffice to become a positive answer to the query. Hence, there is no need to include Museum in the rewriting.
$0.6$
, which does not suffice to become a positive answer to the query. Hence, there is no need to include Museum in the rewriting.
Suppose now that
![]() $d\le 0.6$
; for example, with the query
$d\le 0.6$
; for example, with the query
![]() $q(x)=\textsf{Popular}(x)\ge 0.5$
. In this case, we note that every individual a such that
$q(x)=\textsf{Popular}(x)\ge 0.5$
. In this case, we note that every individual a such that
![]() $\textsf{Museum}^{\mathcal{I}}(a^{\mathcal{I}})\ge 0.5$
must satisfy also that
$\textsf{Museum}^{\mathcal{I}}(a^{\mathcal{I}})\ge 0.5$
must satisfy also that
![]() $\textsf{Popular}^{\mathcal{I}}(a^{\mathcal{I}})\ge 0.5$
. Indeed, recall that under the Gödel semantics,
$\textsf{Popular}^{\mathcal{I}}(a^{\mathcal{I}})\ge 0.5$
. Indeed, recall that under the Gödel semantics,
![]() $f\Rightarrow e$
is either e if
$f\Rightarrow e$
is either e if
![]() $e\le f$
or 1 otherwise. Since
$e\le f$
or 1 otherwise. Since
![]() ${\mathcal{I}}$
satisfies the axiom
${\mathcal{I}}$
satisfies the axiom
![]() ${\left<{\textsf{Museum}\sqsubseteq \textsf{Popular}},[0.6]\right>}$
, whenever
${\left<{\textsf{Museum}\sqsubseteq \textsf{Popular}},[0.6]\right>}$
, whenever
![]() $f=\textsf{Museum}^{\mathcal{I}}(a^{\mathcal{I}})\ge 0.5$
holds, we know that the degree e of
$f=\textsf{Museum}^{\mathcal{I}}(a^{\mathcal{I}})\ge 0.5$
holds, we know that the degree e of
![]() $\textsf{Popular}^{\mathcal{I}}(a^{\mathcal{I}})$
must be such that
$\textsf{Popular}^{\mathcal{I}}(a^{\mathcal{I}})$
must be such that
![]() $f\Rightarrow e\ge 0.6$
. If
$f\Rightarrow e\ge 0.6$
. If
![]() $e\le f$
, this can only be true if
$e\le f$
, this can only be true if
![]() $e\ge 0.6>0.5$
. Otherwise, we know that
$e\ge 0.6>0.5$
. Otherwise, we know that
![]() $e>f\ge 0.5$
, and hence any individual belonging to the concept Museum to degree at least
$e>f\ge 0.5$
, and hence any individual belonging to the concept Museum to degree at least
![]() $0.5$
is an answer to the query q(x).
$0.5$
is an answer to the query q(x).
This example shows that during the rewriting process, we only need to consider the axioms that hold to a degree greater than the threshold of the current atom of interest. During the rewriting step, the original threshold is preserved regardless of the bound from the axioms. We now proceed to describe the rewriting process in detail, following the ideas developed originally for classical
![]() $\text{DL-Lite}_{R}$
and other members of the DL-Lite family through the PerfectRef algorithm. To aid understanding from readers knowledgeable with the original method, we preserve as much of the terminology from Calvanese et al. (Reference Calvanese, De Giacomo, Lembo, Lenzerini and Rosati2007) as possible. From now on, in a query
$\text{DL-Lite}_{R}$
and other members of the DL-Lite family through the PerfectRef algorithm. To aid understanding from readers knowledgeable with the original method, we preserve as much of the terminology from Calvanese et al. (Reference Calvanese, De Giacomo, Lembo, Lenzerini and Rosati2007) as possible. From now on, in a query
![]() $q({\mathbf{x}})=\varphi({\mathbf{x}},{\mathbf{y}})$
, we call all the variables in
$q({\mathbf{x}})=\varphi({\mathbf{x}},{\mathbf{y}})$
, we call all the variables in
![]() ${\mathbf{x}}$
distinguished, and any variable that appears at least twice within a query shared. Note that there is no need to keep track of the variables that are not distinguished nor shared (from now on, called undistinguished, unshared variables); it is only relevant that they can be adequately assigned a value. Hence, those variables will be denoted by an underscore (“_”), and use
${\mathbf{x}}$
distinguished, and any variable that appears at least twice within a query shared. Note that there is no need to keep track of the variables that are not distinguished nor shared (from now on, called undistinguished, unshared variables); it is only relevant that they can be adequately assigned a value. Hence, those variables will be denoted by an underscore (“_”), and use
![]() $y=\rule{2mm}{1pt}$
to express that y is one such variable.
$y=\rule{2mm}{1pt}$
to express that y is one such variable.
Definition 23
(applicability) An axiom
![]() $\alpha$
is applicable to the threshold atom
$\alpha$
is applicable to the threshold atom
![]() $A(x)\ge d$
iff
$A(x)\ge d$
iff
![]() $\alpha$
is of the form
$\alpha$
is of the form
![]() ${\left<{C\sqsubseteq A},[e]\right>}$
and
${\left<{C\sqsubseteq A},[e]\right>}$
and
![]() $d\le e$
. It is applicable to the threshold atom
$d\le e$
. It is applicable to the threshold atom
![]() $P(x_1,x_2)$
iff either (i)
$P(x_1,x_2)$
iff either (i)
![]() $x_2=\rule{2mm}{1pt}$
and
$x_2=\rule{2mm}{1pt}$
and
![]() $\alpha$
is of the form
$\alpha$
is of the form
![]() ${\left<{C\sqsubseteq \exists P},[e]\right>}$
with
${\left<{C\sqsubseteq \exists P},[e]\right>}$
with
![]() $d\le e$
; (ii)
$d\le e$
; (ii)
![]() $x_1=\rule{2mm}{1pt}$
and
$x_1=\rule{2mm}{1pt}$
and
![]() $\alpha$
is of the form
$\alpha$
is of the form
![]() ${\left<{C\sqsubseteq\exists P^-},[e]\right>}$
; or (iii)
${\left<{C\sqsubseteq\exists P^-},[e]\right>}$
; or (iii)
![]() $\alpha$
is of the form
$\alpha$
is of the form
![]() ${\left<{Q\sqsubseteq P},[e]\right>}$
or
${\left<{Q\sqsubseteq P},[e]\right>}$
or
![]() ${\left<{Q\sqsubseteq P^-},[e]\right>}$
with
${\left<{Q\sqsubseteq P^-},[e]\right>}$
with
![]() $d\le e$
.
$d\le e$
.
If
![]() $\alpha$
is applicable to the threshold atom
$\alpha$
is applicable to the threshold atom
![]() $\gamma$
, the result of the application is the atom
$\gamma$
, the result of the application is the atom
![]() $gr(\gamma,\alpha)$
defined through the rules in Figure 4.
$gr(\gamma,\alpha)$
defined through the rules in Figure 4.

Figure 4. The result
![]() $gr(\gamma,\alpha)$
of applying the axiom
$gr(\gamma,\alpha)$
of applying the axiom
![]() $\alpha$
to the threshold atom
$\alpha$
to the threshold atom
![]() $\gamma$
.
$\gamma$
.
The PerfectRef algorithm constructs a union of threshold queries by iteratively substituting atoms
![]() $\gamma$
for which an axiom
$\gamma$
for which an axiom
![]() $\alpha$
is applicable, with the result
$\alpha$
is applicable, with the result
![]() $gr(\gamma,\alpha)$
of the application. This follows the idea of tracing backwards the axioms in order to absorb the TBox into the query which was previously outlined. The pseudocode for PerfectRef is more formally described in Algorithm 4. In the algorithm,
$gr(\gamma,\alpha)$
of the application. This follows the idea of tracing backwards the axioms in order to absorb the TBox into the query which was previously outlined. The pseudocode for PerfectRef is more formally described in Algorithm 4. In the algorithm,
![]() $q[\gamma,\eta]$
is the query resulting from substituting in q the atom
$q[\gamma,\eta]$
is the query resulting from substituting in q the atom
![]() $\gamma$
with the atom
$\gamma$
with the atom
![]() $\eta$
. The function
$\eta$
. The function
![]() $reduce(p,\gamma_1,\gamma_2)$
called in line 4 simply returns the query obtained by applying the most general unifier between
$reduce(p,\gamma_1,\gamma_2)$
called in line 4 simply returns the query obtained by applying the most general unifier between
![]() $\gamma_1$
and
$\gamma_1$
and
![]() $\gamma_2$
to p. For unification, all nondistinguished, unshared variables are considered different. For simplicity, we always assume that all nondistinguished, unshared variables are known, and hence call them
$\gamma_2$
to p. For unification, all nondistinguished, unshared variables are considered different. For simplicity, we always assume that all nondistinguished, unshared variables are known, and hence call them
![]() $\_$
when testing applicability.
$\_$
when testing applicability.

Note that, just as in the classical case, the application of the reduce function is necessary to guarantee correctness of the rewriting. Specifically, a variable that is bound in a query p may become unbound after the unification process, which may allow more axioms to be applied for the rewriting.
Once again, the algorithm takes as input a threshold query q, and returns a union of threshold queries T which is constructed by taking into account the information from the TBox
![]() ${\mathcal{T}}$
. The importance of this rewriting is that at this point, the answers to the original query q w.r.t. an ontology
${\mathcal{T}}$
. The importance of this rewriting is that at this point, the answers to the original query q w.r.t. an ontology
![]() ${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
can be obtained by applying the query T to the ABox
${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
can be obtained by applying the query T to the ABox
![]() ${\mathcal{A}}$
, seen as a standard database.
${\mathcal{A}}$
, seen as a standard database.
Let
![]() $db({\mathcal{A}})$
be the ABox
$db({\mathcal{A}})$
be the ABox
![]() ${\mathcal{A}}$
seen as a database. Note that since we have fuzzy assertions, the database will contain binary relations (representing concept assertions) and ternary relations (representing the role assertions), where the last element of the relation is the degree; a number in the interval [0,1]. Under this view, a threshold query can also be seen as a conjunctive query, taking into account the inequalities in the selection. Given a union of threshold queries T, UCQ(T) denotes the fact that T is being read as a UCQ in this sense. Given an ABox
${\mathcal{A}}$
seen as a database. Note that since we have fuzzy assertions, the database will contain binary relations (representing concept assertions) and ternary relations (representing the role assertions), where the last element of the relation is the degree; a number in the interval [0,1]. Under this view, a threshold query can also be seen as a conjunctive query, taking into account the inequalities in the selection. Given a union of threshold queries T, UCQ(T) denotes the fact that T is being read as a UCQ in this sense. Given an ABox
![]() ${\mathcal{A}}$
and a union of TQs T, we denote by
${\mathcal{A}}$
and a union of TQs T, we denote by
![]() ${\mathsf{ans}}(db({\mathcal{A}}),UCQ(T))$
the set of answers to T w.r.t.
${\mathsf{ans}}(db({\mathcal{A}}),UCQ(T))$
the set of answers to T w.r.t.
![]() $db({\mathcal{A}})$
from a database perspective. We also denote by
$db({\mathcal{A}})$
from a database perspective. We also denote by
![]() ${\mathsf{ans}}(q,{\mathcal{O}})$
the set of answers to the TQ q w.r.t. the ontology
${\mathsf{ans}}(q,{\mathcal{O}})$
the set of answers to the TQ q w.r.t. the ontology
![]() ${\mathcal{O}}$
. We then obtain the following result.
${\mathcal{O}}$
. We then obtain the following result.
Theorem 24 Let
![]() ${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
be a consistent G-
${\mathcal{O}}=({\mathcal{T}},{\mathcal{A}})$
be a consistent G-
![]() $\text{DL-Lite}_{R}$
ontology, q a TQ, and T the union of TQs obtained through the rewriting. Then
$\text{DL-Lite}_{R}$
ontology, q a TQ, and T the union of TQs obtained through the rewriting. Then
![]() ${\mathsf{ans}}(q,{\mathcal{O}})={\mathsf{ans}}(db({\mathcal{A}}),UCQ(T))$
.
${\mathsf{ans}}(q,{\mathcal{O}})={\mathsf{ans}}(db({\mathcal{A}}),UCQ(T))$
.
A consequence of Theorem 24 is that, in terms of data complexity, answering a TQ w.r.t. a
![]() $\text{DL-Lite}_{R}$
ontology is at most as costly as answering a CQ over a database. Indeed, note that although the query q is transformed into a larger UCQ, the data itself remains unchanged. This yields the following result.
$\text{DL-Lite}_{R}$
ontology is at most as costly as answering a CQ over a database. Indeed, note that although the query q is transformed into a larger UCQ, the data itself remains unchanged. This yields the following result.
Theorem 25 Answering threshold queries w.r.t. consistent G-
![]() $\text{DL-Lite}_{R}$
ontologies is in
$\text{DL-Lite}_{R}$
ontologies is in
![]() ${AC}^{0}$
w.r.t. data complexity.
${AC}^{0}$
w.r.t. data complexity.
Before finishing this section, we return to a question on complexity left open in the previous section; namely, the precise complexity of finding the degree of an answer to a conjunctive query. To answer this question, we first note that under the Gödel semantics, we can always see a degree query as a special case of a threshold query.
Given a CQ q, let
![]() ${\mathsf{At}}(q)$
be the set of all the atoms in q. For a degree
${\mathsf{At}}(q)$
be the set of all the atoms in q. For a degree
![]() $d\in[0,1]$
, we can define the TQ
$d\in[0,1]$
, we can define the TQ
![]() $TQ(q,d)=\bigwedge_{\gamma\in{\mathsf{At}}(q)}\gamma\ge d$
. That is, TQ(q,d) uses the same atoms as q, but assigns a minimum degree of d to each of them. Since the Gödel semantics interprets the conjunction through the minimum operator, any answer of TQ(q) yields a degree of at least d to the original query q.
$TQ(q,d)=\bigwedge_{\gamma\in{\mathsf{At}}(q)}\gamma\ge d$
. That is, TQ(q,d) uses the same atoms as q, but assigns a minimum degree of d to each of them. Since the Gödel semantics interprets the conjunction through the minimum operator, any answer of TQ(q) yields a degree of at least d to the original query q.
Lemma 26 Let
![]() ${\mathcal{O}}$
be a consistent G-
${\mathcal{O}}$
be a consistent G-
![]() $\text{DL-Lite}_{R}$
ontology, q a CQ,
$\text{DL-Lite}_{R}$
ontology, q a CQ,
![]() ${\mathbf{a}}$
an answer tuple, and
${\mathbf{a}}$
an answer tuple, and
![]() $d\in[0,1]$
. It holds that
$d\in[0,1]$
. It holds that
![]() ${\mathcal{O}}\models q({\mathbf{a}})\ge d$
iff
${\mathcal{O}}\models q({\mathbf{a}})\ge d$
iff
![]() ${\mathcal{O}}\models TQ(q({\mathbf{a}}),d)$
.
${\mathcal{O}}\models TQ(q({\mathbf{a}}),d)$
.
In order to find the degree of an answer, we can simply add as an answer variable after the rewriting one that looks at the degrees from the database
![]() $db({\mathcal{A}})$
. This does not affect the overall data complexity, and hence remains in
$db({\mathcal{A}})$
. This does not affect the overall data complexity, and hence remains in
![]() ${AC}^{0}$
.
${AC}^{0}$
.
Corollary 27 Answering conjunctive queries w.r.t. consistent G-
![]() $\text{DL-Lite}_{R}$
ontologies is in
$\text{DL-Lite}_{R}$
ontologies is in
![]() ${AC}^{0}$
in data complexity.
${AC}^{0}$
in data complexity.
This finishes our analysis of the Gödel t-norm, which also provides our main results. In the following section we briefly visit the case where the underlying t-norm is not idempotent, and showcase that in general dealing with such semantics becomes harder.
6 Non-idempotent t-norms
We now move our attention to the t-norms that are not idempotent; in particular the product and Łukasiewicz t-norms. Unfortunately, as we will see, the correctness of the reductions and algorithms presented in the previous sections rely strongly on the idempotency of the Gödel t-norm, and does not transfer directly to the other cases. However, at least for the product t-norm, it is still possible to answer some kinds of queries efficiently.
First recall that Proposition 15 holds for the product t-norm as well. Hence, deciding consistency of a
![]() $\Pi-\text{DL-Lite}_{R}$
ontology remains reducible to the classical case and thus, efficient. We now show with simple examples that the other results do not transfer so easily.
$\Pi-\text{DL-Lite}_{R}$
ontology remains reducible to the classical case and thus, efficient. We now show with simple examples that the other results do not transfer so easily.
Example 28 Consider the ontology
![]() ${\mathcal{O}_\textsf{exb}}:=({\mathcal{T}_\textsf{exb}},{\mathcal{A}_\textsf{exb}})$
where
${\mathcal{O}_\textsf{exb}}:=({\mathcal{T}_\textsf{exb}},{\mathcal{A}_\textsf{exb}})$
where
![]() ${\mathcal{T}_\textsf{exb}}:=\{\left<A_i\sqsubseteq A_{i+1},0.9\right>\mid 0\le i <n\}$
and
${\mathcal{T}_\textsf{exb}}:=\{\left<A_i\sqsubseteq A_{i+1},0.9\right>\mid 0\le i <n\}$
and
![]() ${\mathcal{A}_\textsf{exb}}:=\{\left<A_0(a),1\right>\}$
. Note that
${\mathcal{A}_\textsf{exb}}:=\{\left<A_0(a),1\right>\}$
. Note that
![]() ${\mathcal{O}_\textsf{exb}}=({{\mathcal{O}_\textsf{exb}}})_{\ge 0.9}$
, but the degree for the query
${\mathcal{O}_\textsf{exb}}=({{\mathcal{O}_\textsf{exb}}})_{\ge 0.9}$
, but the degree for the query
![]() $q()=A_n(a)$
is
$q()=A_n(a)$
is
![]() $0.9^n$
which can be made arbitrarily small by making n large.
$0.9^n$
which can be made arbitrarily small by making n large.
Similarly, it is not possible to find the top-k answers simply by layering the
![]() $\theta$
-cuts for decreasing values of
$\theta$
-cuts for decreasing values of
![]() $\theta$
until enough answers can be found.
$\theta$
until enough answers can be found.
Example 29 Let
![]() ${\mathcal{O}_\textsf{exb}}':=({\mathcal{T}_\textsf{exb}},{\mathcal{A}_\textsf{exb}}')$
, where
${\mathcal{O}_\textsf{exb}}':=({\mathcal{T}_\textsf{exb}},{\mathcal{A}_\textsf{exb}}')$
, where
![]() ${\mathcal{A}_\textsf{exb}}':={\mathcal{A}_\textsf{exb}}\cup\{\left<A_n(b),0.85\right>\}$
and
${\mathcal{A}_\textsf{exb}}':={\mathcal{A}_\textsf{exb}}\cup\{\left<A_n(b),0.85\right>\}$
and
![]() ${\mathcal{T}_\textsf{exb}}$
,
${\mathcal{T}_\textsf{exb}}$
,
![]() ${\mathcal{A}_\textsf{exb}}$
are as in Example 28. The top answer for
${\mathcal{A}_\textsf{exb}}$
are as in Example 28. The top answer for
![]() $q(x)=A_n(x)$
is b with degree 0.85, but from
$q(x)=A_n(x)$
is b with degree 0.85, but from
![]() $({{\mathcal{O}_\textsf{exb}}'})_{\ge 0.9}$
we already find the answer a, which is not the top one.
$({{\mathcal{O}_\textsf{exb}}'})_{\ge 0.9}$
we already find the answer a, which is not the top one.
The main point with these examples is that, from the lack of idempotency of the t-norm
![]() $\otimes$
, we can obtain low degrees in a match which arises from combining several axioms and assertions having a high degree. On the other hand, the product behaves well for positive values in the sense that applying the t-norm to two positive values always results in a positive value; formally, if
$\otimes$
, we can obtain low degrees in a match which arises from combining several axioms and assertions having a high degree. On the other hand, the product behaves well for positive values in the sense that applying the t-norm to two positive values always results in a positive value; formally, if
![]() $d,e>0$
, then
$d,e>0$
, then
![]() $d\otimes e>0$
. Thus, if we are only interested in knowing whether the result of a query is positive or not, there is no difference between the Gödel t-norm and the product t-norm.
$d\otimes e>0$
. Thus, if we are only interested in knowing whether the result of a query is positive or not, there is no difference between the Gödel t-norm and the product t-norm.
Definition 30 A tuple
![]() ${\mathbf{a}}$
is a positive answer to the query
${\mathbf{a}}$
is a positive answer to the query
![]() $q({\mathbf{x}})$
w.r.t. the ontology
$q({\mathbf{x}})$
w.r.t. the ontology
![]() ${\mathcal{O}}$
(denoted by
${\mathcal{O}}$
(denoted by
![]() ${\mathcal{O}}\models q({\mathbf{a}})>0$
) iff for every model
${\mathcal{O}}\models q({\mathbf{a}})>0$
) iff for every model
![]() ${\mathcal{I}}$
of
${\mathcal{I}}$
of
![]() ${\mathcal{O}}$
it holds that
${\mathcal{O}}$
it holds that
![]() $q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}})>0$
.
$q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}})>0$
.
Theorem 31 If
![]() ${\mathcal{O}}$
is a consistent
${\mathcal{O}}$
is a consistent
![]() $\Pi-\text{DL-Lite}_{R}$
ontology, then
$\Pi-\text{DL-Lite}_{R}$
ontology, then
![]() ${\mathcal{O}}\models q({\mathbf{a}})>0$
iff
${\mathcal{O}}\models q({\mathbf{a}})>0$
iff
![]() $\widehat{\mathcal{O}}\models q({\mathbf{a}})$
.
$\widehat{\mathcal{O}}\models q({\mathbf{a}})$
.
Proof. Every model of
![]() $\widehat{\mathcal{O}}$
is also a model of
$\widehat{\mathcal{O}}$
is also a model of
![]() ${\mathcal{O}}$
, with the additional property that the interpretation function maps all elements to
${\mathcal{O}}$
, with the additional property that the interpretation function maps all elements to
![]() $\{0,1\}$
. If
$\{0,1\}$
. If
![]() ${\mathcal{O}}\models q({\mathbf{a}})>0$
, then for every model
${\mathcal{O}}\models q({\mathbf{a}})>0$
, then for every model
![]() ${\mathcal{I}}$
of
${\mathcal{I}}$
of
![]() $\widehat{\mathcal{O}}$
it holds that
$\widehat{\mathcal{O}}$
it holds that
![]() $q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}})>0$
and thus
$q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}})>0$
and thus
![]() $q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}})=1$
, which means that
$q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}})=1$
, which means that
![]() $\widehat{\mathcal{O}}\models q({\mathbf{a}})$
.
$\widehat{\mathcal{O}}\models q({\mathbf{a}})$
.
Conversely, if
![]() $\widehat{\mathcal{O}}\models q({\mathbf{a}})$
, then the canonical interpretation is such that
$\widehat{\mathcal{O}}\models q({\mathbf{a}})$
, then the canonical interpretation is such that
![]() $q^{{\mathcal{I}_\mathsf{can}}}({\mathbf{a}}^{{\mathcal{I}_\mathsf{can}}})>0$
, and hence for every model
$q^{{\mathcal{I}_\mathsf{can}}}({\mathbf{a}}^{{\mathcal{I}_\mathsf{can}}})>0$
, and hence for every model
![]() ${\mathcal{I}}$
it also holds that
${\mathcal{I}}$
it also holds that
![]() $q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}})>0$
.
$q^{\mathcal{I}}({\mathbf{a}}^{\mathcal{I}})>0$
.
This means that, for the sake of answering positive queries over the product t-norm, one can simply ignore all the truth degrees and answer a classical query using any state-of-the-art engine. In particular, this means that positive answers can be found in
![]() ${AC}^{0}$
in data complexity just as in the classical case.
${AC}^{0}$
in data complexity just as in the classical case.
We now briefly consider the Łukasiewicz t-norm, which is known to be the hardest to handle due to its involutive negation and nilpotence, despite being in many cases the most natural choice for fuzzy semantics (Borgwardt et al. Reference Borgwardt, Cerami and Peñaloza2017). As mentioned already, Proposition 15 does not apply to the Łukasiewicz t-norm. That is, there are consistent Ł-
![]() $\text{DL-Lite}_{R}$
ontologies whose classical version is inconsistent (see Example 10). As a result, there is currently no known method for deciding consistency of these ontologies, let alone answering queries. The culprits for this are the involutive negation, which is weaker than the negation used in the other two t-norms, but also the nilpotence, which may combine positive degrees to produce a degree of 0. The latter also means that, even if one could check consistency, it is still not clear how to answer even positive queries.
$\text{DL-Lite}_{R}$
ontologies whose classical version is inconsistent (see Example 10). As a result, there is currently no known method for deciding consistency of these ontologies, let alone answering queries. The culprits for this are the involutive negation, which is weaker than the negation used in the other two t-norms, but also the nilpotence, which may combine positive degrees to produce a degree of 0. The latter also means that, even if one could check consistency, it is still not clear how to answer even positive queries.
Example 32 Consider the ontology
![]() ${\mathcal{O}_2}:=({\mathcal{T}_2},{\mathcal{A}_2})$
where
${\mathcal{O}_2}:=({\mathcal{T}_2},{\mathcal{A}_2})$
where
Note that
![]() ${\mathcal{O}_2}$
is consistent, but there is a model
${\mathcal{O}_2}$
is consistent, but there is a model
![]() $ {\mathcal{I}}$
(e.g. the canonical interpretation) of this ontology which sets
$ {\mathcal{I}}$
(e.g. the canonical interpretation) of this ontology which sets
![]() $A_2^{\mathcal{I}}(a^{\mathcal{I}})=0$
. Hence, a is not a positive answer to the query
$A_2^{\mathcal{I}}(a^{\mathcal{I}})=0$
. Hence, a is not a positive answer to the query
![]() $q(x)=A_2(x)$
even though it is an answer of q(x) over
$q(x)=A_2(x)$
even though it is an answer of q(x) over
![]() $\widehat{\mathcal{O}_2}$
.
$\widehat{\mathcal{O}_2}$
.
Importantly, if we extend
![]() $\text{DL-Lite}_{R}$
with the possibility of using conjunctions as constructors for complex concepts, one can show following the ideas from Borgwardt et al. (Reference Borgwardt, Cerami and Peñaloza2017) and Borgwardt et al. (Reference Borgwardt, Cerami and Peñaloza2014) that deciding consistency of a Ł-
$\text{DL-Lite}_{R}$
with the possibility of using conjunctions as constructors for complex concepts, one can show following the ideas from Borgwardt et al. (Reference Borgwardt, Cerami and Peñaloza2017) and Borgwardt et al. (Reference Borgwardt, Cerami and Peñaloza2014) that deciding consistency of a Ł-
![]() $\text{DL-Lite}_{R}$
ontology is
$\text{DL-Lite}_{R}$
ontology is
![]() $\text{NP}$
-hard in combined complexity even if negations are disallowed; see 8 for full details. In the classical case, this logic – which is called
$\text{NP}$
-hard in combined complexity even if negations are disallowed; see 8 for full details. In the classical case, this logic – which is called
![]() $\text{DL-Lite}_{\text{Horn}}$
– has a polynomial time consistency problem (Artale et al. Reference Artale, Calvanese, Kontchakov and Zakharyaschev2009). This gives an indication that dealing with Ł-
$\text{DL-Lite}_{\text{Horn}}$
– has a polynomial time consistency problem (Artale et al. Reference Artale, Calvanese, Kontchakov and Zakharyaschev2009). This gives an indication that dealing with Ł-
![]() $\text{DL-Lite}_{R}$
may also lead to an increase in complexity.
$\text{DL-Lite}_{R}$
may also lead to an increase in complexity.
Interestingly, the rewriting technique from Section 5 also works for other t-norms – modulo some basic modifications – when answering threshold queries. Recall, for example, that given an axiom
![]() ${\left<{A\sqsubseteq B},[e]\right>}$
, and a threshold atom
${\left<{A\sqsubseteq B},[e]\right>}$
, and a threshold atom
![]() $B(x)\ge d$
, if
$B(x)\ge d$
, if
![]() $e\ge d$
then the rewriting technique would substitute this atom with
$e\ge d$
then the rewriting technique would substitute this atom with
![]() $A(x)\ge d$
. Although this substitution is sound for the idempotent Gödel t-norm, it does not work directly for the other ones. For example, under the product t-norm, if we set
$A(x)\ge d$
. Although this substitution is sound for the idempotent Gödel t-norm, it does not work directly for the other ones. For example, under the product t-norm, if we set
![]() $d=e=0.9$
we note that guaranteeing
$d=e=0.9$
we note that guaranteeing
![]() $A^{\mathcal{I}}(x)\ge 0.9$
does not necessarily implies, in a model
$A^{\mathcal{I}}(x)\ge 0.9$
does not necessarily implies, in a model
![]() ${\mathcal{I}}$
of
${\mathcal{I}}$
of
![]() ${\left<{A\sqsubseteq B},[e]\right>}$
that
${\left<{A\sqsubseteq B},[e]\right>}$
that
![]() $B^{\mathcal{I}}(x)\ge 0.9$
. Indeed, as long as
$B^{\mathcal{I}}(x)\ge 0.9$
. Indeed, as long as
![]() $B^{\mathcal{I}}(x)\ge 0.81$
, the axiom is satisfied in this case. A similar argument can be made for the Łukasiewicz t-norm. Hence, we need to increase the required degree for the rewritten atom.
$B^{\mathcal{I}}(x)\ge 0.81$
, the axiom is satisfied in this case. A similar argument can be made for the Łukasiewicz t-norm. Hence, we need to increase the required degree for the rewritten atom.
Recall from the properties of the residuum that for every t-norm
![]() $\otimes$
it holds that
$\otimes$
it holds that
![]() $A^{\mathcal{I}}(x)\Rightarrow B^{\mathcal{I}}(x)\ge e$
iff
$A^{\mathcal{I}}(x)\Rightarrow B^{\mathcal{I}}(x)\ge e$
iff
![]() $B^{\mathcal{I}}(x)\ge A^{\mathcal{I}}(x)\otimes e$
. Thus, to ensure that
$B^{\mathcal{I}}(x)\ge A^{\mathcal{I}}(x)\otimes e$
. Thus, to ensure that
![]() $B^{\mathcal{I}}(x)\ge d$
it suffices to guarantee that
$B^{\mathcal{I}}(x)\ge d$
it suffices to guarantee that
![]() $A^{\mathcal{I}}(x)\otimes e\ge d$
. In the case of the product t-norm, this is akin to the condition
$A^{\mathcal{I}}(x)\otimes e\ge d$
. In the case of the product t-norm, this is akin to the condition
![]() $A^{\mathcal{I}}(x)\ge d/e$
. For the Łukasiewicz t-norm the condition translates to the inequality
$A^{\mathcal{I}}(x)\ge d/e$
. For the Łukasiewicz t-norm the condition translates to the inequality
![]() $A^{\mathcal{I}}(x)\ge \min\{1, d+1-e\}$
. We can then apply the same PerfectRef algorithm, with a new definition of the function gr that changes the last degree (which is always
$A^{\mathcal{I}}(x)\ge \min\{1, d+1-e\}$
. We can then apply the same PerfectRef algorithm, with a new definition of the function gr that changes the last degree (which is always
![]() $\ge d$
in Figure 4) with the new degree developed here. Overall, this yields the following complexity result.
$\ge d$
in Figure 4) with the new degree developed here. Overall, this yields the following complexity result.
Theorem 33 Answering threshold queries w.r.t. consistent DL-Lite ontologies is in
![]() ${AC}^{0}$
in data complexity.
${AC}^{0}$
in data complexity.
Note that this theorem does not solve the problems sketched before for non-idempotent t-norms. Indeed, it is still not clear how to check for consistency of a Ł-DL-Lite ontology. Moreover, this result cannot be used to answer CQs because the analogous to Lemma 26 does not hold. Indeed, suppose that we have a simple CQ with only two atoms:
To turn
![]() $q(x)\ge d$
into a TQ, we need to assign a threshold to each of the atoms. Note however that, under a non-idempotent t-norm, we cannot assign the same degree d to each atom, as their conjunction would become in fact lower than d. To be more precise consider the product t-norm and
$q(x)\ge d$
into a TQ, we need to assign a threshold to each of the atoms. Note however that, under a non-idempotent t-norm, we cannot assign the same degree d to each atom, as their conjunction would become in fact lower than d. To be more precise consider the product t-norm and
![]() $d=0.9$
. Note that an answer to the TQ
$d=0.9$
. Note that an answer to the TQ
![]() $A(x)\ge 0.9 \land B(x)\ge 0.9$
is not necessarily an answer to
$A(x)\ge 0.9 \land B(x)\ge 0.9$
is not necessarily an answer to
![]() $q(x)\ge 0.9$
because there could be a model that assigns both atoms to degree 0.9; hence the product of those degrees is
$q(x)\ge 0.9$
because there could be a model that assigns both atoms to degree 0.9; hence the product of those degrees is
![]() $0.81<0.9$
. To use a TQ, we need to choose two degrees
$0.81<0.9$
. To use a TQ, we need to choose two degrees
![]() $d_1,d_2$
such that
$d_1,d_2$
such that
![]() $d_1\cdot d_2=0.9$
, and construct the TQ
$d_1\cdot d_2=0.9$
, and construct the TQ
![]() $A(x)\ge d_1 \land B(x)\ge d_2$
. But there are infinitely many choices to make in this regard, hence we cannot even construct a finite UTQ. Thus, unfortunately, although we are able to answer TQs efficiently (if the ontology is known to be consistent), degree queries remain an open problem for non-idempotent t-norms.
$A(x)\ge d_1 \land B(x)\ge d_2$
. But there are infinitely many choices to make in this regard, hence we cannot even construct a finite UTQ. Thus, unfortunately, although we are able to answer TQs efficiently (if the ontology is known to be consistent), degree queries remain an open problem for non-idempotent t-norms.
7 Conclusions
In this paper we have studied the problem of answering queries over fuzzy ontologies written in DL-Lite. Our goal was to cover the gap in this area left by previous research. Indeed, although query answering w.r.t. ontologies is still an active topic, most work referring to fuzzy terminologies or ABoxes focused on the so-called Zadeh semantics, which does not preserve desired properties from the mathematical fuzzy logic point of view. To our knowledge, only Mailis and Turhan (Reference Mailis and Turhan2014) and Mailis et al. (Reference Mailis, Turhan, Zenker, Calvanese and Konev2015) have studied this problem based on t-norms, and found solutions based on the Gödel t-norm. However, they limited their approach to classical TBoxes. They left open the problems of dealing with graded TBoxes, handling threshold queries, and dealing with non-idempotent t-norms.
A second goal of our work was to reuse as much as possible the classical techniques, in order to avoid an implementation overhead when our algorithms will be, in future work, implemented and tested. As a result, we developed a method for answering degree queries which relies heavily on a classical query answering tool as a black box. Through this method, we can take advantage of all the existing optimizations and improvements from that area, and simply use a better tool whenever it becomes available without having to worry about the internal intricacies that make it work. In few words, our algorithm for answering CQs w.r.t. the Gödel semantics simply considers the classical version of the cut of the ontology. That is, the method ignores all axioms that hold to a degree lower than the threshold imposed, and then sees the remaining query answering question as a classical one. We emphasize that this approach works perfectly even if the TBox is graded. This means that our results improve those by Mailis and Turhan (Reference Mailis and Turhan2014) by allowing for fuzzy TBox axioms and not requiring a new rewriting of the query.
Dealing with threshold queries, where each atom can be independently assigned a different degree, turns out to be more complex technically. In fact, we were not able to produce a direct reduction to a classical query answering problem – and it is unlikely that such a reduction could exist, given the nature of the graded axioms. However, we could still exploit the main ideas from the classical scenario, adapting the well-known PerfectRef method to the fuzzy scenario. In some sense PerfectRef absorbs the TBox into the query, forming a larger UCQ which can be answered classically, seeing the ABox as a database. In our case, we also need to take care of the degree at which the rewritten atoms should hold, when creating the new query. Under the Gödel semantics, it suffices to preserve the same degree from the original query, but for non-idempotent t-norms the degree has to be increased accordingly to avoid including spurious answers. Importantly, this shows that answering threshold queries w.r.t. consistent fuzzy ontologies is in the same complexity class (
![]() ${AC}^{0}$
) in data complexity as for the classical case, regardless of the t-norm underlying the semantics. The only caveat is that it is not known how to verify consistency of a fuzzy DL-Lite ontology in general. The idempotency of the Gödel t-norm allowed us then to show that CQ answering w.r.t. consistent G-DL-Lite ontologies is also in
${AC}^{0}$
) in data complexity as for the classical case, regardless of the t-norm underlying the semantics. The only caveat is that it is not known how to verify consistency of a fuzzy DL-Lite ontology in general. The idempotency of the Gödel t-norm allowed us then to show that CQ answering w.r.t. consistent G-DL-Lite ontologies is also in
![]() ${AC}^{0}$
in data complexity. This latter bound does not hold for non-idempotent t-norms.
${AC}^{0}$
in data complexity. This latter bound does not hold for non-idempotent t-norms.
It is worth noting that the methods for answering degree and threshold queries both ultimately rely on a rewriting of the query to represent the information expressed in the TBox. While the rewriting does not affect the data complexity, it is well-known that the UCQ obtained through PerfectRef may grow exponentially (Calvanese et al. Reference Calvanese, De Giacomo, Lembo, Lenzerini and Rosati2007; Pérez-Urbina et al. Reference Pérez-Urbina, Motik and Horrocks2010). This means that, depending on the instance, answering these queries may still be impractical. For that reason, different rewriting and answering techniques have been developed and tested; for example, rewriting into a Datalog program instead of an UCQ (Gottlob and Schwentick Reference Gottlob and Schwentick2012; Gottlob et al. Reference Gottlob, Orsi and Pieris2011). Our approach for solving threshold queries, given its reliance on PerfectRef, suffers from the same drawbacks. In order to use more optimized approaches, it is necessary to study whether other existing rewritings can also be adapted to the fuzzy setting. On the other hand, the approach to degree queries is, as mentioned already, fully black box: we only need to call an unmodified classical query answering tool repeatedly. This allows us to directly plug whichever system performs best, without worrying about the implementation overhead of understanding and adapting the existing tools.
Through illustrative examples, we showed that dealing with CQs is in general harder when the underlying t-norm is not idempotent. The main issue is that there is no unique way to decide the bounds for the different degrees to which atoms should hold to satisfy the lower bound for a conjunction of atoms. The problem is exacerbated by the fact that it is not even clear how to decide consistency of ontologies under the nilpotent t-norm. Indeed, even in the absence of an ABox, the Łukasiewicz t-norm may impose upper bounds in the degrees of some assertions which are not obvious to detect and could contradict other conditions.
As future work, we are also interested in implementing and testing our ideas, with the help of some fuzzy ontologies which will be developed for specific application domains.
A. NP-Hardness for the Horn case
In this appendix we show that ontology consistency in Ł-
![]() $\text{DL-Lite}_{\text{Horn}}$
, a DL closely related to Ł-DLLR, is
$\text{DL-Lite}_{\text{Horn}}$
, a DL closely related to Ł-DLLR, is
![]() $\text{NP}$
-hard. The proof builds on the idea originally developed for a finitely-valued logic (Borgwardt et al. Reference Borgwardt, Cerami and Peñaloza2014),
Footnote 7
extended with the methods from Borgwardt et al. (Reference Borgwardt, Cerami and Peñaloza2017) and Borgwardt et al. (Reference Borgwardt, Cerami and Peñaloza2015) to deal with infinitely-valued t-norms. For brevity, we consider only a restricted version of Ł-
$\text{NP}$
-hard. The proof builds on the idea originally developed for a finitely-valued logic (Borgwardt et al. Reference Borgwardt, Cerami and Peñaloza2014),
Footnote 7
extended with the methods from Borgwardt et al. (Reference Borgwardt, Cerami and Peñaloza2017) and Borgwardt et al. (Reference Borgwardt, Cerami and Peñaloza2015) to deal with infinitely-valued t-norms. For brevity, we consider only a restricted version of Ł-
![]() $\text{DL-Lite}_{\text{Horn}}$
which already suffices to show hardness.
$\text{DL-Lite}_{\text{Horn}}$
which already suffices to show hardness.
A Ł-
![]() $\text{DL-Lite}_{\text{Horn}}$
GCI is an expression of the form
$\text{DL-Lite}_{\text{Horn}}$
GCI is an expression of the form
![]() $\left<B\sqsubseteq C,d\right>$
where B,C are built through the grammar
$\left<B\sqsubseteq C,d\right>$
where B,C are built through the grammar
![]() $B::= A\mid B\sqcap B\mid \bot$
, where
$B::= A\mid B\sqcap B\mid \bot$
, where
![]() $A\in {N_C}$
; that is, they are conjunctions of concept names, and
$A\in {N_C}$
; that is, they are conjunctions of concept names, and
![]() $d\in[0,1]$
. The notion of an ABox, a TBox, and an ontology are analogous to the
$d\in[0,1]$
. The notion of an ABox, a TBox, and an ontology are analogous to the
![]() $\text{DL-Lite}_{R}$
setting. The semantics of this logic is defined as for
$\text{DL-Lite}_{R}$
setting. The semantics of this logic is defined as for
![]() $\text{DL-Lite}_{R}$
, with the addition that the interpretation function is defined for conjunctions as
$\text{DL-Lite}_{R}$
, with the addition that the interpretation function is defined for conjunctions as
![]() $(B\sqcap C)^{\mathcal{I}}(\delta):=B^{\mathcal{I}}(\delta)\otimes C^{\mathcal{I}}(\delta)$
and for bottom as
$(B\sqcap C)^{\mathcal{I}}(\delta):=B^{\mathcal{I}}(\delta)\otimes C^{\mathcal{I}}(\delta)$
and for bottom as
![]() $\bot^{\mathcal{I}}(\delta):=0$
.
$\bot^{\mathcal{I}}(\delta):=0$
.
We show
![]() $\text{NP}$
-hardness through a reduction from the well-known problem of satisfiability of 3-CNF formulas (Cook Reference Cook1971). Very briefly, a 3-clause is a disjunction of exactly three literals (variables or negated variables) and a 3-CNF formula is a conjunction of 3-clauses.
$\text{NP}$
-hardness through a reduction from the well-known problem of satisfiability of 3-CNF formulas (Cook Reference Cook1971). Very briefly, a 3-clause is a disjunction of exactly three literals (variables or negated variables) and a 3-CNF formula is a conjunction of 3-clauses.
The main idea behind the reduction is to use an intermediate degree greater than 0 to simulate the logical truth value false from classical propositional logic. This allows us to simulate the disjunction from the 3-clauses through a conjunction of concepts. This idea is formalized in full detail next.
Consider the set
![]() ${\mathcal{V}}$
of propositional variables. For each
${\mathcal{V}}$
of propositional variables. For each
![]() $v\in{\mathcal{V}}$
we define two concept names
$v\in{\mathcal{V}}$
we define two concept names
![]() $A_v$
and
$A_v$
and
![]() $A'_v$
with the intuitive meaning that
$A'_v$
with the intuitive meaning that
![]() $A_v$
stands for the valuation making v true, and
$A_v$
stands for the valuation making v true, and
![]() $A'_v$
for the valuation making v false. We define the function
$A'_v$
for the valuation making v false. We define the function
![]() $\rho$
which maps propositional literals to concept names as:
$\rho$
which maps propositional literals to concept names as:
 \begin{equation*}\rho(\ell) := \begin{cases} A_v & \text{if } \ell=v\in{\mathcal{V}} \\ A'_v & \text{if } \ell=\neg v, v\in{\mathcal{V}}. \end{cases}\end{equation*}
\begin{equation*}\rho(\ell) := \begin{cases} A_v & \text{if } \ell=v\in{\mathcal{V}} \\ A'_v & \text{if } \ell=\neg v, v\in{\mathcal{V}}. \end{cases}\end{equation*}
This function is extended to 3-clauses by defining
![]() $\rho(\ell_1\lor \ell_2\lor \ell_3):=\rho(\ell_1)\sqcap \rho(\ell_2)\sqcap \rho(\ell_3)$
. Abusing the notation, we identify the 3-CNF formula
$\rho(\ell_1\lor \ell_2\lor \ell_3):=\rho(\ell_1)\sqcap \rho(\ell_2)\sqcap \rho(\ell_3)$
. Abusing the notation, we identify the 3-CNF formula
![]() $\varphi$
with the set of 3-clauses it contains.
$\varphi$
with the set of 3-clauses it contains.
Let
![]() $\varphi$
be a propositional formula in 3-CNF, and
$\varphi$
be a propositional formula in 3-CNF, and
![]() ${\mathsf{var}}(\varphi)$
represent the set of all propositional variables appearing in
${\mathsf{var}}(\varphi)$
represent the set of all propositional variables appearing in
![]() $\varphi$
. We construct the ontology
$\varphi$
. We construct the ontology
![]() ${\mathcal{O}}_\varphi$
consisting of the very simple ABox
${\mathcal{O}}_\varphi$
consisting of the very simple ABox
![]() ${\mathcal{A}}_\varphi:=\{\left<A_0(a),1\right>\}$
and the TBox
${\mathcal{A}}_\varphi:=\{\left<A_0(a),1\right>\}$
and the TBox
Theorem 34 The formula
![]() $\varphi$
is satisfiable iff the ontology
$\varphi$
is satisfiable iff the ontology
![]() ${\mathcal{O}}_\varphi=({\mathcal{A}}_\varphi,{\mathcal{T}}_\varphi)$
is consistent.
${\mathcal{O}}_\varphi=({\mathcal{A}}_\varphi,{\mathcal{T}}_\varphi)$
is consistent.
Proof. We start with some observations about the TBox
![]() ${\mathcal{T}}_\varphi$
. The axioms in lines (A1) and (A2) require that every model
${\mathcal{T}}_\varphi$
. The axioms in lines (A1) and (A2) require that every model
![]() ${\mathcal{I}}=(\Delta^{\mathcal{I}},\cdot^{\mathcal{I}})$
of
${\mathcal{I}}=(\Delta^{\mathcal{I}},\cdot^{\mathcal{I}})$
of
![]() ${\mathcal{T}}_\varphi$
is such that
${\mathcal{T}}_\varphi$
is such that
![]() $A_v^{\mathcal{I}}(\delta)\in [0,2/3]\cup\{1\}$
and
$A_v^{\mathcal{I}}(\delta)\in [0,2/3]\cup\{1\}$
and
![]() ${A'_v}^{\mathcal{I}}(\delta)\in [0,2/3]\cup\{1\}$
for all
${A'_v}^{\mathcal{I}}(\delta)\in [0,2/3]\cup\{1\}$
for all
![]() $\delta\in\Delta^{\mathcal{I}}$
.
Footnote 8
Given the ABox axiom, the GCIs from line (A3) guarantee that exactly one between
$\delta\in\Delta^{\mathcal{I}}$
.
Footnote 8
Given the ABox axiom, the GCIs from line (A3) guarantee that exactly one between
![]() $A_v^{\mathcal{I}}(a^{\mathcal{I}})$
and
$A_v^{\mathcal{I}}(a^{\mathcal{I}})$
and
![]() ${A'_v}^{\mathcal{I}}(a^{\mathcal{I}})$
is interpreted as 1, and the other one as
${A'_v}^{\mathcal{I}}(a^{\mathcal{I}})$
is interpreted as 1, and the other one as
![]() $2/3$
. Intuitively, the value
$2/3$
. Intuitively, the value
![]() $2/3$
will be read as “false” and 1 as “true.” Finally, the axioms in line (A4) guarantee that for every clause
$2/3$
will be read as “false” and 1 as “true.” Finally, the axioms in line (A4) guarantee that for every clause
![]() $c\in\varphi$
, at least one of the conjuncts in
$c\in\varphi$
, at least one of the conjuncts in
![]() $\rho(c)$
is interpreted as 1 (i.e. “true”) at the element
$\rho(c)$
is interpreted as 1 (i.e. “true”) at the element
![]() $a^{\mathcal{I}}$
. Now we prove the property.
$a^{\mathcal{I}}$
. Now we prove the property.
If
![]() $\varphi$
is satisfiable, let
$\varphi$
is satisfiable, let
![]() ${\mathcal{V}}$
be a valuation making
${\mathcal{V}}$
be a valuation making
![]() $\varphi$
true. As customary, a valuation is a subset of
$\varphi$
true. As customary, a valuation is a subset of
![]() ${\mathsf{var}}(\varphi)$
that expresses which variables are mapped to true. We construct the interpretation
${\mathsf{var}}(\varphi)$
that expresses which variables are mapped to true. We construct the interpretation
![]() ${\mathcal{I}}_{\mathcal{V}}=(\{a\},\cdot^{\mathcal{I}})$
having a singleton domain, where
${\mathcal{I}}_{\mathcal{V}}=(\{a\},\cdot^{\mathcal{I}})$
having a singleton domain, where
![]() $A_0^{\mathcal{I}}(a)=1$
and for each
$A_0^{\mathcal{I}}(a)=1$
and for each
![]() $v\in{\mathsf{var}}(\varphi)$
$v\in{\mathsf{var}}(\varphi)$
 \begin{align*}A_v^{\mathcal{I}}(a) = {} & \begin{cases} 1 & \text{if } v\in{\mathcal{V}} \\ 2/3 & \text{otherwise} \end{cases},\end{align*}
\begin{align*}A_v^{\mathcal{I}}(a) = {} & \begin{cases} 1 & \text{if } v\in{\mathcal{V}} \\ 2/3 & \text{otherwise} \end{cases},\end{align*}
It is easy to see that this interpretation satisfies
![]() ${\mathcal{A}}_\varphi$
and all the axioms in lines (A1)–(A3) of
${\mathcal{A}}_\varphi$
and all the axioms in lines (A1)–(A3) of
![]() ${\mathcal{T}}_\varphi$
. Since
${\mathcal{T}}_\varphi$
. Since
![]() ${\mathcal{V}}$
is a model of
${\mathcal{V}}$
is a model of
![]() $\varphi$
, for every 3-clause
$\varphi$
, for every 3-clause
![]() $c\in\varphi$
, there exists a literal
$c\in\varphi$
, there exists a literal
![]() $\ell$
in c that
$\ell$
in c that
![]() ${\mathcal{V}}$
maps to true. By construction,
${\mathcal{V}}$
maps to true. By construction,
![]() $(\rho(\ell))^{\mathcal{I}}(a)=1$
, and hence,
$(\rho(\ell))^{\mathcal{I}}(a)=1$
, and hence,
![]() ${\mathcal{I}}_\varphi$
is also a model of these axioms. Hence
${\mathcal{I}}_\varphi$
is also a model of these axioms. Hence
![]() ${\mathcal{O}}_\varphi$
is consistent.
${\mathcal{O}}_\varphi$
is consistent.
Conversely, let
![]() ${\mathcal{I}}=(\Delta^{\mathcal{I}},\cdot^{\mathcal{I}})$
be a model of
${\mathcal{I}}=(\Delta^{\mathcal{I}},\cdot^{\mathcal{I}})$
be a model of
![]() ${\mathcal{O}}_\varphi$
and let
${\mathcal{O}}_\varphi$
and let
![]() $\delta=a^{\mathcal{I}}$
. We construct the propositional valuation
$\delta=a^{\mathcal{I}}$
. We construct the propositional valuation
![]() ${\mathcal{V}}_{\mathcal{I}}$
as follows: for every
${\mathcal{V}}_{\mathcal{I}}$
as follows: for every
![]() $v\in{\mathsf{var}}(\varphi)$
,
$v\in{\mathsf{var}}(\varphi)$
,
![]() $v\in{\mathcal{V}}$
iff
$v\in{\mathcal{V}}$
iff
![]() $A_v^{\mathcal{I}}(\delta)=1$
. By construction, for every
$A_v^{\mathcal{I}}(\delta)=1$
. By construction, for every
![]() $v\notin{\mathcal{V}}$
it holds that
$v\notin{\mathcal{V}}$
it holds that
![]() ${A'_v}^{\mathcal{I}}(\delta)=1$
. Since
${A'_v}^{\mathcal{I}}(\delta)=1$
. Since
![]() ${\mathcal{I}}$
is a model of
${\mathcal{I}}$
is a model of
![]() ${\mathcal{T}}_\varphi$
, it satisfies the axioms in line (A4), and hence for each clause c, there is a literal
${\mathcal{T}}_\varphi$
, it satisfies the axioms in line (A4), and hence for each clause c, there is a literal
![]() $\ell$
such that
$\ell$
such that
![]() $\rho(\ell)^{\mathcal{I}}(\delta)=1$
. This is true iff
$\rho(\ell)^{\mathcal{I}}(\delta)=1$
. This is true iff
![]() ${\mathcal{V}}_{\mathcal{I}}$
makes
${\mathcal{V}}_{\mathcal{I}}$
makes
![]() $\ell$
true, and in particular the whole clause c true. Hence
$\ell$
true, and in particular the whole clause c true. Hence
![]() ${\mathcal{V}}_{\mathcal{I}}$
satisfies
${\mathcal{V}}_{\mathcal{I}}$
satisfies
![]() $\varphi$
.
$\varphi$
.