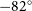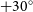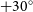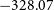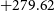1. Introduction
The construction of an all-sky grid of polarised sources with which to probe the large-scale magnetised Universe is one of the high-priority goals of many surveys with next-generation radio telescopes. For example, the POlarisation Sky Survey of the Universe’s Magnetism (POSSUM; Gaensler et al. Reference Gaensler, Landecker and Taylor2010) project with the Australian Square Kilometre Array Pathfinder (ASKAP; Johnston et al. Reference Johnston2007) is predicted to detect up to million polarised sources across the Southern sky (South of Declination around ![]() $+30^\circ$). Such all-sky grids can be used as statistical probes of cosmic magnetism, and a number of large-N studies have already been performed using previous state-of-the-art polarisation catalogues to probe both the Galactic magnetised foreground (e.g., Oppermann et al. Reference Oppermann2012, Reference Oppermann2015; Hutschenreuter & Enßlin Reference Hutschenreuter and Enßlin2020) and the extragalactic magnetised Universe (e.g., Vernstrom et al. Reference Vernstrom, Gaensler, Vacca, Farnes, Haverkorn and O’Sullivan2019).
$+30^\circ$). Such all-sky grids can be used as statistical probes of cosmic magnetism, and a number of large-N studies have already been performed using previous state-of-the-art polarisation catalogues to probe both the Galactic magnetised foreground (e.g., Oppermann et al. Reference Oppermann2012, Reference Oppermann2015; Hutschenreuter & Enßlin Reference Hutschenreuter and Enßlin2020) and the extragalactic magnetised Universe (e.g., Vernstrom et al. Reference Vernstrom, Gaensler, Vacca, Farnes, Haverkorn and O’Sullivan2019).
However, these previous all-sky polarisation surveys—principally the catalogue of Taylor, Stil, & Sunstrum (Reference Taylor2009), produced from the National Radio Astronomy Observatory (NRAO) Very Large Array (VLA) Sky Survey (NVSS; Condon et al. Reference Condon, Cotton, Greisen, Yin, Perley, Taylor and Broderick1998)—contain large systematic uncertainties, due to their poor frequency sampling (e.g., Van Eck et al. Reference Van Eck2011; Ma et al. Reference Ma, Mao, Stil, Basu, West, Heiles, Hill and Betti2019a). However, next-generation surveys (such as POSSUM and the Karl G. Jansky Very Large Array Sky Survey; Lacy et al. 2020) possess large fractional bandwidths that are finely sampled in frequency, which mitigates many of the systematic uncertainties of the Taylor et al. (Reference Taylor2009) catalogue.
Towards longer wavelengths, with the advent of next-generation interferometers such as the LOw-Frequency ARray (LOFAR; van Haarlem et al. Reference van Haarlem2013) and the Murchison Widefield Array (MWA; Tingay et al. Reference Tingay2013), low-frequency polarimetry has experienced a renaissance. Historically, such studies were extremely challenging, due to the poor sensitivity of previous instruments as well as calibration difficulties (related often to ionospheric effects). However, recent advances in calibration and imaging software, such as the MWA’s Real-Time System (RTS; Mitchell et al. Reference Mitchell, Greenhill, Wayth, Sault, Lonsdale, Cappallo, Morales and Ord2008) as well as techniques for correcting for instrumental leakage and ionospheric effects (e.g., Lenc et al. Reference Lenc2017, Reference Lenc, Murphy, Lynch, Kaplan and Zhang2018; Mevius Reference Mevius2018) have enabled rapid progress in the field of low-frequency polarimetry. Another critical element that has enabled this renaissance is the availability of high-performance computing resources in the Square Kilometre Array precursor era.
Indeed, in recent years, the low-frequency polarised sky has been explored in greater detail than ever before, with detections of large-scale diffuse Galactic foreground along many lines of sight (LOSs) (e.g., Jelić et al. Reference Jelić2015; Lenc et al. Reference Lenc2016; Van Eck et al. Reference Van Eck2017, Reference Van Eck2019) as well as many surveys that have begun to study the polarised extragalactic source population (e.g., Bernardi et al. Reference Bernardi2013; Mulcahy et al. Reference Mulcahy2014; Van Eck et al. Reference Van Eck2017; Lenc et al. Reference Lenc, Murphy, Lynch, Kaplan and Zhang2018; Neld et al. Reference Neld2018; O’Sullivan et al. Reference O’Sullivan2019, Reference O’Sullivan2020; Stuardi et al. 2020; Cantwell et al. 2020).
1.1. Faraday rotation
Following, for example, Sokoloff et al. (Reference Sokoloff, Bykov, Shukurov, Berkhuijsen, Beck and Poezd1998), the complex narrowband linear polarisation P can be expressed as
where I, Q, and U are the measured Stokes parameters, ![]() $\Pi$ is the fractional polarisation, and
$\Pi$ is the fractional polarisation, and ![]() $\chi$ is the polarisation angle.
$\chi$ is the polarisation angle.
When a linearly polarised radio wave encounters magnetised thermal plasma with some magnetic field component along the LOS from a given source to an observer, the plane of polarised emission rotates. This is known as Faraday rotation, and the observed frequency-dependent polarisation angle, ![]() $\chi(\lambda^2)$, is rotated according to:
$\chi(\lambda^2)$, is rotated according to:
where ![]() $\lambda$ is the observing wavelength and
$\lambda$ is the observing wavelength and ![]() $\chi_0$ is the intrinsic source polarisation angle. The rotational measure (RM) (in rad m−2) is defined as
$\chi_0$ is the intrinsic source polarisation angle. The rotational measure (RM) (in rad m−2) is defined as
where ![]() $\ell$ is the distance to the source of polarised emission (in parsecs),
$\ell$ is the distance to the source of polarised emission (in parsecs), ![]() $n_{\rm{e}}$ is the number density of free electrons (in cm−3), and
$n_{\rm{e}}$ is the number density of free electrons (in cm−3), and ![]() $B_{\|}$ is the magnetic field strength component along the LOS (in
$B_{\|}$ is the magnetic field strength component along the LOS (in ![]() $\mu$G). The accepted sign convention is that positive RM indicates a magnetic field oriented towards the observer, and negative RM indicates a magnetic field oriented away from the observer.
$\mu$G). The accepted sign convention is that positive RM indicates a magnetic field oriented towards the observer, and negative RM indicates a magnetic field oriented away from the observer.
In regions where linearly polarised emission and Faraday rotation are co-located, interference effects along the LOS lead to more complex observed behaviour in ![]() $P(\lambda^2)$. Such behaviour carries a lot of physical information (e.g., Sokoloff et al. Reference Sokoloff, Bykov, Shukurov, Berkhuijsen, Beck and Poezd1998) but is beyond the scope of our low-frequency polarimetry work. As quantified later in Section 2, we are only sensitive to polarised emission that lies along the LOS through a medium that is purely Faraday-rotating (i.e., does not also emit any polarised synchrotron emission itself, e.g., Heald 2009).
$P(\lambda^2)$. Such behaviour carries a lot of physical information (e.g., Sokoloff et al. Reference Sokoloff, Bykov, Shukurov, Berkhuijsen, Beck and Poezd1998) but is beyond the scope of our low-frequency polarimetry work. As quantified later in Section 2, we are only sensitive to polarised emission that lies along the LOS through a medium that is purely Faraday-rotating (i.e., does not also emit any polarised synchrotron emission itself, e.g., Heald 2009).
1.2. Surveys with the phase I MWA
The GaLactic and Extragalactic All-sky MWA survey (GLEAM; Wayth et al. Reference Wayth2015) covers the entire sky South of Declination ![]() $+30^\circ$. The GLEAM Extragalactic Catalogue (Hurley-Walker et al. Reference Hurley-Walker2017) covers 24 831 square degrees of sky below this Declination and at Galactic latitudes
$+30^\circ$. The GLEAM Extragalactic Catalogue (Hurley-Walker et al. Reference Hurley-Walker2017) covers 24 831 square degrees of sky below this Declination and at Galactic latitudes ![]() $|b| \geq 10^\circ$. In Riseley et al. (Reference Riseley2018) (hereafter Reference PurcellPaper I), we applied recent technical advances in low-frequency polarisation calibration, as well as source-finding and verification techniques, to begin probing the low-frequency linearly polarised source population across a wide area of the Southern sky.
$|b| \geq 10^\circ$. In Riseley et al. (Reference Riseley2018) (hereafter Reference PurcellPaper I), we applied recent technical advances in low-frequency polarisation calibration, as well as source-finding and verification techniques, to begin probing the low-frequency linearly polarised source population across a wide area of the Southern sky.
Paper I presented the first results from the POlarised GLEAM Survey (POGS). We applied these novel data processing techniques to a subset of GLEAM data covering approximately 6 400 square degrees of sky in the frequency range 200−231 MHz. This region covered 24 h in Right Ascension and ![]() $20^\circ$ in Declination centred on Declination
$20^\circ$ in Declination centred on Declination ![]() $-27^\circ$. We detected 81 sources with polarised flux densities in excess of 18 mJy at 216 MHz. In this paper, we present the full results from POGS, covering the entire Southern sky South of Declination
$-27^\circ$. We detected 81 sources with polarised flux densities in excess of 18 mJy at 216 MHz. In this paper, we present the full results from POGS, covering the entire Southern sky South of Declination ![]() $+30^\circ$ in the frequency range 169−231 MHz. All errors are quoted to
$+30^\circ$ in the frequency range 169−231 MHz. All errors are quoted to ![]() $1\sigma$, and we adopt the spectral index convention that
$1\sigma$, and we adopt the spectral index convention that ![]() $S\propto \nu^{\alpha}$, where S is the measured flux density,
$S\propto \nu^{\alpha}$, where S is the measured flux density, ![]() $\nu$ is the frequency and
$\nu$ is the frequency and ![]() $\alpha$ is the spectral index.
$\alpha$ is the spectral index.
2. Data processing
2.1. Observations
The GLEAM observations were performed in a drift-scan observing mode, where all tiles were pointed to the meridian, and the sky drifts through the MWA field of view (see Wayth et al. Reference Wayth2015). This drift-scan observing mode ensures that the MWA maintains a consistent primary beam throughout a given observing run. Observations were taken during four epochs between 2013 August and 2014 June. Each epoch covered approximately 8 h in Right Ascension, with a ![]() $\sim$2–4 h overlap between epochs. The entire sky South of Declination
$\sim$2–4 h overlap between epochs. The entire sky South of Declination ![]() $+30^\circ$ was covered in seven ‘Declination strips’. The details of each GLEAM observing run are presented by Hurley-Walker et al. (Reference Hurley-Walker2017) and Lenc et al. (Reference Lenc, Murphy, Lynch, Kaplan and Zhang2018).
$+30^\circ$ was covered in seven ‘Declination strips’. The details of each GLEAM observing run are presented by Hurley-Walker et al. (Reference Hurley-Walker2017) and Lenc et al. (Reference Lenc, Murphy, Lynch, Kaplan and Zhang2018).
In completing POGS, we have opted to use the top two GLEAM frequency bands, covering the contiguous frequency range 169–231 MHz. This frequency range provides a balance between achieving improved resolution in both image space and Faraday space, while reducing the impact of depolarisation and retaining sensitivity to large RMs. We note that the MWA beam model is less accurate at these frequencies, and we suffer increased polarisation leakage compared to lower frequencies (e.g., Sutinjo et al. Reference Sutinjo, O’Sullivan, Lenc, Wayth, Padhi, Hall and Tingay2015; Lenc et al. Reference Lenc2016).
2.2. Data reduction
Calibration and imaging were performed with the RTS (Mitchell et al. Reference Mitchell, Greenhill, Wayth, Sault, Lonsdale, Cappallo, Morales and Ord2008) using the process detailed by Lenc et al. (Reference Lenc2017; Reference Lenc, Murphy, Lynch, Kaplan and Zhang2018) and discussed in Reference PurcellPaper I, performed separately on each frequency band. Archival online flagging (Offringa, van de Gronde, & Roerdink Reference Offringa, van de Gronde and Roerdink2012) was applied to mitigate RFI. Gains were derived for a single calibrator scan on each GLEAM night, selected to maximise signal-to-noise ratio (SNR). Images were generated using the RTS, employing Briggs weighting (Briggs Reference Briggs1995) using robust![]() $=-1.0$ to reduce sidelobe confusion. We selected baselines in the range
$=-1.0$ to reduce sidelobe confusion. We selected baselines in the range ![]() $50\lambda$ to
$50\lambda$ to ![]() $1{\rm{k}}\lambda$ in order to (i) reduce contamination from diffuse Galactic foreground emission and (ii) maintain near-constant resolution for a given Declination strip across the entire frequency band. Image cubes were generated using the native GLEAM channel resolution (40 kHz) for a
$1{\rm{k}}\lambda$ in order to (i) reduce contamination from diffuse Galactic foreground emission and (ii) maintain near-constant resolution for a given Declination strip across the entire frequency band. Image cubes were generated using the native GLEAM channel resolution (40 kHz) for a ![]() $20\times20$ deg
$20\times20$ deg![]() $^2$ region on a per-snapshot basis, with a 40 arcsec pixel size to ensure our point spread function (PSF) is oversampled by a factor
$^2$ region on a per-snapshot basis, with a 40 arcsec pixel size to ensure our point spread function (PSF) is oversampled by a factor ![]() $\sim$5. Note that the RTS does not perform deconvolution without a priori knowledge of the source population. While deconvolution is not critical in our case, as the surface density of linearly polarised sources is sufficiently low to avoid confusion and the majority of polarised sources remain unresolved at the resolution of the Phase I MWA, it can help mitigate leakage due to sidelobes from brighter Stokes I sources in the field.
$\sim$5. Note that the RTS does not perform deconvolution without a priori knowledge of the source population. While deconvolution is not critical in our case, as the surface density of linearly polarised sources is sufficiently low to avoid confusion and the majority of polarised sources remain unresolved at the resolution of the Phase I MWA, it can help mitigate leakage due to sidelobes from brighter Stokes I sources in the field.
We then applied corrections for instrumental leakage to correct for inaccuracies in the MWA beam model (Sutinjo et al. Reference Sutinjo, O’Sullivan, Lenc, Wayth, Padhi, Hall and Tingay2015), as described in Section 2.1 of Reference PurcellPaper I. This correction uses the snapshot nature of GLEAM to reconstruct an empirical ‘leakage surface’ from the apparent Stokes Q and U flux densities as sources drift through the beam (see for full details Lenc et al. Reference Lenc2017, Reference Lenc, Murphy, Lynch, Kaplan and Zhang2018). In a similar manner, a flux scaling correction was derived and subsequently applied by comparing apparent flux densities for sources with entries in the GLEAM catalogue (Hurley-Walker et al. Reference Hurley-Walker2017). This corrects for position-dependent flux calibration errors that were noted by Hurley-Walker et al. (Reference Hurley-Walker2014; Reference Hurley-Walker2017).
Following instrumental leakage correction, we applied a correction for ionospheric Faraday rotation using the RMextract tool (Mevius Reference Mevius2018), as per Section 2.2 of Reference PurcellPaper I. The ionospheric RMs reported by RMextract for a given epoch were used to perform a frequency-dependent de-rotation of the Stokes Q and U image cubes on a per-snapshot basis. We note that the expected residual ionospheric RM correction error is of the order of 0.1−0.3 rad m−2 for an 8-h observing run (Sotomayor-Beltran et al. Reference Sotomayor-Beltran2013).
Our leakage- and ionospheric-RM-corrected Stokes Q and U images were then mosaicked using swarp (Bertin et al. Reference Bertin, Mellier, Radovich, Missonnier, Didelon, Morin, Durand and Handley2002) to boost our sensitivity (as per Section 2.3 of Reference PurcellPaper I), due to the significant overlap between GLEAM snapshots. Finally, the images for each GLEAM frequency band were stacked into one larger cube covering the full frequency range 169–231 MHz.
We then performed RM synthesis (e.g., Burn Reference Burn1966; Brentjens & de Bruyn Reference Brentjens and de Bruyn2005) using the Compute Unified Device Architecture-accelerated Fast Faraday Synthesis (cuFFS; Sridhar, Heald, & van der Hulst Reference Sridhar, Heald and van der Hulst2018) software. As presented by Brentjens & de Bruyn (Reference Brentjens and de Bruyn2005), the key parameters for RM synthesis—the RM resolution ![]() $(\Delta({\rm{RM}}))$, maximum RM
$(\Delta({\rm{RM}}))$, maximum RM ![]() $(|{\rm{RM}}_{\rm{max}}|),$ and maximum scale in RM space
$(|{\rm{RM}}_{\rm{max}}|),$ and maximum scale in RM space ![]() $(\rm{max. scale})$—are defined as
$(\rm{max. scale})$—are defined as
where ![]() $\Delta(\lambda^2)$ is the span in wavelength-squared across the observing bandwidth,
$\Delta(\lambda^2)$ is the span in wavelength-squared across the observing bandwidth, ![]() $\delta(\lambda^2)$ is the wavelength-squared difference across each observed frequency channel, and
$\delta(\lambda^2)$ is the wavelength-squared difference across each observed frequency channel, and ![]() $\lambda_{\rm{min}}$ is the wavelength of the highest-frequency channel.
$\lambda_{\rm{min}}$ is the wavelength of the highest-frequency channel.
From Equation (4a), we have ![]() $\Delta({\rm{RM}}) \simeq2.6$ rad m−2, which provides high RM precision. From Equation (4b), the maximum scale size we can recover is also small, at around 1.9 rad m−2, meaning that all polarised sources will appear point-like in Faraday space (e.g., Van Eck et al. Reference Van Eck2017). However, from Equation (4c), our use of the native 40 kHz GLEAM channel resolution retains sensitivity to very large RMs, up to
$\Delta({\rm{RM}}) \simeq2.6$ rad m−2, which provides high RM precision. From Equation (4b), the maximum scale size we can recover is also small, at around 1.9 rad m−2, meaning that all polarised sources will appear point-like in Faraday space (e.g., Van Eck et al. Reference Van Eck2017). However, from Equation (4c), our use of the native 40 kHz GLEAM channel resolution retains sensitivity to very large RMs, up to ![]() $\sim$1100 rad m−2. For our full POGS sample, we explored Faraday rotations
$\sim$1100 rad m−2. For our full POGS sample, we explored Faraday rotations ![]() $|{\rm{RM}}| \leq 1000 $ rad m−2. We do not anticipate significant bias due to this limit, as typically
$|{\rm{RM}}| \leq 1000 $ rad m−2. We do not anticipate significant bias due to this limit, as typically ![]() $|{\rm{RM}}| \ll 200$ rad m−2 away from the Galactic plane (e.g., Taylor et al. Reference Taylor2009; Schnitzeler Reference Schnitzeler2010). Additionally, no sources in the NVSS RM catalogue have
$|{\rm{RM}}| \ll 200$ rad m−2 away from the Galactic plane (e.g., Taylor et al. Reference Taylor2009; Schnitzeler Reference Schnitzeler2010). Additionally, no sources in the NVSS RM catalogue have ![]() $| {\rm{RM}} | \gtrsim760$ rad m−2 (Taylor et al. Reference Taylor2009). Finally, given our long observing wavelength, we also expect complete depolarisation for sources that exhibit variation in RM (i.e.,
$| {\rm{RM}} | \gtrsim760$ rad m−2 (Taylor et al. Reference Taylor2009). Finally, given our long observing wavelength, we also expect complete depolarisation for sources that exhibit variation in RM (i.e., ![]() $\sigma_{\rm{RM}}$) at levels much lower than our maximum scale.
$\sigma_{\rm{RM}}$) at levels much lower than our maximum scale.
We note that, at the time of data processing, cuFFS cannot perform deconvolution of the RM spread function (RMSF; analogous to the PSF in aperture synthesis). This technique is better known as ‘RM-clean’ (e.g., Heald 2009). There are two principal areas of improvement that RM-clean can provide: first, in recovering structures that are extended in Faraday space (‘Faraday-thick’), and second, in providing improved precision in the recovered RMs.
Simulations by Van Eck et al. (Reference Van Eck2018) have demonstrated that low-frequency observations can recover Faraday-thick structures, but that they (i) are heavily depolarised, with ![]() $\sim$90% of the input flux density unrecovered and (ii) appear as Faraday-thin ‘skins’ on the outer edges of the Faraday-thick structure. Likewise, the dominant contribution to the uncertainty in our RM precision arises not as a result of our RMSF width, but from the precision of the ionospheric RM correction (Sotomayor-Beltran et al. Reference Sotomayor-Beltran2013). Given the relatively shallow depth of our survey and our insensitivity to Faraday-thick structures, and that RM-clean will not provide significant improvement in our RM precision, plus the significant residual leakage in our RM spectra, we opted not to perform RM-clean and instead solely performed RM synthesis.
$\sim$90% of the input flux density unrecovered and (ii) appear as Faraday-thin ‘skins’ on the outer edges of the Faraday-thick structure. Likewise, the dominant contribution to the uncertainty in our RM precision arises not as a result of our RMSF width, but from the precision of the ionospheric RM correction (Sotomayor-Beltran et al. Reference Sotomayor-Beltran2013). Given the relatively shallow depth of our survey and our insensitivity to Faraday-thick structures, and that RM-clean will not provide significant improvement in our RM precision, plus the significant residual leakage in our RM spectra, we opted not to perform RM-clean and instead solely performed RM synthesis.
3. Source identification and verification
3.1. Noise characterisation
As discussed in Section 3 of Reference PurcellPaper I, we opted to perform source finding directly on our ![]() $P({\rm{RM}})$-cubes. For each epoch, we characterised the noise following the method described by Van Eck et al. (Reference Van Eck2018). In short, we fitted a Rayleigh distribution to the histogram of
$P({\rm{RM}})$-cubes. For each epoch, we characterised the noise following the method described by Van Eck et al. (Reference Van Eck2018). In short, we fitted a Rayleigh distribution to the histogram of ![]() $P({\rm{RM}})$ along each pixel, excluding the range
$P({\rm{RM}})$ along each pixel, excluding the range ![]() $|{\rm{RM}}|\leq 20$ rad m−2, as this contained the majority of both residual instrumental leakage as well as residual Galactic foreground contamination.
$|{\rm{RM}}|\leq 20$ rad m−2, as this contained the majority of both residual instrumental leakage as well as residual Galactic foreground contamination.
We measure a typical noise of ![]() $\sim$1–2 mJy beam−1 RMSF−1 near zenith (the declination
$\sim$1–2 mJy beam−1 RMSF−1 near zenith (the declination ![]() $-27^\circ$ strip). There is noticeable reduction in sensitivity far from zenith: for example, we measured a typical noise of
$-27^\circ$ strip). There is noticeable reduction in sensitivity far from zenith: for example, we measured a typical noise of ![]() $\sim$4–8 mJy beam−1 RMSF−1 for the Declination
$\sim$4–8 mJy beam−1 RMSF−1 for the Declination ![]() $-72^\circ$ and
$-72^\circ$ and ![]() $+18^\circ$ strips, as these pointings lie at
$+18^\circ$ strips, as these pointings lie at ![]() ${\sim}45^\circ$ elevation for the MWA.
${\sim}45^\circ$ elevation for the MWA.
3.2. Source finding
While the Phase I MWA is limited by confusion noise in Stokes I at the depth reached by GLEAM, the surface density of polarised sources is significantly lower, meaning our image cubes are limited by thermal noise. However, due to a lack of 3D source-finding algorithms in the literature, combined with the non-Gaussian nature of polarisation image noise, we opted to perform ‘priorised’ source finding, that is, source finding at the location of known Stokes I sources. In order to strike a balance between probing the faint source population and selecting reliable sources, we took GLEAM sources with a 200 MHz Stokes I flux density in excess of 90 mJy. For discussion regarding polarisation source finding, we refer the reader to Farnes et al. (Reference Farnes2018).
The source-finding process used in POGS (as per Section 3.1 of Reference PurcellPaper I) closely follows that described by Van Eck et al. (Reference Van Eck2018). Regions were extracted centred on the location of known Stokes I sources. The RM spectrum of pixels within the source full width at half maximum (‘on-source’) was then searched for peaks by identifying local maxima. A peak was considered a ‘candidate’ if it fulfilled three criteria.
A peak must be in excess of
 $7{\sigma_{\rm{P}}}$, where
$7{\sigma_{\rm{P}}}$, where  ${\sigma_{\rm{P}}}$ is the local noise derived in the previous section.
${\sigma_{\rm{P}}}$ is the local noise derived in the previous section.A peak must have a flux density greater than the sum of the off-source foreground plus
 $2{\sigma_{\rm{P}}}$. This off-source foreground is taken as the maximum value of the RM spectrum of pixels below the 1 per cent level of the PSF, centred on the source peak.
$2{\sigma_{\rm{P}}}$. This off-source foreground is taken as the maximum value of the RM spectrum of pixels below the 1 per cent level of the PSF, centred on the source peak.A peak must appear outside the instrumental leakage region. This exclusion zone was centred on
 ${\rm{RM}}=0$ rad m−2, with upper and lower limits defined by the absolute maximum value of the ionospheric RM for that observing epoch.
${\rm{RM}}=0$ rad m−2, with upper and lower limits defined by the absolute maximum value of the ionospheric RM for that observing epoch.
The enforcement of this third criterion means that we are likely excluding some real polarised sources with low RM. From the NVSS RM catalogue of Taylor et al. (Reference Taylor2009), about 11% of sources have RMs that would be excluded by this criterion. However, this was a necessary step, given our current inability to fully mitigate instrumental leakage. Future improvements in the MWA beam model may help reduce leakage and allow us to probe this low-RM regime further; however, such efforts are beyond the scope of this paper.
Two separate targeted searches were performed. Our primary science goal with POGS was to characterise the low-frequency linearly polarised extragalactic source population, so the GLEAM Extragalactic Catalogue was used (Hurley-Walker et al. Reference Hurley-Walker2017). As discussed by those authors (Table 1 of Hurley-Walker et al. Reference Hurley-Walker2017), a handful of sky regions were excluded from the GLEAM catalogue due to data processing issues. The largest region outside the Galactic plane covered 859 square degrees in the region ![]() $0^{\circ} < {\rm{Declination}} < +30^{\circ}$ and
$0^{\circ} < {\rm{Declination}} < +30^{\circ}$ and ![]() $22^{\rm{h}} < \text{Right Ascension} < 0^{\rm{h}}$. From visual inspection, we found a handful of polarised sources in this region; a more robust search was performed using the catalogue from the First Alternative Data Release from the Tata Institute of Fundamental Research-Giant Metrewave Radio Telescope Sky Survey (TGSS-ADR1; Intema et al. Reference Intema, Jagannathan, Mooley and Frail2017). A second targeted search was performed across the entire sky, South of Declination
$22^{\rm{h}} < \text{Right Ascension} < 0^{\rm{h}}$. From visual inspection, we found a handful of polarised sources in this region; a more robust search was performed using the catalogue from the First Alternative Data Release from the Tata Institute of Fundamental Research-Giant Metrewave Radio Telescope Sky Survey (TGSS-ADR1; Intema et al. Reference Intema, Jagannathan, Mooley and Frail2017). A second targeted search was performed across the entire sky, South of Declination ![]() $+30^\circ$ using the Australia Telescope National Facility (ATNF) Pulsar Catalogue (Manchester et al. Reference Manchester, Hobbs, Teoh and Hobbs2005) v1.59 to hunt for known pulsars.
$+30^\circ$ using the Australia Telescope National Facility (ATNF) Pulsar Catalogue (Manchester et al. Reference Manchester, Hobbs, Teoh and Hobbs2005) v1.59 to hunt for known pulsars.
Table 1. List of columns in POGS ExGal and POGS PsrCat that are fixed for all sources

a The rms noise was not measured on a per-channel basis, but from our RM cube, as discussed in the text.b This will be changed to the bibcode of this paper after publication.c This column is intended to provide a link between the catalogue and the paper describing the origin survey.
3.3. Candidate evaluation
As per Section 3.2 of Reference PurcellPaper I, for each candidate source identified by our routine, we fitted a 3D Gaussian (Right Ascension/Declination/RM) using a nine-parameter model, chosen to match the expected form of a source that is unresolved in both image space (as any extended polarised emission from an extragalactic source will tend to rapidly depolarise at our ![]() $3^{\prime}$–
$3^{\prime}$–![]() $7^{\prime}$ resolution) and Faraday space (as Equations (4a) and (4b) suggest that any sources detected by the MWA will appear point-like). The nine parameters were
$7^{\prime}$ resolution) and Faraday space (as Equations (4a) and (4b) suggest that any sources detected by the MWA will appear point-like). The nine parameters were
broadband peak polarised intensity (P);
background polarised intensity (C);
image-plane centroids in pixel coordinates (X,Y);
image-plane semi-major
 $(\sigma_{\rm{maj}})$ and semi-minor
$(\sigma_{\rm{maj}})$ and semi-minor  $(\sigma_{\rm{min}})$ axes, measured as Gaussian
$(\sigma_{\rm{min}})$ axes, measured as Gaussian  $\sigma$;
$\sigma$;image-plane position angle (PA);
RM centroid
 $({\rm{RM}})$;
$({\rm{RM}})$;RM width
 $(\sigma_{{\rm{RM}}})$, measured as Gaussian
$(\sigma_{{\rm{RM}}})$, measured as Gaussian  $\sigma$.
$\sigma$.
Note that the ‘background polarised intensity’ is not the same as the foreground discussed in the previous section, but rather the ‘zero level’ of the 3D Gaussian fitted to a candidate. We optimised our model using the scipy ‘curve-fit’ algorithm, employing a Levenberg–Marquardt solver, with initial parameter estimates defined by the initial peak identification. Our candidate list contained a large number of sources that were clearly identified (by visual inspection) as sidelobes of the main instrumental leakage peak, rather than any astrophysical polarised signal. These were frequently poorly constrained or failed to fit and were eliminated from our catalogue.
To quantify the uncertainties on our fitted model, as described in Section 3.3 of Reference PurcellPaper I, we followed the method described by Van Eck et al. (Reference Van Eck2018). We established a Monte–Carlo (MC) simulation, performing 1 000 realisations of noise, adding the best-fit candidate source model, and re-fitting our nine-parameter model. The standard deviation of the fit results was then used to estimate the uncertainty. Note that the theoretical uncertainty on the measured RM of a source is inversely proportional to the SNR of the detection (e.g., Brentjens & de Bruyn Reference Brentjens and de Bruyn2005) according to
We found that our MC uncertainties are comparable to the theoretical uncertainty for candidates with high SNR (consistent with previous findings by, e.g., George, Stil, & Keller Reference George, Stil and Keller2012). For candidates with lower SNR ![]() $({\lesssim}20)$, the MC uncertainties are typically 30–50% larger than predicted by Equation (5).
$({\lesssim}20)$, the MC uncertainties are typically 30–50% larger than predicted by Equation (5).
Of all candidates that were successfully fitted, we then rejected any with fitted sizes more than ![]() $2\times$ the extent of the PSF or RMSF. Our motivation behind this filtering was twofold: first, given the low-frequency nature of our observations, we are only sensitive to Faraday-thin sources (as indicated by Equations (4b) and (4c)). Second, due to our moderate resolution with the Phase I MWA, any extended extragalactic polarised sources would likely exhibit RM variance within the PSF (whether due to intrinsic or foreground variation) and rapidly depolarise. As a result of this filtering, plus rejecting fits with poorly constrained parameters, some
$2\times$ the extent of the PSF or RMSF. Our motivation behind this filtering was twofold: first, given the low-frequency nature of our observations, we are only sensitive to Faraday-thin sources (as indicated by Equations (4b) and (4c)). Second, due to our moderate resolution with the Phase I MWA, any extended extragalactic polarised sources would likely exhibit RM variance within the PSF (whether due to intrinsic or foreground variation) and rapidly depolarise. As a result of this filtering, plus rejecting fits with poorly constrained parameters, some ![]() ${\sim}35\%$ of candidates were rejected.
${\sim}35\%$ of candidates were rejected.
Note that we did not enforce a criterion that the polarised peak must be coincident with the Stokes I peak. Many single sources that appear compact in Stokes I become resolved into multiple components at higher resolution, and it was frequently the case that a polarised source offset from the GLEAM Stokes I peak was in fact associated with one of these components.
As a final verification step, each fitted candidate was visually inspected in both total intensity and polarisation, with the associated RM spectrum and fitted peak identification. This step was necessary to remove many spurious candidates and chance alignments with sparsely sampled patches of diffuse Galactic polarised emission. All candidates that conformed to these criteria and passed our tests were considered real, and are henceforth referred to as ‘sources’. This comprised some ![]() ${\sim}5\%$ of initial identifications.
${\sim}5\%$ of initial identifications.
3.4. Final measurements
There is significant overlap between differing epochs of the same Declination strip (some ![]() $\sim$2–4 h in Right Ascension) as well as overlap between different Declination strip observations of the same hour angle range. As such, a total of 63 sources among our GLEAM-selected population were detected in more than one epoch. For all such sources, the final flux density and RM were determined using the mean of all detections. In all cases of multiple detections, the peak RMs were found to be consistent (to within the
$\sim$2–4 h in Right Ascension) as well as overlap between different Declination strip observations of the same hour angle range. As such, a total of 63 sources among our GLEAM-selected population were detected in more than one epoch. For all such sources, the final flux density and RM were determined using the mean of all detections. In all cases of multiple detections, the peak RMs were found to be consistent (to within the ![]() $1\sigma$ uncertainties) between epochs. However, we note some variation, up to around
$1\sigma$ uncertainties) between epochs. However, we note some variation, up to around ![]() ${\sim}30\%$, in the measured peak polarised flux density between epochs.
${\sim}30\%$, in the measured peak polarised flux density between epochs.
We believe that this variation may be tied to some second-order ionospheric effect that is not yet accurately quantifiable or correctable (private communication Cameron Van Eck & the LOFAR Magnetism Key Science Project). Investigating the cause of this effect is beyond the scope of this work. Under the assumption that the measured background is largely dominated by noise, we determined final polarised flux density measurements for each source through the quadrature subtraction of the noise from the fitted flux density (e.g., George et al. Reference George, Stil and Keller2012). As a final step, we manually compared our nominally extragalactic catalogue with our pulsar catalogue to remove duplicate detections.
4. Results
In total, we detect 517 linearly polarised radio sources: 33 of these are known pulsars, and the remaining 484 are assumed to be extragalactic in origin. We thus present two catalogues from this work: POGS ExGal (containing our detected extragalactic radio sources) and POGS PsrCat (containing the known pulsars we have detected).
4.1. Extragalactic radio sources
We have attempted to make each catalogue ‘value-added’ by including a number of cross-identifications that the end user may find helpful, and we have also ensured that our catalogue is compliant with the ongoing community effort to standardise reporting of polarisation catalogue data.Footnote a To that end, POGS ExGal contains the following columns:
POGS ID;
Right Ascension (J2000) (degrees);
Declination (J2000) (degrees)
Galactic Longitude (degrees);
Galactic Latitude (degrees);
Position uncertainty (degrees);
200 MHz RM and uncertainty (rad m−2);
Faraday complexity flag (
 $\ast$);
$\ast$);Faraday complexity identification method (
 $\ast$);
$\ast$);RM determination method (
 $\ast$);
$\ast$);Ionospheric RM correction method (
 $\ast$);
$\ast$);Number of RM components (
 $\ast$);
$\ast$);200 MHz Stokes I flux density and uncertainty (Jy);
Spectral index and uncertainty (see below);
Stokes I reference frequency (
 $\ast$);
$\ast$);200 MHz linear polarisation flux density and uncertainty (Jy);
Polarisation bias correction method (
 $\ast$);
$\ast$);Polarised flux density type (
 $\ast$);
$\ast$);Fractional polarisation and uncertainty;
Linear polarisation reference frequency (
 $\ast$);
$\ast$);Beam major axis, minor axis, and PA (degrees);
Beam reference frequency (
 $\ast$);
$\ast$);Minimum and maximum frequency (Hz) (
 $\ast$);
$\ast$);Channel width (Hz) (
 $\ast$);
$\ast$);Number of channels;
Channel noise (
 $\ast$);
$\ast$);Telescope used (
 $\ast$);
$\ast$);Polarisation catalogue reference (
 $\ast$);
$\ast$);Stokes I catalogue reference;
Stokes I catalogue ID;
GLEAM 4 Jy sample ID;
Morphological classification (see below);
Stokes I local rms (Jy beam−1);
Linear polarisation local rms (Jy beam−1);
NVSS RM catalogue counterpart;
1.4 GHz NVSS RM and uncertainty (rad m−2);
S band Polarisation All Sky Survey (S-PASS)/Australia Telescope Compact Array (ATCA) RM catalogue counterpart;
2.2 GHz S-PASS/ATCA RM and uncertainty (rad m−2);
Host Flag (see below);
Host ID (see below);
Host Redshift (see below);
Galactic Foreground RM and uncertainty (rad m−2);
where all columns listed above that are marked with ![]() $\ast$ have identical values for all sources. These are given in Table 1.
$\ast$ have identical values for all sources. These are given in Table 1.
For 465 sources in POGS ExGal, we use the spectral index and fitted 200 MHz Stokes I flux density (with their uncertainties) from the GLEAM Extragalactic Catalogue (respectively, ‘alpha’ and ‘int_flux_fit_200’; Hurley-Walker et al. Reference Hurley-Walker2017). However, 12 POGS ExGal sources have fitted Stokes I flux densities with significant fractional uncertainty (50% or greater). Additionally, six sources in POGS ExGal lay in one of the gaps in the GLEAM catalogue (Figure 11 and Table 3 of Hurley-Walker et al. Reference Hurley-Walker2017). These were identified using the 150 MHz TGSS-ADR1 catalogue as location prior and thus do not have measured 200 MHz Stokes I flux densities.
For these 18 sources, we estimated a 200 MHz flux density using a power-law spectral energy distribution (SED) fit to flux density measurements from the literature. We selected those GLEAM measurements from Hurley-Walker et al. (Reference Hurley-Walker2017) that were reliably constrained, plus data from the following surveys, where available:
74 MHz VLA Low-Frequency Sky Survey redux (VLSSr; Lane et al. Reference Lane, Cotton, van Velzen, Clarke, Kassim, Helmboldt, Lazio and Cohen2014);
150 MHz TGSS-ADR1 (Intema et al. Reference Intema, Jagannathan, Mooley and Frail2017);
365 MHz Texas Radio Survey (TXS; Douglas et al. Reference Douglas, Bash, Bozyan, Torrence and Wolfe1996);
408 MHz Molonglo Reference Catalogue (MRC; Large et al. Reference Large, Mills, Little, Crawford and Sutton1981);
1.4 GHz NVSS (Condon et al. Reference Condon, Cotton, Greisen, Yin, Perley, Taylor and Broderick1998);
4.85 GHz Green Bank 6cm survey (GB6; Gregory et al. Reference Gregory, Scott, Douglas and Condon1996).
The resulting SED fits for the 12 GLEAM sources and six TGSS-ADR1 sources are, respectively, shown in Figures A.1 and A.2.
4.1.1. Host identification
Host identification was performed using the same method as for the GLEAM 4-Jy (G4Jy) Sample (see White et al. Reference White2018, Reference White2020a, Reference White2020b). For each source, we created an overlay with GLEAM and higher resolution survey data (specifically, the TGSS-ADR1, Sydney University Molonglo Sky Survey (SUMSS), and NVSS where available) superimposed on Widefield Infrared Survey Explorer (WISE; Wright et al. Reference Wright2010) mid-infrared images. These were visually inspected, attempting to associate the radio emission to a core galaxy. Once a core was identified, we inspected a WISE Band 1 (![]() $3.4\,\upmu$m) cutout at that location and selected the most likely host, where one could be identified. The overwhelming majority of identified hosts had entries in the AllWISE catalogue (Cutri et al. Reference Cutri2013); a handful had clear hosts not catalogued in AllWISE; in these instances, we used entries from the WISE catalogue. It is noted in POGS ExGal when this is the case. With the ‘Host Flag’ column, we thus adopt the same formalism as for the G4Jy catalogue, where
$3.4\,\upmu$m) cutout at that location and selected the most likely host, where one could be identified. The overwhelming majority of identified hosts had entries in the AllWISE catalogue (Cutri et al. Reference Cutri2013); a handful had clear hosts not catalogued in AllWISE; in these instances, we used entries from the WISE catalogue. It is noted in POGS ExGal when this is the case. With the ‘Host Flag’ column, we thus adopt the same formalism as for the G4Jy catalogue, where
‘i’: sources which have a clearly identified WISE/AllWISE catalogue entry.
‘u’: sources which do not have a clear WISE/AllWISE catalogue entry, either due to the complexity of the Stokes I radio emission or the distribution of nearby WISE/AllWISE sources.
‘m’: sources for which a host galaxy cannot be identified, either due to being too faint to identify in the AllWISE survey, or due to contamination by nearby, bright mid-infrared sources.
The WISE catalogue position was then cross-referenced with other surveys to determine a redshift, where possible. We used the following catalogues: the Million Quasars Catalogue v6.3 (Milliquas; Flesch Reference Flesch2015), the 6dF Galaxy Survey Redshift Catalogue Data Release 3 (6dF; Jones et al. Reference Jones2009), the Sloan Digital Sky Survey Photometric Catalogue, Release 12 (SDSS DR12; Alam et al. Reference Alam2015) and a number of other specific studies (Simpson et al. Reference Simpson, Clements, Rawlings and Ward1993; Ellison et al. Reference Ellison, York, Pettini and Kanekar2008; Khabibullina & Verkhodanov Reference Khabibullina and Verkhodanov2009).
4.1.2. Morphological classification
For the morphological classification, we again adopt the same formalism as for the G4Jy Sample. We used the same overlays described above to classify our sources according to the following:
‘single’: sources which have simple (typically compact) morphologies in higher-resolution data (TGSS-ADR1/SUMSS/NVSS);
‘double’: sources which have two lobe-like components identified in higher-resolution data (TGSS-ADR1/SUMSS/NVSS) or show elongated structure (suggesting multiple components) but a single catalogued entry in the TGSS-ADR1/SUMSS/NVSS catalogues;
‘triple’: sources which have two clear lobes in higher-resolution surveys, as well as a clear detection of a core in the same survey;
‘complex’: sources which do not clearly fit into any of the above categories.
Finally, the Galactic foreground RM and uncertainty are measured from the all-sky Galactic RM reconstruction of Oppermann et al. (Reference Oppermann2015) at the location of each POGS ExGal source.
4.2. Known pulsars
As with POGS ExGal, we have attempted to add value to POGS PsrCat by including properties from other catalogues that the user may find useful. As such, POGS PsrCat contains the following columns:
POGS ID;
Right Ascension (J2000) (degrees);
Declination (J2000) (degrees);
Galactic Longitude (degrees);
Galactic Latitude (degrees);
Position uncertainty (degrees);
200 MHz RM and uncertainty (rad m−2);
Faraday complexity flag (
 $\ast$);
$\ast$);Faraday complexity identification method (
 $\ast$);
$\ast$);RM determination method (
 $\ast$);
$\ast$);Ionospheric RM correction method (
 $\ast$);
$\ast$);Number of RM components (
 $\ast$);
$\ast$);200 MHz Stokes I flux density and uncertainty (Jy);
Spectral index and uncertainty (see below);
Stokes I reference frequency (
 $\ast$);
$\ast$);200 MHz linear polarisation flux density and uncertainty (Jy);
Polarisation bias correction method (
 $\ast$);
$\ast$);Polarised flux density type (
 $\ast$);
$\ast$);Fractional polarisation and uncertainty;
Linear polarisation reference frequency (
 $\ast$);
$\ast$);Beam major axis, minor axis, and PA (degrees);
Beam reference frequency (
 $\ast$);
$\ast$);Minimum and maximum frequency (Hz) (
 $\ast$);
$\ast$);Channel width (Hz) (
 $\ast$);
$\ast$);Number of channels;
Channel noise (
 $\ast$);
$\ast$);Telescope used (
 $\ast$);
$\ast$);Polarisation catalogue reference (
 $\ast$);
$\ast$);Stokes I catalogue reference;
Pulsar catalogue ID;
Notes;
Number of spectral index components (see below);
Spin period (s);
Dispersion measure (DM) (pc cm−3);
Catalogue reference RM (rad m−3);
where all columns listed above that are marked with ![]() $\ast$ have identical values for all sources. These are given in Table 1. The ‘Notes’ column contains additional information, provided as comma-separated-variable (csv) text. This includes whether a pulsar is a known millisecond pulsar (MSP) according to the literature.
$\ast$ have identical values for all sources. These are given in Table 1. The ‘Notes’ column contains additional information, provided as comma-separated-variable (csv) text. This includes whether a pulsar is a known millisecond pulsar (MSP) according to the literature.
A number of columns in POGS PsrCat are sourced from the GLEAM Pulsar Catalogue (Murphy et al. Reference Murphy2017). These are (i) Stokes I flux density measurements at 200 MHz, (ii) spectral index (plus the associated uncertainties), and (iii) number of spectral index components. Of the 60 known pulsars detected by Murphy et al. (Reference Murphy2017), we detect 21 in polarisation. We also note one pulsar, PSR J1747-4036, that was undetected by Murphy et al. (Reference Murphy2017), but has a compact radio source within 30 arcsec that was detected in the ‘GLEAM-II: Galactic Plane’ reprocessing by Hurley-Walker et al. (Reference Hurley-Walker2019). This source is GLEAM J174749-403650, and we suggest that it is PSR J1747-4036. There are a further 11 pulsars in POGS PsrCat that do not have 200 MHz Stokes I flux density measurements, due to their absence from the GLEAM Pulsar Catalogue or GLEAM Galactic Plane Catalogue. We also note that the spectral index fitted by Murphy et al. (Reference Murphy2017) was derived using a single-component power-law fit or a two-component broken power-law fit to the available data, and as such does not always span the same frequency range. Where a pulsar has a broken power-law fit, we quote the spectral index value for the ‘side’ of the break on which our observing frequency range lies.
The remainder of this paper is devoted to the discussion of the properties of sources in POGS ExGal (Section 5) and POGS PsrCat (Section 6). In the appropriate sections of this paper, we present an excerpt from POGS ExGal and the full POGS PsrCat. Unless otherwise stated, all properties are reported at our central frequency of 200 MHz. All unfilled text entries (e.g., where a POGS source does not have a counterpart in the NVSS RM catalogue) are marked with a ‘-’; all unfilled numerical entries (e.g., the 1.4 GHz RM for a POGS source does not have an NVSS RM catalogue counterpart) list a ‘ NaN’. However, for display purposes in this manuscript, all such entries list a ‘-’. Both catalogues will be made available (in the accompanying online material and through Vizier) upon publication of this manuscript.
5. Extragalactic radio sources
As a brief overview, POGS ExGal contains 484 sources with linearly polarised flux densities between 9.9 mJy and 1.1 Jy. Our sources have RMs between ![]() $-328.07$ rad m−2 and
$-328.07$ rad m−2 and ![]() $+279.62$ rad m−2, with a noticeable dearth of sources at
$+279.62$ rad m−2, with a noticeable dearth of sources at ![]() $|{\rm{RM}}|\lesssim6$ rad m−2. The mean uncertainty is
$|{\rm{RM}}|\lesssim6$ rad m−2. The mean uncertainty is ![]() $0.38$ rad m−2; with a worst-case uncertainty of
$0.38$ rad m−2; with a worst-case uncertainty of ![]() $10.65$ rad m−2. We find a total of 80 sources in common with the G4Jy Sample. An excerpt from POGS ExGal is presented in Table 2.
$10.65$ rad m−2. We find a total of 80 sources in common with the G4Jy Sample. An excerpt from POGS ExGal is presented in Table 2.
Table 2. Sample rows from POGS ExGal, showing only columns that vary by source. Note that, for display purposes, unfilled entries are marked with a ‘ −’

BPA: beam position angle; RA: Right Ascension.
We detect a total of ten ‘polarised doubles’, by which we mean a pair of physically associated polarised sources, in our catalogue. These are discussed later in Section 5.2 and presented in Figures 5 and B.1. We present the RM spectra of the remaining 464 POGS ExGal sources in Appendix D, Figure D.1.
5.1. Surface distribution
The total sky area covered by POGS ExGal is 25 489 square degrees. Hence, our average surface density is 0.019 per square degree, or one polarised extragalactic radio source per 53 square degrees. This represents a 60% improvement on the source numbers predicted in Reference PurcellPaper I, and a factor ![]() ${\sim}2$ improvement compared to predictions by other MWA polarisation studies (Lenc et al. Reference Lenc2017).
${\sim}2$ improvement compared to predictions by other MWA polarisation studies (Lenc et al. Reference Lenc2017).
We present the sky distribution for POGS ExGal (circles) and POGS PsrCat (squares) in Figure 1, overlaid on different maps of the radio sky (the Galactic foreground RM map of Oppermann et al. Reference Oppermann2015 and the all-sky 408 MHz map of Haslam et al. Reference Haslam, Salter, Stoffel and Wilson1982). A number of trends are evident in the distribution of sources. First, there is noticeable decrease in the density of detections towards higher Declinations, with few sources detected at ![]() ${\rm{Declination}}\gtrsim+15^\circ$. We notice a similar trend towards the south celestial pole, although it is less pronounced. This can be attributed to the reduced sensitivity of the MWA far from zenith, as these pointings were observed at
${\rm{Declination}}\gtrsim+15^\circ$. We notice a similar trend towards the south celestial pole, although it is less pronounced. This can be attributed to the reduced sensitivity of the MWA far from zenith, as these pointings were observed at ![]() ${\sim}44^\circ$ elevation—the typical polarised flux density of sources detected in these regions of sky (median
${\sim}44^\circ$ elevation—the typical polarised flux density of sources detected in these regions of sky (median ![]() $P\sim53\,$mJy) is about a factor two higher than that measured at higher elevations (median
$P\sim53\,$mJy) is about a factor two higher than that measured at higher elevations (median ![]() $P\sim29\,$mJy). Second, away from these low-elevation regions, the distribution of sources appears to be non-uniform. We note a particular clustering of ExGal sources in the region of
$P\sim29\,$mJy). Second, away from these low-elevation regions, the distribution of sources appears to be non-uniform. We note a particular clustering of ExGal sources in the region of ![]() $(l,b)\sim(230^\circ,-20^\circ)$, whereas to the Galactic South-West of this region, there is a noticeable dearth of sources around
$(l,b)\sim(230^\circ,-20^\circ)$, whereas to the Galactic South-West of this region, there is a noticeable dearth of sources around ![]() $(l,b)\sim(260^\circ,-35^\circ)$. Two questions arise: first, are these features significant, and if so, what is their physical origin?
$(l,b)\sim(260^\circ,-35^\circ)$. Two questions arise: first, are these features significant, and if so, what is their physical origin?

Figure 1. Sky surface distribution of sources in POGS ExGal (circles) and POGS PsrCat (squares), shown in Galactic coordinates, colourised according to the sign and magnitude of RM as indicated by the colourbar in the upper panel. The background colourscale shows the Galactic RM from Oppermann et al. (Reference Oppermann2015) saturating at ![]() $|{\rm{RM}}|=200$ rad m−2 (top panel) and the 408 MHz Galactic synchrotron emission from Haslam et al. (Reference Haslam, Salter, Stoffel and Wilson1982) (bottom panel). The solid lines denote the upper and lower Declination limits of our survey coverage (
$|{\rm{RM}}|=200$ rad m−2 (top panel) and the 408 MHz Galactic synchrotron emission from Haslam et al. (Reference Haslam, Salter, Stoffel and Wilson1982) (bottom panel). The solid lines denote the upper and lower Declination limits of our survey coverage (![]() $+30^\circ$ and
$+30^\circ$ and ![]() $-82^\circ$, respectively); dashed black lines denote gaps in the GLEAM coverage, where source finding was performed using the TGSS-ADR1 catalogue. Red dashed lines denote the Galactic plane region excluded from the GLEAM Extragalactic Catalogue (
$-82^\circ$, respectively); dashed black lines denote gaps in the GLEAM coverage, where source finding was performed using the TGSS-ADR1 catalogue. Red dashed lines denote the Galactic plane region excluded from the GLEAM Extragalactic Catalogue (![]() $|b| < 10^\circ$; Hurley-Walker et al. Reference Hurley-Walker2017).
$|b| < 10^\circ$; Hurley-Walker et al. Reference Hurley-Walker2017).
5.1.1. Clustering significance
To quantify the significance of these over- and under-density regions, we divided the sky into a set of tiles using Hierarchical Equal Area isoLatitude Pixelisation (HEALPix; Górski et al. Reference Górski, Hivon and Banday2005) with NSIDE![]() $=4$. This yields 192 tiles of approximately 214 square degrees covering the entire sky; the surface density is then simply given by the number of sources within a given tile. The surface density of sources is shown in Figure 2.
$=4$. This yields 192 tiles of approximately 214 square degrees covering the entire sky; the surface density is then simply given by the number of sources within a given tile. The surface density of sources is shown in Figure 2.

Figure 2. Surface density of POGS ExGal sources (black circles) derived using a HEALPix Mollweide projection in Galactic coordinates (top panel) and Equatorial J2000 coordinates (bottom panel) with NSIDE ![]() $=4$. Dashed and solid curves denote exclusion regions as per Figure 1.
$=4$. Dashed and solid curves denote exclusion regions as per Figure 1.
From Figure 2, the surface density appears to vary substantially from tile to tile, supporting the suggestion that our sources are not uniformly distributed across the sky. Note that, as suggested by Figure 2, this appears to be irrespective of coordinate projection, suggesting the distribution is not a related to decreases in instrumental sensitivity away from zenith. From inspection of our rms noise maps, we can also discount the idea that this clustering is simply the result of local noise variations.
We then estimated the median surface density exclusively using those tiles whose central coordinates lay outside the exclusion zones shown in Figures 1 and 2, leading us to discard those tiles at ![]() ${\rm{Declination}}\geq+30^\circ$ and
${\rm{Declination}}\geq+30^\circ$ and ![]() $|b|\leq10^\circ$. We find the resulting median density is 0.014 deg−2, with a standard deviation of 0.016 deg−2. The apparent under-dense region around
$|b|\leq10^\circ$. We find the resulting median density is 0.014 deg−2, with a standard deviation of 0.016 deg−2. The apparent under-dense region around ![]() $(l,b)\sim(260^\circ,-35^\circ)$ has a typical density of 0.0047 deg−2 which, while much lower than the median, is not significant. This is also visible in Figure 2, where many tiles exhibit a similar density.
$(l,b)\sim(260^\circ,-35^\circ)$ has a typical density of 0.0047 deg−2 which, while much lower than the median, is not significant. This is also visible in Figure 2, where many tiles exhibit a similar density.
The ‘cluster’ of sources visually identified in Figure 1 around ![]() $(l,b)\sim(230^\circ,-20^\circ)$ lies within a tile where the source density is 0.05 deg−2. Some
$(l,b)\sim(230^\circ,-20^\circ)$ lies within a tile where the source density is 0.05 deg−2. Some ![]() $5.4\%$ of tiles have a surface density equal to or greater than this, so we do not consider this clustering particularly significant. Only two tiles (out of 112 that do not lie within the ‘exclusion zones’ defined in Figure 2) show a surface density in excess of
$5.4\%$ of tiles have a surface density equal to or greater than this, so we do not consider this clustering particularly significant. Only two tiles (out of 112 that do not lie within the ‘exclusion zones’ defined in Figure 2) show a surface density in excess of ![]() $3\sigma$. These are the tile centred on
$3\sigma$. These are the tile centred on ![]() $(l,b) = (230^\circ,-30^\circ)$, where the surface density is 0.079 deg−2 (a
$(l,b) = (230^\circ,-30^\circ)$, where the surface density is 0.079 deg−2 (a ![]() $4\sigma$ outlier) and the tile centred on
$4\sigma$ outlier) and the tile centred on ![]() $(l,b) = (45^\circ, -78^\circ)$, which has a surface density of 0.070 deg−2
$(l,b) = (45^\circ, -78^\circ)$, which has a surface density of 0.070 deg−2![]() $(\sim3.5\sigma)$. However, this is still only
$(\sim3.5\sigma)$. However, this is still only ![]() ${\sim}2\%$ of tiles in Figure 2, so we cannot conclusively discount that this is simply random chance.
${\sim}2\%$ of tiles in Figure 2, so we cannot conclusively discount that this is simply random chance.
5.1.2. Large-RM sources
A total of 14 sources in our catalogue have large RM values, defined as ![]() $|{\rm{RM}}| > 100$ rad m−2. We summarise the Galactic coordinates, RMs, and associations of these sources in Table 3. Two of these, GLEAM J161719-100227 and GLEAM J163927-124141, lie along the LOS through the nearby H ii region, Sharpless 2-27. Sources along the LOS through this H ii region are known to have significant RM enhancement (e.g., Harvey-Smith, Madsen, & Gaensler Reference Harvey-Smith, Madsen and Gaensler2011).
$|{\rm{RM}}| > 100$ rad m−2. We summarise the Galactic coordinates, RMs, and associations of these sources in Table 3. Two of these, GLEAM J161719-100227 and GLEAM J163927-124141, lie along the LOS through the nearby H ii region, Sharpless 2-27. Sources along the LOS through this H ii region are known to have significant RM enhancement (e.g., Harvey-Smith, Madsen, & Gaensler Reference Harvey-Smith, Madsen and Gaensler2011).
Table 3. Population of POGS ExGal sources with large absolute RM values, defined as ![]() $|{\text{RM}}| > 100$ rad m−2
$|{\text{RM}}| > 100$ rad m−2

We also detect a single high-|RM| source, GLEAM J031522-031643, which lies coincident with ‘Arc B’ of the Orion-Eridanus Superbubble (e.g., Ochsendorf et al. Reference Ochsendorf, Brown, Bally and Tielens2015; Soler, Bracco, & Pon Reference Soler, Bracco and Pon2018). The high-|RM| source GLEAM J120238-294841 has no apparent association with any Galactic foreground structure in total intensity, H![]() $\alpha$ or Galactic linear polarisation, from, for example, the S-PASS (S-PASS; Carretti et al. Reference Carretti2019).
$\alpha$ or Galactic linear polarisation, from, for example, the S-PASS (S-PASS; Carretti et al. Reference Carretti2019).
Five sources in our large-RM sample (GLEAM J092317-213744, GLEAM J094056-335914, GLEAM J095750-283808, GLEAM J100206-265606, and GLEAM J101236-425901) lie along multiple LOS through the northern H![]() $\alpha$ arc of the Gum Nebula (e.g., Purcell et al. Reference Purcell2015). We show a close-up of this region in Figure 3. Note that one of these sources was detected in Reference PurcellPaper I. A large magnetic bubble was identified in this region by Vallée & Bignell (Reference Vallée and Bignell1983) who detected enhanced RMs (up to
$\alpha$ arc of the Gum Nebula (e.g., Purcell et al. Reference Purcell2015). We show a close-up of this region in Figure 3. Note that one of these sources was detected in Reference PurcellPaper I. A large magnetic bubble was identified in this region by Vallée & Bignell (Reference Vallée and Bignell1983) who detected enhanced RMs (up to ![]() $|{\rm{RM}}| \sim 200$ rad m−2) within
$|{\rm{RM}}| \sim 200$ rad m−2) within ![]() $\sim20^\circ$ of the Gum Nebula. The typical absolute RM of these five sources is 160 rad m−2, suggesting that we detect the same feature, although our sample is limited by its proximity to the Galactic plane.
$\sim20^\circ$ of the Gum Nebula. The typical absolute RM of these five sources is 160 rad m−2, suggesting that we detect the same feature, although our sample is limited by its proximity to the Galactic plane.

Figure 3. Close-up image of the Gum Nebula region. The background image shows H![]() $\alpha$ emission (Finkbeiner Reference Finkbeiner2003) on an arcsinh stretch. Circular (square) markers denote POGS ExGal (PsrCat) sources, colourised according to |RM| as indicated by the colour bar. POGS ExGal sources with large absolute RMs, defined as
$\alpha$ emission (Finkbeiner Reference Finkbeiner2003) on an arcsinh stretch. Circular (square) markers denote POGS ExGal (PsrCat) sources, colourised according to |RM| as indicated by the colour bar. POGS ExGal sources with large absolute RMs, defined as ![]() $|{\rm{RM}}| > 100$ rad m−2, are indicated by the larger markers. Red dashed lines denote the Galactic plane exclusion zone omitted from the GLEAM catalogue.
$|{\rm{RM}}| > 100$ rad m−2, are indicated by the larger markers. Red dashed lines denote the Galactic plane exclusion zone omitted from the GLEAM catalogue.
A further five sources in our large-|RM| sample (GLEAM J055905-201306, GLEAM J060840-304130, GLEAM J062028-274020, GLEAM J062213-155817 and GLEAM J063228-272109) are members of the source ‘cluster’ around ![]() $(l,b)\sim(230^\circ,-20^\circ)$, discussed in Section 5.1.1. The LOS to these sources passes between the Gum Nebula and Barnard’s Loop. We have shown that the density of sources in this region is not significantly enhanced compared to the average sky distribution; neither is the mean |RM| significantly higher in this region, as might be expected if there were a magnetic shell similar to that detected to the North of the Gum Nebula.
$(l,b)\sim(230^\circ,-20^\circ)$, discussed in Section 5.1.1. The LOS to these sources passes between the Gum Nebula and Barnard’s Loop. We have shown that the density of sources in this region is not significantly enhanced compared to the average sky distribution; neither is the mean |RM| significantly higher in this region, as might be expected if there were a magnetic shell similar to that detected to the North of the Gum Nebula.
5.2. Notes on individual sources
We detect polarised emission from regions of a number of sources that exhibit extended and/or complex Stokes I continuum morphologies. Examples of these are given in Figure 4, where we show cutouts around the location of polarised emission as well as the RM spectrum along the LOS through the polarised peak. Note that none of the sources in Figure 4 were detected in polarisation by either Taylor et al. (Reference Taylor2009) or Schnitzeler et al. (Reference Schnitzeler, Carretti, Wieringa, Gaensler, Haverkorn and Poppi2019).

Figure 4. Examples of POGS ExGal sources that have complex and/or extended Stokes I continuum morphologies. From top to bottom, sources are GLEAM J000936-321640, GLEAM J034026-183545, GLEAM J222510-162001, and TGSS-ADR J222603.3![]() $+$172208. Left panels show WISE W1 (
$+$172208. Left panels show WISE W1 (![]() $3.4\,\upmu$m) infrared surface brightness in grayscale, with total intensity contours from GLEAM 200 MHz (red), the TGSS-ADR1 150 MHz (yellow), and the NVSS 1.4 GHz (blue). In the lower panel, archival C-configuration VLA data at 1.4 GHz are overlaid in magenta. Note that this source does not have GLEAM continuum contours as it lies within one of the ‘gaps’ in the GLEAM survey coverage. Cyan stars denote the coordinates of the polarised peak. The resolution of the survey used for the source search (i.e., GLEAM for the first three panels, TGSS-ADR1 for the lower panel) is shown as the hatched ellipse in the lower-left corner. Right panels show the source RM spectrum along the LOS through the cyan star (black) plus the foreground RM spectrum (red) as well as the instrumental leakage avoidance zone (shaded gray region). Green dashed line denotes the fitted RM; blue dot-dashed line denotes the
$3.4\,\upmu$m) infrared surface brightness in grayscale, with total intensity contours from GLEAM 200 MHz (red), the TGSS-ADR1 150 MHz (yellow), and the NVSS 1.4 GHz (blue). In the lower panel, archival C-configuration VLA data at 1.4 GHz are overlaid in magenta. Note that this source does not have GLEAM continuum contours as it lies within one of the ‘gaps’ in the GLEAM survey coverage. Cyan stars denote the coordinates of the polarised peak. The resolution of the survey used for the source search (i.e., GLEAM for the first three panels, TGSS-ADR1 for the lower panel) is shown as the hatched ellipse in the lower-left corner. Right panels show the source RM spectrum along the LOS through the cyan star (black) plus the foreground RM spectrum (red) as well as the instrumental leakage avoidance zone (shaded gray region). Green dashed line denotes the fitted RM; blue dot-dashed line denotes the ![]() $7\sigma$ level.
$7\sigma$ level.
From the top panel of Figure 4, the source spectrum of GLEAM J000936-321640 shows a single significant peak outside the leakage zone of avoidance, but three peaks in the off-source foreground spectrum that are at the ![]() $7\sigma$ level. These foreground peaks are examples of contamination by residual Galactic foreground emission: when inspecting the RM cube, the emission corresponding to these peaks appears extended in the image plane, whereas the emission associated with this source is compact in the image plane.
$7\sigma$ level. These foreground peaks are examples of contamination by residual Galactic foreground emission: when inspecting the RM cube, the emission corresponding to these peaks appears extended in the image plane, whereas the emission associated with this source is compact in the image plane.
The lower panel of Figure 4 shows the source TGSS-ADR J222603.3![]() $+$172208, which was detected in our alternative search using the TGSS-ADR1 catalogue for prior positions. In this overlay, we also include archival C-configuration VLA data at 1.4 GHz (project AS13, observed 1983 May 15) which was retrieved from the NRAO VLA Archive Survey (NVASFootnote b) in an effort to identify a host object. However, as can be seen in the lower panel of Figure 4, the polarised emission from this source measured at 200 MHz appears offset from the emission at 1.4 GHz. Given that it lies within the 150 MHz TGSS-ADR1 Stokes I emission, this polarised emission is likely associated with a steep-spectrum component of this complex radio source. We were unable to confidently identify a host object for TGSS-ADR J222603.3
$+$172208, which was detected in our alternative search using the TGSS-ADR1 catalogue for prior positions. In this overlay, we also include archival C-configuration VLA data at 1.4 GHz (project AS13, observed 1983 May 15) which was retrieved from the NRAO VLA Archive Survey (NVASFootnote b) in an effort to identify a host object. However, as can be seen in the lower panel of Figure 4, the polarised emission from this source measured at 200 MHz appears offset from the emission at 1.4 GHz. Given that it lies within the 150 MHz TGSS-ADR1 Stokes I emission, this polarised emission is likely associated with a steep-spectrum component of this complex radio source. We were unable to confidently identify a host object for TGSS-ADR J222603.3![]() $+$172208.
$+$172208.
In Reference PurcellPaper I, we also identified a handful of radio galaxies where two polarised sources were detected, each associated with one of a pair of radio lobes. These were the radio galaxies PMN J0351-2744 (e.g., Lenc et al. Reference Lenc2017), ESO 422-G028 (also known as MSH 05-22, e.g., Subrahmanyan et al. Reference Subrahmanyan, Ekers, Saripalli and Sadler2008), PKS J0636-2036 (e.g., O’Sullivan et al. Reference O’Sullivan2012), and PKS 0707-35 (e.g., Burgess & Hunstead Reference Burgess and Hunstead2006). We identify these four sources plus a further six physical pairs of polarised sources (‘polarised doubles’) in POGS ExGal, two examples of which are shown in Figure 5. Samples of such physical pairs of polarised sources can be used to provide constraints on the magnetised Cosmic Web (e.g., Vernstrom et al. Reference Vernstrom, Gaensler, Vacca, Farnes, Haverkorn and O’Sullivan2019; O’Sullivan et al. 2020), but in order to derive meaningful constraints, we would require significantly higher surface density than is achieved with our MWA Phase I polarisation work.

Figure 5. Examples of ‘polarised doubles’, where two POGS ExGal sources are associated with a single, extended radio galaxy. Sources are POGSII-EG-250 and POGSII-EG-251 (PKS B0800-09, G4Jy 680; top) and POGSII-EG-265 and POGSII-EG-266 (‘J0947-1338’; bottom). The grayscale is WISE W1 (![]() $3.4\,\upmu$m) infrared surface brightness, and contours are as per Figure 4. The top-right panel shows a close-up of the core of PKS B0800-09, with archival B/C configuration VLA data at 4.89 GHz in magenta. These data were used to select the correct host galaxy for this source. Placement of the RM spectrum subplots denotes which LOS in the postage stamp they are shown along. Hatched ellipses denote the resolution of the GLEAM 200 MHz continuum image.
$3.4\,\upmu$m) infrared surface brightness, and contours are as per Figure 4. The top-right panel shows a close-up of the core of PKS B0800-09, with archival B/C configuration VLA data at 4.89 GHz in magenta. These data were used to select the correct host galaxy for this source. Placement of the RM spectrum subplots denotes which LOS in the postage stamp they are shown along. Hatched ellipses denote the resolution of the GLEAM 200 MHz continuum image.
These sources are (i) POGSII-EG-250 and POGSII-EG-251 (GLEAM J080225-095823 and GLEAM J080253-095822), which together form the radio lobes of PKS B0800-09 (e.g., Bolton Reference Bolton1968), catalogued by White et al. (Reference White2020a) as ‘G4Jy 680’, and (ii) POGSII-EG-265 and POGSII-EG-266 (GLEAM J094633-132703 and GLEAM J094739-134806), which comprise the hotspots associated with the giant radio galaxy ‘J0947-1338’ (e.g., Kuźmicz et al. Reference Kuźmicz, Jamrozy, Bronarska, Janda-Boczar and Saikia2018). The host galaxy of J0947-1338, AllWISE J094708.00-133827.6, is associated with the compact radio source that falls on the ![]() $3\sigma$ GLEAM contour from the South-Eastern radio lobe (see the lower panel of Figure 5).
$3\sigma$ GLEAM contour from the South-Eastern radio lobe (see the lower panel of Figure 5).
We note some disagreement in the literature regarding the host galaxy of PKS B0800-09. The host currently adopted by the NASA/Infrared Processing & Analysis Center Extragalactic Database (NED), marked by the green ‘x’ in Figure 5, is AllWISE J080239.90-095809.8 at ![]() $z=0.0892$ (SDSS DR12; Alam et al. Reference Alam2015). However, archival B/C configuration VLA data at 4.89 GHz (project AJ 141, observed 1986 Oct 1) sourced from the NVAS reveal a probable radio core and one-sided jet associated with AllWISE J080236.28-095739.9 (
$z=0.0892$ (SDSS DR12; Alam et al. Reference Alam2015). However, archival B/C configuration VLA data at 4.89 GHz (project AJ 141, observed 1986 Oct 1) sourced from the NVAS reveal a probable radio core and one-sided jet associated with AllWISE J080236.28-095739.9 (![]() $z=0.0699$; Jones et al. Reference Jones2009), and so we suggest that this is in fact the correct host for PKS B0800-09 (marked by a white ‘+’). We note that, as discussed by White et al. (Reference White2020a), this was the host identification favoured by Schilizzi (Reference Schilizzi1975).
$z=0.0699$; Jones et al. Reference Jones2009), and so we suggest that this is in fact the correct host for PKS B0800-09 (marked by a white ‘+’). We note that, as discussed by White et al. (Reference White2020a), this was the host identification favoured by Schilizzi (Reference Schilizzi1975).
5.3. RM consistency
There are two other RM catalogues in the literature which, between them, cover the full POGS survey area. The first of these is the 1.4 GHz NVSS RM catalogue of Taylor et al. (Reference Taylor2009), which contains RMs for 37 543 sources at Declination ![]() $> -40^\circ$, derived from the NVSS catalogue (which contains flux density measurements in both total intensity and linear polarisation; Condon et al. Reference Condon, Cotton, Greisen, Yin, Perley, Taylor and Broderick1998).
$> -40^\circ$, derived from the NVSS catalogue (which contains flux density measurements in both total intensity and linear polarisation; Condon et al. Reference Condon, Cotton, Greisen, Yin, Perley, Taylor and Broderick1998).
In the Southern sky, this is complemented by the 2.2 GHz S-PASS/ATCA catalogue (Schnitzeler et al. Reference Schnitzeler, Carretti, Wieringa, Gaensler, Haverkorn and Poppi2019), containing RMs for 3 811 sightlines at Declination ![]() $<0^\circ$ at a resolution of
$<0^\circ$ at a resolution of ![]() $2\times1$ arcmin. This catalogue is also uniquely suited to compare with POGS ExGal, as Schnitzeler et al. used their broadband data to investigate the potential for multiple RM components along their sightlines.
$2\times1$ arcmin. This catalogue is also uniquely suited to compare with POGS ExGal, as Schnitzeler et al. used their broadband data to investigate the potential for multiple RM components along their sightlines.
We cross-matched POGS ExGal with the NVSS-RM and S-PASS/ATCA-RM catalogues using a radius of 3 arcmin (our typical PSF) and visually inspected the results to confirm associations between polarised sources. We find a total of 286 POGS ExGal sources with NVSS-RM counterparts, and 124 with S-PASS/ATCA-RM counterparts. Figure 6 shows the comparison between our POGS ExGal RMs and the RMs from these reference catalogues.

Figure 6. Comparison of POGS ExGal RM with NVSS RM (left) and S-PASS/ATCA RM (right). Dashed red line denotes unity, dotted lines denote zero RM. The dot-dashed lines denote the ![]() $3\sigma$ scatter in the RM/RM plane. Individual markers are colourised according to the density in the RM/RM plane to assist the reader. Note that we show different axis ranges in each subplot.
$3\sigma$ scatter in the RM/RM plane. Individual markers are colourised according to the density in the RM/RM plane to assist the reader. Note that we show different axis ranges in each subplot.
From Figure 6, the overwhelming majority of sources lie within ![]() $3\sigma$ of unity, suggesting that there is good agreement between POGS ExGal and the RMs derived at higher frequencies. Given that low-frequency RM studies are only sensitive to Faraday-thin sources, this suggests that the majority of these sources are also dominated by a single Faraday-rotating component.
$3\sigma$ of unity, suggesting that there is good agreement between POGS ExGal and the RMs derived at higher frequencies. Given that low-frequency RM studies are only sensitive to Faraday-thin sources, this suggests that the majority of these sources are also dominated by a single Faraday-rotating component.
Instead, we search for clear outliers away from the unity line. From Figure 6, there are a number of clear outliers. The clearest outlier in the right panel of Figure 6 is GLEAM J182331-705604, which has ![]() ${\rm{RM}}_{\rm{POGS}} = -11.86\pm0.68$ rad m−2 and
${\rm{RM}}_{\rm{POGS}} = -11.86\pm0.68$ rad m−2 and ![]() ${\rm{RM}}_{\rm{S-PASS/ATCA}} = +229.66\pm6.94$ rad m−2. This source is identified in the peaked-spectrum sample of Callingham et al. (Reference Callingham2017) and exhibits steep spectral behaviour above 1 GHz with a flattening in the GLEAM band, so we suggest that this stark RM difference may be the result of different spectral index properties of two polarised emission components within this source. Polarisation observations across a wide frequency range, which would allow QU-fitting, would be required to study this further.
${\rm{RM}}_{\rm{S-PASS/ATCA}} = +229.66\pm6.94$ rad m−2. This source is identified in the peaked-spectrum sample of Callingham et al. (Reference Callingham2017) and exhibits steep spectral behaviour above 1 GHz with a flattening in the GLEAM band, so we suggest that this stark RM difference may be the result of different spectral index properties of two polarised emission components within this source. Polarisation observations across a wide frequency range, which would allow QU-fitting, would be required to study this further.
There are also a handful of clear outliers in the left panel of Figure 6. These sources are GLEAM J100123-263720, GLEAM J120533-263407, and GLEAM J181835![]() $+$240055. From inspection, we find that (i) all are associated with active galactic nuclei and (ii) all remain unresolved by both the MWA and the NVSS. Unresolved polarised radio sources can exhibit complex spectropolarimetric behaviour, often showing different spectral indices in continuum and polarisation (e.g., Schnitzeler et al. Reference Schnitzeler, Carretti, Wieringa, Gaensler, Haverkorn and Poppi2019). Alternatively, these may represent examples of RM time variability (e.g., Anderson et al. Reference Anderson, O’Sullivan, Heald, Hodgson, Pasetto and Gaensler2019). Further polarisation observations across a broad frequency range would be required to study this behaviour further.
$+$240055. From inspection, we find that (i) all are associated with active galactic nuclei and (ii) all remain unresolved by both the MWA and the NVSS. Unresolved polarised radio sources can exhibit complex spectropolarimetric behaviour, often showing different spectral indices in continuum and polarisation (e.g., Schnitzeler et al. Reference Schnitzeler, Carretti, Wieringa, Gaensler, Haverkorn and Poppi2019). Alternatively, these may represent examples of RM time variability (e.g., Anderson et al. Reference Anderson, O’Sullivan, Heald, Hodgson, Pasetto and Gaensler2019). Further polarisation observations across a broad frequency range would be required to study this behaviour further.
5.4. Polarisation properties of POGS ExGal
Figure 7 summarises the fractional polarisation ![]() $(\Pi)$ properties of POGS ExGal. The top panel shows the polarisation fraction at 200 MHz
$(\Pi)$ properties of POGS ExGal. The top panel shows the polarisation fraction at 200 MHz ![]() $(\Pi_{\rm{200\,MHz}})$ as a function of Stokes I flux density. Note that we have not merged the ten ‘polarised doubles’ mentioned in the previous section, as these contribute a small fraction of our full sample. The central and lower panels show comparisons of our 200 MHz fractional polarisation with that measured in the 1.4 GHz NVSS RM catalogue.
$(\Pi_{\rm{200\,MHz}})$ as a function of Stokes I flux density. Note that we have not merged the ten ‘polarised doubles’ mentioned in the previous section, as these contribute a small fraction of our full sample. The central and lower panels show comparisons of our 200 MHz fractional polarisation with that measured in the 1.4 GHz NVSS RM catalogue.
5.4.1. Properties of the full sample
In the top panel of Figure 7, we also show the evolution in the mean fractional polarisation, ![]() $\Bar{\Pi}$, and the standard deviation,
$\Bar{\Pi}$, and the standard deviation, ![]() $\sigma({\Pi})$, as a function of Stokes I flux density. These curves were derived by binning our sources according to Stokes I flux density in adjacent bins of 25 sources, and then calculating
$\sigma({\Pi})$, as a function of Stokes I flux density. These curves were derived by binning our sources according to Stokes I flux density in adjacent bins of 25 sources, and then calculating ![]() $\Bar{\Pi}$ and
$\Bar{\Pi}$ and ![]() $\sigma({\Pi})$ per bin.
$\sigma({\Pi})$ per bin.

Figure 7. Polarisation properties of extragalactic radio sources detected in POGS. Upper: fractional polarisation as a function of 200 MHz Stokes I flux density. Solid (dashed) red lines denote the mean ![]() $({\rm{mean}}+1\sigma)$
$({\rm{mean}}+1\sigma)$![]() $\Pi$, derived in adjacent bins of 25 sources. Dot-dashed and dotted lines denote the lower detectability bound for the Declination
$\Pi$, derived in adjacent bins of 25 sources. Dot-dashed and dotted lines denote the lower detectability bound for the Declination ![]() $-27^\circ$ strip and the Declination
$-27^\circ$ strip and the Declination ![]() $+18^\circ$ strip, derived using typical off-source rms noise of 1.4 and 6 mJy, respectively. Lower: fractional polarisation histogram for POGS ExGal (blue) and the NVSS RM catalogue (red). Dashed lines denote the median polarisation fraction for each sample. For POGS ExGal, this value is
$+18^\circ$ strip, derived using typical off-source rms noise of 1.4 and 6 mJy, respectively. Lower: fractional polarisation histogram for POGS ExGal (blue) and the NVSS RM catalogue (red). Dashed lines denote the median polarisation fraction for each sample. For POGS ExGal, this value is ![]() $\Tilde{\Pi}_{\text{200\,MHz}} = 2.67\%$; for the NVSS RM catalogue,
$\Tilde{\Pi}_{\text{200\,MHz}} = 2.67\%$; for the NVSS RM catalogue, ![]() $\Tilde{\Pi}_{\text{1.4\,GHz}} = 5.83\%$.
$\Tilde{\Pi}_{\text{1.4\,GHz}} = 5.83\%$.
From Figure 7, two trends are visible in the ![]() $\Pi_{\rm{200\,MHz}}/S_{200\,{\rm{MHz}}}$ plane. The first trend is that there appears to be an inverse relationship between
$\Pi_{\rm{200\,MHz}}/S_{200\,{\rm{MHz}}}$ plane. The first trend is that there appears to be an inverse relationship between ![]() $\Pi_{\rm{200\,MHz}}$ and
$\Pi_{\rm{200\,MHz}}$ and ![]() $S_{200\,{\rm{MHz}}}$. For the fainter source regime, where
$S_{200\,{\rm{MHz}}}$. For the fainter source regime, where ![]() $S_{200\,{\rm{MHz}}} < 0.5$ Jy, the mean fractional polarisation is
$S_{200\,{\rm{MHz}}} < 0.5$ Jy, the mean fractional polarisation is ![]() $\Bar{\Pi}_{\rm{200\,MHz}}=7.8\%$, whereas for sources with
$\Bar{\Pi}_{\rm{200\,MHz}}=7.8\%$, whereas for sources with ![]() $0.5\,{\rm{Jy}} < S_{200\,{\rm{MHz}}} < 3\,{\rm{Jy}}$, the mean is
$0.5\,{\rm{Jy}} < S_{200\,{\rm{MHz}}} < 3\,{\rm{Jy}}$, the mean is ![]() $\Bar{\Pi}_{200\,{\rm{MHz}}}=3.0\%$.
$\Bar{\Pi}_{200\,{\rm{MHz}}}=3.0\%$.
Similar trends have previously been observed at higher frequencies in large samples of polarised sources, where ![]() $\Pi$ rises from
$\Pi$ rises from ![]() ${\sim}2.5\%$ at
${\sim}2.5\%$ at ![]() $S_{\rm{1.4\,GHz}}>10$ mJy to
$S_{\rm{1.4\,GHz}}>10$ mJy to ![]() ${\sim}15\%$ below 1 mJy (e.g., Taylor et al. Reference Taylor2007; Subrahmanyan et al. Reference Subrahmanyan, Saripalli, Safouris and Hunstead2010). However, given that extragalactic radio sources typically exhibit low fractional polarisation, at fainter Stokes I flux densities we are naturally biased towards sources with higher fractional polarisation. Indeed, by stacking polarised intensity images from the NVSS, Stil et al. (Reference Stil, Taylor and Sunstrum2014) showed that while
${\sim}15\%$ below 1 mJy (e.g., Taylor et al. Reference Taylor2007; Subrahmanyan et al. Reference Subrahmanyan, Saripalli, Safouris and Hunstead2010). However, given that extragalactic radio sources typically exhibit low fractional polarisation, at fainter Stokes I flux densities we are naturally biased towards sources with higher fractional polarisation. Indeed, by stacking polarised intensity images from the NVSS, Stil et al. (Reference Stil, Taylor and Sunstrum2014) showed that while ![]() $\Pi$ still increases with decreasing
$\Pi$ still increases with decreasing ![]() $S_{\rm{1.4\,GHz}}$, the slope is far more gradual than shown by previous surveys.
$S_{\rm{1.4\,GHz}}$, the slope is far more gradual than shown by previous surveys.
The second noticeable trend is that, for ![]() $S_{200\,{\rm{MHz}}} \gtrsim 3$ Jy, the median polarisation fraction appears to flatten, before increasing above
$S_{200\,{\rm{MHz}}} \gtrsim 3$ Jy, the median polarisation fraction appears to flatten, before increasing above ![]() ${\sim}8$ Jy. However, for this population of increasingly bright sources, any leakage of Stokes I signal into the linear polarisation products (due to inaccuracies in the beam model or calibration errors, for example) can come to dominate any polarised signal. This means that again we are biased towards only sources with higher fractional polarisation, where the real polarised signal can be separated from instrumental leakage. Improvements in either the MWA beam model and/or advanced calibration techniques would be required to mitigate instrumental leakage further and probe the polarisation properties of this bright source population.
${\sim}8$ Jy. However, for this population of increasingly bright sources, any leakage of Stokes I signal into the linear polarisation products (due to inaccuracies in the beam model or calibration errors, for example) can come to dominate any polarised signal. This means that again we are biased towards only sources with higher fractional polarisation, where the real polarised signal can be separated from instrumental leakage. Improvements in either the MWA beam model and/or advanced calibration techniques would be required to mitigate instrumental leakage further and probe the polarisation properties of this bright source population.
5.4.2. Comparison with the NVSS RM catalogue
The lower panel of Figure 7 shows a histogram of fractional polarisation for POGS ExGal (484 sources) and the NVSS RM catalogue (37 543 sources), normalised according to the sample size. For clarity, we show the region ![]() $\Pi<30\%$, which excludes only a single source from POGS ExGal and 10 sources from the NVSS RM catalogue.
$\Pi<30\%$, which excludes only a single source from POGS ExGal and 10 sources from the NVSS RM catalogue.
The histogram suggests that the two populations exhibit different distributions in polarisation fraction. While both populations exhibit broadly similar scatter, with ![]() $\sigma(\Pi_{\rm{200\,MHz}})\sim3.62\%$ and
$\sigma(\Pi_{\rm{200\,MHz}})\sim3.62\%$ and ![]() $\sigma(\Pi_{\rm{1.4\,GHz}})\sim4.81\%$, the median polarisation fraction for POGS ExGal is
$\sigma(\Pi_{\rm{1.4\,GHz}})\sim4.81\%$, the median polarisation fraction for POGS ExGal is ![]() $\Tilde{\Pi}_{\rm{200\,MHz}} = 2.67\%$, about half that for the NVSS RM catalogue,
$\Tilde{\Pi}_{\rm{200\,MHz}} = 2.67\%$, about half that for the NVSS RM catalogue, ![]() $\Tilde{\Pi}_{\rm{1.4\,GHz}} = 5.83\%$. We also note that the NVSS RM catalogue is likely biased at the low end of the fractional polarisation distribution, as Taylor et al. (Reference Taylor2009) exclude sources with
$\Tilde{\Pi}_{\rm{1.4\,GHz}} = 5.83\%$. We also note that the NVSS RM catalogue is likely biased at the low end of the fractional polarisation distribution, as Taylor et al. (Reference Taylor2009) exclude sources with ![]() $\Pi_{\rm{1.4\,GHz}}<0.5\%$.
$\Pi_{\rm{1.4\,GHz}}<0.5\%$.
5.5. POGS ExGal as a probe of the extragalactic magnetised universe
For all our POGS ExGal sources, the observed RM combines contributions from multiple screens along the LOS. While we have already corrected for the Earth’s ionosphere, there remains a contribution from the Milky Way’s magnetised foreground: the Galactic RM.
We have used POGS ExGal to probe the extragalactic RM component by deriving the residual rotation measure (RRM), defined as
where ![]() ${\rm{RM_{Galactic}}}$ was measured using the all-sky Galactic RM reconstructed by Oppermann et al. (Reference Oppermann2015). We note, however, that at Declination
${\rm{RM_{Galactic}}}$ was measured using the all-sky Galactic RM reconstructed by Oppermann et al. (Reference Oppermann2015). We note, however, that at Declination ![]() $\leq-40^\circ$, the Galactic RM reconstruction is based on a comparatively small sample of sources (some
$\leq-40^\circ$, the Galactic RM reconstruction is based on a comparatively small sample of sources (some ![]() $\sim900$; Oppermann et al. Reference Oppermann2015) compared to the sky at Declination
$\sim900$; Oppermann et al. Reference Oppermann2015) compared to the sky at Declination ![]() $>-40^\circ$ (based on some
$>-40^\circ$ (based on some ![]() $>$40 000 sources).
$>$40 000 sources).
The upper row of Figure 8 shows the observed-RM/Galactic-RM plane for POGS ExGal sources, both across the whole sky (upper-left panel) and solely those at Declination ![]() $\leq-40^\circ$ (upper-right panel). From the upper-left panel of Figure 8, it appears that there is broadly good agreement between POGS ExGal RM and Galactic RM, suggesting that the majority of the Faraday rotation we are measuring is being caused by the Galactic foreground. However, the relatively large number of outliers, far from the 1:1 line, suggests that there is a non-negligible extragalactic Faraday rotation component. It is also readily apparent that at Declination
$\leq-40^\circ$ (upper-right panel). From the upper-left panel of Figure 8, it appears that there is broadly good agreement between POGS ExGal RM and Galactic RM, suggesting that the majority of the Faraday rotation we are measuring is being caused by the Galactic foreground. However, the relatively large number of outliers, far from the 1:1 line, suggests that there is a non-negligible extragalactic Faraday rotation component. It is also readily apparent that at Declination ![]() $<-40^\circ$, there is little correlation between POGS ExGal RM and Galactic RM. This lies below the NVSS Declination limit, so the significantly lower source density used in the Galactic RM reconstruction of Oppermann et al. (Reference Oppermann2015) results in larger uncertainty. Furthermore, the typical magnitude of source RMs in this region appears to be lower, thus increasing the fractional uncertainty. Future polarisation surveys with ASKAP (such as POSSUM, which includes a specific ‘RM-grid’ goal; Gaensler et al. Reference Gaensler, Landecker and Taylor2010) will be critical to fill in this sparsely sampled (in polarisation) region of sky.
$<-40^\circ$, there is little correlation between POGS ExGal RM and Galactic RM. This lies below the NVSS Declination limit, so the significantly lower source density used in the Galactic RM reconstruction of Oppermann et al. (Reference Oppermann2015) results in larger uncertainty. Furthermore, the typical magnitude of source RMs in this region appears to be lower, thus increasing the fractional uncertainty. Future polarisation surveys with ASKAP (such as POSSUM, which includes a specific ‘RM-grid’ goal; Gaensler et al. Reference Gaensler, Landecker and Taylor2010) will be critical to fill in this sparsely sampled (in polarisation) region of sky.
Finally, we note that a handful of POGS ExGal sources have extremely large uncertainties on their RRMs; this results from the large fractional uncertainty in Galactic RM along the LOS to these sources, which is readily apparent in the upper-right panel of Figure 8. Thus, in the following sections, we will not only examine the whole sample together, but also a sub-sample at Declination ![]() $>-40^\circ$, where the higher density of sources used to reconstruct the foreground will mean that our RRMs are likely to be more reliable.
$>-40^\circ$, where the higher density of sources used to reconstruct the foreground will mean that our RRMs are likely to be more reliable.
5.5.1. RRM/redshift relation
While it is well established that there is no redshift evolution of RRM out to ![]() $z\sim4$ (e.g., Kronberg, Reinhardt, & Simard-Normandin Reference Kronberg, Bernet, Miniati, Lilly, Short and Higdon1977; Oren & Wolfe Reference Oren and Wolfe1995; Kronberg et al. Reference Kronberg, Reinhardt and Simard-Normandin2008; Vernstrom et al. Reference Vernstrom, Gaensler, Rudnick and Andernach2018), the debate over the dependence (or lack thereof) of the variance in RRM with redshift has been more contentious. For example, the sample of
$z\sim4$ (e.g., Kronberg, Reinhardt, & Simard-Normandin Reference Kronberg, Bernet, Miniati, Lilly, Short and Higdon1977; Oren & Wolfe Reference Oren and Wolfe1995; Kronberg et al. Reference Kronberg, Reinhardt and Simard-Normandin2008; Vernstrom et al. Reference Vernstrom, Gaensler, Rudnick and Andernach2018), the debate over the dependence (or lack thereof) of the variance in RRM with redshift has been more contentious. For example, the sample of ![]() ${\sim}300$ sources catalogued by Kronberg et al. (Reference Kronberg, Reinhardt and Simard-Normandin2008) suggested a significant increase in the variance of RRM with redshift, suggesting strong magnetic fields were present in galaxies in the relatively early Universe. However, from their larger sample of
${\sim}300$ sources catalogued by Kronberg et al. (Reference Kronberg, Reinhardt and Simard-Normandin2008) suggested a significant increase in the variance of RRM with redshift, suggesting strong magnetic fields were present in galaxies in the relatively early Universe. However, from their larger sample of ![]() $\sim$3 650 sources at
$\sim$3 650 sources at ![]() $|b|\geq20^\circ$, Hammond, Robishaw, & Gaensler (Reference Hammond, Robishaw and Gaensler2012) find no significant evolution of RRM variance out to redshift
$|b|\geq20^\circ$, Hammond, Robishaw, & Gaensler (Reference Hammond, Robishaw and Gaensler2012) find no significant evolution of RRM variance out to redshift ![]() $z\sim5.3$.
$z\sim5.3$.
We present the RRM/z plane in the central row of Figure 8, for two different cuts on our source population. Following Hammond et al. (Reference Hammond, Robishaw and Gaensler2012), we also show the mean and standard deviation of RM for this population as a function of redshift, derived using adjacent bins of 25 sources (although we note that we are using a smaller population in each bin as a result of our smaller overall population size).
From Figure 8, there is no clear trend in either the mean or standard deviation of RRM with redshift, either for the full POGS ExGal population or the sources at Declination ![]() $>-40^\circ$. This is consistent with previous results derived from larger samples of polarised sources with known redshifts (Bernet, Miniati, & Lilly Reference Bernet, Miniati and Lilly2012; Hammond et al. Reference Hammond, Robishaw and Gaensler2012; Vernstrom et al. Reference Vernstrom, Gaensler, Rudnick and Andernach2018). This suggests that the observed Faraday rotation is not internal to the sources but is caused by an external screen.
$>-40^\circ$. This is consistent with previous results derived from larger samples of polarised sources with known redshifts (Bernet, Miniati, & Lilly Reference Bernet, Miniati and Lilly2012; Hammond et al. Reference Hammond, Robishaw and Gaensler2012; Vernstrom et al. Reference Vernstrom, Gaensler, Rudnick and Andernach2018). This suggests that the observed Faraday rotation is not internal to the sources but is caused by an external screen.
5.5.2. RRM/polarisation fraction relation
In Reference PurcellPaper I, we performed an initial study of the relation between RM and polarisation fraction for our extragalactic source population, following the work of Hammond et al. (Reference Hammond, Robishaw and Gaensler2012). We have revisited this with our larger POGS ExGal sample, the result of which is shown in the lower panels of Figure 8. Note that for clarity, we show the region ![]() $\Pi_{200\,\rm{MHz}} \leq 20\%$; this region excludes only two sources from POGS ExGal. We note that the sources which exhibit the highest polarisation fraction also show the largest measurement uncertainty. However, this is to be expected—these are among the faintest sources in our catalogue so can only be detected because they have a high polsarisation fraction.
$\Pi_{200\,\rm{MHz}} \leq 20\%$; this region excludes only two sources from POGS ExGal. We note that the sources which exhibit the highest polarisation fraction also show the largest measurement uncertainty. However, this is to be expected—these are among the faintest sources in our catalogue so can only be detected because they have a high polsarisation fraction.
From Figure 8, we see no significant evolution of RRM with ![]() $\Pi$, consistent with previous studies. Interpreting the standard deviation of RRM is slightly more complex. Towards higher fractional polarisation, we are relatively limited by small number statistics, so we focus on the region
$\Pi$, consistent with previous studies. Interpreting the standard deviation of RRM is slightly more complex. Towards higher fractional polarisation, we are relatively limited by small number statistics, so we focus on the region ![]() $\Pi_{\rm{200\,MHz}} \lesssim 8\%$, which contains some
$\Pi_{\rm{200\,MHz}} \lesssim 8\%$, which contains some ![]() ${\sim}95\%$ of our sources (from Figure 7, middle panel). In this region, we see roughly a 50% decrease in the standard deviation of RRM (from
${\sim}95\%$ of our sources (from Figure 7, middle panel). In this region, we see roughly a 50% decrease in the standard deviation of RRM (from ![]() ${\sim}48$ to
${\sim}48$ to ![]() ${\sim}24$ rad m−2).
${\sim}24$ rad m−2).
Using the NVSS RM catalogue, Hammond et al. (Reference Hammond, Robishaw and Gaensler2012) found a similar trend—an anticorrelation between RRM variance and fractional polarisation (their Figure 19). However, as recently shown by Ma et al. (Reference Ma, Mao, Stil, Basu, West, Heiles, Hill and Betti2019a), (Reference Ma, Mao, Stil, Basu, West, Heiles, Hill and Betti2019b) towards lower fractional polarisation (![]() $\Pi_{\rm{1.4\,GHz}}\lesssim1\%$), the NVSS RM catalogue may be contaminated by off-axis leakage effects, which introduces extra RM uncertainties of about 13.5 rad m−2 (see Ma et al. Reference Ma, Mao, Stil, Basu, West, Heiles, Hill and Betti2019b). Nevertheless, when taking only sources with
$\Pi_{\rm{1.4\,GHz}}\lesssim1\%$), the NVSS RM catalogue may be contaminated by off-axis leakage effects, which introduces extra RM uncertainties of about 13.5 rad m−2 (see Ma et al. Reference Ma, Mao, Stil, Basu, West, Heiles, Hill and Betti2019b). Nevertheless, when taking only sources with ![]() $\Pi_{\rm{1.4\,GHz}}\gtrsim2\%$, a similar
$\Pi_{\rm{1.4\,GHz}}\gtrsim2\%$, a similar ![]() ${\sim}60\%$ decrease in RRM variance is visible in Figure 19 of Hammond et al. (Reference Hammond, Robishaw and Gaensler2012), from
${\sim}60\%$ decrease in RRM variance is visible in Figure 19 of Hammond et al. (Reference Hammond, Robishaw and Gaensler2012), from ![]() ${\sim}25$ to
${\sim}25$ to ![]() $\sim10$ rad m−2.
$\sim10$ rad m−2.

Figure 8. Upper: observed RM and Galactic RM for POGS ExGal sources. Different cuts are shown according to the inset. Dashed red line denotes unity, dotted lines denote zero RM. The dot-dashed ellipses denote the ![]() $1\sigma$,
$1\sigma$, ![]() $2\sigma$, and
$2\sigma$, and ![]() $3\sigma$ scatter in the RM/RM plane. Individual markers are colourised according to the density in the RM/RM plane to assist the reader. Middle: RRM as a function of redshift for the 179/484 POGS ExGal sources where a host with measured redshift could be found. Lower: RRM as a function of polarisation fraction
$3\sigma$ scatter in the RM/RM plane. Individual markers are colourised according to the density in the RM/RM plane to assist the reader. Middle: RRM as a function of redshift for the 179/484 POGS ExGal sources where a host with measured redshift could be found. Lower: RRM as a function of polarisation fraction ![]() $(\Pi_{\text{200\,MHz}})$ for POGS ExGal sources, whether or not a redshift could be found. For clarity, we show the region
$(\Pi_{\text{200\,MHz}})$ for POGS ExGal sources, whether or not a redshift could be found. For clarity, we show the region ![]() $\Pi_{\text{200\,MHz}}\leq20\%$, excluding two sources. Different cuts on the population are indicated in the inset. Solid (dashed) red lines denote the mean
$\Pi_{\text{200\,MHz}}\leq20\%$, excluding two sources. Different cuts on the population are indicated in the inset. Solid (dashed) red lines denote the mean ![]() $(\pm1\sigma)$ RRM in each plane, derived in adjacent bins of 25 sources.
$(\pm1\sigma)$ RRM in each plane, derived in adjacent bins of 25 sources.
As discussed by Hammond et al. (Reference Hammond, Robishaw and Gaensler2012), this anticorrelation likely has an astrophysical origin, resulting from some depolarisation mechanism (e.g., Burn Reference Burn1966; Sokoloff et al. Reference Sokoloff, Bykov, Shukurov, Berkhuijsen, Beck and Poezd1998). Given the long wavelength of our observations, ![]() $\lambda^2 \gg 1$, we are extremely sensitive to depolarisation, so it is likely that this is the cause of the behaviour we observe.
$\lambda^2 \gg 1$, we are extremely sensitive to depolarisation, so it is likely that this is the cause of the behaviour we observe.
We do not consider it likely that we suffer from significant bandwidth depolarisation, as we are sensitive to RMs up to ![]() $|{\rm{RM}}|\sim1100$ rad m−2, whereas all our sources have
$|{\rm{RM}}|\sim1100$ rad m−2, whereas all our sources have ![]() $|{\rm{RM}}|\lesssim330$ rad m−2. Faraday depth depolarisation could play a role, as our observations are insensitive to structures thicker than around
$|{\rm{RM}}|\lesssim330$ rad m−2. Faraday depth depolarisation could play a role, as our observations are insensitive to structures thicker than around ![]() $1.9$ rad m−2. However, given that we observe no evolution of RRM with redshift (Figure 8, central panels), it is likely that the Faraday rotation we are measuring is occurring along the LOS to these sources, whereas Faraday-thick structures arise from a medium that both emits and rotates polarised emission.
$1.9$ rad m−2. However, given that we observe no evolution of RRM with redshift (Figure 8, central panels), it is likely that the Faraday rotation we are measuring is occurring along the LOS to these sources, whereas Faraday-thick structures arise from a medium that both emits and rotates polarised emission.
It has been demonstrated that low-frequency observations may recover the outer ‘skins’ of a Faraday-thick structure (e.g., Van Eck et al. Reference Van Eck2018). In these circumstances, the two skins would appear as separate Faraday-thin peaks in the RM spectrum (whereas none of our sources exhibited signs of multiple RM peaks) and would suffer significant depolarisation. As such, we also consider the Faraday depth depolarisation explanation unlikely. Thus the remaining explanation is beam depolarisation, whereby RM variations on scales smaller than the PSF cause the polarisation angle to rotate, decreasing the observed polarisation. Given that our study uses exclusively long-wavelength data, and the Faraday rotation is a function of wavelength-squared, we will be extremely sensitive to such fluctuations.
While all of our sources remain unresolved with our moderate resolution of around 3–8 arcmin, the effect of beam depolarisation has been observed in unresolved sources (e.g., Haverkorn et al. Reference Haverkorn, Brown, Gaensler and McClure-Griffiths2008). Considering that Figure 8 shows no redshift evolution of RRM (either magnitude or standard deviation), this RM variation must occur along the LOS between a source and the observer. A natural explanation for this could be small-scale variation (i.e., at or below the scale of our PSF) in the Galactic foreground RM, which a number of sensitive, small-area studies have shown to be significant (e.g., Mao et al. Reference Mao, Gaensler, Haverkorn, Zweibel, Madsen, McClure-Griffiths, Shukurov and Kronberg2010; Wolleben et al. Reference Wolleben2010; Stil, Taylor, & Sunstrum Reference Stil, Keller, George and Taylor2011; Sun et al. Reference Sun2015; Anderson et al. Reference Anderson, Gaensler, Feain and Franzen2015).
As shown by Stil et al. (Reference Stil, Keller, George and Taylor2011), the standard deviation in RM on angular scales at or below ![]() $1^\circ$ (the typical sampling of sources used by Oppermann et al. Reference Oppermann2015 to reconstruct the Galactic foreground RM) is
$1^\circ$ (the typical sampling of sources used by Oppermann et al. Reference Oppermann2015 to reconstruct the Galactic foreground RM) is ![]() $\sim$12–17 rad m−2 for Galactic latitudes
$\sim$12–17 rad m−2 for Galactic latitudes ![]() $|b| \geq 20^\circ$. Selecting only those POGS ExGal sources at Declination
$|b| \geq 20^\circ$. Selecting only those POGS ExGal sources at Declination ![]() $\geq -40^\circ$ and
$\geq -40^\circ$ and ![]() $|b| \geq 20^\circ$ and subtracting (in quadrature) a typical 15 rad m−2 from our observed RRM variance, we find a persistent excess RRM variance of
$|b| \geq 20^\circ$ and subtracting (in quadrature) a typical 15 rad m−2 from our observed RRM variance, we find a persistent excess RRM variance of ![]() $\sim$10–25 rad m−2. This is broadly consistent with the predicted RM due to the halo of a Milky-Way-like galaxy (e.g., Mao et al. Reference Mao, Gaensler, Haverkorn, Zweibel, Madsen, McClure-Griffiths, Shukurov and Kronberg2010, Reference Mao2012).
$\sim$10–25 rad m−2. This is broadly consistent with the predicted RM due to the halo of a Milky-Way-like galaxy (e.g., Mao et al. Reference Mao, Gaensler, Haverkorn, Zweibel, Madsen, McClure-Griffiths, Shukurov and Kronberg2010, Reference Mao2012).
6. Pulsars
6.1. Known pulsars
Our catalogue contains 33 known pulsars from the ATNF Pulsar CatalogueFootnote c (hereafter ATNF psrcat; Manchester et al. Reference Manchester, Hobbs, Teoh and Hobbs2005). For six of these pulsars, we provide the first recorded RMs. We measure linearly polarised flux densities between 17 mJy and 1.7 Jy, with RMs between ![]() $-185.99$ and
$-185.99$ and ![]() $+150.74$ rad m−2. The mean RM uncertainty is
$+150.74$ rad m−2. The mean RM uncertainty is ![]() $0.22$ rad m−2, and the worst-case RM uncertainty is
$0.22$ rad m−2, and the worst-case RM uncertainty is ![]() $2.84$ rad m−2.
$2.84$ rad m−2.
An excerpt from our catalogue is presented in Table 4, along with ancillary information sourced from the GLEAM Pulsar Catalogue (Murphy et al. Reference Murphy2017) and the ATNF psrcat. We also present the RM spectra for all 33 known pulsars in Figure C.1. The properties of some pulsars in our catalogue are not listed in either of these catalogues and were sourced from alternative references. These are listed here for completeness.
PSR J1747-4036: This pulsar was not detected by Murphy et al. (Reference Murphy2017), but a compact radio source (GLEAM J174749-403650) was catalogued within 30 arcsec by Hurley-Walker et al. (Reference Hurley-Walker2019). We suggest that they are the same source, so we quote that object’s 200 MHz flux density.
PSR J0509
 $+$0856: The literature RM and DM for this pulsar are quoted from Martinez et al. (Reference Martinez2019).
$+$0856: The literature RM and DM for this pulsar are quoted from Martinez et al. (Reference Martinez2019).
Table 4. Sample rows from POGS PsrCat, showing only columns that vary by source. Note that, for display purposes, unfilled entries are marked with a ‘ −’

BPA: beam position angle; RA: Right Ascension.
There are two pulsars in our catalogue that are part of a pulsar binary system (J0737-3039A) or are located in a globular cluster that is known to host multiple pulsars (J1824-2452A, located in globular cluster M28). For the pulsar binary, the companion pulsar (J0737-3039B) precessed out of our LOS in 2008 March and is expected to reappear around 2035, due to relativistic spin (or geodetic) precession (e.g., Perera et al. Reference Perera2010).
Globular cluster M28 is known to host multiple pulsars, so it is possible that we are detecting an amalgamation of polarised emission from a number of these with our moderate resolution. However, we consider this unlikely for a number of reasons. First, J1824-2452A is the dominant pulsar in M28, with a 1.4 GHz flux density of ![]() ${\sim}2.3$ mJy (Dai et al. Reference Dai2015), whereas the second-brightest pulsar, J1824-2452C, has a 1.4 GHz flux density of
${\sim}2.3$ mJy (Dai et al. Reference Dai2015), whereas the second-brightest pulsar, J1824-2452C, has a 1.4 GHz flux density of ![]() ${\sim}0.17$ mJy. While the low-frequency spectral behaviour of the other pulsars is not known, with a spectral index
${\sim}0.17$ mJy. While the low-frequency spectral behaviour of the other pulsars is not known, with a spectral index ![]() $\alpha=-3.2\pm0.1$ (Murphy et al. Reference Murphy2017), ‘pulsar A’ likely dominates the low-frequency continuum. Second, we do not detect any additional peaks in the RM spectrum of this source that might indicate other pulsars within our PSF. Third, if we detected emission from other pulsars within our PSF at similar RM to pulsar A, it could result in a broadening of the apparent RM peak. However, for J1824-2452A, the width of the RM spectrum peak is consistent with that of other isolated pulsars in our catalogue.
$\alpha=-3.2\pm0.1$ (Murphy et al. Reference Murphy2017), ‘pulsar A’ likely dominates the low-frequency continuum. Second, we do not detect any additional peaks in the RM spectrum of this source that might indicate other pulsars within our PSF. Third, if we detected emission from other pulsars within our PSF at similar RM to pulsar A, it could result in a broadening of the apparent RM peak. However, for J1824-2452A, the width of the RM spectrum peak is consistent with that of other isolated pulsars in our catalogue.
Thus, for both J0737-3039A and J1824-2452A, we assume that the emission we are detecting is associated with ‘pulsar A’ of each system.
In Figure 9, we present properties of the pulsars we have detected in linear polarisation at 200 MHz. The top panel presents a comparison of our 200 MHz RMs with those measured in the literature; our RMs are typically in very good agreement with the values determined at other frequencies. We also note that our median uncertainty ![]() $(0.12$ rad m
$(0.12$ rad m![]() $^{-2})$ represents a 40% improvement on the median uncertainty for sources with known RMs
$^{-2})$ represents a 40% improvement on the median uncertainty for sources with known RMs ![]() $(0.20$ rad m
$(0.20$ rad m![]() $^{-2})$. Based on our relatively small sample, this suggests that there is no frequency-dependence of the RMs, and therefore no contribution to the observed RM from the pulsar magnetosphere, at least to the precision of our measurements, in agreement with previous studies (e.g., Sobey et al. Reference Sobey2019, and references therein).
$^{-2})$. Based on our relatively small sample, this suggests that there is no frequency-dependence of the RMs, and therefore no contribution to the observed RM from the pulsar magnetosphere, at least to the precision of our measurements, in agreement with previous studies (e.g., Sobey et al. Reference Sobey2019, and references therein).

Figure 9. Polarisation properties of known pulsars detected in POGS. Top panel: Comparison of RMs for known pulsars in the ATNF psrcat and POGS PsrCat at 200 MHz. Pulsars without RMs in the ATNF psrcat are shown as empty markers in the right-hand panel. Red dashed lines mark zero RM; black line denotes unity. The median and worst-case measurement uncertainties from these pulsars in each catalogue are indicated, respectively, by the black and red error symbols in the upper-left quadrant. Bottom panel: Histogram of 200 MHz fractional polarisation for the 22/33 pulsars with continuum image-plane detections in GLEAM survey data (Murphy et al. Reference Murphy2017; Hurley-Walker et al. Reference Hurley-Walker2019). Dashed and dot-dashed lines represent Gaussians fitted to the population, with typical polarisation fractions of ![]() $\Pi_{200\,\rm{MHz}}=24.7\pm1.4\%$ and
$\Pi_{200\,\rm{MHz}}=24.7\pm1.4\%$ and ![]() $46.7\pm1.4\%$, respectively.
$46.7\pm1.4\%$, respectively.

Figure 10. Polarisation properties of the 33 pulsars in POGS PsrCat (filled symbols) and the 686 pulsars in the ATNF psrcat that have both RM and DM values (small, semitransparent symbols). Top panel: absolute RM (i.e., ![]() $|{\rm{RM}}|$) as a function of absolute Galactic latitude (i.e.,
$|{\rm{RM}}|$) as a function of absolute Galactic latitude (i.e., ![]() $|b|$). Bottom panel: relation between absolute RM and DM. Colours represent different Galactic latitudes above and below the plane: red denotes
$|b|$). Bottom panel: relation between absolute RM and DM. Colours represent different Galactic latitudes above and below the plane: red denotes ![]() $|b|\leq5^\circ$, orange indicates
$|b|\leq5^\circ$, orange indicates ![]() $5<|b|<30^\circ,$ and yellow denotes
$5<|b|<30^\circ,$ and yellow denotes ![]() $|b|\geq30^\circ$. Gray lines show constant
$|b|\geq30^\circ$. Gray lines show constant ![]() $|\langle B_{\|} \rangle|$ derived according to Equation (7).
$|\langle B_{\|} \rangle|$ derived according to Equation (7).
The lower panel of Figure 9 shows a histogram of the polarisation fraction for POGS PsrCat pulsars that have continuum image-plane detections in GLEAM survey data (Murphy et al. Reference Murphy2017; Hurley-Walker et al. Reference Hurley-Walker2019). Note that only three of these pulsars are known to exhibit long-term variability, likely due to magnetospheric emission mode changes (PSRs J0034-0721 and J0828-3417; e.g., McSweeney et al. Reference McSweeney, Bhat and Tremblay2017; Esamdin et al. Reference Esamdin, Lyne, Graham-Smith, Kramer, Manchester and Wu2005) or refractive interstellar scintillation (PSR J0630-2834; e.g., Bell et al. Reference Bell2016). Our use of GLEAM data means that both continuum and polarisation data will have been taken in the same epoch.
The histogram appears to exhibit a bimodal distribution. We performed a one-sample Kolmogorov–Smirnov (K–S) test on our measured ![]() $\Pi_{200\,\rm{MHz}}$ values to determine the likelihood that this apparent bimodality was due to random chance. Our test yielded a K–S statistic of 0.53 and associated p-value of
$\Pi_{200\,\rm{MHz}}$ values to determine the likelihood that this apparent bimodality was due to random chance. Our test yielded a K–S statistic of 0.53 and associated p-value of ![]() $1.67\times10^{-6}$, so we can confidently reject the null hypothesis that our polarisation fraction measurements are drawn from the same normal distribution.
$1.67\times10^{-6}$, so we can confidently reject the null hypothesis that our polarisation fraction measurements are drawn from the same normal distribution.
We thus fitted a pair of Gaussians to describe the population. We find our catalogue contains a dominant population of pulsars with typical polarisation fraction and variance of ![]() $\Pi_{200\,\rm{MHz}}=0.25$ and
$\Pi_{200\,\rm{MHz}}=0.25$ and ![]() $\sigma_{\Pi}=0.08$, and a smaller population with
$\sigma_{\Pi}=0.08$, and a smaller population with ![]() $\Pi_{200\,\rm{MHz}}=0.47$ and
$\Pi_{200\,\rm{MHz}}=0.47$ and ![]() $\sigma_{\Pi}=0.04$. None of the pulsars in this latter group show any common traits in terms of DM, spin period, location, or spectral index properties. Note that, as a general rule, pulsar emission tends to increase in polarisation fractions towards low frequencies, thought to be due to the pulsar magnetospheric radio emission mechanism (e.g., Johnston et al. Reference Johnston, Karastergiou, Mitra and Gupta2008; Noutsos et al. Reference Noutsos2015), with some exceptions (e.g., Xue et al. Reference Xue, Ord, Tremblay, Bhat, Sobey, Meyers, McSweeney and Swainston2019).
$\sigma_{\Pi}=0.04$. None of the pulsars in this latter group show any common traits in terms of DM, spin period, location, or spectral index properties. Note that, as a general rule, pulsar emission tends to increase in polarisation fractions towards low frequencies, thought to be due to the pulsar magnetospheric radio emission mechanism (e.g., Johnston et al. Reference Johnston, Karastergiou, Mitra and Gupta2008; Noutsos et al. Reference Noutsos2015), with some exceptions (e.g., Xue et al. Reference Xue, Ord, Tremblay, Bhat, Sobey, Meyers, McSweeney and Swainston2019).
6.1.1. Comparison with VCS data
Xue et al. (Reference Xue2017) present a catalogue of 50 pulsars detected using the MWA’s Voltage Capture System (VCS; Tremblay et al. Reference Tremblay2015) at 185 MHz. Of the 33 pulsars that we detect, 13 are common to the catalogue of Xue et al. Recently, Xue et al. (Reference Xue, Ord, Tremblay, Bhat, Sobey, Meyers, McSweeney and Swainston2019) have demonstrated that the VCS can be reliably calibrated in full-polarisation by observing two known, bright, and strongly polarised pulsars: J0742-2822 and J1752-2806. Both of these are in our catalogue, allowing additional cross-verification between our imaging data and MWA-VCS observations.
For PSR J0742-2822, we cannot compare polarisation fraction measurements with those found by Xue et al. (Reference Xue, Ord, Tremblay, Bhat, Sobey, Meyers, McSweeney and Swainston2019), as this source was not detected by Murphy et al. (Reference Murphy2017). However, we can compare RMs. From our image-plane data, we find an ![]() ${\rm{RM}}=+150.74\pm0.02$ rad m−2 at 200 MHz; the VCS data indicate an
${\rm{RM}}=+150.74\pm0.02$ rad m−2 at 200 MHz; the VCS data indicate an ![]() ${\rm{RM}}=+150.975\pm0.097$ rad m−2 at 179 MHz. For PSR J1752-2806, our image-plane RM is
${\rm{RM}}=+150.975\pm0.097$ rad m−2 at 179 MHz. For PSR J1752-2806, our image-plane RM is ![]() ${\rm{RM}}=+95.74\pm0.08$ rad m−2; Xue et al. (Reference Xue, Ord, Tremblay, Bhat, Sobey, Meyers, McSweeney and Swainston2019) determine an RM of
${\rm{RM}}=+95.74\pm0.08$ rad m−2; Xue et al. (Reference Xue, Ord, Tremblay, Bhat, Sobey, Meyers, McSweeney and Swainston2019) determine an RM of ![]() ${\rm{RM}}=+95.871\pm0.078$ rad m−2 from their VCS data at 154 MHz. While these discrepancies are relatively significant (respectively,
${\rm{RM}}=+95.871\pm0.078$ rad m−2 from their VCS data at 154 MHz. While these discrepancies are relatively significant (respectively, ![]() $2.4\sigma$ and
$2.4\sigma$ and ![]() $1.7\sigma$), this is likely due to differences in the ionospheric RM correction applied to our different datasets. With the naturally high precision RMs that can be determined by our long-wavelength data, uncertainties in the ionospheric RM correction become the dominant contribution to the overall measurement uncertainty, so we consider our results broadly consistent with the VCS data.
$1.7\sigma$), this is likely due to differences in the ionospheric RM correction applied to our different datasets. With the naturally high precision RMs that can be determined by our long-wavelength data, uncertainties in the ionospheric RM correction become the dominant contribution to the overall measurement uncertainty, so we consider our results broadly consistent with the VCS data.
We also note that PSR J0742-2822 is known to change emission mode on the timescale of ![]() ${\sim}95$ days (Keith, Shannon, & Johnston Reference Keith, Shannon and Johnston2013). The observations of Xue et al. (Reference Xue, Ord, Tremblay, Bhat, Sobey, Meyers, McSweeney and Swainston2019) were performed in 2016, whereas the GLEAM observations from which our catalogue was compiled were performed in 2013, so it is plausible that the data were taken when this pulsar was in different emission modes. This is not expected to cause a discrepancy in the RM, since we expect this effect to be the result of the interstellar medium propagation, with no/negligible contribution from the relativistic electron–positron plasma in the pulsar magnetosphere (e.g., Melrose & Rafat Reference Melrose and Rafat2017), particularly at low observing frequencies (e.g., Wang, Han, & Lai Reference Wang, Han and Lai2011; Noutsos et al. Reference Noutsos2015).
${\sim}95$ days (Keith, Shannon, & Johnston Reference Keith, Shannon and Johnston2013). The observations of Xue et al. (Reference Xue, Ord, Tremblay, Bhat, Sobey, Meyers, McSweeney and Swainston2019) were performed in 2016, whereas the GLEAM observations from which our catalogue was compiled were performed in 2013, so it is plausible that the data were taken when this pulsar was in different emission modes. This is not expected to cause a discrepancy in the RM, since we expect this effect to be the result of the interstellar medium propagation, with no/negligible contribution from the relativistic electron–positron plasma in the pulsar magnetosphere (e.g., Melrose & Rafat Reference Melrose and Rafat2017), particularly at low observing frequencies (e.g., Wang, Han, & Lai Reference Wang, Han and Lai2011; Noutsos et al. Reference Noutsos2015).
For PSR J1752-2806, we measure a polarisation fraction of ![]() $\Pi_{200\,\rm{MHz}} = 7.0\pm1.3\%$. This is about half that determined for this pulsar from VCS data and significantly discrepant with the general trend exhibited in measurements from the literature (Figure 10 of Xue et al. Reference Xue, Ord, Tremblay, Bhat, Sobey, Meyers, McSweeney and Swainston2019). The cause of this is likely to be the polarisation angle discontinuity across the pulse profile of PSR J1752-2806 (Figure 11 of Xue et al. Reference Xue, Ord, Tremblay, Bhat, Sobey, Meyers, McSweeney and Swainston2019), which will cause depolarisation when averaging over the pulse profile in the image domain.
$\Pi_{200\,\rm{MHz}} = 7.0\pm1.3\%$. This is about half that determined for this pulsar from VCS data and significantly discrepant with the general trend exhibited in measurements from the literature (Figure 10 of Xue et al. Reference Xue, Ord, Tremblay, Bhat, Sobey, Meyers, McSweeney and Swainston2019). The cause of this is likely to be the polarisation angle discontinuity across the pulse profile of PSR J1752-2806 (Figure 11 of Xue et al. Reference Xue, Ord, Tremblay, Bhat, Sobey, Meyers, McSweeney and Swainston2019), which will cause depolarisation when averaging over the pulse profile in the image domain.
6.1.2. Consistency of our image-plane pulsar measurements
PSR J1752-2806 was only detected in a single GLEAM epoch, so we cannot determine the cause of this discrepancy between our measured polarisation fraction and that determined by Xue et al. (Reference Xue, Ord, Tremblay, Bhat, Sobey, Meyers, McSweeney and Swainston2019). However, PSR J0742-2822 was in detected in two separate epochs of GLEAM observations, during observations on 2013 November 25 and 2014 March 3. Both epochs were observations of the Declination ![]() $-27^\circ$ strip, meaning that the primary beam response to this pulsar should be consistent.
$-27^\circ$ strip, meaning that the primary beam response to this pulsar should be consistent.
The RMs were broadly consistent between epochs: in the first epoch, ![]() ${\rm{RM}}=+150.67\pm0.01$ rad m−2; for the second,
${\rm{RM}}=+150.67\pm0.01$ rad m−2; for the second, ![]() ${\rm{RM}}=+150.80\pm0.02$ rad m−2. However, the polarised flux density measurements are inconsistent for these two epochs:
${\rm{RM}}=+150.80\pm0.02$ rad m−2. However, the polarised flux density measurements are inconsistent for these two epochs: ![]() $284.7\pm3.8$ and
$284.7\pm3.8$ and ![]() $241.5\pm4.1$ mJy. These observing epochs are separated by 105 days, so these differences could be caused by a change in emission mode in the intervening period. However, as mentioned previously, our observations may suffer from some second-order ionospheric effect that may explain this discrepancy—this was observed in long-track observations of a known pulsar during LOFAR polarisation commissioning (private communication LOFAR Magnetism Key Science Project). Ten pulsars in our catalogue were detected in multiple epochs; all exhibit some level of apparent variability in polarised flux density between epochs (between
$241.5\pm4.1$ mJy. These observing epochs are separated by 105 days, so these differences could be caused by a change in emission mode in the intervening period. However, as mentioned previously, our observations may suffer from some second-order ionospheric effect that may explain this discrepancy—this was observed in long-track observations of a known pulsar during LOFAR polarisation commissioning (private communication LOFAR Magnetism Key Science Project). Ten pulsars in our catalogue were detected in multiple epochs; all exhibit some level of apparent variability in polarised flux density between epochs (between ![]() ${\sim}5\%$ and
${\sim}5\%$ and ![]() ${\sim}250\%$). However, three of these pulsars were each detected in four epochs, and our measured polarised flux densities are consistent in a subset of epochs. As with the POGS ExGal sources, we also note that our RMs were consistent between all multi-epoch detections.
${\sim}250\%$). However, three of these pulsars were each detected in four epochs, and our measured polarised flux densities are consistent in a subset of epochs. As with the POGS ExGal sources, we also note that our RMs were consistent between all multi-epoch detections.
Interstellar scintillation may also explain this phenomenon; when comparing single-epoch VCS data with the GLEAM Pulsar Catalogue, Xue et al. (Reference Xue2017) noted variations in continuum flux density measurements for many pulsars common to both catalogues. These differences ranged from the ![]() ${\sim}1.5\%$ level to the
${\sim}1.5\%$ level to the ![]() ${\sim}85\%$ level. The LOS to PSR J0742-2822 passes through the Gum Nebula, which has been shown to be responsible for significant turbulence along this LOS (Johnston, Nicastro, & Koribalski Reference Johnston, Nicastro and Koribalski1998).
${\sim}85\%$ level. The LOS to PSR J0742-2822 passes through the Gum Nebula, which has been shown to be responsible for significant turbulence along this LOS (Johnston, Nicastro, & Koribalski Reference Johnston, Nicastro and Koribalski1998).
6.1.3. Relation to Galactic structure
This new era of low-frequency polarimetry has allowed observers to determine very precise RMs for many known pulsars, unlocking a new window into probing the Galactic magnetic field. For example, Sobey et al. (Reference Sobey2019) used beam-formed LOFAR High-Band Antenna detections of 137 known pulsars to study the 3D Galactic halo magnetic field. For pulsars at distance d, with known RM and DM, the ratio between RM and DM can be used to estimate the electron-density-weighted average magnetic field strength along the LOS, via:
where ![]() $n_{\rm{e}}$ is the electron density (cm−3) and
$n_{\rm{e}}$ is the electron density (cm−3) and ![]() ${\rm{d}}l$ is the unit path length along the LOS. We note that this relation relies on the assumption that there is no correlation between electron density and magnetic field strength (e.g., Beck et al. Reference Beck, Shukurov, Sokoloff and Wielebinski2003). If there is positive correlation between these quantities, RM will be enhanced and thus Equation (7) will overestimate
${\rm{d}}l$ is the unit path length along the LOS. We note that this relation relies on the assumption that there is no correlation between electron density and magnetic field strength (e.g., Beck et al. Reference Beck, Shukurov, Sokoloff and Wielebinski2003). If there is positive correlation between these quantities, RM will be enhanced and thus Equation (7) will overestimate ![]() $\langle B_{\|}\rangle$; likewise, anti-correlation would result in an underestimate of
$\langle B_{\|}\rangle$; likewise, anti-correlation would result in an underestimate of ![]() $\langle B_{\|}\rangle$.
$\langle B_{\|}\rangle$.
While our sample is much smaller, and based on imaging (rather than tied-array) data, we can also attempt to investigate this using catalogue DMs from the ATNF psrcat. Since the uncertainty in RM is usually the dominant source of uncertainty in ![]() $|\langle B_{\|} \rangle|$, our low-frequency RM measurements provide more accurate
$|\langle B_{\|} \rangle|$, our low-frequency RM measurements provide more accurate ![]() $|\langle B_{\|} \rangle|$.
$|\langle B_{\|} \rangle|$.
The top panel of Figure 10 shows the relation between absolute RM value and absolute Galactic latitude, for POGS PsrCat entries (filled points) and ATNF psrcat entries (open markers). Two clear trends are visible. First, absolute RM decreases with increasing absolute Galactic latitude. Second, the scatter in absolute RM is significantly greater at low Galactic latitude. For POGS pulsars at ![]() $|b|\leq5^\circ$,
$|b|\leq5^\circ$, ![]() $\sigma_{|{\rm{RM}}|} = 56.5$ rad m−2, whereas for
$\sigma_{|{\rm{RM}}|} = 56.5$ rad m−2, whereas for ![]() $|b|>5^\circ$,
$|b|>5^\circ$, ![]() $\sigma_{|{\rm{RM}}|} = 20.7$ rad m−2.
$\sigma_{|{\rm{RM}}|} = 20.7$ rad m−2.
The bottom panel of Figure 10 also shows the variation of absolute RM with DM for the same population, for ![]() $|{\rm{RM}}| \leq200$ rad m−2 and
$|{\rm{RM}}| \leq200$ rad m−2 and ![]() $|{\rm{DM}}| \leq550$ pc cm−3. Markers are colourised according to Galactic latitude, with low-, medium-, and high-latitude pulsars indicated, respectively, in red, orange, and yellow.
$|{\rm{DM}}| \leq550$ pc cm−3. Markers are colourised according to Galactic latitude, with low-, medium-, and high-latitude pulsars indicated, respectively, in red, orange, and yellow.
Broadly speaking, the lower panel of Figure 10 indicates that pulsars located towards higher Galactic latitudes tend to have lower values of RM and DM and are distributed across a fairly narrow range of Galactic magnetic field strengths, ![]() $|\langle B_{\|}\rangle| \leq 1.5\,\upmu$G. Pulsars towards lower Galactic latitudes tend to have larger RM and/or DM values yet are also distributed across a fairly small range of Galactic magnetic field,
$|\langle B_{\|}\rangle| \leq 1.5\,\upmu$G. Pulsars towards lower Galactic latitudes tend to have larger RM and/or DM values yet are also distributed across a fairly small range of Galactic magnetic field, ![]() $|\langle B_{\|}\rangle| \leq 3.1\,\upmu$G. This is largely consistent with the LOFAR results presented by Sobey et al. (Reference Sobey2019).
$|\langle B_{\|}\rangle| \leq 3.1\,\upmu$G. This is largely consistent with the LOFAR results presented by Sobey et al. (Reference Sobey2019).
For two pulsars, J1601-5244 and J1851-0241, their position in the DM![]() $/|{\rm{RM}}|$ plane suggests very low magnetic field strength: from Equation 7,
$/|{\rm{RM}}|$ plane suggests very low magnetic field strength: from Equation 7, ![]() $|\langle B_{\|}\rangle| = 0.035\,\upmu$G for J1851-0241 and
$|\langle B_{\|}\rangle| = 0.035\,\upmu$G for J1851-0241 and ![]() $0.046\,\upmu$G for J1601-5244. However, their locations towards the Galactic centre, proximity to the Galactic plane, and DM distances (
$0.046\,\upmu$G for J1601-5244. However, their locations towards the Galactic centre, proximity to the Galactic plane, and DM distances (![]() $\sim$4.09 and 7.92 kpc; Yao, Manchester, & Wang Reference Yao, Manchester and Wang2017) could also mean that their emission traverses through the magnetic field reversal(s) within the Galactic disk (e.g., Van Eck et al. Reference Van Eck2011).
$\sim$4.09 and 7.92 kpc; Yao, Manchester, & Wang Reference Yao, Manchester and Wang2017) could also mean that their emission traverses through the magnetic field reversal(s) within the Galactic disk (e.g., Van Eck et al. Reference Van Eck2011).
From Figure 10, it appears that, similarly to Sobey et al. (Reference Sobey2019), we detect very few pulsars with both large DM and large ![]() $|{\rm{RM}}|$. This is converse to the population of pulsars in the ATNF PsrCat, which are largely uniformly distributed in DM
$|{\rm{RM}}|$. This is converse to the population of pulsars in the ATNF PsrCat, which are largely uniformly distributed in DM![]() $/|{\rm{RM}}|$ space.
$/|{\rm{RM}}|$ space.
We also note that our image-domain search retains sensitivity to pulsars with large DMs. The highest-DM pulsar for which we find a RM has a DM of 515 pc cm−3, which is significantly larger than the highest-DM pulsars typically detected in low-frequency, time-domain, beamformed data. For example, from the incoherent beamformed data presented by Xue et al. (Reference Xue2017), the highest-DM pulsar has a DM of 147.45 pc cm−3. The highest-DM for which Sobey et al. (Reference Sobey2019) detected an RM was 161 pc cm−3; the highest-DM pulsar yet detected by LOFAR is around 217 pc cm−3 (Pilia et al. Reference Pilia2016). A number of effects may account for this, such as dispersion smearing (for incoherent dedispersion) or scattering effects (that may smear the pulse profile over a larger number of profile bins); spectral index effects (particularly towards areas of increased sky temperature from the Galactic foreground where a pulsar’s spectral index may be unfavourably small); propagation effects (e.g., scintillation) or instrumental effects (e.g., beam jitter). For further discussion of such effects, see, for example, Kondratiev et al. (Reference Kondratiev2016) or Bilous et al. (Reference Bilous2016).
Table 5. New pulsar candidates identified from our nominally extragalactic source population, selected according to compactness and polarisation fraction

6.2. New pulsar candidates
In Reference PurcellPaper I, we attempted to search for new pulsar candidates among our nominally extragalactic source population. We applied three selection criteria: a source must (a) be compact at the resolution of GLEAM and the NVSS, (b) exhibit a high polarisation fraction ![]() $(\gtrsim10\%),$ and (c) have a steep radio spectrum
$(\gtrsim10\%),$ and (c) have a steep radio spectrum ![]() $(\alpha \lesssim -1)$. By applying these criteria, we found a single candidate pulsar among the 80 sources detected in polarisation (excluding the known pulsar PSR B0628-28).
$(\alpha \lesssim -1)$. By applying these criteria, we found a single candidate pulsar among the 80 sources detected in polarisation (excluding the known pulsar PSR B0628-28).
However, statistical samples have shown that pulsars may exhibit a wide range of spectral properties. For example, Bilous et al. (Reference Bilous2016) showed that while 75% of their sample were well described by a single power-law spectrum, this strongly depends on the availability of multi-frequency flux density measurements. Furthermore, the index of this power law varied significantly, with single-component spectra having ![]() $-3\lesssim\alpha<-0.5$ and the low-frequency spectral index of multi-component SED fits having
$-3\lesssim\alpha<-0.5$ and the low-frequency spectral index of multi-component SED fits having ![]() $-3\lesssim\alpha_{\rm{low}}<+5$. Likewise, around half the sample of 60 pulsars detected by Murphy et al. (Reference Murphy2017) were not well described using a single power law, with a number showing low-frequency flattening or turn-overs. As such, when searching our new all-sky catalogue for new candidate pulsars, we relaxed criterion (c) and instead searched for pulsar candidates by compactness and polarisation fraction.
$-3\lesssim\alpha_{\rm{low}}<+5$. Likewise, around half the sample of 60 pulsars detected by Murphy et al. (Reference Murphy2017) were not well described using a single power law, with a number showing low-frequency flattening or turn-overs. As such, when searching our new all-sky catalogue for new candidate pulsars, we relaxed criterion (c) and instead searched for pulsar candidates by compactness and polarisation fraction.
Among our 484 nominally extragalactic sources, we found four additional candidates which are not visibly spatially extended,Footnote d exhibit a polarisation fraction ![]() $\Pi_{200\,\rm{MHz}} \geq10\%$, and do not have a likely infrared counterpart in AllWISE. We note that the pulsar candidate presented in Reference PurcellPaper I, GLEAM J134038-340234, is not detected in this all-sky catalogue. This suggests that this source is unlikely to be a true pulsar, as pulsars are expected to be Faraday-thin and would not depolarise significantly with the shift in reference frequency between Reference PurcellPaper I (
$\Pi_{200\,\rm{MHz}} \geq10\%$, and do not have a likely infrared counterpart in AllWISE. We note that the pulsar candidate presented in Reference PurcellPaper I, GLEAM J134038-340234, is not detected in this all-sky catalogue. This suggests that this source is unlikely to be a true pulsar, as pulsars are expected to be Faraday-thin and would not depolarise significantly with the shift in reference frequency between Reference PurcellPaper I (![]() $\nu_{\rm{ref}}=216$ MHz) and this work (
$\nu_{\rm{ref}}=216$ MHz) and this work (![]() $\nu_{\rm{ref}}=200$ MHz).
$\nu_{\rm{ref}}=200$ MHz).
We present these pulsar candidates in Table 5. For the spectral index values listed in Table 5, we also sourced ancillary measurements from various radio surveys. As well as the VLSSr, TGSS-ADR1, TXS, and NVSS catalogues, measurements were also found in catalogues from VLSSr the VLA’s Faint Images of the Radio Sky at Twenty-cm survey (Becker, White, & Helfand Reference Becker, White and Helfand1994) and the Westerbork in the Southern Hemisphere survey (De Breuck et al. Reference De Breuck, Tang, de Bruyn, Röttgering and van Breugel2002). Flux density measurements from these surveys (where available) were combined with the GLEAM catalogue measurements and used to derive a single-component power-law fit, with the uncertainty region explored using an MC routine employed as part of the EMCEE package (Foreman-Mackey et al. Reference Foreman-Mackey, Hogg, Lang and Goodman2013). The resulting SEDs are presented in Figure A.3, except for TGSS-ADR J230010.0![]() $+$184537, where the SED is already shown in Figure A.2.
$+$184537, where the SED is already shown in Figure A.2.
From Table 5 (as well as Figure A.3), our candidate pulsars exhibit fairly typical synchrotron spectra, with ![]() $-0.8 < \alpha < -0.6$. While the GLEAM measurements for some of the candidates exhibit significant scatter, none of the spectra show clear signs of variability, or of multiple components. Time-domain observations with the MWA’s VCS, for example, would be required to determine whether these sources are true pulsars, or simply strongly polarised compact extragalactic radio sources.
$-0.8 < \alpha < -0.6$. While the GLEAM measurements for some of the candidates exhibit significant scatter, none of the spectra show clear signs of variability, or of multiple components. Time-domain observations with the MWA’s VCS, for example, would be required to determine whether these sources are true pulsars, or simply strongly polarised compact extragalactic radio sources.
7. Conclusions and outlook
7.1. Conclusions
In this paper, we have presented the all-sky results from the POlarised GLEAM Survey (POGS). We have catalogued the low-frequency polarised radio source population, applying the RM synthesis technique to the GLEAM survey data, covering 25 489 square degrees of sky between Declination ![]() $+30^\circ$ and
$+30^\circ$ and ![]() $-82^\circ$. We have detected a total of 517 radio sources, of which 33 are known radio pulsars and the remaining 484 are nominally extragalactic in origin. We have reported the bulk properties of our two catalogues at a reference frequency of 200 MHz.
$-82^\circ$. We have detected a total of 517 radio sources, of which 33 are known radio pulsars and the remaining 484 are nominally extragalactic in origin. We have reported the bulk properties of our two catalogues at a reference frequency of 200 MHz.
Our extragalactic catalogue, POGS ExGal, contains sources with linearly polarised flux densities between 9.9 mJy and 1.1 Jy. All sources in POGS ExGal have RMs between ![]() $-328.07$ and
$-328.07$ and ![]() $+279.62$ rad m−2. We find that our RMs are largely consistent with previous RM catalogues at higher frequencies. We determine RMs for these sources that are typically one or two orders of magnitude more precise than previous studies, with a mean and worst-case uncertainty of
$+279.62$ rad m−2. We find that our RMs are largely consistent with previous RM catalogues at higher frequencies. We determine RMs for these sources that are typically one or two orders of magnitude more precise than previous studies, with a mean and worst-case uncertainty of ![]() $0.38$ and
$0.38$ and ![]() $10.65$ rad m−2, respectively. Our results suggest that the dominant component of the RM is contributed by the Galactic foreground, although there is sufficient discrepancy that some extragalactic RM contribution must also be present. We have compared the bulk polarisation properties of our sources with the 1.4 GHz polarised source population, finding that sources depolarise by about 55% between 1.4 GHz and 200 MHz.
$10.65$ rad m−2, respectively. Our results suggest that the dominant component of the RM is contributed by the Galactic foreground, although there is sufficient discrepancy that some extragalactic RM contribution must also be present. We have compared the bulk polarisation properties of our sources with the 1.4 GHz polarised source population, finding that sources depolarise by about 55% between 1.4 GHz and 200 MHz.
We find that the population of extragalactic radio sources shows significantly increasing fractional polarisation with decreasing Stokes I flux density. From our sample, fainter Stokes I sources (![]() $S<0.5$ Jy) tend to have a fractional polarisation that is
$S<0.5$ Jy) tend to have a fractional polarisation that is ![]() ${\sim}2.6$ higher than brighter Stokes I sources (
${\sim}2.6$ higher than brighter Stokes I sources (![]() $0.5<S<3$ Jy). While this is consistent with some previous studies at higher frequencies, we are naturally biased towards fainter Stokes I sources with higher fractional polarisation.
$0.5<S<3$ Jy). While this is consistent with some previous studies at higher frequencies, we are naturally biased towards fainter Stokes I sources with higher fractional polarisation.
We identify 10 ‘polarised doubles’, that is, extended radio galaxies where a physical pair of polarised sources are detected, associated with opposing radio lobes. All show statistically significant RM variations between physically related emission components. Our catalogue also contains 14 sources with large RMs, which we define as ![]() $|{\rm{RM}}| > 100$ rad m−2. The majority of these lie along LOSs that pass through ionised Galactic foregrounds, visible in H
$|{\rm{RM}}| > 100$ rad m−2. The majority of these lie along LOSs that pass through ionised Galactic foregrounds, visible in H![]() $\alpha$ emission.
$\alpha$ emission.
For our extragalactic source population, we observe no significant evolution in RRM (which can be used to probe extragalactic magnetic fields) as a function of redshift. This has been seen previously at higher frequencies but is seen here for the first time at low frequencies, which suggests that the observed Faraday rotation is occurring external to the radio sources. We also see an anticorrelation between RRM and polarisation fraction, which we attribute to a depolarisation mechanism. Given our long observing wavelength and our moderate resolution of around 3–7 arcmin, we suggest that the responsible mechanism is beam depolarisation due to small-scale variations in the Galactic RM that occur within our beam element.
Among our nominally extragalactic radio source population, we find four sources that are compact, exhibit a high polarisation fraction ![]() $(\Pi \geq 10\%),$ and do not have a clear infrared host; these we identify as new pulsar candidates.
$(\Pi \geq 10\%),$ and do not have a clear infrared host; these we identify as new pulsar candidates.
Our known-pulsar catalogue, POGS PsrCat, contains pulsars with linearly polarised flux density measurements between 17 mJy and 1.7 Jy. Our pulsar RMs span the range ![]() $-185.99$ to
$-185.99$ to ![]() $+150.74$ rad m−2. We find that our RMs are broadly consistent with known values, with a typical
$+150.74$ rad m−2. We find that our RMs are broadly consistent with known values, with a typical ![]() ${\sim}40\%$ improvement in the RM precision compared to previous measurements: our mean and worst-case uncertainties are
${\sim}40\%$ improvement in the RM precision compared to previous measurements: our mean and worst-case uncertainties are ![]() $0.22$ and
$0.22$ and ![]() $2.84$ rad m−2, respectively. There are 11 pulsars for which we make the first image-plane detection at low frequencies, and six pulsars for which we determine the first RMs.
$2.84$ rad m−2, respectively. There are 11 pulsars for which we make the first image-plane detection at low frequencies, and six pulsars for which we determine the first RMs.
Our image-domain search for pulsars has yielded RMs and fractional polarisations that are broadly consistent with previous time-domain, beam-formed, studies, although we note that we likely suffer from strong scintillation. Our study also demonstrates that image-domain searches retain sensitivity to significantly dispersed pulsars, as we find RMs for pulsars with DMs up to a factor ![]() ${\sim}2.5$ larger than previous time-domain beam-formed data.
${\sim}2.5$ larger than previous time-domain beam-formed data.
7.2. Further work
While this paper represents the final catalogue from our all-sky linear polarisation survey with the Phase I MWA, there are a number of novel aspects of the linearly polarised source population that are left to explore.
Foremost among these is the low-frequency linearly polarised source counts, which remain entirely unexplored. However, due to our non-standard source identification and verification method, the completeness of our catalogue is non-trivial to establish and will require injection of 3D source models into RM spectra—a novel adaptation of standard methods used in continuum source completeness evaluation. Such work is beyond the scope of this paper, but crucial for establishing the completeness, which is in turn key to probing the differential source counts.
Looking forward, polarisation work with the Phase II MWA will build on our work. The factor ![]() ${\sim}2$ improvement in resolution achievable with the extended configuration (up to
${\sim}2$ improvement in resolution achievable with the extended configuration (up to ![]() ${\sim}6$ km; Wayth et al. Reference Wayth2018) will provide a huge step forward for low-frequency polarimetry by significantly reducing beam depolarisation. Not only should this yield an increased number of detections across the sky, but a direct comparison of Phase I and Phase II MWA polarimetry using the same sources could provide insight into the scale size of Galactic foreground RM fluctuations. Both our work and Phase II MWA polarimetry also provide a crucial step in ‘filling in’ the gap in the Southern RM sky.
${\sim}6$ km; Wayth et al. Reference Wayth2018) will provide a huge step forward for low-frequency polarimetry by significantly reducing beam depolarisation. Not only should this yield an increased number of detections across the sky, but a direct comparison of Phase I and Phase II MWA polarimetry using the same sources could provide insight into the scale size of Galactic foreground RM fluctuations. Both our work and Phase II MWA polarimetry also provide a crucial step in ‘filling in’ the gap in the Southern RM sky.
Acknowledgements
This work makes use of the Murchison Radioastronomy Observatory, operated by the Commonwealth Scientific and Industrial Research Organisation. We acknowledge the Wajarri Yamatji people as the traditional owners of the Observatory site. Support for the operation of the MWA is provided by the Australian Government (National Collaborative Research Infrastructure Strategy) under a contract to Curtin University, administered by Astronomy Australia Limited. This work was supported by resources provided by the Pawsey Supercomputing Centre, with funding from the Australian Government and the Government of Western Australia.
CJR acknowledges financial support from the European Research Council Starting Grant ‘DRANOEL’, number 714 245. The Dunlap Institute is funded through an endowment established by the David Dunlap family and the University of Toronto. B.M.G. acknowledges the support of the Natural Sciences and Engineering Research Council of Canada through grant RGPIN-2015-05948, and of the Canada Research Chairs program. CSA is a Jansky Fellow of the National Radio Astronomy Observatory. NH-W is supported by an Australian Research Council Future Fellowship (project number FT190100231) funded by the Australian Government. We acknowledge the International Centre for Radio Astronomy Research, which is a joint venture between Curtin University and The University of Western Australia, funded by the Western Australian State Government. The financial assistance of the South African Radio Astronomy Observatory towards this research is hereby acknowledged (www.ska.ac.za). We thank Phil Edwards for helpful comments during the internal ATNF review process, and we thank our anonymous referee for their supportive and constructive feedback during peer review.
This work has made use of S-PASS data. All NVAS images used in this work were produced as part of the NVAS, (c) Associated Universities, Inc./NRAO. This research has made use of NASA’s Astrophysics Data System as well as the VizieR catalogue access tool, Centre de Données astronomiques de Strasbourg, Strasbourg, France. This research has made use of the NED, which is funded by the National Aeronautics and Space Administration and operated by the California Institute of Technology. Additionally, this research made use of the Tool for OPerations on Catalogues And Tables software (Taylor Reference Taylor, Stil and Sunstrum2005). We also used ionospheric Total Electron Content maps produced by the Centre for Orbital Determination in Europe (http://aiuws.unibe.ch/ionosphere/). We acknowledge the use of NASA’s SkyView service (http://skyview.gsfc.nasa.gov), located at the NASA Goddard Space Flight Center. Finally, we wish to acknowledge the developers of the following python packages, which were used extensively during this project: aplpy (Robitaille & Bressert Reference Robitaille and Bressert2012), astropy (Astropy Collaboration et al. 2013), lmfit (Newville et al. Reference Newville2017), matplotlib (Hunter Reference Hunter2007), numpy (van der Walt, Colbert, & Varoquaux Reference van der Walt, Colbert and Varoquaux2011), and scipy (Jones et al. Reference Jones, Oliphant and Peterson2001).
A. Spectral energy distribution fits
In this section, we show SED fits used to derive 200 MHz Stokes I flux densities for some sources in our catalogues. Figure A.1 shows the SEDs for GLEAM sources which have large fractional uncertainty in‘int_flux_fit_200’ from Hurley-Walker et al. (Reference Hurley-Walker2017). Figure A.2 shows the SEDs for TGSS-ADR1 sources. Figure A.3 shows the SEDs for new pulsar candidates identified in this work.

Figure A.1. SED plots for the 12 GLEAM sources with large fractional uncertainty in int_flux_fit_200 from Hurley-Walker et al. (Reference Hurley-Walker2017). Black markers denote GLEAM measurements, white markers denote measurements from the literature, using catalogues from TGSS-ADR1, SUMSS and the NVSS, where available. Dashed blue line denotes the best-fit power-law spectral index; shaded region denotes the ![]() $1\sigma$ uncertainty region mapped by EMCEE. All subplots are shown on matching x- and y-ranges.
$1\sigma$ uncertainty region mapped by EMCEE. All subplots are shown on matching x- and y-ranges.

Figure A.2. SED plots for sources detected using the TGSS-ADR1 Catalogue as a positional prior. White markers denote flux density measurements from the literature, using catalogues from the VLSSr, TGSS-ADR1, TXS, MRC, NVSS and GB6 surveys. Dashed blue line denotes the best-fit power-law spectral index; shaded region denotes the ![]() $1\sigma$ uncertainty region mapped by EMCEE. All subplots are shown on matching x- and y-ranges.
$1\sigma$ uncertainty region mapped by EMCEE. All subplots are shown on matching x- and y-ranges.

Figure A.3. SED plots for three of the four pulsar candidates in our catalogue. The SED for our fourth pulsar candidate, TGSS-ADR J230010.0![]() $+$184537, is already shown in Figure A.2. Filled points denote flux density measurements from GLEAM, empty points denote ancillary measurements from various radio surveys. Dashed blue line denotes the best-fit power-law spectral index; shaded region denotes the
$+$184537, is already shown in Figure A.2. Filled points denote flux density measurements from GLEAM, empty points denote ancillary measurements from various radio surveys. Dashed blue line denotes the best-fit power-law spectral index; shaded region denotes the ![]() $1\sigma$ uncertainty region mapped by EMCEE. All subplots are shown on matching x- and y-ranges.
$1\sigma$ uncertainty region mapped by EMCEE. All subplots are shown on matching x- and y-ranges.
B. Polarised doubles
Two ‘polarised doubles’—where we define a ‘polarised double’ as a pair of physically associated polarised sources—were previously presented in Figure 5. We present the remaining eight polarised doubles in POGS ExGal in Figure B.1.

POGS ExGal ‘Polarised doubles’. Panels show the following sources: POGSII-EG-005 & POGSII-EG-006 (G4Jy 7; top left), POGSII-EG-152 & POGSII-EG-153 (PMN J0351-2744/G4Jy 386; top right), POGSII-EG-174 & POGSII-EG-175 (ESO 422-G028/MSH 05-22/G4Jy 517; bottom left) and POGSII-EG-210 & POGSII-EG-211 (bottom right). Red, blue and yellow contours denote Stokes I surface brightness from GLEAM (200 MHz), the NVSS and TGSS-ADR1 respectively, starting at ![]() $3 \sigma$ and scaling by a factor
$3 \sigma$ and scaling by a factor ![]() $\sqrt{2}$. Where a host galaxy could be found, it is identified by a white ‘+’. Note that a host could not confidently be identified for POGSII-EG-210 & POGSII-EG-211. Right panels in each subplot show the source RM spectrum along the LOS through the cyan star (black) plus the foreground RM spectrum (red) as well as the instrumental leakage avoidance zone (shaded gray region). Green dashed line denotes the fitted RM; blue dot-dashed line denotes the
$\sqrt{2}$. Where a host galaxy could be found, it is identified by a white ‘+’. Note that a host could not confidently be identified for POGSII-EG-210 & POGSII-EG-211. Right panels in each subplot show the source RM spectrum along the LOS through the cyan star (black) plus the foreground RM spectrum (red) as well as the instrumental leakage avoidance zone (shaded gray region). Green dashed line denotes the fitted RM; blue dot-dashed line denotes the ![]() $7\sigma$ level.
$7\sigma$ level.

Panels show the following sources: POGSII-EG-221 & POGSII-EG-222 (PKS J0636-2036/G4Jy 619; top left), POGSII-EG-235 & POGSII-EG-236 (PKS 0707-35/G4Jy 644; top right), POGSII-EG-365 & POGSII-EG-366 (PKS 1733-56/G4Jy 1423; bottom left) and POGSII-EG-400 & POGSII-EG-401 (bottom right). Blue contours in the bottom left panel show SUMSS surface brightness starting at ![]() $20\sigma$ and scaling by a factor
$20\sigma$ and scaling by a factor ![]() $\sqrt{2}$, due to the presence of strong artefacts associated with bright sources in SUMSS.
$\sqrt{2}$, due to the presence of strong artefacts associated with bright sources in SUMSS.
C. Pulsar RM spectra
We present the RM spectra for the 33 known pulsars identified in POGS PsrCat in Figure C.1. As with RM spectra shown elsewhere in this paper, the source spectrum is shown in black and the off-source foreground spectrum is shown in red. The blue ![]() $7\sigma$ level is shown by the blue dot-dashed horizontal line, and the fitted peak shown as a vertical green dashed line. The polarised flux density is shown in mJy beam−1.
$7\sigma$ level is shown by the blue dot-dashed horizontal line, and the fitted peak shown as a vertical green dashed line. The polarised flux density is shown in mJy beam−1.

Figure C.1. RM spectra for the 33 known pulsars in POGS PsrCat. The x-axes show RM (rad m-2), y-axes show linearly polarised flux density (mJy beam-1). The source RM spectrum (off-source foreground RM) is shown in black (red). The instrumental leakage avoidance zone is shown in shaded gray; the green dashed line denotes the fitted RM, and the blue dot-dashed line denotes the ![]() $7\sigma$ level.
$7\sigma$ level.
D. Extragalactic source RM spectra
Figure D.1 presents the RM spectra of all POGS ExGal sources, aside from the 10 ‘polarised doubles’. As with previous RM spectra, the source spectrum is shown in black and the off-source foreground spectrum is shown in red. The ![]() $7\sigma$ level is shown by the blue dot-dashed horizontal line, and the fitted peak shown as a vertical green dashed line. The polarised flux density is shown in mJy beam−1.
$7\sigma$ level is shown by the blue dot-dashed horizontal line, and the fitted peak shown as a vertical green dashed line. The polarised flux density is shown in mJy beam−1.
















Figure D.1. RM spectra for POGS ExGal sources. The x-axes show RM (rad m-2), y-axes show linearly polarised flux density (mJy beam-1). The source RM spectrum (off-source foreground RM) is shown in black (red). The instrumental leakage avoidance zone is shown in shaded gray; the green dashed line denotes the fitted RM, and the blue dot-dashed line denotes the ![]() $7\sigma$ level.
$7\sigma$ level.