1. Introduction
In 2017, GW170817, a gravitational wave produced by the merging of two neutron stars (NS), was observed by Advanced LIGO/Virgo (Abbott et al. Reference Abbott2017). Its transient counterparts were detected across almost the entire electromagnetic spectra (e.g., Abbott et al. Reference Abbott2017; Arcavi et al. Reference Arcavi2017; Cowperthwaite et al. Reference Cowperthwaite2017), hence hailing the advent of a new era in multi-messenger astronomy.
Notably, only two seconds after the discovery of GW170817, a short γ-ray burst (GRB) was detected by both the Fermi and INTEGRAL space telescopes (Abbott et al. Reference Abbott2017). Traditionally, GRBs are divided into long GRBs and short GRBs. Long GRBs (T 90 ≥ 2s) result from the death of massive stars and their accompanying supernovae. Short GRBs (T 90 ≤ 2s), however, are a result of the merging of two compact objects (Paczynski Reference Paczynski1986; Eichler et al. Reference Eichler, Livio, Piran and Schramm1989; Piran Reference Piran1992). Therefore, the discovery of a short GRB provides the tantalising prospect that GW170817 may have originated from a double NS merger. According to Abbott et al. (Reference Abbott2017), the product of GW170817 was a compact object with a solar mass of 2.7 Mʘ. It is possible that this object may form a millisecond pulsar (MSP), a magnetar, in the future, or it may even rapidly collapse into a black hole (Dai & Lu Reference Dai and Lu1998; Dai et al. Reference Dai, Wang, Wu and Zhang2006), but due to its sheer distance, there are no telescopes or astronomical equipment in the world capable of confirming its current state.
In 2006, Gehrels et al. (Reference Gehrels2006), Della Valle et al. (Reference Della Valle2006), and Gal-Yam et al. (Reference Gal-Yam2006) published the discovery of a special GRB: GRB060614. It was a long GRB (∼100s) and was not associated with any supernova (Gehrels et al. Reference Gehrels2006; Della Valle et al. Reference Della Valle2006; Gal-Yam et al. Reference Gal-Yam2006). About this, King, Olsson, & Davies (Reference King, Olsson and Davies2007) suggest that GRB060614 may have originated from the merging of an NS and a massive white dwarf (WD). Currently, a total of 10 GRBs have been observed as having GRB060614-esque properties (Ruffini et al. Reference Ruffini2016).
What’s more, the subset of NS + WD binaries, resulting from a merger, would be likely source for so-called ‘calcium-rich gap’ transients. These are a class of optical events characterised by subluminous type-I supernovae, such as SN 2005E (Perets et al. Reference Perets2010; Kasliwal et al. Reference Kasliwal2012).
In theory, merging an NS and a massive WD could produce an isolated millisecond pulsar (IMSP) (van den Heuvel & Bonsema 1984). IMSPs are a special type of pulsar. According to data from Manchester et al. (Reference Manchester, Hobbs, Teoh and Hobbs2005), approximately 2 600 different pulsars have been observed, most of which are ‘normal pulsars’ with pulse periods of P∼ 0.1–10 s. However, there are roughly 325 other pulsars, which exhibit pulse periods of ∼1.4–20 ms (Pan, Wang, & Zhang Reference Pan, Wang and Zhang2013). These are so-called MSPs. The typical age (τ c) of ‘normal pulsars’ is 107 yr, with a surface magnetic field strength (B) of 1012 G. For MSPs, however, these values are 109 yr and 108 G, respectively (Lorimer Reference Lorimer2008). Generally, MSPs are thought to be NSs with a high rotation rate, being formed from the accreting matter of an NS and its companion star (see Alpar et al. Reference Alpar, Cheng, Ruderman and Shaham1982; Bhattacharya & van den Heuvel Reference Bhattacharya and van den Heuvel1991).
For this reason, one might surmise that all MSPs evolved from binary systems. However, according to the Australia Telescope National Facility (ATNF) catalogue, approximately 1/3 of MSPs are isolated (Manchester et al. Reference Manchester, Hobbs, Teoh and Hobbs2005). Their origins are highly debated, with different scholars proposing a variety of different possible scenarios.
First, van den Heuvel & Bonsema (Reference van den Heuvel and Bonsema1984) proposed that IMSPs were a product of gravitational wave emissions after the merging of an NS and a massive WD. However, after the MSP PSR 1957+20 was discovered by Fruchter, Stinebring, & Taylor (Reference Fruchter, Stinebring and Taylor1988), it was proposed that pulsar wind was the major cause of IMSP formation (Kluzniak et al. Reference Kluzniak, Ruderman, Shaham and Tavani1988). In other words, a low-mass helium WD (with a solar mass ∼0.02 Mʘ) would be left when the mass transfer results in a low-mass X-ray binary. Due to the high energetic radiation emitted from the MSP, the WD would then be completely ablated. This process was known as the Standard Model. However, Stappers et al. (Reference Stappers, Bailes, Manchester, Sandhu and Toscano1998) found that the timescale for ablation provided in the Standard Model was too long for an NS to evolve into an IMSP in Hubble time (see also Chen et al. Reference Chen, Chen, Tauris and Han2013). Though the ∼9-h orbit of PSR 1957+20 has a relatively short ablation timescale of merely 3×107 yr (Ryba & Taylor Reference Ryba and Taylor1991), it is unlikely that this could truly be observed in such a short time phase.
Second, Bhattacharya & van den Heuvel (Reference Bhattacharya and van den Heuvel1991) proposed another possible evolutionary scenario. They believed that the MSPs formed from high-mass X-ray binaries can evolve into IMSPs when such binaries are disrupted by a core-collapse supernova from their companion stars. Although this scenario may be suitable for some IMSPs in these systems, it is unlikely to represent the most common formation models (Belczynski et al. Reference Belczynski, Lorimer, Ridley and Curran2010). Recently, a possible solution in the form of a triple-star formation model was discussed by Freire et al. (Reference Freire2011), based on ideas previously put forward by Eggleton & Verbunt (Reference Eggleton and Verbunt1986). In their model, the orbit of a triple star system expands when materials transfer from the donor star to the NS. Subsequently, the accreting NS will then evolve into an MSP. If the triple star system becomes dynamically unstable, then it is possible for the MSP to be ejected, hence forming an IMSP. Portegies Zwart et al. (Reference Portegies Zwart, van den Heuvel, van Leeuwen and Nelemans2011), however, contradict this model, stating that these phenomena in fact contribute very little to the formation of IMSPs.
As can be seen from the discussion above, none of the three scenarios above have been able to provide a definitive explanation for the origin of IMSPs. In the first model, Nelemans, Yungelson, & Portegies Zwart (Reference Nelemans, Yungelson and Portegies Zwart2001) estimate that there are, theoretically, ∼2.2×106 NS + WD binaries in the Galaxy and the merger rate of these systems ranges from about 1.0×10−6y−1 (Cooray Reference Cooray2004) to 1.4 ×10−4yr−1 (Nelemans et al. Reference Nelemans, Yungelson and Portegies Zwart2001). Similarly, Thompson, Kistler, & Stanek (Reference Thompson, Kistler and Stanek2009), with 95% confidence, state that the lowest galactic merger rate for NS + WD systems is 2.5 ×10−5yr−1.
This paper builds on the previous research mentioned above, undertaking its own investigation into the possibility of forming IMSPs via the merging of NSs and WDs. Section 2 below presents both the authors’ assumptions and details on the modelling algorithms. This is then followed by a set of results in Section 3 and final conclusions in Section 4.
2. Models
In this paper, the authors draw on the rapid binary star evolution (BSE) code, as expounded in Hurley, Pols, & Tout (Reference Hurley, Pols and Tout2000), Hurley, Tout, & Pols (Reference Hurley, Tout and Pols2002), and updated by Kiel & Hurley (Reference Kiel and Hurley2006). Unless specifically mentioned, our default input parameters are also based on those found in the above literature.
2.1. Kick velocity
During its formation, non-spherical symmetry of an NS creates additional ‘kick’ velocity. The physical origin of this non-spherical symmetry, however, remains somewhat enigmatic. In 1975, Katz (Reference Katz1975) suggested that these kicks may have a dichotomous nature, which was later confirmed by Hartman et al. (Reference Hartman, Bhattacharya, Wijers and Verbunt1997) and Pfahl, Rappaport, & Podsiadlowski (Reference Pfahl, Rappaport and Podsiadlowski2002). Despite this, kick velocity cannot be easily controlled during observation, due to its numerous and complicated selection effects.
Typically, the distribution of the kick velocity is a Maxwellian with a dispersion (σk) of
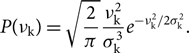 \begin{equation}P({\nu _{\rm{k}}}) = \sqrt{{2 \over \pi }} {{\nu _{\rm{k}}^2} \over {\sigma _{\rm{k}}^3}}{e^{ - \nu _{\rm{k}}^2/2\sigma _{\rm{k}}^2}}.\end{equation}
(1)
\begin{equation}P({\nu _{\rm{k}}}) = \sqrt{{2 \over \pi }} {{\nu _{\rm{k}}^2} \over {\sigma _{\rm{k}}^3}}{e^{ - \nu _{\rm{k}}^2/2\sigma _{\rm{k}}^2}}.\end{equation}
(1)
In Hansen & Phinney (Reference Hansen and Phinney1997), analysis of the proper motion of approximately 100 pulsars found σk to be equal to 190 km s−1. Hobbs et al. (Reference Hobbs, Lorimer, Lyne and Kramer2005), however, examined the proper motion of 233 pulsars and found that the kick velocity could be described by a single Maxwellian with σk = 265 km s−1. In the present investigation, we apply different velocity dispersions in different cases.
2.2. Evolution of NS + WD binary systems
NSs and WDs are both stellar remnants. Once binary systems are formed from them, there can often be disastrous consequences. In NS + WD systems, gravitational wave radiation can cause the orbital angular momentum (Jorb) to decay. Faulkner (Reference Faulkner1971) noted that the decay ratio of Jorb was the following formula, where c is the speed of light and a is the separation of the binary system:
As the orbital period shrinks, the WD fills its Roche lobe and begins to act as a donor, transferring its mass to the NS. This mass transfer can be either dynamically stable or unstable—at this point, either outcome is possible. Based on an investigation into stable mass transfer, using polytropic models, Hjellming & Webbink (Reference Hjellming and Webbink1987) and Hurley et al. (Reference Hurley, Tout and Pols2002) concluded that if the mass ratio of the components (q = M
donor/M
gainer) is larger than a certain value, q
c, at the onset of Roche lobe overflow, then the mass transfer will be dynamically unstable. Otherwise, the mass transfer will be stable. According to Hurley et al. (Reference Hurley, Tout and Pols2002), the value of q
c, in an NS + WD binary system is 0.628. However, based on the isotropic re-emission mechanism,Footnote
a
van Haaften et al. (Reference van Haaften, Nelemans, Voss, Wood and Kuijpers2012) put forward even stricter criteria for mass transfers in an NS + WD system to be stable, i.e. the critical mass of the WD (
![]() $ M_{{\rm{W}}D}^{\rm{c}} $
) donor must be 0.37 Mʘ. Recent scholarship into the angular momentum of material lost in disc winds, such as Bobrick, Davies, & Church (Reference Bobrick, Davies and Church2017), has found that the
$ M_{{\rm{W}}D}^{\rm{c}} $
) donor must be 0.37 Mʘ. Recent scholarship into the angular momentum of material lost in disc winds, such as Bobrick, Davies, & Church (Reference Bobrick, Davies and Church2017), has found that the
![]() $ M_{{\rm{W}}D}^{\rm{c}} $
may also be equal to 0.2 Mʘ, significantly lower than previously thought. If the mass transfer does, for some reason, become dynamically unstable, then the WD will be tidally disrupted by the NS, which, in turn, may lead to a merger and a gravitational wave event (Paschalidis et al. Reference Paschalidis, MacLeod, Baumgarte and Shapiro2009; van den Heuvel & Bonsema Reference van den Heuvel and Bonsema1984). However, according to Margalit & Metzger (Reference Margalit and Metzger2016), in most circumstances, the mass accreted by an NS is insufficient to induce a gravitational collapse. It is often capable, however, of simply increasing the rotational velocity of the NS by several milliseconds. For this reason, it is critically important to consider the parameters of dynamically unstable mass transfer in our investigative models.
$ M_{{\rm{W}}D}^{\rm{c}} $
may also be equal to 0.2 Mʘ, significantly lower than previously thought. If the mass transfer does, for some reason, become dynamically unstable, then the WD will be tidally disrupted by the NS, which, in turn, may lead to a merger and a gravitational wave event (Paschalidis et al. Reference Paschalidis, MacLeod, Baumgarte and Shapiro2009; van den Heuvel & Bonsema Reference van den Heuvel and Bonsema1984). However, according to Margalit & Metzger (Reference Margalit and Metzger2016), in most circumstances, the mass accreted by an NS is insufficient to induce a gravitational collapse. It is often capable, however, of simply increasing the rotational velocity of the NS by several milliseconds. For this reason, it is critically important to consider the parameters of dynamically unstable mass transfer in our investigative models.
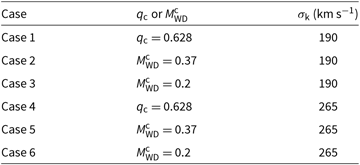
In order to discuss the effect of q c on the formation of IMSPs, the authors calculated a total six possible cases, each of which contain different combinations of mass and kick velocity values, such as those mentioned above (see Table 1).
Table 1. Parameters of the population models for NS + WD binaries
2.3. Post-merger NS
As mentioned above, this paper is built on the assumption that the merging of an NS and a WD can produce an IMSP. After a merge, Metzger (Reference Metzger2012) estimated that about 20–50% of the WD’s matter is accreted by the NS and then the remainder is ejected as energy, released by both gravity and nuclear reactions during the tidal disruption of the WD. Here, we assume that the post-merger mass of the NS is equal to M NS + 0.5 MWD.
After merging, the spin (P s) of the NS is also affected by its surrounding matter. There is a great deal of scholarship on the interaction between rotating magnetised NSs and their surrounding matter (e.g. Pringle & Rees, Reference Pringle and Rees1972; Illarionov & Sunyaev, Reference Illarionov and Sunyaev1975; Lipunov, Börner, & Wadhwa, Reference Lipunov, Börner and Wadhwa1992; Lovelace, Romanova, & Bisnovatyi-Kogan, Reference Lovelace, Romanova and Bisnovatyi-Kogan1999). In these works, the value of P s chiefly depends on both the NS’ mass accretion rate and also its magnetic field. What’s more, during the merging process, the mass accretion rate (∼10−2 Mʘ yr−1) is significantly higher than the Eddington accretion rate (Metzger Reference Metzger2012). Lipunov (Reference Lipunov1982) investigated magnetised NSs with a super-Eddington rate of accretion, giving the NS’ equilibrium spin period as
In the above, μ30 = μ/(1030 G cm3), where
![]() $ \mu = {B_{{\rm{N}}S}}R_{{\rm{N}}S}^3/2 $
denotes the magnetic dipole momentum, B
NS is the magnetic field, and RNS is the radius of the NS. In this particular case, the RNS = 106 cm. After the merger, the spin then decreases due to a brake in the current (Beskin Reference Beskin1993). Hence, the evolution of spin can be given approximately as
$ \mu = {B_{{\rm{N}}S}}R_{{\rm{N}}S}^3/2 $
denotes the magnetic dipole momentum, B
NS is the magnetic field, and RNS is the radius of the NS. In this particular case, the RNS = 106 cm. After the merger, the spin then decreases due to a brake in the current (Beskin Reference Beskin1993). Hence, the evolution of spin can be given approximately as
The evolution of NS’ magnetic fields is still unknown. Using their death and spin-increase line as evidence, Urpin & Konenkov (Reference Urpin and Konenkov1997) calculated a decrease in an NS’ magnetic field strength as it evolved into an MSP. Their calculation was as follows:
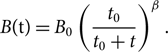 \begin{equation}B({{t}}) = {{\rm{B}}_0}{\left( {{{{{{t}}_0}} \over {{{{t}}_0} + {{t}}}}} \right)^\beta }.\end{equation}
(5)
\begin{equation}B({{t}}) = {{\rm{B}}_0}{\left( {{{{{{t}}_0}} \over {{{{t}}_0} + {{t}}}}} \right)^\beta }.\end{equation}
(5)
In the above, B 0, t 0, and t, respectively, denote the initial field strength, the time-scale of decay, and the age of the NS. β is a free parameter. Based on figures from the ATNF, pulsars which age less than 105 yr have magnetic fields of between roughly 1012 and 1013 G, averaging out at approximately 8×1012 G. Hence, this work takes the value of B 0 as 8×1012 G and t 0 as 105 yr. In the majority of cases, the time it takes for an NS to form and then merge with its companion star may range from around 106–108yr. For this reason, the authors follow in the footsteps of Urpin & Konenkov (Reference Urpin and Konenkov1997), taking β as 1.0. Whilst merging, the magnetic field of the NS may either increase via a so-called winding-up process (Ohlmann et al. Reference Ohlmann, Röpke, Pakmor, Springel and Müller2016) or decrease due to an enhanced Ohmic dissipation of accreted matter. However, to the authors’ knowledge, there are currently no models available to simulate this event. For this reason, the models used in this paper assume that magnetic fields do not change during the merging process.
3. Results
In order to understand more about the birth rate of IMSPs and their physical properties, the authors use population synthesis to simulate the evolution of 107 binary systems.
The cases considered in the present study show a similarity to those in Lü, Yungelson, & Han (Reference Lü, Yungelson and Han2006), Lü et al. (Reference Lü, Zhu, Han and Wang2008, Reference Lü, Zhu, Wang and Wang2009, Reference Lü2012), and Lü, Zhu, & Podsiadlowski (Reference Lü, Zhu and Podsiadlowski2013). Notably, the authors use a simple approximation to the initial mass function (IMF), based on Miller & Scalo (Reference Miller and Scalo1979). The primary mass is then generated using the formula suggested by Eggleton, Fitchett, & Tout (Reference Eggleton, Fitchett and Tout1989). The distribution of separations is given by log a = 5X + 1, where X is a random variable between 0 and 1 and a is orbital separation in units of Rʘ. In our models, all binaries have initial circular orbits and the metallicity Z is set to 0.02 for PopulationI stars.
Furthermore, in the case of a constant star formation rate, the authors assume that one binary, with a primary body more massive than 0.8 Mʘ, is formed annually in the Galaxy (Yungelson, Tutukov, & Livio Reference Yungelson, Tutukov and Livio1993; Han, Podsiadlowski, & Eggleton Reference Han, Podsiadlowski and Eggleton1995; Yisikandeer et al. Reference Yisikandeer, Zhu, Wang and Lü2016).
3.1. NS + WD binaries
There are three possible evolutionary pathways for NS + WD binaries. Firstly, the WD is unable to fill its Roche lobe, due to its long orbital period within Hubble time. Secondly, the WD can fill its Roche lobe and its matter can undergo a stable transfer to the NS, hence evolving into an ultra-compact X-ray binary. Thirdly, the WD successfully fills its Roche lobe and the merging process begins. It is the latter of the three pathways that is the focus of this investigation.
According to ATNF, there are a total of 147 binaries, composed of one pulsar and one WD (Manchester et al. Reference Manchester, Hobbs, Teoh and Hobbs2005). Figure 1 gives a comparison of WD masses and orbital periods between the NS + WD binaries in our simulation and those from ATNF. On average, our results tend to show overall larger masses than those observed in other systems, where figures are usually recorded as around 0.2–0.3 Mʘ. For example, there were even systems in which the mass of the WD is between 0.4 and 0.8 Mʘ. Since these WDs have smaller radii, they will never fill their Roche lobes in Hubble time. In fact, the majority of NSs recorded in these systems appear to have already passed their deadline, hence should no longer be observed as pulsars.
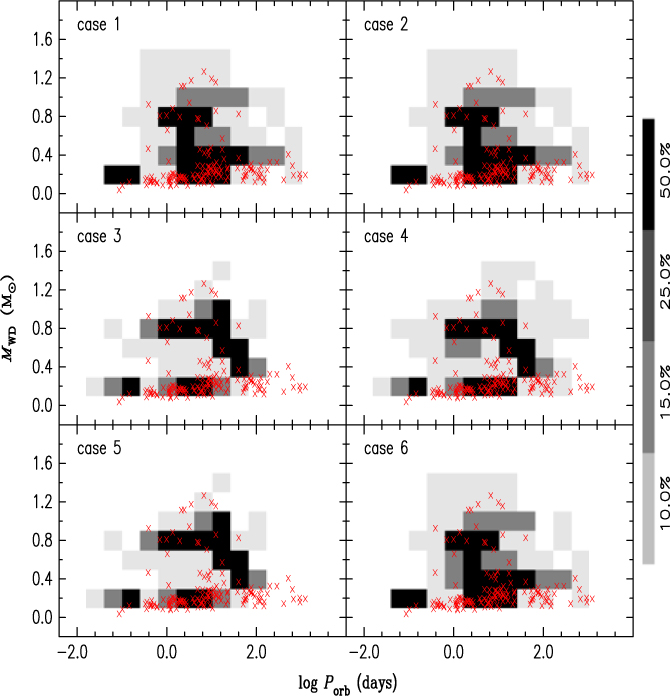
Figure 1. Grey-scale maps of WD masses and orbital periods in NS + WD binaries. The red multiplication sign (×)represents observational values for the binaries composed of a pulsar and a WD. The observational data comes from the ATNF, as cited in Manchester et al. (Reference Manchester, Hobbs, Teoh and Hobbs2005).
If the WDs in NS + WD binaries fill their Roche lobes within Hubble time, then mass transfer shall inevitably occur. Once mass transfer begins, if q < q
c or
![]() $ M_{{\rm{WD}}} \lt M_{{\rm{WD}}}^{\rm{c}} $
, then it will be dynamically stable and the original binaries will, in turn, evolve into new ultra-compact X-ray binaries. At present, there are a total of 30 known ultra-compact X-ray binaries and formation candidates in the Galaxy (Liu, van Paradijs, & van den Heuvel Reference Nelemans and Jonker2007; Nelemans & Jonker Reference Liu, van Paradijs and van den Heuvel2010). The evolution of such ultra-compact X-ray binaries has been investigated by previous researchers, such as Yungelson (Reference Yungelson2008), vanHaaften et al. (Reference van Haaften, Nelemans, Voss, Wood and Kuijpers2012), and Lü et al. (Reference Lü, Zhu, Wang and Iminniyaz2017). Contrastingly, if q > q
c or
$ M_{{\rm{WD}}} \lt M_{{\rm{WD}}}^{\rm{c}} $
, then it will be dynamically stable and the original binaries will, in turn, evolve into new ultra-compact X-ray binaries. At present, there are a total of 30 known ultra-compact X-ray binaries and formation candidates in the Galaxy (Liu, van Paradijs, & van den Heuvel Reference Nelemans and Jonker2007; Nelemans & Jonker Reference Liu, van Paradijs and van den Heuvel2010). The evolution of such ultra-compact X-ray binaries has been investigated by previous researchers, such as Yungelson (Reference Yungelson2008), vanHaaften et al. (Reference van Haaften, Nelemans, Voss, Wood and Kuijpers2012), and Lü et al. (Reference Lü, Zhu, Wang and Iminniyaz2017). Contrastingly, if q > q
c or
![]() $ {M_{{\rm{WD}}}} \lt M_{{\rm{WD}}}^{\rm{c}} $
, then a dynamical mass transfer will occur stably and the NS and WD will begin to merge into an IMSP.
$ {M_{{\rm{WD}}}} \lt M_{{\rm{WD}}}^{\rm{c}} $
, then a dynamical mass transfer will occur stably and the NS and WD will begin to merge into an IMSP.
3.2. IMSP population
In our investigative models, an IMSP’s mass equals M NS + 0.5M WD. Figure 2 uses a chart to illustrate the distribution of IMSP mass in our models. From the chart, one can see that when q c = 0.628, the solar mass of the IMSP ranges from 1.7 to 2.0 Mʘ, whereas the mass of other models lies between 1.5 and 1.7 Mʘ. This shows that IMSPs are generally more massive than normal pulsars, which themselves have a total mass of around 1.4 Mʘ. Unfortunately, academia has not yet been able to provide any accurate measurements for the exact mass of an IMSP. What’s more, the highest left peak in Figure 2 reaches approximately 2.5 Mʘ. This highlights the possibility that the progenitors of NSs may have had a higher initial mass and shorter initial period, causing NSs to gain a total solar mass of approximately >2.0 Mʘ during their pre-merging period.
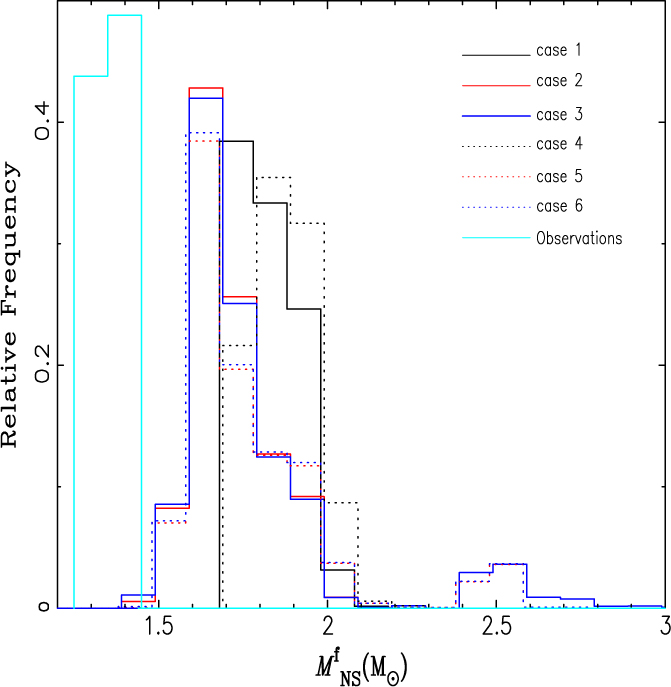
Figure 2. The mass distribution of IMSPs in the paper’s investigative models. The observational data consist of currently known normal stars’ pulsar masses, which are taken from https://stellarcollapse.org/nsmasses (Lattimer Reference Lattimer2012).
In addition to mass, spin periods are also one of the most important physical parameters of an IMSP. Figure 3 presents spin distributions for the IMSPs recorded in the present study. In general, the data correlates with previous observations, but some peaks in our model seem to show a somewhat slower spin than those observed in previous studies. This leads one to surmise that the widely accepted figures for the magnetic field of a post-merger NS could possibly be an overestimation. Nevertheless, the magnetic field of an NS is notoriously hard to determine. Furthermore, researchers have not yet reached a common understanding on the decay of an accreting NS’ magnetic field. One possibility was proposed by Bisnovatyi-Kogan & Komberg (Reference Bisnovatyi-Kogan and Komberg1974), who, through the examination of original magnetic fields, concluded that the decay of an NS may be caused by its accreted matter.
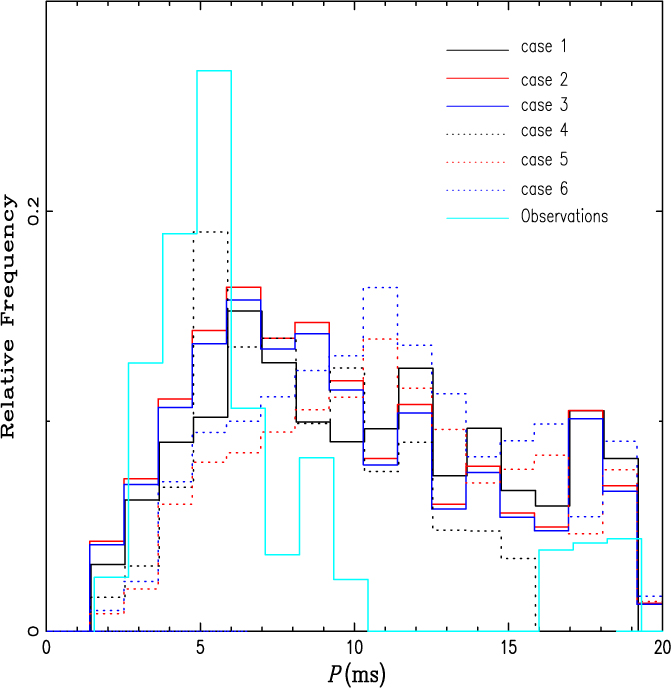
Figure 3. The distributions of spin periods for IMSPs in different models. The data included comes from the ATNF, as cited in Manchester et al. (Reference Manchester, Hobbs, Teoh and Hobbs2005).
3.3. Merger rate
Using the method of population synthesis, the present study estimates that the merger rate of NS + WD binaries lies between 5.8×10−5 yr−1 (case 4) and 2.0×10−4 yr−1 (case 3). From case 1 to case 3, the numbers of NS + WD binaries also increased from 666 to 1981, thanks to differing critical values. In other words, one can conclude that the smaller the critical mass of a WD, the more IMSPs will be formed. In addition to this, comparing case 1 with case 4, case 2 with case 5, and case 3 with case 6 suggests that the higher the kick velocity is, the less IMSPs are formed. This is because the nascent NS’ kick velocity plays a determining role in whether the binary can continue to survive or whether, if the kick velocity is too high, it will be disrupted by a supernova explosion.
Furthermore, the authors of the present survey also consider NS + WD mergers as a potential progenitor of calcium-rich supernovae. According to According to Kennicutt (Reference Kennicutt1998), the Milky Way took 0–10 Mʘ yr−1 to form. If one takes the median of this range, then that makes 5 Mʘyr−1 the rate of star formation. Kasliwal et al. (Reference Kasliwal2012), however, put forward a possible a lower limit for calcium-rich gap events of 7×10−7 Mpc−3 yr−1.
To calculate the total star production rate, one can use the following formula from Strolger et al. (Reference Strolger2004):
Therein, t denotes the age of the Universe in Gyr and t 0 is the current age of the Universe. If one follows through with Strolger et al.’s (Reference Strolger2004) method and takes t 0 to be 13.47 Gyr, and the parameters a = 0.021, b = 2.12, c = 1.69, and d = 0.207, then one can infer that the rate of Ca-rich gap transients in the Galaxy is roughly 5×10−4 yr−1. This result is relatively close to our simulation-base estimations.
In general, our results are consistent with Nelemans et al. (Reference Nelemans, Yungelson and Portegies Zwart2001). The merger rate of NS + WD binaries is approximately 3–10 times that of double NS systems (Portegies Zwart & Yungelson Reference Portegies Zwart and Yungelson1999). Although gravitational waves are released during the merging of an NS and a WD, they can hardly be detected, due to their relatively low amplitude and frequency. It is their electro-magnetic counterparts that should be observed, as they eject significantly more observable matter. As for whether GRBs, such as GRB060614, originate from the merger of an NS and a WD binary, this hypothesis is certainly possible, but many more multiband observations are still needed until we get a more defined and clear-cut answer.
4. Conclusion
In this paper, the authors investigated the merging of NS and WDs as the possible origin of IMSP. This paper not only estimated that IMSPs’ galactic birth rate is between approximately 5.8×10−5yr−1 and 2.0×10−4yr−1, depending on variables such as stable mass transfer via the Roche lobe and kick velocity, but also predicted that the solar mass of IMSPs lies between 1.5 and 2.0 Mʘ, which makes them more massive than normal pulsars. What’s more, most of the IMSPs in our simulations have a spin period of several to 20 ms, which is consistent with previous observations.
If it is true that the majority of IMSPs originate from the merging of NSs and WDs, then this event may trigger a GRB060614-esque reaction and produce gravitational waves. If it be possible to detect these in the future, then our field will be one step closer to a fuller understanding of GRBs and gravitational waves.
Acknowledgements
We would like to take this opportunity to thank an anonymous referee for all their useful comments. This work received the generous support of the National Natural Science Foundation of China, projects No. 11763007, 11473024, 11463005, 11863005, and 11503008. We would also like to express our gratitude to the Tianshan Youth Project of Xinjiang (No. 2017Q014).






