1 INTRODUCTION
The Earth’s ionosphere, being a dispersive medium at radio wavelengths, causes a change in the propagation velocity of radio waves, among other effects. The ionosphere is directly dependent on the solar activity through the high-energy far ultraviolet and X-rays. The ionosphere further varies depending on various transportation and depletion processes, namely, due to the influence of tides and atmospheric (gravity) waves, solar winds, and vertical transport through eddy’s diffusion and the geomagnetic disturbances (Zolesi & Cander Reference Zolesi and Cander2014). Considering the ionosphere to be highly variable and uncertain, it becomes important to monitor the ionosphere on a regular basis for a number of applications.
Early ground-based ionospheric sensors like ionosondes were effective for understanding the bottomside ionosphere. Ground-based coherent and incoherent radars operating at High Frequency (HF, 3–30 MHz), Very-High Frequency (VHF, 30–300 MHz) and Ultra-High Frequency (UHF, 300–3000 MHz), are able to probe the middle and upper ionosphere. Example of coherent radars include the Super Dual Auroral Radar Network consisting of around 34 HF radars located at mid-latitudes and extending into the polar regions. The radars are pointed towards the North and the South poles to study ionospheric convection (Zolesi & Cander Reference Zolesi and Cander2014). Incoherent radars include the Jicamarca Radio Observatory located along the geomagnetic equator in Lima, Peru, (49.92 MHz), the Arecibo dish in Puerto Rico (430 MHz), and European Incoherent Scatter, northern Scandinavia, operating at UHF (931 and 500 MHz) and VHF (224 MHz) (Zolesi & Cander Reference Zolesi and Cander2014). To access information about the topside ionosphere, satellite-based topside sounders have also been used (Hunsucker Reference Hunsucker2013). With the advent of radio communication satellites, the signals from such satellite systems were used to obtain spatial and temporal information on the ionosphere (Leitinger et al. Reference Leitinger, Hartmann, Lohmar and Putz1984).
The Global Positioning System (GPS) was designed by the Department of Defence, US, in the early 1970s to fulfil US military requirements (FRP 2001). It has since been used in various civilian applications, from navigation to precise geodetic positioning. The promise of GPS to operate in all weather conditions, 24 × 7, in addition to its multi-frequency transmission, has made it a useful tool to monitor ionospheric parameters (El-Rabbany Reference El-Rabbany2006). In comparison to ground-based ionospheric sensors like radars and ionosondes, the satellite-based system like GPS can provide continuous near-real-time global coverage of the ionosphere.
For precise positioning applications using GPS, new control points can be established by applying constraints using positions from the established control points. Global GPS data processing centres like the International GNSS (Global Navigation Satellite System) Service (IGS), with international multi-agency members, provide support for such global geodetic activities. In addition to the positions of the global network of GPS/GNSS stations, a number of products such as precise satellite ephemerides, satellite clock parameters, Earth rotation parameters, global ionosphere maps, and zenith tropospheric path delays are routinely generated (Beutler et al. Reference Beutler, Rothacher, Schaer, Springer, Kouba and Neilan1999). Global ionospheric maps are also generated by various IGS analysis centres, namely, the Center for Orbit Determination in Europe (CODE), the Astronomical Institute at the University of Bern, Switzerland (Rothacher et al. Reference Rothacher1997), and the Jet Propulsion Laboratory (JPL), California Institute of Technology, U.S (Mannucci et al. Reference Mannucci, Wilson, Yuan, Ho, Lindqwister and Runge1998; Komjathy et al. Reference Komjathy, Sparks, Wilson and Mannucci2005), among others. The temporal and spatial resolution of global maps is generally of 2 h and 5°/2.5° in longitude/latitude, respectively.
Real-time GPS positioning accuracy can be improved by providing ionospheric and other corrections directly to the user. This is the role of space-based augmentation systems such as the Wide Area Augmentation System in the US (Parkinson & Spilker Reference Parkinson and Spilker1996). Vertical ionosphere corrections are generated at temporal and spatial resolution of 3 min and 5°/5° in latitude/longitude, respectivelyFootnote 1.
The Global GPS data are also processed at the MIT Haystack Observatory by the mapgps software package in order to generate global Total Electron Content (TEC) maps (see Rideout & Coster Reference Rideout and Coster2006). The TEC maps are generated with a greater temporal and spatial resolution of 10 min and 1°/1° in longitude/latitude, respectively, and are distributed through an open source, web-based systemFootnote 2. To achieve even finer spatial resolution, regional ionosphere modelling must be performed. Regional ionosphere data centres like the Royal Observatory of Belgium (ROB) are able to model the ionosphere over small spatial areas with higher sampling of ground GPS stations with a temporal and spatial resolution of 15 min and 0.5°/0.5° in longitude/latitude, respectively (Chevalier et al. Reference Chevalier, Bergeot, Bruyninx, Legrand, Baire, Defrainge and Aerts2013).
Since the early days of radio astronomy, the ionosphere has been found to have a profound effect on astrometric observations. In a study of discrete radio sources, fluctuations in the signal from Cygnus A at observing frequency of 68 MHz were reported by Hey, Parsons, & Phillips (Reference Hey, Parsons and Phillips1946). Further investigation confirmed this to be a result of ionospheric structures. Hewish (Reference Hewish1951) and Booker (Reference Booker1958), among others, used this information to quantify ionospheric fluctuations and present some insights into the nature and behaviour of the ionosphere. Radio astronomy can be used to extract information on the ionosphere, however an external source for deriving information on the ionosphere is needed to calibrate astrometric observations.
Ros et al. (Reference Ros, Marcaide, Guirado, Sardón and Shapiro2000) evaluated the quality of GPS-based ionosphere corrections for Very Long Baseline Interferometry (VLBI) at 8.4 and 2.3 GHz. In his study, Ros et al. corrected the ionosphere for continental (~ 200 to ~ 700 km) and inter-continental (~ 7 800 to ~ 8 300 km) baseline lengths and concluded that GPS maps of TEC can usefully contribute to VLBI astrometric analysis. Erickson et al. (Reference Erickson, Perley, Flatters and Kassim2001) made use of the ionospheric corrections generated from an experimental set-up of four GPS receivers at the Very Large Array site to correct for the ionospheric effect. Erickson et al. found that large-scale structures (> 1 000 km) could be resolved observing at frequencies of 322 and 333 MHz, whereas small-scale fluctuations (< 100 km) could not be seen using a global model; it was noted that global ionosphere models perform averaging over the ionosphere and hence lose their capacity to monitor small-scale ionospheric changes. Erickson et al. argue that a dense GPS network is required to correct for small-scale fluctuations in the ionosphere.
In work by Sotomayor-Beltran et al. (Reference Sotomayor-Beltran2013), CODE and ROB maps were used to compute the rotation measure due to the ionosphere for polarised sources that were observed by the Low-Frequency Array for radio astronomy. However, the CODE maps presented in Sotomayor-Beltran et al. Figure 2 show an error in the location of the equatorial anomaly. This error is further investigated and discussed in Appendix A of this paper. This error is also discussed by Herne, Lynch, & Kennewell (Reference Herne, Lynch and Kennewellsubmitted).
GPS-based estimation of the ionosphere has also been carried out by Herne et al. (Reference Herne, Kennewell, Lynch and Carrano2013). High-fidelity GPS systems were specially deployed by the US Air Force for measurement of ionospheric TEC and scintillation indices at the location of the Murchison Radio-astronomy Observatory (MRO) and Australian Space Academy campus (Meckering, Western Australia). Two periods of time corresponding to low (2008–2009) and high (2012–2013) ionospheric activity were studied. During 2008–2009, the F10.7 Index varied between 65 and 82 (10−22 Wm−2 Hz−1), the monthly variation was found to be insignificant for most of the period. The Ap index reached a maximum of 35 during this period. However, during high solar activity (2012–2013), F10.7 led between 85 and 190, the monthly variation was significant throughout the period. Ap index reached a maximum of 90. The ionosphere at the MRO was expected to exhibit very low levels of scintillation (Kennewell et al. Reference Kennewell, Caruana, Terkildsen, Wu, Wilkinson and Cole2005). For Kp=9, scintillation at MRO reached about 0.2. In Herne et al., during 2012–2013, scintillation was found to reached a maximum of about 0.3.
The Murchison Widefield Array (MWA) is a recently operational low-frequency radio telescope located within the MRO in Western Australia. The instrument exemplifies exceptional wide-field imaging capability at low frequencies (see Lonsdale et al. Reference Lonsdale2009 and Tingay et al. Reference Tingay2013 for a technical overview of the instrument). These capabilities make it ideal for a range of science investigations with an emphasis on the following: detection of the 21 cm line from the epoch of reionoisation; large-scale surveys; searches for radio transients; continuum surveys; and solar, heliospheric and ionospheric studies (Bowman et al. Reference Bowman2013). In the recent survey by Hurley-Walker et al. (Reference Hurley-Walker2014), over 14 000 radio sources were detected in just four nights of observing.
Since a fundamental observable of an interferometer is the phase difference between elements, such instruments are unable to measure the TEC towards a particular source directly (though it may be inferred indirectly from polarisation measurements). However, for a single source located at infinity, the radiation reaching each element of an interferometer will have passed through a different part of the ionosphere providing information on the differential ionosphere or ionospheric gradients.
Excellent summaries of how the ionosphere affects radio interferometers are given in Lonsdale (Reference Lonsdale2004) and Wijnholds et al. (Reference Wijnholds, van der Tol, Nijboer and van der Veen2010). In the specific case of the MWA, the instrument has a very wide field of view, but relatively short baselines. Thus, while the effects of the ionosphere may change across the instrument’s field of view, the complex structure of the ionosphere is on larger spatial scales than the dimensions of the array, and the wavefront arriving at the array from a source will be largely coherent. However more complicated effects may be seen. Unless explicitly corrected in the calibration process, a TEC gradient across the array will manifest itself as a shift in source position; the incoming radiation gets refracted by the ionosphere.
The MWA has recently commenced operations and ionospheric effects are routinely detected. For example, observations have revealed variations in the rotation measure of polarised point sources and the diffuse galactic background (E. Lenc 2014, private communication). Loi et al. (Reference Loi2015c) demonstrate the utility of the MWA as a powerful imager for studying high-altitude irregularities, revealing a population of field-aligned density ducts that appear regularly over the observatory. The spatial distributions of celestial source refractive offsets over the field of view, combined with a novel parallax technique for altitude measurement, enable the 3D characterisation of ionospheric structures at high temporal cadence. Travelling ionospheric disturbances (TIDs), sinusoidal perturbations with wavelengths of 100–1 000 km and periods of several tens of minutes to an hour, are also often observed in MWA data. A technique for the spatio-temporal power spectrum analysis of ionospheric gradients, presented by Loi et al. (Reference Loi2015b), enables characteristic wavelengths and periods of fluctuation to be measured. A quantitative study of the statistical properties of ionosphere-induced position and amplitude variations of sources in MWA images (Loi et al. Reference Loi2015a) has yielded information about characteristic density gradients and the diffractive scale in the ionosphere. This illustrates the capability of the MWA to probe ionospheric structure in great detail.
All previous attempts at GPS-based ionosphere calibration for radio astronomy made use of ionosphere information from TEC maps which have a temporal resolution of 2 h. Ionospheric structures such as TIDs have a period of several tens of minutes, hence it is important to generate ionospheric information with higher resolution. We present here a method where publicly available data from GPS stations are used to generate location-specific ionosphere models at 10 min intervals. This requires the calibration of GPS receiver/transmitter instrumental biases in order to accurately model the ionosphere, also known as Differential Code Bias (DCB).
We perform a simultaneous fit for both GPS DCBs and ionospheric parameters. While the bernese software provides the GPS DCBs and ionospheric parameters (Dach, R. and others, Reference Dach2007), our work allows much higher time resolution of the ionospheric parameters than is commonly obtained, while simultaneously solving for the DCBs.
This paper is organised as follows. In Section 2, the methodology concerning the GPS-based ionospheric modelling is fully described. In this section, the basic GPS observation equations, estimating the Vertical Total Electron Content (VTEC) are formulated. In particular, we show how the VTEC and DCBs are determined simultaneously through Kalman filtering. Section 3 briefly describes the methodology adopted by CODE to generate ionosphere maps. Section 4 presents the procedure to model the ionosphere seen by the MWA in the form of position shifts. The results are presented and discussed in Section 5. Results from the IGS analysis centre, CODE, serve as reference to validate our VTEC results. In particular, we compare our estimated receiver DCBs, the inter-frequency biases on code observables, with those determined by the bernese processing software employed by CODE. The ionosphere observed by the MWA and the GPS are analysed and the agreement discussed. Finally, we make some concluding remarks in Section 6.
2 ESTIMATION OF THE IONOSPHERE USING GPS OBSERVATIONS
A GPS constellation consists of up to 32 operational satellites placed in 6 orbital planes at an altitude of 20 200 km above the Earth’s surface. With this constellation geometry and an orbital period of about 12 h, 4–10 GPS satellites are visible anywhere in the world at any given time. The earlier GPS satellites [Block IIA (2nd generation, ‘Advanced’) and Block IIR (‘Replenishment’)] transmitted on two carrier frequencies (L1 and L2), each encoded with one or two digital codes, and navigation messages (El-Rabbany Reference El-Rabbany2006). The BLOCK IIR(M) (‘Modernized’) satellites have an additional civil signal on L2 (L2C) (Hofmann-Wellenhof, Lichtenegger, & Collins Reference Hofmann-Wellenhof, Lichtenegger, Collins, Hofmann-Wellenhof, Lichtenegger and Collins1993). The BLOCK IIF (‘Follow-on’) satellites transmit an additional third frequency, L5, which has higher transmitted power and greater bandwidth, to support high-performance applications (El-Rabbany Reference El-Rabbany2006).
The signals transmitted by the GPS satellites form the observables, namely the phase (of the carrier frequency) and code (digital code) measurements. A phase measurement is the number of cycles at the corresponding carrier frequency between the satellite and the receiver. The phase delay between the receiver and the satellite is obtained by multiplying the number of phase cycles with the wavelength of the corresponding carrier. The phase measurements are biased by an unknown number of phase cycles, in addition to other errors. When a GPS receiver is switched on or tracks a newly risen satellite, it cannot determine the total number of complete cycles between the receiver and the satellite. Hence the initial number of complete cycles remains ambiguous, known as phase ambiguity bias.
The GPS code measurements have two types of code observables, namely the C/A-code (Coarse/Acquisition code, modulated only on the L1 carrier, denoted as C1) and P-code (Precise code, modulated on both L1 and L2 carriers, denoted as P1 and P2, respectively). The code modulation is different for each GPS satellite, with code signals sometimes also referred to as Pseudo Random Noise. The C/A-code measurement is less precise than the P-code, since the bit rate of C/A-code is 10 times lower than P-code (Langley Reference Langley1993). The GPS receiver generates replicas of the transmitted code signals. By comparing the code signal to its replica, the signal travel time is obtained (Hofmann-Wellenhof et al. Reference Hofmann-Wellenhof, Lichtenegger, Collins, Hofmann-Wellenhof, Lichtenegger and Collins1993). For a more detailed description, one can refer to Hofmann-Wellenhof et al. (Reference Hofmann-Wellenhof, Lichtenegger, Collins, Hofmann-Wellenhof, Lichtenegger and Collins1993), Langley (Reference Langley1993), and El-Rabbany (Reference El-Rabbany2006). This work uses two GPS carrier frequencies, namely f 1 = 1 575.42 MHz (for carrier L1) and f 2 = 1 227.60 MHz (for L2).
2.1 The GPS observation equation
The terms contributing to the GPS phase and code observables can be given as follows (Teunissen & Kleusberg Reference Teunissen and Kleusberg1998):
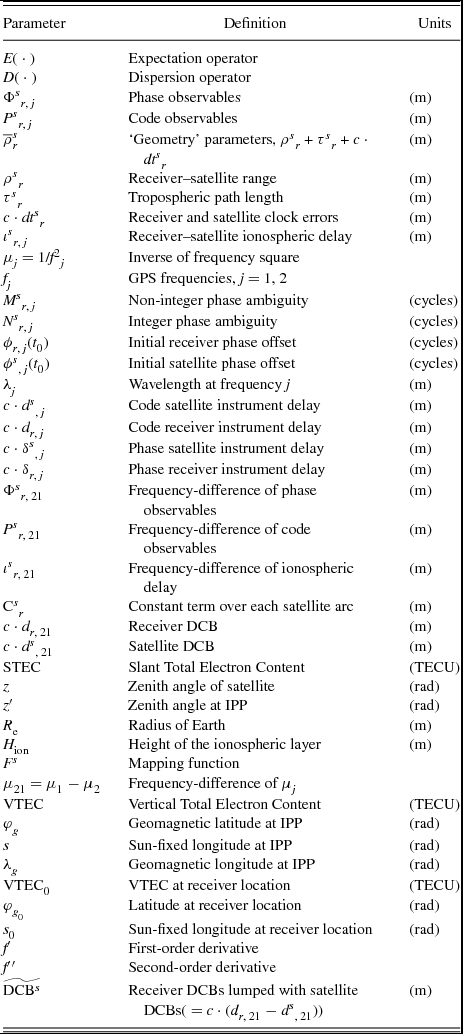
The parameters used in Sections 2.1 and 2.2 are listed in Table 1. Here subscripts s, r, and j indicate satellite, receiver and GPS frequency number, respectively.
Table 1. GPS model parameters and definitions.

Ms r, j are the non-integer ambiguities on the phase observables which contain the unknown integer ambiguities, Ns r, j, and the non-integer initial phase offsets for the receiver (ϕr, j(t 0)) and satellite (ϕs, j(t 0)), i.e.,
The phase ambiguities remain constant for any given receiver, frequency, and continuous satellite arc unless there is a loss of signal lock.
Since the effect of the ionospheric delay is a function of frequency, a frequency difference of phase and code observables can be formed which retains the ionospheric delay while the geometry-related parameters are eliminated. Along with the ionospheric delay (ιsr), the phase and code instrumental delays (δr, j, δs, j, d r, j, ds , j) and phase ambiguities (λjMs r, j) remain. The frequency-difference phase and code observation equations for dual frequency GPS observables, formed using Equations (1) and (2), are given as follows:
Here, ds , 21 and d r, 21 are the inter-frequency code delays for the satellite and the receiver and the constant phase term Csr is given as follows:
The slant ionospheric delay, ιsr, j, is related to the Slant Total Electron Content (STEC) as follows (Hofmann-Wellenhof et al. Reference Hofmann-Wellenhof, Lichtenegger, Collins, Hofmann-Wellenhof, Lichtenegger and Collins1993):
As shown in Figure 1, the STEC can be mapped to the VTEC, using the obliquity factor Fs, also known as the ionosphere mapping function. Fs is a function of zenith angle at the Ionosphere Pierce Point (IPP), z′, given as follows:
 \begin{eqnarray}
\left. \begin{array}{lll}\displaystyle \text{STEC} &=& \displaystyle \text{VTEC} \cdot F^{s} \\
\\
\displaystyle F^{s} &=& \displaystyle \frac{1}{\cos (z^{\prime })} =\frac{1}{\sqrt{1-\sin ^{2} z^{\prime }}} \\
\\
\displaystyle \sin z^{\prime } &=& \displaystyle \frac{R_{\rm e}}{R_{\rm e}+H_{\text{ion}}} \sin (z) \end{array}\right\rbrace
\end{eqnarray}
\begin{eqnarray}
\left. \begin{array}{lll}\displaystyle \text{STEC} &=& \displaystyle \text{VTEC} \cdot F^{s} \\
\\
\displaystyle F^{s} &=& \displaystyle \frac{1}{\cos (z^{\prime })} =\frac{1}{\sqrt{1-\sin ^{2} z^{\prime }}} \\
\\
\displaystyle \sin z^{\prime } &=& \displaystyle \frac{R_{\rm e}}{R_{\rm e}+H_{\text{ion}}} \sin (z) \end{array}\right\rbrace
\end{eqnarray}
where z′ is the zenith angle at the IPP, R e is the mean radius of the Earth, considered to be 6 371 km and assuming a spherical Earth, H ion is the height at the sub-ionospheric point, assumed to be 450 km, and z is the zenith angle of the satellite as seen by the receiver. The geometry of the model is illustrated in Figure 1. This study aims to compare and analyse ionosphere gradients, the height, H ion, of 450 km was chosen in order to compare the VTEC with CODE analysis center published values.

Figure 1. Ionosphere single layer model representation.
We can now map the GPS observables to the VTEC as follows:
 \begin{eqnarray}
\left. \begin{array}{lll}\displaystyle E\left(\frac{\Phi _{r,21}^{s}}{40.3 \ \mu _{21}}\right) &=& \displaystyle -F^{s} \ \text{VTEC} + \displaystyle \frac{\mathrm{C}_{r}^{s}}{40.3 \ \mu _{21}} \\
&&\\
\displaystyle E\left(\frac{P_{r,21}^{s}}{40.3 \ \mu _{21}}\right) &=& \displaystyle F^{s} \ \text{VTEC} + \displaystyle \frac{c \cdot (d_{r,21} - d^{s}_{,21})}{40.3 \ \mu _{21}} \end{array}\right\rbrace
\end{eqnarray}
\begin{eqnarray}
\left. \begin{array}{lll}\displaystyle E\left(\frac{\Phi _{r,21}^{s}}{40.3 \ \mu _{21}}\right) &=& \displaystyle -F^{s} \ \text{VTEC} + \displaystyle \frac{\mathrm{C}_{r}^{s}}{40.3 \ \mu _{21}} \\
&&\\
\displaystyle E\left(\frac{P_{r,21}^{s}}{40.3 \ \mu _{21}}\right) &=& \displaystyle F^{s} \ \text{VTEC} + \displaystyle \frac{c \cdot (d_{r,21} - d^{s}_{,21})}{40.3 \ \mu _{21}} \end{array}\right\rbrace
\end{eqnarray}
Here c · (d r, 21) and c · (ds , 21) constitute terms known as DCB for the receiver and the satellite, respectively, where
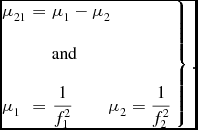 \begin{eqnarray}
\left. \begin{array}{lll}\mu _{21} &=& \mu _{1} - \mu _{2}\\
&&\\
&& \textrm {and}\\
&&\\
\mu _{1} &=& \displaystyle \frac{1}{f_{1}^{2}} \qquad \mu _{2} = \displaystyle \frac{1}{f_{2}^{2}} \end{array}\right\rbrace.
\end{eqnarray}
\begin{eqnarray}
\left. \begin{array}{lll}\mu _{21} &=& \mu _{1} - \mu _{2}\\
&&\\
&& \textrm {and}\\
&&\\
\mu _{1} &=& \displaystyle \frac{1}{f_{1}^{2}} \qquad \mu _{2} = \displaystyle \frac{1}{f_{2}^{2}} \end{array}\right\rbrace.
\end{eqnarray}
2.2 GPS ionospheric modelling
The VTEC can be modelled by assuming that the ionosphere is concentrated at a single layer at height H ion as illustrated in Figure 1 (Schaer Reference Schaer1999; Wang, Wang, & Morton Reference Wang, Wang, Morton, Sun, Jiao, Wu and Lu2014). The intersection of the GPS receiver–satellite line-of-sight with the ionospheric layer is called as IPP. The slant TEC is mapped to the vertical TEC by an obliquity factor (Equation 8), which is a function of the zenith angle at the IPP, z′. VTEC is modelled as a function of geomagnetic latitude, φg, and Sun-fixed longitude, s, using the following polynomial function (Wang et al. Reference Wang, Wang, Morton, Sun, Jiao, Wu and Lu2014):
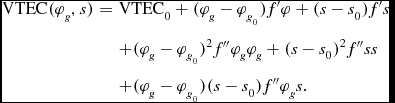 \begin{eqnarray}
\nonumber \text{VTEC} (\varphi _{g},s) &=& \text{VTEC}_{0} + (\varphi _{g} - \varphi _{g_{0}})f^{\prime } \varphi + (s - s_{0})f^{\prime } s\nonumber \\
\nonumber & & + (\varphi _{g} - \varphi _{g_{0}})^{2}f^{\prime \prime } \varphi _{g} \varphi _{g} + (s - s_{0})^{2}f^{\prime \prime } s s\nonumber \\
&& + (\varphi _{g} - \varphi _{g_{0}}) (s - s_{0}) f^{\prime \prime } \varphi _{g} s.
\end{eqnarray}
\begin{eqnarray}
\nonumber \text{VTEC} (\varphi _{g},s) &=& \text{VTEC}_{0} + (\varphi _{g} - \varphi _{g_{0}})f^{\prime } \varphi + (s - s_{0})f^{\prime } s\nonumber \\
\nonumber & & + (\varphi _{g} - \varphi _{g_{0}})^{2}f^{\prime \prime } \varphi _{g} \varphi _{g} + (s - s_{0})^{2}f^{\prime \prime } s s\nonumber \\
&& + (\varphi _{g} - \varphi _{g_{0}}) (s - s_{0}) f^{\prime \prime } \varphi _{g} s.
\end{eqnarray}
The Sun-fixed longitude, s, is related to the local solar time (LT) as s = λg + LT − π, where λg is the geomagnetic longitude at IPP, LT is in radians, VTEC0 is the VTEC at the receiver location and f′s, f′φg, f′′ss, f′′φgφg, f′′φgs are the first- and second-order derivatives of VTEC along the Sun-fixed longitude and latitude, respectively.
The single layer ionospheric model is a computation efficient model to estimate local ionospheric gradients at the zenith. However, the ionospheric features, for example those along the magnetic field lines, cannot be resolved using this model.
2.3 VTEC determination through Kalman filtering
The GPS model to estimate unknowns can be formed from Equation (5). In our method, the DCBs for receiver and satellite are estimated as a single parameter, ![]() $\widetilde{\text{DCB}^{s}} = c \cdot (d_{r,21} - d^{s}_{,21})$, since the model presented in Equation (9) is rank deficient. The parameters, namely the receiver and the satellite DCBs, cannot be separated from each other, hence cannot be independently estimated. A minimum set of parameters, known as the
$\widetilde{\text{DCB}^{s}} = c \cdot (d_{r,21} - d^{s}_{,21})$, since the model presented in Equation (9) is rank deficient. The parameters, namely the receiver and the satellite DCBs, cannot be separated from each other, hence cannot be independently estimated. A minimum set of parameters, known as the ![]() $\mathcal {S}$-basis, are chosen which can be lumped with the remaining parameters in order to overcome the rank deficiency in the underlying model (Teunissen Reference Teunissen, Grafarend and Sansò1985). For m satellites seen by receiver r, a weighted least-squares model is formed using Equations (5) and (11), given as follows:
$\mathcal {S}$-basis, are chosen which can be lumped with the remaining parameters in order to overcome the rank deficiency in the underlying model (Teunissen Reference Teunissen, Grafarend and Sansò1985). For m satellites seen by receiver r, a weighted least-squares model is formed using Equations (5) and (11), given as follows:
 \begin{eqnarray}
\begin{array}{rcl}E(\kern0.7pt{{{\bf y}}_{\bf i}}) &=& {{\bf A}_{\bf i}} \ \bf{x_{i}} \\
\\
D({{\bf y}}_{\bf i}) &=& \bf{\mathrm{Q_{yi}}} \\
\\
\bf{x_{i}} &=& \left[ \mathrm{C}_{r}^{s} \ \widetilde{DCB^{s}} \ \text{VTEC}_{0} \ f^{\prime } \varphi _{g} \ f^{\prime } s \ f^{\prime \prime } \varphi _{g} \varphi _{g} \ f^{\prime \prime } s s \ f^{\prime \prime } \varphi _{g} s \right]^{T} \end{array}
\end{eqnarray}
\begin{eqnarray}
\begin{array}{rcl}E(\kern0.7pt{{{\bf y}}_{\bf i}}) &=& {{\bf A}_{\bf i}} \ \bf{x_{i}} \\
\\
D({{\bf y}}_{\bf i}) &=& \bf{\mathrm{Q_{yi}}} \\
\\
\bf{x_{i}} &=& \left[ \mathrm{C}_{r}^{s} \ \widetilde{DCB^{s}} \ \text{VTEC}_{0} \ f^{\prime } \varphi _{g} \ f^{\prime } s \ f^{\prime \prime } \varphi _{g} \varphi _{g} \ f^{\prime \prime } s s \ f^{\prime \prime } \varphi _{g} s \right]^{T} \end{array}
\end{eqnarray}
where E(·) and D(·) denote the expectation and dispersion operators, yi denotes a vector of observables of size [2m × 1] at time stamp i, Ai is the design matrix of size [2m × (2m + 6)], the unknowns given by xi are of size [(2m + 6) × 1], and Qyi is the stochastic model for observables in yi given as
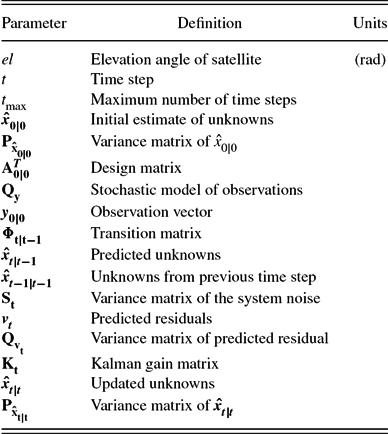
el is the vector of elevation angles of all the visible satellites, and σ0 is the measurement noise of the observables.
To solve the above model, a cut-off for the satellite zenith angle of 70° was chosen. The model given in Equation (12) cannot be solved in a single epoch. An ionosphere refreshing interval of 20 epochs (1 epoch = 30 s) is chosen over which the ionosphere is assumed to remain constant. The phase bias term Csr constitutes an integer phase ambiguity and non-integer receiver and satellite phase bias terms. The integer phase ambiguities remain constant for a single continuous satellite arc unless there is a loss of signal lock, hence Csr is assumed to remain constant for a continuous satellite arc. The GPS observables were free of multipath and cycle slips. The code bias terms, ![]() $\widetilde{\text{DCB}^{s}}$, are assumed to remain constant over a period of 24 h for any satellite.
$\widetilde{\text{DCB}^{s}}$, are assumed to remain constant over a period of 24 h for any satellite.
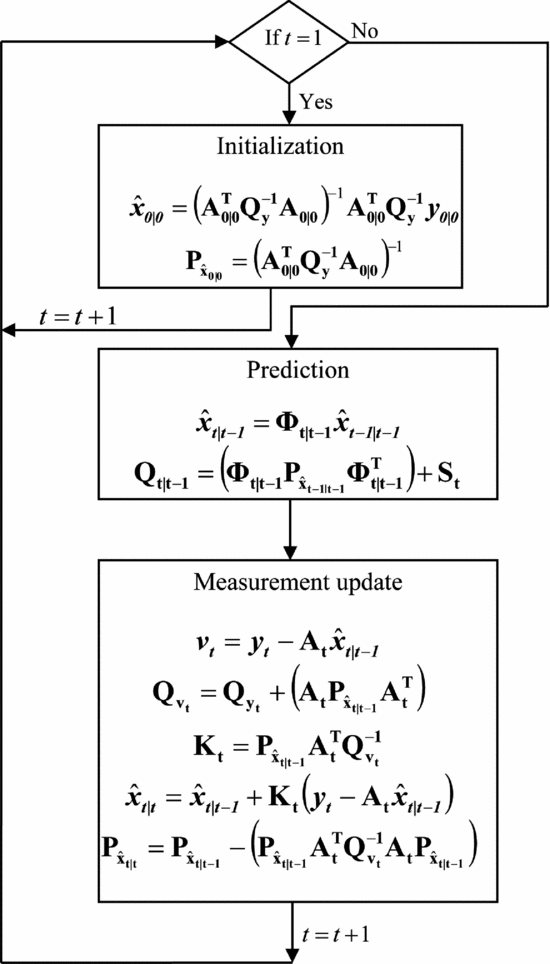
With the above considerations, the unknowns given in Equation (12) are estimated using the Kalman filter approach (Kalman Reference Kalman1960; Kailath Reference Kailath1981; Grewal & Andrews Reference Grewal and Andrews2011). In this work, Kalman filter is used in data assimilation mode. A Kalman filter can be described as a three-step procedure, with initialisation, prediction, and measurement update executed at different time steps t, t = 1, . . . , t max. The implementation of the Kalman filter is shown in Figure 2, where, ![]() $\bf{\hat{x}_{0|0}}, \bf{\mathrm{\mathrm{A}_{0|0}^{T}}}, \bf{\mathrm{Q_{y}}}$, and y0|0 indicate the unknowns, the design matrix, the Variance Covariance (VC) matrix of the measurements, and the measurements, respectively. Φt|t − 1 is the transition matrix which relates the unknowns at the current
$\bf{\hat{x}_{0|0}}, \bf{\mathrm{\mathrm{A}_{0|0}^{T}}}, \bf{\mathrm{Q_{y}}}$, and y0|0 indicate the unknowns, the design matrix, the Variance Covariance (VC) matrix of the measurements, and the measurements, respectively. Φt|t − 1 is the transition matrix which relates the unknowns at the current ![]() $\bf{\hat{x}_{t|t-1}}$ and previous
$\bf{\hat{x}_{t|t-1}}$ and previous ![]() $\bf{\hat{x}_{t-1|t-1}}$ time step with a system noise given by the VC matrix. St, vt are the predicted residuals and Qvt its VC matrix. Kt is the Kalman gain which is used to compute the measurement update given by
$\bf{\hat{x}_{t-1|t-1}}$ time step with a system noise given by the VC matrix. St, vt are the predicted residuals and Qvt its VC matrix. Kt is the Kalman gain which is used to compute the measurement update given by ![]() $\bf{\hat{x}_{t|t}}$ and its VC matrix
$\bf{\hat{x}_{t|t}}$ and its VC matrix ![]() $\bf{\mathrm{P_{\hat{x}_{t|t}}}}$. The parameters used in Kalman filter are presented in Table 2.
$\bf{\mathrm{P_{\hat{x}_{t|t}}}}$. The parameters used in Kalman filter are presented in Table 2.

Figure 2. Flow chart describing the implementation of a Kalman filter.
Table 2. Kalman filter parameters and definition.

2.4 GPS data preparation
The data from the three GPS/GNSS stations nearest to the MRO were used for this analysis, namely the Geoscience Australia (GA) stations MRO1 (Murchison), MTMA (Mount Magnet), YAR3 (Yarragadee), and WILU (Wiluna) were chosen (Figure 3). A description of the selected GPS/GNSS stations is given in Table 3. The data for the selected GA GNSS network were downloaded from the GA archiveFootnote 3 for 2014 March 3, 4, 6, and 16 corresponding to Day of Year (DOY) 062, 063, 065, and 075, respectively. The four days chosen for this analysis were the first four nights of GLEAM (GaLactic and Extragalactic All-sky MWA) observations for which suitable MWA data was available. Also, by choosing data from the year 2014, data from the recently active GPS receiver MRO1 could be included. Only YAR3 is included in CODE analysis, illustrating why our analysis is required to establish dense GPS networks near the MWA. Table 4 presents the summary of ionospheric weather on the selected four days; the parameters, F10.7 solar flux, and Planetary Kp indices are presented. The data presented in Table 4 indicate quiet ionospheric conditions, which are ideal for testing the methods described in this paper.

Figure 3. Selected GPS station locations from Geoscience Australia’s network (red), MWA location (blue) and MWA IPP (green) for the four MWA observation nights (DOY 062, 063, 065, and 075 marked by 1–4).
Table 3. Description of the selected GA network GPS/GNSS stations and the MWA.

a Partial data available, from 00:00:00 UTC to 18:07:00 UTC.
Table 4. Daily solar and geomagnetic indices for the selected MWA observation days.

aNational Geophysical Data Center (NGDC), National Oceanic and Atmospheric Administration (NOAA): ftp://ftp.ngdc.noaa.gov/STP/GEOMAGNETIC_DATA/INDICES/KP_AP/2014.
bSpace Weather Prediction Center (SWPC), NOAA, Boulder, USA: ftp://ftp.swpc.noaa.gov/pub/warehouse/2014.
3 CODE IONEX MAPS
The daily ionosphere maps from the CODE are based on a global network of ~ 200 GPS/GNSS stations. The line of sight GPS ionospheric delay is mapped to VTEC using a Modified Single Layer Model (MSLM) mapping function approximating the JPL Extended Slab Model (ESM) (for ESM mapping function see, Coster, Gaposchkin, & Thornton Reference Coster, Gaposchkin and Thornton1992). The MSLMFootnote 4 is given as follows:
where H = 506.7 km and α = 0.9782.
The VTEC is modelled using spherical harmonic coefficients of order and degree 15 in the solar magnetic reference frame as snapshots with an ionosphere refreshing interval of 2 h (Schaer et al. Reference Schaer, Beutler, Rothacher, Springer, Neilan, Van Scoy and Zumberge1996). The spatial resolution of CODE maps is 5°/2.5° in longitude/latitude, respectively. The spherical harmonic model used by CODE to interpret the global ionosphere is described in Schaer et al. (Reference Schaer, Beutler, Rothacher, Springer, Neilan, Van Scoy and Zumberge1996).
CODE maps are available as daily final solutions in CODE’s online archiveFootnote 5. Figure 4 presents the 2 h snapshots for the day 2014 March 03 (DOY 062), which is one day of interest for the MWA observations. The average CODE VTEC RMS is shown in Figure 5. The RMS of the VTEC fit is higher over oceans and regions with sparse GPS/GNSS receivers coverage, due to limited data points available for the fit.

Figure 4. Global TEC (TECU) from CODE IONEX maps for DOY 062, year 2014.

Figure 5. Average RMS (1σ uncertainties) in TECU, of CODE IONEX maps for DOY 062, year 2014, marked in white are the GPS/GNSS stations considered for the solution.
4 MEASUREMENT OF THE IONOSPHERE USING MWA OBSERVATIONS
4.1 Observations
For comparison with our GPS modelling of the ionosphere, we used observations from the GLEAM survey (Wayth et al. Reference Wayth2015; N. Hurley-Walker et al., in preparation). In this survey, the MWA observes in meridian drift-scan mode, where the telescope remains pointing at a single point on the meridian throughout the night. Four nights from 2014 March were chosen, when the telescope was pointed close to the zenith. The IPP corresponding to the pointing centre of the telescope is shown for each night in Figure 6.

Figure 6. GA station locations (red) with satellite IPPs in earth fixed reference frame over a period of 24 h (grey) and for 1 h during MWA observations (black). MWA is marked in blue, whereas the IPP of MWA is shown in green.
During GLEAM observations, the instrument cycles five frequency bands, centred on approximately 88 MHz, 118 MHz, 154 MHz 185 MHz, and 215 MHz, with a dwell time of 2 min on each band, and each band having an instantaneous bandwidth of 30.72 MHz. Each 2 min observation is then imaged with separate images being generated for four sub-bands (each having a bandwidth of 7.68 MHz). The position of a prepared list of bright sources was then determined for each of these images.
4.2 Ionospheric modelling
By comparing the position of each source in all four sub-bands, it is possible to quantify the effect of the ionosphere, separating it from instrumental and calibration effects. By making a least-squares fit to all four points, the contribution of the ionosphere (the gradient) can be determined for each source. The offset in position at each frequency is shown in Figure 8 for a single strong source. It can be seen that the change in apparent position of the source depends precisely on λ2, exactly as would be expected from ionospheric refraction.
A comprehensive analysis of this data set using MWA observations is underway (J. Morgan et al., in preparation). For this analysis, ionospheric gradient were estimated over all sources detected in each snapshot. This is shown in Figure 7 which shows the gradient of this fit for each source, scaled by λ2 for the highest frequency offset shown in the left panel. The fact that the average reduced χ2 for each observation is ~ 1, and the fact that λ = 0 position of the sources remains at zero throughout the night, both serve to reinforce the hypothesis that the shift in sources is largely due to the ionosphere.

Figure 7. Offset (extrapolated to λ = 0), gradient, and reduced χ2 of a fit of source position offset as a function of λ2. Each point is for a single observation, all quantities are averaged over all (100) sources detected in that observation. Left panels are for the EW position offset (Right Ascension) right panels are for the NS position offset (Declination). Red, yellow, green, blue, and purple are for the 88, 118, 154, 185, and 215 MHz bands, respectively. Note that the gradients (in arcmin m1) have been multiplied by 4, representing an offset at a wavelength of 2 m (=150 MHz).

Figure 8. Source position offset against λ2 (m2) for a strong source. Each line represents a measurement of the source in each of four sub-bands in a single 2-min observation. There are many lines since the source in multiple observations as it passes through the field of view. Left panels are for the EW position offset (Right Ascension) right panels are for the NS position offset (Declination). Red, yellow, green, blue, and purple are for the 88, 118, 154, 185, and 215 MHz bands, respectively. More significant detections are given a darker colour.
For simplicity, only the lowest-frequency data were used, since these observations are the most sensitive to ionospheric effects, and still yield sufficient time resolution. This yields two time series (one in the north–south, NS, direction and one in the east–west, EW, direction) representing the average shift due to the ionosphere of ~ 100 sources within a 35° radius of the pointing centre. In order that these shifts could be compared directly with GPS measurements, both measurements were scaled to a common reference frequency of 150 MHz and the (angular) offset was converted to radians.
5 RESULTS AND DISCUSSION
5.1 Comparison of VTEC with CODE IONEX
The VTEC was estimated by our software at a time resolution of 10 min as described in Section 2 with software developed in matlab for the location of the four GPS stations, MRO1, MTMA, YAR3, and WILU. The CODE values of VTEC are available at intervals of 2 h. Values of the VTEC corresponding to our time resolution were interpolated from CODE VTEC maps (see Schaer et al. Reference Schaer, Gurtner, Feltens, Noll, Gowey and Neilan1998) for each of the four GPS locations. Our estimated values of VTEC along with the CODE VTEC values are presented in Figure 9 for DOY 062, year 2014. Figures 9(a)–(d), present VTEC for MRO1, MTMA, YAR3, and WILU, respectively, for DOY 062. Figure 10 shows the difference between our VTEC estimates with respect to CODE. The F10.7 solar flux, presented in Table 4, is highest on DOY 062 and lowest on 075. This is reflected in the VTEC values; they reach a maximum of ~ 68 TECU on DOY 062 and ~ 57 TECU on DOY 075 for MRO1; refer Figures 9(a) and A4(a). The 1σ uncertainties in CODE maps reach a maximum of 8 TECU (Figure 5). The differences between CODE and our VTEC are found to lie within the errors, with the differences ranging between − 6 to 6 TECU for four different days of observations (Figure 10).

Figure 9. VTEC at stations (a) MRO1, (b) MTMA, (c) YAR3, and (d) WILU estimated using the method described in the text (blue curve) and CODE IONEX (red curve) on DOY 062, year 2014.

Figure 10. Differences in VTEC with respect to CODE for stations MRO1, MTMA, YAR3, and WILU for (a) DOY 062, year 2014 (b) DOY 063, year 2014 (c) DOY 065, year 2014, and (d) DOY 075, year 2014.
5.2 Comparison of receiver DCBs
The receiver DCBs given by c · d r, 21 in Equation (5) are the inter-frequency biases on code GPS data. Estimation of receiver DCBs is important for correct estimation of ionospheric parameters from GPS/GNSS observables (Gaposchkin & Coster Reference Gaposchkin and Coster1992; Sardon, Rius, & Zarraoa Reference Sardon, Rius and Zarraoa1994; Teunissen & Kleusberg Reference Teunissen and Kleusberg1998). The receiver DCBs were estimated as described in Section 2. In addition, the bernese GNSS data processing software (Dach, R. and others, Reference Dach2007) was used to estimate receiver DCBs for the selected GA GPS/GNSS stations given in Table 3. bernese 5.0 Precise Point Positioning (PPP) processing estimates one set of station specific ionosphere parameters for the entire session as well as receiver DCBs using the script ![]() $\texttt{PPP\underline{ }ION}$ (Dach, R. and others, Reference Dach2007). With bernese PPP it is possible to obtain centimetre level station positions using precise satellite orbits, satellite clock and Earth Orientation Parameters along with the receiver DCB.
$\texttt{PPP\underline{ }ION}$ (Dach, R. and others, Reference Dach2007). With bernese PPP it is possible to obtain centimetre level station positions using precise satellite orbits, satellite clock and Earth Orientation Parameters along with the receiver DCB.
The station specific ionosphere parameters are estimated by bernese PPP by forming frequency-differenced geometry-free observables. In this work, frequency-differenced observables were used to estimate station specific parameters. Unlike bernese PPP where quotidian ionosphere parameters are estimated for a given session, we make use of a Kalman filter to estimate the ionosphere every 10 min and a single value of receiver–satellite DCB for an entire session.
There exists a rank deficiency between the receiver and satellite DCBs. To overcome this rank deficiency, CODEFootnote 6 assumes a zero-mean condition over all the satellite DCBs, ![]() $\sum _{s=1}^{m} \text{DCB}^{s} =0$. By assuming a zero-mean condition it implies that the DCB results may be shifted by a common offset value (see Dach, R. and others, Reference Dach2007, Chapter 13), which is a function of total number of satellites m considered for the solution. Hence an independent
$\sum _{s=1}^{m} \text{DCB}^{s} =0$. By assuming a zero-mean condition it implies that the DCB results may be shifted by a common offset value (see Dach, R. and others, Reference Dach2007, Chapter 13), which is a function of total number of satellites m considered for the solution. Hence an independent ![]() $\mathcal {S}$-basis was formed for estimation of DCBs.
$\mathcal {S}$-basis was formed for estimation of DCBs.
Our estimated receiver DCBs and bernese PPP estimates are compared in this section. CODE also provides estimates of receiver DCBs which are estimated while performing a global fit for ionosphere parameters. However, of the selected stations used in this study, only receiver DCBs for station YAR3 are available from CODE.
Figure 11 shows our estimated receiver DCBs (blue), with bernese (red) and from CODE (cyan) for DOY 062. Table 5 presents the differences between our estimated receiver DCBs and bernese and CODE values. In comparison with bernese estimated DCBs, differences are between − 0.475 and − 1.311 ns which corresponds to − 1.356 to − 3.743 TECU. Whereas comparing to CODE DCBs, the DCB for YAR3 differed by 0.055–0.553 ns, 0.157–1.579 TECU.

Figure 11. Comparison of our estimated receiver DCBs (blue) with bernese estimates (red) and CODE DCBs (cyan) for (a) DOY 062, year 2014, (b) DOY 063, year 2014, (c) DOY 065, year 2014, and (d) DOY 075, year 2014.
Table 5. Differences between our estimated receiver DCBs with bernese and CODE for DOY 062, 063, 065, and 075, year 2014.
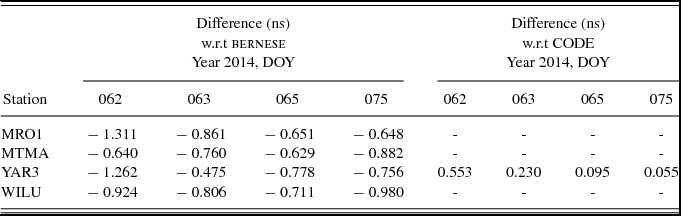
Hong, Grejner-Brzezinska, & Kwon (Reference Hong, Grejner-Brzezinska and Kwon2008) estimated the receiver DCBs by initially estimating single differenced DCBs. Further, by finding the time t 0 for which the single difference geometric range is zero, absolute receiver DCBs were computed. Hong et al. compared the estimated receiver DCBs with bernese values and found the maximum difference to lie around 15 cm or 0.5 ns. Arikan et al. (Reference Arikan, Nayir, Sezen and Arikan2008) estimated the receiver DCBs using IONOsphere research LABoratories single-station receiver BIAS estimation algorithm (IONOLAB-BIAS) method and compared them with CODE estimates. Arikan et al. found the differences in receiver DCBs to lie between − 0.552 and 0.110 ns for different receivers.
5.3 Comparison of GPS ionosphere gradients with MWA observations
The gradients in the EW and NS directions were computed from the ionosphere first-order coefficients given in Equation (11) for each of the selected stations and compared with MWA observed gradients. Figure 12 presents each of the EW and NS gradients for all the GA GPS stations and MWA. Figures 12(a), (c), (e), and (g), show the EW gradients for DOY 062, 063, 065, and 075 of year 2014, respectively. The NS gradients are presented in Figures 12(b), (d), (f), and (h) for DOY 062, 063, 065, and 075 of year 2014, respectively. In each of the subplots, along with the GPS ionospheric gradients, the MWA-observed gradients are shown.

Figure 12. EW and NS ionosphere gradients for selected GA stations and MWA for DOY 062, 063, 065, and 072 for year 2014. The time window related to MWA observations is shown by red line. (a) EW gradient for DOY 062. (b) NS gradient for DOY 062. (c) EW gradient for DOY 063. (d) NS gradient for DOY 063. (e) EW gradient for DOY 065. (f) NS gradient for DOY 065. (g) EW gradient for DOY 075. (h) NS gradient for DOY 075.
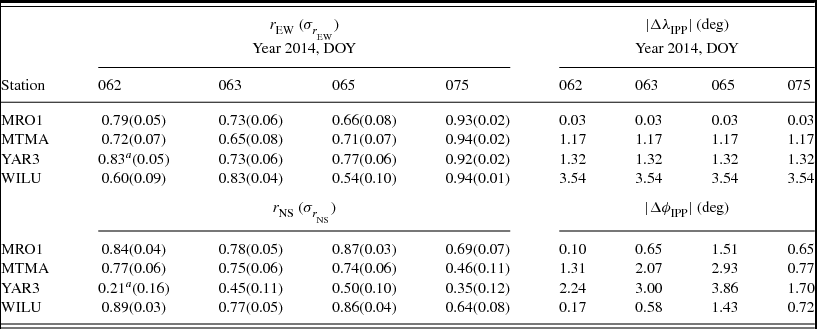
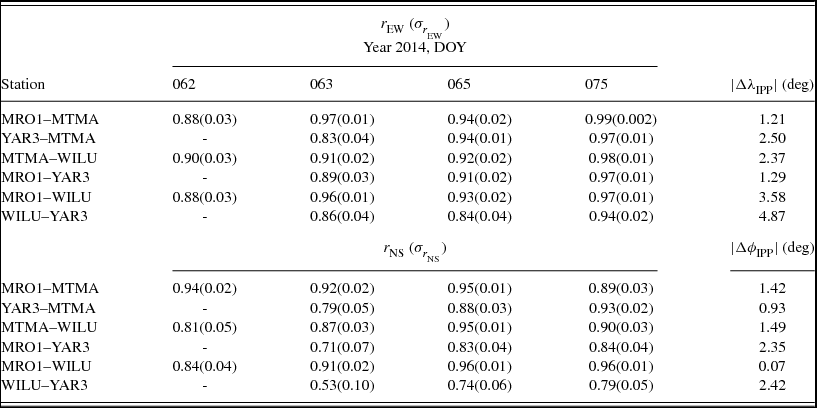
Table 6 presents the correlation between GPS and MWA gradients in the EW and NS directions for the four days of observations. The IPP separations in longitude (![]() $|\Delta \lambda _{\text{IPP}}|$) and latitude (
$|\Delta \lambda _{\text{IPP}}|$) and latitude (![]() $|\Delta \phi _{\text{IPP}}|$) for each of the GPS stations and MWA are presented in Table 6. The correlation between the GPS and MWA ionosphere gradients is computed using Pearson’s coefficient of correlation, r, for an assumed mean method along with the standard error, σr; refer Fisher (Reference Fisher1936).
$|\Delta \phi _{\text{IPP}}|$) for each of the GPS stations and MWA are presented in Table 6. The correlation between the GPS and MWA ionosphere gradients is computed using Pearson’s coefficient of correlation, r, for an assumed mean method along with the standard error, σr; refer Fisher (Reference Fisher1936).
Table 6. Correlation between the GPS- and MWA-observed gradients in EW (r EW) and NS (r NS) components, its standard error (σr), and IPP separations in longitude (![]() $|\Delta \lambda _{\text{IPP}}|$) and latitude (
$|\Delta \lambda _{\text{IPP}}|$) and latitude (![]() $|\Delta \phi _{\text{IPP}}|$) of GPS stations and MWA (ΔIPP) for DOY 062, 063, 065, and 075, year 2014.
$|\Delta \phi _{\text{IPP}}|$) of GPS stations and MWA (ΔIPP) for DOY 062, 063, 065, and 075, year 2014.

aPartial data available, from 00:00:00 to 18:07:00 UTC (MWA observation window = ~ 11–21 UTC).
There is a high correlation in the EW and NS gradient between GPS and MWA for most of the GPS stations for all the days (Table 6). The NS gradients had a weak correlation with YAR3 for most days. The correlation was highest on DOY 075 while the IPP was closest among the four days of observation (Table 6). The EW gradient showed consistent good correlation with MRO1 GPS stations, whereas correlation with WILU seemed to be most inconsistent (Table 6). A general trend seemed to show that the EW gradient was proportional to the longitudinal difference and the NS gradient to the latitude difference. For DOY 075 while the solar activity was the lowest among the selected days (Table 4), the EW gradient was found to be high for all the stations. NS gradient did not have a similar behaviour.
Table 7 and Figure 12 present the comparison of zenith EW and NS gradients between GPS stations. Correlation for the EW and NS gradients, presented in Table 7, were computed between each of the selected GPS stations for the time window of MWA observations (marked by the red line in Figure 12). Table 7 summarises the inter-station EW and NS gradient correlations. Inter-station correlation is strong for the EW and NS gradient for almost all the days between all the stations. The EW gradient is consistently strong between all the stations, however the NS gradient is found to be weakest between WILU and YAR3 which have a distinguished latitudinal and longitudinal separation (Figure 3).
Table 7. Inter-station correlation for the EW and NS gradients (r), its standard error (σr), and IPP separations in longitude (![]() $|\Delta \lambda _{\text{IPP}}|$) and latitude (
$|\Delta \lambda _{\text{IPP}}|$) and latitude (![]() $|\Delta \phi _{\text{IPP}}|$) between GPS stations.
$|\Delta \phi _{\text{IPP}}|$) between GPS stations.

6 CONCLUSIONS
This work presents a single-station approach to estimate VTEC ionosphere gradients. The VTEC and ionosphere gradients were estimated at intervals of 10 min. The ionosphere gradients in the EW and NS direction at the GPS station locations are in good agreement with the MWA-observed gradients.
The ionosphere gradient analysis presented in this research brings forth various questions, namely, the variation of EW and NS gradients with respect to IPP separation, and the elevation dependency reflected by the correlation of gradients between the GPS station, MRO1, and MWA. With the limited data set, these questions cannot be resolved comprehensively. The future work will focus on including more MWA observation and will attempt to closely probe the above questions in a statistical sense.
With our single-station approach, the GPS receiver DCBs can be accurately estimated for any available GPS receiver. Thus our method can be applied to local GPS receiver data for which the DCBs are not publicly available.
To develop a regional model for the ionosphere, a multi-station approach needs to be adopted. Furthermore, the spatial resolution of ionosphere gradients is closely related to the scale of the GPS/GNSS receiver network on the ground. The scales at which MWA sees the ionosphere lie between 10–100 km. In order to estimate the ionosphere gradients on such scales, dense GPS networks of the order of the ionosphere scales seen by the MWA need to be present around MWA site. The existing GPS network near the MWA site is of scale 150–250 km, which limits the GPS-based ionosphere research possible for the MWA.
In addition to GPS satellite data, other satellite systems can be used to densify the IPPs over the study area. Other global navigation systems like GLONASS, launched by Russia, BeiDou from China, and the European Union’s Galileo could be adopted in our model. Of these three global navigation systems, only the GLONASS system is close to completely operational; it currently has 23 operational satellites in orbit. GA receivers are able to capture data from the GLONASS system, and using GLONASS data along with the GPS data has been shown to improve ionospheric modelling (Coster et al. Reference Coster, Pratt, Burke and Misra1999).
Future work will focus on developing a regional ionosphere model using data from both GPS and GLONASS satellite systems.
We find that the Australian SKA site (where the MWA is located) is well suited for low-frequency astronomy. Appendix A shows that the conclusions drawn in Sotomayor-Beltran et al. (Reference Sotomayor-Beltran2013) regarding the suitability of MRO for low-frequency radio astronomy are a result of an incorrect interpretation of CODE maps.
Acknowledgements
The authors wish to thank Anthony Willis from National Research Council of Canada for the valuable discussions. This scientific work makes use of the MRO, operated by Commonwealth Scientific and Industrial Research Organisation (CSIRO). We acknowledge the Wajarri Yamatji people as the traditional owners of the Observatory site. Support for the MWA comes from the US National Science Foundation (grants AST-0457585, PHY-0835713, CAREER-0847753, and AST-0908884), the Australian Research Council (LIEF grants LE0775621 and LE0882938), the US Air Force Office of Scientific Research (grant FA9550-0510247), and the Centre for All-sky Astrophysics (an Australian Research Council Centre of Excellence funded by grant CE110001020). Support is also provided by the Smithsonian Astrophysical Observatory, the MIT School of Science, the Raman Research Institute, the Australian National University, and the Victoria University of Wellington (via grant MED-E1799 from the New Zealand Ministry of Economic Development and an IBM Shared University Research Grant). The Australian Federal government provides additional support via the CSIRO, National Collaborative Research Infrastructure Strategy, Education Investment Fund, and the Australia India Strategic Research Fund, and Astronomy Australia Limited, under contract to Curtin University. We acknowledge the iVEC Petabyte Data Store, the Initiative in Innovative Computing and the CUDA Center for Excellence sponsored by NVIDIA at Harvard University, and the International Centre for Radio Astronomy Research (ICRAR), a Joint Venture of Curtin University and The University of Western Australia, funded by the Western Australian State government.
A CODE IONOSPHERE MAP INTERPRETATION DISCREPANCY
The CODE maps presented in Sotomayor-Beltran et al. (Reference Sotomayor-Beltran2013) show a behaviour of the equatorial anomaly different to what is seen in this work. To underline this inconsistency, the CODE maps for the day 2014 April 11 presented by Sotomayor-Beltran et al. (Figure A1 a) were plotted with our software (Figure A1 b). The possible source of inconsistency lies in the way CODE maps are plotted by Sotomayor-Beltran et al. On close inspection it is clear that the latitudes provided in CODE IONEX files are inverted in the plot presented by Sotomayor-Beltran et al. This results in the equatorial anomaly appearing to pass directly over the MRO, which is not the case. This conclusion is supported in the literature, (Seeber Reference Seeber2003, Figure 7.52 Kennewell et al. Reference Kennewell, Caruana, Terkildsen, Wu, Wilkinson and Cole2005).

Figure A1. CODE IONEX plot for 06 UTC by Sotomayor-Beltran et al. (Reference Sotomayor-Beltran2013) (a) and by our software (b) for 2011 April 11.

Figure A2. VTEC at stations (a) MRO1, (b) MTMA, (c) YAR3, and (d) WILU estimated using the method described in the text (blue curve) and CODE IONEX (red curve) on DOY 063, year 2014.

Figure A3. VTEC at stations (a) MRO1, (b) MTMA, (c) YAR3, and (d) WILU estimated using the method described in the text (blue curve) and CODE IONEX (red curve) on DOY 065, year 2014.

Figure A4. VTEC at stations (a) MRO1, (b) MTMA, (c) YAR3, and (d) WILU estimated using the method described in the text (blue curve) and CODE IONEX (red curve) on DOY 075, year 2014.