1 INTRODUCTION
Over the last two decades star-forming clouds (SFCs) have been studied in ever increasing detail with telescopes on the ground like the JCMT (e.g., Ward-Thompson et al. Reference Ward-Thompson2007), and those in space like Spitzer (Kirk, Ward-Thompson, & André Reference Kirk, Ward-Thompson and André2007), and Herschel (e.g., André et al. Reference André2010). While improving our understanding about the initial conditions for the formation of stars on the one hand, these studies, on the other, have also posed a few challenging questions. Consequently, recent years have seen considerable investment of observational and computational efforts in this subject. Modulo the effect of magnetic field, which is also believed to play a significant role in the formation of stars, purely hydrodynamic models have, to a large extent, successfully reconciled the physical conditions found in typical SFCs (for e.g., see review by Hennebelle & Falgarone Reference Hennebelle and Falgarone2012).
Presently, we face at least two major questions that demand investigation: (i) the formation and evolution of prestellar cores in putative SFCs, and (ii) the relationship, if any, between the distribution of stellar masses, as described by the stellar initial mass function, and that for prestellar coresFootnote 1 (e.g., Alves Lombardi, & Lada Reference Alves, Lombardi and Lada2007; Nutter & Ward-Thompson Reference Nutter and Ward-Thompson2007; Enoch et al. Reference Enoch, Evans, Sargent, Glenn, Rosolowsky and Myers2008; Anathpindika Reference Anathpindika2011). At the moment though, our interest lies in studying the formation of cores and the development of their physical properties. The question has evoked considerable interest among a number of authors and there has been a growing consensus on the formation of cores via fragmentation of dense clumps within turbulent MCs. This model envisages a competition between self-gravity and turbulence (see e.g., Hartmann Reference Hartmann2002; Klessen et al. Reference Klessen, Ballesteros-Paredes, Vázquez-Semadeni and Roman-Duval2005; Bonnell, Clarke, & Bate Reference Bonnell, Clarke and Bate2006; Heitsch, Hartmann, & Burkert Reference Heitsch, Hartmann and Burkert2008 b; Schmidt et al. Reference Schmidt, Kern, Federrath and Klessen2010; Price, Federrath, & Brunt Reference Federrath, Sur, Schleicher, Banerjee and Klessen2011; Federrath & Klessen 2012; Anathpindika Reference Anathpindika2013). The cascading nature of turbulence makes it crucial in the evolutionary cycle of MCs. On the sub-parsec scales, it induces the formation of local compression that may self-gravitate if the Jeans condition is satisfied (see e.g., Mac Low & Klessen Reference Low and Klessen2004; Audit & Hennebelle Reference Audit and Hennebelle2010; Bonnell, Dobbs, & Smith Reference Bonnell, Dobbs and Smith2013).
Turbulence and the fragmentation of turbulent gas is scale-free which makes it plausible that clouds and cores form in identical processes. Indeed, sub-fragmentation within larger clouds has been reported and a more recent example being the starless cloud, IRDC18310-4. The length-scale of internal fragmentation within this cloud was found to be consistent with the local thermal Jeans length (Beuther et al. Reference Beuther2013). A number of similar examples have been reported and now form part of the voluminous literature on this subject. Clouds and smaller clumps that form in this fashion could be bound, although evidence from numerical simulations suggests otherwise. It has been suggested, fragmentation of shocked bodies though rapid, is more likely to produce unbound fragments, confined by external pressure and may merge to form larger clumps. These fragments are unlike those that form under the assumption of isothermality in which case they are likely to be relatively short-lived on account of their propensity towards re-expansion due to insufficient confining pressure (see e.g., Vázquez-Semadeni et al. Reference Vázquez-Semadeni, Gómez, Jappsen, Ballesteros-Paredes, González and Klessen2007; Heitsch et al. Reference Heitsch, Hartmann and Burkert2008 b; Anathpindika Reference Anathpindika2009).
Surveys of MCs have revealed populations of both bound, as well as unbound cores, either of which could remain starless. Despite their relatively high levels of turbulence, some do indeed have a population of cores, most of which are unbound and therefore starless (see e.g., Hatchell et al. Reference Hatchell, Richer, Fuller, Qualtrough, Ladd and Chandler2005 for the Perseus MC; Hily-Blant & Falgarone 2009 for Polaris Flare; Roman-Duval et al. Reference Roman-Duval, Jackson, Heyer, Rathborne and Simon2010 for MCs in the Galactic ring survey; Ragan et al. Reference Ragan, Heitsch, Bergin and Wilner2012 for a number of IRDCsFootnote 2 and Ripple et al. Reference Ripple, Heyer, Gutermuth, Snell and Brunt2013 for the Orion MC). Starless cores are believed to be supported by turbulence, and perhaps the magnetic field. The occurrence of a weak velocity field within these cores is attributed to the cascading nature of turbulence as it trickles down from large spatial scales to smaller ones (see e.g., Goodman et al. Reference Goodman, Barranco, Wilner and Heyer1998; Vazquez-Semadeni, Ballesteros-Paredes, & Klessen Reference Vázquez-Semadeni, Ballesteros-Paredes and Klessen2003; Federrath et al. Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010; Federrath Reference Federrath2013). Broadening of optically thick emission lines from molecular tracers such as CO, NH3, H2O and SiO is a good tracer of the turbulent nature of clouds on the sub-parsec scale, i.e., on the scale of cores.
More stable fragments forming out of weakly turbulent gas successfully reproduce crucial properties such as the mass-spectrum and further fragmentation produces smaller prestellar cores, as argued analytically by Hennebelle & Chabrier (Reference Hennebelle and Chabrier2008) and Anathpindika (Reference Anathpindika2013). Numerical simulations on the subject also demonstrate the formation of an extensive network of dense filaments within turbulent gas (e.g., Price & Bate Reference Price and Bate2008, Reference Bate2009; Bate Reference Bate2009; Federrath & Klessen 2012). Thus, we would like to see first, how sheet-like clouds are converted into filaments, second, how cores form in these filaments, and third, the occurrence of a relatively weak velocity-field on the scale of prestellar cores. The problem has been attempted both, analytically as well as numerically. For instance, stability analysis of pressure-confined and/or unconfined isothermal sheet-like clouds has shown that the fastest growing unstable mode is in the order of a fraction of the slab-thickness (Elmegreen & Elmegreen Reference Elmegreen and Elmegreen1978; Lubow & Pringle Reference Lubow and Pringle1993).
Pressure-confined slabs in the limiting case of confinement due to thermal pressure or those due to shocks, show mutually different behaviour. For example, numerical work by Inutsuka & Miyama (Reference Inutsuka and Miyama1997) and Anathpindika (Reference Anathpindika2009) demonstrated that a shocked slab, after its formation, soon lost thermal support due to internal dissipation as fluid layers excited by hydrodynamic instabilities sheared against each other. Unsupported clouds then lost thermal support and collapsed to the central-plane before expanding out laterally to form a filament. Slabs confined by thermal pressure of course, behave differently as they break-up into smaller fragments. The susceptibility of these sheets to changes in external pressure was first discussed by Hunter (Reference Hunter1979), Whitworth (Reference Whitworth1981) and Hunter & Fleck (Reference Hunter and Fleck1982), and more recently, by Heyer et al. (Reference Heyer, Krawczyk, Duval and Jackson2009). Similarly, the importance of cooling in shocked gas-bodies was demonstrated by Tohline, Bodenheimer, & Christodoulou (Reference Tohline, Bodenheimer and Christodoulou1987). According to the hypothesis, efficient cooling of a pressure compressed gas-body raised its propensity towards fragmentation so that one/many of these fragments could eventually spawn stars. Pressure-confined isothermal gas slabs were also examined by Whitworth et al. (Reference Whitworth, Bhattal, Chapman, Disney and Turner1994), Yamada & Nishi (Reference Yamada and Nishi1998) and Clarke (Reference Clarke1999).
It is evident that strength of the external pressure could possibly control the evolutionary cycle of a confined cloud. In the present work, we propose to examine the behaviour of an initially isothermal sheet-like cloud subject to strong pressure confinement, but not a shock, and is allowed to cool over the course of its evolution. In particular, we are interested in (a) examining the interplay between the gravitational and the TI during the process of gas fragmentation, (b) examine the behaviour of gas in the warm and cold phase and finally, (c) test the consistency between the properties of cores derived here and those reported for field cores. This contribution is divided as follows: the initial conditions for the simulations and the numerical algorithm used are discussed in Section 2. Then in Section 3, the evolution of the pressure-confined slab is discussed and useful diagnostics are presented in Sections 4 and 5. We conclude in Section 6.
2 INITIAL CONDITIONS
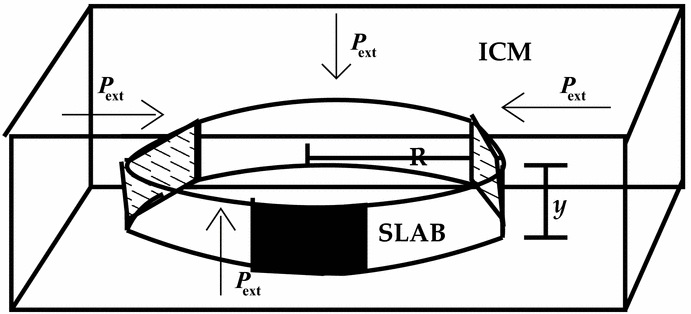
The set-up for our simulations is simple and consists of a uniform density slab that is marginally gravitationally super-critical in Case 1 (slab mass approximately 1.4 times the initial thermal Jeans mass), and gravitationally sub-critical (slab mass only a fraction of the initial thermal Jeans mass) in the remaining two cases (see Table 1). The slab is circular with radius, R, and is in pressure equilibrium with the inter-cloud medium (ICM), that confines it. Note that particles in the slab and the ICM were so distributed that the number density of particles across the slab-ICM interface is constant. The entire assembly was placed in a box, but without periodic-boundary conditions, meant only to prevent the ICM from diffusing away so that particles escaping from one face of the box re-enter from the opposite face. That SPH particles representing the ICM are mobile and exert only hydrodynamic force on normal gas particles would serve as a useful reminder to our readers at this point. The schematic sketch in Figure 1 illustrates this initial set-up for the simulations. Gas within the slab is composed of the usual cosmic mixture maintained initially at temperature, T gas. We set μ = 4 × 10−24 gms, the mean molecular mass of the gas particles.

Figure 1. A sketch of the gas-slab of radius, R, and height, y, confined by the ICM has been shown in this cartoon. The small ICM exerts pressure, p ext, externally on all faces of the slab as demonstrated by the direction of arrows.
Table 1. Physical parameters for the two cases.

aNumber density for gas and the ICM listed in columns 2 & 3 in units of [cm−3].
bComponents of pressure listed in columns 6, 7, & 8 in units of 104 × [K cm−3].
cScale-height for the slab
dTotal number of particles including those representing the ICM.
eAverage smoothing length for gas particles.
fM Jeans is the thermal Jeans mass calculated for the initial gas temperature, T gas.
The slab was characterised by radius, R = 2.5 pc, uniform initial number density, ![]() $\bar{n}$ = 250 cm−3, gas temperature, T gas, and thickness, y = 2h 0, where the scale-height, h 0, for the slab has been calculated below. Values of the relevant physical parameters have been listed in Table 1. For a slab in pressure equilibrium, the pressure exerted by the ICM, P ext, balances the thermal pressure, P therm, and the gravitational pressure, P grav, within the slab so that
$\bar{n}$ = 250 cm−3, gas temperature, T gas, and thickness, y = 2h 0, where the scale-height, h 0, for the slab has been calculated below. Values of the relevant physical parameters have been listed in Table 1. For a slab in pressure equilibrium, the pressure exerted by the ICM, P ext, balances the thermal pressure, P therm, and the gravitational pressure, P grav, within the slab so that
(e.g., Whitworth et al. Reference Whitworth, Bhattal, Chapman, Disney and Turner1994), where the gas surface density, ![]() $\Sigma _{g} = \bar{n}\mu h_{0}$. The gas temperature, T gas, corresponds to sound-speed a, so that the scale-height for the slab,
$\Sigma _{g} = \bar{n}\mu h_{0}$. The gas temperature, T gas, corresponds to sound-speed a, so that the scale-height for the slab, ![]() $h_{0}\ =\ \frac{a}{\sqrt{2\pi G\bar{n}\mu }}$ (Ledoux Reference Ledoux1951; Lubow & Pringle Reference Lubow and Pringle1993). The length of the fastest growing mode in a cooling medium is
$h_{0}\ =\ \frac{a}{\sqrt{2\pi G\bar{n}\mu }}$ (Ledoux Reference Ledoux1951; Lubow & Pringle Reference Lubow and Pringle1993). The length of the fastest growing mode in a cooling medium is
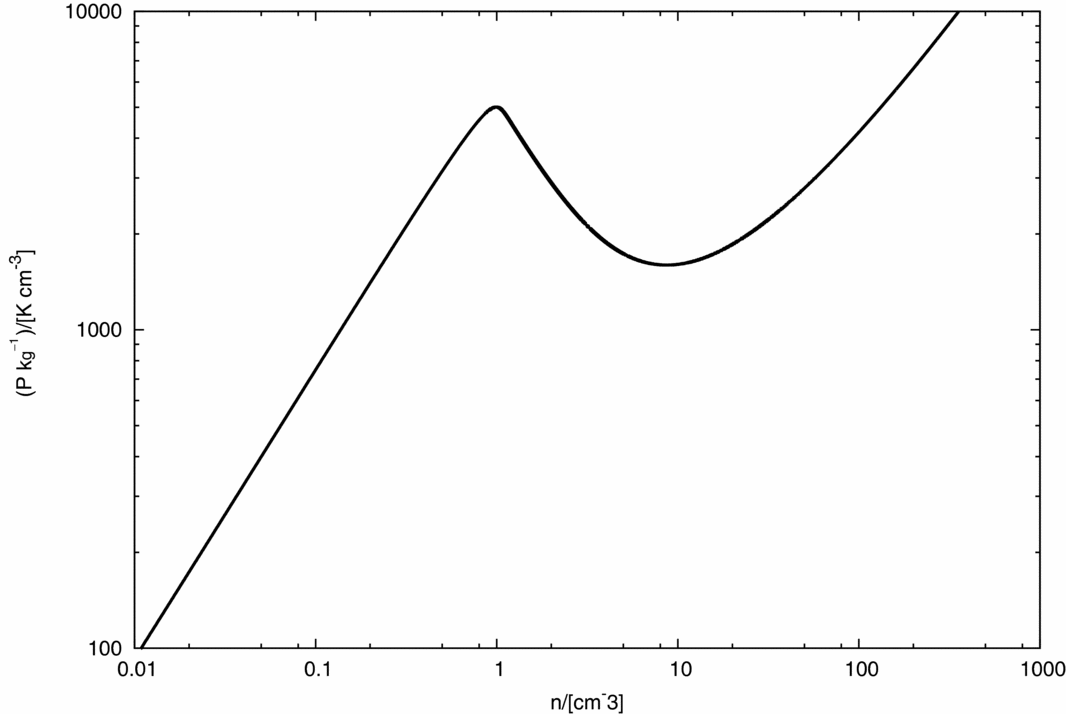
Vázquez-Semadeni, Passot, & Pouquet (Reference Vázquez-Semadeni, Passot and Pouquet1996); γe, is the effective polytropic exponent, i.e., slope of the cooling curve shown in Figure 2, which for our choice of the initial gas density, ![]() $\bar{n}$, turns out to be ~ 0.9 where as, γ = 5/3, is the adiabatic gas constant. The equilibrium pressure at density,
$\bar{n}$, turns out to be ~ 0.9 where as, γ = 5/3, is the adiabatic gas constant. The equilibrium pressure at density, ![]() $\bar{n}$, according to the cooling curve is ~7500 K cm−3. We perform three realisations with different choice of the initial gas temperature, and therefore, thermal pressure, P therm, away from its equilibrium magnitude as can be seen from Table 1.
$\bar{n}$, according to the cooling curve is ~7500 K cm−3. We perform three realisations with different choice of the initial gas temperature, and therefore, thermal pressure, P therm, away from its equilibrium magnitude as can be seen from Table 1.

Figure 2. The thermal equilibrium curve showing a plot of gas pressure against its density.
2.1 Numerical algorithm
Numerical simulations were performed using the well-tested smoothed particle hydrodynamics (SPH) code SEREN in its energy and momentum conserving formalism with an adaptive gravitational softening length (Hubber et al. Reference Hubber, Batty, McLeod and Whitworth2011). Simulations were developed with the standard cubic spline kernel with each SPH particle having approximately 50 neighbours. We note some concerns have been reported in the literature (e.g., Hobbs et al. Reference Hobbs, Read, Power and Cole2013), about the suitability of the classical SPH algorithm to investigate the fragmentation of a cooling gas on account of its inability to handle the mixing between hot and cold gas particles. It would be appropriate to point out that the said problem reported by these authors is in the extreme environment of galactic accretion where gas temperature is at least five orders of magnitude higher than that in the present work, so that the supposed difficulty with the mixing between two species of SPH particles could present a problem. This is unlikely in the present work where we are working with gas at a temperature not greater than a few hundred Kelvin. On the contrary, SPH has been routinely used to study problems such as the formation of giant molecular clouds (GMCs) in the galactic disk via fragmentation of gas that is allowed to cool (e.g., Dobbs, Pringle, & Burkert Reference Dobbs, Pringle and Burkert2012; Bonnell et al. Reference Bonnell, Dobbs and Smith2013), a problem that is of a similar nature to the one at hands in this work, but of course, on a much larger spatial scale. Nevertheless, in order to mitigate any such eventuality, we use the prescription of artificial conductivity suggested by Price (Reference Price2008). The Riemann artificial viscosity prescribed by Monaghan (Reference Monaghan1997) is used in these calculations with the corresponding viscosity parameter, α = 0.5.
The average initial smoothing length of a particle, h avg, is defined as
 \begin{equation*}
h_{{\rm avg}}^{3}\sim \frac{3V_{{\rm gas}}}{32\pi }\Big (\frac{N_{{\rm neibs}}=50}{N_{{\rm gas}}}\Big ),
\end{equation*}
\begin{equation*}
h_{{\rm avg}}^{3}\sim \frac{3V_{{\rm gas}}}{32\pi }\Big (\frac{N_{{\rm neibs}}=50}{N_{{\rm gas}}}\Big ),
\end{equation*}
V gas is the volume of the slab. Each simulation in this work was developed using 3.83 × 105 gas particles. For the magnitude of the average smoothing length, h avg, listed in column 11 of Table 1, the resolution criterion defined by Hubber, Goodwin, & Whitworth (Reference Hubber, Goodwin and Whitworth2006), the SPH equivalent of the well-known Truelove condition (Truelove et al. Reference Truelove, Klein, McKee, Holliman, Howell and Greenhough1997), is readily satisfied down to the typical size of a prestellar core (~0.2 pc), at 104 cm−3 and 10 K. This is good enough to study the formation of filaments and clumps in the post-fragmentation gas-slab. Also, note that the average smoothing length, h avg, is at least an order of magnitude smaller than the slab-height so that there is sufficient spatial resolution along this direction as well. However, although this choice of resolution is sufficient to prevent artificial fragmentation on the scale of a typical prestellar core in this work (at l ~ 0.2 pc), it is inadequate to achieve convergence in the calculation of physical quantities such as energy and momentum of the gas on this scale (see Federrath et al. Reference Federrath, Sur, Schleicher, Banerjee and Klessen2011, Reference Federrath, Schrön, Banerjee and Klessen2014). To this end these authors have suggested a much more stringent criterion, ![]() $\frac{l}{h_{{\rm avg}}}\gtrsim 30$, to be able to satisfactorily follow the dynamics on this scale. This adventure would of course, demand at least an order of magnitude increase in the number of gas particles. But we are not particularly concerned about this matter as it is not our intention to follow here the evolution of individual cores. Our immediate interest lies in demonstrating the initial stage of prestellar core-formation, i.e., the formation of dense clumps via fragmentation of gas that is allowed to cool. The average smoothing length, h avg, in each of the three realisations is sufficiently small to satisfy the above mentioned resolution criterion at the length-scale of fragmentation, λfast, defined by Equation (2).
$\frac{l}{h_{{\rm avg}}}\gtrsim 30$, to be able to satisfactorily follow the dynamics on this scale. This adventure would of course, demand at least an order of magnitude increase in the number of gas particles. But we are not particularly concerned about this matter as it is not our intention to follow here the evolution of individual cores. Our immediate interest lies in demonstrating the initial stage of prestellar core-formation, i.e., the formation of dense clumps via fragmentation of gas that is allowed to cool. The average smoothing length, h avg, in each of the three realisations is sufficiently small to satisfy the above mentioned resolution criterion at the length-scale of fragmentation, λfast, defined by Equation (2).
In SPH, the ICM is modelled with special type of particles that interact with normal gas particles only via the hydrodynamic force and are maintained at a fixed temperature, Ticm, throughout the entire length of each simulation. The temperature of ordinary gas particles, on the other hand, was determined by solving the equation for internal energy, modified suitably using the function below to account for cooling of the warm gas. Gas particles were allowed to cool by employing a parametric cooling function(Λ), defined by Equation (3) below and plotted in Figure 2. The curve can be readily identified as the thermal equilibrium curve for gas in the interstellar medium (ISM) (e.g., Wolfire et al. Reference Wolfire, McKee, Hollenbach and Tielens1995). We also assume a constant background source of heating defined by the heating function(Γ),
 \begin{eqnarray}
\frac{\Lambda (T)}{\Gamma } & =& 10^{7}\mathrm{exp}\Big (\frac{-1.184\times 10^{5}}{T + 1000}\Big )\nonumber\\
&& +\, 1.4\times 10^{-2}\surd {T}\ \mathrm{exp}\Big (\frac{-92}{T}\Big )\ \mathrm{cm}^{3},
\end{eqnarray}
\begin{eqnarray}
\frac{\Lambda (T)}{\Gamma } & =& 10^{7}\mathrm{exp}\Big (\frac{-1.184\times 10^{5}}{T + 1000}\Big )\nonumber\\
&& +\, 1.4\times 10^{-2}\surd {T}\ \mathrm{exp}\Big (\frac{-92}{T}\Big )\ \mathrm{cm}^{3},
\end{eqnarray}
(Koyama & Inutsuka Reference Koyoma and Inutsuka2002; Vázquez-Semadeni et al. Reference Vázquez-Semadeni, Gómez, Jappsen, Ballesteros-Paredes, González and Klessen2007).
2.1.1 Identifying gas clumps
We employed the robust HOP algorithm suggested by Eisenstein & Hut (Reference Eisenstein and Hut1998) to identify clumps within the density field. The algorithm proceeds by first identifying the local density peaks in a given density field, followed by a neighbour search for each of the identified density peaks. For the purpose, we need three density thresholds: ρpeak, ρsaddle and ρouter. An initial scan of the density field was carried out and SPH particles with density higher than, ![]() $\rho _{{\rm peak}}\sim 10^{4} \text{ cm}^{-3}$, were identified as density peaks, or in other words, the seed-particles for clumps. This choice of the density threshold is sufficiently large for the extant purpose of studying the onset of core-formation. The density at the edge of a fragment is denoted as, ρouter, and ρouter ~ 0.2ρpeak. The density field was then re-scanned with this density threshold to identify immediate neighbours of the previously identified density peaks. Finally, two clumps were merged together to form a contiguous object, if a particle and its nearest neighbour appeared in two different clumps and if the average density of these two particles turned out to be greater than ρsaddle ~ 0.1ρpeak. The radius of a clump was calculated as, r clump = max(< rc − ri >), i ∈ (1, N clump) and c, the identifier of the seed-particle for a clump. Finally, the mass of a clump was calculated as, M clump = Σclumpr 2clump; Σclump, being the average surface density of a detected clump, and
$\rho _{{\rm peak}}\sim 10^{4} \text{ cm}^{-3}$, were identified as density peaks, or in other words, the seed-particles for clumps. This choice of the density threshold is sufficiently large for the extant purpose of studying the onset of core-formation. The density at the edge of a fragment is denoted as, ρouter, and ρouter ~ 0.2ρpeak. The density field was then re-scanned with this density threshold to identify immediate neighbours of the previously identified density peaks. Finally, two clumps were merged together to form a contiguous object, if a particle and its nearest neighbour appeared in two different clumps and if the average density of these two particles turned out to be greater than ρsaddle ~ 0.1ρpeak. The radius of a clump was calculated as, r clump = max(< rc − ri >), i ∈ (1, N clump) and c, the identifier of the seed-particle for a clump. Finally, the mass of a clump was calculated as, M clump = Σclumpr 2clump; Σclump, being the average surface density of a detected clump, and
 \begin{equation*}
\Sigma _{{\rm clump}} \sim \frac{1}{N_{{\rm clump}}}\sum _{p=1}^{N_{{\rm clump}}}\rho _{p} h_{p},
\end{equation*}
\begin{equation*}
\Sigma _{{\rm clump}} \sim \frac{1}{N_{{\rm clump}}}\sum _{p=1}^{N_{{\rm clump}}}\rho _{p} h_{p},
\end{equation*}
where, hp and, ρp, are respectively the smoothing length and density, of a particle belonging to a clump. The summation in the expression above is over the number of particles, N clump, that constituted a clump.
3 RESULTS
3.1 Evolution of the pressure-confined slab
Under confinement from external pressure, p ext, the gas-slab fragments to produce clumps, some of which are isolated, many other appear contiguousFootnote 3. In the absence of any external perturbations structure in the density field is seeded purely by numerical noise. While the slab in each of the three cases evolves in a mutually similar fashion, in Case 1, where the slab was initially gravitationally super-critical, it also exhibits a tendency to contract in the radial direction. In the remaining two realisations the slab does not contract in the radial direction, but fragments, though the fragmentation-timescale successively increases in these two realisations, viz. 2 and 3. Shown in Figure 3 are rendered images of the mid-plane of the slab in Case 2. That the slab soon becomes flocculated can be seen from the picture on the central panel of this figure. On the right-hand panel in this figure is the picture showing the fragmented slab at the time of terminating calculations in this realisation. At this epoch, the slab is replete with filamentary structure and smaller cores appear to have begun forming along the length of some of these filaments.

Figure 3. Plot showing rendered density images of a projection of the mid-plane of the slab in Case 2. Time measured in Myrs has been marked on the top right-hand corner and spatial coordinates in units of parsecs.
Rendered images in Figure 3 also suggest that the fragmentation has probably been hierarchical, in the sense that we observe formation of larger, contiguous clumps that appear filament-like, which then sub-fragment to form smaller cores. However, we could not track the process further due to lack of adequate computational resources. Indeed, during the early stages of fragmentation some clumps do merge to form larger clumps. Shown on the upper panel of Figure 4 for instance, is the rendered density plot of a small section of the fragmented slab. These pictures demonstrate the merger of clumps to form a single contiguous object that incidentally looks filament-like. But this is not to suggest that filamentary objects form exclusively via merger of smaller fragments. Observational evidence for such occurrence in molecular clouds has been reported; star-formation in the Serpens molecular cloud, for instance, appears to have been triggered due to collision between two smaller clumps of molecular gas (e.g., Duarte-Cabral et al. Reference Duarte-Cabral2010; Graves et al. Reference Graves2010). Furthermore, André et al. (Reference André, Belloche, Motte and Peretto2007) have estimated the collision time on the order of ~ 1 Myr for cores in the Ophiuchus molecular cloud. More recently, Tsitali et al. (Reference Tsitali, Belloche, Garrod, Parise and Menten2014), have deduced an even shorter collision time on the order of ~ 0.7 Myr for cores in the Chamaeleon I North region.

Figure 4. Shown on the upper panel, in a set of images, is a small section of the fragmenting slab, fairly early in its evolution, for Case 2. Of particular interest is the region between x ∈ (3.5, 3.7) and z ∈ (4.6, 5.2), on these plots which shows the merger of smaller clumps leading to the formation of a single large clump that incidentally appears filament-like. Shown on the lower panel are rendered images of net pressure (in units of log (K cm−3)) over this region at the same epoch as that for pictures on the upper panel. The merger of clumps to form a single contiguous object is reflected by contiguous nature of the gas pressure over this region. As in Figure 3, unit of time is Myrs and has been marked at the top right-hand corner of the upper panel.
Merger of fragments has also been reported previously in numerical simulations (e.g., Banerjee et al. Reference Banerjee2009), and probably, is the result of clumps having lower thermal pressure relative to that in the medium between clumps, the inter-clump medium. Clumps floating in the tenuous inter-clump medium and confined by the pressure exerted by this medium may be thought of as analogous to nuts distributed on cake top. The inter-clump medium is non-stationary and clump-merger is likely triggered by the motion of this medium that drags the clumps floating in it. To examine if this was indeed the case, we have, in the lower panel of Figure 4, plotted rendered images of gas pressure in the region of merging clumps shown in the upper panel of this same figure. The gas pressure for this plot is a sum of the thermal and the non-thermal contributions (by which we mean the kinematic pressure due to the velocity of gas particles, the magnitude of which has been discussed in Section 4.1 b below). From these plots, it is evident that regions of relatively low pressure marked in yellow-red shades join to form a single elongated structure. The density field is now segregated into the warm and cold phase. However, this observation does not support the hypothesis suggested by Koyama & Inutsuka (Reference Koyoma and Inutsuka2004), according to which clumps must have a higher pressure relative to the inter-clump medium so they could wade through this medium to make merger possible. The difficulty with this hypothesis is that clumps would disperse quickly if they were to have a pressure greater than that of the medium in which they reside; there is no evidence to suggest dispersal of clumps in these simulations.
Temperature distribution of molecular gas within the fragmented slab at two epochs has been shown in the rendered plots of Figure 5. Cooler and relatively dense regions in the fragmented slab can be identified as those shaded red on this image. The rendered image on the left-hand panel of this figure shows the gas temperature within the fragmented slab at t = 2.21 Myrs which in conjunction with the corresponding density plot in Figure 3 can be used to estimate the length of the fastest growing mode, L fast, defined by Equation (2) above. A simple calculation yields, L fast ~ 1.3 pc, which, as can be seen on the central panel of the second row of Figure 3, is indeed consistent with the length of fragments visible in this image. The picture on the right-hand panel of Figure 5 shows the distribution of gas temperature at the time when calculations for this case were terminated (t ~ 6.1 Myrs). The red areas on this image, and therefore colder regions in the fragmented slab, denote regions where smaller cores have probably begun forming via sub-fragmentation of larger clumps. The rarefied gas between clumps, which in the rest of this article will be described as the inter-clump medium, is an order of magnitude warmer than the gas in the dense phase. These two phases, as expected, are in approximate pressure equilibrium; the average density and temperature of the inter-clump medium are respectively ~ 2.5 × 103 cm−3, and ~ 120 K which corresponds to a pressure, ~ 3 × 105 K cm−3, is comparable to the pressure in the dense phase at ~ 104 cm−3 and ~ 30 K.

Figure 5. Rendered images of the distribution of gas temperature in the mid-plane of the slab in Case 2 for two epochs (t = 2.21 Myrs and 6.07 Myrs for the plot, respectively on the left and right-hand panel), has been shown here.
Figures 3 and 5 further highlight the importance of cooling in the process of gas fragmentation within clouds, and therefore, in the overall process of core-formation. Note that the pictures shown in Figure 5 were prepared by distributing particles over a grid of 1 000 cells in each dimension so that temperature has been averaged over pixels and could therefore, easily blanket some of the coldest particles in the calculation. Since the nature of the dynamical processes within the slab remain unaltered despite changes in gas temperature, we have shown here plots only from Case 2 listed in Table 1 above. Below we will present a mutual comparison of the dynamical processes that lead to fragmentation of the slab in each of the three realisations. This will be followed by a comparison of other diagnostic properties of gas in the post-fragmentation slab.
3.2 Dynamical instabilities within a cooling slab
The slab evolves in the wake of an interplay primarily between two instabilities, viz. (i) the TI and (ii) the gravitational instability (GI). As is common knowledge, a gas-body becomes susceptible to the TI, when it is perturbed from its state of thermal equilibrium. In these simulations, we achieve this by setting the initial gas temperature above its equilibrium temperature (T eq ~ 30 K; initial equilibrium pressure, ![]() $\frac{P_{{\rm eq}}}{k_{B}}\sim$ 7500 K cm−3), as dictated by the cooling curve shown in Figure 2. The calculations steadily converge to a new equilibrium state that depends on gas density; we are essentially looking to minimise the quantity,
$\frac{P_{{\rm eq}}}{k_{B}}\sim$ 7500 K cm−3), as dictated by the cooling curve shown in Figure 2. The calculations steadily converge to a new equilibrium state that depends on gas density; we are essentially looking to minimise the quantity, ![]() $\mathcal {L}\equiv (n^{2}\Lambda (T) - n\Gamma )$, for gas number density, n, and
$\mathcal {L}\equiv (n^{2}\Lambda (T) - n\Gamma )$, for gas number density, n, and ![]() $\mathcal {L}\rightarrow 0$ close to equilibrium temperature. The absolute timescale over which the slab attains its thermal equilibrium, therefore does not really carry much physical significance and must be interpreted in a comparative sense only. Without the thermal conductivity, we cannot define the Field length in these calculations and so, the minimum length-scale for the TI, in these simulations, is supplanted by the SPH smoothing length. A volume of gas becomes susceptible to the TI if,
$\mathcal {L}\rightarrow 0$ close to equilibrium temperature. The absolute timescale over which the slab attains its thermal equilibrium, therefore does not really carry much physical significance and must be interpreted in a comparative sense only. Without the thermal conductivity, we cannot define the Field length in these calculations and so, the minimum length-scale for the TI, in these simulations, is supplanted by the SPH smoothing length. A volume of gas becomes susceptible to the TI if,
Field (Reference Field1965); ![]() $\mathcal {L} = n^{2}\Lambda - n\Gamma$. However, the gas may also be destabilised due to
$\mathcal {L} = n^{2}\Lambda - n\Gamma$. However, the gas may also be destabilised due to
Clarke & Carswell (Reference Clarke and Carswell2007). Equivalently, while the Field criterion must be satisfied for the gas to become thermally unstable, it may also become unstable according to the latter condition. In the present work, the slab, initially held at uniform pressure becomes thermally unstable most likely by satisfying the Field criterion and then, during the course of its evolution, the next criterion is also likely satisfied as gas is segregated into the dense and the rarefied phase.
Furthermore, if at least one side of the gas is also confined by ram pressure, the slab-ICM interface demonstrates propensity towards growth of corrugations such as those associated with the thin-shell instability (TSI) (Vishniac Reference Vishniac1983). In the present work, though, thermal pressure confines the slab and the amplitude of perturbations on the slab-ICM interface are much smaller than the thickness of the slab itself. So in the rest of this article, we will refer to the growth of the corrugations as the shell-instability, keeping in mind that the corrugations appear only on this interface.
During the course of evolution, as perturbations in the density field begin to grow, gas within the slab gets segregated into the dense and rarefied phase. Each subsequently acquired state of thermal equilibrium is impermanent as density and pressure adjustments happen quickly and the gas is no longer in gravo-thermal equilibrium. The implications of this observed fragmentation for the evolution of molecular clouds will be discussed in Section 5.1. The typical fragmentation length-scale of this cooling gas is given by Equation (2). Of the two instabilities, the TI grows more rapidly in comparison to the GI in realisations 2 and 3 whereas the latter dominates the former in the first realisation. The image on the central panel of Figure 3, for instance, shows that the mid-plane of the slab becomes flocculated as it cools simultaneously.
In an earlier contribution, we have demonstrated that growth of the shell-instability induces a velocity field in the underlying gas and have explored the non-linear excursion of this instability (Anathpindika Reference Anathpindika2009). In this latter case, the amplitude of perturbations become comparable to the slab thickness which is not the case here. In this work, however, we are interested in examining the growth of the GI in a cooling slab. For although the TI initially generates structure in the density field, the GI sets in as gas continues to cool and induces sub-fragmentation, once the Jeans condition is satisfied. It must be remembered though, the fragments had not become isothermal when simulations were terminated and so the thermal Jeans length can only serve as a rough estimate for the typical size of a core (or a clump, in general). The thermal Jeans length, as is well-known, is defined as,
(Jeans Reference Jeans1928), which at ![]() $\bar{n}\sim$ 2 × 104 cm−3, our choice of density threshold to detect clumps, and temperature, T gas ~ 10 K, becomes, λJeans ~ 0.2 pc, which is significantly larger than the extent of the smallest resolvable spatial region in these simulations and satisfies the Truelove criterion for resolution so that artificial fragmentation is unlikely. Although, we have demonstrated here the process of clump-formation using only a relatively simple cooling function, a more realistic treatment of the process in which molecular gas attains thermal equilibrium would need the appropriate molecular chemistry (see e.g., Glover et al. Reference Glover, Federrath, Mac Low and Klessen2010). We leave this for a future work.
$\bar{n}\sim$ 2 × 104 cm−3, our choice of density threshold to detect clumps, and temperature, T gas ~ 10 K, becomes, λJeans ~ 0.2 pc, which is significantly larger than the extent of the smallest resolvable spatial region in these simulations and satisfies the Truelove criterion for resolution so that artificial fragmentation is unlikely. Although, we have demonstrated here the process of clump-formation using only a relatively simple cooling function, a more realistic treatment of the process in which molecular gas attains thermal equilibrium would need the appropriate molecular chemistry (see e.g., Glover et al. Reference Glover, Federrath, Mac Low and Klessen2010). We leave this for a future work.
At this point, a comparison of rates at which the TI and the GI grows, will prove useful in unravelling the fragmentation process. It will help us understand which of the two instabilities are responsible for clump-formation in a MC. During fragmentation it is likely, cooling at a given pressure and density, both have a destabilising effect on gas within the slab. In this case, the TI grows approximately on the thermal timescale as perturbations need not wait for a pressure equilibrium to become unstable. The thermal timescale
so that its growth-rate,
The growth-rate, ωTI, given by Equation (8) above was calculated by distributing the SPH particles on a 2563 grid in the k-space. The average density weighted temperature for each cell on this grid was then calculated and followed by the evaluation of the cooling function, (nΛ(T) − Γ), for that cell. The expression for the growth-rate of the GI on the surface of the slab, on the other hand, from the usual Jeans analysis, is
Jeans (Reference Jeans1928), which is also similar to that suggested by Ledoux (Reference Ledoux1951) and Elmegreen & Elmegreen (Reference Elmegreen and Elmegreen1978), though the former suggest growth-rate higher by a factor of 2 than that given by Equation (9), and therefore, is unlikely to alter conclusions drawn here.
Plotted on the upper, middle, and the lower panel of Figure 6 are respectively, the measured growth-rates for the TI and the GI for Cases 1, 2, and 3. It is clear that in each of the three test cases the slab fragments via a confluence of the TI and the GI. A common feature visible in these plots for Cases 2 and 3 is the subservience of the GI relative to the TI suggesting, the fragmentation is largely driven by the TI, the growth of which is the strongest in Case 3. On the contrary, the GI grows more strongly as compared to the TI in Case 1, where the initial distribution of gas in the slab was gravitationally super-critical (see Col. 12 of Table 1). Realisation 3 is the one that has the highest initial gas temperature and therefore departed strongly from thermal equilibrium (equilibrium temperature, T eq ~ 30 K). The TI-induced fragmentation is hierarchical as the slab first fragments on large spatial scales and then trickles down to smaller spatial scales, i.e., higher wave-numbers. Growth of either instability in each realisation begins on the length-scale, L fast, defined by Equation (2) and can be seen from the plots shown in Figure 6.

Figure 6. Comparative plots of the growth-rates of the gravitational and the thermal instability in Cases 1, 2 and 3 have been shown on respectively, the top, middle and the lower panel.
Fall in the growth-rate of the TI at a length-scale indicates a lower rate of cooling at that length-scale which means gas there is closer to acquiring thermal equilibrium. The reduction in the growth-rate of the TI, as is visible from these plots is impermanent and picks up as the slab continues to fragment. The situation in the fragmenting slab is dynamic so that pressure adjustments happen quickly. The relatively large fragments break up further as they continue to cool, a process that is simultaneously associated with the steadily rising strength of gravity. This is evident from the observed rise in the growth-rate of the GI with passage of time. Also, it appears, the TI-induced fragmentation was not complete at the time of terminating these calculations. However, in all the test cases its growth does appear to be slowing at higher wave-numbers (smaller spatial scales), as it should when fragments are approaching their equilibrium temperature. This slowing is more prominently visible in the plots for Case 1, where the slow down is visible at all wave-numbers. As noted earlier, we could not follow the later stages when these smaller fragments would likely begin to collapse. In the following section, we will separately examine some physical properties of the gas and the clumps detected in these simulations.
4 SOME DIAGNOSTIC PROPERTIES OF GAS
As we are concerned with the behaviour of gas in the prestellar phase, it is crucial to examine the distribution of its other physical properties. In this regard, we call attention to the distribution of gas velocity and density before examining the properties of cores detected in each realisation.
(1) The velocity probability distribution function (PDF). Of significant importance to the process of fragmentation is the behaviour of the relatively cool gas, typically found at a few ten Kelvin. We therefore describe as cold, gas cooler than 15 K, and warm, that is at temperature higher than 15 K. This threshold of gas temperature is suitable to study the kinematic properties of potential star-forming gas. Histograms showing the distribution of gas velocity on either side of the temperature threshold have been plotted on the upper and the lower panel of Figure 7 for each of the three realisations. We note that apart from the variation in the magnitude of velocity, the respective histograms show little mutual variation. The magnitude of gas velocity increases successively with increasing initial gas temperature in the three realisations. Also, in each of these cases the histogram for cold gas peters-off steeply at the high velocity end. This suggests, velocity field within a potential star-forming clump is likely to have a magnitude lower than a certain turnover value, perhaps determined by the prevailing physical conditions. It is, however, difficult to draw any specific inferences from these PDFs, or in general, from similar ones derived for MCs. At best they are indicative of the relative strength in the velocity bins. Observationally deduced velocity PDFs for typical SFCs are known to have a variety of shapes. For instance, similar looking PDFs have been derived for MCs such as the Orion, Monoceres, and a few others by Miesch & Scalo (Reference Miesch and Scalo1995). Interestingly, velocity magnitudes seen here are also comparable to those reported for gas within these clouds (e.g., Falgarone, Pety, & Hily-Blant Reference Falgarone, Pety and Hily-Blant2009; Hatchell et al. Reference Hatchell, Richer, Fuller, Qualtrough, Ladd and Chandler2005; Curtis, Richer, & Buckle Reference Curtis, Richer and Buckle2010; and references therein).
Figure 7. Shown here are the plots of the local velocity distribution for gas in the cold and warm phase within the fragmented slab at the time of terminating calculations for each of the three realisations.
(2) The density probability distribution function. Shown in Figure 8 are density PDFs for each of the three realisations, plotted at the time calculations were terminated in each case. Although similar looking, the PDFs for Cases 1 and 2 evolve on a timescale that is significantly different although it is comparable for Cases 2 and 3. This is because growth of the TI is much more sluggish in Case 1 as compared to that in the remaining two realisations as was demonstrated in Figure 6. The PDFs for the latter two realisations viz., 2 and 3, are bi-modal, a combination of two log-normal distributions, which is consistent with the behaviour of a two-phase medium. The log-normal fit to these PDFs was obtained using the following expression
(10)(e.g., Padoan, Jones, & Nordlund Reference Padoan, Jones and Nordlund1997; Federrath, Klessen, & Schmidt Reference Federrath, Klessen and Schmidt2008; Audit & Hennebelle Reference Audit and Hennebelle2010; Federrath et al. Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010 and Gazol & Kim Reference Gazol and Kim2013); σ, being the full width at half-maximum. The PDF for Case 1, on the other hand, appears to be developing a power-law tail at higher densities. However, this latter stage when fragments could begin to collapse was not followed in these simulations (see e.g., Klessen & Burkert Reference Klessen and Burkert2000; Dib & Burkert Reference Dib and Burkert2005; Vázquez-Semadeni et al. Reference Vázquez-Semadeni, González, Ballesteros-Paredes, Gazol and Kim2008; Kritsuk, Norman, & Wagner Reference Kritsuk, Norman and Wagner2011; Ballesteros-Paredes et al. Reference Ballesteros-Paredes, Vázquez-Semadeni, Gazol, Hartmann, Heitsch and Colin2011 and Federrath & Klessen 2013). \begin{equation}
p(\ln \ n) = \frac{1}{(2\pi \sigma ^{2})^{1/2}}\exp \Big [-\frac{(\ln \ n - \ln \bar{n})^{2}}{2\sigma ^{2}}\Big ],
\end{equation}
\begin{equation}
p(\ln \ n) = \frac{1}{(2\pi \sigma ^{2})^{1/2}}\exp \Big [-\frac{(\ln \ n - \ln \bar{n})^{2}}{2\sigma ^{2}}\Big ],
\end{equation}
Figure 8. The density probability distribution for gas within the fragmented slab in each of the three test cases has been shown here. As for the velocity PDFs shown in Figure 7, this plot was also made at the time of terminating calculations. Apart from the difference in timescale on which these PDFs take shape, the distributions for Cases 2 and 3 are bi-modal while that for case appears to be developing a power-law tail at higher densities.
PDFs have now been derived for a number of galactic MCs. For instance, André et al. (Reference André2010) have derived one for the Aquila SFC while Kainulainen et al. (Reference Kainulainen, Beuther, Henning, Henning and Plume2009), for nearly two dozen other galactic MCs (see also Schneider et al. Reference Schneider2012, Reference Schneider2013; Kainulainen, Federrath, & Henning Reference Kainulainen, Federrath and Henning2014). The density PDF for the Aquila MC has a distinct power-law tail at its high-density end. Similarly, other SFCs such the Taurus and Lupus I also demonstrates a tail at the high-density end. On the contrary, relatively quiescent clouds such as Lupus V and Coalsack have approximately log-normal density PDFs (Kainulainen et al. Reference Kainulainen, Beuther, Henning, Henning and Plume2009). In general, however, the density PDF shows considerable variation across MCs.
(3) Velocity power-spectrum. Growth of the dynamical instabilities discussed above induces a velocity field within slab-layers. The power-spectrum is a vital diagnostic of energy distribution across the spatial scales of a given velocity field (Federrath Reference Federrath2013). Observationally spectral indices have been determined for molecular clouds using emissions from the CO molecule and its isotopologues. Spectral indices in these cases have usually been suggested to lie between − 2 and − 4; see Miville-Desch$\rm{\hat{e}}$nes et al. (Reference Miville-Deschênes2010), review by Hennebelle & Falgarone (Reference Hennebelle and Falgarone2012). Shown in Figure 9 is the spectrum for the three test cases generated at the time of termination of calculations in these respective realisations and evidently has two peaks. A double-peaked spectrum is often reported for MCs (e.g., Schneider et al. Reference Schneider2011), and indicates the characteristic length-scale of dense structure in a MC. The spectra derived for realisations discussed in this work peak at ~ 1 pc, the typical length of filaments and ~ 0.2 pc, the characteristic size of clumps detected in the fragmented slab. However, unlike the spectra for typical SFCs, the spectra derived here peters-off at small spatial scales as protostellar feedback has not been included in these simulations. The spectrum was calculated by first interpolating the SPH particles on to a grid having resolution 2563 in the k-space. For this, we followed the procedure described by Price (Reference Price2007) while developing the publicly available visualisation algorithm SPLASH. Then the velocity vector field in the k-space was generated using the relation
(11)The corresponding power, P(k), was then calculated according to \begin{equation}
\mathbf {v}(\mathbf {k}) = \frac{1}{(2\pi )^{3}}\int _{V}\mathbf {v}(\mathbf {r})\exp (-i\mathbf {k\cdot r})\ d\mathbf {r}.
\end{equation}
(12)
\begin{equation}
\mathbf {v}(\mathbf {k}) = \frac{1}{(2\pi )^{3}}\int _{V}\mathbf {v}(\mathbf {r})\exp (-i\mathbf {k\cdot r})\ d\mathbf {r}.
\end{equation}
(12) \begin{equation}
P(k) = \langle \mathbf {v(k)}\cdot \mathbf {v}^{\ast }(\mathbf {k})\rangle.
\end{equation}
\begin{equation}
P(k) = \langle \mathbf {v(k)}\cdot \mathbf {v}^{\ast }(\mathbf {k})\rangle.
\end{equation}
At the epoch, when the spectrum was made, turbulence between wave-numbers (1 100) has not decayed yet. There is, however, no evidence of a significant decrease in power at smaller wave-numbers, i.e., larger spatial scales. Consequently, relatively large fragments are still probably sub-fragmenting at this epoch. On smaller spatial scales, or higher wave-numbers though, the decrease in the spectrum shows that TI induced fragmentation has probably terminated. The resulting clumps on small spatial scales are thermally supported, although most at this stage could be unbound at this stage. The spectrum is significantly steeper than the Kolmogorov spectrum and can be reasonably well approximated by a power-law of the type, P(k)∝ k −2.5. Thus, gas motions within the slab induced by pressure confinement and the confluence of various instabilities described above, appear to be compressive in nature and interestingly, is similar to the spectra derived for simulations where isothermal supersonic turbulence is injected. In these later cases, the power-spectrum is usually observed to have a slope slightly in excess of − 2 (e.g., Padoan et al. Reference Padoan, Jones and Nordlund1997; Kim & Ryu Reference Kim and Ryu2005; Price & Federrath Reference Price and Federrath2010; Federrath Reference Federrath2013).
The other striking feature of these spectra is that each of them exhibits secondary peaks at higher wave-numbers, k ≳ 100. As argued by Kitsionas et al. (Reference Kitsionas2009); Federrath et al. (Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010; Reference Federrath, Sur, Schleicher, Banerjee and Klessen2011) and Price & Federrath (Reference Price and Federrath2010), this feature and the somewhat excessive steepness of the spectra are both apparently the prognosis associated with inadequate numerical resolution, though it does not call into question the conclusion that dynamic instabilities in the slab generate compressive motions within its layers. Kitsionas et al. (Reference Kitsionas2009) argue that a minimum of 32 grid cells (i.e., 16 SPH smoothing kernels), are necessary to eliminate numerical artifacts that could possibly be introduced by dissipation mechanisms employed in a hydrodynamic code and more crucially, achieve numerical convergence in calculations of statistical quantities such as the power-spectrum associated with the underlying turbulent velocity field. The critical wave-number below which numerical convergence can be obtained is,
 $k_{\text{crit}}\le (\frac{N{\,=\,}\, ^{3\!\!\!\!\!}\sqrt{N}_{\rm gas}}{32})$, which for the current numerical exercise is ~ 3. In other words, the turbulent power-spectrum derived here is not resolved on the typical length-scale of fragmentation observed in these realisations. In order to be able to resolve the spectrum on the length-scale of the fastest growing mode defined by Equation (2) above, we will have to increase the number of particles by at least 1 order of magnitude above that used in this work, and by up to 3 orders of magnitude to resolve it on the length-scale of a typical core defined by Equation (6) above. We can therefore neither associate much significance to the observed slope of the spectra derived here, nor associate a causal relationship between the observed slope and the gas motions generated by the dynamic instabilities attending the slab. The secondary peaks in the power-spectra visible at higher wave-numbers are likely due to the accumulation of energy in these wave-number bins as density builds up on the corresponding length-scales. This problem would also be alleviated with an enhanced resolution as the observed accumulation of power in specific wave-vector bins will be more evenly distributed over smaller bins.
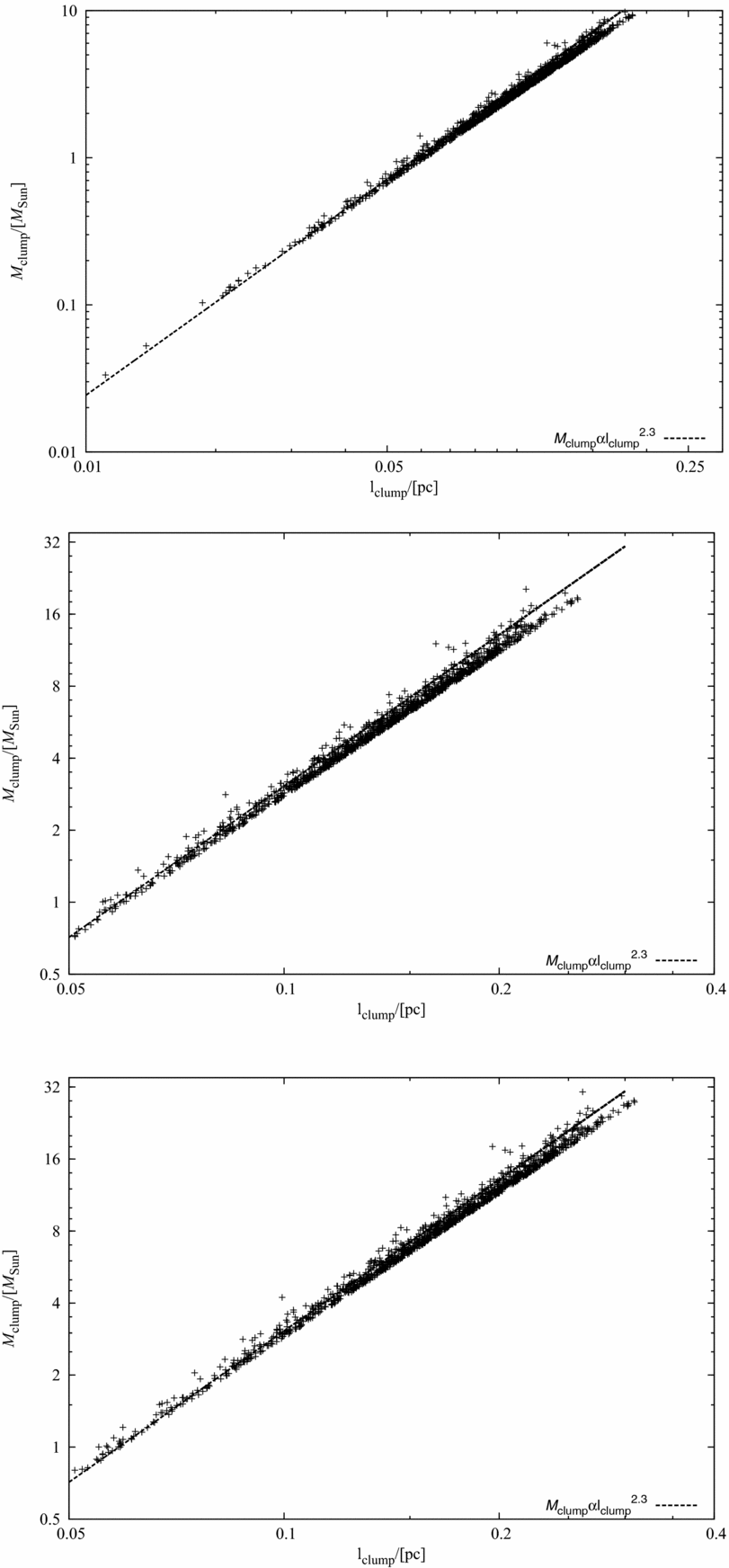
$k_{\text{crit}}\le (\frac{N{\,=\,}\, ^{3\!\!\!\!\!}\sqrt{N}_{\rm gas}}{32})$, which for the current numerical exercise is ~ 3. In other words, the turbulent power-spectrum derived here is not resolved on the typical length-scale of fragmentation observed in these realisations. In order to be able to resolve the spectrum on the length-scale of the fastest growing mode defined by Equation (2) above, we will have to increase the number of particles by at least 1 order of magnitude above that used in this work, and by up to 3 orders of magnitude to resolve it on the length-scale of a typical core defined by Equation (6) above. We can therefore neither associate much significance to the observed slope of the spectra derived here, nor associate a causal relationship between the observed slope and the gas motions generated by the dynamic instabilities attending the slab. The secondary peaks in the power-spectra visible at higher wave-numbers are likely due to the accumulation of energy in these wave-number bins as density builds up on the corresponding length-scales. This problem would also be alleviated with an enhanced resolution as the observed accumulation of power in specific wave-vector bins will be more evenly distributed over smaller bins.(4) Mass-size correlation. Shown in the top, middle, and the lower panel of Figure 10 is the correlation between the mass and size of the fragments detected in realisations 1, 2 and 3, respectively. The fit, M clump∝Lp clump, with p = 2.3, for these test cases is remarkably tight. It is also well above the M clump∝L 2clump relation that signifies constant column density for the detected sample of clumps and their bounded nature. Interestingly, isothermal simulations by Federrath et al. (Reference Federrath, Klessen and Wolfram2009), for instance, yielded a similar correlation, M clump∝L 2.3clump, for clumps detected in simulations of compressionally driven turbulence. On the other hand, for simulations of solenoidally driven turbulence they deduced a much steeper correlation, M clump∝L 2.6clump. Elmegreen & Falgarone (Reference Elmegreen and Falgarone1996) have reported a similarly steep correlation, M clump∝L 2.35clump, for CO clumps. Also, cores have been found in the Serpens and Ophiuchus MCs with a similarly steep slope such as those reported here (e.g., Enoch et al. Reference Enoch, Evans, Sargent, Glenn, Rosolowsky and Myers2008). Similar slopes have also been reported for CO clumps by a few other authors, e.g., Heithausen et al. (Reference Heithausen, Bensch, Stutzki, Falgarone and Parnis1998), Kramer et al. (Reference Kramer, Stutzki, Rohrig and Corneliussen1998) and Falgarone, Hily-Blant, & Levrier (Reference Falgarone, Hily-Blant and Levrier2004). Other recent observations of SFCs by for instance, Roman-Duval et al. (Reference Roman-Duval, Jackson, Heyer, Rathborne and Simon2010) and Donovan-Meyer et al. (Reference Meyer2013) also suggest a similar correlation. This suggests, SFCs are likely governed by supersonic, compressive turbulence that generates dense sheets of gas.
Figure 10. The upper, middle, and the lower panel shows the distribution of mass against the size of cores detected in each of the three realisations. The correlation is tight and well approximated by the M core∝L 3core.
4.1 Diagnostic properties of clumps
We have seen in the above sub-section that despite the similarity in the general evolutionary sequence of the slab for different choices of the confining pressure, p ext, the timescale of evolution and the magnitude of physical entities such as gas velocity and density vary across the three realisations. Consequently, differences in the properties of clumps condensing out of this gas across the three test cases are not altogether unexpected. Below, we will examine some physical properties of prestellar cores detected in each realisation.
(a) Gas temperature in clumps. The distribution of gas temperature in the clumps detected in each of the three realisations has been shown in Figure 11. The nature of temperature distribution is similar for each of the three realisations, however, the coldest clumps were found in realisation 1, followed by those that are successively warmer, in the remaining two realisations. Also, the dual-peaked temperature distributions suggest, one set of clumps that is relatively colder than the other. The implication of which is, this latter set of clumps is likely to sub-fragment as they continue to cool. In what follows, we will investigate if other physical properties such as the mass and size of these clumps also depend on their temperature. Observational surveys of typical SFCs such as those by Jijina et al. (Reference Jijina, Myers and Adams1999) and Enoch et al. (Reference Enoch, Evans, Sargent, Glenn, Rosolowsky and Myers2008), have deduced temperatures in the range of 7–40 K for prestellar cores and gas clumps. Apparently, this deduced temperature distribution peaks at about 12 K, though cores with even cooler molecular gas have also been reported frequently. We get a similar distribution for clumps detected in our simulations with the coldest clumps being detected in realisation 1.
(b) Velocity field within clumps. The histogram showing the distribution of gas velocity dispersion, V, within the clumps detected in the three realisations has been shown on the top right-hand panel of Figure 12. Although the nature of the PDF is similar for the three test cases, the magnitude of velocity dispersion increases successively from Case 1 through to 3. This is probably due to the stronger growth of the TI that triggers early fragmentation of the slab. In particular, the growth of this instability is stronger in Cases 2 and 3 in comparison to that in Case 1. That the TI indeed, grows strongly in these two realisations has been demonstrated above. Also, a stronger confining pressure also assists stronger growth of corrugations on the slab-ICM interface, associated with the shell-instability. Growth of this latter instability on the slab-ICM interface causes the interface to buckle as density perturbations amplify rapidly. This amplification is associated with momentum transfer between local peaks and troughs in the density field. A stronger confining pressure assists momentum transfer between density perturbations and therefore, their amplification. The combined effect of these instabilities probably holds the key to the observed velocity field in the detected clumps. Interestingly, the magnitude of this velocity field is consistent with that found within clumps and cores in typical star-forming regions; see e.g., Enoch et al. (Reference Enoch, Evans, Sargent, Glenn, Rosolowsky and Myers2008) and other references therein.
(c) Clump-size. The calculation of clump-size was discussed earlier in Section 2.1 where the algorithm to detect clumps was described. The resulting distribution of clump-size for those detected in the respective test cases has been shown in Figure 13. The detected clumps have sizes comparable to those of potential star-forming clumps and reported in the previously cited literature. Evidently, the sub-fragmentation of larger fragments into smaller cores must be still underway at the time of terminating these calculations. The sub-fragmentation of gas filaments, as can be seen in the rendered density plots of Figure 3, occurs on the scale of the local Jeans length. For instance, the temperature distribution of clumps detected in Case 2 peaks at ~ 15 K, which at the clump-detection threshold of ~ 104 cm−3, corresponds λJeans ~ 0.2 pc, which is indeed where the distribution of clump-sizes for Case 2 peaks. This is also true for the other two realisations.
(d) Mass-spectrum. The distribution of masses for the cores detected in each realisation has been shown in Figure 14. Across the three realisations, the nature of the distribution of clump masses is largely similar, though the spectrum for Cases 2 and 3 shifts rightward relative to that for Case 1. This is likely because, and as demonstrated in item (a) above, the clumps detected in these latter realisations are relatively warmer than those detected in Case 1. It was also demonstrated in item (c) above that the fragmentation probably occurs on the scale of the local Jeans length, so that the turnover of mass-spectra shown in Figure 14 at the respective Jeans mass should be hardly surprising. The shift in the turnover mass suggests that it is sensitive to the prevailing physical conditions. At this stage, it is evident that sub-fragmentation of larger clumps into smaller cores is still likely underway as there is a significant population of massive fragments. However, even at this fairly early stage in their life cycle, this initial mass-spectrum appears similar to that derived for cores detected in SFCs (see e.g., Motte, André, & Neri Reference Motte, André and Neri1998; Nutter & Ward-Thompson Reference Nutter and Ward-Thompson2007; Enoch et al. Reference Enoch, Evans, Sargent, Glenn, Rosolowsky and Myers2008; André et al. Reference André, Men’shchikov, Könyves and Arzoumanian2011), and is very well approximated by a power-law at the high-mass end. Using the peaks in respective histograms for M clump and L clump, the condition for gravitational boundedness,
 $V^{2}\equiv \frac{2GM_{{\rm clump}}}{L_{{\rm clump}}}$, yields escape velocities on the order of ~ 0.3 km s−1 to ~ 0.4 km s−1 for the detected clumps in Cases 1, 2, and 3, respectively. From the plots shown in Figure 12, it is evident that the magnitude of gas velocity dispersion for most, if not all the detected clumps is significantly larger than the escape velocity calculated above. The implication being, most clumps at this stage are likely unbound.
$V^{2}\equiv \frac{2GM_{{\rm clump}}}{L_{{\rm clump}}}$, yields escape velocities on the order of ~ 0.3 km s−1 to ~ 0.4 km s−1 for the detected clumps in Cases 1, 2, and 3, respectively. From the plots shown in Figure 12, it is evident that the magnitude of gas velocity dispersion for most, if not all the detected clumps is significantly larger than the escape velocity calculated above. The implication being, most clumps at this stage are likely unbound.
Figure 11. Shown here is the distribution of gas temperature in clumps detected in Cases 1, 2, and 3.
Figure 12. As in Figure 11, the distribution of velocity dispersion for gas in the clumps detected in our simulations has been shown in these plots.
Figure 13. The distribution of sizes for clumps detected in Cases 1, 2 and 3 has been shown in these plots.
Figure 14. The initial mass distribution for clumps detected in Cases 1, 2, and 3 has been shown in these plots.
5 DISCUSSION
Molecular clouds are replete with density structure that is often found to be filament-like with potential star-forming regions usually located at the junctions of these gas filaments (Schneider et al. Reference Schneider2012). Filamentary clouds and potential star-forming clumps that form at the junctions of gas filaments fragment further on the scale of local Jeans length to form prestellar cores. Interestingly though, cores, clumps, and larger clouds all appear to follow empirical scaling relations first introduced by Larson (Reference Larson1981), which makes turbulence ubiquitously important. The fractal nature of molecular clouds suggests that clouds may not be collapsing universally instead, pockets of dense gas probably assembled via interactions between turbulent flows could collapse locally. Hydrodynamic instabilities are usually triggered due to shocks generated by strongly supersonic turbulent flows. One of the properties of these instabilities is their relatively short growth timescales that tends to fragment rapidly the shocked clouds while damping the gravitational instability (see eg. Vázquez-Semadeni et al. Reference Vázquez-Semadeni, Gómez, Jappsen, Ballesteros-Paredes, González and Klessen2007; Heitsch et al. Reference Heitsch, Hartmann and Burkert2008 b; Anathpindika Reference Anathpindika2009).
As demonstrated by the above authors, despite their rapid appearance within a shocked cloud, fragments generated via growth of hydrodynamic instabilities are unlikely to be bound and usually are transient by nature. Thus, they are more likely to be either sheared apart by turbulent flows or perhaps merge with other neighbouring fragments. On the other hand, confinement by relatively weaker shocks, or indeed, thermal pressure, yields radically different results as it is more likely to aid the growth of gravitational instability and produce more stable fragments that demonstrate a greater propensity towards a radial in-fall. However, irrespective of the type of confinement, gas cooling appears to play a fundamental role in the process of fragmentation. A fragment (which could be a core), that cools efficiently becomes susceptible to gravitational collapse as it loses thermal support and as turbulence decays gradually. For the moment, though we neglect the effects of magnetic field on dynamic stability.
Under appropriate physical conditions, the gravitational instability grows quickly and fragments the underlying gas cloud. The timescale of fragmentation, ![]() $\tau \equiv \frac{\lambda _{{\rm fast}}}{a}$, where a is the average sound-speed within the gas slab and λfast, length of the fastest growing unstable mode. If E rad is the excess energy radiated away by a pressure-confined cloud over its fragmentation timescale then,
$\tau \equiv \frac{\lambda _{{\rm fast}}}{a}$, where a is the average sound-speed within the gas slab and λfast, length of the fastest growing unstable mode. If E rad is the excess energy radiated away by a pressure-confined cloud over its fragmentation timescale then, ![]() $E_{{\rm rad}}\equiv \frac{p_{{\rm ext}}}{n}$, and finally, the rate at which it loses energy,
$E_{{\rm rad}}\equiv \frac{p_{{\rm ext}}}{n}$, and finally, the rate at which it loses energy, ![]() $\frac{dE_{{\rm rad}}}{dt}\equiv n\Lambda - \Gamma$. Thus, the timescale on which the gas cools,
$\frac{dE_{{\rm rad}}}{dt}\equiv n\Lambda - \Gamma$. Thus, the timescale on which the gas cools, ![]() $\tau _{{\rm cool}}\equiv \frac{E_{{\rm rad}}}{dE_{{\rm rad}}/dt}\equiv \frac{p_{{\rm ext}}}{n^{2}\Lambda - n\Gamma }$. In a calculation such as this one, the cooling-timescale, of course, is determined by the functional dependence of the cooling function, Λ, on temperature. Eliminating time from the above expressions, we get an expression for the average sound-speed, a, within the fragmenting gas,
$\tau _{{\rm cool}}\equiv \frac{E_{{\rm rad}}}{dE_{{\rm rad}}/dt}\equiv \frac{p_{{\rm ext}}}{n^{2}\Lambda - n\Gamma }$. In a calculation such as this one, the cooling-timescale, of course, is determined by the functional dependence of the cooling function, Λ, on temperature. Eliminating time from the above expressions, we get an expression for the average sound-speed, a, within the fragmenting gas,
Equation (13) also shows that the average gas temperature attained by a gas-body, over a length scale, λfast, by radiating excess energy depends on the balance between the net heating and cooling. For the GI to grow, gas within a cloud must cool to a sufficiently low temperature which makes cooling rate crucial for the fragmentation process.
While the canonical Jeans analysis can account for the fragmentation process in the simplest case of an unconfined gas-body, pressure confinement adds a degree of complication. The gas-slab in this work evolved via a complex interplay of three instabilities, viz. the (i) TI, (ii) shell-instability, and (iii) gravitational instability. Fragmentation of the slab during its early stages is triggered by the confluence of the TI and the shell-instability. Analytic arguments suggest, change in the confining pressure alone can possibly induce a change to the fate of a pressure-confined cloud. Equations (2) and (13) support this argument and the scale of fragmentation is determined by the details of thermal physics. In the case of a cooling medium, the functional dependence of the cooling function on the gas temperature must hold the key to determining the fate of the slab, or a cloud, in general.
5.1 Thermal instability(TI) in Giant molecular clouds (GMCs)
Depending on the magnitude of gravitational pressure in a GMC, it may be classified as pressure-confined or gravitationally bound. The magnitude of gravitational pressure in the former type of cloud is significantly smaller than its surface pressure whereas in the latter, the gravitational pressure dominates the surface pressure (e.g., Bertoldi & Mc Kee Reference Bertoldi and McKee1992). It has been suggested that pressure-confined clouds may be considered part of the usual three-phase model of the ISM, while a more complex, four-component model could be invoked for gravitationally bound GMCs (McKee Reference McKee1995). The reason being, gravitational bound GMCs are not isobaric. However, it is now widely accepted that GMCs, irrespective of their gravitational state, are far from uniform and exhibit turbulent motions (e.g., Hughes et al. Reference Hughes2013). In general, GMCs are therefore unlikely to be isobaric, though they are usually in approximate pressure equilibrium with the ambient ISM. So, the suggested four-component model may then be extended to GMCs without invoking the qualifying condition about gravitational boundedness.
The essence of this model is, GMCs are multi-phase media themselves and processes that regulate thermal pressure in the diffuse ISM could very well regulate thermal pressure in GMCs also. This model can then reconcile the fact that dense clumps in GMCs could possibly have thermal pressure comparable to, or even greater than that in typical HI clouds in the diffuse ISM. Now, the slab considered in numerical exercises discussed in this work is initially pressure confined (see Table 1). It is rendered gravo-thermally unstable by continuous gas cooling. Early growth of density perturbations in this slab disturb its initial isobaric nature. The rapid growth of these density perturbations cause redistribution of thermal pressure in the slab and the resulting fragmentation on the length-scale, L fast, segregates the gas into the dense and a relatively tenuous phase, which we describe as the inter-clump medium.
The resulting fragments continue to cool and during the process enhance their self-gravity. Though, a majority of the fragments in each realisation were still gravitationally unbound when calculations were terminated. Thermal pressure between the fragments and the inter-clump medium in which they float undergoes rapid redistribution during the course of evolution. Earlier, in Section 3.1 we demonstrated, fragments, soon after their formation, are at a relatively lower pressure relative to the inter-clump medium and some of them merge to form more contiguous objects. Eventually, the fragments acquire an approximate pressure equilibrium with this inter-clump medium. This explains why the inter-clump medium is relatively warm compared to the dense phase. Our conclusion is that a cooling molecular cloud with a non-uniform density distribution presents itself as a multi-phase medium and supports the hypothesis suggested by McKee (Reference McKee1995). It is also supported by observations that have demonstrated the tenuous nature of the inter-clump medium (e.g., Falgarone & Puget Reference Falgarone, Puget, Pudritz and Fich1988; Blitz Reference Blitz, Lada and Kylafis1991). More recently, Bailey, Basu, & Caselli (Reference Bailey, Basu and Caselli2014), have demonstrated that cores in molecular clouds are confined by a tenuous medium that is warm. Although, we have succeeded in demonstrating the segregation of the density field, we could not follow the evolution of fragments to the stage when they would begin to collapse under self-gravity, but this is not the subject of this investigation.
6 CONCLUSIONS
In our calculations, we observed unstable modes first appearing on the slab-surface via its interaction with the ICM confining it. These modes were associated with the simultaneous onset of the TI that induced fragmentation within the slab. This is true in all three realisations as is reflected by the higher growth-rate of the TI in comparison to that of the GI. We have demonstrated that molecular clouds are themselves three-phase media and contain a dense phase, represented by clumps and cores, in approximate pressure equilibrium with the relatively tenuous inter-clump medium in which these clumps float and an intermediate unstable phase between these two phases. Growth of these instabilities injected a velocity field within slab layers at large k which then trickled down to small k. Gas in the dense phase continued to cool and fragmentation on the scale of the local Jeans length ensued. Interestingly, following a recent study of the dynamical properties of MCs across the M51, M33, and the LMC, the authors suggested, pressure within a cloud and that confining it were correlated (Hughes et al. Reference Hughes2013). This result is interesting since the induced velocity field, in a purely non-magnetic calculation, is a major contributor to the internal pressure and the magnitude of the externally confining pressure could affect the strength of this velocity field.
The effects of gas thermodynamics on physical properties of dense gas clumps is evident in this work.
Clumps detected in the post-fragmentation slab are not only more massive, but predominantly unbound in the realisations where the temperature of the initial volume of gas deviated strongly from its equilibrium value. These clumps formed on a longer timescale and also had a relatively large velocity dispersion. Sub-fragmentation of these clumps to form smaller cores is possible once they acquire sufficient mass, or conversely, have cooled sufficiently. Irrespective of this difference, the mass-spectrum qualitatively resembles the mass-spectrum for clumps and/or cores found in typical SFCs. This re-emphasises the suggestion that the core mass-spectrum is probably seeded by the core-formation process itself (e.g., Heitsch et al. Reference Heitsch, Hartmann and Burkert2008a).
A comparison of the results obtained from this work with those in the literature for an isothermal slab demonstrate the effects of gas thermodynamics on the evolution of the slab. Although the outcome is broadly consistent, i.e., the slab fragments irrespective of its thermodynamic state, the timescale and the length-scale on which this happens is significantly different in either type. Unlike the isothermal slab, the timescale of fragmentation for a dynamically cooling slab is determined by the cooling function as demonstrated the expression for the cooling timescale, τcool, defined by Equation (13). Although sufficient to demonstrate the ongoing dynamic processes, the assumption of an isothermal gas will most probably bias results in a direction dictated by the initial choice of temperature; see for instance Bonnell et al. (Reference Bonnell, Clarke and Bate2006). A self-consistent calculation of gas temperature with a cooling function permits us to demonstrate the effect of prevailing physical conditions on various properties of clumps as was demonstrated in the previous section.
Prestellar cores are found at sub-parsec scale and more recent observations of cores have shown that gas within potential star-forming cores is cold at only a few Kelvin and is pervaded by a weak velocity field, often referred to as micro-turbulence. Low-magnitude velocity fields have been observed in both, bound prestellar cores as well as unbound cores (see e.g., Motte et al. Reference Motte, André and Neri1998; Jijina, Myers, & Adams Reference Jijina, Myers and Adams1999; Hatchell et al. Reference Hatchell, Richer, Fuller, Qualtrough, Ladd and Chandler2005; Nutter & Ward-Thompson Reference Nutter and Ward-Thompson2007; Enoch et al. Reference Enoch, Evans, Sargent, Glenn, Rosolowsky and Myers2008; among a number of other authors working on the subject). It is commonly believed, this velocity field within cores is introduced during their natal phase itself, while they are yet accreting gas from their parent clouds. Although this is quite likely, results from this work show that a turbulent velocity field is probably first injected in virgin clouds via interactions with the confining ICM, followed by growth of other dynamical instabilities such as the TI.
From our test simulations, it appears that cores and their parent clumps forms on different timescales which makes the cooling timescale, τcool, of molecular gas within clumps, crucial. We have seen that interaction with a warmer ICM in the case of a strongly confined slab introduces a relatively strong velocity field. So, although the initial fragmentation in these realisations happens on a relatively short timescale, fragments are unbound and some of them do merge to form larger objects. Thus, while a turbulent velocity field need not necessarily delay fragmentation, the formation of potential SFCs is likely to take longer.
Using a relatively simple prescription of the cooling function, we have demonstrated the possible variation in properties of cores in response to changes in the externally confining pressure. We have also shown that a confluence of various dynamic instabilities could possibly seed a weak velocity field in dense clumps of gas. Thus, it is clear that dynamic processes preceding the prestellar cores are responsible for their observed physical properties. The apparent importance of the thermodynamic properties of gas in the process of fragmentation is consonant with the canonical Jeans analysis. Although in the present work we demonstrated this using a relatively simple cooling function, the real gas dynamics is much more complex and must be accounted for.
Pure hydrodynamic models such as those discussed here must be coupled with the appropriate molecular chemistry so that evolution of molecular gas can be understood better. Such integrated models can then be used to gauge the effects of cooling of molecular gas on its dynamical stability and study the onset of fragmentation, in other words, formation of dense clumps and cores. While reproducing the typical nature of the distribution of clump masses, apart from other important physical properties, we have demonstrated here that the seeds of core-formation are introduced during the process of dynamical fragmentation itself and of course, the rate with which molecular gas cools likely determines the efficiency of core-formation. We have also demonstrated that the weak velocity field often found within cores is probably injected during the fragmentation phase itself. It is also apparent that turbulence in the virgin clouds can appear without any artificial injection and is probably seeded by the growth of various dynamical instabilities. For a further understanding of the process of core-formation and the evolution of cores however, we must supplement purely hydrodynamic models of MCs with the appropriate molecular chemistry.
ACKNOWLEDGEMENTS
The author gratefully acknowledges an anonymous referee for a helpful report that helped improve the original manuscript.