Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alibert, Jean -Jacques
and
Dacorogna, Bernard
1992.
An example of a quasiconvex function that is not polyconvex in two dimensions.
Archive for Rational Mechanics and Analysis,
Vol. 117,
Issue. 2,
p.
155.
Gremaud, P. A.
1995.
Numerical optimization and quasiconvexity.
European Journal of Applied Mathematics,
Vol. 6,
Issue. 1,
p.
69.
Rosakis, Phoebus
and
Simpson, Henry C.
1995.
On the relation between polyconvexity and rank-one convexity in nonlinear elasticity.
Journal of Elasticity,
Vol. 37,
Issue. 2,
p.
113.
Hartwig, H.
1995.
A polyconvexity condition in dimension two.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 125,
Issue. 5,
p.
901.
Bousselsal, M.
and
Chipot, M.
1995.
Relaxation of some functionals of the calculus of variations.
Archiv der Mathematik,
Vol. 65,
Issue. 4,
p.
316.
Dacorogna, Bernard
and
Haeberly, Jean-Pierre
1996.
Variational Methods for Discontinuous Structures.
p.
143.
Pedregal, Pablo
1996.
Some remarks on quasiconvexity and rank-one convexity.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 126,
Issue. 5,
p.
1055.
Iwaniec, Tadeusz
and
Lutoborski, Adam
1996.
Polyconvex Functionals for Nearly Conformal Deformations.
SIAM Journal on Mathematical Analysis,
Vol. 27,
Issue. 3,
p.
609.
1997.
Relaxation in Optimization Theory and Variational Calculus.
p.
443.
Šilhavý, Miloslav
2002.
Applied Nonlinear Analysis.
p.
513.
TRABELSI, KARIM
2005.
NONLINEARLY ELASTIC THIN PLATE MODELS FOR A CLASS OF OGDEN MATERIALS: I.
Analysis and Applications,
Vol. 03,
Issue. 02,
p.
195.
Chełmiński, Krzysztof
and
Kałamajska, Agnieszka
2006.
New convexity conditions in the calculus of variations and compensated compactness theory.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 12,
Issue. 1,
p.
64.
Gutiérrez, Sergio
and
Villavicencio, Jorge
2007.
An optimization algorithm applied to the Morrey conjecture in nonlinear elasticity.
International Journal of Solids and Structures,
Vol. 44,
Issue. 10,
p.
3177.
Pedregal, Pablo
and
Bandeira, Luís
2009.
Finding new families of rank-one convex polynomials.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 26,
Issue. 5,
p.
1621.
Bandeira, Luís
and
Pedregal, Pablo
2011.
Quasiconvexity: the quadratic case revisited, and some consequences for fourth-degree polynomials.
Advances in Calculus of Variations,
Vol. 4,
Issue. 2,
Neff, Patrizio
Lankeit, Johannes
Ghiba, Ionel-Dumitrel
Martin, Robert
and
Steigmann, David
2015.
The exponentiated Hencky-logarithmic strain energy. Part II: Coercivity, planar polyconvexity and existence of minimizers.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 66,
Issue. 4,
p.
1671.
Voss, Jendrik
Martin, Robert J.
Sander, Oliver
Kumar, Siddhant
Kochmann, Dennis M.
and
Neff, Patrizio
2022.
Numerical Approaches for Investigating Quasiconvexity in the Context of Morrey’s Conjecture.
Journal of Nonlinear Science,
Vol. 32,
Issue. 6,


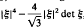 indicating that this function is quasiconvex.
indicating that this function is quasiconvex.