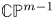1. Introduction
One of the most useful ways to construct concrete examples of Einstein metrics is by considering Riemannian manifolds with a large symmetry group, for example, homogeneous spaces and manifolds of cohomogeneity one, see e.g. [Reference Besse10, Reference Wang56, Reference Wang57] and references therein. As another useful tool, the Calabi–Yau theorem assures the existence of Einstein metrics on compact complex Kähler manifolds with non-positive first-Chern class [Reference Aubin8, Reference Yau59], and also the existence of Kähler–Einstein metrics on Fano manifolds has been recently understood.
The first non-homogeneous example of compact Riemannian Einstein manifold with positive scalar curvature has been provided by Page [Reference Page45, Reference Page and Pope46] on $\mathbb {C}\mathbb {P}^{2} \# \overline {\mathbb {C}\mathbb {P}}{}^{2}$![]() , and then generalized by Bérard-Bergery in [Reference Bérard-Bergery9] as follows. Let $P$
, and then generalized by Bérard-Bergery in [Reference Bérard-Bergery9] as follows. Let $P$![]() be a compact Kähler–Einstein manifold with positive scalar curvature [Reference Alekseevsky and Perelomov1, Reference Koiso and Sakane34, Reference Koiso and Sakane35], for example, $P=\mathbb {C} \mathbb {P}^{1}$
be a compact Kähler–Einstein manifold with positive scalar curvature [Reference Alekseevsky and Perelomov1, Reference Koiso and Sakane34, Reference Koiso and Sakane35], for example, $P=\mathbb {C} \mathbb {P}^{1}$![]() in case of the Page example. Let the first-Chern class be $c_1(P)=p\alpha$
in case of the Page example. Let the first-Chern class be $c_1(P)=p\alpha$![]() , with $p>0$
, with $p>0$![]() integer and $\alpha \in H^{2}(P;\mathbb {Z})$
integer and $\alpha \in H^{2}(P;\mathbb {Z})$![]() indivisible. For $n>0$
indivisible. For $n>0$![]() integer, consider the line bundle $\mathbb {C} \to E_n\to P$
integer, consider the line bundle $\mathbb {C} \to E_n\to P$![]() with $c_1(E_n)=n\alpha$
with $c_1(E_n)=n\alpha$![]() , and the associated projective bundle $\mathbb {C} \mathbb {P}^{1} \to M_n\to P$
, and the associated projective bundle $\mathbb {C} \mathbb {P}^{1} \to M_n\to P$![]() . Then one can use the theory of Riemannian submersion [Reference O'Neill43] to compute the Riemannian curvature of both $E_n$
. Then one can use the theory of Riemannian submersion [Reference O'Neill43] to compute the Riemannian curvature of both $E_n$![]() and $M_n$
and $M_n$![]() . In particular, when $P=\mathsf {G}/\mathsf {K}$
. In particular, when $P=\mathsf {G}/\mathsf {K}$![]() is a Hermitian symmetric space, then $E_n$
is a Hermitian symmetric space, then $E_n$![]() and $M_n$
and $M_n$![]() are cohomogeneity one, and by consequence their curvature is determined by the structure constants of the Lie algebra $\mathfrak {g}:=\operatorname {Lie}(\mathsf {G})$
are cohomogeneity one, and by consequence their curvature is determined by the structure constants of the Lie algebra $\mathfrak {g}:=\operatorname {Lie}(\mathsf {G})$![]() and by the induced 1-parameter family of scalar products [Reference Bérard-Bergery9]. The Einstein equation is then reduced to a system of second-order ordinary differential equations (ODEs), in both the spaces $E_n$
and by the induced 1-parameter family of scalar products [Reference Bérard-Bergery9]. The Einstein equation is then reduced to a system of second-order ordinary differential equations (ODEs), in both the spaces $E_n$![]() and $M_n$
and $M_n$![]() , that can be integrated to get Einstein metrics which are also Hermitian, see [Reference Bérard-Bergery9, théorèmes 1.10 and 1.13].
, that can be integrated to get Einstein metrics which are also Hermitian, see [Reference Bérard-Bergery9, théorèmes 1.10 and 1.13].
In the complex setting, Kähler C-spaces (i.e. compact, simply-connected, homogeneous Kähler manifolds) are well understood [Reference Alekseevsky and Perelomov1, Reference Bordermann, Forger and Römer12, Reference Wang55]: in particular, they always admit a unique Kähler–Einstein metric, up to scaling. On the other hand, cohomogeneity one Kähler metrics have been studied in [Reference Alekseevsky and Zuddas4, Reference Alekseevsky and Zuddas5, Reference Dancer and Wang17, Reference Guan and Chen28, Reference Koiso and Sakane35, Reference Podestà and Spiro48–Reference Sakane50].
In the Hermitian non-Kählerian context, since the Levi-Civita connection does not preserve the complex structure, one is led to introduce a more suitable notion of canonical metrics, for example, the second-Chern–Einstein condition. Here, by second-Chern–Einstein metric on a complex manifold, we mean a Hermitian metric on the tangent bundle that is Hermite–Einstein with respect to itself [Reference Gauduchon22], see also [Reference Angella, Calamai and Spotti7, Reference Streets and Tian51]. Examples of compact second-Chern–Einstein manifolds include the homogeneous Hopf surface [Reference Gauduchon22, Reference Gauduchon and Ivanov24, Reference Liu and Yang37], holomorphically parallelizable manifolds [Reference Boothby11] and the homogeneous non-Kähler C-spaces studied by Podestà [Reference Podestá47]; see also [Reference Alekseevsky and Podestà2] for the almost-Kähler case. In particular, the only compact complex non-Kähler surface admitting second-Chern–Einstein metrics is the Hopf surface [Reference Gauduchon and Ivanov24, theorem 2], see also [Reference Gauduchon22]. Note that there still miss (if any) non-Kähler examples of second-Chern–Einstein metrics with negative Chern-scalar curvature on compact complex manifolds. Further problems, e.g. the constant Chern-scalar curvature problem, also known as Chern–Yamabe problem [Reference Angella, Calamai and Spotti6], are still not completely understood. Non-homogeneous examples of Hermitian metrics of positive constant Chern-scalar curvature on Hirzebruch surfaces, using the Page and Bérard-Bergery ansatz, have been constructed in [Reference Koca and Lejmi33].
In this note, motivated by the above questions, we start to investigate the curvature and the properties of Hermitian non-Kähler manifolds with large isometry groups. In particular, we focus on the Bérard-Bergery [Reference Bérard-Bergery9] standard [Reference Podestà and Spiro48] cohomogeneity one Hermitian manifolds $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J},\, {\mathbb g})$![]() , with $i \in \{1,\,2,\,3,\,4\}$
, with $i \in \{1,\,2,\,3,\,4\}$![]() and $n \in \mathbb {N}$
and $n \in \mathbb {N}$![]() , that are defined as (the total spaces of) bundles over a simply connected, irreducible, compact Hermitian symmetric space $P=\mathsf {G}/\mathsf {K}$
, that are defined as (the total spaces of) bundles over a simply connected, irreducible, compact Hermitian symmetric space $P=\mathsf {G}/\mathsf {K}$![]() , see definition 3.7. We compute the Chern–Ricci and Chern-scalar curvatures, see proposition 3.15. This is aimed at getting the second-Chern–Einstein and the constant Chern-scalar curvature equations, that we investigate in the last section. Here, we continue by describing the existence of special metrics.
, see definition 3.7. We compute the Chern–Ricci and Chern-scalar curvatures, see proposition 3.15. This is aimed at getting the second-Chern–Einstein and the constant Chern-scalar curvature equations, that we investigate in the last section. Here, we continue by describing the existence of special metrics.
Our first result concerns the locally conformally Kähler condition. We recall that a Hermitian metric $ {\mathbb g}$![]() is called locally conformally Kähler if it admits a local conformal change to a Kähler metric [Reference Dragomir and Ornea19], which is equivalent to say that $\operatorname {d\!}\omega =\frac {1}{m-1}\vartheta \wedge \omega$
is called locally conformally Kähler if it admits a local conformal change to a Kähler metric [Reference Dragomir and Ornea19], which is equivalent to say that $\operatorname {d\!}\omega =\frac {1}{m-1}\vartheta \wedge \omega$![]() with $\operatorname {d\!}\vartheta =0$
with $\operatorname {d\!}\vartheta =0$![]() , where $\omega = {\mathbb g}(\mathbb {J} \cdot,\, \cdot )$
, where $\omega = {\mathbb g}(\mathbb {J} \cdot,\, \cdot )$![]() is the fundamental $2$
is the fundamental $2$![]() -form associated with the metric, $m$
-form associated with the metric, $m$![]() denotes the complex dimension and $\vartheta$
denotes the complex dimension and $\vartheta$![]() is the Lee form of $ {\mathbb g}$
is the Lee form of $ {\mathbb g}$![]() [Reference Gauduchon23], see § 3.3. In the particular case when $\vartheta$
[Reference Gauduchon23], see § 3.3. In the particular case when $\vartheta$![]() is also exact, say $\vartheta =(m-1)\operatorname {d\!}\phi$
is also exact, say $\vartheta =(m-1)\operatorname {d\!}\phi$![]() , then $\exp (-\phi )\omega$
, then $\exp (-\phi )\omega$![]() is Kähler, and $ {\mathbb g}$
is Kähler, and $ {\mathbb g}$![]() is called globally conformally Kähler (this includes the case $\vartheta =0$
is called globally conformally Kähler (this includes the case $\vartheta =0$![]() , corresponding to $ {\mathbb g}$
, corresponding to $ {\mathbb g}$![]() itself being Kähler). When $\vartheta$
itself being Kähler). When $\vartheta$![]() is not exact, we say that the metric is strictly locally conformally Kähler. Moreover, a strictly locally conformally Kähler metric is called Vaisman if the Lee form $\vartheta$
is not exact, we say that the metric is strictly locally conformally Kähler. Moreover, a strictly locally conformally Kähler metric is called Vaisman if the Lee form $\vartheta$![]() is parallel with respect to the Levi-Civita connection.
is parallel with respect to the Levi-Civita connection.
It is worth noticing that homogeneous, strictly locally conformally Kähler metrics on compact manifolds are Vaisman [Reference Gauduchon, Moroianu and Ornea25, Reference Hasegawa and Kamishima29]. On the other hand, in the cohomogeneity one case, we prove the following.
Theorem A (see proposition 4.1, corollary 4.2 and proposition 4.3)
Let $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J},\, {\mathbb g})$![]() be one of the Bérard-Bergery standard cohomogeneity one Hermitian manifolds. Then, $ {\mathbb g}$
be one of the Bérard-Bergery standard cohomogeneity one Hermitian manifolds. Then, $ {\mathbb g}$![]() is locally conformally Kähler. Furthermore, $ {\mathbb g}$
is locally conformally Kähler. Furthermore, $ {\mathbb g}$![]() is strictly locally conformally Kähler if and only if $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$
is strictly locally conformally Kähler if and only if $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$![]() is compact without singular orbits (case $i=3$
is compact without singular orbits (case $i=3$![]() ) and, on such manifolds, $ {\mathbb g}$
) and, on such manifolds, $ {\mathbb g}$![]() is Vaisman if and only if it is homogeneous.
is Vaisman if and only if it is homogeneous.
Our second result concerns other kinds of special conditions for Hermitian metrics. To this regard, we recall that the balanced condition in the sense of Michelsohn [Reference Michelsohn40] amounts to $\operatorname {d\!}{}^{*}\omega =0$![]() . The pluriclosed condition, a.k.a. strong Kähler with torsion (SKT for short), means that $\operatorname {d\!}\operatorname {d\!}^{\,c}\omega =0$
. The pluriclosed condition, a.k.a. strong Kähler with torsion (SKT for short), means that $\operatorname {d\!}\operatorname {d\!}^{\,c}\omega =0$![]() . Moreover, the Gauduchon condition [Reference Gauduchon21] refers to $\operatorname {d\!}{}^{*}\vartheta =0$
. Moreover, the Gauduchon condition [Reference Gauduchon21] refers to $\operatorname {d\!}{}^{*}\vartheta =0$![]() , equivalently, $\operatorname {d\!}\operatorname {d\!}^{\,c}\omega ^{m-1}=0$
, equivalently, $\operatorname {d\!}\operatorname {d\!}^{\,c}\omega ^{m-1}=0$![]() .
.
Theorem B (see corollaries 4.7, 4.9 and proposition 4.6)
Let $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J},\, {\mathbb g})$![]() be one of the Bérard-Bergery standard cohomogeneity one Hermitian manifolds. The following three conditions are equivalent: $ {\mathbb g}$
be one of the Bérard-Bergery standard cohomogeneity one Hermitian manifolds. The following three conditions are equivalent: $ {\mathbb g}$![]() is pluriclosed, $ {\mathbb g}$
is pluriclosed, $ {\mathbb g}$![]() is balanced, $ {\mathbb g}$
is balanced, $ {\mathbb g}$![]() is Kähler. Moreover, if $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
is Kähler. Moreover, if $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() has singular orbits, then $ {\mathbb g}$
has singular orbits, then $ {\mathbb g}$![]() is Gauduchon if and only if it is Kähler.
is Gauduchon if and only if it is Kähler.
Finally, we investigate the second-Chern–Einstein and the constant Chern-scalar curvature problems (see § 2.2) on this class of manifolds. Firstly, we prove a local existence and uniqueness result for second-Chern–Einstein metrics with prescribed Chern-scalar curvature (see theorem 5.1), by using a method due to Malgrange [Reference Malgrange39] already exploited by Eschenburg and Wang [Reference Eschenburg and Wang20] and by Böhm [Reference Böhm14, Reference Böhm15]. Then, concerning the existence of complete solutions to the second-Chern–Einstein equations, we prove the following.
Theorem C (see remark 5.2, theorem 5.3, proposition 5.5)
Let $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$![]() be one of the Bérard-Bergery standard cohomogeneity one complex manifolds.
be one of the Bérard-Bergery standard cohomogeneity one complex manifolds.
(a) If $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$
 has no singular orbits (cases $i=1$
has no singular orbits (cases $i=1$ and $i=3$
and $i=3$ ), then it admits homogeneous second-Chern–Einstein metrics.
), then it admits homogeneous second-Chern–Einstein metrics.(b) If $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$
 has one singular orbit (case $i=2$
has one singular orbit (case $i=2$ ), then it admits a complete, non-Kähler, second-Chern–Einstein metrics of cohomogeneity one.
), then it admits a complete, non-Kähler, second-Chern–Einstein metrics of cohomogeneity one.(c) If $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$
 has two singular orbits (case $i=4$
has two singular orbits (case $i=4$ ), then it does not admit any cohomogeneity one, submersion-type metrics which are second-Chern–Einstein.
), then it does not admit any cohomogeneity one, submersion-type metrics which are second-Chern–Einstein.
Let us stress that the homogeneous second-Chern–Einstein metrics on $(M_{(1,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() and $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
and $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() , corresponding to case (a) in theorem C, are clearly of constant Chern-scalar curvature. They include the classical example of the standard metric on the diagonal Hopf manifold, which corresponds in our notation to $M_{(3,1)}(\mathsf {G},\,\mathsf {K})$
, corresponding to case (a) in theorem C, are clearly of constant Chern-scalar curvature. They include the classical example of the standard metric on the diagonal Hopf manifold, which corresponds in our notation to $M_{(3,1)}(\mathsf {G},\,\mathsf {K})$![]() with $\mathsf {G}=\mathsf {SU}(m)$
with $\mathsf {G}=\mathsf {SU}(m)$![]() and $\mathsf {K}=\mathsf {S}(\mathsf {U}(1)\times \mathsf {U}(m-1))$
and $\mathsf {K}=\mathsf {S}(\mathsf {U}(1)\times \mathsf {U}(m-1))$![]() . On the other hand, the metrics that we constructed on manifolds with singular orbits, corresponding to cases (b) and (c) in theorem C, are weakly second-Chern–Einstein, namely, they do not have constant Chern-scalar curvature. Therefore, this brings us to investigate the constant Chern-scalar curvature problem for such manifolds. In this direction, we obtain
. On the other hand, the metrics that we constructed on manifolds with singular orbits, corresponding to cases (b) and (c) in theorem C, are weakly second-Chern–Einstein, namely, they do not have constant Chern-scalar curvature. Therefore, this brings us to investigate the constant Chern-scalar curvature problem for such manifolds. In this direction, we obtain
Theorem D (see remark 5.2, theorems 5.7, 5.8)
All the Bérard-Bergery standard cohomogeneity one complex manifolds $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$![]() admit complete, non-Kähler metrics of cohomogeneity one with constant Chern-scalar curvature.
admit complete, non-Kähler metrics of cohomogeneity one with constant Chern-scalar curvature.
Note that, in complex dimension $m=2$![]() , the compact case with two singular orbits (corresponding to $i=4$
, the compact case with two singular orbits (corresponding to $i=4$![]() ) reduces to the Hirzebruch surfaces. This case has been treated by Koca and Lejmi [Reference Koca and Lejmi33], who proved the existence of positive constant Chern-scalar curvature of cohomogeneity one.
) reduces to the Hirzebruch surfaces. This case has been treated by Koca and Lejmi [Reference Koca and Lejmi33], who proved the existence of positive constant Chern-scalar curvature of cohomogeneity one.
The paper is organized as follows. In § 2, we recall some basics on the Chern connection and cohomogeneity one actions. In § 3, we recall the construction of $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J},\, {\mathbb g})$![]() following Bérard-Bergery, and we compute the Hermitian curvatures and torsion of such manifolds. In § 4, we investigate the existence of special non-Kähler Hermitian metrics, proving theorems A and B. In § 5, we prove theorems C and D. Finally, in Appendix A, we collect the detailed computations needed in § 3, precisely to prove propositions 3.15 and 3.17, and in § 4, namely to prove equation (4.3).
following Bérard-Bergery, and we compute the Hermitian curvatures and torsion of such manifolds. In § 4, we investigate the existence of special non-Kähler Hermitian metrics, proving theorems A and B. In § 5, we prove theorems C and D. Finally, in Appendix A, we collect the detailed computations needed in § 3, precisely to prove propositions 3.15 and 3.17, and in § 4, namely to prove equation (4.3).
2. Preliminaries
In this section, we briefly recall some facts on the Chern connection and on Hermitian manifolds with cohomogeneity one actions by holomorphic isometries.
2.1 The Chern connection
Let $(M,\,\mathbb {J},\, {\mathbb g})$![]() be a connected, complete, Hermitian manifold of real dimension $\dim _{\mathbb {R}}M=2\,m$
be a connected, complete, Hermitian manifold of real dimension $\dim _{\mathbb {R}}M=2\,m$![]() . Let us denote by $\omega := {\mathbb g}(\mathbb {J} \,\cdot \,,\, \cdot \,)$
. Let us denote by $\omega := {\mathbb g}(\mathbb {J} \,\cdot \,,\, \cdot \,)$![]() its fundamental $2$
its fundamental $2$![]() -form, by $D$
-form, by $D$![]() its Levi-Civita connection and by $\nabla$
its Levi-Civita connection and by $\nabla$![]() its Chern connection, which is defined by
its Chern connection, which is defined by
for any $A,\,B,\,C \in \Gamma (TM)$![]() . Since, by the Koszul formula,
. Since, by the Koszul formula,
and
it follows that
Moreover, it is well-known that the Chern connection is characterized by the following properties
where $\tau (A,\,B) := \nabla _AB -\nabla _BA - [A,\,B]$![]() is the torsion tensor of $\nabla$
is the torsion tensor of $\nabla$![]() .
.
For later use, we observe the following straightforward
Lemma 2.1 For any $A \in \Gamma (TM)$![]() it holds that
it holds that
Proof. If $E \in \Gamma (\operatorname {End}(TM))$![]() , then
, then

Then, equation (2.6) follows by setting $E=\mathbb {J}$![]() and using equation (2.5). On the other hand, from equations (2.5) and (2.6) we get
and using equation (2.5). On the other hand, from equations (2.5) and (2.6) we get
and so the thesis follows.
A real vector field $A \in \Gamma (TM)$![]() is holomorphic if $\mathcal {L}_A\mathbb {J}=0$
is holomorphic if $\mathcal {L}_A\mathbb {J}=0$![]() . Hence, we get
. Hence, we get
Corollary 2.2 Let $A \in \Gamma (TM)$![]() . Then it holds:
. Then it holds:
• $A$
 is holomorphic if and only if
\[ \nabla_{\mathbb{J} B}A=\mathbb{J}\nabla_BA \quad \text{ for any } B \in \Gamma(TM); \]
is holomorphic if and only if
\[ \nabla_{\mathbb{J} B}A=\mathbb{J}\nabla_BA \quad \text{ for any } B \in \Gamma(TM); \]
• $A$
 is holomorphic if and only if $\mathbb {J} A$
is holomorphic if and only if $\mathbb {J} A$ is holomorphic.
is holomorphic.
Finally, we set $\operatorname {d\!}^{\,c} := \mathbb {J}^{-1} \! \circ \operatorname {d\!}\, \circ \mathbb {J}$![]() , so that
, so that
and, for any smooth function $f: M \to \mathbb {R}$![]() , we denote by $\Delta _{ {\mathbb g}}^{\rm Ch}f := {\mathbb g}(\operatorname {d\!}\operatorname {d\!}^{\,c}\!f,\,\omega )$
, we denote by $\Delta _{ {\mathbb g}}^{\rm Ch}f := {\mathbb g}(\operatorname {d\!}\operatorname {d\!}^{\,c}\!f,\,\omega )$![]() the Chern–Laplacian of $f$
the Chern–Laplacian of $f$![]() .
.
2.2 Second-Chern–Einstein metrics
Let $(M,\,\mathbb {J},\, {\mathbb g})$![]() be a connected, complete, Hermitian manifold of real dimension $\dim _{\mathbb {R}}M=2\,m$
be a connected, complete, Hermitian manifold of real dimension $\dim _{\mathbb {R}}M=2\,m$![]() . We recall that, by the lack of symmetries of the Chern-curvature
. We recall that, by the lack of symmetries of the Chern-curvature
we have (at least) two ways to trace the Ricci tensor. We call first Chern–Ricci curvature the tensor defined by
where $(e_\alpha,\, \mathbb {J} e_\alpha )$![]() is a $(\mathbb {J},\, {\mathbb g})$
is a $(\mathbb {J},\, {\mathbb g})$![]() -unitary frame for the tangent space at $x$
-unitary frame for the tangent space at $x$![]() . Similarly, we call second Chern–Ricci curvature the tensor defined by
. Similarly, we call second Chern–Ricci curvature the tensor defined by
Finally, the Chern-scalar curvature is the function given by
We remark that, according to our notation, when $ {\mathbb g}$![]() is Kähler it holds that $\operatorname {Ric}^{\rm Ch[1]}( {\mathbb g})=\operatorname {Ric}^{\rm Ch[2]}( {\mathbb g})=\operatorname {Ric}( {\mathbb g})$
is Kähler it holds that $\operatorname {Ric}^{\rm Ch[1]}( {\mathbb g})=\operatorname {Ric}^{\rm Ch[2]}( {\mathbb g})=\operatorname {Ric}( {\mathbb g})$![]() and $\operatorname {scal}^{\rm Ch}( {\mathbb g})=\operatorname {scal}( {\mathbb g})$
and $\operatorname {scal}^{\rm Ch}( {\mathbb g})=\operatorname {scal}( {\mathbb g})$![]() , where $\operatorname {Ric}( {\mathbb g})$
, where $\operatorname {Ric}( {\mathbb g})$![]() and $\operatorname {scal}( {\mathbb g})$
and $\operatorname {scal}( {\mathbb g})$![]() denote the Riemannian Ricci tensor and the Riemannian scalar curvature of $ {\mathbb g}$
denote the Riemannian Ricci tensor and the Riemannian scalar curvature of $ {\mathbb g}$![]() , respectively.
, respectively.
This yields to the following
Definition 2.3 Let $i \in \{1,\,2\}$![]() . The metric $ {\mathbb g}$
. The metric $ {\mathbb g}$![]() is said to be weakly (respectively, strongly) $i{\rm th}$
is said to be weakly (respectively, strongly) $i{\rm th}$![]() -Chern–Einstein if there exists $\lambda \in \mathcal {C}^{\infty }(M,\, \mathbb {R})$
-Chern–Einstein if there exists $\lambda \in \mathcal {C}^{\infty }(M,\, \mathbb {R})$![]() (respectively, $\lambda \in \mathbb {R}$
(respectively, $\lambda \in \mathbb {R}$![]() ) such that
) such that
We stress that the first-Chern–Einstein problem is basically understood for compact complex manifolds $X=(M,\,\mathbb {J})$![]() , see [Reference Angella, Calamai and Spotti7, Reference Tosatti52]. Indeed, strongly first-Chern–Einstein metrics with non-zero Chern-scalar curvature are Kähler–Einstein. Moreover, by conformal methods, if a Hermitian metric $ {\mathbb g}$
, see [Reference Angella, Calamai and Spotti7, Reference Tosatti52]. Indeed, strongly first-Chern–Einstein metrics with non-zero Chern-scalar curvature are Kähler–Einstein. Moreover, by conformal methods, if a Hermitian metric $ {\mathbb g}$![]() is weakly first-Chern–Einstein with non-identically zero Chern-scalar curvature, then it is conformal to a Kähler metric in the class $\pm c_1(X)$
is weakly first-Chern–Einstein with non-identically zero Chern-scalar curvature, then it is conformal to a Kähler metric in the class $\pm c_1(X)$![]() (see [Reference Angella, Calamai and Spotti7, theorem A]). Finally, compact complex manifolds with first-Bott–Chern class $c_1^{BC}(X)=0$
(see [Reference Angella, Calamai and Spotti7, theorem A]). Finally, compact complex manifolds with first-Bott–Chern class $c_1^{BC}(X)=0$![]() are the so-called non-Kähler Calabi–Yau manifolds [Reference Tosatti52] and always admit Chern–Ricci flat metrics [Reference Tosatti52, theorem 1.2], see also [Reference Tosatti and Weinkove53, corollary 2].
are the so-called non-Kähler Calabi–Yau manifolds [Reference Tosatti52] and always admit Chern–Ricci flat metrics [Reference Tosatti52, theorem 1.2], see also [Reference Tosatti and Weinkove53, corollary 2].
On the other hand, the second-Chern–Einstein problem seems to be geometrically more appealing, see e.g. [Reference Angella, Calamai and Spotti7, Reference Gauduchon and Ivanov24, Reference Podestá47, Reference Streets and Tian51]. Note that a Hermitian metric $ {\mathbb g}$![]() on $X=(M,\,\mathbb {J})$
on $X=(M,\,\mathbb {J})$![]() is second-Chern–Einstein according to definition 2.3 if and only if the induced Hermitian metric $h(V,\,W) := {\mathbb g}(V,\,\overline {W})$
is second-Chern–Einstein according to definition 2.3 if and only if the induced Hermitian metric $h(V,\,W) := {\mathbb g}(V,\,\overline {W})$![]() on the holomorphic tangent bundle $T^{1,0}X$
on the holomorphic tangent bundle $T^{1,0}X$![]() is Hermite–Einstein by taking trace with itself [Reference Gauduchon22].
is Hermite–Einstein by taking trace with itself [Reference Gauduchon22].
Remark 2.4 We observe that the second-Chern–Einstein condition is satisfied by a Hermitian metric $ {\mathbb g}$![]() if and only if it is satisfied by all the metrics in its conformal class (see [Reference Gauduchon22]), since for any smooth function $f: M \to \mathbb {R}$
if and only if it is satisfied by all the metrics in its conformal class (see [Reference Gauduchon22]), since for any smooth function $f: M \to \mathbb {R}$![]() it holds that
it holds that
We remark that this is strongly different from the Riemannian analogue, i.e. the Einstein condition. On the other hand, we stress that a Kähler metric is second-Chern–Einstein if and only if it is Einstein.
Note that, up to our knowledge, a non-Kähler example of second-Chern–Einstein metric on a compact complex manifold of complex dimension $m > 2$![]() with negative scalar curvature is still missing.
with negative scalar curvature is still missing.
2.3 Cohomogeneity one group actions on Hermitian manifolds
Let us consider a compact, connected real Lie group $\mathsf {G}$![]() which acts effectively by holomorphic isometries on $(M,\,\mathbb {J},\, {\mathbb g})$
which acts effectively by holomorphic isometries on $(M,\,\mathbb {J},\, {\mathbb g})$![]() with cohomogeneity one [Reference Bérard-Bergery9, Reference Besse10, Reference Mostert41, Reference Podestà and Spiro48]. Then, the orbit space $\Omega := \mathsf {G} \backslash M$
with cohomogeneity one [Reference Bérard-Bergery9, Reference Besse10, Reference Mostert41, Reference Podestà and Spiro48]. Then, the orbit space $\Omega := \mathsf {G} \backslash M$![]() is homeomorphic to one of the following:
is homeomorphic to one of the following:
Up to homothety, we can choose a unit speed geodesic $\gamma :\overline {I} \to M$![]() which intersects orthogonally any $\mathsf {G}$
which intersects orthogonally any $\mathsf {G}$![]() -orbit [Reference Bérard-Bergery9, § 2.7], where the interval $I \subset \mathbb {R}$
-orbit [Reference Bérard-Bergery9, § 2.7], where the interval $I \subset \mathbb {R}$![]() is defined as
is defined as
Then, for $r \in I$![]() , the orbit $\mathcal {S}_r := \mathsf {G} \cdot \gamma (r)$
, the orbit $\mathcal {S}_r := \mathsf {G} \cdot \gamma (r)$![]() is principal and can be identified with a fixed homogeneous space by means of the $1$
is principal and can be identified with a fixed homogeneous space by means of the $1$![]() -parameter family of $\mathsf {G}$
-parameter family of $\mathsf {G}$![]() -equivariant diffeomorphisms
-equivariant diffeomorphisms
where $\mathsf {H} \subset \mathsf {G}$![]() is a closed subgroup. For $r \in \partial I$
is a closed subgroup. For $r \in \partial I$![]() , the following cases occur:
, the following cases occur:
(i) $\partial I = \emptyset$
 and all the orbits are principal;
and all the orbits are principal;(ii) $\partial I = \{0\}$
 , the orbit $\mathcal {S}_0 := \mathsf {G} \cdot \gamma (0)$
, the orbit $\mathcal {S}_0 := \mathsf {G} \cdot \gamma (0)$ is non-principal and $\mathsf {G}$
is non-principal and $\mathsf {G}$ -equivariantly diffeomorphic to a homogeneous space $\mathsf {G}/\mathsf {L}$
-equivariantly diffeomorphic to a homogeneous space $\mathsf {G}/\mathsf {L}$ , where $\mathsf {H} \subset \mathsf {L} \subset \mathsf {G}$
, where $\mathsf {H} \subset \mathsf {L} \subset \mathsf {G}$ is an intermediate subgroup and $\mathsf {L} / \mathsf {H}$
is an intermediate subgroup and $\mathsf {L} / \mathsf {H}$ is a sphere, see e.g. [Reference Bérard-Bergery9, § 2.12];
is a sphere, see e.g. [Reference Bérard-Bergery9, § 2.12];(iii) $\partial I = \{\pm \pi \}$
 , the orbits $\mathcal {S}_{\pm \pi } := \mathsf {G} \cdot \gamma (\pm \pi )$
, the orbits $\mathcal {S}_{\pm \pi } := \mathsf {G} \cdot \gamma (\pm \pi )$ are principal but in general $\gamma (-\pi ) \neq \gamma (\pi )$
are principal but in general $\gamma (-\pi ) \neq \gamma (\pi )$ , see e.g. [Reference Bérard-Bergery9, § 2.10];
, see e.g. [Reference Bérard-Bergery9, § 2.10];(iv) $\partial I = \{0,\,\pi \}$
 , the orbits $\mathcal {S}_0 := \mathsf {G} \cdot \gamma (0)$
, the orbits $\mathcal {S}_0 := \mathsf {G} \cdot \gamma (0)$ , $\mathcal {S}_{\pi } := \mathsf {G} \cdot \gamma (\pi )$
, $\mathcal {S}_{\pi } := \mathsf {G} \cdot \gamma (\pi )$ are non-principal and $\mathsf {G}$
are non-principal and $\mathsf {G}$ -equivariantly diffeomorphic to two homogeneous space $\mathsf {G}/\mathsf {L}_{\pm }$
-equivariantly diffeomorphic to two homogeneous space $\mathsf {G}/\mathsf {L}_{\pm }$ , with $\mathsf {H} \subset \mathsf {L}_- \cap \mathsf {L}_+$
, with $\mathsf {H} \subset \mathsf {L}_- \cap \mathsf {L}_+$ and $\mathsf {L}_{\pm } / \mathsf {H}$
and $\mathsf {L}_{\pm } / \mathsf {H}$ are spheres, see e.g. [Reference Bérard-Bergery9, § 2.13].
are spheres, see e.g. [Reference Bérard-Bergery9, § 2.13].
The subset $M^{\rm reg} := \bigcup _{r \in I} \mathcal {S}_r$![]() of regular points is an open, dense submanifold of $M$
of regular points is an open, dense submanifold of $M$![]() which projects onto $I$
which projects onto $I$![]() by means of the canonical projection $M \to \Omega$
by means of the canonical projection $M \to \Omega$![]() and the restricted Riemannian metric splits as
and the restricted Riemannian metric splits as
where $r$![]() is the coordinate on $I$
is the coordinate on $I$![]() . We fix an $\operatorname {Ad}(\mathsf {G})$
. We fix an $\operatorname {Ad}(\mathsf {G})$![]() -invariant inner product $Q$
-invariant inner product $Q$![]() on the Lie algebra $\mathfrak {g} := \operatorname {Lie}(\mathsf {G})$
on the Lie algebra $\mathfrak {g} := \operatorname {Lie}(\mathsf {G})$![]() and a $Q$
and a $Q$![]() -orthogonal decomposition $\mathfrak {g}=\mathfrak {h}+\mathfrak {m}$
-orthogonal decomposition $\mathfrak {g}=\mathfrak {h}+\mathfrak {m}$![]() , with $\mathfrak {h} := \operatorname {Lie}(\mathsf {H})$
, with $\mathfrak {h} := \operatorname {Lie}(\mathsf {H})$![]() . We consider identified $\mathfrak {m} \simeq T_{e\mathsf {H}}\mathsf {G}/\mathsf {H}$
. We consider identified $\mathfrak {m} \simeq T_{e\mathsf {H}}\mathsf {G}/\mathsf {H}$![]() by means of the evaluation map $X \mapsto \frac {\rm d}{{\rm d}s}\exp (sX)\mathsf {H} \big |_{s=0}$
by means of the evaluation map $X \mapsto \frac {\rm d}{{\rm d}s}\exp (sX)\mathsf {H} \big |_{s=0}$![]() , where $\exp : \mathfrak {g} \to \mathsf {G}$
, where $\exp : \mathfrak {g} \to \mathsf {G}$![]() denotes the Lie exponential map of $\mathsf {G}$
denotes the Lie exponential map of $\mathsf {G}$![]() . We also identify any $\mathsf {G}$
. We also identify any $\mathsf {G}$![]() -invariant tensor field on $\mathsf {G}/\mathsf {H}$
-invariant tensor field on $\mathsf {G}/\mathsf {H}$![]() with the corresponding $\operatorname {Ad}(\mathsf {H})$
with the corresponding $\operatorname {Ad}(\mathsf {H})$![]() -invariant tensor on $\mathfrak {m}$
-invariant tensor on $\mathfrak {m}$![]() in the usual way.
in the usual way.
Firstly, we define the $1$![]() -parameter family $(g_r) \subset \mathrm {Sym}^{2}(\mathfrak {m}^{*})^{\operatorname {Ad}(\mathsf {H})}$
-parameter family $(g_r) \subset \mathrm {Sym}^{2}(\mathfrak {m}^{*})^{\operatorname {Ad}(\mathsf {H})}$![]() by
by
We also set

Then, for any $r \in I$![]() , the complex structure $\mathbb {J}$
, the complex structure $\mathbb {J}$![]() induces a linear complex structure $J_r$
induces a linear complex structure $J_r$![]() on $\mathfrak {p}_r := \ker (\theta _r) \subset \mathfrak {m}$
on $\mathfrak {p}_r := \ker (\theta _r) \subset \mathfrak {m}$![]() by setting
by setting
The integrability of $\mathbb {J}$![]() implies that, for any $X,\,Y \in \mathfrak {p}_r$
implies that, for any $X,\,Y \in \mathfrak {p}_r$![]() ,
,

Moreover, since the subgroup $\mathsf {H} \subset \mathsf {G}$![]() leaves any point of the geodesic $\gamma$
leaves any point of the geodesic $\gamma$![]() fixed and $\mathsf {G}$
fixed and $\mathsf {G}$![]() acts by holomorphic isometries, it follows that
acts by holomorphic isometries, it follows that
and so $(\theta _r,\,J_r)$![]() is a $1$
is a $1$![]() -parameter family of $\mathsf {G}$
-parameter family of $\mathsf {G}$![]() -invariant CR structures on $\mathsf {G}/\mathsf {H}$
-invariant CR structures on $\mathsf {G}/\mathsf {H}$![]() , see e.g. [Reference Alekseevsky and Spiro3].
, see e.g. [Reference Alekseevsky and Spiro3].
We recall now the following definition [Reference Podestà and Spiro48]: $\mathsf {G}/\mathsf {H}$![]() is said to be ordinary if $\mathsf {G}$
is said to be ordinary if $\mathsf {G}$![]() is semisimple, the normalizer $\mathsf {K}:= \mathsf {N}_{\mathsf {G}}(\mathsf {H}^{\operatorname {o}})$
is semisimple, the normalizer $\mathsf {K}:= \mathsf {N}_{\mathsf {G}}(\mathsf {H}^{\operatorname {o}})$![]() of the connected component $\mathsf {H}^{\operatorname {o}}$
of the connected component $\mathsf {H}^{\operatorname {o}}$![]() of $\mathsf {H}$
of $\mathsf {H}$![]() is the centralizer of a torus and $\dim \mathsf {K}=1+\dim \mathsf {H}$
is the centralizer of a torus and $\dim \mathsf {K}=1+\dim \mathsf {H}$![]() . This implies that:
. This implies that:
• $T \equiv T_r$
 and $\mathfrak {p} \equiv \mathfrak {p}_r$
and $\mathfrak {p} \equiv \mathfrak {p}_r$ do not depend on $r \in I$
do not depend on $r \in I$ ;
;• the Lie algebra $\mathfrak {k} := \operatorname {Lie}(\mathsf {K})$
 splits $Q$
splits $Q$ -orthogonally as $\mathfrak {k} = \mathfrak {h} \oplus \mathbb {R} T$
-orthogonally as $\mathfrak {k} = \mathfrak {h} \oplus \mathbb {R} T$ .
.
Moreover, the complex structure $\mathbb {J}$![]() is said to be projectable if each $J_r$
is said to be projectable if each $J_r$![]() is $\operatorname {Ad}(\mathsf {K})$
is $\operatorname {Ad}(\mathsf {K})$![]() -invariant. In this case, $(J_r)_{r \in I}$
-invariant. In this case, $(J_r)_{r \in I}$![]() is mapped onto a $1$
is mapped onto a $1$![]() -parameter family of $\mathsf {G}$
-parameter family of $\mathsf {G}$![]() -invariant complex structures on the flag manifold $\mathsf {G} / \mathsf {K}$
-invariant complex structures on the flag manifold $\mathsf {G} / \mathsf {K}$![]() . Since the set of invariant complex structures on a flag manifold is discrete [Reference Alekseevsky and Perelomov1, Reference Nishiyama42], it follows that $J \equiv J_r$
. Since the set of invariant complex structures on a flag manifold is discrete [Reference Alekseevsky and Perelomov1, Reference Nishiyama42], it follows that $J \equiv J_r$![]() is constant.
is constant.
Definition 2.5 [Reference Alekseevsky and Zuddas4, Reference Podestà and Spiro48]
The Hermitian manifold $(M,\,\mathbb {J},\, {\mathbb g})$![]() acted by $\mathsf {G}$
acted by $\mathsf {G}$![]() is said to be standard if the following conditions are satisfied:
is said to be standard if the following conditions are satisfied:
• the principal orbits are ordinary and the complex structure $\mathbb {J}$
 is projectable;
is projectable;• the non-principal orbits, if they exist, are flag manifolds with the induced complex structure.
In § 3, a distinguished kind of cohomogeneity one standard Hermitian manifolds will be investigated.
3. Bérard-Bergery standard cohomogeneity one Hermitian manifolds
In this section, we consider a special class of standard cohomogeneity one Hermitian manifolds, following the construction of Bérard-Bergery [Reference Bérard-Bergery9]. Then, we compute the Chern connection and the Chern–Ricci tensors of such manifolds.
3.1 Chern connection of standard cohomogeneity one Hermitian manifolds
Let $(M,\,\mathbb {J},\, {\mathbb g})$![]() be a standard cohomogeneity one Hermitian manifolds acted effectively by holomorphic isometries by a compact, connected real Lie group $\mathsf {G}$
be a standard cohomogeneity one Hermitian manifolds acted effectively by holomorphic isometries by a compact, connected real Lie group $\mathsf {G}$![]() .
.
Hereafter, we adopt the same notation introduced in § 2. Note that the complement $\mathfrak {m}$![]() of $\mathfrak {h}$
of $\mathfrak {h}$![]() in $\mathfrak {g}$
in $\mathfrak {g}$![]() admits a $Q$
admits a $Q$![]() -orthogonal, $\operatorname {Ad}(\mathsf {H})$
-orthogonal, $\operatorname {Ad}(\mathsf {H})$![]() -invariant decomposition $\mathfrak {m}= \mathfrak {a} + \mathfrak {p}$
-invariant decomposition $\mathfrak {m}= \mathfrak {a} + \mathfrak {p}$![]() , where $\mathfrak {a} := \mathbb {R} T$
, where $\mathfrak {a} := \mathbb {R} T$![]() is the trivial submodule. Since, by hypothesis, $\mathfrak {p}$
is the trivial submodule. Since, by hypothesis, $\mathfrak {p}$![]() does not contain any trivial $\operatorname {Ad}(\mathsf {H})$
does not contain any trivial $\operatorname {Ad}(\mathsf {H})$![]() -submodule, the metrics $g_r$
-submodule, the metrics $g_r$![]() induced by $ {\mathbb g}$
induced by $ {\mathbb g}$![]() on $\mathfrak {m}$
on $\mathfrak {m}$![]() split uniquely as
split uniquely as
by means of the Schur lemma, where $F: I \to \mathbb {R}$![]() is a smooth, positive function, possibly satisfying some appropriate boundary condition.
is a smooth, positive function, possibly satisfying some appropriate boundary condition.
From now on, given $V \in \mathfrak {g}$![]() , we denote by $V^{*} \in \Gamma (TM)$
, we denote by $V^{*} \in \Gamma (TM)$![]() the fundamental vector field on $M$
the fundamental vector field on $M$![]() associated with $V$
associated with $V$![]() , that is $V^{*}_p := \frac {\rm d}{{\rm d}s}\exp (sV)\cdot p \big |_{s=0}$
, that is $V^{*}_p := \frac {\rm d}{{\rm d}s}\exp (sV)\cdot p \big |_{s=0}$![]() , and we also set
, and we also set
Note that, by construction,
and, for any $V,\,W \in \mathfrak {g}$![]() , it holds
, it holds
We observe also that, for any $X \in \mathfrak {p}$![]() and for any $Y_1,\,Y_2 \in \mathfrak {m}$
and for any $Y_1,\,Y_2 \in \mathfrak {m}$![]() , we have
, we have
By hypothesis, the fundamental vector fields $V^{*}$![]() are holomorphic, i.e.
are holomorphic, i.e.
By using equations (2.2) and (2.3), one can directly obtain the explicit formulas for the Levi-Civita connection and the $3$![]() -form $\operatorname {d\!}\omega$
-form $\operatorname {d\!}\omega$![]() . Here and in the following statements, we consider the context and assume the notation as above.
. Here and in the following statements, we consider the context and assume the notation as above.
Proposition 3.1 Let $X,\, Y,\, Z \in \mathfrak {p}$![]() . Then, the non-vanishing components of the Levi-Civita connection are given by
. Then, the non-vanishing components of the Levi-Civita connection are given by

Proposition 3.2 Let $X,\,Y,\,Z \in \mathfrak {p}$![]() . Then, the $3$
. Then, the $3$![]() -form $\operatorname {d\!}\omega$
-form $\operatorname {d\!}\omega$![]() is given by
is given by

By combining propositions 3.1 and 3.2, and by equation (2.1), we obtain explicit formulas for the Chern connection along the geodesic $\gamma (r)$![]() . More precisely
. More precisely
Proposition 3.3 Let $X,\,Y,\,Z \in \mathfrak {p}$![]() . Then the non-vanishing components of the Chern connection are
. Then the non-vanishing components of the Chern connection are

As a direct consequence of proposition 3.3 and equation (2.6), we get
Corollary 3.4 It holds that $(\mathcal {L}_{N}\mathbb {J})_{\gamma (r)} = 0,$![]() i.e. $[N,\,\mathbb {J} A]_{\gamma (r)} = \mathbb {J}[N,\, A]_{\gamma (r)}$
i.e. $[N,\,\mathbb {J} A]_{\gamma (r)} = \mathbb {J}[N,\, A]_{\gamma (r)}$![]() for any $A \in \Gamma (TM)$
for any $A \in \Gamma (TM)$![]() .
.
We can also characterize the Kähler metrics as follows. By proposition 3.2 it follows that
if and only if the restriction $g_r|_{\mathfrak {p}{\otimes }\mathfrak {p}}$![]() is $\operatorname {Ad}(\mathsf {K})$
is $\operatorname {Ad}(\mathsf {K})$![]() -invariant for any $r \in I$
-invariant for any $r \in I$![]() . This is equivalent to say that the metrics $(g_r)$
. This is equivalent to say that the metrics $(g_r)$![]() on $\mathsf {G}/\mathsf {H}$
on $\mathsf {G}/\mathsf {H}$![]() are of submersion-type with respect to the homogeneous circle bundle $\mathsf {K}/\mathsf {H} \to \mathsf {G}/\mathsf {H} \to \mathsf {G}/\mathsf {K}$
are of submersion-type with respect to the homogeneous circle bundle $\mathsf {K}/\mathsf {H} \to \mathsf {G}/\mathsf {H} \to \mathsf {G}/\mathsf {K}$![]() , namely, they induce metrics on the base such that the projection is a Riemannian submersion. Moreover, if $g_r|_{\mathfrak {p}{\otimes }\mathfrak {p}}$
, namely, they induce metrics on the base such that the projection is a Riemannian submersion. Moreover, if $g_r|_{\mathfrak {p}{\otimes }\mathfrak {p}}$![]() is $\operatorname {Ad}(\mathsf {K})$
is $\operatorname {Ad}(\mathsf {K})$![]() -invariant, then the condition
-invariant, then the condition
holds true if and only if the induced metrics on the flag manifold $\mathsf {G}/\mathsf {K}$![]() are Kähler. Let us fix now a $Q$
are Kähler. Let us fix now a $Q$![]() -orthogonal, $\operatorname {Ad}(\mathsf {K})$
-orthogonal, $\operatorname {Ad}(\mathsf {K})$![]() -invariant, irreducible decomposition
-invariant, irreducible decomposition
Since flag manifolds are equal rank homogeneous spaces, namely ${\rm rank}(\mathsf {K})={\rm rank}(\mathsf {G})$![]() , it follows that their isotropy representations are always monotypic, namely $\mathfrak {p}_i \not \simeq \mathfrak {p}_j$
, it follows that their isotropy representations are always monotypic, namely $\mathfrak {p}_i \not \simeq \mathfrak {p}_j$![]() for any $1 \leq i < j \leq \ell$
for any $1 \leq i < j \leq \ell$![]() . Hence, the decomposition (3.6) is unique (up to order) and, by the Schur lemma, the metrics $g_r$
. Hence, the decomposition (3.6) is unique (up to order) and, by the Schur lemma, the metrics $g_r$![]() splits uniquely as
splits uniquely as
Then, the condition
holds true if and only if
3.2 Construction of Bérard-Bergery manifolds
Let us assume that $P = P(\mathsf {G},\,\mathsf {K}):= \mathsf {G}/\mathsf {K}$![]() is a simply-connected, irreducible compact Hermitian symmetric space, i.e. $\mathsf {G}$
is a simply-connected, irreducible compact Hermitian symmetric space, i.e. $\mathsf {G}$![]() is a connected, compact, simple Lie group and $\mathsf {K} \subset \mathsf {G}$
is a connected, compact, simple Lie group and $\mathsf {K} \subset \mathsf {G}$![]() is a maximal, connected, compact subgroup with centre isomorphic to the circle group [Reference Helgason30, theorem 6.1]. Set $\dim _{\mathbb {R}}P=2(m-1)$
is a maximal, connected, compact subgroup with centre isomorphic to the circle group [Reference Helgason30, theorem 6.1]. Set $\dim _{\mathbb {R}}P=2(m-1)$![]() , with $m\geq 2$
, with $m\geq 2$![]() , and let $p \in \mathbb {N}$
, and let $p \in \mathbb {N}$![]() be the unique positive integer such that $p^{-1}c_1(P)$
be the unique positive integer such that $p^{-1}c_1(P)$![]() is an indivisible (positive) class in the cohomology group $H^{2}(P;\mathbb {Z})$
is an indivisible (positive) class in the cohomology group $H^{2}(P;\mathbb {Z})$![]() , see [Reference Borel and Hirzebruch13, chapter 5, § 16]. In the following, we list the possibilities for $P$
, see [Reference Borel and Hirzebruch13, chapter 5, § 16]. In the following, we list the possibilities for $P$![]() , following [Reference Besse10, § 7.102 and § 9.124].
, following [Reference Besse10, § 7.102 and § 9.124].

Denote by $\mathsf {H} := [\mathsf {K},\,\mathsf {K}]$![]() the commutator of $\mathsf {K}$
the commutator of $\mathsf {K}$![]() . By hypothesis, there exists an integer $s\geq 1$
. By hypothesis, there exists an integer $s\geq 1$![]() such that $\mathsf {H} \cap \mathsf {Z}(\mathsf {K}) \simeq \mathbb {Z}_s$
such that $\mathsf {H} \cap \mathsf {Z}(\mathsf {K}) \simeq \mathbb {Z}_s$![]() . Fix an isomorphism $\imath : \mathsf {U}(1) \to \mathsf {Z}(\mathsf {K})$
. Fix an isomorphism $\imath : \mathsf {U}(1) \to \mathsf {Z}(\mathsf {K})$![]() and consider the generator $\alpha := \imath ({\rm e}^{\sqrt {-1}({2\pi }/{s})})$
and consider the generator $\alpha := \imath ({\rm e}^{\sqrt {-1}({2\pi }/{s})})$![]() of $\mathsf {H} \cap \mathsf {Z}(\mathsf {K})$
of $\mathsf {H} \cap \mathsf {Z}(\mathsf {K})$![]() . Then, consider the right action of $\mathbb {Z}_s$
. Then, consider the right action of $\mathbb {Z}_s$![]() on $\mathsf {H} \times \mathsf {U}(1)$
on $\mathsf {H} \times \mathsf {U}(1)$![]() given by $(h,\,z)\cdot j := (h\alpha ^{j},\,{\rm e}^{-\sqrt {-1}({2j\pi }/{s})}z)$
given by $(h,\,z)\cdot j := (h\alpha ^{j},\,{\rm e}^{-\sqrt {-1}({2j\pi }/{s})}z)$![]() and take the quotient $\mathsf {H}{\cdot }\mathsf {U}(1) := \mathsf {H} \times _{\mathbb {Z}_s}\!\! \mathsf {U}(1)$
and take the quotient $\mathsf {H}{\cdot }\mathsf {U}(1) := \mathsf {H} \times _{\mathbb {Z}_s}\!\! \mathsf {U}(1)$![]() . We can consider identified $\mathsf {K} = \mathsf {H}{\cdot }\mathsf {U}(1)$
. We can consider identified $\mathsf {K} = \mathsf {H}{\cdot }\mathsf {U}(1)$![]() by means of a Lie group isomorphism (see e.g. [Reference Bredon16, chapter 0, theorem 6.9]) and, for any positive integer $n$
by means of a Lie group isomorphism (see e.g. [Reference Bredon16, chapter 0, theorem 6.9]) and, for any positive integer $n$![]() , we take the representation
, we take the representation
Then, consider the associated bundle
with the projection $\pi _n: \S _n \to P$![]() given by $\pi _n([a,\,z]):= a \mathsf {K}$
given by $\pi _n([a,\,z]):= a \mathsf {K}$![]() . Note that $\mathsf {G}$
. Note that $\mathsf {G}$![]() acts transitively on the left on $\S _n$
acts transitively on the left on $\S _n$![]() by $\tilde {a} \cdot [a,\,z] := [\tilde {a}a,\,z]$
by $\tilde {a} \cdot [a,\,z] := [\tilde {a}a,\,z]$![]() and the stabilizer of $[e,\,1]$
and the stabilizer of $[e,\,1]$![]() is the subgroup $\ker (\rho _n) = \mathsf {H} {\times } \mathbb {Z}_n \subset \mathsf {K}$
is the subgroup $\ker (\rho _n) = \mathsf {H} {\times } \mathbb {Z}_n \subset \mathsf {K}$![]() , where
, where
We are ready to construct the family $M_{(i,n)}(\mathsf {G},\,\mathsf {K})$![]() , with $1 \leq i \leq 4$
, with $1 \leq i \leq 4$![]() and $n \in \mathbb {N}$
and $n \in \mathbb {N}$![]() , of standard cohomogeneity one Hermitian manifolds in the following way.
, of standard cohomogeneity one Hermitian manifolds in the following way.
(i) We set $M_{(1,n)}(\mathsf {G},\,\mathsf {K}) := \S _n \times \mathbb {R}$
 and we let $\mathsf {G}$
and we let $\mathsf {G}$ act on $M_{(1,n)}$
act on $M_{(1,n)}$ via $a \cdot (x,\, r) := (a\cdot x,\,r)$
via $a \cdot (x,\, r) := (a\cdot x,\,r)$ . The orbit space is $\Omega =\mathbb {R}$
. The orbit space is $\Omega =\mathbb {R}$ .
.(ii) We let $M_{(2,n)}(\mathsf {G},\,\mathsf {K}) := \S _n \times _{\mathsf {U}(1)} \mathbb {C}$
 be the homogeneous complex line bundle over $P$
be the homogeneous complex line bundle over $P$ associated with $\pi _n: \S _n \to P$
associated with $\pi _n: \S _n \to P$ by means of the standard action of $\mathsf {U}(1)$
by means of the standard action of $\mathsf {U}(1)$ on $\mathbb {C}$
on $\mathbb {C}$ . Then, $M_{(2,n)}(\mathsf {G},\,\mathsf {K})$
. Then, $M_{(2,n)}(\mathsf {G},\,\mathsf {K})$ is equivariantly diffeomorphic to the quotient of $\S _n \times [0,\,+\infty )$
is equivariantly diffeomorphic to the quotient of $\S _n \times [0,\,+\infty )$ by the fibration $\S _n \times \{0\} \to P$
by the fibration $\S _n \times \{0\} \to P$ , on which $\mathsf {G}$
, on which $\mathsf {G}$ acts by left multiplication on the first factor.
acts by left multiplication on the first factor.(iii) We set $M_{(3,n)}(\mathsf {G},\,\mathsf {K}) := \S _n \times S^{1}$
 and we let $\mathsf {G}$
and we let $\mathsf {G}$ act on $M_{(3,n)}(\mathsf {G},\,\mathsf {K})$
act on $M_{(3,n)}(\mathsf {G},\,\mathsf {K})$ via $a \cdot (x,\, z) := (a\cdot x,\,z)$
via $a \cdot (x,\, z) := (a\cdot x,\,z)$ . The orbit space is $\Omega =S^{1}$
. The orbit space is $\Omega =S^{1}$ .
.(iv) We let $M_{(4,n)}(\mathsf {G},\,\mathsf {K}) := \S _n \times _{\mathsf {U}(1)} \mathbb {C} \mathbb {P}^{1}$
 be the homogeneous $\mathbb {C} \mathbb {P}^{1}$
be the homogeneous $\mathbb {C} \mathbb {P}^{1}$ -bundle over $P$
-bundle over $P$ associated with $\pi _n: \S _n \to P$
associated with $\pi _n: \S _n \to P$ by means of the standard action of $\mathsf {U}(1)$
by means of the standard action of $\mathsf {U}(1)$ on $\mathbb {C} \mathbb {P}^{1}$
on $\mathbb {C} \mathbb {P}^{1}$ . Then, $M_{(4,n)}(\mathsf {G},\,\mathsf {K})$
. Then, $M_{(4,n)}(\mathsf {G},\,\mathsf {K})$ is equivariantly diffeomorphic to the quotient of $\S _n \times [0,\,\pi ]$
is equivariantly diffeomorphic to the quotient of $\S _n \times [0,\,\pi ]$ under the identification of the two boundaries by means of the fibrations $\S _n \times \{0\} \to P$
under the identification of the two boundaries by means of the fibrations $\S _n \times \{0\} \to P$ and $\S _n \times \{\pi \} \to P$
and $\S _n \times \{\pi \} \to P$ , on which $\mathsf {G}$
, on which $\mathsf {G}$ acts by left multiplication on the first factor.
acts by left multiplication on the first factor.
We observe that the manifolds in families $M_{(3,n)}(\mathsf {G},\,\mathsf {K})$![]() and $M_{(4,n)}(\mathsf {G},\,\mathsf {K})$
and $M_{(4,n)}(\mathsf {G},\,\mathsf {K})$![]() are compact, and the manifolds in families $M_{(2,n)}(\mathsf {G},\,\mathsf {K})$
are compact, and the manifolds in families $M_{(2,n)}(\mathsf {G},\,\mathsf {K})$![]() and $M_{(4,n)}(\mathsf {G},\,\mathsf {K})$
and $M_{(4,n)}(\mathsf {G},\,\mathsf {K})$![]() are simply connected. Moreover, manifolds in family $M_{(4,n)}(\mathsf {G},\,\mathsf {K})$
are simply connected. Moreover, manifolds in family $M_{(4,n)}(\mathsf {G},\,\mathsf {K})$![]() are almost-homogeneous in the sense of [Reference Huckleberry and Snow31], i.e. the complexified Lie group $\mathsf {G}^{\mathbb {C}}$
are almost-homogeneous in the sense of [Reference Huckleberry and Snow31], i.e. the complexified Lie group $\mathsf {G}^{\mathbb {C}}$![]() acts on them by biholomorphisms with one open orbit, see [Reference Podestà and Spiro49].
acts on them by biholomorphisms with one open orbit, see [Reference Podestà and Spiro49].
Let $M_{(i,n)}(\mathsf {G},\,\mathsf {K})$![]() be as above. We denote by $B$
be as above. We denote by $B$![]() be the Cartan–Killing form of $\mathfrak {g} := \operatorname {Lie}(\mathsf {G})$
be the Cartan–Killing form of $\mathfrak {g} := \operatorname {Lie}(\mathsf {G})$![]() and we set $\mathfrak {k} := \operatorname {Lie}(\mathsf {K})$
and we set $\mathfrak {k} := \operatorname {Lie}(\mathsf {K})$![]() , $\mathfrak {h} := \operatorname {Lie}(\mathsf {H})$
, $\mathfrak {h} := \operatorname {Lie}(\mathsf {H})$![]() , $\mathfrak {a} := \mathfrak {z}(\mathfrak {k}) = \operatorname {Lie}(\mathsf {Z}(\mathsf {K}))$
, $\mathfrak {a} := \mathfrak {z}(\mathfrak {k}) = \operatorname {Lie}(\mathsf {Z}(\mathsf {K}))$![]() . Then, the positive definite $\operatorname {Ad}(\mathsf {G})$
. Then, the positive definite $\operatorname {Ad}(\mathsf {G})$![]() -invariant scalar product $Q := \frac 1{4m}(-B)$
-invariant scalar product $Q := \frac 1{4m}(-B)$![]() on $\mathfrak {g}$
on $\mathfrak {g}$![]() determines a $\operatorname {Ad}(\mathsf {H})$
determines a $\operatorname {Ad}(\mathsf {H})$![]() -invariant, $Q$
-invariant, $Q$![]() -orthogonal decomposition
-orthogonal decomposition

We fix a vector $T \in \mathfrak {a}$![]() with $Q(T,\,T)=1$
with $Q(T,\,T)=1$![]() and we pick the only $\lambda >0$
and we pick the only $\lambda >0$![]() such that
such that
is a linear complex structure on $\mathfrak {p}$![]() [Reference Kobayashi and Nomizu32, chapter XI, theorem 9.6]. Note that a direct computation implies
[Reference Kobayashi and Nomizu32, chapter XI, theorem 9.6]. Note that a direct computation implies
and so
Remark 3.5 [Reference Podestà and Spiro48, p. 814]
The linear complex structure $J$![]() on $\mathfrak {p}$
on $\mathfrak {p}$![]() determines uniquely a $\mathsf {G}$
determines uniquely a $\mathsf {G}$![]() -invariant, projectable, complex structure $\mathbb {J}$
-invariant, projectable, complex structure $\mathbb {J}$![]() on $M_{(i,n)}(\mathsf {G},\,\mathsf {K})$
on $M_{(i,n)}(\mathsf {G},\,\mathsf {K})$![]() .
.
Moreover, we stress that:
• the restriction $Q_{\mathfrak {p}} := Q|_{\mathfrak {p}{\otimes }\mathfrak {p}}$
 induces a $\mathsf {G}$
induces a $\mathsf {G}$ -invariant Kähler–Einstein metric on the base space $P$
-invariant Kähler–Einstein metric on the base space $P$ satisfying the equation $\operatorname {Ric}(Q_{\mathfrak {p}}) =2\,m Q_{\mathfrak {p}}$
satisfying the equation $\operatorname {Ric}(Q_{\mathfrak {p}}) =2\,m Q_{\mathfrak {p}}$
• the scalar product $\frac {2m(m-1)n^{2}}{p^{2}}Q_{\mathfrak {a}}$
 , with $Q_{\mathfrak {a}}:= Q |_{\mathfrak {a}{\otimes }\mathfrak {a}}$
, with $Q_{\mathfrak {a}}:= Q |_{\mathfrak {a}{\otimes }\mathfrak {a}}$ , corresponds to the standard metric of radius $1$
, corresponds to the standard metric of radius $1$ on the fibres of $\pi _n: \S _n \to P$
on the fibres of $\pi _n: \S _n \to P$
Then, being $P$![]() irreducible, any $\mathsf {G}$
irreducible, any $\mathsf {G}$![]() -invariant Hermitian metric $ {\mathbb g}$
-invariant Hermitian metric $ {\mathbb g}$![]() on $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
on $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() which is of submersion-type with respect to $M_{(i,n)}(\mathsf {G},\,\mathsf {K}) \to P$
which is of submersion-type with respect to $M_{(i,n)}(\mathsf {G},\,\mathsf {K}) \to P$![]() is completely determined by two positive, smooth functions $f,\,h: I \to \mathbb {R}$
is completely determined by two positive, smooth functions $f,\,h: I \to \mathbb {R}$![]() , satisfying some appropriate smoothness conditions, by means of the splitting
, satisfying some appropriate smoothness conditions, by means of the splitting
where $(g_r)$![]() is again the 1-parameter family of $\mathsf {G}$
is again the 1-parameter family of $\mathsf {G}$![]() -invariant metrics induced by $ {\mathbb g}$
-invariant metrics induced by $ {\mathbb g}$![]() on the principal orbits. Case by case, the smoothness conditions are the following (see e.g. [Reference Verdiani and Ziller54, p. 7] and [Reference Bérard-Bergery9, p. 39]).
on the principal orbits. Case by case, the smoothness conditions are the following (see e.g. [Reference Verdiani and Ziller54, p. 7] and [Reference Bérard-Bergery9, p. 39]).
(i) For $i=1$
 , $I=\mathbb {R}$
, $I=\mathbb {R}$ and there are no boundary conditions.
and there are no boundary conditions.(ii) For $i=2$
 , $I=(0,\,+\infty )$
, $I=(0,\,+\infty )$ and the conditions are: $f$
and the conditions are: $f$ is the restriction of a smooth odd function on $\mathbb {R}$
is the restriction of a smooth odd function on $\mathbb {R}$ with $f'(0) = 1$
with $f'(0) = 1$ and $h$
and $h$ is the restriction of a smooth even function on $\mathbb {R}$
is the restriction of a smooth even function on $\mathbb {R}$ .
.(iii) For $i=3$
 , $f,\,h$
, $f,\,h$ need to be $S^{1}$
need to be $S^{1}$ -periodic.
-periodic.(iv) For $i=4$
 , $I=(0,\,\pi )$
, $I=(0,\,\pi )$ and the conditions are: $f$
and the conditions are: $f$ is the restriction of a smooth odd function on $\mathbb {R}$
is the restriction of a smooth odd function on $\mathbb {R}$ satisfying $f(\pi +r)=-f(\pi -r)$
satisfying $f(\pi +r)=-f(\pi -r)$ with $f'(0) = 1 = -f'(\pi )$
with $f'(0) = 1 = -f'(\pi )$ and $h$
and $h$ is the restriction of a smooth even function on $\mathbb {R}$
is the restriction of a smooth even function on $\mathbb {R}$ satisfying $h(\pi +r)=h(\pi -r)$
satisfying $h(\pi +r)=h(\pi -r)$ .
.
Conversely, any pair of smooth functions $(f,\,h)$![]() satisfying the appropriate smoothness condition uniquely defines a smooth $\mathsf {G}$
satisfying the appropriate smoothness condition uniquely defines a smooth $\mathsf {G}$![]() -invariant Hermitian metric $ {\mathbb g}= {\mathbb g}(f,\,h)$
-invariant Hermitian metric $ {\mathbb g}= {\mathbb g}(f,\,h)$![]() , which is of submersion-type.
, which is of submersion-type.
By equations (3.7), (3.9) and (3.10), it follows that the metric $ {\mathbb g}(f,\,h)$![]() is Kähler if and only if the functions $f,\,h$
is Kähler if and only if the functions $f,\,h$![]() verify
verify
Remark 3.6 We note that the smoothness condition in (iii) and equation (3.11) imply immediately that the complex manifolds $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() cannot admit cohomogeneity one, submersion-type Kähler metrics (see also [Reference Alekseevsky and Zuddas4, corollary 20]). Actually, it holds more: it can be easily check that $\pi _1(\S _n)$
cannot admit cohomogeneity one, submersion-type Kähler metrics (see also [Reference Alekseevsky and Zuddas4, corollary 20]). Actually, it holds more: it can be easily check that $\pi _1(\S _n)$![]() is finite, and so its first Betti number is $b_1(\S _n)=0$
is finite, and so its first Betti number is $b_1(\S _n)=0$![]() . In particular, this implies that $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
. In particular, this implies that $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() do not admit Kähler metrics at all.
do not admit Kähler metrics at all.
From now on, we will adopt the following
Definition 3.7 A Bérard-Bergery standard cohomogeneity one Hermitian manifold is a triple $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J},\, {\mathbb g})$![]() , where $M_{(i,n)}(\mathsf {G},\,\mathsf {K})$
, where $M_{(i,n)}(\mathsf {G},\,\mathsf {K})$![]() is the bundle over $P=\mathsf {G}/\mathsf {K}$
is the bundle over $P=\mathsf {G}/\mathsf {K}$![]() constructed as above, $\mathbb {J}$
constructed as above, $\mathbb {J}$![]() is the unique $\mathsf {G}$
is the unique $\mathsf {G}$![]() -invariant projectable complex structure on $M_{(i,n)}(\mathsf {G},\,\mathsf {K})$
-invariant projectable complex structure on $M_{(i,n)}(\mathsf {G},\,\mathsf {K})$![]() as in remark 3.5 and $ {\mathbb g}= {\mathbb g}(f,\,h)$
as in remark 3.5 and $ {\mathbb g}= {\mathbb g}(f,\,h)$![]() is the Riemannian metric described in equation (3.10). Accordingly, any pair $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$
is the Riemannian metric described in equation (3.10). Accordingly, any pair $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$![]() will be called Bérard-Bergery standard cohomogeneity one complex manifold.
will be called Bérard-Bergery standard cohomogeneity one complex manifold.
Let us point out that the above construction can be performed in a more general setting, i.e. by requiring that the base space $P=\mathsf {G}/\mathsf {K}$![]() is a Kähler C-space, see [Reference Bérard-Bergery9]. However, in this work, we will just focus in the case of $P$
is a Kähler C-space, see [Reference Bérard-Bergery9]. However, in this work, we will just focus in the case of $P$![]() being symmetric and irreducible.
being symmetric and irreducible.
Example 3.8 Consider the Hermitian symmetric space $P=\mathbb {C} \mathbb {P}^{m-1}$![]() , corresponding to $\mathsf {G}=\mathsf {SU}(m)$
, corresponding to $\mathsf {G}=\mathsf {SU}(m)$![]() and $\mathsf {K}=\mathsf {S}(\mathsf {U}(1){\times }\mathsf {U}(m-1))$
and $\mathsf {K}=\mathsf {S}(\mathsf {U}(1){\times }\mathsf {U}(m-1))$![]() . Here, the $\operatorname {Ad}(\mathsf {G})$
. Here, the $\operatorname {Ad}(\mathsf {G})$![]() -invariant scalar product $Q(A_1,\,A_2):= -\frac {1}{2}\operatorname {Tr}(A_1A_2)$
-invariant scalar product $Q(A_1,\,A_2):= -\frac {1}{2}\operatorname {Tr}(A_1A_2)$![]() on the Lie algebra $\mathfrak {g}=\mathfrak {su}(m)$
on the Lie algebra $\mathfrak {g}=\mathfrak {su}(m)$![]() , defined following the above normalization, induces on $P$
, defined following the above normalization, induces on $P$![]() the Fubini–Study metric with sectional curvature satisfying $1\leq \sec \leq 4$
the Fubini–Study metric with sectional curvature satisfying $1\leq \sec \leq 4$![]() . In this case, the principal orbits are equivariantly diffeomorphic to the lens space $\S _n = \mathbb {Z}_n \backslash S^{2m-1}$
. In this case, the principal orbits are equivariantly diffeomorphic to the lens space $\S _n = \mathbb {Z}_n \backslash S^{2m-1}$![]() , where $\mathbb {Z}_n$
, where $\mathbb {Z}_n$![]() acts on $S^{2m-1} \subset \mathbb {C}^{m}$
acts on $S^{2m-1} \subset \mathbb {C}^{m}$![]() via $k \cdot z := {\rm e}^{-i({2k\pi }/n)}z$
via $k \cdot z := {\rm e}^{-i({2k\pi }/n)}z$![]() , and
, and

Here, we denoted by $\mathcal {O}_{\mathbb {C} \mathbb {P}^{m-1}}$![]() the trivial line bundle over $\mathbb {C} \mathbb {P}^{m-1}$
the trivial line bundle over $\mathbb {C} \mathbb {P}^{m-1}$![]() , by $\mathcal {O}_{\mathbb {C} \mathbb {P}^{m-1}}(-1)$
, by $\mathcal {O}_{\mathbb {C} \mathbb {P}^{m-1}}(-1)$![]() the tautological line bundle and by $\mathcal {O}_{\mathbb {C} \mathbb {P}^{m-1}}(-n) := \mathcal {O}_{\mathbb {C} \mathbb {P}^{m-1}}(-1)^{\otimes n}$
the tautological line bundle and by $\mathcal {O}_{\mathbb {C} \mathbb {P}^{m-1}}(-n) := \mathcal {O}_{\mathbb {C} \mathbb {P}^{m-1}}(-1)^{\otimes n}$![]() . In particular:
. In particular:
• if $(i,\,n)=(3,\,1)$
 , then we get a diagonal Hopf manifold;
, then we get a diagonal Hopf manifold;• if $(i,\,n)=(4,\,1)$
 , then we get the connected sum $\mathbb {C}\mathbb {P}^{m} \# \overline {\mathbb {C}\mathbb {P}}{}^{m}$
, then we get the connected sum $\mathbb {C}\mathbb {P}^{m} \# \overline {\mathbb {C}\mathbb {P}}{}^{m}$ ;
;• if $m=2$
 and $i=4$
and $i=4$ , then we get all the Hirzebruch surfaces.
, then we get all the Hirzebruch surfaces.
Remark 3.9 Let us consider $P=\mathbb {C} \mathbb {P}^{m-1}$![]() and assume that $m\geq 3$
and assume that $m\geq 3$![]() . Since the isotropy representation of the odd sphere $\S _1 = S^{2m-1}=\mathsf {SU}(m)/\mathsf {SU}(m-1)$
. Since the isotropy representation of the odd sphere $\S _1 = S^{2m-1}=\mathsf {SU}(m)/\mathsf {SU}(m-1)$![]() is monotypic, all the cohomogeneity one Hermitian metrics on $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
is monotypic, all the cohomogeneity one Hermitian metrics on $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() are of submersion type with respect to the fibration $M_{(i,n)}(\mathsf {G},\,\mathsf {K}) \to \mathbb {C}\mathbb {P}^{m-1}$
are of submersion type with respect to the fibration $M_{(i,n)}(\mathsf {G},\,\mathsf {K}) \to \mathbb {C}\mathbb {P}^{m-1}$![]() . This fact does not hold true in general. For example, starting from the Grassmannian $P=\widetilde {\rm Gr}(2,\,\mathbb {R}^{m+1})= \mathsf {SO}(m+1)/(\mathsf {SO}(2){\times }\mathsf {SO}(m-1))$
. This fact does not hold true in general. For example, starting from the Grassmannian $P=\widetilde {\rm Gr}(2,\,\mathbb {R}^{m+1})= \mathsf {SO}(m+1)/(\mathsf {SO}(2){\times }\mathsf {SO}(m-1))$![]() of the oriented $2$
of the oriented $2$![]() -planes in $\mathbb {R}^{m+1}$
-planes in $\mathbb {R}^{m+1}$![]() , we get that $\S _1 = V(2,\,\mathbb {R}^{m+1}) = \mathsf {SO}(m+1)/\mathsf {SO}(m-1)$
, we get that $\S _1 = V(2,\,\mathbb {R}^{m+1}) = \mathsf {SO}(m+1)/\mathsf {SO}(m-1)$![]() is the Stiefel manifold of the orthonormal $2$
is the Stiefel manifold of the orthonormal $2$![]() -frames in $\mathbb {R}^{m+1}$
-frames in $\mathbb {R}^{m+1}$![]() , whose isotropy representation contains two equivalent irreducible summands.
, whose isotropy representation contains two equivalent irreducible summands.
Remark 3.10 Note that, by means of the action of $\mathsf {G}$![]() , there is a bijective correspondence between the set of
, there is a bijective correspondence between the set of ![]() $\mathsf{G}$-invariant smooth functions $\tilde {\varphi }: M_{(i,n)}(\mathsf {G},\,\mathsf {K}) \to \mathbb {R}$
$\mathsf{G}$-invariant smooth functions $\tilde {\varphi }: M_{(i,n)}(\mathsf {G},\,\mathsf {K}) \to \mathbb {R}$![]() and the set of functions $\varphi : I \to \mathbb {R}$
and the set of functions $\varphi : I \to \mathbb {R}$![]() satisfying the appropriate smoothness condition:
satisfying the appropriate smoothness condition:
(i) if $i=1$
 , $I=\mathbb {R}$
, $I=\mathbb {R}$ and $\varphi$
and $\varphi$ is smooth;
is smooth;(ii) if $i=2$
 , $I=(0,\,+\infty )$
, $I=(0,\,+\infty )$ and $\varphi$
and $\varphi$ is the restriction of a smooth even function on $\mathbb {R}$
is the restriction of a smooth even function on $\mathbb {R}$ ;
;(iii) if $i=3$
 , $\varphi$
, $\varphi$ is smooth and $S^{1}$
is smooth and $S^{1}$ -periodic;
-periodic;(iv) if $i=4$
 , $I=(0,\,\pi )$
, $I=(0,\,\pi )$ and $\varphi$
and $\varphi$ is the restriction of a smooth even function on $\mathbb {R}$
is the restriction of a smooth even function on $\mathbb {R}$ satisfying $\varphi (\pi +r)=\varphi (\pi -r)$
satisfying $\varphi (\pi +r)=\varphi (\pi -r)$ .
.
From now on, any function $\varphi : I \to \mathbb {R}$![]() satisfying the appropriate smoothness condition will be called admissible.
satisfying the appropriate smoothness condition will be called admissible.
Remark 3.11 Let $ {\mathbb g}= {\mathbb g}(f,\,h)$![]() a cohomogeneity one, submersion-type metric on a manifold $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
a cohomogeneity one, submersion-type metric on a manifold $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() and $\varphi : I \to \mathbb {R}$
and $\varphi : I \to \mathbb {R}$![]() a positive, admissible function. Then, the metric $\varphi ^{2} {\mathbb g}$
a positive, admissible function. Then, the metric $\varphi ^{2} {\mathbb g}$![]() is still a cohomogeneity one, submersion-type metric on $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
is still a cohomogeneity one, submersion-type metric on $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() and $\varphi ^{2} {\mathbb g} = {\mathbb g}(\hat {f}_{\varphi },\,\hat {h}_{\varphi })$
and $\varphi ^{2} {\mathbb g} = {\mathbb g}(\hat {f}_{\varphi },\,\hat {h}_{\varphi })$![]() , with
, with
where $\xi _{\varphi }(r) := \int _0^{r}\varphi (t)\operatorname {d\!} t$![]() . However we stress that, even if $ {\mathbb g}$
. However we stress that, even if $ {\mathbb g}$![]() is complete, in general the conformal metric $\varphi ^{2} {\mathbb g}$
is complete, in general the conformal metric $\varphi ^{2} {\mathbb g}$![]() is not.
is not.
3.3 Curvature and torsion computations for Bérard-Bergery manifolds
We begin this section by listing the Levi-Civita connection and the Riemannian Ricci tensor of the manifolds $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J},\, {\mathbb g})$![]() . By straightforward computations, from proposition 3.1 and equations (3.10), (3.8) we get
. By straightforward computations, from proposition 3.1 and equations (3.10), (3.8) we get
Proposition 3.12 Let $X,\,Y,\,Z \in \mathfrak {p}$![]() . Then
. Then

Moreover, from [Reference Grove and Ziller27, proposition 1.14], we directly obtain
Proposition 3.13 Let $X \in \mathfrak {p}$![]() with $Q(X,\,X)=1$
with $Q(X,\,X)=1$![]() . Then the Riemannian Ricci tensor is given by
. Then the Riemannian Ricci tensor is given by

and
Furthermore, the Riemannian scalar curvature is

We compute now the Chern connection and the Chern–Ricci tensors of the manifolds $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J},\, {\mathbb g})$![]() . From proposition 3.3 and equations (3.10), (3.8) we get
. From proposition 3.3 and equations (3.10), (3.8) we get
Proposition 3.14 Let $X,\,Y,\,Z \in \mathfrak {p}$![]() . Then
. Then

We are ready to state the following proposition, whose proof will be given in Appendix A.
Proposition 3.15 Let $X \in \mathfrak {p}$![]() with $Q(X,\,X)=1$
with $Q(X,\,X)=1$![]() .
.
(a) The first Chern–Ricci tensor verifies
(3.12)\begin{equation} \begin{aligned} & \operatorname{Ric}^{\rm Ch[1]}( {\mathbb g})(T^{*},T^{*})_{\gamma(r)}\\ & \quad= \frac{2m(m-1)n^{2}}{p^{2}}f(r)^{2}\\ & \qquad \times \left(-\frac{f''(r)}{f(r)} +(m-1)\left(-\frac{h''(r)}{h(r)} +\frac{h'(r)^{2}}{h(r)^{2}} -\frac{f'(r)}{f(r)}\frac{h'(r)}{h(r)}\right)\right), \\ & \operatorname{Ric}^{\rm Ch[1]}( {\mathbb g})(X^{*},X^{*})_{\gamma(r)}\\ & \quad = h(r)^{2}\left(\frac{2mn}p\frac{f(r)}{h(r)^{2}}\left(\frac{f'(r)}{f(r)} +(m-1)\frac{h'(r)}{h(r)}\right) +\frac{2m}{h(r)^{2}}\right). \end{aligned} \end{equation}
(b) The second Chern–Ricci tensor verifies
(3.13)\begin{equation} \begin{aligned} & \operatorname{Ric}^{\rm Ch[2]}( {\mathbb g})(T^{*},T^{*})_{\gamma(r)}\\ & \quad = \frac{2m(m-1)n^{2}}{p^{2}}f(r)^{2} \\ & \qquad \times\left(-\frac{f''(r)}{f(r)} +\frac{2m(m-1)n}{p}\frac{f'(r)}{h(r)^{2}} +\frac{2m^{2}(m-1)n^{2}}{p^{2}}\frac{f(r)^{2}}{h(r)^{4}}\right), \\ & \operatorname{Ric}^{\rm Ch[2]}( {\mathbb g})(X^{*},X^{*})_{\gamma(r)}\\ & \quad = h(r)^{2}\left(-\frac{h''(r)}{h(r)}+\frac{h'(r)^{2}}{h(r)^{2}}-\frac{f'(r)}{f(r)}\frac{h'(r)}{h(r)}+\frac{2m(m-1)n}{p}f(r)\frac{h'(r)}{h(r)^{3}}\right.\\ & \qquad -\left.2\left(\frac{mn}{p}\right)^{2}\frac{f(r)^{2}}{h(r)^{4}}+\frac{2m}{h(r)^{2}}\right). \end{aligned} \end{equation}
(c) Both the Chern–Ricci tensors satisfy
(3.14)\begin{equation} \begin{aligned} \operatorname{Ric}^{\rm Ch[i]}( {\mathbb g})(N,N)_{\gamma(r)} & = \operatorname{Ric}^{\rm Ch[i]}( {\mathbb g})(T^{*},T^{*})_{\gamma(r)}, \\ \operatorname{Ric}^{\rm Ch[i]}( {\mathbb g})(N,T^{*})_{\gamma(r)} & = \operatorname{Ric}^{\rm Ch[i]}( {\mathbb g})(N,X^{*})_{\gamma(r)} = \operatorname{Ric}^{\rm Ch[i]}( {\mathbb g})(T^{*},X^{*})_{\gamma(r)} =0. \end{aligned} \end{equation}
(d) The Chern-scalar curvature is given by
(3.15)\begin{align} \operatorname{scal}^{\rm Ch}( {\mathbb g})(r) & =-2\frac{f''(r)}{f(r)} -2(m-1)\frac{h''(r)}{h(r)} +2(m-1)\notag\\ & \quad \times \left(\frac{h'(r)}{h(r)} -\frac{f'(r)}{f(r)}\right)\frac{h'(r)}{h(r)} +4m(m-1)\frac 1{h(r)^{2}} \nonumber\\ & \quad +\frac{4m(m-1)n}{p}\left(f'(r) +(m-1)f(r)\frac{h'(r)}{h(r)}\right) \frac 1{h(r)^{2}}. \end{align}
Given proposition 3.15, we are now able to study the second-Chern–Einstein equations and the constant Chern-scalar curvature equation for this special class of Hermitian cohomogeneity one manifolds. This will be done in § 5.
Finally, we recall that the torsion $\tau$![]() of the Chern connection is given by
of the Chern connection is given by
and that its trace $\vartheta (A) := \operatorname {Tr}(\tau (A,\,\cdot ))$![]() is called Lee form. We recall that it satisfies $\operatorname {d\!}\omega ^{m-1}=\vartheta \wedge \omega ^{m-1}$
is called Lee form. We recall that it satisfies $\operatorname {d\!}\omega ^{m-1}=\vartheta \wedge \omega ^{m-1}$![]() , see [Reference Gauduchon23, p 500].
, see [Reference Gauduchon23, p 500].
From proposition 3.2 and formulas (3.8), (3.10) we obtain
Corollary 3.16 Let $X,\,Y,\,Z \in \mathfrak {p}$![]() . Then
. Then

where $\rho (X,\,Y) := Q_{\mathfrak {p}}(JX,\,Y)$![]() is the $\mathsf {G}$
is the $\mathsf {G}$![]() -invariant Kähler–Einstein form on $P$
-invariant Kähler–Einstein form on $P$![]() , and
, and
and, by consequence
Proposition 3.17 Let $X,\,Y \in \mathfrak {p}$![]() . Then it holds $\tau (N,\,T^{*})_{\gamma (r)} = \tau (X^{*},\,Y^{*})_{\gamma (r)} = 0$
. Then it holds $\tau (N,\,T^{*})_{\gamma (r)} = \tau (X^{*},\,Y^{*})_{\gamma (r)} = 0$![]() and
and

Moreover, the Lee form $\vartheta$![]() satisfies
satisfies
and $\vartheta (T^{*})_{\gamma (r)} = \vartheta (X^{*})_{\gamma (r)} = 0$![]() .
.
As a direct consequence of proposition 3.17, whose proof will be given in Appendix A, we get the following
Corollary 3.18 For any $A,\,B \in \Gamma (TM),$![]() it holds that
it holds that
4. Special Hermitian metrics on Bérard-Bergery manifolds
In this section, we investigate the existence of special non-Kähler Hermitian metrics, such as balanced, pluriclosed, locally conformally Kähler, Vaisman and Gauduchon, on the Bérard-Bergery standard cohomogeneity one Hermitian manifolds. In particular, we prove theorems A and B.
4.1 Proof of theorem A
We begin by pointing out the following
Proposition 4.1 All the cohomogeneity one Hermitian metrics $ {\mathbb g}$![]() of submersion-type on the complex manifold $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
of submersion-type on the complex manifold $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() are locally conformally Kähler.
are locally conformally Kähler.
Proof. By [Reference Dragomir and Ornea19, corollary 1.1], we know that $ {\mathbb g}$![]() is locally conformally Kähler if and only if the complex structure $\mathbb {J}$
is locally conformally Kähler if and only if the complex structure $\mathbb {J}$![]() is parallel with respect to the Weyl connection associated with $( {\mathbb g},\,\frac {1}{m-1}\vartheta )$
is parallel with respect to the Weyl connection associated with $( {\mathbb g},\,\frac {1}{m-1}\vartheta )$![]() , equivalently, the following is satisfied:
, equivalently, the following is satisfied:
for any $A,\, B \in \Gamma (TM)$![]() , where $\vartheta ^\# \in \Gamma (TM)$
, where $\vartheta ^\# \in \Gamma (TM)$![]() is defined by the relation $ {\mathbb g}(\vartheta ^\#,\,\cdot ) = \vartheta$
is defined by the relation $ {\mathbb g}(\vartheta ^\#,\,\cdot ) = \vartheta$![]() . By using equations (2.1) and (3.16), a straightforward computation shows that the above equation is equivalent to equation (3.18). Indeed, for any $C\in \Gamma (TM)$
. By using equations (2.1) and (3.16), a straightforward computation shows that the above equation is equivalent to equation (3.18). Indeed, for any $C\in \Gamma (TM)$![]() ,
,

which shows the above mentioned equivalence.
Corollary 4.2 Let $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J},\, {\mathbb g})$![]() be a Bérard-Bergery standard cohomogeneity one Hermitian manifold. Then, $ {\mathbb g}$
be a Bérard-Bergery standard cohomogeneity one Hermitian manifold. Then, $ {\mathbb g}$![]() is strictly locally conformally Kähler if and only if $i=3$
is strictly locally conformally Kähler if and only if $i=3$![]() .
.
Proof. Since the complex manifolds $(M_{(2,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$![]() and $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$
and $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$![]() are simply connected, any closed $1$
are simply connected, any closed $1$![]() -form on them is necessarily exact. Moreover, by remark 3.6, it holds that $b_1(M_{(1,n)}(\mathsf {G},\,\mathsf {K}))=0$
-form on them is necessarily exact. Moreover, by remark 3.6, it holds that $b_1(M_{(1,n)}(\mathsf {G},\,\mathsf {K}))=0$![]() . Therefore, any locally conformally Kähler metrics on them are necessarily globally conformally Kähler. Finally, by using again remark 3.6, the complex manifolds $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$
. Therefore, any locally conformally Kähler metrics on them are necessarily globally conformally Kähler. Finally, by using again remark 3.6, the complex manifolds $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\, \mathbb {J})$![]() do not admit any Kähler metric.
do not admit any Kähler metric.
Let now $ {\mathbb g}$![]() be a cohomogeneity one, submersion-type Hermitian metric on a complex manifold $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
be a cohomogeneity one, submersion-type Hermitian metric on a complex manifold $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() . By proposition 4.1, it follows that $\operatorname {d\!}\omega =\frac {1}{m-1}\vartheta \wedge \omega$
. By proposition 4.1, it follows that $\operatorname {d\!}\omega =\frac {1}{m-1}\vartheta \wedge \omega$![]() which in turn implies that $\mathcal {L}_A\vartheta =0$
which in turn implies that $\mathcal {L}_A\vartheta =0$![]() for any holomorphic Killing vector field $A \in \Gamma (TM)$
for any holomorphic Killing vector field $A \in \Gamma (TM)$![]() . Hence, by equations (3.1), (3.10) and proposition 3.12, the non-vanishing components of the Levi-Civita covariant derivative of $\vartheta$
. Hence, by equations (3.1), (3.10) and proposition 3.12, the non-vanishing components of the Levi-Civita covariant derivative of $\vartheta$![]() are
are

where $\lambda$![]() is given by equation (3.9). By corollary 4.2, the complex manifolds $(M_{(1,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
is given by equation (3.9). By corollary 4.2, the complex manifolds $(M_{(1,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() , $(M_{(2,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
, $(M_{(2,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() and $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
and $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() cannot admit cohomogeneity one, Hermitian metric of submersion-type that are Vaisman. Moreover, from equation (4.1), we get
cannot admit cohomogeneity one, Hermitian metric of submersion-type that are Vaisman. Moreover, from equation (4.1), we get
Proposition 4.3 A cohomogeneity one Hermitian metric $ {\mathbb g}$![]() of submersion-type on the complex manifolds $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
of submersion-type on the complex manifolds $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() is Vaisman if and only if both $f,$
is Vaisman if and only if both $f,$![]() $h$
$h$![]() are constant.
are constant.
Proof. The if part is immediate. Indeed, since $\vartheta$![]() is necessarily non-exact, if both $f$
is necessarily non-exact, if both $f$![]() and $h$
and $h$![]() are constant, then by equations (3.17) and (4.1) it follows that $D\vartheta =0$
are constant, then by equations (3.17) and (4.1) it follows that $D\vartheta =0$![]() .
.
Conversely, assume that $D\vartheta =0$![]() . Note that either $\vartheta (N)_{\gamma (r_{\operatorname {o}})}=0$
. Note that either $\vartheta (N)_{\gamma (r_{\operatorname {o}})}=0$![]() for some $r_{\operatorname {o}}\in I$
for some $r_{\operatorname {o}}\in I$![]() , or $\vartheta (N)_{\gamma (r)}$
, or $\vartheta (N)_{\gamma (r)}$![]() is nowhere vanishing. In the former case, the first equation in (4.1) yields that $\vartheta (N)_{\gamma (r)}$
is nowhere vanishing. In the former case, the first equation in (4.1) yields that $\vartheta (N)_{\gamma (r)}$![]() is constantly zero. In fact, one gets that $\vartheta =0$
is constantly zero. In fact, one gets that $\vartheta =0$![]() , that is, $ {\mathbb g}$
, that is, $ {\mathbb g}$![]() is Kähler. In particular, if $ {\mathbb g}$
is Kähler. In particular, if $ {\mathbb g}$![]() is Vaisman, then the above observation implies that $D\vartheta =0$
is Vaisman, then the above observation implies that $D\vartheta =0$![]() and $\vartheta (N)_{\gamma (r)}$
and $\vartheta (N)_{\gamma (r)}$![]() is nowhere vanishing. Hence, equations (4.1) immediately imply that $f$
is nowhere vanishing. Hence, equations (4.1) immediately imply that $f$![]() and $h$
and $h$![]() are constant.
are constant.
Finally, we note that the manifolds $(M_{(1,n)} (\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() (respectively $(M_{(3,n)} (\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
(respectively $(M_{(3,n)} (\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() ) are acted transitively by the larger group $\mathsf {G}\times \mathbb {R}$
) are acted transitively by the larger group $\mathsf {G}\times \mathbb {R}$![]() (respectively $\mathsf {G}\times \mathsf {U}(1)$
(respectively $\mathsf {G}\times \mathsf {U}(1)$![]() ), and any metric $ {\mathbb g}= {\mathbb g}(f,\,h)$
), and any metric $ {\mathbb g}= {\mathbb g}(f,\,h)$![]() is invariant under this action if and only if the functions $f$
is invariant under this action if and only if the functions $f$![]() and $h$
and $h$![]() are constant. This completes the proof of theorem A.
are constant. This completes the proof of theorem A.
Remark 4.4 By propositions 4.1 and 4.3, the compact complex manifolds $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() admit cohomogeneity one, strictly locally conformally Kähler metrics that are non-Vaisman. Remarkably, in the homogeneous case, this is excluded by [Reference Gauduchon, Moroianu and Ornea25, Reference Hasegawa and Kamishima29]. We stress that the Hopf manifold, which is the main example of Vaisman manifold [Reference Ornea and Verbitsky44], corresponds, in our notation, to $(M_{(3,1)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
admit cohomogeneity one, strictly locally conformally Kähler metrics that are non-Vaisman. Remarkably, in the homogeneous case, this is excluded by [Reference Gauduchon, Moroianu and Ornea25, Reference Hasegawa and Kamishima29]. We stress that the Hopf manifold, which is the main example of Vaisman manifold [Reference Ornea and Verbitsky44], corresponds, in our notation, to $(M_{(3,1)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() with $\mathsf {G}=\mathsf {SU}(m)$
with $\mathsf {G}=\mathsf {SU}(m)$![]() and $\mathsf {K}=\mathsf {S}(\mathsf {U}(1)\times \mathsf {U}(m-1))$
and $\mathsf {K}=\mathsf {S}(\mathsf {U}(1)\times \mathsf {U}(m-1))$![]() , see example 3.8.
, see example 3.8.
Remark 4.5 The locally conformally Kähler metrics by proposition 4.1 include the globally conformally Kähler, Einstein metrics by Bérard-Bergery [Reference Bérard-Bergery9, théorème 1.10]. We also recall that Einstein, locally conformally Käher, non-Kähler metrics are completed classified by [Reference Derdziński and Maschler18, Reference LeBrun36, Reference Madani, Moroianu and Pilca38], and they are either the Einstein, globally conformally Kähler metrics by [Reference Bérard-Bergery9], or they are defined on $\mathbb {C} \mathbb {P}^{2}$![]() by blowing up one or two points.
by blowing up one or two points.
4.2 Proof of theorem B
We begin by characterizing the Gauduchon condition as follows.
Proposition 4.6 A cohomogeneity one Hermitian metric $ {\mathbb g}$![]() of submersion-type on the complex manifolds $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
of submersion-type on the complex manifolds $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() is Gauduchon if and only if it satisfies
is Gauduchon if and only if it satisfies
Moreover, if $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() has singular orbits, then $ {\mathbb g}$
has singular orbits, then $ {\mathbb g}$![]() is Gauduchon if and only if it is Kähler.
is Gauduchon if and only if it is Kähler.
Proof. Let $(\tilde {e}_{\alpha })$![]() be a $Q_{\mathfrak {p}}$
be a $Q_{\mathfrak {p}}$![]() -orthonormal basis for $\mathfrak {p}$
-orthonormal basis for $\mathfrak {p}$![]() . Then, a straightforward computation based on equation (4.1) yields
. Then, a straightforward computation based on equation (4.1) yields

and so $ {\mathbb g}$![]() is Gauduchon if and only if
is Gauduchon if and only if

Since $f(r),\, h(r)$![]() are positive for any $r \in I$
are positive for any $r \in I$![]() and
and

it follows that $ {\mathbb g}$![]() is Gauduchon if and only if equation (4.2) is satisfied.
is Gauduchon if and only if equation (4.2) is satisfied.
Let us assume now that $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() has a singular orbit, that is $i=2$
has a singular orbit, that is $i=2$![]() or $i=4$
or $i=4$![]() . Then, the smoothness conditions at $r=0$
. Then, the smoothness conditions at $r=0$![]() imply that $k=0$
imply that $k=0$![]() in equation (4.2). Therefore, in this case, $ {\mathbb g}$
in equation (4.2). Therefore, in this case, $ {\mathbb g}$![]() is Gauduchon if and only if it is Kähler.
is Gauduchon if and only if it is Kähler.
Since the balanced condition is equivalent to $\vartheta =0$![]() , from proposition 3.17 and equation (3.11) we immediately get
, from proposition 3.17 and equation (3.11) we immediately get
Corollary 4.7 A cohomogeneity one Hermitian metric $ {\mathbb g}$![]() of submersion-type on the complex manifolds $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
of submersion-type on the complex manifolds $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() is balanced if and only if it is Kähler.
is balanced if and only if it is Kähler.
Remark 4.8 In particular, in view of [Reference Yang and Zheng58, theorem 1.3], in the non-Kähler case, both the Levi-Civita and the Chern connections cannot be Kähler-like in the sense of [Reference Gray26, Reference Yang and Zheng58], namely, they do not satisfy the same symmetries as in the Kähler case.
Concerning the pluriclosed condition, a tedious but straightforward computation (see Appendix A) shows that

where $\rho (X,\,Y) = Q_{\mathfrak {p}}(JX,\,Y)$![]() is again the $\mathsf {G}$
is again the $\mathsf {G}$![]() -invariant Kähler–Einstein form on $P$
-invariant Kähler–Einstein form on $P$![]() . Hence, together with equation (3.11), this proves the following
. Hence, together with equation (3.11), this proves the following
Corollary 4.9 A cohomogeneity one Hermitian metric $ {\mathbb g}$![]() of submersion-type on the complex manifolds $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
of submersion-type on the complex manifolds $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() is pluriclosed if and only if it is Kähler.
is pluriclosed if and only if it is Kähler.
which completes the proof of theorem B.
5. Constant Chern-scalar curvature and second-Chern–Einstein metrics
In this section, we investigate the existence of second-Chern–Einstein metrics and of metrics with constant Chern-scalar curvature on the Bérard-Bergery standard cohomogeneity one Hermitian manifolds. In particular, we first prove a local existence and uniqueness result for second-Chern–Einstein metrics with prescribed Chern-scalar curvature. Then, we prove theorems C and D.
5.1 The second-Chern–Einstein equations
Let $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J},\, {\mathbb g})$![]() be a Bérard-Bergery standard cohomogeneity one Hermitian manifold and fix a unit speed geodesic $\gamma :\overline {I} \to M$
be a Bérard-Bergery standard cohomogeneity one Hermitian manifold and fix a unit speed geodesic $\gamma :\overline {I} \to M$![]() which intersects orthogonally any $\mathsf {G}$
which intersects orthogonally any $\mathsf {G}$![]() -orbit. Then, by means of proposition 3.15, the second-Chern–Einstein equation
-orbit. Then, by means of proposition 3.15, the second-Chern–Einstein equation
becomes

where $\lambda : I \to \mathbb {R}$![]() is an admissible function (see remark 3.10). Note that, in this case, it holds that $\lambda =\operatorname {scal}^{\rm Ch}( {\mathbb g})$
is an admissible function (see remark 3.10). Note that, in this case, it holds that $\lambda =\operatorname {scal}^{\rm Ch}( {\mathbb g})$![]() .
.
Our first result in this section concerns the local existence and uniqueness of second-Chern–Einstein metrics, with prescribed Chern-scalar curvature, in a neighbourhood of a singular orbit. More precisely
Theorem 5.1 Assume that the complex manifold $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() has a singular orbit, corresponding to the value $r=0$
has a singular orbit, corresponding to the value $r=0$![]() of the orthogonal geodesic $\gamma$
of the orthogonal geodesic $\gamma$![]() . For any constant $a \in \mathbb {R}_{>0}$
. For any constant $a \in \mathbb {R}_{>0}$![]() and for any admissible function $\lambda : I \to \mathbb {R}$
and for any admissible function $\lambda : I \to \mathbb {R}$![]() , there exist $\varepsilon >0$
, there exist $\varepsilon >0$![]() and two smooth functions $f,\,h : [0,\,\varepsilon ) \to \mathbb {R}$
and two smooth functions $f,\,h : [0,\,\varepsilon ) \to \mathbb {R}$![]() satisfying the following conditions:
satisfying the following conditions:
(I) $f,\,h$
 solve the second-Chern–Einstein equations (5.1);
solve the second-Chern–Einstein equations (5.1);(II) $f,\,h$
 determine a smooth Hermitian metric $ {\mathbb g}= {\mathbb g}(f,\,h)$
determine a smooth Hermitian metric $ {\mathbb g}= {\mathbb g}(f,\,h)$ on the open set
\[ \mathcal{U}^{\rm reg}_{\varepsilon} := \bigcup_{r \in (0,\varepsilon)} \mathsf{G} \cdot \gamma(r) \subset M_{(i,n)}(\mathsf{G},\mathsf{K})^{\rm reg} \]which extends smoothly over the singular orbit $\mathsf {G} \cdot \gamma (0);$
on the open set
\[ \mathcal{U}^{\rm reg}_{\varepsilon} := \bigcup_{r \in (0,\varepsilon)} \mathsf{G} \cdot \gamma(r) \subset M_{(i,n)}(\mathsf{G},\mathsf{K})^{\rm reg} \]which extends smoothly over the singular orbit $\mathsf {G} \cdot \gamma (0);$

(III) $h(0)=a$
 and the Chern-scalar curvature of $ {\mathbb g}$
and the Chern-scalar curvature of $ {\mathbb g}$ verifies $\operatorname {scal}^{\rm Ch}( {\mathbb g})(r)=\lambda (r)$
verifies $\operatorname {scal}^{\rm Ch}( {\mathbb g})(r)=\lambda (r)$ for any $r \in [0,\,\varepsilon )$
for any $r \in [0,\,\varepsilon )$ .
.
Moreover, it holds that:
• if there exist $\tilde {\varepsilon }\geq \varepsilon$
 and $\tilde {f},\,\tilde {h} : [0,\,\tilde {\varepsilon }) \to \mathbb {R}$
and $\tilde {f},\,\tilde {h} : [0,\,\tilde {\varepsilon }) \to \mathbb {R}$ satisfying the conditions (I), (II), (III) above, then $\tilde {f}(r)=f(r)$
satisfying the conditions (I), (II), (III) above, then $\tilde {f}(r)=f(r)$ and $\tilde {h}(r)=h(r)$
and $\tilde {h}(r)=h(r)$ for any $r \in [0,\,\varepsilon );$
for any $r \in [0,\,\varepsilon );$
• $f,\,h$
 depends continuously on the data $a,\, \lambda$
depends continuously on the data $a,\, \lambda$ .
.
Proof. Fix a positive number $a>0$![]() and an admissible function $\lambda : I \to \mathbb {R}$
and an admissible function $\lambda : I \to \mathbb {R}$![]() . Let us write
. Let us write
Then, a straightforward computation shows that equations (5.1) become

with

Moreover, the smoothness conditions for the functions $f$![]() and $h$
and $h$![]() , together with the equation $h(0)=a$
, together with the equation $h(0)=a$![]() , imply that
, imply that
We stress now that the following conditions are satisfied:
• the function $N=N(r,\,v)$
 is smooth in a neighbourhood of $(0,\,v_{\operatorname {o}})$
is smooth in a neighbourhood of $(0,\,v_{\operatorname {o}})$ ,
,• $A \cdot v_{\operatorname {o}} = 0$
 ,
,• $\det (A -k \operatorname {Id}_4) \neq 0$
 for any integer $k\geq 1$
for any integer $k\geq 1$ .
.
Then, by the Malgrange theorem [Reference Malgrange39, theorem 7.1], see also [Reference Böhm14, theorem 2.2], there exists a unique solution $v(r)$![]() , defined on an interval $(-\varepsilon,\,\varepsilon )$
, defined on an interval $(-\varepsilon,\,\varepsilon )$![]() , to equation (5.3) with initial condition (5.4), which depends continuously on the data $a$
, to equation (5.3) with initial condition (5.4), which depends continuously on the data $a$![]() , $\lambda$
, $\lambda$![]() .
.
By equation (5.2), we obtain a pair $(f,\,h)$![]() of smooth functions $f,\,h : (-\varepsilon,\,\varepsilon ) \to \mathbb {R}$
of smooth functions $f,\,h : (-\varepsilon,\,\varepsilon ) \to \mathbb {R}$![]() which satisfy equations (5.1) such that
which satisfy equations (5.1) such that
Since the pair $(\hat {f},\,\hat {h})$![]() of functions defined by
of functions defined by
satisfy equations (5.1) with the initial conditions (5.5), by uniqueness we conclude that $f$![]() is odd and $h$
is odd and $h$![]() is even. Therefore, these functions give rise to a smooth Hermitian metric $ {\mathbb g}= {\mathbb g}(f,\,h)$
is even. Therefore, these functions give rise to a smooth Hermitian metric $ {\mathbb g}= {\mathbb g}(f,\,h)$![]() on the open set $\mathcal {U}^{\rm reg}_{\varepsilon } \subset M_{(i,n)}(\mathsf {G},\,\mathsf {K})^{\rm reg}$
on the open set $\mathcal {U}^{\rm reg}_{\varepsilon } \subset M_{(i,n)}(\mathsf {G},\,\mathsf {K})^{\rm reg}$![]() , which admits a unique smooth extension over the singular orbit $\mathsf {G} \cdot \gamma (0)$
, which admits a unique smooth extension over the singular orbit $\mathsf {G} \cdot \gamma (0)$![]() .
.
Concerning complete solutions to equations (5.1), we point out the following
Remark 5.2 Fundamental examples of complete, non-Kähler, second-Chern– Einstein metrics can be easily found on the manifolds $(M_{(1,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() and $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
and $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() . Indeed, the constant functions
. Indeed, the constant functions
verify the smoothness conditions in case $i=1,\,3$![]() and so they give rise to homogeneous, smooth metrics which are non-Kähler by equation (3.11) and second-Chern–Einstein by equation (5.1) with constant Chern-scalar curvature $\lambda =4m(m-1)$
and so they give rise to homogeneous, smooth metrics which are non-Kähler by equation (3.11) and second-Chern–Einstein by equation (5.1) with constant Chern-scalar curvature $\lambda =4m(m-1)$![]() . These examples include the standard metric on the linear Hopf manifold (see example 3.8).
. These examples include the standard metric on the linear Hopf manifold (see example 3.8).
We also stress that, on manifolds $(M_{(1,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() and $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
and $(M_{(3,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() , all the metrics (not necessarily of cohomogeneity one) in the conformal class of $ {\mathbb g}= {\mathbb g}(f,\,h)$
, all the metrics (not necessarily of cohomogeneity one) in the conformal class of $ {\mathbb g}= {\mathbb g}(f,\,h)$![]() , with $f,\,h$
, with $f,\,h$![]() given by formula (5.6), are second-Chern–Einstein (see remark 2.4). In particular, by remark 3.11, for any admissible positive function $\phi : I \to \mathbb {R}$
given by formula (5.6), are second-Chern–Einstein (see remark 2.4). In particular, by remark 3.11, for any admissible positive function $\phi : I \to \mathbb {R}$![]() , the pair
, the pair
solve equations (5.1) with Chern-scalar curvature $\lambda (r) = 2m\big(-\frac {\phi ''(r)}{\phi (r)} +2(m-1)\frac {\phi '(r)+1}{\phi (r)}\big)$![]() . Therefore, in the following, we will focus on Bérard-Bergery manifolds $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
. Therefore, in the following, we will focus on Bérard-Bergery manifolds $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() with singular orbits, namely, the cases $i=2$
with singular orbits, namely, the cases $i=2$![]() and $i=4$
and $i=4$![]() .
.
5.2 Complete second-Chern–Einstein metrics in case of singular orbits
In this section, we will construct complete second-Chern–Einstein metrics on the manifolds $(M_{(2,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() by using the same technique as [Reference Bérard-Bergery9, § 11].
by using the same technique as [Reference Bérard-Bergery9, § 11].
Let us start by noticing that, for the manifold $\mathcal {O}_{\mathbb {C}\mathbb {P}^{m-1}}(-1)$![]() , the functions
, the functions
solve the second-Chern–Einstein equations (5.1) and define Hermitian metrics $ {\mathbb g}_k= {\mathbb g}(f,\,h_k)$![]() which extend smoothly over the singular orbit. All the metrics $ {\mathbb g}_k$
which extend smoothly over the singular orbit. All the metrics $ {\mathbb g}_k$![]() are non-Kähler and their Chern-scalar curvatures are given by
are non-Kähler and their Chern-scalar curvatures are given by
Note that all these metrics are homothetic, indeed the satisfy $ {\mathbb g}_k = k^{2} {\mathbb g}_1$![]() (see remark 3.11). More in general, we have
(see remark 3.11). More in general, we have
Theorem 5.3 All the complex manifolds $(M_{(2,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() have a complete, Hermitian, non-Kähler, second-Chern–Einstein, cohomogeneity one metric.
have a complete, Hermitian, non-Kähler, second-Chern–Einstein, cohomogeneity one metric.
Proof. Fix a manifold $(M_{(2,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() and set
and set
for some smooth, positive, increasing function $\phi : [0,\,+\infty ) \to \mathbb {R}$![]() . Note that, in this case
. Note that, in this case
and so this metric is necessarily non-Kähler by equation (3.11). Setting the initial condition $h(0)=1$![]() , second-Chern–Einstein equations (5.1) become
, second-Chern–Einstein equations (5.1) become

Cauchy problem (5.10) admits a unique smooth solution on some interval $[0,\,\varepsilon )$![]() , which extends to an even smooth function on $(-\varepsilon,\,\varepsilon )$
, which extends to an even smooth function on $(-\varepsilon,\,\varepsilon )$![]() . Let us prove that this solution can be extended to the whole $[0,\,+\infty )$
. Let us prove that this solution can be extended to the whole $[0,\,+\infty )$![]() .
.
Assume that the solution to equation (5.10) is of the form
Then, from equations (5.10) and (5.11), we get the following Cauchy problem for $u(t)$![]() :
:

The unique solution to equation (5.12) is the function $u: [1,\,+\infty ) \to \mathbb {R}$![]() defined by
defined by
which is smooth, positive and increasing. Hence, the function
is smooth, positive, increasing and, by construction, its inverse $\phi := \varphi ^{-1}$![]() solves the Cauchy problem (5.10). Therefore, by means of equation (5.9), the proof is completed.
solves the Cauchy problem (5.10). Therefore, by means of equation (5.9), the proof is completed.
Remark 5.4 The Chern-scalar curvature of the metric $ {\mathbb g}_{\phi }= {\mathbb g}(f_{\phi },\,h_{\phi })$![]() constructed from equation (5.9) by solving Cauchy problem (5.10) is given by
constructed from equation (5.9) by solving Cauchy problem (5.10) is given by

Note that, if $mn-p=0$![]() , which correspond to the manifolds $\mathcal {O}_{\mathbb {C}\mathbb {P}^{m-1}}(-1)$
, which correspond to the manifolds $\mathcal {O}_{\mathbb {C}\mathbb {P}^{m-1}}(-1)$![]() , function (5.13) is $u(t)=4(t-1)$
, function (5.13) is $u(t)=4(t-1)$![]() . Hence, we recover the family of examples introduced in formula (5.8).
. Hence, we recover the family of examples introduced in formula (5.8).
Finally we observe that, concerning the compact simply-connected manifolds $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() , we have the following
, we have the following
Proposition 5.5 On the complex manifolds $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() there are no cohomogeneity one, submersion-type Hermitian metrics that are second-Chern–Einstein.
there are no cohomogeneity one, submersion-type Hermitian metrics that are second-Chern–Einstein.
Proof. Assume that there exists cohomogeneity one, submersion-type Hermitian metric $ {\mathbb g}$![]() on a complex manifold $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
on a complex manifold $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() which is second-Chern–Einstein. Then, by corollary 4.2, it is globally conformally Kähler. By remark 2.4, this implies the existence of a Kähler–Einstein metric on $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
which is second-Chern–Einstein. Then, by corollary 4.2, it is globally conformally Kähler. By remark 2.4, this implies the existence of a Kähler–Einstein metric on $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() , that is not possible (see [Reference Bérard-Bergery9, remarques 8.14, (1)] and [Reference Besse10, remarks 9.126, (b)]).
, that is not possible (see [Reference Bérard-Bergery9, remarques 8.14, (1)] and [Reference Besse10, remarks 9.126, (b)]).
Remark 5.6 The projective space $\mathbb {C}\mathbb {P}^{m}$![]() is a standard cohomogeneity one manifold with respect to the action of $\mathsf {G}= \mathsf {SU}(m)$
is a standard cohomogeneity one manifold with respect to the action of $\mathsf {G}= \mathsf {SU}(m)$![]() given by $a \cdot [z^{0} : z] := [z^{0} : a \cdot z] \,.$
given by $a \cdot [z^{0} : z] := [z^{0} : a \cdot z] \,.$![]() Even if it is not a Berard–Bérgéry manifold according to definition 3.7, all the formulas in § 3 and § 4 still apply to this specific case. In particular, all the $\mathsf {G}$
Even if it is not a Berard–Bérgéry manifold according to definition 3.7, all the formulas in § 3 and § 4 still apply to this specific case. In particular, all the $\mathsf {G}$![]() -invariant metrics on $\mathbb {C}\mathbb {P}^{m}$
-invariant metrics on $\mathbb {C}\mathbb {P}^{m}$![]() are of the form (3.10) with $n=1$
are of the form (3.10) with $n=1$![]() and $p=m$
and $p=m$![]() , where $f,\,h: [0,\,\frac {\pi }2] \to \mathbb {R}$
, where $f,\,h: [0,\,\frac {\pi }2] \to \mathbb {R}$![]() are smooth, positive function satisfying:
are smooth, positive function satisfying:
• $f$
 is the restriction of a smooth odd function on $\mathbb {R}$
is the restriction of a smooth odd function on $\mathbb {R}$ satisfying
\[ f\left(r+\frac{\pi}2\right) =-f\left(r-\frac{\pi}2\right) \quad \text{ and } \quad f'(0)=1=-f'\left(\frac{\pi}2\right); \]
satisfying
\[ f\left(r+\frac{\pi}2\right) =-f\left(r-\frac{\pi}2\right) \quad \text{ and } \quad f'(0)=1=-f'\left(\frac{\pi}2\right); \]
• $h$
 is the restriction of a smooth even function on $\mathbb {R}$
is the restriction of a smooth even function on $\mathbb {R}$ satisfying
\[ h\left(r+\frac{\pi}2\right) =-h\left(r-\frac{\pi}2\right) \quad \text{ and } \quad h'\left(\frac{\pi}2\right)=-1 \,. \]
satisfying
\[ h\left(r+\frac{\pi}2\right) =-h\left(r-\frac{\pi}2\right) \quad \text{ and } \quad h'\left(\frac{\pi}2\right)=-1 \,. \]
Note that the Fubini–Study metric $ {\mathbb g}_{\rm FS}$![]() with sectional curvature $1 \leq \sec \leq 4$
with sectional curvature $1 \leq \sec \leq 4$![]() corresponds to the functions
corresponds to the functions
As argued in the proof of proposition 5.5, all the $\mathsf {G}$![]() -invariant second-Chern–Einstein metrics on $\mathbb {C}\mathbb {P}^{m}$
-invariant second-Chern–Einstein metrics on $\mathbb {C}\mathbb {P}^{m}$![]() are necessarily conformal to the Fubini–Study metric $ {\mathbb g}_{\rm FS}$
are necessarily conformal to the Fubini–Study metric $ {\mathbb g}_{\rm FS}$![]() . For example, the functions
. For example, the functions
define non-Kähler, second-Chern–Einstein metrics $ {\mathbb g}_k$![]() on $\mathbb {C}\mathbb {P}^{m}$
on $\mathbb {C}\mathbb {P}^{m}$![]() of the form
of the form
5.3 Constant Chern-scalar curvature metrics in case of singular orbits
In this section, we construct complete constant Chern-scalar curvature metrics $ {\mathbb g}= {\mathbb g}(f,\,h)$![]() on the complex manifolds $(M_{(2,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
on the complex manifolds $(M_{(2,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() and $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
and $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() by using again the technique exploited in [Reference Bérard-Bergery9, § 11].
by using again the technique exploited in [Reference Bérard-Bergery9, § 11].
Fix a complex manifold $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() , with $i\in \{2,\,4\}$
, with $i\in \{2,\,4\}$![]() , and set
, and set
for some smooth, increasing, positive, function $\phi : I \to \mathbb {R}$![]() . Note that, in this case,
. Note that, in this case,
and so this metric is necessarily non-Kähler by equation (3.11). Let $c \in \mathbb {R}$![]() to be fixed later. Then, the constant Chern-scalar curvature equation
to be fixed later. Then, the constant Chern-scalar curvature equation
for the metric $ {\mathbb g}_{\phi } := {\mathbb g}(f_{\phi },\,h_{\phi })$![]() becomes
becomes
We look for a solution of the form
for some smooth real function $u=u(t)$![]() . Then, we get the following ODE
. Then, we get the following ODE
which can be explicitly integrated. Indeed, the following cases occur.
• If $m=2$
 , then the solutions to equation (5.17) are
(5.18)\begin{equation} u_{a,b,c}(t) = at^{-4} -2 +bt-\frac{c}6t^{2}, \quad \text{with } a,b \in \mathbb{R} . \end{equation}In this case, the base space of the fibration $M_{(i,n)}(\mathsf {G},\,\mathsf {K}) \to P$
, then the solutions to equation (5.17) are
(5.18)\begin{equation} u_{a,b,c}(t) = at^{-4} -2 +bt-\frac{c}6t^{2}, \quad \text{with } a,b \in \mathbb{R} . \end{equation}In this case, the base space of the fibration $M_{(i,n)}(\mathsf {G},\,\mathsf {K}) \to P$
 is necessarily $P=\mathbb {C} \mathbb {P}^{1}$
is necessarily $P=\mathbb {C} \mathbb {P}^{1}$ and so $p=2$
and so $p=2$ .
.• If $m=3$
 , then the solutions to equation (5.17) are
(5.19)\begin{equation} u_{a,b,c}(t) = at^{-6} -2 +bt^{2}-\frac{c}8\log(t)t^{2},\quad \text{with } a,b \in \mathbb{R}. \end{equation}In this case, the only possibilities for the base space of the fibration $M_{(i,n)}(\mathsf {G},\,\mathsf {K}) \to P$
, then the solutions to equation (5.17) are
(5.19)\begin{equation} u_{a,b,c}(t) = at^{-6} -2 +bt^{2}-\frac{c}8\log(t)t^{2},\quad \text{with } a,b \in \mathbb{R}. \end{equation}In this case, the only possibilities for the base space of the fibration $M_{(i,n)}(\mathsf {G},\,\mathsf {K}) \to P$
 are
\[ P=\mathbb{C} \mathbb{P}^{2} = \mathsf{SU}(3)/\mathsf{S}(\mathsf{U}(1){\times}\mathsf{U}(2)), \quad P={\rm Gr}(2,\mathbb{R}^{5}) = \mathsf{Sp}(2)/\mathsf{U}(2) \]and so $p=3$
are
\[ P=\mathbb{C} \mathbb{P}^{2} = \mathsf{SU}(3)/\mathsf{S}(\mathsf{U}(1){\times}\mathsf{U}(2)), \quad P={\rm Gr}(2,\mathbb{R}^{5}) = \mathsf{Sp}(2)/\mathsf{U}(2) \]and so $p=3$
 .
.• If $m>3$
 , then the solutions to equation (5.17) are given by
(5.20)\begin{equation} u_{a,b,c}(t) = at^{-2m} -2 +\frac{c}{2(m+1)(m-3)}t^{2} +bt^{m-1}, \quad \text{ with } a,b \in \mathbb{R}. \end{equation}
, then the solutions to equation (5.17) are given by
(5.20)\begin{equation} u_{a,b,c}(t) = at^{-2m} -2 +\frac{c}{2(m+1)(m-3)}t^{2} +bt^{m-1}, \quad \text{ with } a,b \in \mathbb{R}. \end{equation}
Then, by means of equations (5.14) and (5.16), we are able to construct constant Chern-scalar curvature metrics on the manifolds $(M_{(2,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() and $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
and $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() .
.
Theorem 5.7 Let $c \in \mathbb {R},$![]() $c\leq 0$
$c\leq 0$![]() . Then, all the complex manifolds $(M_{(2,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
. Then, all the complex manifolds $(M_{(2,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() have a complete, Hermitian, non-Kähler, cohomogeneity one metric $ {\mathbb g}$
have a complete, Hermitian, non-Kähler, cohomogeneity one metric $ {\mathbb g}$![]() with $\operatorname {scal}^{\rm Ch}( {\mathbb g})=c$
with $\operatorname {scal}^{\rm Ch}( {\mathbb g})=c$![]() .
.
Proof. Setting $h(0)=1$![]() , the smoothness conditions for $f,\,h$
, the smoothness conditions for $f,\,h$![]() imply that
imply that
Let us stress that, if there exists a smooth solution $\phi : [0,\,+\infty ) \to \mathbb {R}$![]() to equation (5.15) satisfying the boundary conditions (5.21), then it can be extended to a smooth even function on $\mathbb {R}$
to equation (5.15) satisfying the boundary conditions (5.21), then it can be extended to a smooth even function on $\mathbb {R}$![]() .
.
Note that, by means of equation (5.16), conditions (5.21) imply that the solution $u_{a,b,c}$![]() to the ODE (5.17) verifies
to the ODE (5.17) verifies
Therefore, we obtain two values $a(c) ,\,b(c)$![]() , depending on $c$
, depending on $c$![]() , by imposing conditions (5.22):
, by imposing conditions (5.22):
• if $m=2$
 , then by formula (5.18) we get
\[ a(c):= \frac 25-\frac{c}{30}-\frac 45n , \quad b(c):= \frac 85+\frac{c}5+\frac 45n; \]
, then by formula (5.18) we get
\[ a(c):= \frac 25-\frac{c}{30}-\frac 45n , \quad b(c):= \frac 85+\frac{c}5+\frac 45n; \]
• if $m=3$
 , then by formula (5.19) we get
\[ a(c):= \frac 12-\frac{c}{64}-\frac{n}2, \quad b(c):= \frac 32+\frac{c}{64}+\frac{n}2; \]
, then by formula (5.19) we get
\[ a(c):= \frac 12-\frac{c}{64}-\frac{n}2, \quad b(c):= \frac 32+\frac{c}{64}+\frac{n}2; \]
• if $m>3$
 , then by formula (5.20) we get
\begin{align*} a(c) & := -\frac{(m+1)(4m(2n-p)+4p)+cp}{2p(m+1)(3m-1)}, \\ b(c) & := \frac{4m(m-3)(n+p)-cp}{p(3m-1)(m-3)}. \end{align*}
, then by formula (5.20) we get
\begin{align*} a(c) & := -\frac{(m+1)(4m(2n-p)+4p)+cp}{2p(m+1)(3m-1)}, \\ b(c) & := \frac{4m(m-3)(n+p)-cp}{p(3m-1)(m-3)}. \end{align*}
In all of these three cases it can be directly checked that, for any $c\leq 0$![]() , the function $u_c := u_{a(c),b(c),c}$
, the function $u_c := u_{a(c),b(c),c}$![]() is positive and increasing for $t \in (1,\,+\infty )$
is positive and increasing for $t \in (1,\,+\infty )$![]() . Indeed, by means of conditions (5.22), there exists $\varepsilon _{\operatorname {o}}>0$
. Indeed, by means of conditions (5.22), there exists $\varepsilon _{\operatorname {o}}>0$![]() such that $u_c(t)>0$
such that $u_c(t)>0$![]() and $u'_c(t)>0$
and $u'_c(t)>0$![]() for any $t \in (1,\,1+\varepsilon _{\operatorname {o}})$
for any $t \in (1,\,1+\varepsilon _{\operatorname {o}})$![]() . Assume by contradiction that there exists $t_{\operatorname {o}}>1$
. Assume by contradiction that there exists $t_{\operatorname {o}}>1$![]() such that $u'_c(t)>0$
such that $u'_c(t)>0$![]() for any $t \in [1,\,t_{\operatorname {o}})$
for any $t \in [1,\,t_{\operatorname {o}})$![]() and $u'_c(t_{\operatorname {o}})=0$
and $u'_c(t_{\operatorname {o}})=0$![]() . Then, $t_{\operatorname {o}}$
. Then, $t_{\operatorname {o}}$![]() is a local maximum point or a stationary point of inflection for $u(t)$
is a local maximum point or a stationary point of inflection for $u(t)$![]() , but equation (5.17) implies that
, but equation (5.17) implies that
which is not possible. Hence
is smooth, increasing and, by construction, its inverse $\phi _c := \varphi _c^{-1}$![]() solves equation (5.15) with the initial conditions (5.21).
solves equation (5.15) with the initial conditions (5.21).
Constant Chern-scalar curvature metrics on Hirzebruch surfaces have been constructed by Koca and Lejmi by using the Bérard-Bergery ansatz in [Reference Koca and Lejmi33, theorem 1]. Since in complex dimension $m=2$![]() the complex manifolds $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
the complex manifolds $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() reduces to the Hirzebruch surfaces (see example 3.8), the next theorem extends their result to $m>2$
reduces to the Hirzebruch surfaces (see example 3.8), the next theorem extends their result to $m>2$![]() .
.
Theorem 5.8 Let $c \in \mathbb {R},$![]() $c>0$
$c>0$![]() . Then, all the complex manifolds $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$
. Then, all the complex manifolds $(M_{(4,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J})$![]() have a Hermitian, non-Kähler, cohomogeneity one metric $ {\mathbb g}$
have a Hermitian, non-Kähler, cohomogeneity one metric $ {\mathbb g}$![]() with $\operatorname {scal}^{\rm Ch}( {\mathbb g})=c$
with $\operatorname {scal}^{\rm Ch}( {\mathbb g})=c$![]() .
.
Proof. Setting $h(0)=1$![]() and $h(\pi )=k>1$
and $h(\pi )=k>1$![]() , the smoothness conditions for $f,\,h$
, the smoothness conditions for $f,\,h$![]() imply that
imply that

Let us stress that, if there exists a smooth solution $\phi : [0,\,\pi ] \to \mathbb {R}$![]() to equation (5.15) satisfying the boundary conditions (5.24), then it can be extended to a smooth even function on $\mathbb {R}$
to equation (5.15) satisfying the boundary conditions (5.24), then it can be extended to a smooth even function on $\mathbb {R}$![]() satisfying $\phi (\pi +r)=\phi (\pi -r)$
satisfying $\phi (\pi +r)=\phi (\pi -r)$![]() . Since the case $m=2$
. Since the case $m=2$![]() has already been addressed in [Reference Koca and Lejmi33], we limit ourselves to prove the statement for $m\geq 3$
has already been addressed in [Reference Koca and Lejmi33], we limit ourselves to prove the statement for $m\geq 3$![]() .
.
Assume $m=3$![]() . Then, by means of equation (5.16), conditions (5.24) imply that the solution $u_{a,b,c}$
. Then, by means of equation (5.16), conditions (5.24) imply that the solution $u_{a,b,c}$![]() given in formula (5.19) verifies
given in formula (5.19) verifies
By imposing the first three conditions
we obtain three values $a(k),\,b(k),\,c(k)$![]() depending on $k$
depending on $k$![]() , that are
, that are

Set $u_k := u_{a(k),b(k),c(k)}$![]() and observe that
and observe that
with

Note that

and so there exists $\tilde {k}>1$![]() such that $\alpha (k)>0$
such that $\alpha (k)>0$![]() for any $1< k<\tilde {k}$
for any $1< k<\tilde {k}$![]() and $\alpha (\tilde {k})=0$
and $\alpha (\tilde {k})=0$![]() . Then, we set $u := u_{\tilde {k}}$
. Then, we set $u := u_{\tilde {k}}$![]() , so that the function
, so that the function
is smooth, increasing and its inverse $\phi := \varphi ^{-1}$![]() solves the ODE (5.15) with the boundary conditions (5.24).
solves the ODE (5.15) with the boundary conditions (5.24).
Assume $m>3$![]() . Then, by means of equation (5.16), conditions (5.24) imply that the solution $u_{a,b,c}$
. Then, by means of equation (5.16), conditions (5.24) imply that the solution $u_{a,b,c}$![]() given in formula (5.19) verifies
given in formula (5.19) verifies
By imposing the first three conditions
we obtain three values $a(k),\,b(k),\,c(k)$![]() depending on $k$
depending on $k$![]() , that are
, that are

with

Set $u_k := u_{a(k),b(k),c(k)}$![]() and observe that
and observe that
where $\alpha (k),\, \beta (k)$![]() are the polynomials in $k$
are the polynomials in $k$![]() defined by
defined by

Note that $\beta (1)=0$![]() and
and
hence $\beta (k)>0$![]() for any $k>1$
for any $k>1$![]() . Moreover
. Moreover

and so there exists $\tilde {k}>1$![]() such that $\alpha (k)>0$
such that $\alpha (k)>0$![]() for any $1< k<\tilde {k}$
for any $1< k<\tilde {k}$![]() and $\alpha (\tilde {k})=0$
and $\alpha (\tilde {k})=0$![]() . Then, we set $u := u_{\tilde {k}}$
. Then, we set $u := u_{\tilde {k}}$![]() , so that the function
, so that the function
is smooth, increasing and its inverse $\phi := \varphi ^{-1}$![]() solves the ODE (5.15) with conditions (5.24).
solves the ODE (5.15) with conditions (5.24).
Finally, by means of an argument similar to the one used in the proof of theorem 5.7 (see equation (5.23)), it holds necessarily that $c>0$![]() in all the cases. This concludes the proof.
in all the cases. This concludes the proof.
Acknowledgements
The authors are warmly grateful to Christoph Böhm, Simone Calamai, Liviu Ornea, Alexandra Otiman, Fabio Podestà, Andrea Spiro, Cristiano Spotti and Luigi Verdiani for several interesting discussions and suggestions on the topic.
The authors are supported by project PRIN2017 ‘Real and Complex Manifolds: Topology, Geometry and holomorphic dynamics’ (code 2017JZ2SW5), and by GNSAGA of INdAM.
Appendix A.
In this appendix, we provide the details for the proofs of proposition 3.15 computing the Chern–Ricci tensors of Bérard-Bergery manifolds $(M_{(i,n)}(\mathsf {G},\,\mathsf {K}),\,\mathbb {J},\, {\mathbb g})$![]() , proposition 3.17 computing their torsion and the Lee form and equation (4.3) concerning the pluriclosed condition $\operatorname {d\!}\operatorname {d\!}^{\,c}\!\omega =0$
, proposition 3.17 computing their torsion and the Lee form and equation (4.3) concerning the pluriclosed condition $\operatorname {d\!}\operatorname {d\!}^{\,c}\!\omega =0$![]() .
.
Appendix A.1 Appendix A.1. Proof of proposition 3.15
Let $X,\,Y \in \mathfrak {p}$![]() be such that $Q(X,\,X)=Q(Y,\,Y)=1$
be such that $Q(X,\,X)=Q(Y,\,Y)=1$![]() and $(e_{\alpha },\,Je_{\alpha })$
and $(e_{\alpha },\,Je_{\alpha })$![]() a $(Q_{\mathfrak {p}},\,J)$
a $(Q_{\mathfrak {p}},\,J)$![]() -unitary basis for $\mathfrak {p}$
-unitary basis for $\mathfrak {p}$![]() . Set $F := \frac {2mn}{\lambda p} f$
. Set $F := \frac {2mn}{\lambda p} f$![]() . Then, by using formulas (2.4), (3.1), (3.2), (3.3), (3.4), (3.5), (3.8), (3.9), (3.10), proposition 3.3 and corollary 3.4, we get
. Then, by using formulas (2.4), (3.1), (3.2), (3.3), (3.4), (3.5), (3.8), (3.9), (3.10), proposition 3.3 and corollary 3.4, we get

Hence, we obtain

and

By the symmetries of the tensors $\operatorname {Ric}^{\rm Ch[i]}( {\mathbb g})$![]() , it holds that
, it holds that
Moreover, by a direct computation, we get

and hence
Finally, we have

Note that

Moreover, setting $(\tilde {e}_{\alpha }):= (e_{\alpha },\,Je_{\alpha })$![]() , since $[\mathfrak {p},\,\mathfrak {p}] \subset \mathfrak {k}$
, since $[\mathfrak {p},\,\mathfrak {p}] \subset \mathfrak {k}$![]() and $|X|_Q=1$
and $|X|_Q=1$![]() , by the Schur lemma we obtain
, by the Schur lemma we obtain

Hence, we get

and

which concludes the proof of equations (3.12), (3.13) and (3.14).
For what concerns the scalar curvature, we have

which proves equation (3.15).
Appendix A.2. Proof of proposition 3.17
By equation (3.16) and corollary 3.16, the only non-vanishing components of $\tau$![]() are
are

and so $\tau (N,\,T^{*})_{\gamma (r)}=\tau (X^{*},\,Y^{*})_{\gamma (r)}=0$![]() . Moreover, letting $(e_\alpha,\, Je_a)$
. Moreover, letting $(e_\alpha,\, Je_a)$![]() be a $(Q_\mathfrak {p},\, J)$
be a $(Q_\mathfrak {p},\, J)$![]() -unitary basis for $\mathfrak {p}$
-unitary basis for $\mathfrak {p}$![]() , we get
, we get

Therefore, by equations (3.2) and (3.4), it follows that

Finally

and analogously one can show that $\vartheta (T^{*})_{\gamma (r)} = \vartheta (X^{*})_{\gamma (r)} = 0$![]() , which concludes the proof.
, which concludes the proof.
Appendix A.3. Proof of equation (4.3)
Let us compute $\operatorname {d\!}\operatorname {d\!}^{\,c}\!\omega$![]() . Since $\mathbb {J} \omega =\omega$
. Since $\mathbb {J} \omega =\omega$![]() , it follows that
, it follows that
and so

If $A$![]() is a holomorphic Killing vector field, then $\mathcal {L}_A\operatorname {d\!}\omega = \operatorname {d\!}\mathcal {L}_A\omega =0$
is a holomorphic Killing vector field, then $\mathcal {L}_A\operatorname {d\!}\omega = \operatorname {d\!}\mathcal {L}_A\omega =0$![]() and so
and so
Therefore, if $A,\,B,\,C,\,D$![]() are holomorphic Killing, we get
are holomorphic Killing, we get

Letting $\rho (X,\,Y) = Q_{\mathfrak {p}}(JX,\,Y)$![]() , we have
, we have

and so, by using proposition 3.2 and equations (3.8), (3.10) we get

which concludes the proof.