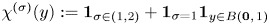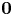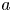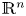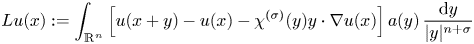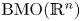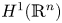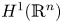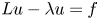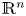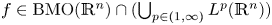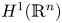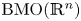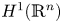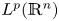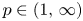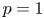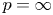On BMO and Hardy regularity estimates for a class of non-local elliptic equations

Wenxian Ma; Sibei Yang

doi:10.1017/prm.2022.82

On BMO and Hardy regularity estimates for a class of non-local elliptic equations

Part of: Special classes of linear operators Partial differential equations Harmonic analysis in several variables Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press: 14 December 2022

Wenxian Ma and

Sibei Yang

Show author details

Wenxian Ma: Affiliation:
School of Mathematics and Statistics, Gansu Key Laboratory of Applied Mathematics and Complex Systems, Lanzhou University, Lanzhou 730000, People's Republic of China (mawx2021@lzu.edu.cn; yangsb@lzu.edu.cn)
Sibei Yang: Affiliation:
School of Mathematics and Statistics, Gansu Key Laboratory of Applied Mathematics and Complex Systems, Lanzhou University, Lanzhou 730000, People's Republic of China (mawx2021@lzu.edu.cn; yangsb@lzu.edu.cn)

Article contents

Abstract
Introduction
Preliminaries
Proofs of theorems and
References

Rights & Permissions

Abstract

Let $\sigma \in (0,\,2)$, $\chi ^{(\sigma )}(y):={\mathbf 1}_{\sigma \in (1,2)}+{\mathbf 1}_{\sigma =1} {\mathbf 1}_{y\in B(\mathbf {0},\,1)}$, where $\mathbf {0}$ denotes the origin of $\mathbb {R}^n$, and $a$ be a non-negative and bounded measurable function on $\mathbb {R}^n$. In this paper, we obtain the boundedness of the non-local elliptic operator

\[ Lu(x):=\int_{\mathbb{R}^n}\left[u(x+y)-u(x)-\chi^{(\sigma)}(y)y\cdot\nabla u(x)\right]a(y)\,\frac{{\rm d}y}{|y|^{n+\sigma}} \]

from the Sobolev space based on $\mathrm {BMO}(\mathbb {R}^n)\cap (\bigcup _{p\in (1,\infty )}L^p(\mathbb {R}^n))$

to the space $\mathrm {BMO}(\mathbb {R}^n)$

, and from the Sobolev space based on the Hardy space $H^1(\mathbb {R}^n)$

to $H^1(\mathbb {R}^n)$

. Moreover, for any $\lambda \in (0,\,\infty )$

, we also obtain the unique solvability of the non-local elliptic equation $Lu-\lambda u=f$

in $\mathbb {R}^n$

, with $f\in \mathrm {BMO}(\mathbb {R}^n)\cap (\bigcup _{p\in (1,\infty )}L^p(\mathbb {R}^n))$

or $H^1(\mathbb {R}^n)$

, in the Sobolev space based on $\mathrm {BMO}(\mathbb {R}^n)$

or $H^1(\mathbb {R}^n)$

. The boundedness and unique solvability results given in this paper are further devolvement for the corresponding results in the scale of the Lebesgue space $L^p(\mathbb {R}^n)$

with $p\in (1,\,\infty )$

, established by H. Dong and D. Kim [J. Funct. Anal. 262 (2012), 1166–1199], in the endpoint cases of $p=1$

and $p=\infty$

Keywords

Non-local elliptic equation BMO space Hardy space Bessel potential space solvability

MSC classification

Primary: 35R11: Fractional partial differential equations

Secondary: 47B38: Operators on function spaces (general) 35B65: Smoothness and regularity of solutions 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.) 42B35: Function spaces arising in harmonic analysis

Type: Research Article
Information: Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 6 , December 2023 , pp. 2025 - 2052

DOI: https://doi.org/10.1017/prm.2022.82 [Opens in a new window]
Copyright: Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

1. Introduction

Let $n\ge 1$, $\sigma \in (0,\,2)$, $\chi ^{(\sigma )}(y):={\mathbf 1}_{\sigma \in (1,2)}+{\mathbf 1}_{\sigma =1} {\mathbf 1}_{y\in B(\mathbf {0},\,1)}$, where $\mathbf {0}$ denotes the origin of $\mathbb {R}^n$, and $a$ be a non-negative and bounded measurable function on ${\mathbb {R}^n}$. In this paper, we first consider the boundedness of the non-local elliptic operator

(1.1)\begin{equation} Lu(x):=\int_{{{\mathbb{R}}}^n}\left[u(x+y)-u(x)-\chi^{(\sigma)}(y)y\cdot\nabla u(x)\right]a(y)\,\frac{{\rm d}y}{|y|^{n+\sigma}} \end{equation}

from the Sobolev space based on $\mathrm {BMO}(\mathbb {R}^n)\cap (\bigcup _{p\in (1,\infty )}L^p(\mathbb {R}^n))$ to the BMO (bounded mean oscillation) space $\mathrm {BMO}(\mathbb {R}^n)$, and from the Sobolev space based on the Hardy space $H^1(\mathbb {R}^n)$ to $H^1(\mathbb {R}^n)$. Assume further that $\lambda \in (0,\,\infty )$, $p\in (1,\,\infty )$, and $f$ belongs to $L^p({\mathbb {R}^n})\cap \mathrm {BMO}({\mathbb {R}^n})$ or the Hardy space $H^1({\mathbb {R}^n})$, we also investigate the unique solvability of the non-local elliptic equation

(1.2)\begin{equation} Lu-\lambda u=f \end{equation}

in the Sobolev space based on $\mathrm {BMO}(\mathbb {R}^n)$ or $H^1(\mathbb {R}^n)$. The results obtained in this paper are further devolvement of the corresponding results in the scale of the Lebesgue space $L^p(\mathbb {R}^n)$ with $p\in (1,\,\infty )$ established by Dong and Kim [Reference Dong and Kim7] in the endpoint cases of $p=1$ and $p=\infty$.

In particular, when $a$ is a fixed appropriate constant, the corresponding operator $L$ is just the fractional Laplacian $-(-\Delta )^{\sigma /2}$. It is said that the function $u$ is a solution of the equation (1.2), if (1.2) holds true in the sense of almost everywhere.

Denote by ${\mathcal {S}}({\mathbb {R}^n})$ the classical Schwartz function space, that is, the set of all infinitely differentiable functions satisfying that all derivatives decrease rapidly at infinity, and by ${\mathcal {S}}'({\mathbb {R}^n})$ its dual space (namely, the space of all tempered distributions).

Recall that, for any given $\alpha \in (0,\,\infty )$, the Bessel potential operator $J_\alpha$ on ${\mathcal {S}}'({\mathbb {R}^n})$ is defined by, for any $f\in {\mathcal {S}}'({\mathbb {R}^n})$ and $\xi \in {\mathbb {R}^n}$,

\[ J_\alpha f(\xi):={\mathcal{F}}^{{-}1}\left(\left(1+|\cdot|^2\right)^{-\alpha/2}{\mathcal{F}}(f)\right)(\xi) \]

(see, for instance, [Reference Grafakos14, definition 1.2.4]). Here and hereafter, ${\mathcal {F}}$ and ${\mathcal {F}}^{-1}$, respectively, denote the Fourier transform and the inverse Fourier transform. Moreover, for any given $\alpha \in (0,\,\infty )$, the Riesz potential operator $I_\alpha$ on ${\mathcal {S}}'({\mathbb {R}^n})$ is defined by, for any $f\in {\mathcal {S}}'({\mathbb {R}^n})$ and $\xi \in {\mathbb {R}^n}$,

\[ I_\alpha f(\xi):={\mathcal{F}}^{{-}1}\left(|\cdot|^{-\alpha}{\mathcal{F}}(f)\right)(\xi) \]

(see, for instance, [Reference Grafakos14, definition 1.2.1]). It is worth pointing out that, when $\alpha \in (0,\,\infty )$, $|\cdot |^{-\alpha }$ has singularity at the origin. Therefore, $I_\alpha$ can only be defined on the space of tempered distributions modulo polynomials. Moreover, for any $\alpha \in (0,\,\infty )$ and $u\in {\mathcal {S}}'({\mathbb {R}^n})$, the fractional derivative of $u$ with order $\alpha$ is defined by

\[ \partial^\alpha u:={-}(-\Delta)^{\alpha/2}u={\mathcal{F}}^{{-}1}\left(|\cdot|^\alpha{\mathcal{F}}(u)\right). \]

Furthermore, for any given $\alpha \in (0,\,2)$ and $u\in {\mathcal {S}}({\mathbb {R}^n})$, the fractional derivative of $u$ with order $\alpha$ has the equivalent definition

(1.3)\begin{align} \partial^\alpha u(x)={-}(-\Delta)^{\alpha/2}u(x)& =c\,{\rm P.V.}\int_{{{\mathbb{R}}}^n}[u(x+y)-u(x)]\,\frac{{\rm d}y}{|y|^{n+\alpha}} \nonumber\\ & =\frac{c}{2}\int_{{{\mathbb{R}}}^n}[u(x+y)+u(x-y)-2u(x)]\frac{{\rm d}y}{|y|^{n+\alpha}}, \end{align}

where

\[ c:=\frac{\alpha(2-\alpha)\Gamma(\frac{n+\alpha}{2})}{\pi^{n-2}2^{2-\alpha}\Gamma(2-\frac\alpha 2)}, \]

$\Gamma$ is the Gamma function, and $\mathrm {P.V.}$ denotes the integral is taken according to the Cauchy principal value sense. It is worth pointing out that (1.3) is well defined for any $u\in C^2_b({\mathbb {R}^n})$ (the set of all $2$-times continuously differentiable bounded functions) (see, for instance, [Reference Garofalo13]).

For any given $\alpha \in (0,\,\infty )$ and function space $X$ on ${\mathbb {R}^n}$, the Sobolev spaces based on $X$, $J_\alpha (X)$ and $I_\alpha (X)$, are defined by the image of $X$ under $J_\alpha$ and $I_\alpha$, respectively. Furthermore, for any $u\in J_\alpha (X)$ [or $u\in I_\alpha (X)$], the (quasi-)norm of $u$ is given by $\|u\|_{J_\alpha (X)}:=\|J_\alpha (u)\|_X$ [or $\|u\|_{I_\alpha (X)}:=\|I_\alpha (u)\|_X$]. By this, we find that, for any function $u\in I_\alpha (X)$, the fractional derivative $\partial ^\alpha u\in X$.

Moreover, recall that the Riesz transform $R_j$, for any given $j\in \{1,\,\ldots,\,n\}$, is defined by, for any $f\in {\mathcal {S}}({\mathbb {R}^n})$,

\[ R_jf(x)=c_n\lim_{\varepsilon\to0}\displaystyle\int_{|y|\ge\varepsilon}\frac{y_j}{|y|^{n+1}}f(x-y)\,{\rm d}y, \]

where $c_n:=\Gamma (\frac {n+1}{2})\pi ^{-\frac {n+1}{2}}$ (see, for instance, [Reference Stein26, Reference Stein27]). When $n=1$, the corresponding operator is known as the Hilbert transform.

The classical Hardy space $H^1({\mathbb {R}^n})$ is defined to be the set of all $f\in L^1({\mathbb {R}^n})$ such that $R_jf\in L^1({\mathbb {R}^n})$ for any $j\in \{1,\,\ldots,\,n\}$, with the norm

(1.4)\begin{equation} \|f\|_{H^1({{{\mathbb{R}}}^n})}=\|f\|_{L^1({{{\mathbb{R}}}^n})}+\sum_{j=1}^{n}\left\|R_jf\right\|_{L^1({{{\mathbb{R}}}^n})} \end{equation}

(see, for instance, [Reference Stein27]). Furthermore, denote by $L^1_{\mathop{\mathrm {loc}}}({\mathbb {R}^n})$ the set of all locally integrable functions on ${\mathbb {R}^n}$. Let $f\in L^1_{\mathop{\mathrm {loc}}}({\mathbb {R}^n})$. It is said that $f$ belongs to the $\mathrm {BMO}$ (bounded mean oscillation) space ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$, if

\[ \|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}:=\sup_{B\subset{{{\mathbb{R}}}^n}}\frac{1}{|B|}\int_B |f(x)-f_B|\,{\rm d}x<\infty, \]

where the supremum is taken over all balls $B$ of ${\mathbb {R}^n}$ and $f_B:=\frac {1}{|B|}\int _Bf(y)\,{\rm d}y$ (see, for instance, [Reference Grafakos14, Reference John and Nirenberg15, Reference Stein27]). Recall that $\|\cdot \|_{{\mathop {\mathrm {BMO}}}({\mathbb {R}^n})}$ is only a semi-norm and ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ modulo constants is a Banach space. To make ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ itself a Banach space, for $f\in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$, we may consider the norm

(1.5)\begin{equation} \|f\|_{{\mathop{\mathrm {BMO}}}+({{{\mathbb{R}}}^n})}:=\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} +\left|\frac{1}{|B_1(\mathbf{0})|} \int_{B_1(\mathbf{0})}f(x)\,{\rm d}x\right|, \end{equation}

which is useful to consider the pointwise multipliers of ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$, where $B_1(\mathbf {0})$ denotes the ball with the centre $\mathbf {0}$ and the radius $1$. It is known that the Hardy space $H^1({\mathbb {R}^n})$ and the ${\mathop {\mathrm {BMO}}}$ space ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$, respectively, are appropriate substitutes of the Lebesgue spaces $L^1({\mathbb {R}^n})$ and $L^\infty ({\mathbb {R}^n})$ when studying the boundedness of some linear operators (see, for instance, [Reference Grafakos14, Reference Stein27–Reference Strichartz29]). Moreover, it is well known that the space ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ is the dual space of the Hardy space $H^1({\mathbb {R}^n})$ (see, for instance, [Reference Grafakos14, Reference Stein27]).

Non-local equations have aroused extensive research interest in recent years. The non-local equations of the form (1.2) naturally arise in the study of jump Lévy processes; they have extensive applications in many fields, such as, economics, physics and probability theory (see, for instance, [Reference Caffarelli and Silvestre3, Reference Cont and Tankov5, Reference Garofalo13, Reference Ros-Oton24]), and have been extensively studied (see, for instance, [Reference Caffarelli and Silvestre3, Reference Caffarelli and Silvestre4, Reference Dong, Jung and Kim6–Reference Dong and Liu11, Reference Karlsen, Petitta and Ulusoy16, Reference Mengesha, Schikorra and Yeepo18–Reference Mikulevičius and Pragarauskas20]).

The study of the boundedness of the non-local elliptic operator $L$ defined as in (1.1) can be founded in many existing literatures. In particular, if the kernel function $a$ satisfies the lower and upper bounds condition, and also satisfies the cancellation condition when $\sigma =1$, Dong and Kim [Reference Dong and Kim7, Reference Dong and Kim8] obtained the boundedness of the operator $L$ from the Sobolev space $J_\sigma (L^p({\mathbb {R}^n}))$ with $p\in (1,\,\infty )$ to $L^p({\mathbb {R}^n})$, and from the Lipschitz space $\Lambda ^{\alpha +\sigma }({\mathbb {R}^n})$ to $\Lambda ^{\alpha }({\mathbb {R}^n})$ for any given $\alpha \in (0,\,\infty )$ (see, for instance, [Reference Stein26, Reference Stein27] or § 2 below for the definition of the Lipschitz space). Afterwards, for the non-local operator associated with the $x$-dependent kernel $a(x,\,\cdot )$ imposed on the Hölder continuity of $x$, by using the boundedness of the singular integral of convolution type on Lebesgue spaces $L^p({\mathbb {R}^n})$ and the partition of unity argument, Mikulevičius and Pragarauskas [Reference Mikulevičius and Pragarauskas20] obtained the boundedness of the operator $L$ from the Sobolev space $J_\sigma (L^p({\mathbb {R}^n}))$ to $L^p({\mathbb {R}^n})$ when $p\in (1,\,\infty )$ is sufficiently large. Recently, Dong et al. [Reference Dong, Jung and Kim6] removed the restriction on $p$ and extended the result established by Mikulevičius and Pragarauskas [Reference Mikulevičius and Pragarauskas20] to the weighted Lebesgue spaces $L^p_\omega({\mathbb {R}^n})$ for any $p\in (1,\,\infty )$ and $\omega \in A_p({\mathbb {R}^n})$ (the Muckenhoupt weight class). Furthermore, when the kernel also depends on the temporal variable, the boundedness of parabolic operators with local or non-local time derivatives was also considered in the existing literatures (see, for instance, [Reference Dong, Jung and Kim6, Reference Dong and Kim9–Reference Dong and Liu11, Reference Mikulevičius and Pragarauskas19, Reference Mikulevičius and Pragarauskas20]).

The research on the solvability and regularity of the solutions of non-local equations is even richer. In particular, for the fraction Laplacian problem $(-\Delta )^su=f$ in ${\mathbb {R}^n}$, with $s\in (\frac 12,\,1)$ and $f\in L^1({\mathbb {R}^n})$, Karlsen et al. [Reference Karlsen, Petitta and Ulusoy16] proved the unique existence by a dual method, and the solution belonging to the local fractional Sobolev space $W^{1-(2-2s)/q,\,q}_{\mathop{\mathrm {loc}}}({\mathbb {R}^n})$ with $q\in (1,\,\frac {n+2-2s}{n+1-2s})$. For the fractional Laplacian equation with $L^p({\mathbb {R}^n})$-data, the existence and regularity of the solution can be obtained by the classical theory of pseudo-differential operators. However, for the general kernel $a$, the theory of pseudo-differential operators is no longer effective. In [Reference Dong and Kim7], by using the boundedness of the non-local operator $L$ as in (1.1) from $J_\sigma (L^p({\mathbb {R}^n}))$ to $L^p({\mathbb {R}^n})$ with $p\in (1,\,\infty )$, Dong and Kim proved that the solution of the non-local elliptic equation (1.2) with $f\in L^p({\mathbb {R}^n})\,(p\in (1,\,\infty ))$ exists and belongs to the Bessel potential space $J_\sigma (L^p({\mathbb {R}^n}))$. Moreover, in [Reference Dong and Kim8], by using the boundedness of the non-local operator $L$ from the Lipschitz space $\Lambda ^{\alpha +\sigma }({\mathbb {R}^n})$ to $\Lambda ^{\alpha }({\mathbb {R}^n})$ with any given $\alpha \in (0,\,\infty )$ and the method of continuity, Dong and Kim established the unique solvability of the equation (1.2) with any given $f\in \Lambda ^\alpha ({\mathbb {R}^n})$, and also proved that the corresponding solution belongs to $\Lambda ^{\alpha +\sigma }({\mathbb {R}^n})$. In the same paper [Reference Dong and Kim8], the solvability of the equation (1.2), with the kernel being $x$-dependent, was also established. Furthermore, the solvability of the non-local parabolic equation, the Dirichlet problem of the non-local equation on domains and the semi-linear non-local equations also have been extensively studied in the existing literatures (see, for instance, [Reference Abdellaoui, Fernández, Leonori and Younes1, Reference Dong, Jung and Kim6, Reference Dong and Liu11, Reference Nowak22–Reference Ros-Oton and Serra25, Reference Wu, Huang and Zhou31]).

Throughout this paper, we always assume that the kernel function $a$ satisfies the following assumption.

Assumption 1.1 Let $\sigma \in (0,\,2)$ and $a$ be a non-negative measurable function on ${\mathbb {R}^n}$.

(i) There are positive constants $\mu$ and $\Lambda$ such that, for any $y\in {\mathbb {R}^n}$,
\[ (2-\sigma)\mu\le a(y)\le(2-\sigma)\Lambda. \]
(ii) If $\sigma =1$, then, for any $0< r< R$,
\[ \displaystyle\int_{r\le|y|\le R}ya(y)\,\frac{{\rm d}y}{|y|^{n+1}}=0. \]

Now, we give the main results of this paper.

Theorem 1.2 Let $n\ge 1$, $\sigma \in (0,\,2)$, $p\in (1,\,\infty )$, and the kernel function $a$ satisfy assumption 1.1. Then the following two assertions hold true.

(i) The operator $L$ defined as in (1.1) is a continuous operator from $J_\sigma (L^p({\mathbb {R}^n}))\cap J_\sigma ({\mathop {\mathrm {BMO}}}({\mathbb {R}^n}))$ to ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n}),$ moreover, there exists a positive constant $C,$ depending only on $n,$ $\sigma,$ $\mu$ and $\Lambda,$ such that, for any $u\in J_\sigma (L^p({\mathbb {R}^n}))\cap J_\sigma ({\mathop {\mathrm {BMO}}}({\mathbb {R}^n})),$
(1.6)\begin{equation} \|Lu\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\le C\left\|\partial^\sigma u\right\|_{{\mathop{\mathrm {BMO}}}+({{{\mathbb{R}}}^n})}, \end{equation}
where, for a function $f\in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n}),$ $\|f\|_{{\mathop {\mathrm {BMO}}}+({\mathbb {R}^n})}$ is defined as in (1.5).
(ii) The operator $L$ defined as in (1.1) is a continuous operator from $J_\sigma (H^1({\mathbb {R}^n}))$ to $H^1({\mathbb {R}^n}),$ moreover, there exists a positive constant $C,$ depending only on $n,$ $\sigma,$ $\mu$ and $\Lambda,$ such that, for any $u\in J_\sigma (H^1({\mathbb {R}^n})),$
(1.7)\begin{equation} \|Lu\|_{H^1({{{\mathbb{R}}}^n})}\le C\left\|\partial^\sigma u\right\|_{H^1({{{\mathbb{R}}}^n})}. \end{equation}

Remark 1.3 In theorem 1.2(i), we need a constraint that $u\in J_\sigma (L^p({\mathbb {R}^n}))$ for some $p\in (1,\,\infty )$ to obtain (1.6). This additional condition is due to our proof method (see (3.20) and (3.21) below for the details). Precisely, let $\lambda \in (0,\,\infty )$ be a constant and $f:=-(-\Delta )^{\sigma /2}u-\lambda u$. To guarantee that there exists a unique solution for the equation $Lw-\lambda w=f$ which is important in the proof of theorem 1.2(i), we need to assume that $f\in L^p({\mathbb {R}^n})$ for some $p\in (1,\,\infty )$. This leads to the constraint that $u\in J_\sigma (L^p({\mathbb {R}^n}))$ for some $p\in (1,\,\infty )$. Meanwhile, because of the lack of the density of $L^p({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ in ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$, we could not replace the condition $u\in J_\sigma (L^p({\mathbb {R}^n}))\cap J_\sigma ({\mathop {\mathrm {BMO}}}({\mathbb {R}^n}))$ with $u\in J_\sigma ({\mathop {\mathrm {BMO}}}({\mathbb {R}^n}))$ by the method used in the proof of theorem 1.2(i).

Next, we show via a counterexample that, for any given $p\in (1,\,\infty )$, $L^p({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ is not dense in ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ with respect to $\|\cdot \|_{{\mathop {\mathrm {BMO}}}({\mathbb {R}^n})}$. Indeed, let $n=1$ and $f_0(x):=\sin x$ for any $x\in {\mathbb {R}}$. Then $f_0\in L^\infty ({\mathbb {R}^n})$ and hence $f_0\in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$. Let $p\in (1,\,\infty )$. Now, we prove that, for any $g\in L^p({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$, $\|f_0-g\|_{{\mathop {\mathrm {BMO}}}({\mathbb {R}^n})}\ge \frac {2}{\pi }$, which implies that $L^p({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ is not dense in ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ with respect to $\|\cdot \|_{{\mathop {\mathrm {BMO}}}({\mathbb {R}^n})}$. For any $k\in {\mathbb {N}}$, let $I_k:=(k\pi,\,(k+2)\pi )$. Then, for any $k\in {\mathbb {N}}$,

(1.8)\begin{align} \|f_0-g\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}& \ge\frac{1}{|I_k|}\int_{I_k}|(f_0-g)-(f_0-g)_{I_k}|\,{\rm d}x \nonumber\\ & \ge\frac{1}{|I_k|}\int_{I_k}|f_0-(f_0)_{I_k}|\,{\rm d}x-\frac{1}{|I_k|}\int_{I_k}|g-(g)_{I_k}|\,{\rm d}x \nonumber\\ & \ge\frac{2}{\pi}-\frac{1}{\pi}\int_{k\pi}^{(k+2)\pi}|g|\,{\rm d}x. \end{align}

Moreover, by $g\in L^p({\mathbb {R}})$, we conclude that $\lim _{k\to \infty }\int _{k\pi }^{(k+2)\pi }|g|\,{\rm d}x=0$. Thus, letting $k\to \infty$ in (1.8), we find that, for any $g\in L^p({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$, $\|f_0-g\|_{{\mathop {\mathrm {BMO}}}({\mathbb {R}^n})}\ge~\frac {2}{\pi }$.

Theorem 1.4 Let $n\ge 1,$ $\lambda \in (0,\,\infty ),$ $\sigma \in (0,\,2),$ $p\in (1,\,\infty ),$ and the kernel function $a$ satisfy assumption 1.1. Then the following two assertions hold true.

(i) For any given $f\in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})\cap L^p({\mathbb {R}^n}),$ the solution $u$ of the equation (1.2) uniquely exists and, moreover, $u\in J_\sigma ({\mathop {\mathrm {BMO}}}({\mathbb {R}^n}))$ and there exists a positive constant $C,$ depending only on $n,$ $\sigma,$ $\mu$ and $\Lambda,$ such that
(1.9)\begin{equation} \lambda\|u\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left\|\partial^\sigma u\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\le C\|f\|_{{\mathop{\mathrm {BMO}}}+({{{\mathbb{R}}}^n})}, \end{equation}
where, for any $f\in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n}),$ $\|f\|_{{\mathop {\mathrm {BMO}}}+({\mathbb {R}^n})}$ is defined as in (1.5).
(ii) For any given $f\in H^1({\mathbb {R}^n}),$ the solution $u$ of the equation (1.2) uniquely exists and, moreover, $u\in J_\sigma (H^1({\mathbb {R}^n}))$ and there exists a positive constant $C,$ depending only on $n,$ $\sigma,$ $\mu$ and $\Lambda,$ such that
(1.10)\begin{equation} \lambda\|u\|_{H^1({{{\mathbb{R}}}^n})}+\left\|\partial^\sigma u\right\|_{H^1({{{\mathbb{R}}}^n})}\le C\|f\|_{H^1({{{\mathbb{R}}}^n})}. \end{equation}

Remark 1.5 (i) Let $\lambda \in (0,\,\infty )$, $\sigma \in (0,\,2)$, $f\in L^\infty ({\mathbb {R}^n})\cap L^p({\mathbb {R}^n})$ with some $p\in (1,\,\infty )$, and $u$ be the solution of the equation (1.2). By the maximum principle, it was proved in [Reference Dong and Kim8, theorem 1.1] that $\lambda \|u\|_{L^\infty ({\mathbb {R}^n})}\le \|f\|_{L^\infty ({\mathbb {R}^n})}$. From this and theorem 1.4, it follows that

\[ \lambda\|u\|_{L^\infty({{{\mathbb{R}}}^n})}+\left\|\partial^\sigma u\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\le C\|f\|_{L^\infty({{{\mathbb{R}}}^n})}, \]

where $C$ is a positive constant depending only on $n$, $\sigma$, $\mu$ and $\Lambda$.

(ii) When $\lambda =0$ in theorem 1.4, we could give a priori estimate for the equation $Lu=f$ in ${\mathbb {R}^n}$. Indeed, if $u\in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})\cap L^p({\mathbb {R}^n})$ is a solution of the equation $Lu=f$ with $f\in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})\cap L^p({\mathbb {R}^n})$ for some $p\in (1,\,\infty )$, then, for any $\lambda \in (0,\,\infty )$, we have $Lu-\lambda u=f-\lambda u$. Since the constant $C$ in (1.9) is independent of $\lambda$, $u$ and $f$, by taking $\lambda \to 0^+$, it follows that (1.9) holds true with $\lambda =0$. Similarly, if $u\in H^1({\mathbb {R}^n})$ is a solution of the equation $Lu=f$ with $f\in H^1({\mathbb {R}^n})$, we also obtain that (1.10) holds true with $\lambda =0$.

(iii) The methods used in this paper to show theorems 1.2 and 1.4 are not effective to deal with the general case that the kernel function $a$ depends on both the variables $x$ and $y$, considered as [Reference Dong, Jung and Kim6, Reference Dong and Liu11, Reference Mikulevičius and Pragarauskas20]. Indeed, in the proofs of theorems 1.2 and 1.4, we use the exchangeability that $(-\Delta )^{\sigma /2}L=L(-\Delta )^{\sigma /2}$ and $R_jL=LR_j$ which plays a key role in the proofs of theorems 1.2 and 1.4, where the operator $L$ is as in (1.1) and $R_j$ with $j\in \{1,\,\ldots,\,n\}$ denotes the Riesz transform. However, these exchangeable properties may not hold true for the operator $L$ when the kernel function $a$ depends on both the variables $x$ and $y$.

The remainder of this paper is organized as follows. In § 2, we recall the notions of the Bessel potential space and the Riesz potential space based on $L^p({\mathbb {R}^n})$, $H^1({\mathbb {R}^n})$ or ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$, and the Lipschitz–Zygmund space. Moreover, we also present the boundedness result of the singular integral operator on the Hardy space $H^1({\mathbb {R}^n})$, and some important results established by Dong and Kim [Reference Dong and Kim7, Reference Dong and Kim8]. In § 3, we prove theorems 1.2 and 1.4. To prove theorem 1.2(i), the key step is to establish the mean oscillation estimates. This method was originated in [Reference Krylov17] and used to treat second-order elliptic and parabolic equations with $\mathrm {VMO}$ coefficients. Moreover, in [Reference Dong and Kim7, Reference Dong and Kim8, Reference Dong and Liu11], this method was further developed to treat non-local elliptic and parabolic equations. To show theorem 1.2(ii), we use the boundedness of the singular integral operator on the Hardy space $H^1({\mathbb {R}^n})$, which is motivated by [Reference Dong, Jung and Kim6]. Meanwhile, to prove theorem 1.4, we also use the method of mean oscillation estimates. Moreover, a duality argument is also used.

Finally, we make some conventions on notations. Throughout the whole paper, we always denote by $C$ a positive constant which is independent of the main parameters, but it may vary from line to line. The symbol $f\lesssim g$ means that $f\le Cg$. For any $x\in {\mathbb {R}^n}$ and $r\in (0,\,\infty )$, let $B_r(x)$ be a ball with centre $x$ and radius $r$. In particular, when $x={\mathbf 0}$ (the origin of ${\mathbb {R}^n}$), we let $B_r:=B_r({\mathbf 0})$. We denote by ${\mathbb {N}}$ the set of all positive integers. Moreover, for an open set $\Omega \subset {\mathbb {R}^n}$, we denote by $C^\infty _{\rm c}(\Omega )$ the set of all infinitely differentiable functions with compact supports on $\Omega$ and by $C^\infty _{b}(\Omega )$ the set of all infinitely differentiable functions with bound derivatives on $\Omega$. For a multiindex $\gamma :=(\gamma _1,\,\ldots,\,\gamma _n)$ with each component $\gamma _i$ being a nonnegative integer, let $|\gamma |=\gamma _1+\cdots +\gamma _n$ and, for any $|\gamma |$-th differentiable function $u$, set $D^\gamma u(x):=\frac {\partial ^{|\gamma |}u(x)}{\partial x_1^{\gamma _1}\cdots \partial x_n^{\gamma _n}}$.

2. Preliminaries

In this section, we recall the notions of some function spaces, such as, the Bessel potential space and the Riesz potential space based on $L^p({\mathbb {R}^n})$, $H^1({\mathbb {R}^n})$ or ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$, and the Lipschitz–Zygmund space. Moreover, we also present the boundedness result of the singular integral operator on $H^1({\mathbb {R}^n})$, and some important results established in [Reference Dong and Kim7, Reference Dong and Kim8].

When $X$ is one of $L^p({\mathbb {R}^n})$, $H^1({\mathbb {R}^n})$ or ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$, we recall the relations of the Sobolev spaces $J_\alpha (X)$ and $I_\alpha (X)$ as follows (see, for instance, [Reference Stein26, Reference Strichartz28, Reference Strichartz29]).

Proposition 2.1 Let $\alpha \in (0,\,\infty )$. Then the following properties hold true.

(i) For any $p\in (1,\,\infty ),$ $J_\alpha (L^p({\mathbb {R}^n}))=L^p({\mathbb {R}^n})\cap I_\alpha (L^p({\mathbb {R}^n}))$.
(ii) $J_\alpha (H^1({\mathbb {R}^n}))=H^1({\mathbb {R}^n})\cap I_\alpha (H^1({\mathbb {R}^n}))$.
(iii) $J_\alpha ({\mathop {\mathrm {BMO}}}({\mathbb {R}^n}))={\mathop {\mathrm {BMO}}}({\mathbb {R}^n})\cap I_\alpha ({\mathop {\mathrm {BMO}}}({\mathbb {R}^n}))$.

Let $u\in L^\infty ({\mathbb {R}^n})$. We recall that the harmonic extension of $u$ to ${\mathbb {R}}^{n+1}_+:={\mathbb {R}^n}\times (0,\,\infty )$ is defined by the convolution

\[ U({\cdot},y):=p({\cdot},y)\ast u({\cdot}) \]

for any $y\in (0,\,\infty )$, where $p(\cdot,\,y)$ is the classical Poisson kernel on ${\mathbb {R}}^{n+1}_+$. Let $\alpha \in (0,\,\infty )$ and $\ell$ be the smallest integer greater that $\alpha$. The Lipschitz–Zygmund space $\Lambda ^\alpha ({\mathbb {R}^n})$ is defined by

\[ \Lambda^\alpha({{{\mathbb{R}}}^n}):=\left\{u\in L^\infty({{{\mathbb{R}}}^n}):\sup_{y\in(0,\infty)}y^{\ell-\alpha} \left\|D^\ell_yU({\cdot},y)\right\|_{L^\infty({{{\mathbb{R}}}^n})}<\infty\right\}, \]

where $D^\ell _y$ denotes the $\ell$-th derivative with respect to $y$, which is equipped with the norm

\[ \|u\|_{\Lambda^\alpha({{{\mathbb{R}}}^n})}:=\|u\|_{L^\infty({{{\mathbb{R}}}^n})} +\sup_{y\in(0,\infty)}y^{\ell-\alpha} \left\|D^\ell_yU({\cdot},y)\right\|_{L^\infty({{{\mathbb{R}}}^n})}. \]

Let $\Omega \subset {\mathbb {R}^n}$ be an open set, $\alpha \in (0,\,\infty )$ be a non-integer and $\ell$ the largest integer smaller than $\alpha$. Denote by $C^\alpha (\Omega )$ the set of all bounded continuous functions on $\Omega$, with satisfying that

\[ \|f\|_{C^\alpha(\Omega)}:=\sum_{|\gamma|\le \ell}\|D^\gamma f\|_{L^\infty(\Omega)}+\left[D^\ell f\right]_{C^{\alpha-\ell}(\Omega)}<\infty, \]

where $[\cdot ]_{C^{\alpha -\ell }(\Omega )}$ denotes the Hölder semi-norm, namely, for a function $g$ on $\Omega$,

\[ [g]_{C^{\alpha-\ell}(\Omega)}:=\sup_{\overset{x,\,y\in\Omega}{x\neq y}}\left\{\frac{|g(x)-g(y)|}{|x-y|^{\alpha-\ell}}\right\}. \]

Then we have the following properties of the Lipschitz–Zygmund space (see, for instance, [Reference Stein26, chapter V] and [Reference Stein27, chapter VI]).

Proposition 2.2 Let $\alpha \in (0,\,\infty )$ and $\Lambda ^\alpha ({\mathbb {R}^n})$ be the Lipschitz–Zygmund space on ${\mathbb {R}^n}$.

(i) For any $0<\alpha _1<\alpha _2<\infty,$ $\Lambda ^{\alpha _2}({\mathbb {R}^n})\subsetneq \Lambda ^{\alpha _1}({\mathbb {R}^n})$.
(ii) If $\alpha$ is a non-integer, then $\Lambda ^\alpha ({\mathbb {R}^n})=C^\alpha ({\mathbb {R}^n})$.
(iii) If $\alpha \in (0,\,2),$ then
\[ \|u\|_{\Lambda^\alpha({{{\mathbb{R}}}^n})}=\|u\|_{L^\infty({{{\mathbb{R}}}^n})} +\sup_{|h|>0}|h|^{-\alpha}\|u({\cdot}{+}h)+u({\cdot}{-}h)-2u({\cdot})\|_{L^\infty({{{\mathbb{R}}}^n})}. \]

The following is the known result of the boundless of the singular integral operator on $H^1({\mathbb {R}^n})$ (see, for instance, [Reference Stein27, chapter III, theorem 3]).

Lemma 2.3 Let $T$ be a singular integral operator on ${\mathbb {R}^n}$. Assume that there exists a kernel function $K$ such that, for any $f\in L^2({\mathbb {R}^n})$ with compact support,

\[ Tf(x)=\int_{{{\mathbb{R}}}^n} K(x-y)f(y)\,{\rm d}y \]

holds true for any $x$ outside the support of $f$. Assume further that there exists a positive constant $A$ such that, for any $y\neq 0,$

\[ \int_{|x|\ge2|y|}|K(x-y)-K(x)|\,{\rm d}x\le A, \]

and, for any $f\in L^2({\mathbb {R}^n}),$

\[ \|Tf\|_{L^2({{{\mathbb{R}}}^n})}\le A\|f\|_{L^2({{{\mathbb{R}}}^n})}. \]

Then there exists a positive constant $C$ depending only on the constant $A$ such that, for any $f\in H^1({\mathbb {R}^n}),$

\[ \|Tf\|_{L^1({{{\mathbb{R}}}^n})}\le C\|f\|_{H^1({{{\mathbb{R}}}^n})}. \]

The following conclusions were established in [Reference Dong and Kim7, Reference Dong and Kim8].

Lemma 2.4 [Reference Dong and Kim7, theorem 2.1]

Let $p\in (1,\,\infty ),$ $\lambda \in [0,\,\infty ),$ $\sigma \in (0,\,2),$ and the kernel function $a$ satisfy assumption 1.1. Then the operator $L$ defined as in (1.1) is a continuous operator from $J_\sigma (L^p({\mathbb {R}^n}))$ to $L^p({\mathbb {R}^n})$ and there exists a positive constant $C,$ depending only on $n,$ $p,$ $\sigma,$ $\mu$ and $\Lambda,$ such that

\[ \lambda\|u\|_{L^p({{{\mathbb{R}}}^n})}+\|Lu\|_{L^p({{{\mathbb{R}}}^n})}\le C\left\|-(-\Delta)^{\sigma/2}u-\lambda u\right\|_{L^p({{{\mathbb{R}}}^n})}. \]

Moreover, for any $\lambda \in (0,\,\infty )$ and $f\in L^p({\mathbb {R}^n}),$ there exists a unique solution $u\in J_\sigma (L^p({\mathbb {R}^n}))$ for the equation (1.2) , and there exists a positive constant $C,$ depending only on $n,$ $p,$ $\sigma,$ $\mu$ and $\Lambda,$ such that

\[ \lambda\|u\|_{L^p({{{\mathbb{R}}}^n})}+\left\|\partial^\sigma u\right\|_{L^p({{{\mathbb{R}}}^n})}\le C\|f\|_{L^p({{{\mathbb{R}}}^n})}. \]

Lemma 2.5 [Reference Dong and Kim8, theorem 1.3]

Let $\alpha \in (0,\,\infty ),$ $\lambda \in (0,\,\infty ),$ $\sigma \in (0,\,2),$ and the kernel function $a$ satisfy assumption 1.1. Then the operator $L-\lambda$ is a continuous operator from $\Lambda ^{\alpha +\sigma }({\mathbb {R}^n})$ to $\Lambda ^\alpha ({\mathbb {R}^n}),$ where $L$ is as in (1.1). Moreover, for any $f\in \Lambda ^\alpha ({\mathbb {R}^n}),$ there exists a unique solution $u\in \Lambda ^{\alpha +\sigma }({\mathbb {R}^n})$ for the equation (1.2), and there exists a positive constant $C,$ depending only on $n,$ $\sigma,$ $\mu,$ $\Lambda,$ $\lambda$ and $\alpha,$ such that

\[ \|u\|_{\Lambda^{\alpha+\sigma}({{{\mathbb{R}}}^n})}\le C\|Lu-\lambda u\|_{\Lambda^\alpha({{{\mathbb{R}}}^n})}. \]

3. Proofs of theorems 1.2 and 1.4

In this section, we prove theorems 1.2 and 1.4. Assume that $\sigma \in (0,\,2)$. Throughout this paper, we always assume that $\omega (x):=\frac {1}{1+|x|^{n+\sigma }}$ for any $x\in {\mathbb {R}^n}$ and

\[ L^1({{{\mathbb{R}}}^n},\omega):=\left\{g\in L^1_{\mathrm{loc}}({{{\mathbb{R}}}^n}):\|g\|_{L^1({{{\mathbb{R}}}^n},\omega)} :=\int_{{{\mathbb{R}}}^n} \dfrac{|g(y)|}{1+|y|^{n+\sigma}}\,{\mathrm d}y<\infty\right\}. \]

Moreover, for an open set $\Omega \subset {\mathbb {R}^n}$, it is said that a function $f\in C^2_{\mathop{\mathrm {loc}}}(\Omega )$, if, for any $\phi \in C^\infty _{\rm c}(\Omega )$, $\phi f\in C^2_{\rm c}(\Omega )$ (the set of all 2-th continuous differentiable functions with compact supports).

We first recall the following property of the space ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ (see, for instance, [Reference Grafakos14, proposition 3.1.5]).

Proposition 3.1 Let $f\in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$. Then, for any $\delta \in (0,\,\infty ),$ there exists a positive constant $C,$ depending only on $n$ and $\delta,$ such that, for any $x_0\in {\mathbb {R}^n}$ and $R\in (0,\,\infty ),$

\[ R^\delta\int_{{{\mathbb{R}}}^n}\frac{|f(x)-(f)_{B_R(x_0)}|}{R^{n+\delta}+|x-x_0|^{n+\delta}}\,{\rm d}x\le C\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}. \]

Now, we need the following lemma 3.2, which was established in [Reference Dong and Kim7, corollary 4.3].

Lemma 3.2 Let $\lambda \in [0,\,\infty ),$ $\sigma \in (0,\,2),$ $f\in L^\infty (B_1),$ and $u\in C^2_{\mathop{\mathrm {loc}}}(B_1)\cap L^1({\mathbb {R}^n},\,\omega )$ be a solution of

\[ Lu-\lambda u=f \]

in $B_1,$ where the operator $L$ is as in (1.1) and the kernel function $a$ satisfies assumption 1.1. Then, for any $\alpha \in (0,\,\min \{1,\,\sigma \}),$ there exists a positive constant $C,$ depending only $n,$ $\sigma,$ $\mu,$ $\Lambda,$ and $\alpha,$ such that

\[ [u]_{C^\alpha(B_{1/2})}\le C\left[\|u\|_{L^1({{{\mathbb{R}}}^n},\omega)}+\mathrm{osc}_{B_1}f\right], \]

where $\mathrm {osc}_{B_1} f:=\sup _{x,\,y\in B_1}|f(x)-f(y)|$.

Moreover, as a corollary of lemma 3.2, we have the following lemma 3.3, which was obtained in [Reference Dong and Kim8, proposition 1].

Lemma 3.3 Let $\lambda \in [0,\,\infty ),$ $\sigma \in (0,\,2),$ $f\in L^\infty (B_1)$ and $u\in C^2_{\mathop{\mathrm {loc}}}(B_1)\cap L^\infty ({\mathbb {R}^n})$ be a solution of

(3.1)\begin{equation} Lu-\lambda u=f \end{equation}

in $B_1,$ where $L$ is as in lemma 3.2. Then, for any $\alpha \in (0,\,\min \{1,\,\sigma \}),$ there exists a positive constant $C,$ depending only $n,$ $\sigma,$ $\mu,$ $\Lambda$ and $\alpha,$ such that

(3.2)\begin{equation} [u]_{C^\alpha(B_{1/2})}\le C\left[\left\|u-(u)_{B_1}\right\|_{L^1({{{\mathbb{R}}}^n},\omega)}+\mathrm{osc}_{B_1}f\right], \end{equation}

where $(u)_{B_1}:=\frac {1}{|B_1|}\int _{B_1}u(x)\,{\rm d}x$.

Lemma 3.4 Let $\lambda \in [0,\,\infty )$, $\sigma \in (0,\,2),$ $f\in C^\infty _{\mathop{\mathrm {loc}}}({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ satisfy that $f=0$ in $B_2$, and $u\in J_\sigma (L^2({\mathbb {R}^n}))\cap C^\infty _b({\mathbb {R}^n})$ be a solution of

(3.3)\begin{equation} Lu-\lambda u=f \end{equation}

in ${\mathbb {R}^n},$ where $L$ is as in lemma 3.2. Then, for any $\alpha \in (0,\,\min \{1,\,\sigma \}),$ there exists a positive constant $C,$ depending only on $n,$ $\sigma,$ $\mu,$ $\Lambda$ and $\alpha,$ such that

(3.4)\begin{equation} [u]_{C^\alpha(B_{1/2})}\le C\left\|u-(u)_{B_1}\right\|_{L^1({{{\mathbb{R}}}^n},\omega)} \end{equation}

and

(3.5)\begin{equation} \left[(-\Delta)^{\sigma/2}u\right]_{C^\alpha(B_{1/2})} \le C\left[\left\|(-\Delta)^{\sigma/2}u-\left((-\Delta)^{\sigma/2}u\right)_{B_1}\right\|_{L^1({{{\mathbb{R}}}^n},\omega)} +\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\right]. \end{equation}

Proof. By lemma 3.3 and the assumption that $f=0$ in $B_2$, we find that (3.4) holds true. Now, we show (3.5). Applying $(-\Delta )^{\sigma /2}$ to both sides of (3.3), we conclude that

\[ L(-\Delta)^{\sigma/2}u-\lambda (-\Delta)^{\sigma/2}u= (-\Delta)^{\sigma/2}f. \]

For any $x\in B_1$, we have $f(x)=0$ and, if $y\in B_{1/2}$, then $f(x+y)=0$. By this, proposition 3.1, and the fact that, for any $x\in B_1$, $(f)_{B_{1/2}(x)}=0$, we find that, for any $x\in B_1$,

\begin{align*} \left|(-\Delta)^{\sigma/2}f(x)\right| & =c\left|\lim_{\varepsilon\to 0^+}\int_{|y|\ge\varepsilon}f(x+y)-f(x)\frac{{\rm d}y}{|y|^{n+\sigma}}\right|\nonumber \\ & =c\left|\int_{|y-x|\ge 1/2}\frac{f(y)}{|y-x|^{n+\sigma}}{\rm d}y\right|\\ & \lesssim\int_{|y-x|\ge 1/2}\frac{\left|f(y)-(f)_{B_{1/2}(x)}\right|}{(1/2)^{n+\sigma}+|y-x|^{n+\sigma}}{\rm d}y\lesssim\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}, \end{align*}

which, combined with the fact that $\mathrm {osc}_{B_1}(-\Delta )^{\sigma /2}f\le 2\|(-\Delta )^{\sigma /2}f\|_{L^\infty (B_1)}$ and lemma 3.3, further implies that (3.5) holds true. This finishes the proof of lemma 3.4.

Then, by lemma 3.4 and a scaling and shifting the coordinates argument, we obtain the following lemma.

Lemma 3.5 Let $\lambda \in [0,\,\infty ),$ $\sigma \in (0,\,2),$ $k\in [2,\,\infty ),$ $f\in C^\infty _{\mathop{\mathrm {loc}}}({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ satisfy that $f=0$ in $B_{2kr}(x_0)$ for some $x_0\in {\mathbb {R}^n}$ and $r\in (0,\,\infty ),$ and $u\in J_\sigma (L^2({\mathbb {R}^n}))\cap C^\infty _b({\mathbb {R}^n})$ be a solution of

\[ Lu-\lambda u=f \]

(3.6)\begin{equation} \left(|u-(u)_{B_r(x_0)}|\right)_{B_r(x_0)} \le Ck^{-\alpha}(kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{|u(x)-(u)_{B_{kr}(x_0)}|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x \end{equation}

and

(3.7)\begin{align} & \left(\left|(-\Delta)^{\sigma/2}u-\left((-\Delta)^{\sigma/2}u\right)_{B_r(x_0)}\right|\right)_{B_r(x_0)} \nonumber\\ & \quad\le C\left[k^{-\alpha}(kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{\left|(\!-\!\Delta)^{\sigma/2}u(x)-\left((-\Delta)^{\sigma/2}u\right)_{B_{kr}(x_0)}\right|} {(kr)^{n+\sigma}\!+\!|x-x_0|^{n+\sigma}}\,{\rm d}x+k^{-\alpha}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\right]\!. \end{align}

Proof. Let $R:=kr$, $U(x):=u(Rx+x_0)$, and $F(x):=R^\sigma f(Rx+x_0)$. Then, we conclude that $U$ satisfies the equation

\[ L_1U(x)-R^\sigma\lambda U(x)=F(x) \]

in ${\mathbb {R}^n}$, where $F(x)=0$ in $B_2$ and $L_1$ is the nonlocal operator with the coefficient $a_1(\cdot )=a(R\cdot )$. Moreover, it is easy to find that $a_1$ also satisfies assumption 1.1.

Therefore, from lemma 3.4 and a change of variables, it follows that

(3.8)\begin{equation} [u]_{C^\alpha(B_{kr/2}(x_0))}=(kr)^{-\alpha}[U]_{C^\alpha(B_{1/2})} \lesssim (kr)^{\sigma-\alpha}\int_{{{\mathbb{R}}}^n}\frac{|u(x)-(u)_{B_{kr}(x_0)}|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x \end{equation}

and

(3.9)\begin{align} \left[(-\Delta)^{\sigma/2}u\right]_{C^\alpha{B_{kr/2}(x_0)}}& =(kr)^{-(\sigma+\alpha)}\left[(-\Delta)^{\sigma/2}U\right]_{C^\alpha(B_{1/2})} \nonumber\\ & \lesssim (kr)^{\sigma-\alpha}\int_{{{\mathbb{R}}}^n}\frac{\left|(-\Delta)^{\sigma/2}u(x)-\left((-\Delta)^{\sigma/2}u\right)_{B_{kr}(x_0)}\right|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x \nonumber\\ & \quad+(kr)^{-\alpha}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}. \end{align}

In addition, for any $k\in [2,\,\infty )$ and any function $g\in C^\alpha (B_{kr/2}(x_0))$, we have

\begin{align*} \left(|g-(g)_{B_r(x_0)}|\right)_{B_r(x_0)} & =\frac{1}{|B_r(x_0)|}\int_{B_r(x_0)}\left|g(y)-\frac{1}{|B_r(x_0)|}\int_{B_r(x_0)}g(x)\,{\rm d}x\right|\,{\rm d}y\\ & \le\frac{1}{|B_r(x_0)|}\frac{1}{|B_r(x_0)|}\int_{B_r(x_0)}\int_{B_r(x_0)}|g(x)-g(y)|\,{\rm d}x{\rm d}y\\ & \quad\lesssim [g]_{C^\alpha(B_{kr/2}(x_0))}r^\alpha, \end{align*}

which, together with (3.8) and (3.9), further implies that (3.6) and (3.7) hold true. This finishes the proof of lemma 3.5.

Lemma 3.6 Let $\sigma \in (0,\,2),$ $\lambda \in (0,\,\infty ),$ $k\in [2,\,\infty ),$ $f\in C^\infty _{\mathop{\mathrm {loc}}}({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ and $u\in J_\sigma (L^2({\mathbb {R}^n}))\cap J_\sigma ({\mathop {\mathrm {BMO}}}({\mathbb {R}^n}))\cap C^\infty _b({\mathbb {R}^n})$ be a solution of

\[ Lu-\lambda u=f \]

in ${\mathbb {R}^n},$ where $L$ is as in lemma 3.2. Then, for any $\alpha \in (0,\,\min \{1,\,\sigma \}),$ $x_0\in {\mathbb {R}^n},$ and $r\in (0,\,\infty ),$ there exists a positive constant $C,$ depending only $n,$ $\sigma,$ $\mu,$ $\Lambda$ and $\alpha,$ such that

\begin{align*} & \lambda\left(|u-(u)_{B_r(x_0)}|\right)_{B_r(x_0)}+\left(\left|(-\Delta)^{\sigma/2}u-\left((-\Delta)^{\sigma/2}u\right)_{B_r(x_0)}\right|\right)_{B_r(x_0)}\\ & \quad\le C\left\{k^{-\alpha}\left[\lambda\left\|u\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} +\left\|(-\Delta)^{\sigma/2}u\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\right] +k^{n/2}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\right\}. \end{align*}

Proof. Let $x_0\in {\mathbb {R}^n}$ and $r\in (0,\,\infty )$. Take $\eta \in C_{\rm c}^\infty ({\mathbb {R}^n})$ such that $\eta \equiv 1$ on $B_{2kr}(x_0)$, $0\le \eta \le 1$, and $\mathop{\mathrm {\,supp\,}}(\eta )\subset B_{4kr}(x_0)$. Then, we have $\eta [f-(f)_{B_{4kr}(x_0)}]\in C_{\rm c}^\infty (B_{4kr}(x_0))$. By this, we find that $\eta [f-(f)_{B_{4kr}(x_0)}]\in L^p({\mathbb {R}^n})\cap C^s({\mathbb {R}^n})$ for any $p\in (1,\,\infty )$ and $s\in (0,\,1)$. From lemmas 2.4 and 2.5, we deduce that there exists a unique solution $w\in J_\sigma (\cap _{p\in (1,\infty )}L^p({\mathbb {R}^n}))\cap \Lambda ^{\sigma +s}({\mathbb {R}^n})$ for the equation (1.2) with $f$ replaced by $\eta [f-(f)_{B_{4kr}(x_0)}]$, and, for any $p\in (1,\,\infty )$, $w$ satisfies that

(3.10)\begin{equation} \lambda\|w\|_{L^p({{{\mathbb{R}}}^n})}+\left\|(-\Delta)^{\sigma/2}w\right\|_{L^p({{{\mathbb{R}}}^n})}\le C\left\|\eta\left[f-(f)_{B_{4kr}(x_0)}\right]\right\|_{L^p({{{\mathbb{R}}}^n})}, \end{equation}

where $C$ is a positive constant independent of $\lambda$, $\eta$, $f$ and $w$. Furthermore, by proposition 2.2(iii) and taking $s\in (0,\,1)$ small enough such that $\sigma +s\in (0,\,2)$, we conclude that $w\in L^{\infty }({\mathbb {R}^n})$ and, for any $x\in {\mathbb {R}^n}$,

\begin{align*} \left|\partial^\sigma w(x)\right| & =\left|\int_{{{\mathbb{R}}}^n}\frac{w(x+y)+w(x-y)-2w(x)}{|y|^{n+\sigma}}\,{\rm d}y\right|\\ & \le\int_{|y|\le1}\frac{|w(x+y)+w(x-y)-2w(x)|}{|y|^{n+\sigma}}\,{\rm d}y\\ & \quad+\int_{|y|>1}\frac{|w(x+y)+w(x-y)-2w(x)|}{|y|^{n+\sigma}}\,{\rm d}y\\ & \lesssim\|w\|_{\Lambda^{\sigma+s}({{{\mathbb{R}}}^n})}\int_{|y|\le1}\frac{1}{|y|^{n-s}}\,{\rm d}y +\|w\|_{L^\infty({{{\mathbb{R}}}^n})}\int_{|y|>1}\frac{1}{|y|^{n+\sigma}}\,{\rm d}y\\ & \lesssim\|w\|_{\Lambda^{\sigma+s}({{{\mathbb{R}}}^n})}. \end{align*}

Thus, $w\in J_\sigma ({\mathop {\mathrm {BMO}}}({\mathbb {R}^n}))$. In addition, from the classical theory of the Fourier transform (see, for instance, [Reference Abels2, remark 2.2]), it follows that $w\in C^\infty _b({\mathbb {R}^n})$.

Let $v:=u-w$. Then, we have $v\in J_\sigma ({\mathop {\mathrm {BMO}}}({\mathbb {R}^n})) \cap J_\sigma (L^2({\mathbb {R}^n}))\cap C_b^\infty ({\mathbb {R}^n})$ and

(3.11)\begin{equation} Lv-\lambda v=(1-\eta)\left[f-(f)_{B_{4kr}(x_0)}\right]+(f)_{B_{4kr}(x_0)}. \end{equation}

By the fact that $(1-\eta )[f-(f)_{B_{4kr}(x_0)}]+(f)_{B_{4kr}(x_0)}$ is a constant in $B_{2kr}(x_0)$, similarly to the proof of lemma 3.5, we find that

(3.12)\begin{equation} \left(|v-(v)_{B_r(x_0)}|\right)_{B_r(x_0)} \lesssim k^{-\alpha}(kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{|v(x)-(v)_{B_{kr}(x_0)}|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x. \end{equation}

Applying $(-\Delta )^{\sigma /2}$ to both sides of (3.11), we conclude that

\[ L(-\Delta)^{\sigma/2}u-\lambda (-\Delta)^{\sigma/2}u= (-\Delta)^{\sigma/2}\left((1-\eta)\left[f-(f)_{B_{4kr}(x_0)}\right]\right). \]

For any $x\in B_{kr}(x_0)$, we have $(1-\eta )\left (x\right )=0$ and, if $y\in B_{kr/2}(x)$, then $(1-\eta) \left (x+y\right )=0$. By this, proposition 3.1, and the fact that, for any $x\in B_{kr}(x_0)$ and $y\notin B_{kr/2}(x)$, $|y-x|\gtrsim |y-x_0|$, we find that, for any $x\in B_{kr}(x_0)$,

\begin{align*} & \left|(-\Delta)^{\sigma/2}\left((1-\eta)\left[f-(f)_{B_{4kr}(x_0)}\right]\right)(x)\right|\\ & \quad =c\left|\lim_{\varepsilon\to 0^+}\int_{|y|\ge\varepsilon}(1-\eta)\left[f-(f)_{B_{4kr}(x_0)}\right](x+y)\frac{{\rm d}y}{|y|^{n+\sigma}}\right|\nonumber \\ & \quad\lesssim\int_{|y-x|\ge kr/2}\frac{\left|f(y)-(f)_{B_{4kr}(x_0)}\right|}{|y-x|^{n+\sigma}}{\rm d}y\\ & \quad\lesssim\int_{|y-x|\ge kr/2}\frac{\left|f(y)-(f)_{B_{4kr}(x_0)}\right|}{(4kr)^{n+\sigma}+|y-x|^{n+\sigma}}{\rm d}y\\ & \quad\lesssim\int_{|y-x|\ge kr/2}\frac{\left|f(y)-(f)_{B_{4kr}(x_0)}\right|}{(4kr)^{n+\sigma}+|y-x_0|^{n+\sigma}}{\rm d}y\\ & \quad\lesssim (kr)^{-\sigma}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}. \end{align*}

This, together with lemma 3.3 and the scaling and shifting the coordinates argument as in lemma 3.5, implies that

(3.13)\begin{align} & \left(\left|(-\Delta)^{\sigma/2}v-\left((-\Delta)^{\sigma/2}v\right)_{B_r(x_0)}\right|\right)_{B_r(x_0)} \nonumber\\ & \quad\lesssim k^{-\alpha}(kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{\left|(-\Delta)^{\sigma/2}v(x)-\left((-\Delta)^{\sigma/2}v\right)_{B_{kr}(x_0)}\right|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x +k^{-\alpha}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}. \end{align}

From (3.13), we deduce that

(3.14)\begin{align} & \left(\left|(-\Delta)^{\sigma/2}u-\left((-\Delta)^{\sigma/2}u\right)_{B_r(x_0)}\right|\right)_{B_r(x_0)} \nonumber\\ & \quad\le\left(\left|(-\Delta)^{\sigma/2}v-\left((-\Delta)^{\sigma/2}v\right)_{B_r(x_0)}\right|\right)_{B_r(x_0)} +2\left(\left|(-\Delta)^{\sigma/2}w\right|\right)_{B_r(x_0)} \nonumber\\ & \quad\lesssim k^{-\alpha}(kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{\left|(-\Delta)^{\sigma/2}v(x)-\left((-\Delta)^{\sigma/2}v\right)_{B_{kr}(x_0)}\right|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x \nonumber\\ & \qquad+\left(\left|(-\Delta)^{\sigma/2}w\right|\right)_{B_r(x_0)}+k^{-\alpha}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} \nonumber\\ & \quad\lesssim k^{-\alpha}(kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{\left|(-\Delta)^{\sigma/2}u(x)-\left((-\Delta)^{\sigma/2}u\right)_{B_{kr}(x_0)}\right|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x \nonumber\\ & \qquad+k^{-\alpha}(kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{\left|(-\Delta)^{\sigma/2}w(x)-\left((-\Delta)^{\sigma/2}w\right)_{B_{kr}(x_0)}\right|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x \nonumber\\ & \qquad+\left(\left|(-\Delta)^{\sigma/2}w\right|\right)_{B_r(x_0)}+k^{-\alpha}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}. \end{align}

Moreover, by (3.10) and the equivalent characterization of $\|f\|_{{\mathop {\mathrm {BMO}}}({\mathbb {R}^n})}$ (see, for instance, [Reference Grafakos14, corollary 3.1.9]), we conclude that, for any $p\in (1,\,\infty )$ and $R\in [r,\,\infty )$,

(3.15)\begin{align} \left(\left|(-\Delta)^{\sigma/2}w\right|\right)_{B_R(x_0)} & \le\left(\frac{1}{|B_R(x_0)|}\int_{B_R(x_0)}\left|(-\Delta)^{\sigma/2}w\right|^p\,{\rm d}x\right)^{1/p} \nonumber\\ & \le\frac{1}{|B_R(x_0)|^{1/p}}\left(\int_{{{\mathbb{R}}}^n}\left|\eta \left[f-(f)_{B_{4kr}(x_0)}\right]\right|^p\,{\rm d}x\right)^{1/p} \nonumber\\ & \lesssim\left(\frac{kr}{R}\right)^{n/p}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}. \end{align}

Furthermore, take $p\in (1,\,\infty )$ small enough such that $n/p+\sigma >1$. Then, from (3.15), it follows that

(3.16)\begin{align} & (kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{\left|(-\Delta)^{\sigma/2}w(x)-\left((-\Delta)^{\sigma/2}w\right)_{B_{kr}(x_0)}\right|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x \nonumber\\ & \quad\le(kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{\left|(-\Delta)^{\sigma/2}w(x)\right|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x +(kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{\left|\left((-\Delta)^{\sigma/2}w\right)_{B_{kr}(x_0)}\right|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x \nonumber\\ & \quad\lesssim(kr)^\sigma\sum_{j=0}^{\infty}\int_{jkr\le|x-x_0|<(j+1)kr}\frac{\left|(-\Delta)^{\sigma/2}w(x)\right|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x+\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} \nonumber\\ & \quad\lesssim(kr)^\sigma\sum_{j=0}^{\infty}\frac{1}{(j^{n+\sigma}+1)(kr)^{n+\sigma}}\int_{|x-x_0|<(j+1)kr}\left|(-\Delta)^{\sigma/2}w(x)\right| \,{\rm d}x\nonumber\\ & \quad\quad+\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} \nonumber\\ & \quad\lesssim \sum_{j=0}^{\infty}\frac{(j+1)^{n-n/p}}{j^{n+\sigma}+1}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} +\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\lesssim \|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}, \end{align}

which, together with (3.14), (3.15) and proposition 3.1, further implies that

(3.17)\begin{align} & \left(\left|(-\Delta)^{\sigma/2}u-\left((-\Delta)^{\sigma/2}u\right)_{B_r(x_0)}\right|\right)_{B_r(x_0)} \nonumber\\ & \quad\lesssim k^{-\alpha}(kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{\left|(-\Delta)^{\sigma/2}u(x)-\left((-\Delta)^{\sigma/2}u\right)_{B_{kr}(x_0)}\right|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x \nonumber\\ & \quad+k^{n/p}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+k^{-\alpha}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} \nonumber\\ & \quad\lesssim k^{-\alpha}\left\|(-\Delta)^{\sigma/2}u\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+k^{n/2}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} +k^{-\alpha}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} \nonumber\\ & \quad\lesssim k^{-\alpha}\left\|(-\Delta)^{\sigma/2}u\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+k^{n/2}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}. \end{align}

Similarly, by (3.10), (3.12) and proposition 3.1, we find that

\begin{align*} & \lambda\left(\left|u-(u)_{B_r(x_0)}\right|\right)_{B_r(x_0)}\nonumber \\ & \quad\le\lambda\left(\left|v-(v)_{B_r(x_0)}\right|\right)_{B_r(x_0)}+2\lambda(|w|)_{B_r(x_0)}\nonumber \\ & \quad\lesssim\lambda k^{-\alpha}(kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{|v(x)-(v)_{B_{kr}(x_0)}|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x+k^{n/2}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\nonumber \\ & \quad\lesssim\lambda k^{-\alpha}(kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{|u(x)-(u)_{B_{kr}(x_0)}|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x\nonumber \\ & \qquad+\lambda k^{-\alpha}(kr)^\sigma\int_{{{\mathbb{R}}}^n}\frac{|w(x)-(w)_{B_{kr}(x_0)}|} {(kr)^{n+\sigma}+|x-x_0|^{n+\sigma}}\,{\rm d}x+k^{n/2}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\nonumber \\ & \quad\lesssim\lambda k^{-\alpha}\left\|u\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} +k^{n/2}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+k^{-\alpha}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\nonumber \\ & \quad\lesssim\lambda k^{-\alpha}\left\|u\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+k^{n/2}\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}, \end{align*}

which, combined with (3.17), further implies that lemma 3.6 holds true. This finishes the proof of lemma 3.6.

Let $\phi$ be a non-negative, real-valued function in $C_{\rm c}^\infty ({\mathbb {R}^n})$ with the property that $\int _{\mathbb {R}^n}\phi (x)\,{\rm d}x=1$ and $\mathop{\mathrm {\,supp\,}}(\phi )\subset B_1$. For any $\varepsilon \in (0,\,\infty )$, let $\phi _\varepsilon (\cdot ): =\frac {1}{\varepsilon ^{n}}\phi (\frac {\cdot }{\varepsilon })$. Let $u\in L^p({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ for some $p\in (1,\,\infty )$. The mollification $u_\varepsilon$ of $u$ is defined by, for any $x\in {\mathbb {R}^n}$,

\[ u_\varepsilon(x):=\phi_\varepsilon\ast u(x) =\int_{{{\mathbb{R}}}^n}\phi_\varepsilon(x-y)u(y)\,{\rm d}y. \]

Then, we have the following well-known properties of $u_\varepsilon$ (see, for instance, [Reference Ziemer32, theorem 1.6.1]).

Lemma 3.7 Let $p\in (1,\,\infty ),$ $u\in L^p({\mathbb {R}^n})\cap L^\infty ({\mathbb {R}^n})$ and $u_\varepsilon$ be the mollification of $u$. Then the following properties hold true.

(i) For any $\varepsilon \in (0,\,\infty ),$ $u_\varepsilon \in C^\infty ({\mathbb {R}^n})$.
(ii) For any $\varepsilon \in (0,\,\infty ),$ $u_\varepsilon \in L^p({\mathbb {R}^n})$ and $\lim _{\varepsilon \to 0}\|u-u_\varepsilon \|_{L^p({\mathbb {R}^n})}=0$.
(iii) For any $\varepsilon \in (0,\,\infty ),$ $\|u_\varepsilon \|_{L^\infty ({\mathbb {R}^n})}\le \|u\|_{L^\infty ({\mathbb {R}^n})}$.

In addition, when $u\in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$, we have the following property of $u_{\varepsilon }$.

Lemma 3.8 Let $u\in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ and $u_\varepsilon$ be the mollification of $u$. Then, for any $\varepsilon \in (0,\,\infty ),$ $u_\varepsilon \in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ and

\[ \|u_\varepsilon\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\le C\|u\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}, \]

where $C$ is a positive constant independent of $\varepsilon$ and $u$.

Proof. Let $\varepsilon \in (0,\,\infty )$ and $B_r(x_0)\subset {\mathbb {R}^n}$ be a ball. By the equivalent characterization of $\|u_\varepsilon \|_{{\mathop {\mathrm {BMO}}}({\mathbb {R}^n})}$ (see, for instance, [Reference Grafakos14, proposition 3.1.2(4)]), to show lemma 3.8, we only need to prove that, for any $B_r(x_0)\subset {\mathbb {R}^n}$, there exists a constant $c$ such that

(3.18)\begin{equation} \frac{1}{|B_r(x_0)|}\int_{B_r(x_0)}|u_\varepsilon(x)-c|\,{\rm d}x\le C\|u\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}. \end{equation}

We first assume that $r\le \varepsilon$. In this case, let $c:=(u)_{B_{3\varepsilon }(x_0)}$. Then, by the fact that, for any $x\in B_r(x_0)$ with $r\le \varepsilon$ and $y\in B_\varepsilon (x)$, $y\in B_{3\varepsilon }(x_0)$, we have

(3.19)\begin{align} & \frac{1}{|B_r(x_0)|}\int_{B_r(x_0)}|u_\varepsilon(x)-c|\,{\rm d}x \nonumber\\ & \quad\le\frac{1}{|B_r(x_0)|}\int_{B_r(x_0)}\frac{1}{\varepsilon^n}\int_{B_\varepsilon(x)}\phi\left(\frac{x-y}{\varepsilon}\right) |u(y)-c|\,{\rm d}y{\rm d}x \nonumber\\ & \quad\le\frac{1}{|B_r(x_0)|}\int_{B_r(x_0)}\frac{1}{\varepsilon^n}\int_{B_{3\varepsilon}(x_0)}|u(y)-(u)_{B_{3\varepsilon}(x_0)}|\,{\rm d}y{\rm d}x \nonumber\\ & \quad\lesssim\|u\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}. \end{align}

Now, we assume that $r\ge \varepsilon$. In this case, let $c:=(u)_{B_{2r}(x_0)}$. Then, from the fact that, for any $y\in B_{\varepsilon }$ and $x\in B_r(x_0-y)$ with $r\ge \varepsilon$, $x\in B_{2r}(x_0)$, it follows that

\begin{align*} & \frac{1}{|B_r(x_0)|}\int_{B_r(x_0)}|u_\varepsilon(x)-c|\,{\rm d}x\nonumber \\ & \quad\le\frac{1}{|B_r(x_0)|}\int_{B_r(x_0)}\frac{1}{\varepsilon^n}\int_{B_\varepsilon}\phi\left(\frac{y}{\varepsilon}\right) |u(x-y)-c|\,{\rm d}y{\rm d}x\nonumber \\ & \quad\le\frac{1}{\varepsilon^n}\int_{B_\varepsilon}\phi\left(\frac{y}{\varepsilon}\right)\frac{1}{|B_r(x_0)|}\int_{B_r(x_0)} |u(x-y)-c|\,{\rm d}x{\rm d}y\nonumber \\ & \quad\le\frac{1}{\varepsilon^n}\int_{B_\varepsilon}\phi\left(\frac{y}{\varepsilon}\right)\frac{1}{|B_r(x_0)|}\int_{B_r(x_0-y)} |u(x)-c|\,{\rm d}x{\rm d}y\nonumber \\ & \quad\le\frac{1}{\varepsilon^n}\int_{B_\varepsilon}\phi\left(\frac{y}{\varepsilon}\right) \frac{1}{|B_r(x_0)|}\int_{B_{2r}(x_0)} |u(x)-c|\,{\rm d}x{\rm d}y\nonumber \\ & \quad\lesssim\|u\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}, \end{align*}

which, together with (3.19), further implies that (3.18) holds true. This finishes the proof of lemma 3.8.

To prove theorems 1.2 and 1.4, we also need the following convergence lemma on the space ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$.

Lemma 3.9 Let $p\in (1,\,\infty ),$ $\{f_k\}_{k\in {\mathbb {N}}}\subset {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})\cap L^p({\mathbb {R}^n})$ be a sequence of functions and $f\in L^p({\mathbb {R}^n})$. Assume that $\lim _{k\to \infty }\|f-f_k\|_{L^p({\mathbb {R}^n})}=0$ and $\lim _{k\to \infty }f_k=f$ in the sense of almost everywhere. Then, $f\in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ and

\[ \|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\le\varliminf_{k\to\infty}\|f_k\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}. \]

Proof. Let $B\subset {\mathbb {R}^n}$ be a ball. Then, by the Hölder inequality, we conclude that, for any $k\in {\mathbb {N}}$,

\begin{align*} \left|\,\left|f-(f)_B\right|-\left|f_k-(f_k)_B\right|\,\right| & \le\left|f-f_k\right|+\frac{1}{|B|}\int_B|f-f_k|\,{\rm d}x\\ & \le\left|f-f_k\right|+\left(\frac{1}{|B|}\int_B|f-f_k|^p\,{\rm d}x\right)^{1/p}.\nonumber \end{align*}

Furthermore, from the assumptions that $\lim _{k\to \infty }\|f-f_k\|_{L^p({\mathbb {R}^n})}=0$ and $\lim _{k\to \infty }f_k=f$ in the sense of almost everywhere, we deduce that

\[ \lim_{k\to\infty}\left|f_k-(f_k)_B\right|=\left|f-(f)_B\right|, \]

which, together with the Fatou lemma, further implies that

\[ \frac{1}{|B|}\int_B\left|f-(f)_B\right|\,{\rm d}x \le\varliminf_{k\to\infty}\frac{1}{|B|}\int_B\left|f_k-(f_k)_B\right|\,{\rm d}x \le\varliminf_{k\to\infty}\|f_k\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}. \]

Since the ball $B$ is arbitrary, it follows that

\[ \|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\le\varliminf_{k\to\infty}\|f_k\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}. \]

This finishes the proof of lemma 3.9.

Now, we prove theorem 1.2 by using lemmas 2.3, 2.4, 2.5, 3.3, 3.6, 3.7 and 3.9.

Proof of theorem 1.2. We first show (i). Let $\lambda \in (0,\,\infty )$, $u\in J_ \sigma (L^p({\mathbb {R}^n}))\cap J_\sigma ({\mathop {\mathrm {BMO}}}({\mathbb {R}^n}))$ and $f=-(-\Delta )^{\sigma /2}u-\lambda u$. Then, we have $f\in L^p({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$. Let $f_\varepsilon$ be the mollification of $f$. Then, by lemmas 3.7 and 3.8, we find that, for any $\varepsilon \in (0,\,\infty )$, $f_\varepsilon \in L^p({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$. From lemma 2.4, it follows that there exists a $u_\varepsilon \in J_\sigma (L^p({\mathbb {R}^n}))$ such that

(3.20)\begin{equation} -(-\Delta)^{\sigma/2}u_\varepsilon-\lambda u_\varepsilon=f_\varepsilon, \end{equation}

moreover, there exists a positive constant $C$, independent of $f$, $f_\varepsilon$, $u$, $u_\varepsilon$ and $\lambda$, such that

(3.21)\begin{equation} \|Lu_\varepsilon-Lu\|_{L^p({{{\mathbb{R}}}^n})}\le C\|f_\varepsilon-f\|_{L^p({{{\mathbb{R}}}^n})}. \end{equation}

Let $\{\chi _j\}_{j\in {\mathbb {N}}}$ be a sequence of smooth functions satisfying that $\chi _j=1$ on the ball $B_j$, $\mathop{\mathrm {\,supp\,}}(\chi _j)\subset B_{j+1}$, and $0\le \chi _j\le 1$, where, for any $j\in {\mathbb {N}}$, $B_j:=B(\mathbf {0},\,j)$. Then, we have $\chi _jf_\varepsilon \in C_{\rm c}^\infty ({\mathbb {R}^n})$ for any $j\in {\mathbb {N}}$ and

(3.22)\begin{equation} \lim_{j\to\infty}\left\|\chi_j f_\varepsilon-f_\varepsilon\right\|_{L^p({{{\mathbb{R}}}^n})}=0. \end{equation}

Moreover, from lemma 2.4 and the theory of Fourier transform (see, for instance, [Reference Abels2, remark 2.2]), we deduce that there exists a unique $u_{\varepsilon,j}\in C^\infty _b({\mathbb {R}^n})\cap J_\sigma (L^2({\mathbb {R}^n}))$ such that

(3.23)\begin{equation} -(-\Delta)^{\sigma/2}u_{\varepsilon,j}-\lambda u_{\varepsilon,j}=\chi_jf_\varepsilon, \end{equation}

meanwhile, there exists a positive constant $C$, independent of $f_\varepsilon$, $u_\varepsilon$, $u_{\varepsilon,j}$, $\chi _j$ and $\lambda$, such that

(3.24)\begin{equation} \left\|Lu_{\varepsilon,j}-Lu_\varepsilon\right\|_{L^p({{{\mathbb{R}}}^n})}\le C\left\|\chi_jf_\varepsilon-f_\varepsilon\right\|_{L^p({{{\mathbb{R}}}^n})}. \end{equation}

Take $\eta \in C_{\rm c}^\infty ({\mathbb {R}^n})$ such that $\eta \equiv 1$ on $B_2$, $\mathop{\mathrm {\,supp\,}}(\eta )\subset B_4$ and $0\le \eta \le 1$. Then, we have $\eta \chi _jf_\varepsilon \subset C_{\rm c}^\infty ({\mathbb {R}^n})$. By using lemma 2.4 and the theory of Fourier transform again, we find that there exists a unique $w_{\varepsilon,j}\in J_\sigma (\cap _{q\in (1,\infty )}L^q({\mathbb {R}^n})) \cap C^\infty _b({\mathbb {R}^n})$ such that

\[ -(-\Delta)^{\sigma/2}w_{\varepsilon,j}-\lambda w_{\varepsilon,j}=\eta\chi_jf_\varepsilon \]

and, for any $q\in (1,\,\infty )$,

(3.25)\begin{equation} \left\|Lw_{\varepsilon,j}\right\|_{L^q({{{\mathbb{R}}}^n})}\le C\left\|\eta\chi_jf_{\varepsilon}\right\|_{L^q({{{\mathbb{R}}}^n})}, \end{equation}

where $C$ is a positive constant independent of $w_{\varepsilon,j}$, $\eta$, $\chi _j$, $f_\varepsilon$ and $\lambda$.

Let $v_{\varepsilon,j}:=u_{\varepsilon,j}-w_{\varepsilon,j}\in J_\sigma (L^2({\mathbb {R}^n}))\cap C^\infty _b({\mathbb {R}^n})$. Then

(3.26)\begin{equation} -(-\Delta)^{\sigma/2}v_{\varepsilon,j}-\lambda v_{\varepsilon,j}=(1-\eta)\chi_jf_\varepsilon. \end{equation}

By applying $L$ to both sides of (3.26), we conclude that

\[ -(-\Delta)^{\sigma/2}Lv_{\varepsilon,j}-\lambda Lv_{\varepsilon,j}=L\left[(1-\eta)\chi_jf_\varepsilon\right]. \]

From the fact that $v_{\varepsilon,j}\in C^\infty _b({\mathbb {R}^n})\subset \Lambda ^s({\mathbb {R}^n})$ for any $s\in (0,\,\infty )$ and lemma 2.5, we deduce that $Lv_{\varepsilon,j}\in \Lambda ^s({\mathbb {R}^n})$ for any $s\in (0,\,\infty )$. Then, by proposition 2.2, we find that $Lv_{\varepsilon,j}\in L^\infty ({\mathbb {R}^n})\cap C^2({\mathbb {R}^n})$, which, together with lemma 3.3, further implies that there exists $\alpha \in (0,\,\min \{1,\,\sigma \})$ such that

(3.27)\begin{equation} \left[Lv_{\varepsilon,j}\right]_{C^\alpha(B_{1/2})}\le C\left\{\left\|Lv_{\varepsilon,j}-(Lv_{\varepsilon,j})_{B_1} \right\|_{L^1({{{\mathbb{R}}}^n},\omega)}+\left\|L\left[(1-\eta)\chi_jf_\varepsilon\right]\right\|_{L^\infty(B_1)}\right\}, \end{equation}

where $C$ is a positive constant independent of $v_{\varepsilon,j}$, $\eta$, $\chi _j$, $f_\varepsilon$ and $\lambda$. For any $x\in B_1$, we have that $(1-\eta )\chi _jf_\varepsilon (x)=0$, and if $y\in B_{1/2}$, then $(1-\eta )\chi _jf_\varepsilon (x+y)=0$. Meanwhile, by $f\in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ and lemma 3.8, we find that, for any $\varepsilon \in (0,\,\infty )$, $f_\varepsilon \in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$, which, combined with the characterization of pointwise multipliers for functions of bounded mean oscillation (see, for instance, [Reference Nakai and Yabuta21, theorem 1]), implies that, for any $j\in {\mathbb {N}}$ and $\varepsilon \in (0,\,\infty )$, $(1-\eta )\chi _jf_\varepsilon \in {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$. Moreover, from [Reference Nakai and Yabuta21, lemmas 3.1 and 3.3] and the proof of [Reference Nakai and Yabuta21, theorem 1] (see [Reference Nakai and Yabuta21, pp. 215-216]), we deduce that

\[ \left\|(1-\eta)\chi_jf_\varepsilon\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\lesssim\left\|f_\varepsilon\right\|_{{\mathop{\mathrm {BMO}}}+({{{\mathbb{R}}}^n})}, \]

which, together with the fact that, for any $x\in B_1$, $((1-\eta )\chi _jf_\varepsilon )_{B_{1/2}(x)} =0$, proposition 3.1, and lemma 3.8, further implies that, for any $x\in B_1$,

\begin{align*} \left|L\left[(1-\eta)\chi_jf_\varepsilon(x)\right]\right| & \le C\int_{|y|\ge\frac12}\frac{|(1-\eta)\chi_j f_\varepsilon(x+y)|}{|y|^{n+\sigma}}\,{\rm d}y\\ & =C\int_{|y-x|\ge\frac12}\frac{|(1-\eta)\chi_j f_\varepsilon(y)-((1-\eta)\chi_jf_\varepsilon)_{B_{1/2}(x)}|}{|y-x|^{n+\sigma}}\,{\rm d}y\\ & \le C\left\|(1-\eta)\chi_jf_\varepsilon\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\le C\left\|f_\varepsilon\right\|_{{\mathop{\mathrm {BMO}}}+({{{\mathbb{R}}}^n})}\\ & \le C\left[\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left|(f_\varepsilon)_{B_1}\right|\right], \end{align*}

where $C$ is a positive constant independent of $\eta$, $\chi _j$, $f_\varepsilon$ and $\lambda$. By this and (3.27), we conclude that

(3.28)\begin{equation} \left[Lv_{\varepsilon,j}\right]_{C^\alpha(B_{1/2})}\le C\left[\left\|Lv_{\varepsilon,j}-(Lv_{\varepsilon,j})_{B_1} \right\|_{L^1({{{\mathbb{R}}}^n},\omega)}+\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left|(f_\varepsilon)_{B_1}\right|\right]. \end{equation}

Then, similarly to the proofs of lemmas 3.5 and 3.6, by (3.25), (3.28), and a scaling and shifting the coordinates argument, we conclude that, for any $k\in [2,\,\infty )$,

\begin{align*} & \left(\left|Lu_{\varepsilon,j}-(Lu_{\varepsilon,j})_{B_r(x_0)}\right|\right)_{B_r(x_0)}\nonumber\\& \quad \le C\left\{k^{-\alpha} \|Lu_{\varepsilon,j}\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} +k^{n/2}\left[\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left|(f_\varepsilon)_{B_1}\right|\right]\right\}, \end{align*}

where $C$ is a positive constant independent of $x_0$, $r$, $k$, $u_{\varepsilon,j}$, $f$ and $\lambda$. Since $x_0$ and $r$ are arbitrary, it follows that, by taking a sufficient large $k$ such that $Ck^{-\alpha }\le \frac 12$, we have

(3.29)\begin{equation} \left\|Lu_{\varepsilon,j}\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\le C\left[\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left|(f_\varepsilon)_{B_1}\right|\right], \end{equation}

where $C$ is a positive constant independent of $f$, $u_{\varepsilon,j}$ and $\lambda$.

Furthermore, by (3.22) and (3.24), we find that there exists a subsequence of $\{Lu_{\varepsilon,j}\}_{j\in {\mathbb {N}}}$, still denoted by $\{Lu_{\varepsilon,j}\}_{j\in {\mathbb {N}}}$, such that

\[ \lim_{j\to\infty}Lu_{\varepsilon,j}=Lu_{\varepsilon} \]

in the sense of almost everywhere, which, together with lemma 3.9 and (3.29), further implies that

(3.30)\begin{equation} \|Lu_{\varepsilon}\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\le C\left[\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left|(f_\varepsilon)_{B_1}\right|\right]. \end{equation}

Similarly, from (3.30), (3.21) and lemmas 3.7 and 3.9, we deduce that

(3.31)\begin{align} \|Lu\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} & \le C\left[\left\|f\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left|(f)_{B_1}\right|\right] \nonumber\\ & =C\left[\left\|-(-\Delta)^{\sigma/2}u-\lambda u\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left|\left(-(-\Delta)^{\sigma/2}u-\lambda u\right)_{B_1}\right|\right]. \end{align}

Since the constant $C$ in (3.31) is independent of $\lambda$, by taking $\lambda \to 0^+$, we obtain (i). This finishes the proof of (i).

Next, we prove (ii) by borrowing some ideas from [Reference Dong, Jung and Kim6] (see also [Reference Mikulevičius and Pragarauskas20]). We first assume that $\sigma \in (0,\,1)$. From the proof of [Reference Dong, Jung and Kim6, proposition 4.1], it follows that

\begin{align*} Lu& =\int_{{{\mathbb{R}}}^n}(u(x+y)-u(x))a(y)\frac{{\rm d}y}{|y|^{n+\sigma}}\\ & =\lim_{\varepsilon\to0^+}C_0\,{\mathrm P.V.}\int_{{{\mathbb{R}}}^n}\left(\int_{{{\mathbb{R}}}^n} k^\sigma(z,y)a_\varepsilon(y)\frac{{\rm d}y} {|y|^{n+\sigma}}\right)\partial^\sigma u(x-z)\,{\rm d}z, \end{align*}

where $C_0:=\frac {\Gamma ((n-\alpha )/2)}{2^\alpha \pi ^{n/2}\Gamma (\alpha /2)}$, $\varepsilon \in (0,\,1)$, $a_\varepsilon (y):=a(y)\mathbf {1}_{\varepsilon \le 1\le \frac {1}{\varepsilon }}$, and $k^\sigma (z,\,y):=|z+y|^{-n+\sigma }-|z|^{-n+\sigma }$.

Let

\[ k_\varepsilon(z):=\int_{{{\mathbb{R}}}^n} k^\sigma(z,y)a_\varepsilon(y)\frac{{\rm d}y}{|y|^{n+\sigma}}. \]

Then, we have

\[ Lu(x)=\lim_{\varepsilon\to0^+}\int_{{{\mathbb{R}}}^n} k_\varepsilon(z)\partial^\sigma u(x-z)\,{\rm d}z=:\lim_{\varepsilon\to0^+}C_0T^\varepsilon\partial^\sigma u(x), \]

where $T^\varepsilon$ denotes the singular integral operator associated with the kernel $k_\varepsilon$. By [Reference Dong, Jung and Kim6, lemmas 4.4 and 4.5], we conclude that the assumptions in lemma 2.3 are satisfied. Thus, from lemma 2.3 and the Fatou lemma, we deduce that

(3.32)\begin{equation} \|Lu\|_{L^1({{{\mathbb{R}}}^n})}\lesssim\varliminf_{\varepsilon\to0^+}\left\|T^\varepsilon\partial^\sigma u\right\|_{L^1({{{\mathbb{R}}}^n})} \lesssim\left\|\partial^\sigma u\right\|_{H^1({{{\mathbb{R}}}^n})}. \end{equation}

For the case $\sigma =1$ and $\sigma \in (1,\,2)$, (1.7) also holds true. Indeed, if $\sigma \in (1,\,2)$, $L_\varepsilon u$ can be written as

\[ \sum_{i=1}^n\int_{{{\mathbb{R}}}^n}\left[D_iu(x+y)-D_iu(x)\right](a_\varepsilon)_i(y)\frac{{\rm d}y}{|y|^{n+\sigma-1}} =\sum_{i=1}^nL^{(a_\varepsilon)_i}(D_iu)(x), \]

where

\[ (a_\varepsilon)_i(y):=\frac{y_i}{|y|}\int_0^1a_\varepsilon\left(\frac{y}{s}\right)s^{{-}1+\sigma}\,ds, \]

and $L^{(a_\varepsilon )_i}$ denotes the non-local elliptic operator defined by

\[ L^{(a_\varepsilon)_i}u(x):=\int_{{{\mathbb{R}}}^n}[u(x+y)-u(x)](a_\varepsilon)_i(y)\frac{{\rm d}y}{|y|^{n+\sigma-1}}. \]

Then, by (3.32) and the boundedness of the Riesz transform on $H^1({\mathbb {R}^n})$ (see, for instance, [Reference Stein27, chapter III, theorem 4]), we conclude that

(3.33)\begin{align} \|Lu\|_{L^1({{{\mathbb{R}}}^n})} & \lesssim\varliminf_{\varepsilon\to0}\sum_{i=1}^n\left\|L^{(a_\varepsilon)_i}(D_i(u))\right\|_{L^1({{{\mathbb{R}}}^n})} \nonumber\\ & \lesssim\sum_{i=1}^n\left\|\partial^{\sigma-1}D_iu\right\|_{H^1({{{\mathbb{R}}}^n})} \!\lesssim\!\left\|\partial^\sigma u\right\|_{H^1({{{\mathbb{R}}}^n})}. \end{align}

Thus, (1.7) holds true in the case of $\sigma \in (1,\,2)$.

If $\sigma =1$, via using assumption 1.1(ii) and an argument used in [Reference Dong, Jung and Kim6, p. 18], we find that

\begin{align*} Lu(x)& =\lim_{\varepsilon\to0^+}L_\varepsilon u(x)\nonumber\\ & :=\lim_{\varepsilon\to0^+}C_0\,{\mathrm P.V.}\int_{{{\mathbb{R}}}^n}\left(\partial^{1/2}u(x-z)-\partial^{1/2}u(x)\right) m_\varepsilon(z)\frac{{\rm d}z}{|z|^{n+\sigma-1/2}}, \end{align*}

where, for any $\varepsilon \in (0,\,\infty )$ and $z\in {\mathbb {R}^n}$ with $z\neq \mathbf {0}$,

\begin{align*} m_\varepsilon(z)& :=\int_{|y|\le\frac12}\left[\frac{1}{\left|z/|z|+y\right|^{n-1/2}}-1-\left({-}n+\frac12\right) \left(\frac{z}{|z|},y\right)\right] a_\varepsilon(|z|y)\,\frac{{\rm d}y}{|y|^{n+\sigma}}\\ & \quad+\int_{|y|>\frac12}\left(\frac{1}{\left|z/|z|+y\right|^{n-1/2}}-1\right)a_\varepsilon\left(|z|y\right)\frac{{\rm d}y}{|y|^{n+\sigma}} \end{align*}

satisfies that there exists a positive constant $C$, depending only on $n$, such that $|m_\varepsilon (z)|\le C$. Since $\sigma -\frac 12\in (\frac 14,\,\frac 34)$ and $|m_\varepsilon (z)|\lesssim 1$ for any $\varepsilon \in (0,\,\infty )$ and $z\in {\mathbb {R}^n}$ with $z\neq \mathbf {0}$, similar to the proof of (3.32), it follows that

\[ \|Lu\|_{L^1({{{\mathbb{R}}}^n})}\le\varliminf_{\varepsilon\to0^+}\left\|L_\varepsilon u\right\|_{L^1({{{\mathbb{R}}}^n})}\lesssim\left\|\partial^{1/2}\partial^{1/2}u\right\|_{H^1({{{\mathbb{R}}}^n})}\lesssim\left\|\partial^1 u\right\|_{H^1({{{\mathbb{R}}}^n})}. \]

This, together with (3.32) and (3.33), implies that

(3.34)\begin{equation} \left\|Lu\right\|_{L^1({{{\mathbb{R}}}^n})}\lesssim\left\|\partial^\sigma u\right\|_{H^1({{{\mathbb{R}}}^n})} \end{equation}

holds true for any $\sigma \in (0,\,2)$.

Furthermore, it is known that $J_\sigma (L^2({\mathbb {R}^n}))\cap I_\sigma (H^1({\mathbb {R}^n}))$ is dense in $I_\sigma (H^1({\mathbb {R}^n}))$ (see, for instance, [Reference Triebel30, chapter 5]). Therefore, for any $u\in J_\sigma (H^1({\mathbb {R}^n}))$, there exists a Cauchy sequence $\{u_k\}_{k\in {\mathbb {N}}}\subset J_\sigma (L^2({\mathbb {R}^n}))\cap I_\sigma (H^1({\mathbb {R}^n}))$ such that $u_k$ converges to $u$ in $I_\sigma (H^1({\mathbb {R}^n}))$. By lemma 2.4 and (3.34), we find that, for any $k\in {\mathbb {N}}$, $Lu_k\in L^2({\mathbb {R}^n})\cap L^1({\mathbb {R}^n})$ and

(3.35)\begin{equation} \|Lu_k\|_{L^1({{{\mathbb{R}}}^n})}\lesssim\|\partial^\sigma u_k\|_{H^1({{{\mathbb{R}}}^n})}. \end{equation}

Moreover, from the boundedness of the Riesz transform $R_j$ on $H^1({\mathbb {R}^n})$ and (3.34), we deduce that, for any $k\in {\mathbb {N}}$,

\begin{align*} \left\|R_jLu_k\right\|_{L^1({{{\mathbb{R}}}^n})}& =\left\|LR_ju_k\right\|_{L^1({{{\mathbb{R}}}^n})}\lesssim\left\|\partial^\sigma R_ju_k\right\|_{H^1({{{\mathbb{R}}}^n})}\\ & =\left\|R_j\partial^\sigma u_k\right\|_{H^1({{{\mathbb{R}}}^n})}\lesssim\left\|\partial^\sigma u_k\right\|_{H^1({{{\mathbb{R}}}^n})}, \end{align*}

which, combined with (3.35), further implies that, for any $k\in {\mathbb {N}}$,

\[ \left\|Lu_k\right\|_{H^1({{{\mathbb{R}}}^n})}\lesssim\left\|\partial^\sigma u_k\right\|_{H^1({{{\mathbb{R}}}^n})}. \]

By this estimate and the density of $J_\sigma (L^2({\mathbb {R}^n}))\cap I_\sigma (H^1({\mathbb {R}^n}))$ in $I_\sigma (H^1({\mathbb {R}^n}))$, we conclude that (1.7) holds true. Therefore, this finishes the proof of (ii) and hence of theorem 1.2.

Next, we prove theorem 1.4 by using lemmas 2.4, 2.5, 3.6, 3.7 and 3.9, and theorem 1.2.

Proof of theorem 1.4. We first show (i). Let $p\in (1,\,\infty )$, $f\in L^p({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ and $f_\varepsilon$ be the mollification of $f$. Then, for any $\varepsilon \in (0,\,\infty )$, $f_\varepsilon \in L^p({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})\cap C^\infty ({\mathbb {R}^n})$. From lemma 2.4, it follows that there exist solutions $u,\,u_\varepsilon \in J_\sigma (L^p({\mathbb {R}^n}))$ for the equation (1.1) with respect to $f$ and $f_\varepsilon$, respectively, with satisfying that

\begin{align*} & \lambda\|u\|_{L^p({{{\mathbb{R}}}^n})}+\left\|\partial^\sigma u\right\|_{L^p({{{\mathbb{R}}}^n})}\le C\|f\|_{L^p({{{\mathbb{R}}}^n})},\\ & \lambda\|u_\varepsilon\|_{L^p({{{\mathbb{R}}}^n})}+\left\|\partial^\sigma u_\varepsilon\right\|_{L^p({{{\mathbb{R}}}^n})}\le C\|f_\varepsilon\|_{L^p({{{\mathbb{R}}}^n})}, \end{align*}

and

(3.36)\begin{equation} \lambda\|u-u_\varepsilon\|_{L^p({{{\mathbb{R}}}^n})}+\left\|\partial^{\sigma}u-\partial^\sigma u_\varepsilon\right\|_{L^p({{{\mathbb{R}}}^n})}\le C\|f-f_\varepsilon\|_{L^p({{{\mathbb{R}}}^n})}, \end{equation}

where $C$ is a positive constant independent of $u$, $f$, $u_\varepsilon$, $f_\varepsilon$ and $\lambda$.

Let $\{\eta _j\}_{j\in {\mathbb {N}}}$ be a sequence of smooth functions satisfying that $\eta _j=1$ on the ball $B_j$, $\mathop{\mathrm {\,supp\,}}({\eta _j})\subset B_{j+1}$ and $0\le \eta _j\le 1$, where, for any $j\in {\mathbb {N}}$, $B_j:=B(\mathbf 0,\,j)$. For any $j\in {\mathbb {N}}$, we have $\eta _j f_\varepsilon \in C_{\rm c}^\infty ({\mathbb {R}^n})\cap L^2({\mathbb {R}^n})\cap L^p({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ and

(3.37)\begin{equation} \lim_{j\to\infty}\left\|\eta_jf_\varepsilon-f_\varepsilon\right\|_{L^p({{{\mathbb{R}}}^n})}=0. \end{equation}

By lemma 2.4, we find that there exists a unique solution $u_{\varepsilon,j}\in J_\sigma (L^2({\mathbb {R}^n}))\cap J_\sigma (L^p({\mathbb {R}^n}))$ for the equation (1.1) with $f$ replaced by $\eta _jf_\varepsilon$, moreover, there exists a positive constant $C$, independent of $u_\varepsilon$, $f_\varepsilon$, $u_{\varepsilon,j}$, $\eta _j$ and $\lambda$, such that

(3.38)\begin{equation} \lambda\left\|u_{\varepsilon,j}-u_\varepsilon\right\|_{L^p({{{\mathbb{R}}}^n})} +\left\|\partial^\sigma u_{\varepsilon,j}-\partial^\sigma u_{\varepsilon}\right\|_{L^p({{{\mathbb{R}}}^n})} \le C\left\|\eta_jf_\varepsilon-f_\varepsilon\right\|_{L^p({{{\mathbb{R}}}^n})}. \end{equation}

Since $\eta _jf_\varepsilon \in C_{\rm c}^\infty ({\mathbb {R}^n})$, it follows that $\eta _jf_\varepsilon \in C^s({\mathbb {R}^n})$ for any $s\in (0,\,1)$. Then, by lemma 2.5, we conclude that $u_{\varepsilon,j}\in \Lambda ^{s+\sigma }({\mathbb {R}^n})$, which, together with proposition 2.2(iii), further implies that $u_{\varepsilon,j}$ and $\partial ^\sigma u_{\varepsilon,j}$ belong to $L^\infty ({\mathbb {R}^n})$. Thus, $u_{\varepsilon,j}\in J_\sigma ({\mathop {\mathrm {BMO}}})({\mathbb {R}^n})$. From the fact that $\eta _jf_\varepsilon \in C_{\rm c}^\infty ({\mathbb {R}^n})$ and the theory of Fourier transform, we deduce that $u_{\varepsilon,j}\in C_b^\infty ({\mathbb {R}^n})$. Then, by lemma 3.6, we find that

\begin{align*} & \lambda\left(\left|u_{\varepsilon,j}-(u_{\varepsilon,j})_{B_r(x_0)}\right|\right)_{B_r(x_0)}+\left(\left|\partial^\sigma u_{\varepsilon,j}-(\partial^\sigma u_{\varepsilon,j})_{B_r(x_0)}\right|\right)_{B_r(x_0)}\\ & \quad\le C\left\{k^{-\alpha}\left[\lambda\left\|u_{\varepsilon,j}\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left\|\partial^\sigma u_{\varepsilon,j}\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\right] +k^{n/2}\left\|\eta_jf_\varepsilon\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\right\}, \end{align*}

where $C$ is a positive constant independent of $u_{\varepsilon,j}$, $f_{\varepsilon }$, $\eta _j$, $x_0$, $r$, $k$ and $\lambda$. Since $x_0\in {\mathbb {R}^n}$ and $r\in (0,\,\infty )$ are arbitrary, it follows that

\begin{align*} & \lambda\left\|u_{\varepsilon,j}\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left\|\partial^\sigma u_{\varepsilon,j}\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\\ & \quad\le C\left\{k^{-\alpha}\left[\lambda\left\|u_{\varepsilon,j}\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left\|\partial^\sigma u_{\varepsilon,j}\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\right] +k^{n/2}\left\|\eta_jf_\varepsilon\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\right\}. \end{align*}

Via taking a sufficient large $k$ such that $Ck^{-\alpha }\le \frac 12$, we then obtain that

\[ \lambda\left\|u_{\varepsilon,j}\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left\|\partial^\sigma u_{\varepsilon,j}\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\le C\left\|\eta_jf_\varepsilon\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}. \]

By the characterization of pointwise multipliers for functions of bounded mean oscillation (see, for instance, [Reference Nakai and Yabuta21]) and lemmas 3.8, we conclude that

(3.39)\begin{equation} \lambda\left\|u_{\varepsilon,j}\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} +\left\|\partial^\sigma u_{\varepsilon,j}\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\le C\left[\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left|(f_\varepsilon)_{B_1}\right|\right]. \end{equation}

Moreover, from (3.37) and (3.38), we deduce that there exists a subsequence of $\{u_{\varepsilon,j}\}_{j\in {\mathbb {N}}}$, still denoted by $\{u_{\varepsilon,j}\}_{j\in {\mathbb {N}}}$, such that

\[ \lim_{j\to\infty}u_{\varepsilon,j}=u_{\varepsilon} \]

and

\[ \lim_{j\to\infty}\partial^\sigma u_{\varepsilon,j}=\partial^\sigma u_{\varepsilon} \]

in the sense of almost everywhere, which, combined with (3.39) and lemma 3.9, further implies that

(3.40)\begin{equation} \lambda\left\|u_{\varepsilon}\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} +\left\|\partial^\sigma u_{\varepsilon}\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\le C\left[\|f\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left|(f_\varepsilon)_{B_1}\right|\right]. \end{equation}

Similarly, by (3.36), lemma 3.7(ii), (3.40) and lemma 3.9, we find that (1.9) holds true. This finishes the proof of (i).

Next, we prove (ii). We first assume that $f\in H^1({\mathbb {R}^n})\cap L^2({\mathbb {R}^n})$. Let $L^\ast$ be the non-local operator associated with the kernel $a(-\cdot )$. Then, we observe that $a(-\cdot )$ also satisfies assumption 1.1. For any $g\in L^\infty ({\mathbb {R}^n})\cap L^2({\mathbb {R}^n})$, by (i) and lemma 2.4, we conclude that there exists a unique $u\in J_\sigma ({\mathop {\mathrm {BMO}}}({\mathbb {R}^n}))\cap J_\sigma (L^2({\mathbb {R}^n}))$ such that

\[ L^\ast u-\lambda u=g, \]

moreover, there exists a positive constant $C$, independent of $u$, $g$ and $\lambda$, such that

(3.41)\begin{equation} \lambda\|u\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+\left\|\partial^\sigma u\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\le C\left[\|g\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}+ \left|(g)_{B_1}\right|\right]\le C\|g\|_{L^\infty({{{\mathbb{R}}}^n})}. \end{equation}

Furthermore, from lemma 2.4, it follows that there exists a unique $v\in J_\sigma (L^2({\mathbb {R}^n}))$ such that

(3.42)\begin{equation} Lv-\lambda v=f. \end{equation}

Then, we find that

\[ \int_{{{\mathbb{R}}}^n} vg\,{\rm d}x=\int_{{{\mathbb{R}}}^n} v(L^*u-\lambda u)\,{\rm d}x=\int_{{{\mathbb{R}}}^n}(Lv-\lambda v)u\,{\rm d}x=\int_{{{\mathbb{R}}}^n} fu\,{\rm d}x, \]

which, together with (3.41) and the characterization of the norm of $L^1({\mathbb {R}^n})$ (see, for instance, [Reference Folland12, theorem 6.14]) and the fact that ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ is the dual space of $H^1({\mathbb {R}^n})$ (see, for instance, [Reference Grafakos14, theorem 3.2.2] and [Reference Stein27, p. 142, theorem 1]), further implies that

(3.43)\begin{align} \lambda\|v\|_{L^1({{{\mathbb{R}}}^n})} & \le\sup_{\overset{\|g\|_{L^\infty({{{\mathbb{R}}}^n})}\le1}{g\in L^\infty({{{\mathbb{R}}}^n})\cap L^2({{{\mathbb{R}}}^n})}}\left|\int_{{{\mathbb{R}}}^n}\lambda vg\,{\rm d}x\right| =\sup_{\overset{\|g\|_{L^\infty({{{\mathbb{R}}}^n})}\le1}{g\in L^\infty({{{\mathbb{R}}}^n})\cap L^2({{{\mathbb{R}}}^n})}}\left|\int_{{{\mathbb{R}}}^n}\lambda fu\,{\rm d}x\right| \nonumber\\ & \le\sup_{\overset{\|g\|_{L^\infty({{{\mathbb{R}}}^n})}\le1}{g\in L^\infty({{{\mathbb{R}}}^n})\cap L^2({{{\mathbb{R}}}^n})}}\lambda\|u\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})} \|f\|_{H^1({{{\mathbb{R}}}^n})}\lesssim\|f\|_{H^1({{{\mathbb{R}}}^n})}. \end{align}

Similarly, for $(-\Delta )^{\sigma /2}v$, we have

\begin{align*} \int_{{{\mathbb{R}}}^n} (-\Delta)^{\sigma/2}vg\,{\rm d}x& =\int_{{{\mathbb{R}}}^n} (-\Delta)^{\sigma/2}v(L^*u-\lambda u)\,{\rm d}x\\ & =\int_{{{\mathbb{R}}}^n}(Lv-\lambda v)(-\Delta)^{\sigma/2}u\,{\rm d}x=\int_{{{\mathbb{R}}}^n} f(-\Delta)^{\sigma/2}u\,{\rm d}x, \end{align*}

which, combined with (3.41) and the characterization of the norm of $L^1({\mathbb {R}^n})$, implies that

(3.44)\begin{align} \left\|(-\Delta)^{\sigma/2}v\right\|_{L^1({{{\mathbb{R}}}^n})}& \le\sup_{\overset{\|g\|_{L^\infty({{{\mathbb{R}}}^n})}\le1}{g\in L^\infty({{{\mathbb{R}}}^n}) \cap L^2({{{\mathbb{R}}}^n})}}\left|\int_{{{\mathbb{R}}}^n} (-\Delta)^{\sigma/2}vg\,{\rm d}x\right| \nonumber\\ & =\sup_{\overset{\|g\|_{L^\infty({{{\mathbb{R}}}^n})}\le1}{g\in L^\infty({{{\mathbb{R}}}^n})\cap L^2({{{\mathbb{R}}}^n})}} \left|\int_{{{\mathbb{R}}}^n} f(-\Delta)^{\sigma/2}u\,{\rm d}x\right| \nonumber\\ & \le\sup_{\overset{\|g\|_{L^\infty({{{\mathbb{R}}}^n})}\le1}{g\in L^\infty({{{\mathbb{R}}}^n})\cap L^2({{{\mathbb{R}}}^n})}} \left\|(-\Delta)^{\sigma/2}u\right\|_{{\mathop{\mathrm {BMO}}}({{{\mathbb{R}}}^n})}\|f\|_{H^1({{{\mathbb{R}}}^n})}\nonumber\\ & \lesssim\|f\|_{H^1({{{\mathbb{R}}}^n})}. \end{align}

By applying the Riesz transform $R_j$ to the two sides of (3.42), we obtain that

\[ LR_jv-\lambda R_jv=R_jf. \]

Since the Riesz transform $R_j$ is bounded on both $L^2({\mathbb {R}^n})$ and $H^1({\mathbb {R}^n})$, it follows that $R_jf\in L^2({\mathbb {R}^n})\cap H^1({\mathbb {R}^n})$. Then, by using an argument similar to that used in (3.43) and (3.44), we conclude that

\begin{align*} \lambda\left\|R_jv\right\|_{L^1({{{\mathbb{R}}}^n})}+\left\|R_j(-\Delta)^{\sigma/2}v\right\|_{L^1({{{\mathbb{R}}}^n})}& =\lambda\left\|R_jv\right\|_{L^1({{{\mathbb{R}}}^n})}+\left\|(-\Delta)^{\sigma/2}R_jv\right\|_{L^1({{{\mathbb{R}}}^n})} \\ & \lesssim\left\|R_jf\right\|_{H^1({{{\mathbb{R}}}^n})}\lesssim\|f\|_{H^1({{{\mathbb{R}}}^n})}, \end{align*}

which, together with (3.43), (3.44) and (1.4), further implies that

(3.45)\begin{equation} \lambda\|v\|_{H^1({{{\mathbb{R}}}^n})}+\left\|(-\Delta)^{\sigma/2}v\right\|_{H^1({{{\mathbb{R}}}^n})}\lesssim\|f\|_{H^1({{{\mathbb{R}}}^n})}. \end{equation}

Finally, for any $f\in H^1({\mathbb {R}^n})$, it is known that there exists a Cauchy sequence $\{f_k\}_{k\in {\mathbb {N}}}\subset L^2({\mathbb {R}^n})\cap H^1({\mathbb {R}^n})$ such that $f_k$ converges to $f$ in $H^1({\mathbb {R}^n})$ (see, for instance, [Reference Grafakos14, proposition 2.1.7] and [Reference Stein27]). Then, from (3.45) and lemma 2.4, we deduce that, for $f_k$ and $f_m$ with $k$, $m\in {\mathbb {N}}$, there exist $v_k,\,v_m\in J_\sigma (L^2({\mathbb {R}^n}))\cap J_\sigma (H^1({\mathbb {R}^n}))$ such that

\[ Lv_k-\lambda v_k=f_k \]

and

\[ Lv_m-\lambda v_m=f_m, \]

moreover, we have

\[ \lambda\|v_k\|_{H^1({{{\mathbb{R}}}^n})}+\left\|(-\Delta)^{\sigma/2}v_k\right\|_{H^1({{{\mathbb{R}}}^n})}\lesssim\|f_k\|_{H^1({{{\mathbb{R}}}^n})} \]

and

\[ \lambda\|v_k-v_m\|_{H^1({{{\mathbb{R}}}^n})} +\left\|(-\Delta)^{\sigma/2}v_k-(-\Delta)^{\sigma/2}v_m\right\|_{H^1({{{\mathbb{R}}}^n})}\lesssim\|f_k-f_m\|_{H^1({{{\mathbb{R}}}^n})}. \]

Therefore, $\{v_k\}_{k\in {\mathbb {N}}}$ is a Cauchy sequence in $J_\sigma (H^1({\mathbb {R}^n}))$, and there exists a $v\in J_\sigma (H^1({\mathbb {R}^n}))$ such that $v_k$ converges to $v$ in $J_\sigma (H^1({\mathbb {R}^n}))$. Then, by theorem 1.2(ii), we conclude that

\[ \|Lv_k-Lv\|_{L^1({{{\mathbb{R}}}^n})}\lesssim\left\|\partial^\sigma v_k-\partial^\sigma v\right\|_{H^1({{{\mathbb{R}}}^n})}, \]

and $Lv_k$ converges to $Lv$ in $L^1({\mathbb {R}^n})$. Furthermore, $v$ is a solution of $Lv-\lambda v=f$ and

\[ \lambda\|v\|_{H^1({{{\mathbb{R}}}^n})}+\left\|(-\Delta)^{\sigma/2}v\right\|_{H^1({{{\mathbb{R}}}^n})}\lesssim\|f\|_{H^1({{{\mathbb{R}}}^n})}. \]

Meanwhile, the uniqueness follows from the above estimate. This finishes the proof of theorem 1.4.

Acknowledgments

The authors would like to thank the referee for her/his many valuable comments which essentially improve the presentation of this paper and, particularly, motivate the authors to improve the conclusions of theorems 1.2(ii) and 1.4(i). The authors would also like to thank Yangyang Zhang very much for some helpful discussions on the counterexample for that $L^p({\mathbb {R}^n})\cap {\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$ with $p\in (1,\,\infty )$ is not dense in ${\mathop {\mathrm {BMO}}}({\mathbb {R}^n})$.

This project is partially supported by the National Natural Science Foundation of China (Grant Nos. 11871254 and 12071431) and the Fundamental Research Funds for the Central Universities (Grant No. lzujbky-2021-ey18).

References

Abdellaoui, B., Fernández, A. J., Leonori, T. and Younes, A., Global fractional Calderón–Zygmund regularity. arXiv: 2107.06535.Google Scholar

Abels, H.. Pseudodifferential and Singular Integral Operators, An Introduction with Applications, De Gruyter Graduate Lectures (Berlin: De Gruyter, 2012).CrossRef Google Scholar

Caffarelli, L. and Silvestre, L.. Regularity results for nonlocal equations by approximation. Arch. Ration. Mech. Anal. 200 (2011), 59–88.CrossRef Google Scholar

Caffarelli, L. and Silvestre, L.. Regularity theory for fully nonlinear integro-differential equations. Comm. Pure Appl. Math. 62 (2009), 597–638.CrossRef Google Scholar

Cont, R. and Tankov, P.. Financial Modelling with Jump Processes, Chapman & Hall/CRC Financial Mathematics Series (Boca Raton, FL: Chapman & Hall/CRC, 2004).Google Scholar

Dong, H., Jung, P. and Kim, D.. Boundedness of non-local operators with spatially dependent coefficients and $L^p$

-estimates for non-local equations. Calc. Var. Partial Differential Equations (to appear) or arXiv: 2111.04029.Google Scholar

Dong, H. and Kim, D.. On $L^p$

-estimates for a class of non-local elliptic equations. J. Funct. Anal. 262 (2012), 1166–1199.CrossRef Google Scholar

Dong, H. and Kim, D.. Schauder estimates for a class of non-local elliptic equations. Discrete Contin. Dyn. Syst. 33 (2013), 2319–2347.CrossRef Google Scholar

Dong, H. and Kim, D.. An approach for weighted mixed-norm estimates for parabolic equations with local and non-local time derivatives. Adv. Math. 377 (2021), 107494.CrossRef Google Scholar

Dong, H. and Kim, D.. Time fractional parabolic equations with measurable coefficients and embeddings for fractional parabolic Sobolev spaces. Int. Math. Res. Not. IMRN 22 (2021), 17563–17610.CrossRef Google Scholar

Dong, H. and Liu, Y.. Sobolev estimates for fractional parabolic equations with space-time non-local operators. arXiv: 2108.11840.Google Scholar

Folland, G. B.. Real Analysis, Modern Techniques and Their Applications, 2nd ed. Pure and Applied Mathematics (New York), A Wiley-Interscience Publication (New York: John Wiley & Sons Inc., 1999).Google Scholar

Garofalo, N.. Fractional thoughts. in New Developments in the Analysis of Nonlocal Operators, Contemp. Math., Vol. 723, pp. 1–135 (Providence, RI: Amer. Math. Soc., 2019).CrossRef Google Scholar

Grafakos, L.. Modern Fourier Analysis, 3rd ed. Graduate Texts in Mathematics 250 (New York: Springer, 2014).CrossRef Google Scholar

John, F. and Nirenberg, L.. On functions of bounded mean oscillation. Comm. Pure Appl. Math. 14 (1961), 415–426.CrossRef Google Scholar

Karlsen, K., Petitta, F. and Ulusoy, S.. A duality approach to the fractional Laplacian with measure data. Publ. Mat. 55 (2011), 151–161.CrossRef Google Scholar

Krylov, N. V.. Parabolic equations with VMO coefficients in Sobolev spaces with mixed norms. J. Funct. Anal. 250 (2007), 521–558.CrossRef Google Scholar

Mengesha, T., Schikorra, A. and Yeepo, S.. Calderón–Zygmund type estimates for nonlocal PDE with Hölder continuous kernel. Adv. Math. 383 (2021), 107692.CrossRef Google Scholar

Mikulevičius, R. and Pragarauskas, H.. On the Cauchy problem for integro-differential operators in Hölder classes and the uniqueness of the martingale problem. Potential Anal. 40 (2014), 539–563.CrossRef Google Scholar

Mikulevičius, R. and Pragarauskas, H.. On the Cauchy problem for integro-differential operators in Sobolev classes and the martingale problem. J. Differ. Eq. 256 (2014), 1581–1626.CrossRef Google Scholar

Nakai, E. and Yabuta, K.. Pointwise multipliers for functions of bounded mean oscillation. J. Math. Soc. Japan 37 (1985), 207–218.CrossRef Google Scholar

Nowak, S.. H ^s,p regularity theory for a class of nonlocal elliptic equations. Nonlinear Anal. 195 (2020), 111730.CrossRef Google Scholar

Nowak, S.. Improved Sobolev regularity for linear nonlocal equations with VMO coefficients. Math. Ann. (2022), 1–56. doi:10.1007/s00208-022-02369-wGoogle Scholar

Ros-Oton, X.. Nonlocal elliptic equations in bounded domains: a survey. Publ. Mat. 60 (2016), 3–26.CrossRef Google Scholar

Ros-Oton, X. and Serra, J.. The extremal solution for the fractional Laplacian. Calc. Var. Partial Differ. Eq. 50 (2014), 723–750.CrossRef Google Scholar

Stein, E. M.. Singular Integrals and Differentiability Properties of Functions (Princeton, NJ: Princeton University Press, 1970).Google Scholar

Stein, E. M.. Harmonic Analysis: Real-variable Methods, Orthogonality, and Oscillatory Integrals (Princeton, NJ: Princeton University Press, 1993).Google Scholar

Strichartz, R.. Bounded mean oscillation and Sobolev spaces. Indiana Univ. Math. J. 29 (1980), 539–558.CrossRef Google Scholar

Strichartz, R.. $H^p$

Sobolev spaces. Colloq. Math. 60/61 (1990), 129–139.CrossRef Google Scholar

Triebel, H.. Theory of Function Spaces, Monographs in Mathematics, Vol. 78 (Basel: Birkhäuser Verlag, 1983).CrossRef Google Scholar

Wu, P., Huang, Y. and Zhou, Y.. Existence and regularity of solutions for a class of fractional Laplacian problems. J. Differ. Equ. 318 (2022), 480–501.CrossRef Google Scholar

Ziemer, W. P.. Weakly Differentiable Functions, Sobolev Spaces and Functions of Bounded Variation, Graduate Texts in Mathematics, Vol. 120 (New York: Springer-Verlag, 1989).CrossRef Google Scholar

Article contents

On BMO and Hardy regularity estimates for a class of non-local elliptic equations

Abstract

Keywords

MSC classification

1. Introduction

2. Preliminaries

Lemma 2.4 [Reference Dong and Kim7, theorem 2.1]

Lemma 2.5 [Reference Dong and Kim8, theorem 1.3]

3. Proofs of theorems 1.2 and 1.4

Acknowledgments

References

Save article to Kindle

Save article to Dropbox

Save article to Google Drive

Reply to: Submit a response

Your details

You have entered the maximum number of contributors

Conflicting interests