Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-19T09:14:34.916Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiparameter Sturm theory

Published online by Cambridge University Press:  14 November 2011

Paul Binding  and
Patrick J. Browne
Paul Binding
Affiliation:
Department of Mathematics and Statistics, The University of Calgary, Calgary, Alberta, CanadaT2N 1N4
Patrick J. Browne
Affiliation:
Department of Mathematics and Statistics, The University of Calgary, Calgary, Alberta, CanadaT2N 1N4
Get access Rights & Permissions [Opens in a new window]

Extract

Let Sturm–Liouville problems

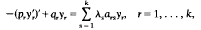
with continuous coefficients and appropriate boundary conditions, be coupled by the eigenvalue λ = (λ1, … λk). When k = 1, there are various oscillation, perturbation and comparison theorems concerning existence and continuous or monotonic dependence of eigenvalues, eigenfunctions and their zeros (i.e. focal points).

We attempt a unified theory for such results, valid for general fc, under conditions known as "left" and “right” definiteness. A representative result may be stated loosely as follows: if LD holds then (elementwise) monotonic dependence of p, q and the matrix [ars] forces monotonic dependence of λ. LD is a generalisation of the “polar” case for k = 1, and was originally conceived for a quite different purpose, viz. completeness of eigenfunctions via elliptic partial differential equation theory.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 99 , Issue 1-2 , 1984 , pp. 173 - 184
Copyright
Copyright © Royal Society of Edinburgh 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Atkinson, F. V.. Discrete and Continuous Boundary Value Problems (New York: Academic Press, 1964).Google Scholar
2Binding, P. A.. Multiparameter definiteness conditions. Proc. Roy. Soc. Edinburgh Sect. A 89 (1981)., 319–332.CrossRefGoogle Scholar
3Binding, P. A.. Abstract oscillation theorems for multiparameter eigenvalue problems. J. Differen- tial Equations 49 (1983)., 331–343.CrossRefGoogle Scholar
4Binding, P. A. and Browne, P. J.. A variational approach to multiparameter eigenvalue problems in Hilbert space. SIAM J. Math. Anal. 9 (1978)., 1054–1067.CrossRefGoogle Scholar
5Binding, P. A. and Browne, P. J.. Comparison cones for multiparameter eigenvalue problems. J. Math. Anal. Appl. 77 (1980)., 132–149.CrossRefGoogle Scholar
6Coddington, E. A. and Levison, N.. Theory of Ordinary Differential Equations (New York: McGraw-Hill, 1955).Google Scholar
7Crandall, M. G. and Rabinowitz, P. H.. Bifurcation from simple eigenvalues. J. Funct. Anal. 8 (1971)., 321–340.CrossRefGoogle Scholar
8Dieudonne, J.. Foundations of Modern Analysis (New York: Academic Press, 1969).Google Scholar
9Faierman, M.. An oscillation theorem for a two parameter system of ordinary differential equations. Quaestiones Math. 3 (1979)., 313–321.CrossRefGoogle Scholar
10Ince, E. L.. Ordinary Differential Equations (New York: Dover, 1956).Google Scholar
11Morse, M.. Calculus of Variations in the Large (Amer. Math. Soc. Colloq. Publications 18) (Providence, R.I.: 1934).Google Scholar
12Reid, W. T.. Sturmian Theory for Ordinary Differential Equations (New York: Springer, 1980).CrossRefGoogle Scholar
13Sleeman, B. D.. Klein oscillation theorems for multiparameter eigenvalue problems in ordinary differential equations. Nieuw Arch. Wisk. 27 (1979)., 341–352.Google Scholar