Article contents
Corrigendum: On the Dirichlet problem for weakly non-linear elliptic partial differential equations
Published online by Cambridge University Press: 14 November 2011
Extract
The proof of Lemma 6 (and thus of Theorem 9) has a gap in it. While m(B) → 0 as r → ∞ for each fixed h in Ni, it is not clear (and probably false) that this holds uniformly for h in 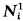 . However Lemma 6 (and thus Theorem 9) holds with only trivial modifications of the given proof if one of the following holds: (i) ygi(y) → ∞ as |y| → ∞; (ii) m{x∈Ω: h(x) = 0} = 0 for every h in
. However Lemma 6 (and thus Theorem 9) holds with only trivial modifications of the given proof if one of the following holds: (i) ygi(y) → ∞ as |y| → ∞; (ii) m{x∈Ω: h(x) = 0} = 0 for every h in 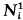 (iii) Niis one dimensional; (iv) there is a subset A of Ω such that h(x) = 0 if x ∈ A and h ∈
(iii) Niis one dimensional; (iv) there is a subset A of Ω such that h(x) = 0 if x ∈ A and h ∈ 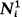 and m{x∈Ω\A: h(x) = 0} = 0 for every h ∈
and m{x∈Ω\A: h(x) = 0} = 0 for every h ∈ 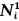 . Assumption (ii) holds under very weak conditions. For example, the methods in [1] and regularity theorems imply that (ii) holds if there is a closed subset T of Ω of measure zero such that either (a) Ω\T is connected and aij (i, j = 1, …, n) are locally Lipschitz continuous on Ω\T or (b) for each component A of Ω\T, the aij have Lipschitz extensions to Ā and T is a “nice” set. (For example, it suffices to assume that T is a smooth submanifold of Ω though much weaker conditions would suffice.) Remember that we are assuming Ω is connected.
. Assumption (ii) holds under very weak conditions. For example, the methods in [1] and regularity theorems imply that (ii) holds if there is a closed subset T of Ω of measure zero such that either (a) Ω\T is connected and aij (i, j = 1, …, n) are locally Lipschitz continuous on Ω\T or (b) for each component A of Ω\T, the aij have Lipschitz extensions to Ā and T is a “nice” set. (For example, it suffices to assume that T is a smooth submanifold of Ω though much weaker conditions would suffice.) Remember that we are assuming Ω is connected.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 89 , Issue 1-2 , 1981 , pp. 15
- Copyright
- Copyright © Royal Society of Edinburgh 1981
References
- 1
- Cited by




