Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-23T20:01:45.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Borderline gradient continuity for fractional heat type operators

Part of: Miscellaneous topics - Partial differential equations Partial differential equations

Published online by Cambridge University Press:  14 October 2022

Vedansh Arya  and
Dharmendra Kumar
Vedansh Arya
Affiliation:
Tata Institute of Fundamental Research, Centre For Applicable Mathematics, Bangalore 560065, India (vedansh@tifrbng.res.in, dharmendra2020@tifrbng.res.in)
Dharmendra Kumar
Affiliation:
Tata Institute of Fundamental Research, Centre For Applicable Mathematics, Bangalore 560065, India (vedansh@tifrbng.res.in, dharmendra2020@tifrbng.res.in)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we establish gradient continuity for solutions to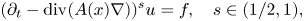

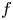\[ (\partial_t - \operatorname{div}(A(x) \nabla ))^{s} u =f,\quad s \in (1/2, 1), \]
when $f$ belongs to the scaling critical function space $L\left (\frac {n+2}{2s-1}, 1\right )$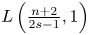. Our main results theorems 1.1 and 1.2 can be seen as a nonlocal generalization of a well-known result of Stein in the context of fractional heat type operators and sharpen some of the previous gradient continuity results which deal with $f$ 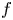in subcritical spaces. Our proof is based on an appropriate adaptation of compactness arguments, which has its roots in a fundamental work of Caffarelli in [13].

Keywords

Extension problemFractional heat operatorMaster equationsBorderline gradient continuity

MSC classification

Primary: 35R11: Fractional partial differential equations
Secondary: 35B65: Smoothness and regularity of solutions 35R09: Integro-partial differential equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 5 , October 2023 , pp. 1651 - 1682
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adimurthi, K. and Banerjee, A.. Borderline regularity for fully nonlinear equations in Dini domains. To appear in Adv. Calc. Var. arXiv:1806.07652v2.Google Scholar
Athanasopoulos, I., Caffarelli, L. and Milakis, E.. On the regularity of the non-dynamic parabolic fractional obstacle problem. J. Differ. Equ. 265 (2018), 2614–2647.CrossRefGoogle Scholar
Audrito, A. and Terracini, S.. On the nodal set of solutions to a class of nonlocal parabolic reaction-diffusion equations.arXiv:1807.10135.Google Scholar
Audrito, A.. On the existence and Hölder regularity of solutions to some nonlinear Cauchy-Neumann problems. arXiv:2107.03308.Google Scholar
Balakrishnan, A.. Fractional powers of closed operators and the semigroups generated by them. Pac. J. Math. 10 (1960), 419–437.CrossRefGoogle Scholar
Banerjee, A., Danielli, D., Garofalo, N. and Petrosyan, A.. The regular free boundary in the thin obstacle problem for degenerate parabolic equations. Algebra Anal. 32 (2020), 84–126.Google Scholar
Banerjee, A., Danielli, D., Garofalo, N. and Petrosyan, A.. The structure of the singular set in the thin obstacle problem for degenerate parabolic equations. Calc. Var. Partial Differ. Equ. 60 (2021), 91.CrossRefGoogle Scholar
Banerjee, A. and Garofalo, N.. Monotonicity of generalized frequencies and the strong unique continuation property for fractional parabolic equations. Adv. Math. 336 (2018), 149–241.CrossRefGoogle Scholar
Banerjee, A., Garofalo, N., Munive, I. and Nhieu, D.. The Harnack inequality for a class of nonlocal parabolic equations. Commun. Contemp. Math. 23 (2021), 2050050.CrossRefGoogle Scholar
Banerjee, A. and Munive, I.. Gradient continuity estimates for the normalized p-Poisson equation. Commun. Contemp. Math. 22 (2020), 1950069.CrossRefGoogle Scholar
Biswas, A., De Leon-Contreras, M. and Stinga, P.. Harnack inequalities and Hölder estimates for master equations. SIAM J. Math. Anal. 53 (2021), 2319–2348.CrossRefGoogle Scholar
Biswas, A. and Stinga, P. R.. Regularity estimates for nonlocal space-time master equations in bounded domains. J. Evol. Equ. 21 (2021), 503–565.CrossRefGoogle Scholar
Caffarelli, L.. Interior estimates for fully nonlinear equations. Ann. Math. 130 (1989), 189–213.CrossRefGoogle Scholar
Caffarelli, L. and Kenig, C. E.. Gradient estimates for variable coefficient parabolic equations and singular perturbation problems. Am. J. Math. 120 (1998), 391–439.CrossRefGoogle Scholar
Caffarelli, L. and Silvestre, L.. An extension problem related to the fractional Laplacian. Commun. Partial Differ. Equ. 32 (2007), 1245–1260.CrossRefGoogle Scholar
Caffarelli, L. and Silvestre, L.. Hölder regularity for generalized master equations with rough kernels. Advances in Analysis: The Legacy of Elias M. Stein, Princeton Math. Ser., vol. 50, pp. 63–83 (Princeton, NJ: Princeton University Press, 2014).Google Scholar
Chiarenza, F. and Serapioni, R.. A remark on a Harnack inequality for degenerate parabolic equations. Rend. Sem. Mat. Univ. Padova 73 (1985), 179–190.Google Scholar
Daskalopoulos, P., Kuusi, T. and Mingione, G.. Borderline estimates for fully nonlinear elliptic equations. Commun. Partial Differ. Equ. 39 (2014), 574–590.CrossRefGoogle Scholar
Dong, H. and Phan, T.. Regularity for parabolic equations with singular or degenerate coefficients. Calc. Var. Partial Differ. Equ. 60 (2021), 44.CrossRefGoogle Scholar
Duvaut, G. and Lions, J.-L.. Les inéquations en mécanique et en physique. (French) Travaux et Recherches Mathématiques, vol. 21, p. xx+387 (Paris: Dunod, 1972).Google Scholar
Duzaar, F. and Mingione, G.. Gradient estimates via non-linear potentials. Am. J. Math. 133 (2011), 1093–1149.CrossRefGoogle Scholar
Fabes, E. B., Kenig, C. E. and Serapioni, R. P.. The local regularity of solutions of degenerate elliptic equations. Commun. Partial Differ. Equ. 7 (1982), 77–116.CrossRefGoogle Scholar
Hardy, G. H., Littlewood, J. E. and Pólya, G., Inequalities. p. xii+324 (Cambridge: Cambridge University Press, 1988).Google Scholar
Kenkre, M., Montroll, E. W. and Shlesinger, M. F.. Generalized master equations for continuous-time random walks. J. Stat. Phys. 9 (1973), 45–50.CrossRefGoogle Scholar
Kuusi, T. and Mingione, G.. Universal potential estimates. J. Funct. Anal. 262 (2012), 4205–4269.CrossRefGoogle Scholar
Kuusi, T. and Mingione, G.. Linear potentials in nonlinear potential theory. Arch. Ration. Mech. Anal. 207 (2013), 215–246.CrossRefGoogle Scholar
Kuusi, T. and Mingione, G.. Guide to nonlinear potential estimates. Bull. Math. Sci. 4 (2014), 1–82.CrossRefGoogle ScholarPubMed
Kuusi, T. and Mingione, G.. A nonlinear Stein theorem. Calc. Var. Partial Differ. Equ. 51 (2014), 45–86.CrossRefGoogle Scholar
Lai, R., Lin, Y. and Ruland, A.. The Calderón problem for a space-time fractional parabolic equation. SIAM J. Math. Anal. 52 (2020), 2655–2688.CrossRefGoogle Scholar
Litsgard, M. and Nystrom, K.. Fractional powers of parabolic operators with time-dependent measurable coefficients. arXiv:2104.07313.Google Scholar
Lorentz, G. G.. Approximation of functions (New York-Chicago, Ill.-Toronto, ON: Holt, Rinehart and Winston, 1966).Google Scholar
Metzler, R. and Klafter, J.. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339 (2000), 1–77.CrossRefGoogle Scholar
Montroll, E. W. and Weiss, G. H.. Random walks on lattices. II. J. Math. Phys. 6 (1965), 167–181.CrossRefGoogle Scholar
Nekvinda, A.. Characterization of traces of the weighted Sobolev space $W^{1}, p(\Omega, d^{\epsilon }_M)$ on $M$. Czech. Math. J. 43 (1993), 695–711.CrossRefGoogle Scholar
Nyström, K. and Sande, O.. Extension properties and boundary estimates for a fractional heat operator. Nonlinear Anal. 140 (2016), 29–37.CrossRefGoogle Scholar
O'Neil, R.. Integral transforms and tensor products on Orlicz spaces and $L(p, q)$ spaces. J. Anal. Math. 21 (1968), 4–276.CrossRefGoogle Scholar
Riesz, M.. Intégrales de Riemann-Liouville et potentiels. Acta Sci. Math. Szeged 9 (1938), 1–42.Google Scholar
Riesz, M.. L'intégrale de Riemann-Liouville et le problème de Cauchy. Acta Math. 81 (1949), 1–223.CrossRefGoogle Scholar
Stein, E. M.. Editor's note: the differentiability of functions in Rn. Ann. Math. 113 (1981), 383–385.Google Scholar
Stinga, P. R. and Torrea, J. L.. Regularity theory and extension problem for fractional nonlocal parabolic equations and the master equation. SIAM J. Math. Anal. 49 (2017), 3893–3924.CrossRefGoogle Scholar