No CrossRef data available.
Article contents
Asymptotics for some polynomial patterns in the primes
Published online by Cambridge University Press: 17 January 2019
Abstract
We prove asymptotic formulae for sums of the form
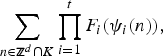 $$\sum\limits_{n\in {\open z}^d\cap K} {\prod\limits_{i = 1}^t {F_i} } (\psi _i(n)),$$
$$\sum\limits_{n\in {\open z}^d\cap K} {\prod\limits_{i = 1}^t {F_i} } (\psi _i(n)),$$
The paper combines ingredients from the work of Green and Tao on linear equations in primes and that of Matthiesen on linear correlations amongst integers represented by a quadratic form. To make the von Mangoldt function compatible with the representation function of a quadratic form, we provide a new pseudorandom majorant for both – an average of the known majorants for each of the functions – and prove that it has the required pseudorandomness properties.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 5 , October 2019 , pp. 1241 - 1290
- Copyright
- Copyright © Royal Society of Edinburgh 2019




