Article contents
On the optimization of the first weighted eigenvalue
Published online by Cambridge University Press: 12 September 2022
Abstract
For $N\geq 2$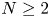 , a bounded smooth domain $\Omega$
, a bounded smooth domain $\Omega$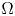 in $\mathbb {R}^{N}$
in $\mathbb {R}^{N}$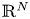 , and $g_0,\, V_0 \in L^{1}_{loc}(\Omega )$
, and $g_0,\, V_0 \in L^{1}_{loc}(\Omega )$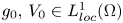 , we study the optimization of the first eigenvalue for the following weighted eigenvalue problem:
, we study the optimization of the first eigenvalue for the following weighted eigenvalue problem: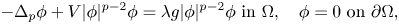
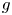 and $V$
and $V$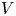 vary over the rearrangement classes of $g_0$
vary over the rearrangement classes of $g_0$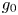 and $V_0$
and $V_0$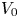 , respectively. We prove the existence of a minimizing pair $(\underline {g},\,\underline {V})$
, respectively. We prove the existence of a minimizing pair $(\underline {g},\,\underline {V})$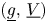 and a maximizing pair $(\overline {g},\,\overline {V})$
and a maximizing pair $(\overline {g},\,\overline {V})$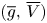 for $g_0$
for $g_0$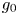 and $V_0$
and $V_0$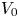 lying in certain Lebesgue spaces. We obtain various qualitative properties such as polarization invariance, Steiner symmetry of the minimizers as well as the associated eigenfunctions for the case $p=2$
lying in certain Lebesgue spaces. We obtain various qualitative properties such as polarization invariance, Steiner symmetry of the minimizers as well as the associated eigenfunctions for the case $p=2$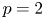 . For annular domains, we prove that the minimizers and the corresponding eigenfunctions possess the foliated Schwarz symmetry.
. For annular domains, we prove that the minimizers and the corresponding eigenfunctions possess the foliated Schwarz symmetry.
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 6 , December 2023 , pp. 1777 - 1804
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 1
- Cited by



