No CrossRef data available.
Article contents
BP-cohomology of projective Stiefel manifolds
Published online by Cambridge University Press: 21 March 2022
Abstract
In this paper, we compute the $BP$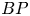 -cohomology of complex projective Stiefel manifolds. The method involves the homotopy fixed point spectral sequence, and works for complex oriented cohomology theories. We also use these calculations and $BP$
-cohomology of complex projective Stiefel manifolds. The method involves the homotopy fixed point spectral sequence, and works for complex oriented cohomology theories. We also use these calculations and $BP$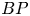 -operations to prove new results about equivariant maps between Stiefel manifolds.
-operations to prove new results about equivariant maps between Stiefel manifolds.
Keywords
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 2 , April 2023 , pp. 679 - 701
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh



