Hostname: page-component-758b78586c-qvhcc Total loading time: 0 Render date: 2023-11-29T03:11:40.749Z Has data issue: false Feature Flags: { "corePageComponentGetUserInfoFromSharedSession": true, "coreDisableEcommerce": false, "useRatesEcommerce": true } hasContentIssue false
  • English
  • Français

Asymptotically autonomous robustness of random attractors for a class of weakly dissipative stochastic wave equations on unbounded domains

Part of: Infinite-dimensional dissipative dynamical systems Partial differential equations Topological dynamics

Published online by Cambridge University Press:  05 November 2020

Tomás Caraballo ,
Boling Guo ,
Nguyen Huy Tuan  and
Renhai Wang
Tomás Caraballo
Affiliation:
Departamento de Ecuaciones Diferenciales y Análisis Numérico, Facultad de Matemáticas, Universidad de Sevilla, C/ Tarfia s/n, 41012-Sevilla, Spain
Boling Guo
Affiliation:
Institute of Applied Physics and Computational Mathematics, PO Box 8009, Beijing100088, China
Nguyen Huy Tuan
Affiliation:
Department of Mathematics and Computer Science, University of Science-VNUHCM, 227 Nguyen Van Cu Str., Dist. 5, Ho Chi Minh City, Viet Nam
Renhai Wang*
Affiliation:
Institute of Applied Physics and Computational Mathematics, PO Box 8009, Beijing100088, China (rwang-math@outlook.com)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

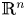This paper is concerned with the asymptotic behaviour of solutions to a class of non-autonomous stochastic nonlinear wave equations with dispersive and viscosity dissipative terms driven by operator-type noise defined on the entire space $\mathbb {R}^n$. The existence, uniqueness, time-semi-uniform compactness and asymptotically autonomous robustness of pullback random attractors are proved in 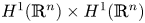$H^1(\mathbb {R}^n)\times H^1(\mathbb {R}^n)$ when the growth rate of the nonlinearity has a subcritical range, the density of the noise is suitably controllable, and the time-dependent force converges to a time-independent function in some sense. The main difficulty to establish the time-semi-uniform pullback asymptotic compactness of the solutions in 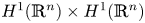$H^1(\mathbb {R}^n)\times H^1(\mathbb {R}^n)$ is caused by the lack of compact Sobolev embeddings on 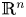$\mathbb {R}^n$, as well as the weak dissipativeness of the equations is surmounted at light of the idea of uniform tail-estimates and a spectral decomposition approach. The measurability of random attractors is proved by using an argument which considers two attracting universes developed by Wang and Li (Phys. D 382: 46–57, 2018).

Keywords

Weakly dissipative wave equationpullback random attractorsasymptotically autonomous robustnesstime-semi-uniform compactnessoperator-type noise

MSC classification

Primary: 37L55: Infinite-dimensional random dynamical systems; stochastic equations
Secondary: 37B55: Nonautonomous dynamical systems 35B41: Attractors 35B40: Asymptotic behavior of solutions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 6 , December 2021 , pp. 1700 - 1730
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bates, P. W., Lu, K. and Wang, B.. Random attractors for stochastic reaction-diffusion equations on unbounded domains. J. Differ. Equ. 246 (2009), 845–869.CrossRefGoogle Scholar
Brzeźniak, Z., Capiński, M. and Flandoli, F.. Pathwise global attractors for stationary random dynamical systems. Probab. Theory Relat. Fields 95 (1993), 87–102.CrossRefGoogle Scholar
Caraballo, T. and Langa, J. A.. On the upper semicontinuity of cocycle attractors for non-autonomous and random dynamical systems. Dyn. Contin. Discrete Impuls. Syst. Ser. A Math. Anal. 10 (2003), 491–513.Google Scholar
Caraballo, T. and Lu, K. Attractors for stochastic lattice dynamical systems with a multiplicative noise. Front. Math. China 3 (2008), 317–335.CrossRefGoogle Scholar
Caraballo, T., Langa, J. A. and Robinson, J. C.. Attractors for differential equations with variable delays. J. Math. Anal. Appl. 260 (2001), 421–438.CrossRefGoogle Scholar
Caraballo, T., Langa, J. A. and Robinson, J. C.. A stochastic pitchfork bifurcation in a reaction-diffusion equation. Proc. R. Soc. Lond. Ser. A 457 (2001), 2041–2061.CrossRefGoogle Scholar
Caraballo, T., Langa, J. A., Melnik, V. S. and Valero, J.. Pullback attractors for nonautonomous and stochastic multivalued dynamical systems. Set-Valued Anal. 11 (2003), 153–201.CrossRefGoogle Scholar
Caraballo, T., Kloeden, P. E. and Schmalfuß, B.. Exponentially stable stationary solutions for stochastic evolution equations and their perturbation. Appl. Math. Optim. 50 (2004), 183–207.CrossRefGoogle Scholar
Caraballo, T., Garrido-Atienza, M. J., Schmalfuß, B. and Valero, J.. Asymptotic behaviour of a stochastic semilinear dissipative functional equation without uniqueness of solutions. Discrete Contin. Dyn. Syst. Ser. B 14 (2010), 439–455.Google Scholar
Caraballo, T., Garrido-Atienza, M. J. and Taniguchi, T.. The existence and exponential behavior of solutions to stochastic delay evolution equations with a fractional Brownian motion. Nonlinear Anal. 74 (2011), 3671–3684.CrossRefGoogle Scholar
Carvalho, A. N. and Cholewa, J. W.. Local well posedness, asymptotic behavior and asymptotic bootstrapping for a class of semilinear evolution equations of the second order in time. Trans. Amer. Math. Soc. 361 (2009), 2567–586.CrossRefGoogle Scholar
Carvalho, A. N., Langa, J. A. and Robinson, J. C.. Structure and bifurcation of pullback attractors in a non-autonomous Chafee-Infante equation. Proc. Amer. Math. Soc. 140 (2012), 2357–2373.CrossRefGoogle Scholar
Carvalho, A. N., Langa, J. A. and Robinson, J. C.. Attractors for infinite-dimensional non-autonomous dynamical systems. Appl. Math. Sciences, Springer 182 (2013).Google Scholar
Crauel, H. and Flandoli, F.. Attractors for random dynamical systems. Probab. Theory Relat. Fields 100 (1994), 365–393.CrossRefGoogle Scholar
Crauel, H., Debussche, A. and Flandoli, F.. Random attractors. J. Dyn. Differ. Equ. 9 (1997), 307–341.CrossRefGoogle Scholar
Cui, H. and Kloeden, P. E.. Invariant forward attractors of non-autonomous random dynamical systems. J. Differ. Equ. 265 (2018), 6166–6186.CrossRefGoogle Scholar
Fan, X.. Random attractors for damped stochastic wave equations with multiplicative noise. Int. J. Math. 19 (2008), 421–437.CrossRefGoogle Scholar
Flandoli, F. and Schmalfuß, B.. Random attractors for the 3D stochastic Navier-Stokes equation with multiplicative noise. Stoch. Rep. 59 (1996), 21–45.CrossRefGoogle Scholar
Garrido-Atienza, M. J. and Schmalfuss, B.. Ergodicity of the infinite dimensional fractional Brownian motion. J. Dyn. Differ. Equ. 23 (2011), 671–681.CrossRefGoogle Scholar
Gu, A., Li, D., Wang, B. and Yang, H.. Regularity of random attractors for fractional stochastic reaction-diffusion equations on $\mathbb {R}^n$. J. Differ. Equ. 264 (2018), 7094–7137.CrossRefGoogle Scholar
Hayashi, N., Kaikina, E. I. and Naumkin, P. I.. Damped wave equation with a critical nonlinearity. Trans. Amer. Math. Soc. 358 (2006), 1165–1185.CrossRefGoogle Scholar
Jones, R. and Wang, B.. Asymptotic behavior of a class of stochastic nonlinear wave equations with dispersive and dissipative terms. Nonlinear Anal. RWA 14 (2013), 1308–1322.CrossRefGoogle Scholar
Kloeden, P. E. and Langa, J. A.. Flattening, squeezing and the existence of random attractors. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 463 (2007), 163–181.Google Scholar
Kloeden, P. E. and Simsen, J.. Attractors of asymptotically autonomous quasi-linear parabolic equation with spatially variable exponents. J. Math. Anal. Appl. 425 (2015), 911–918.CrossRefGoogle Scholar
Kloeden, P. E. and Lorenz, T.. Construction of nonautonomous forward attractors. Proc. Amer. Math. Soc. 144 (2016), 259–268.CrossRefGoogle Scholar
Kloeden, P. E., Simsen, J. and Simsen, M. S.. Asymptotically autonomous multivalued cauchy problems with spatially variable exponents. J. Math. Anal. Appl. 445 (2017), 513–531.CrossRefGoogle Scholar
Langa, J. A., Robinson, J. C. and Suárez, A. Forwards and pullback behaviour of a non-autonomous Lotka-Volterra system. Nonlinearity 16 (2003), 1277.CrossRefGoogle Scholar
Langa, J. A., Robinson, J. C. and Vidal-López, A.. The stability of attractors for non-autonomous perturbations of gradient-like systems. J. Differ. Equ. 234 (2007), 607–625.CrossRefGoogle Scholar
Li, Y., Gu, A. and Li, J.. Existence and continuity of bi-spatial random attractors and application to stochastic semilinear Laplacian equations. J. Differ. Equ. 258 (2015), 504–534.CrossRefGoogle Scholar
Li, Y., Wang, R. and Yin, J.. Backward compact attractors for non-autonomous Benjamin-Bona-Mahony equations on unbounded channels. Discrete Contin. Dyn. Syst. Ser. B 22 (2017), 2569–2586.Google Scholar
Li, Y., She, L. and Wang, R.. Asymptotically autonomous dynamics for parabolic equation. J. Math. Anal. Appl. 459 (2018), 1106–1123.CrossRefGoogle Scholar
Li, Y., She, L. and Yin, J.. Longtime robustness and semi-uniform compactness of a pullback attractor via nonautonomous PDE, Discrete Contin. Dyn. Syst. Ser. B, 23 (2018), 1535–1557.Google Scholar
Lu, K. and Wang, B.. Wong-Zakai approximations and long term behavior of stochastic partial differential equations. J. Dyn. Differ. Equ. 31 (2019), 1341–1371.CrossRefGoogle Scholar
Marín-Rubio, P. and Robinson, J. C.. Attractors for the stochastic 3D Navier-Stokes equations. Stoch. Dyn. 3 (2008), 279–297.CrossRefGoogle Scholar
Robinson, J. C.. Infinite-Dimensional Dynamical Systems: An Introduction to Dissipative Parabolic PDEs and the Theory of Global Attractors. Cambridge Texts in Applied Mathematics. (Math Inst, Univ of Warwick, UK). Cambridge University Press, Cambridge, UK. 2001. 461 pp. (Softcover). ISBN 0-521-63564-0.CrossRefGoogle Scholar
Robinson, J. C., Rodríguez-Bernal, A. and Vidal-López, A.. Pullback attractors and extremal complete trajectories for non-autonomous reaction-diffusion problems. J. Differ. Equ. 238 (2007), 289–337.CrossRefGoogle Scholar
Sun, C., Cao, D. and Duan, J.. Uniform attractors for nonautonomous wave equations with nonlinear damping. SIAM J. Appl. Dyn. Syst. 6 (2007), 293–318.CrossRefGoogle Scholar
Sun, C., Yang, L. and Duan, J.. Asymptotic behavior for a semilinear second order evolution equation. Trans. Amer. Math. Soc. 363 (2011), 6085–6109.CrossRefGoogle Scholar
Wang, B.. Attractors for reaction-diffusion equations in unbounded domains. Physica D 128 (1999), 41–52.CrossRefGoogle Scholar
Wang, B.. Asymptotic behavior of stochastic wave equations with critical exponents on $\mathbb {R}^3$. Trans. Amer. Math. Soc. 363 (2011), 3639–3663.CrossRefGoogle Scholar
Wang, B.. Sufficient and necessary criteria for existence of pullback attractors for non-compact random dynamical systems. J. Differ. Equ. 253 (2012), 1544–1583.CrossRefGoogle Scholar
Wang, B.. Random attractors for non-autonomous stochastic wave equations with multiplicative noise. Discrete Contin. Dyn. Syst. 34 (2014), 269–300.CrossRefGoogle Scholar
Wang, S. and Li, Y.. Longtime robustness of pullback random attractors for stochastic magneto-hydrodynamics equations. Physica D 382 (2018), 46–57.CrossRefGoogle Scholar
Wang, R. and Li, Y.. Backward compactness and periodicity of random attractors for stochastic wave equations with varying coefficients. Discrete Contin. Dyn. Syst. Ser. B 24 (2019), 4145–4167.Google Scholar
Wang, R. and Li, Y.. Asymptotic autonomy of kernel sections for Newton-Boussinesq equations on unbounded zonary domains. Dyn. Partial Differ. Equ. 16 (2019), 295–316.CrossRefGoogle Scholar
Wang, R. and Wang, B.. Asymptotic behavior of non-autonomous fractional stochastic p-laplacian equations. Comput. Math. Appl. 78 (2019), 3527–3543.CrossRefGoogle Scholar
Wang, Z. and Zhou, S.. Random attractor for stochastic non-autonomous damped wave equation with critical exponent. Discrete Contin. Dyn. Syst. 37 (2017), 545–573.CrossRefGoogle Scholar
Wang, Z. and Zhou, S.. Random attractor and random exponential attractor for stochastic non-autonomous damped cubic wave equation with linear multiplicative white noise. Discrete Contin. Dyn. Syst. 38 (2018), 4767–4817.CrossRefGoogle Scholar
Wang, Z., Zhou, S. and Gu, A.. Random attractor for a stochastic damped wave equation with multiplicative noise on unbounded domains. Nonlinear Anal. RWA 12 (2011), 3468–3482.CrossRefGoogle Scholar
Wang, X., Lu, K. and Wang, B.. Wong-Zakai approximations and attractors for stochastic reaction-diffusion equations on unbounded domains. J. Differ. Equ. 246 (2018), 378–424.CrossRefGoogle Scholar
Wang, R., Li, Y. and Li, F.. Probabilistic robustness for dispersive-dissipative wave equations driven by small Laplace-multiplier noise. Dyn. Syst. Appl. 27 (2018), 165–183.Google Scholar
Wang, R., Li, Y. and Wang, B.. Random dynamics of fractional nonclassical diffusion equations driven by colored noise. Discrete Contin. Dyn. Syst. 39 (2019), 4091–4126.CrossRefGoogle Scholar
Wang, R., Shi, L. and Wang, B.. Asymptotic behavior of fractional nonclassical diffusion equations driven by nonlinear colored noise on $\mathbb {R}^N$. Nonlinearity 32 (2019), 4524.CrossRefGoogle Scholar
Yang, M. and Sun, C.. Dynamics of strongly damped wave equations in locally uniform spaces: attractors and asymptotic regularity. Trans. Amer. Math. Soc. 361 (2009), 1069–1101.CrossRefGoogle Scholar
Yin, J., Gu, A. and Li, Y.. Backwards compact attractors for non-autonomous damped 3D Navier-Stokes equations. Dyn. Partial Differ. Equ. 14 (2017), 201–218.CrossRefGoogle Scholar
Yin, J., Li, Y. and Gu, A.. Backwards compact attractors and periodic attractors for non-autonomous damped wave equations on an unbounded domain. Comput. Math. Appl. 74 (2017), 744–758.CrossRefGoogle Scholar
Zhou, S. and Zhao, M.. Fractal dimension of random attractor for stochastic non-autonomous damped wave equation with linear multiplicative white noise. Discrete Contin. Dyn. Syst. 36 (2017), 2887–2914.CrossRefGoogle Scholar
Zhou, S., Yin, F. and Ouyang, Z.. Random attractor for damped nonlinear wave equations with white noise. SIAM J. Appl. Dyn. Syst. 4 (2005), 883–903.CrossRefGoogle Scholar