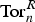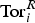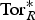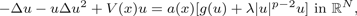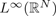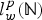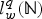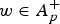Research Article
Rigidity of Ext and Tor with Coefficients in Residue Fields of a Commutative Noetherian Ring
- Part of:
-
- Published online by Cambridge University Press:
- 16 November 2018, pp. 305-321
-
- Article
- Export citation
Biholomorphic Mappings on Banach Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2019, pp. 913-924
-
- Article
- Export citation
The Spectra of Algebras of Group-Symmetric Functions
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2018, pp. 609-623
-
- Article
- Export citation
Least Energy Nodal Solutions for a Defocusing Schrödinger Equation with Supercritical Exponent
- Part of:
-
- Published online by Cambridge University Press:
- 16 August 2018, pp. 1-23
-
- Article
- Export citation
A Modular André–Oort Statement with Derivatives
- Part of:
-
- Published online by Cambridge University Press:
- 16 November 2018, pp. 323-365
-
- Article
- Export citation
Algebraic EHP Sequences Revisited
- Part of:
-
- Published online by Cambridge University Press:
- 03 December 2018, pp. 625-640
-
- Article
- Export citation
On the Integral Degree of Integral Ring Extensions
- Part of:
-
- Published online by Cambridge University Press:
- 20 August 2018, pp. 25-46
-
- Article
- Export citation
Grothendieck Ring of Varieties with Actions of Finite Groups
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2019, pp. 925-948
-
- Article
- Export citation
Higher Summability and Discrete Weighted Muckenhoupt and Gehring Type Inequalities
- Part of:
-
- Published online by Cambridge University Press:
- 11 March 2019, pp. 949-973
-
- Article
- Export citation
Grothendieck–Plücker Images of Hilbert Schemes are Degenerate
- Part of:
-
- Published online by Cambridge University Press:
- 22 August 2018, pp. 47-60
-
- Article
- Export citation
Unitary and Symmetric Units of a Commutative Group Algebra
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 641-654
-
- Article
- Export citation
Rigid C*-Tensor Categories and their Realizations as Hilbert C*-Bimodules
- Part of:
-
- Published online by Cambridge University Press:
- 16 November 2018, pp. 367-393
-
- Article
- Export citation
An Elementary Proof of Bevan's Theorem on the Growth of Grid Classes of Permutations
- Part of:
-
- Published online by Cambridge University Press:
- 11 March 2019, pp. 975-984
-
- Article
- Export citation
Geodesic Flows Modelled by Expansive Flows
- Part of:
-
- Published online by Cambridge University Press:
- 28 August 2018, pp. 61-95
-
- Article
- Export citation
Factorizations in Bounded Hereditary Noetherian Prime Rings
- Part of:
-
- Published online by Cambridge University Press:
- 19 November 2018, pp. 395-442
-
- Article
- Export citation
Compactness of Commutators of One-Sided Singular Integrals in Weighted Lebesgue Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 10 January 2019, pp. 655-665
-
- Article
- Export citation
Asymptotic Behaviour of the Energy Integral of a Two-Parameter Homogenization Problem with Nonlinear Periodic Robin Boundary Conditions
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2019, pp. 985-1016
-
- Article
- Export citation
On a Criterion of Local Invertibility and Conformality for Slice Regular Quaternionic Functions
- Part of:
-
- Published online by Cambridge University Press:
- 28 August 2018, pp. 97-105
-
- Article
- Export citation
Stable Rationality of Cyclic Covers of Projective Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2019, pp. 667-682
-
- Article
- Export citation
Szemerédi's Theorem in the Primes
- Part of:
-
- Published online by Cambridge University Press:
- 19 November 2018, pp. 443-457
-
- Article
- Export citation