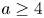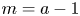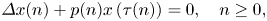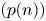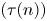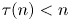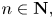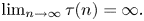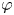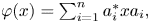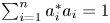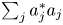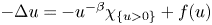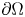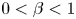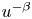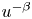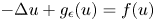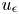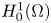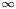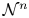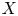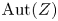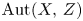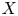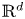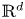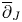Research Article
On birationally trivial families and adjoint quadrics
- Part of:
-
- Published online by Cambridge University Press:
- 04 July 2022, pp. 587-617
-
- Article
- Export citation
Upper and lower limit oscillation conditions for first-order difference equations
- Part of:
-
- Published online by Cambridge University Press:
- 07 July 2022, pp. 618-631
-
- Article
- Export citation
Which states can be reached from a given state by unital completely positive maps?
- Part of:
-
- Published online by Cambridge University Press:
- 05 July 2022, pp. 632-651
-
- Article
- Export citation
Singular elliptic equations with nonlinearities of subcritical and critical growth
- Part of:
-
- Published online by Cambridge University Press:
- 27 July 2022, pp. 652-690
-
- Article
- Export citation
On the analyticity of WLUD∞ functions of one variable and WLUD∞ functions of several variables in a complete non-Archimedean valued field
- Part of:
-
- Published online by Cambridge University Press:
- 07 July 2022, pp. 691-704
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the dynamics of extensions of free-abelian times free groups endomorphisms to the completion
- Part of:
-
- Published online by Cambridge University Press:
- 12 August 2022, pp. 705-735
-
- Article
- Export citation
Strongly Jordan property and free actions of non-abelian free groups
- Part of:
-
- Published online by Cambridge University Press:
- 11 August 2022, pp. 736-746
-
- Article
- Export citation
On dense intermingling of exact overlaps and the open set condition
- Part of:
-
- Published online by Cambridge University Press:
- 22 August 2022, pp. 747-759
-
- Article
- Export citation
On the Fatou theorem for ∂̄J-subsolutions in wedges
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2022, pp. 760-774
-
- Article
- Export citation
Truncated versions of three identities of Euler and Gauss
- Part of:
-
- Published online by Cambridge University Press:
- 30 August 2022, pp. 775-798
-
- Article
- Export citation
Examples of multiparameter CCR flows with non-trivial index
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2022, pp. 799-832
-
- Article
- Export citation
On a class of Hilbert-type inequalities in the whole plane involving some classical kernel functions
- Part of:
-
- Published online by Cambridge University Press:
- 06 October 2022, pp. 833-846
-
- Article
- Export citation
Some analytical properties of the matrix related to q-coloured Delannoy numbers
- Part of:
-
- Published online by Cambridge University Press:
- 06 October 2022, pp. 847-860
-
- Article
- Export citation
A correspondence between inverse subsemigroups, open wide subgroupoids and cartan intermediate C*-subalgebras
- Part of:
-
- Published online by Cambridge University Press:
- 07 October 2022, pp. 861-879
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PEM series 2 volume 65 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 October 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PEM series 2 volume 65 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 October 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation