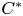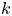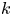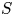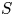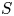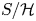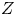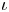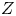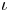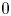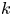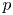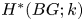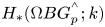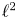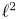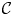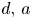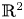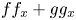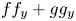Research Article
Crystal flex bases and the RUM spectrum
- Part of:
-
- Published online by Cambridge University Press:
- 24 November 2021, pp. 735-761
-
- Article
- Export citation
Invariance of KMS states on graph C*-algebras under classical and quantum symmetry
- Part of:
-
- Published online by Cambridge University Press:
- 20 September 2021, pp. 762-778
-
- Article
- Export citation
Benson's cofibrants, Gorenstein projectives and a related conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 23 September 2021, pp. 779-799
-
- Article
- Export citation
On holomorphic reflexivity conditions for complex Lie groups
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2021, pp. 800-821
-
- Article
- Export citation
Structure theory and stable rank for C*-algebras of finite higher-rank graphs
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2021, pp. 822-847
-
- Article
- Export citation
Semigroups whose right ideals are finitely generated
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2021, pp. 848-883
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic cycles and Lehn–Lehn–Sorger–van Straten eightfolds
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2021, pp. 884-907
-
- Article
- Export citation
Massey products in the homology of the loop space of a p-completed classifying space: finite groups with cyclic Sylow p-subgroups
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2021, pp. 908-915
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The first $\ell ^{2}$
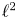 -betti number and groups acting on trees
-betti number and groups acting on trees
- Part of:
-
- Published online by Cambridge University Press:
- 25 October 2021, pp. 916-923
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Free quotients of fundamental groups of smooth quasi-projective varieties
- Part of:
-
- Published online by Cambridge University Press:
- 27 October 2021, pp. 924-946
-
- Article
- Export citation
Tilting pairs in extriangulated categories
- Part of:
-
- Published online by Cambridge University Press:
- 26 October 2021, pp. 947-981
-
- Article
- Export citation
On minimal log discrepancies and kollár components
- Part of:
-
- Published online by Cambridge University Press:
- 04 November 2021, pp. 982-1001
-
- Article
- Export citation
Extrapolation to weighted Morrey spaces with variable exponents and applications
- Part of:
-
- Published online by Cambridge University Press:
- 09 November 2021, pp. 1002-1027
-
- Article
- Export citation
A weight-homogenous condition to the real Jacobian conjecture in $ {\mathbb {R}}^{2}$
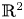
- Part of:
-
- Published online by Cambridge University Press:
- 19 November 2021, pp. 1028-1036
-
- Article
- Export citation
Erratum
On non-separated zero sequences of solutions of a linear differential equation – ERRATUM
-
- Published online by Cambridge University Press:
- 24 November 2021, p. 1037
-
- Article
-
- You have access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
PEM series 2 volume 64 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 December 2021, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PEM series 2 volume 64 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 December 2021, pp. b1-b2
-
- Article
-
- You have access
- Export citation