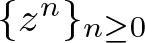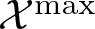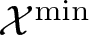1. Introduction and main results
A number of new Banach spaces of analytic functions over the unit disk arisenaturally as the symbol spaces during the study of random analytic functions in Hardy spaces, Bergman spaces, Dirichlet spaces and their multipliers, analytic functions of bounded mean oscillation (BMOA), etc. [Reference Cheng, Fang and Liu11–Reference Cochran, Shapiro and Ullrich13, Reference Littlewood29, Reference Marcus and Pisier32, Reference Nishry and Paquette34]. Let ![]() $\mathcal{X}$ be a Banach space of analytic functions over the unit disk
$\mathcal{X}$ be a Banach space of analytic functions over the unit disk ![]() $\mathbb{D}.$ Let
$\mathbb{D}.$ Let ![]() $\{X_n\}_{n\geq 0}$ be independent, identically distributed symmetric random variables over a probability space
$\{X_n\}_{n\geq 0}$ be independent, identically distributed symmetric random variables over a probability space ![]() $(\Omega, \mathcal{F}, \mathbb{P}).$ The symbol space
$(\Omega, \mathcal{F}, \mathbb{P}).$ The symbol space ![]() $\mathcal{X}_{\star}$ for random
$\mathcal{X}_{\star}$ for random ![]() $\mathcal{X}$-functions is another deterministic space, consisting of ‘symbols’ for random elements in
$\mathcal{X}$-functions is another deterministic space, consisting of ‘symbols’ for random elements in ![]() $\mathcal{X}$:
$\mathcal{X}$:
where ![]() $\mathcal{R} f(z) = \mathcal{R}^{\{(X_n)_n\}} f(z)$ is given by
$\mathcal{R} f(z) = \mathcal{R}^{\{(X_n)_n\}} f(z)$ is given by ![]() $
\mathcal{R} f(z) \doteq \sum_{n=0}^{\infty} a_nX_nz^n,
$ where
$
\mathcal{R} f(z) \doteq \sum_{n=0}^{\infty} a_nX_nz^n,
$ where ![]() $f(z)=\sum_{n=0}^{\infty}a_nz^n\in H(\mathbb{D}).$ By the Kolmogorov zero-one law, for any f(z),
$f(z)=\sum_{n=0}^{\infty}a_nz^n\in H(\mathbb{D}).$ By the Kolmogorov zero-one law, for any f(z), ![]() $\mathbb{P}(\mathcal{R} f\in \mathcal{X}) \in \{0, 1\}$ under mild conditions. This justifies the introduction of
$\mathbb{P}(\mathcal{R} f\in \mathcal{X}) \in \{0, 1\}$ under mild conditions. This justifies the introduction of ![]() $\mathcal{X}_\star$.
$\mathcal{X}_\star$.
The first nontrivial example of ![]() $\mathcal{X}_\star$ is perhaps the Littlewood theorem, reformulated as follows. Let
$\mathcal{X}_\star$ is perhaps the Littlewood theorem, reformulated as follows. Let ![]() $f(z)=a_0+a_1z+a_2z^2+\cdots \in H^2(\mathbb{D})$ be an element of the Hardy space over the unit disk. Let
$f(z)=a_0+a_1z+a_2z^2+\cdots \in H^2(\mathbb{D})$ be an element of the Hardy space over the unit disk. Let ![]() $\{\epsilon_n\}_{n\geq 0}$ be a sequence of independent, identically distributed Bernoulli random variables, that is,
$\{\epsilon_n\}_{n\geq 0}$ be a sequence of independent, identically distributed Bernoulli random variables, that is,  $\mathbb{P}(\epsilon_n=1)=\mathbb{P}(\epsilon_n=-1)=\frac{1}{2}$ for all
$\mathbb{P}(\epsilon_n=1)=\mathbb{P}(\epsilon_n=-1)=\frac{1}{2}$ for all ![]() $n\geq0.$ Littlewood’s theorem, proved in 1930 [Reference Littlewood29], states that
$n\geq0.$ Littlewood’s theorem, proved in 1930 [Reference Littlewood29], states that ![]() $(\mathcal{R}f)(z)=\sum_{n=0}^\infty a_n \epsilon_n z^n \in H^p(\mathbb{D})$ almost surely for all
$(\mathcal{R}f)(z)=\sum_{n=0}^\infty a_n \epsilon_n z^n \in H^p(\mathbb{D})$ almost surely for all ![]() $p \ge 0.$ When
$p \ge 0.$ When ![]() $f \notin H^2(\mathbb{D})$, for almost every choice of signs,
$f \notin H^2(\mathbb{D})$, for almost every choice of signs, ![]() $\mathcal{R} f$ has a radial limit almost nowhere. This implies, in particular,
$\mathcal{R} f$ has a radial limit almost nowhere. This implies, in particular, ![]() $H^p(\mathbb{D})_\star = H^2(\mathbb{D})$ for any p > 0. The same is true for a standard Steinhaus sequence [Reference Littlewood28, Reference Paley and Zygmund36] and a standard Gaussian sequence ([Reference Kahane22], p. 54). More generally, a Gaussian process version is obtained in [Reference Cheng, Fang, Guo and Liu10].
$H^p(\mathbb{D})_\star = H^2(\mathbb{D})$ for any p > 0. The same is true for a standard Steinhaus sequence [Reference Littlewood28, Reference Paley and Zygmund36] and a standard Gaussian sequence ([Reference Kahane22], p. 54). More generally, a Gaussian process version is obtained in [Reference Cheng, Fang, Guo and Liu10].
When the random series ![]() $\mathcal{R} f$ represents an
$\mathcal{R} f$ represents an ![]() $H^{\infty}(\mathbb{D})$-function almost surely is much harder, where
$H^{\infty}(\mathbb{D})$-function almost surely is much harder, where ![]() $H^{\infty}(\mathbb{D})$ denotes the bounded analytic functions. Paley, Zygmund and Salem [Reference Paley and Zygmund35, Reference Salem and Zygmund38] gave some necessary conditions and sufficient conditions. In [Reference Billard6], Billard showed that the Bernoulli case is equivalent to the Steinhaus case. A remarkable characterization was finally obtained by Marcus and Pisier in 1978 [Reference Marcus and Pisier31] (see also [Reference Kahane22, Reference Marcus and Pisier32]). Their characterization, or, in other words, a description of
$H^{\infty}(\mathbb{D})$ denotes the bounded analytic functions. Paley, Zygmund and Salem [Reference Paley and Zygmund35, Reference Salem and Zygmund38] gave some necessary conditions and sufficient conditions. In [Reference Billard6], Billard showed that the Bernoulli case is equivalent to the Steinhaus case. A remarkable characterization was finally obtained by Marcus and Pisier in 1978 [Reference Marcus and Pisier31] (see also [Reference Kahane22, Reference Marcus and Pisier32]). Their characterization, or, in other words, a description of ![]() $H^\infty(\mathbb{D})_\star$, builds on the celebrated Dudley–Fernique theorem. The space
$H^\infty(\mathbb{D})_\star$, builds on the celebrated Dudley–Fernique theorem. The space ![]() $H^\infty(\mathbb{D})_\star$ can be equipped with a Banach space norm and lies strictly between the standard Dirichlet space and
$H^\infty(\mathbb{D})_\star$ can be equipped with a Banach space norm and lies strictly between the standard Dirichlet space and ![]() $H^2(\mathbb{D})$. Further understanding of
$H^2(\mathbb{D})$. Further understanding of ![]() $H^\infty(\mathbb{D})_\star$ appears desirable.
$H^\infty(\mathbb{D})_\star$ appears desirable.
In 1974, Anderson, Clunie and Pommerenke [Reference Anderson, Clunie and Pommerenke2] studied the case of the Bloch space ![]() $\mathcal{B}.$ Among other things, they showed that the condition
$\mathcal{B}.$ Among other things, they showed that the condition ![]() $
\sum_{n=1}^{\infty}|a_n|^2\log n \lt \infty
$ implies that
$
\sum_{n=1}^{\infty}|a_n|^2\log n \lt \infty
$ implies that ![]() $
\sum_{n=0}^{\infty}\mathrm{e}^{2\pi i\alpha_n}a_nz^n\in\mathcal{B}
$ a.s. By Paley and Zygmund [Reference Paley and Zygmund35], this condition does not imply that
$
\sum_{n=0}^{\infty}\mathrm{e}^{2\pi i\alpha_n}a_nz^n\in\mathcal{B}
$ a.s. By Paley and Zygmund [Reference Paley and Zygmund35], this condition does not imply that ![]() $
\sum_{n=0}^{\infty} a_n \epsilon_n z^n\in H^\infty(\mathbb{D})
$ a.s. On the other hand, the condition
$
\sum_{n=0}^{\infty} a_n \epsilon_n z^n\in H^\infty(\mathbb{D})
$ a.s. On the other hand, the condition ![]() $
\sum_{n=1}^{\infty}|a_n|^2(\log n)^{1+\epsilon} \lt \infty
$ for some ϵ > 0 implies that
$
\sum_{n=1}^{\infty}|a_n|^2(\log n)^{1+\epsilon} \lt \infty
$ for some ϵ > 0 implies that ![]() $\sum_{n=0}^{\infty} a_n\epsilon_n z^n\in {\mathcal{A} }$ a.s., where
$\sum_{n=0}^{\infty} a_n\epsilon_n z^n\in {\mathcal{A} }$ a.s., where ![]() $\mathcal{A}$ denotes the disk algebra. A necessary and sufficient condition for a random Taylor series to represent a Bloch function is given by Gao [Reference Gao18]. The space
$\mathcal{A}$ denotes the disk algebra. A necessary and sufficient condition for a random Taylor series to represent a Bloch function is given by Gao [Reference Gao18]. The space ![]() $\mathcal{B}_*$ is less understood so far, and although not explicitly discussed in [Reference Gao18], it differs for the Gaussian and the Rademacher/Steinhaus randomization methods.
$\mathcal{B}_*$ is less understood so far, and although not explicitly discussed in [Reference Gao18], it differs for the Gaussian and the Rademacher/Steinhaus randomization methods.
In 1981, Sledd [Reference Sledd39] showed that the condition ![]() $
\sum_{n=1}^{\infty}|a_n|^2\log n \lt \infty
$ implies that
$
\sum_{n=1}^{\infty}|a_n|^2\log n \lt \infty
$ implies that ![]() $
\sum_{n=0}^{\infty}a_n\epsilon_nz^n\in\text{BMOA a.s.}
$ Actually, he proved that it is indeed in the class of analytic functions of vanishing mean oscillation (VMOA). Then, some related results were extended by [Reference Wulan42]. Sledd and Stegenga [Reference Sledd and Stegenga40] showed that
$
\sum_{n=0}^{\infty}a_n\epsilon_nz^n\in\text{BMOA a.s.}
$ Actually, he proved that it is indeed in the class of analytic functions of vanishing mean oscillation (VMOA). Then, some related results were extended by [Reference Wulan42]. Sledd and Stegenga [Reference Sledd and Stegenga40] showed that ![]() $
\sum_{n=0}^{\infty}\epsilon_na_nz^n\notin\text{BMOA a.s.}
$ for some sequence
$
\sum_{n=0}^{\infty}\epsilon_na_nz^n\notin\text{BMOA a.s.}
$ for some sequence ![]() $\{a_n\}_{n\geq 0}\in\ell^2.$ In [Reference Duren16], Duren explored the difference between
$\{a_n\}_{n\geq 0}\in\ell^2.$ In [Reference Duren16], Duren explored the difference between  $\bigcap_{0 \lt p \lt \infty}H^p(\mathbb{D})$ and BMOA for the random Taylor series. Konyagin–Queffélec–Saksman–Seip provide one sufficient condition for a random Dirichlet series belonging to BMOA [Reference Konyagin, Queffélec, Saksman and Seip24]. It remains an outstanding open problem to characterize
$\bigcap_{0 \lt p \lt \infty}H^p(\mathbb{D})$ and BMOA for the random Taylor series. Konyagin–Queffélec–Saksman–Seip provide one sufficient condition for a random Dirichlet series belonging to BMOA [Reference Konyagin, Queffélec, Saksman and Seip24]. It remains an outstanding open problem to characterize ![]() $\text{BMOA}_\star$ and
$\text{BMOA}_\star$ and ![]() $\text{VMOA}_\star$, which are different according to Nishry and Paquette [Reference Nishry and Paquette34].
$\text{VMOA}_\star$, which are different according to Nishry and Paquette [Reference Nishry and Paquette34].
Another elegant example is a theorem due to Cochran, Shapiro and Ullrich on the Dirichlet space [Reference Cochran, Shapiro and Ullrich13]. They proved in 1993 that a Dirichlet function with random signs is a.s. a Dirichlet multiplier. Equivalently, ![]() $\mathcal{M(\mathcal{D})}_\star=\mathcal{D}.$ This result is generalized in [Reference Liu30]. Our preliminary investigation suggests that extending this result from
$\mathcal{M(\mathcal{D})}_\star=\mathcal{D}.$ This result is generalized in [Reference Liu30]. Our preliminary investigation suggests that extending this result from ![]() $\mathcal{D}\doteq\mathcal{D}^2$ to
$\mathcal{D}\doteq\mathcal{D}^2$ to ![]() $\mathcal{D}^p$, p > 0, leads to a new family of nontrivial Banach spaces.
$\mathcal{D}^p$, p > 0, leads to a new family of nontrivial Banach spaces.
On the other hand, for essentially every example of ![]() $\mathcal{X}_{\star}$ which we encounter, the monomials
$\mathcal{X}_{\star}$ which we encounter, the monomials ![]() $\{z^n\}_{n\geq 0}$ exhibit features of an unconditional basis, yet they often don’t even form a Schauder basis. When this happens, the space under consideration is usually non-separable. There is clearly a lack of proper technical tools in the current literature to describe such a phenomenon, and it prompts us to introduce the following definition, which is the focus of this study. Let
$\{z^n\}_{n\geq 0}$ exhibit features of an unconditional basis, yet they often don’t even form a Schauder basis. When this happens, the space under consideration is usually non-separable. There is clearly a lack of proper technical tools in the current literature to describe such a phenomenon, and it prompts us to introduce the following definition, which is the focus of this study. Let ![]() $\mathfrak{S}=\big\{a=(a_1, a_2, \cdots, a_n, \cdots ): \ a_n\in \mathbb{C}, \ n\geq 1\big\}$ denote the vector space of sequences of complex scalars. Then,
$\mathfrak{S}=\big\{a=(a_1, a_2, \cdots, a_n, \cdots ): \ a_n\in \mathbb{C}, \ n\geq 1\big\}$ denote the vector space of sequences of complex scalars. Then, ![]() $\mathfrak{S}$ is a locally convex vector space under the seminorms
$\mathfrak{S}$ is a locally convex vector space under the seminorms ![]() $p_n(a)=|a_n|,\ n\geq 1.$ For simplicity, let
$p_n(a)=|a_n|,\ n\geq 1.$ For simplicity, let ![]() $\mathbf{e}_n\doteq (0, \cdots, 0, 1, 0, \cdots), \ n\geq 1.$
$\mathbf{e}_n\doteq (0, \cdots, 0, 1, 0, \cdots), \ n\geq 1.$
Definition 1. Let E be a Banach space, or a p-Banach space with ![]() $p\in (0, 1)$, and
$p\in (0, 1)$, and ![]() $\{e_n\}_{n\geq 1}$ a sequence of unit vectors in E. We say that
$\{e_n\}_{n\geq 1}$ a sequence of unit vectors in E. We say that ![]() $\{e_n\}_{n\geq 1}$ is a solid basis for E if there exists a linear map
$\{e_n\}_{n\geq 1}$ is a solid basis for E if there exists a linear map ![]() $\mathcal{T}: E \to \mathfrak{S},$ called the coefficient map, with
$\mathcal{T}: E \to \mathfrak{S},$ called the coefficient map, with ![]() $\mathcal{T} x=\big((\mathcal{T} x)_1, \cdots, (\mathcal{T} x)_n, \cdots \big)$ and
$\mathcal{T} x=\big((\mathcal{T} x)_1, \cdots, (\mathcal{T} x)_n, \cdots \big)$ and ![]() $\mathcal{T} e_n=\mathbf{e}_n, \ n\geq 1,$ such that
$\mathcal{T} e_n=\mathbf{e}_n, \ n\geq 1,$ such that
(i)
 $\big\|\sum_{n=1}^{N}\lambda_na_ne_n\big\|_E \leq \big\|\sum_{n=1}^{N}a_ne_n\big\|_E $ for
$\big\|\sum_{n=1}^{N}\lambda_na_ne_n\big\|_E \leq \big\|\sum_{n=1}^{N}a_ne_n\big\|_E $ for  $\lambda_n\in\mathbb{C}$,
$\lambda_n\in\mathbb{C}$,  $|\lambda_n|\leq 1,$
$|\lambda_n|\leq 1,$  $N\in\mathbb{N}$ and
$N\in\mathbb{N}$ and  $a_n\in\mathbb{C};$ and
$a_n\in\mathbb{C};$ and(ii)
 $\lim\limits_{N\to\infty}\big\|\sum_{n=1}^N(\mathcal{T} x)_ne_n\big\|_E=\|x\|_E,\ x\in E.$
$\lim\limits_{N\to\infty}\big\|\sum_{n=1}^N(\mathcal{T} x)_ne_n\big\|_E=\|x\|_E,\ x\in E.$
Remarks. (a) Recall that a functional ![]() $\|\cdot\|: E \to [0, \infty)$ is called a p -norm with
$\|\cdot\|: E \to [0, \infty)$ is called a p -norm with ![]() $p\in (0, 1)$ if E is a complex vector space and
$p\in (0, 1)$ if E is a complex vector space and ![]() $x, y\in E,$ then
$x, y\in E,$ then
(i)
 $\|x\| \gt 0$ if
$\|x\| \gt 0$ if  $x\neq 0,$ and
$x\neq 0,$ and  $\|\lambda x\|=|\lambda|\|x\|,\ \lambda\in\mathbb{C};$ and
$\|\lambda x\|=|\lambda|\|x\|,\ \lambda\in\mathbb{C};$ and(ii)
 $\|x+y\|^p\leq \|x\|^p+\|y\|^p.$
$\|x+y\|^p\leq \|x\|^p+\|y\|^p.$
If (E, d), with ![]() $d(x, y)=\|x-y\|^p$, is a complete metric space, then it is called a p -Banach space. Banach spaces are p-Banach spaces for each
$d(x, y)=\|x-y\|^p$, is a complete metric space, then it is called a p -Banach space. Banach spaces are p-Banach spaces for each ![]() $p\in (0, 1),$ although we don’t need such an identification in this paper.
$p\in (0, 1),$ although we don’t need such an identification in this paper.
(b) For convenience, let  $P_N(x)=\sum_{n=1}^N(\mathcal{T} x)_n{e}_n, \ x\in E$, which we view as an abstract Taylor polynomial.
$P_N(x)=\sum_{n=1}^N(\mathcal{T} x)_n{e}_n, \ x\in E$, which we view as an abstract Taylor polynomial.
(c) By Definition 1, the quantity ![]() $\|P_N(x)-x\|_E$ is necessarily decreasing in N; hence, the limit
$\|P_N(x)-x\|_E$ is necessarily decreasing in N; hence, the limit ![]() $\text{gap}(x)\doteq\lim_{N\to\infty} \|P_N(x)-x\|_E$ exists. Those elements such that
$\text{gap}(x)\doteq\lim_{N\to\infty} \|P_N(x)-x\|_E$ exists. Those elements such that ![]() $\text{gap}(x)=0$ form a closed subspace of E. The situation when
$\text{gap}(x)=0$ form a closed subspace of E. The situation when ![]() $\text{gap}(x) \gt 0$ is the more interesting part of our study, and this happens usually when E is non-separable.
$\text{gap}(x) \gt 0$ is the more interesting part of our study, and this happens usually when E is non-separable.
In order to quantify the clause ‘essentially every example of ![]() $\mathcal{X}_\star$’ above and to put our study on a proper footing, we are led to revisit the axioms satisfied by canonical Banach spaces of analytic functions over the unit disk. This is a subject with a long history. The first systematic investigation is probably due to Taylor in 1951 [Reference Taylor41]. Two subsequent developments, somehow similar to our study in spirit, are due to Brown and Shields [Reference Brown and Shields9], in which the authors proposed a set of axioms suitable for their research of cyclic vectors, and due to Blasco and Pavlović [Reference Blasco and Pavlović7], in which they presented a framework suitable for the study of coefficient multipliers. In this paper, we present another set of axioms (Definition 2), which are suitable not only for our study of random analytic functions but also of interests for the general study of Banach spaces of analytic functions. Compared with earlier works, a feature of our axioms is that they lead to several functorial constructions.
$\mathcal{X}_\star$’ above and to put our study on a proper footing, we are led to revisit the axioms satisfied by canonical Banach spaces of analytic functions over the unit disk. This is a subject with a long history. The first systematic investigation is probably due to Taylor in 1951 [Reference Taylor41]. Two subsequent developments, somehow similar to our study in spirit, are due to Brown and Shields [Reference Brown and Shields9], in which the authors proposed a set of axioms suitable for their research of cyclic vectors, and due to Blasco and Pavlović [Reference Blasco and Pavlović7], in which they presented a framework suitable for the study of coefficient multipliers. In this paper, we present another set of axioms (Definition 2), which are suitable not only for our study of random analytic functions but also of interests for the general study of Banach spaces of analytic functions. Compared with earlier works, a feature of our axioms is that they lead to several functorial constructions.
For any (p-)Banach space ![]() $\mathcal{X}$ of analytic functions over the unit disk
$\mathcal{X}$ of analytic functions over the unit disk ![]() $\mathbb{D},$ let δz denote the point evaluation functional:
$\mathbb{D},$ let δz denote the point evaluation functional: ![]() $\delta_z(f)=f(z),\ f\in \mathcal{X}, z\in\mathbb{D}$ and let
$\delta_z(f)=f(z),\ f\in \mathcal{X}, z\in\mathbb{D}$ and let ![]() $f_{w}(z)=f(wz)$ for
$f_{w}(z)=f(wz)$ for ![]() $ z\in\mathbb{D}$ and
$ z\in\mathbb{D}$ and ![]() $w \in \overline{\mathbb{D}}.$ Our axioms for canonical Banach spaces of analytic functions are the following:
$w \in \overline{\mathbb{D}}.$ Our axioms for canonical Banach spaces of analytic functions are the following:
Definition 2. A functional Banach space, or a functional p-Banach space with ![]() $p\in (0, 1)$,
$p\in (0, 1)$, ![]() $\mathcal{X}$ of analytic functions over
$\mathcal{X}$ of analytic functions over ![]() $\mathbb{D}$, which contains all the polynomials, is called of homogeneous type if
$\mathbb{D}$, which contains all the polynomials, is called of homogeneous type if
(i) the point evaluations are continuous:
 $\big\{\delta_z:\ z\in\mathbb{D}\big\} \subset \mathcal{X}^{\ast};$
$\big\{\delta_z:\ z\in\mathbb{D}\big\} \subset \mathcal{X}^{\ast};$(ii) the rotations preserve the norm:
 $\|f_{\xi}\|_{\mathcal{X}} = \|f\|_{\mathcal{X}}$ for
$\|f_{\xi}\|_{\mathcal{X}} = \|f\|_{\mathcal{X}}$ for  $f\in \mathcal{X}$ and
$f\in \mathcal{X}$ and  $\xi\in\mathbb{T};$
$\xi\in\mathbb{T};$(iii) the dilation is continuous: The function
 $F=F_f(\cdot): \mathbb{D} \to \mathcal{X}$, defined by
$F=F_f(\cdot): \mathbb{D} \to \mathcal{X}$, defined by  $F(z)=f_z$ for
$F(z)=f_z$ for  $f\in \mathcal{X}$, is well-defined and continuous; and
$f\in \mathcal{X}$, is well-defined and continuous; and(iv) the norm is increasingly continuous:
 $\sup_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}} = \|f\|_{\mathcal{X}}$ for
$\sup_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}} = \|f\|_{\mathcal{X}}$ for  $f\in \mathcal{X}.$
$f\in \mathcal{X}.$
Each of the above four axioms is clearly familiar to a practitioner in the field, and they are inclusive enough to accommodate every example of interests to us. The main point, which we stress again, is that they turn out to suit our study of ![]() $\mathcal{X}_\star$ well. Note that the function
$\mathcal{X}_\star$ well. Note that the function ![]() $r \mapsto \|f_r\|_{\mathcal{X}} $ is necessarily continuous and increasing over
$r \mapsto \|f_r\|_{\mathcal{X}} $ is necessarily continuous and increasing over ![]() $(0,1)$ which follows from (iii) and (iv) in Definition 2. In this paper, we usually use E to denote an abstract (p-)Banach space and
$(0,1)$ which follows from (iii) and (iv) in Definition 2. In this paper, we usually use E to denote an abstract (p-)Banach space and ![]() $\mathcal{X}$ a functional (p-)Banach space. Moreover, let SNf denote the degree-N Taylor polynomial for
$\mathcal{X}$ a functional (p-)Banach space. Moreover, let SNf denote the degree-N Taylor polynomial for ![]() $f\in H(\mathbb{D})$ (
$f\in H(\mathbb{D})$ (![]() $N\geq 0).$
$N\geq 0).$
Measurability assumption. Several results in this paper involve not only ![]() $\mathcal{X}$ above, but also
$\mathcal{X}$ above, but also ![]() $\mathcal{X}_{\star}$, its symbol space. In order to make a statement about
$\mathcal{X}_{\star}$, its symbol space. In order to make a statement about ![]() $\mathcal{X}_{\star}$, we still need to impose another very weak but necessary assumption: For any
$\mathcal{X}_{\star}$, we still need to impose another very weak but necessary assumption: For any ![]() $f \in H(\mathbb{D})$, the event
$f \in H(\mathbb{D})$, the event ![]() $\{\mathcal{R} f \in \mathcal{X}\}$ is Borel measurable, so that
$\{\mathcal{R} f \in \mathcal{X}\}$ is Borel measurable, so that ![]() $\mathbb{P}(\mathcal{R} f \in \mathcal{X})$ is defined. The Kolmogorov zero-one law implies, then,
$\mathbb{P}(\mathcal{R} f \in \mathcal{X})$ is defined. The Kolmogorov zero-one law implies, then, ![]() $\mathbb{P}(\mathcal{R} f \in \mathcal{X}) \in \{0,1\}$, and hence,
$\mathbb{P}(\mathcal{R} f \in \mathcal{X}) \in \{0,1\}$, and hence, ![]() $\mathcal{X}_{\star}$ is well defined. Subsequently, in this paper, whenever we mention
$\mathcal{X}_{\star}$ is well defined. Subsequently, in this paper, whenever we mention ![]() $\mathcal{X}_{\star}$, we assume that this measurability assumption is in force. On the other hand, once
$\mathcal{X}_{\star}$, we assume that this measurability assumption is in force. On the other hand, once ![]() $\mathcal{X}_{\star}$ is defined, this assumption will no longer enter any argument.
$\mathcal{X}_{\star}$ is defined, this assumption will no longer enter any argument.
The following is our principal example of solid bases.
Theorem A. Let ![]() $\{X_n\}_{n\geq 0}$ be a standard random sequence (Definition 6).
$\{X_n\}_{n\geq 0}$ be a standard random sequence (Definition 6).
(i) Let
 $\mathcal{X}$ be a functional Banach space of homogeneous type. Then
$\mathcal{X}$ be a functional Banach space of homogeneous type. Then(i.1)
 $\mathcal{X}_{\star}$ is a functional Banach space of homogeneous type under the norm
$\mathcal{X}_{\star}$ is a functional Banach space of homogeneous type under the norm  $
\|f\|_{\mathcal{X}_{\star}} = \mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}},
$ which is necessarily finite.
$
\|f\|_{\mathcal{X}_{\star}} = \mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}},
$ which is necessarily finite.(i.2) If
 $\{X_n\}_{n\geq 0}$ is a standard Steinhaus or complex Gaussian sequence, then
$\{X_n\}_{n\geq 0}$ is a standard Steinhaus or complex Gaussian sequence, then  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for  $\mathcal{X}_{\star}.$
$\mathcal{X}_{\star}.$(i.3) If
 $\{X_n\}_{n\geq 0}$ is a standard Rademacher or real Gaussian sequence, then
$\{X_n\}_{n\geq 0}$ is a standard Rademacher or real Gaussian sequence, then  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for  $\mathcal{X}_{\star}.$ Moreover,
$\mathcal{X}_{\star}.$ Moreover,  $\|f\|_{\mathcal{X}_{\star}}=\lim\limits_{N\to\infty}\|S_Nf\|_{\mathcal{X}_{\star}}$ for
$\|f\|_{\mathcal{X}_{\star}}=\lim\limits_{N\to\infty}\|S_Nf\|_{\mathcal{X}_{\star}}$ for  $ f\in \mathcal{X}_{\star}.$
$ f\in \mathcal{X}_{\star}.$
(ii) Let
 $\mathcal{X}$ be a functional p-Banach space of homogeneous type with
$\mathcal{X}$ be a functional p-Banach space of homogeneous type with  $p\in (0, 1).$ Assume that
$p\in (0, 1).$ Assume that  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ Then
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ Then(ii.1)
 $\mathcal{X}_{\star}$ is a functional p-Banach space of homogeneous type under the p-norm
$\mathcal{X}_{\star}$ is a functional p-Banach space of homogeneous type under the p-norm  $
\|f\|_{\mathcal{X}_{\star}} = \big(\mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}}^p\big)^{1/p},
$ which is necessarily finite.
$
\|f\|_{\mathcal{X}_{\star}} = \big(\mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}}^p\big)^{1/p},
$ which is necessarily finite.(ii.2)
 $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for  $\mathcal{X}_{\star}.$
$\mathcal{X}_{\star}.$
Definition 3. A sequence of unit vectors ![]() $\{e_n\}_{n\geq 1}$ is said to be a solid frame for E, a Banach or p-Banach space, if there exists a linear coefficient map
$\{e_n\}_{n\geq 1}$ is said to be a solid frame for E, a Banach or p-Banach space, if there exists a linear coefficient map ![]() $\mathcal{T}: E \to \mathfrak{S}$ with
$\mathcal{T}: E \to \mathfrak{S}$ with ![]() $\mathcal{T} x=\big((\mathcal{T} x)_1, \cdots, (\mathcal{T} x)_n, \cdots \big)$ and
$\mathcal{T} x=\big((\mathcal{T} x)_1, \cdots, (\mathcal{T} x)_n, \cdots \big)$ and ![]() $\mathcal{T} e_n=\mathbf{e}_n, n\geq 1,$ such that
$\mathcal{T} e_n=\mathbf{e}_n, n\geq 1,$ such that
(i) there exists a constant C such that
 $
\big\|\sum_{n=1}^{N}\lambda_na_ne_n\big\|_E \leq C\big\|\sum_{n=1}^{N}a_ne_n\big\|_E
$ for any
$
\big\|\sum_{n=1}^{N}\lambda_na_ne_n\big\|_E \leq C\big\|\sum_{n=1}^{N}a_ne_n\big\|_E
$ for any  $\lambda_n\in\mathbb{C}$,
$\lambda_n\in\mathbb{C}$,  $|\lambda_n|\leq 1$, and
$|\lambda_n|\leq 1$, and  $N\in\mathbb{N}, \ a_n\in\mathbb{C};$ and
$N\in\mathbb{N}, \ a_n\in\mathbb{C};$ and(ii) there exist
 $
C'{~and~}C''{~such~that~} C'\|x\|_E \leq \sup_{N\geq 1}\|P_N(x)\|_E \leq C''\|x\|_E, x\in E.
$
$
C'{~and~}C''{~such~that~} C'\|x\|_E \leq \sup_{N\geq 1}\|P_N(x)\|_E \leq C''\|x\|_E, x\in E.
$
Theorem E below explains how to transform solid frames into solid bases.
Remarks. (a) By the contraction principle ([Reference Hytönen, van Neerven, Veraar and Weis21, Theorem 6.1.13, p. 9]) and Lemma 8, we can choose ![]() $C=\frac{\pi}{2}, C'=C''=1 $ and
$C=\frac{\pi}{2}, C'=C''=1 $ and  $C'=1, C''=2^{\frac{1}{p}-1},$ respectively, for the constants of solid frames in (i.3) and (ii.2), Theorem A.
$C'=1, C''=2^{\frac{1}{p}-1},$ respectively, for the constants of solid frames in (i.3) and (ii.2), Theorem A.
(b) From the assumption ![]() $\{\delta_z: \ z\in\mathbb{D}\}\subset \mathcal{X}^{\ast},$ one can show that
$\{\delta_z: \ z\in\mathbb{D}\}\subset \mathcal{X}^{\ast},$ one can show that  $\liminf\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}\geq 1.$
$\liminf\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}\geq 1.$
Functorial constructions. Next, we summarize various functorial constructions for ![]() $\mathcal{X}$ and
$\mathcal{X}$ and ![]() $E,$ which are features following from our choice of axioms for a typical (p-)Banach space of analytic functions. Although they are motivated by the study of random analytic functions, these constructions are clearly of independent interests for the general study of functional (p-)Banach spaces.
$E,$ which are features following from our choice of axioms for a typical (p-)Banach space of analytic functions. Although they are motivated by the study of random analytic functions, these constructions are clearly of independent interests for the general study of functional (p-)Banach spaces.
(a)
 $\mathcal{X}^\mathrm{min}$ and
$\mathcal{X}^\mathrm{min}$ and  $\mathcal{X}^\mathrm{max}:$ We shall introduce a notion called homogeneous extension (Definition 4), and in this sense, for any homogeneous
$\mathcal{X}^\mathrm{max}:$ We shall introduce a notion called homogeneous extension (Definition 4), and in this sense, for any homogeneous  $\mathcal{X},$ we show that there exists a unique
$\mathcal{X},$ we show that there exists a unique  $\mathcal{X}^\mathrm{min}$ and a unique
$\mathcal{X}^\mathrm{min}$ and a unique  $\mathcal{X}^\mathrm{max}$ such that
$\mathcal{X}^\mathrm{max}$ such that
 \begin{equation*}
\mathcal{X}^\mathrm{min}\subset \mathcal{X} \subset \mathcal{X}^\mathrm{max}.
\end{equation*}
\begin{equation*}
\mathcal{X}^\mathrm{min}\subset \mathcal{X} \subset \mathcal{X}^\mathrm{max}.
\end{equation*}Examples of the pair
 $(\mathcal{X}^\mathrm{min}, \mathcal{X}^\mathrm{max})$ include
$(\mathcal{X}^\mathrm{min}, \mathcal{X}^\mathrm{max})$ include–
 $(A(\mathbb{D}), H^{\infty}(\mathbb{D})),$ the disk algebra and bounded analytic functions
$(A(\mathbb{D}), H^{\infty}(\mathbb{D})),$ the disk algebra and bounded analytic functions–
 $(\mathcal{B}_0, \mathcal{B}),$ the little Bloch and Bloch spaces, and
$(\mathcal{B}_0, \mathcal{B}),$ the little Bloch and Bloch spaces, and–
 $(\text{VMOA}, \text{BMOA})$.
$(\text{VMOA}, \text{BMOA})$.
(b)
 $E_{\mathcal{P}}$ and
$E_{\mathcal{P}}$ and  $E^\mathrm{s\text{-}max}:$ We shall introduce a notion called solid extension (Definition 5). This allows us to introduce sequential analogs of
$E^\mathrm{s\text{-}max}:$ We shall introduce a notion called solid extension (Definition 5). This allows us to introduce sequential analogs of  $\mathcal{X}^\mathrm{min}$ and
$\mathcal{X}^\mathrm{min}$ and  $\mathcal{X}^\mathrm{max}$ for E, denoted by
$\mathcal{X}^\mathrm{max}$ for E, denoted by  $E_{\mathcal{P}}$ and
$E_{\mathcal{P}}$ and  $E^\mathrm{s\text{-}max}$, respectively. Then, for any E with a solid basis
$E^\mathrm{s\text{-}max}$, respectively. Then, for any E with a solid basis  $\{{e}_n\}_{n\geq 1}$,
$\{{e}_n\}_{n\geq 1}$,  $
E_{\mathcal{P}}$ is simply given by
$
E_{\mathcal{P}}$ is simply given by  $\overline{\text{span}} \{{e}_n: n\geq 1\}
$ and
$\overline{\text{span}} \{{e}_n: n\geq 1\}
$ and  $E^\mathrm{s\text{-}max}$ by (7). Examples of the pair
$E^\mathrm{s\text{-}max}$ by (7). Examples of the pair  $(E_{\mathcal{P}}, E^\mathrm{s\text{-}max})$ include
$(E_{\mathcal{P}}, E^\mathrm{s\text{-}max})$ include–
 $(c_0, \ell^{\infty})$, and
$(c_0, \ell^{\infty})$, and–
 $\big((H^{\infty}(\mathbb{D}))_{\star}, (H^{\infty}(\mathbb{D}))_{\star}\big).$
$\big((H^{\infty}(\mathbb{D}))_{\star}, (H^{\infty}(\mathbb{D}))_{\star}\big).$
(c)
 $(\mathcal{X}, \|\cdot\|_{\sharp}):$ The construction
(1)
$(\mathcal{X}, \|\cdot\|_{\sharp}):$ The construction
(1) \begin{align}
\|f\|_{\sharp}=\sup_{N\geq 0}\sup_{\|\lambda\|_{\ell^{\infty}}\leq 1}\Big\|\sum_{k=0}^{N}\lambda_ka_kz^k\Big\|_{\mathcal{X}},
\end{align}
\begin{align}
\|f\|_{\sharp}=\sup_{N\geq 0}\sup_{\|\lambda\|_{\ell^{\infty}}\leq 1}\Big\|\sum_{k=0}^{N}\lambda_ka_kz^k\Big\|_{\mathcal{X}},
\end{align}where
 $f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{X},$ allows us to transform a solid frame into a solid basis; see Theorem E.
$f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{X},$ allows us to transform a solid frame into a solid basis; see Theorem E.(d) A pseudo-canonical embedding
 $\mathfrak {J}: E\to E^{\ast\ast}:$ Let E be a Banach space with a solid basis
$\mathfrak {J}: E\to E^{\ast\ast}:$ Let E be a Banach space with a solid basis  $\{{e}_n\}_{n\geq 1}.$ Let
$\{{e}_n\}_{n\geq 1}.$ Let  $J:E \to E^{\ast\ast}$ be the canonical embedding map into its second dual. We shall establish the weak-star convergence of
$J:E \to E^{\ast\ast}$ be the canonical embedding map into its second dual. We shall establish the weak-star convergence of  $J(P_Nx)$ as
$J(P_Nx)$ as  $N \to \infty$, leading to what we call a pseudo-canonical map
$N \to \infty$, leading to what we call a pseudo-canonical map  $\mathfrak {J}: E\to E^{\ast\ast},$ which stands in interesting contrast to the map J; see Theorem D. In particular,
$\mathfrak {J}: E\to E^{\ast\ast},$ which stands in interesting contrast to the map J; see Theorem D. In particular,  $Jx=\mathfrak {J} x$ if and only if
$Jx=\mathfrak {J} x$ if and only if  $x\in E_{\mathcal{P}}.$ A related map
$x\in E_{\mathcal{P}}.$ A related map  $\Phi: E^\mathrm{s\text{-}max}\to (E_{\mathcal{P}})^{\ast\ast}$ is constructed in order to see how large
$\Phi: E^\mathrm{s\text{-}max}\to (E_{\mathcal{P}})^{\ast\ast}$ is constructed in order to see how large  $E^\mathrm{s\text{-}max}$ usually is. Two examples of
$E^\mathrm{s\text{-}max}$ usually is. Two examples of  $E\mathrm{^{s\text{-}max}}$ are
$E\mathrm{^{s\text{-}max}}$ are  $
E=c_0,\ E^\mathrm{s\text{-}max}=E^{\ast\ast}=\ell^{\infty}
$ and
$
E=c_0,\ E^\mathrm{s\text{-}max}=E^{\ast\ast}=\ell^{\infty}
$ and
 \begin{equation*}
E=\ell^{\infty},\ E\mathrm{^{s\text{-}max}}=\ell^{\infty}
\subset (\ell^{\infty})^{\ast\ast}=
E^{\ast\ast}.
\end{equation*}
\begin{equation*}
E=\ell^{\infty},\ E\mathrm{^{s\text{-}max}}=\ell^{\infty}
\subset (\ell^{\infty})^{\ast\ast}=
E^{\ast\ast}.
\end{equation*}To get a grasp of
 $E^\mathrm{s\text{-}max}$ in general, we construct an embedding map
$E^\mathrm{s\text{-}max}$ in general, we construct an embedding map  $\Phi: E^\mathrm{s\text{-}max}\to (E_{\mathcal{P}})^{\ast\ast},$ which fixes
$\Phi: E^\mathrm{s\text{-}max}\to (E_{\mathcal{P}})^{\ast\ast},$ which fixes  $E_{\mathcal{P}}$ (under the natural identification).
$E_{\mathcal{P}}$ (under the natural identification).
Precise statements of results related to the above constructions are presented next.
Definition 4. Let ![]() $\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with
$\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with ![]() $p\in (0, 1),$ of homogeneous type. We say that
$p\in (0, 1),$ of homogeneous type. We say that ![]() $\mathcal{Y}$ is a homogeneous extension of
$\mathcal{Y}$ is a homogeneous extension of ![]() $\mathcal{X}$ if
$\mathcal{X}$ if
(i)
 $\mathcal{Y}$ is a functional Banach space, or a functional p-Banach space with
$\mathcal{Y}$ is a functional Banach space, or a functional p-Banach space with  $p\in (0, 1),$ of homogeneous type;
$p\in (0, 1),$ of homogeneous type;(ii)
 $\mathcal{X}\subset \mathcal{Y},$ and
$\mathcal{X}\subset \mathcal{Y},$ and  $f_r\in \mathcal{X}$ if
$f_r\in \mathcal{X}$ if  $0\leq r \lt 1, \ f\in \mathcal{Y}$; and
$0\leq r \lt 1, \ f\in \mathcal{Y}$; and(iii)
 $\|f\|_{\mathcal{Y}}=\|f\|_{\mathcal{X}}$ for any
$\|f\|_{\mathcal{Y}}=\|f\|_{\mathcal{X}}$ for any  $f\in \mathcal{X}.$
$f\in \mathcal{X}.$
![]() $\mathcal{X}^\mathrm{min}$ and
$\mathcal{X}^\mathrm{min}$ and ![]() $\mathcal{X}^\mathrm{max}$. For any
$\mathcal{X}^\mathrm{max}$. For any ![]() $\mathcal{X}$ as above, we set
$\mathcal{X}$ as above, we set ![]() $\mathcal{X}^\mathrm{min} =\mathcal{X}_{\mathcal{P}},$ the closure of polynomials in
$\mathcal{X}^\mathrm{min} =\mathcal{X}_{\mathcal{P}},$ the closure of polynomials in ![]() $\mathcal{X}$. Two facts need to be verified and both are straightforward:
$\mathcal{X}$. Two facts need to be verified and both are straightforward:
•
 $\mathcal{X}_{\mathcal{P}}$ is of homogeneous type, and
$\mathcal{X}_{\mathcal{P}}$ is of homogeneous type, and•
 $\mathcal{X}$ is a homogeneous extension of
$\mathcal{X}$ is a homogeneous extension of  $\mathcal{X}_{\mathcal{P}}.$
$\mathcal{X}_{\mathcal{P}}.$
For ![]() $\mathcal{X}^\mathrm{max}$, we prove
$\mathcal{X}^\mathrm{max}$, we prove
Theorem B. Let ![]() $\{X_n\}_{n\geq 0}$ be a standard random sequence (Definition 6). Let
$\{X_n\}_{n\geq 0}$ be a standard random sequence (Definition 6). Let ![]() $\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with
$\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with ![]() $p\in (0, 1),$ of homogeneous type; for the latter, we also assume
$p\in (0, 1),$ of homogeneous type; for the latter, we also assume  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ Then,
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ Then,
(i) there exists a unique maximal homogeneous extension, denoted by
 $\mathcal{X}^\mathrm{max};$ and
$\mathcal{X}^\mathrm{max};$ and(ii) both
 $(\mathcal{X}^\mathrm{max})_{\star}$ and
$(\mathcal{X}^\mathrm{max})_{\star}$ and  $(\mathcal{X}_{\mathcal{P}})_{\star}$ are solid spaces.
$(\mathcal{X}_{\mathcal{P}})_{\star}$ are solid spaces.
A solid space, introduced by Anderson and Shields [Reference Anderson and Shields3], is a sequence space E such that ![]() $\{b_n\}_{n\geq 1}\in E$ whenever
$\{b_n\}_{n\geq 1}\in E$ whenever ![]() $\{a_n\}_{n\geq 1}\in E$ and
$\{a_n\}_{n\geq 1}\in E$ and ![]() $|b_n|\leq |a_n|.$ Although a solid space is not a space with a solid basis, our Definition 1 is clearly motivated by it. Note that, in this paper, a function
$|b_n|\leq |a_n|.$ Although a solid space is not a space with a solid basis, our Definition 1 is clearly motivated by it. Note that, in this paper, a function ![]() $f\in H(\mathbb{D})$ is often identified with its sequence of Taylor coefficients. In general,
$f\in H(\mathbb{D})$ is often identified with its sequence of Taylor coefficients. In general, ![]() $\mathcal{X}_{\star}$ may fail to be solid; see the example after the proof of Theorem B in Section 4. Fortunately, Theorem B is quite applicable, since, indeed, most natural examples of
$\mathcal{X}_{\star}$ may fail to be solid; see the example after the proof of Theorem B in Section 4. Fortunately, Theorem B is quite applicable, since, indeed, most natural examples of ![]() $\mathcal{X}$ are of the forms:
$\mathcal{X}$ are of the forms: ![]() $\mathcal{X}^\mathrm{max}$ or
$\mathcal{X}^\mathrm{max}$ or ![]() $\mathcal{X}_{\mathcal{P}}$.
$\mathcal{X}_{\mathcal{P}}$.
Remark. When ![]() $\{X_n\}_{n\geq 0}$ is a standard random sequence (Definition 6), it is known that
$\{X_n\}_{n\geq 0}$ is a standard random sequence (Definition 6), it is known that ![]() $(H^{\infty}(\mathbb{D}))_{\star}$ is solid. This follows from the celebrated characterization of
$(H^{\infty}(\mathbb{D}))_{\star}$ is solid. This follows from the celebrated characterization of ![]() $(H^{\infty}(\mathbb{D}))_{\star}$ in terms of the modulus of the Taylor coefficients of its elements [Reference Marcus and Pisier32]. Theorem B implies that
$(H^{\infty}(\mathbb{D}))_{\star}$ in terms of the modulus of the Taylor coefficients of its elements [Reference Marcus and Pisier32]. Theorem B implies that
are solid as well, and this is not obvious. It is of value to characterize when ![]() $\mathcal{X}_{\star}$ is solid, and we present it as Problem A in order to spur more interests.
$\mathcal{X}_{\star}$ is solid, and we present it as Problem A in order to spur more interests.
Unconditional bases. Next, we discuss the relationship between solid bases and unconditional bases. A Schauder basis ![]() $\{{e}_n\}_{n\geq 1}$ in a Banach space or a p-Banach space E is called an unconditional basis if for every
$\{{e}_n\}_{n\geq 1}$ in a Banach space or a p-Banach space E is called an unconditional basis if for every ![]() $x\in E,$ there exists a unique sequence of scalars
$x\in E,$ there exists a unique sequence of scalars ![]() $\{a_n(x)\}_{n\geq 1}$ such that
$\{a_n(x)\}_{n\geq 1}$ such that ![]() $
x=\sum_{n=1}^{\infty}a_n(x){e}_n,
$ and the series
$
x=\sum_{n=1}^{\infty}a_n(x){e}_n,
$ and the series ![]() $\sum_{n=1}^{\infty}a_n(x){e}_n$ converges unconditionally, that is,
$\sum_{n=1}^{\infty}a_n(x){e}_n$ converges unconditionally, that is, ![]() $\sum_{n=1}^{\infty}a_{\pi(n)}(x)\mathrm{e}_{\pi(n)}$ converges for every permutation π of positive integers. Equivalently, for any choice of phases
$\sum_{n=1}^{\infty}a_{\pi(n)}(x)\mathrm{e}_{\pi(n)}$ converges for every permutation π of positive integers. Equivalently, for any choice of phases ![]() $\theta=(\theta_k)_{k\geq 1}\in \mathbb{T}^{\mathbb{N}},$ the symmetries
$\theta=(\theta_k)_{k\geq 1}\in \mathbb{T}^{\mathbb{N}},$ the symmetries ![]() $
M_{\theta}: \sum_{n=1}^{\infty}a_n(x){e}_n \mapsto \sum_{n=1}^{\infty}\theta_na_n(x){e}_n
$ are continuous on E and
$
M_{\theta}: \sum_{n=1}^{\infty}a_n(x){e}_n \mapsto \sum_{n=1}^{\infty}\theta_na_n(x){e}_n
$ are continuous on E and ![]() $\sup_{\theta}\|M_{\theta}\| \lt \infty;$ see [Reference Li and Queffélec25, Proposition III.3, p. 91], [Reference Lindenstrauss and Tzafriri27, p. 18] or [Reference Albiac, Ansorena, Berná and Wojtaszczyk1, Theorem 1.10]. The quantity
$\sup_{\theta}\|M_{\theta}\| \lt \infty;$ see [Reference Li and Queffélec25, Proposition III.3, p. 91], [Reference Lindenstrauss and Tzafriri27, p. 18] or [Reference Albiac, Ansorena, Berná and Wojtaszczyk1, Theorem 1.10]. The quantity ![]() $K=\sup_{\theta}\|M_{\theta}\|$ is called the unconditional constant of the basis
$K=\sup_{\theta}\|M_{\theta}\|$ is called the unconditional constant of the basis ![]() $\{{e}_n\}_{n\geq 1}.$
$\{{e}_n\}_{n\geq 1}.$
(i) Let
 $\mathcal{X}$ be a functional Banach space of homogeneous type. Then, the following are equivalent:
$\mathcal{X}$ be a functional Banach space of homogeneous type. Then, the following are equivalent:(i.1)
 $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for  $\mathcal{X};$
$\mathcal{X};$(i.2)
 $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for  $\mathcal{X}_{\mathcal{P}};$
$\mathcal{X}_{\mathcal{P}};$(i.3)
 $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for  $\mathcal{X}_{\mathcal{P}}$ with constant 1;
$\mathcal{X}_{\mathcal{P}}$ with constant 1;(i.4)
 $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for  $\mathcal{X}^\mathrm{max}.$
$\mathcal{X}^\mathrm{max}.$
(ii) Let
 $\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with
$\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with  $p\in (0, 1),$ of homogeneous type; for the latter we assume
$p\in (0, 1),$ of homogeneous type; for the latter we assume  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ Then, the following are equivalent:
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ Then, the following are equivalent:(ii.1)
 $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for  $\mathcal{X};$
$\mathcal{X};$(ii.2)
 $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for  $\mathcal{X}_{\mathcal{P}};$
$\mathcal{X}_{\mathcal{P}};$(ii.3)
 $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for  $\mathcal{X}_{\mathcal{P}};$
$\mathcal{X}_{\mathcal{P}};$(ii.4)
 $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for  $\mathcal{X}^\mathrm{max}.$
$\mathcal{X}^\mathrm{max}.$
For an abstract Banach space ![]() $E,$ the relationship between solid bases/frames and unconditional bases is presented in Lemma 16.
$E,$ the relationship between solid bases/frames and unconditional bases is presented in Lemma 16.
Weak-star convergence of Taylor polynomials. Next, we claim that, in the presence of a solid basis, partial summations, viewed as abstract Taylor polynomials, are weak-star sequentially convergent in the double dual. This stands in interesting contrast to a typical existing result, say, Proposition 1 in [Reference Zhu43], which concerns the norm convergence and where the Banach space is separable; hence, the interest in Theorem D below lies in the non-separable case. Also note that, under mild conditions, weak convergence and norm convergence of Taylor polynomials are equivalent – see the discussion at the beginning of Section 6 – but weak-star sequential convergence results are indeed rare. Let ![]() $J: E\to E^{\ast\ast}$ denote the canonical imbedding of a Banach space into its second dual.
$J: E\to E^{\ast\ast}$ denote the canonical imbedding of a Banach space into its second dual.
Theorem D. Let E be a Banach space with a solid basis ![]() $\{{e}_n\}_{n\geq 1}.$ For each
$\{{e}_n\}_{n\geq 1}.$ For each ![]() $x\in E,$
$x\in E,$ ![]() $J(P_Nx)$ converges in
$J(P_Nx)$ converges in ![]() $w^{\ast}$-topology as
$w^{\ast}$-topology as ![]() $N\to\infty.$
$N\to\infty.$
The Banach–Alaoglu theorem implies that ![]() $\{P_Nx\}_{N\geq 1}$ has a
$\{P_Nx\}_{N\geq 1}$ has a ![]() $w^{\ast}$-convergent subnet since
$w^{\ast}$-convergent subnet since ![]() $\sup_{N\geq 1}\|P_Nx\|_E\leq \|x\|_E \lt \infty.$ A subtle point here is that the subnet is not necessarily a subsequence. Our contribution, hence, is to boost to the sequential convergence. Let
$\sup_{N\geq 1}\|P_Nx\|_E\leq \|x\|_E \lt \infty.$ A subtle point here is that the subnet is not necessarily a subsequence. Our contribution, hence, is to boost to the sequential convergence. Let ![]() $\mathfrak {J}(x)$ denote the limit in Theorem D. It is interesting to gain more insight, in comparison with the canonical embedding J, about the map
$\mathfrak {J}(x)$ denote the limit in Theorem D. It is interesting to gain more insight, in comparison with the canonical embedding J, about the map ![]() $
\mathfrak {J}: E \longrightarrow E^{\ast\ast}.
$ In particular, we shall show that ‘
$
\mathfrak {J}: E \longrightarrow E^{\ast\ast}.
$ In particular, we shall show that ‘![]() $\mathfrak {J}(x) = J(x)$ if and only if
$\mathfrak {J}(x) = J(x)$ if and only if ![]() $x \in E_\mathcal{P}$’; hence, the two maps appear to be considerably different when E is non-separable. The existence of
$x \in E_\mathcal{P}$’; hence, the two maps appear to be considerably different when E is non-separable. The existence of ![]() $\mathfrak {J} x$ depends only on (8), and it can be modified to yield an embedding
$\mathfrak {J} x$ depends only on (8), and it can be modified to yield an embedding ![]() $\Phi: E^\mathrm{s\text{-}max} \longrightarrow (E_{\mathcal{P}})^{\ast\ast}.$ This Φ may be viewed as an abstract extension of some classical embedding maps.
$\Phi: E^\mathrm{s\text{-}max} \longrightarrow (E_{\mathcal{P}})^{\ast\ast}.$ This Φ may be viewed as an abstract extension of some classical embedding maps.
Remark. The motivation for Theorem D comes from the so-called w.u.C. condition in Banach space theory; see, in particular, [Reference Diestel15, p. 44] or [Reference Li and Queffélec25, Proposition II.5, p. 87]. Given a Banach space ![]() $E,$ a (formal) series
$E,$ a (formal) series ![]() $\sum_{n=1}^{\infty}x_n$ is called weakly unconditionally Cauchy if
$\sum_{n=1}^{\infty}x_n$ is called weakly unconditionally Cauchy if  $
\sum\limits_{n=1}^{\infty}|\phi(x_n)| \lt \infty
$ for every
$
\sum\limits_{n=1}^{\infty}|\phi(x_n)| \lt \infty
$ for every ![]() $\phi\in E^{\ast}.$
$\phi\in E^{\ast}.$
From frames to bases. Next, we show how to transform a solid frame into a solid basis, with the help of the norm ![]() $\|\cdot\|_{\sharp}$, which is motivated by [Reference Megginson33, Definitions 4.1.13, 4.2.15].
$\|\cdot\|_{\sharp}$, which is motivated by [Reference Megginson33, Definitions 4.1.13, 4.2.15].
Theorem E. Let ![]() $\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with
$\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with ![]() $p\in (0, 1),$ of homogeneous type; for the latter, we also assume
$p\in (0, 1),$ of homogeneous type; for the latter, we also assume  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ For each
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ For each  $f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in \mathcal{X},$ let
$f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in \mathcal{X},$ let  $
\|f\|_{\sharp}=\sup\limits_{N\geq 0}\sup\limits_{\|\lambda\|_{\ell^{\infty}}\leq 1}\Big\|\sum_{k=0}^{N}\lambda_ka_kz^k\Big\|_{\mathcal{X}}.
$ Then, the following are equivalent:
$
\|f\|_{\sharp}=\sup\limits_{N\geq 0}\sup\limits_{\|\lambda\|_{\ell^{\infty}}\leq 1}\Big\|\sum_{k=0}^{N}\lambda_ka_kz^k\Big\|_{\mathcal{X}}.
$ Then, the following are equivalent:
(i)
 $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for  $\mathcal{X}.$
$\mathcal{X}.$(ii)
 $(\mathcal{X}, \|\cdot\|_{\sharp})$ is a Banach space (or p-Banach space), and
$(\mathcal{X}, \|\cdot\|_{\sharp})$ is a Banach space (or p-Banach space), and  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for  $(\mathcal{X}, \|\cdot\|_{\sharp}).$
$(\mathcal{X}, \|\cdot\|_{\sharp}).$
A large class of examples. Next, we present a characterization of solid frames in a case, which covers a large class of natural examples.
Theorem F. Let ![]() $\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with
$\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with ![]() $p\in (0, 1),$ of homogeneous type; for the latter, we also assume
$p\in (0, 1),$ of homogeneous type; for the latter, we also assume  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ If
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ If ![]() $\mathcal{X}=\mathcal{X}^\mathrm{max}$ or
$\mathcal{X}=\mathcal{X}^\mathrm{max}$ or ![]() $\mathcal{X}=\mathcal{X}_{\mathcal{P}},$ then
$\mathcal{X}=\mathcal{X}_{\mathcal{P}},$ then  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for ![]() $\mathcal{X}$ if and only if
$\mathcal{X}$ if and only if ![]() $\sup_{N\geq 0}\|S_N\| \lt \infty$ and
$\sup_{N\geq 0}\|S_N\| \lt \infty$ and ![]() $\mathcal{X}$ is a solid space. Here,
$\mathcal{X}$ is a solid space. Here, ![]() $\|S_N\|$ is the operator norm.
$\|S_N\|$ is the operator norm.
Remark. Since ![]() $(\mathcal{X}_{\star})_{\mathcal{P}}=(\mathcal{X}_{\mathcal{P}})_{\star}$ and
$(\mathcal{X}_{\star})_{\mathcal{P}}=(\mathcal{X}_{\mathcal{P}})_{\star}$ and ![]() $ (\mathcal{X}_{\star})^\mathrm{max}=(\mathcal{X}^\mathrm{max})_{\star}$ (Lemma 10), the above result should be compared with (ii) in Theorem B.
$ (\mathcal{X}_{\star})^\mathrm{max}=(\mathcal{X}^\mathrm{max})_{\star}$ (Lemma 10), the above result should be compared with (ii) in Theorem B.
Solid span. A sequence ![]() $\{{e}_n\}_{n\geq 1}$ in a Banach space E is said to be a basic sequence if it is a Schauder basis for the closure of its span, i.e.,
$\{{e}_n\}_{n\geq 1}$ in a Banach space E is said to be a basic sequence if it is a Schauder basis for the closure of its span, i.e., ![]() $\overline{\text{span}\{{e}_n: \ n\geq1\}}.$ For a new notion of Banach space basis, such as the one we propose in this paper, a natural question to ask is: How to construct the solid span of a basic sequence? This does not have an easy answer since c 0 and
$\overline{\text{span}\{{e}_n: \ n\geq1\}}.$ For a new notion of Banach space basis, such as the one we propose in this paper, a natural question to ask is: How to construct the solid span of a basic sequence? This does not have an easy answer since c 0 and ![]() $\ell^{\infty}$ show that we can find two Banach spaces
$\ell^{\infty}$ show that we can find two Banach spaces ![]() $E\subsetneq F$ such that
$E\subsetneq F$ such that ![]() $\{{e}_n\}_{n\geq 1}$ is a solid basis for both. This discrepancy can be nicely resolved by introducing the following:
$\{{e}_n\}_{n\geq 1}$ is a solid basis for both. This discrepancy can be nicely resolved by introducing the following:
Definition 5. Let E be a Banach space with a solid basis ![]() $\{{e}_n\}_{n\geq 1}.$ A Banach space F is called a solid extension of E if
$\{{e}_n\}_{n\geq 1}.$ A Banach space F is called a solid extension of E if
(i) there exists an isometric embedding
 $\imath: E\hookrightarrow F;$ and
$\imath: E\hookrightarrow F;$ and(ii)
 $\{\imath {e}_n\}_{n\geq 1}$ is also a solid basis for
$\{\imath {e}_n\}_{n\geq 1}$ is also a solid basis for  $F.$
$F.$
Theorem G. Let E be a Banach space with a solid basis ![]() $\{{e}_n\}_{n\geq 1}.$
$\{{e}_n\}_{n\geq 1}.$
(i) There exists a unique maximal solid extension under the isometric isomorphism, denoted by
 $E^\mathrm{s\text{-}max}$ (which is necessarily given by (7)).
$E^\mathrm{s\text{-}max}$ (which is necessarily given by (7)).(ii) Let W be a Banach space. Assume that
 $\imath :E_{\mathcal{P}}\hookrightarrow W$ is an isometric embedding. Then
$\imath :E_{\mathcal{P}}\hookrightarrow W$ is an isometric embedding. Then  $\{\imath {e}_n\}_{n\geq 1}$ is a solid basis for W if and only if W can be embedded into
$\{\imath {e}_n\}_{n\geq 1}$ is a solid basis for W if and only if W can be embedded into  $(E_{\mathcal{P}})^\mathrm{s\text{-}max}$ isometrically.
$(E_{\mathcal{P}})^\mathrm{s\text{-}max}$ isometrically.
Remark. This theorem may be viewed as an abstract extension of Theorem C for ![]() $\mathcal{X}$.
$\mathcal{X}$.
The role of c 0. At last, we highlight the curious roles played by c 0 in our study. This part is motivated by the corresponding action of c 0 in the theory of unconditional bases; see, for example, [Reference Li and Queffélec25, Chapter 3]. Recall that c 0 is the subspace of ![]() $\mathfrak{S}$ consisting of sequences convergent to 0. Let E be a Banach space with a solid basis
$\mathfrak{S}$ consisting of sequences convergent to 0. Let E be a Banach space with a solid basis ![]() $\{{e}_n\}_{n\geq 1}.$ Let
$\{{e}_n\}_{n\geq 1}.$ Let  $
c_0\cdot E \doteq \Big\{\sum_{n=1}^{\infty}t_n(\mathcal{T} x)_n{e}_n:\ (t_n)_{n\geq 1}\in c_0,\ x\in E\Big\}.
$ Similarly, for
$
c_0\cdot E \doteq \Big\{\sum_{n=1}^{\infty}t_n(\mathcal{T} x)_n{e}_n:\ (t_n)_{n\geq 1}\in c_0,\ x\in E\Big\}.
$ Similarly, for ![]() $a=(a_1, a_2, \cdots)\in \mathfrak{S},$ let
$a=(a_1, a_2, \cdots)\in \mathfrak{S},$ let ![]() $
c_0\cdot a=\big\{(a_nt_n)_{n\geq 1}:\ (t_n)_{n\geq 1}\in c_0\big\}.
$ The proofs of the following two theorems involve the dual space
$
c_0\cdot a=\big\{(a_nt_n)_{n\geq 1}:\ (t_n)_{n\geq 1}\in c_0\big\}.
$ The proofs of the following two theorems involve the dual space ![]() $E^{\ast},$ hence confined to Banach spaces.
$E^{\ast},$ hence confined to Banach spaces.
Theorem H. Let E be a Banach space with a solid basis ![]() $\{{e}_n\}_{n\geq 1}.$ Then,
$\{{e}_n\}_{n\geq 1}.$ Then,
(i)
 $c_0\cdot E=E_{\mathcal{P}}.$
$c_0\cdot E=E_{\mathcal{P}}.$(ii) For each
 $a\in \mathfrak{S}$,
$a\in \mathfrak{S}$,  $c_0\cdot a\in E_{\mathcal{P}}$ if and only if
$c_0\cdot a\in E_{\mathcal{P}}$ if and only if  $a\in E^\mathrm{s\text{-}max}.$
$a\in E^\mathrm{s\text{-}max}.$
Theorem I. Let E be a Banach space with a solid basis ![]() $\{{e}_n\}_{n\geq 1}.$ Then,
$\{{e}_n\}_{n\geq 1}.$ Then, ![]() $\{\mathbf{e}_n\}_{n\geq 1}$ is an unconditional basis for
$\{\mathbf{e}_n\}_{n\geq 1}$ is an unconditional basis for ![]() $E^\mathrm{s\text{-}max}$ if and only if
$E^\mathrm{s\text{-}max}$ if and only if ![]() $E^\mathrm{s\text{-}max}$ does not contain
$E^\mathrm{s\text{-}max}$ does not contain ![]() $c_0.$
$c_0.$
The proof of the last result is a quick application of one of the famous James’ theorems [Reference Li and Queffélec25, Theorem V.4, p. 98].
2. Preliminary issues
For the reader’s convenience, in this section, we collect standard definitions and technical tools which are used repeatedly in this paper. Let ![]() $H(\mathbb{D})$ denote the collection of all analytic functions over the unit disk
$H(\mathbb{D})$ denote the collection of all analytic functions over the unit disk ![]() $\mathbb{D}$ in the complex plane, and we often identify
$\mathbb{D}$ in the complex plane, and we often identify  $f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in H(\mathbb{D})$ with its sequence of Taylor coefficients
$f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in H(\mathbb{D})$ with its sequence of Taylor coefficients ![]() $\{a_n\}_{n\geq 0}.$ For
$\{a_n\}_{n\geq 0}.$ For ![]() $0 \lt p \lt \infty,$
$0 \lt p \lt \infty,$ ![]() $H^p(\mathbb{D})$ [Reference Duren17] denotes the Hardy space, consisting of
$H^p(\mathbb{D})$ [Reference Duren17] denotes the Hardy space, consisting of ![]() $f\in H(\mathbb{D})$ such that
$f\in H(\mathbb{D})$ such that
 \begin{equation*}
\|f\|_{H^p(\mathbb{D})}=\sup\limits_{0\leq r \lt 1}\Big(\frac{1}{2\pi}\int_0^{2\pi}|f(r\mathrm{e}^{\mathrm{i}\theta})|^p\,\mathrm{d}\theta\Big)^{1/p} \lt \infty.
\end{equation*}
\begin{equation*}
\|f\|_{H^p(\mathbb{D})}=\sup\limits_{0\leq r \lt 1}\Big(\frac{1}{2\pi}\int_0^{2\pi}|f(r\mathrm{e}^{\mathrm{i}\theta})|^p\,\mathrm{d}\theta\Big)^{1/p} \lt \infty.
\end{equation*} The Bergman space ![]() $L_a^p(\mathbb{D})$ [Reference Hedenmalm, Korenblum and Zhu19] consists of
$L_a^p(\mathbb{D})$ [Reference Hedenmalm, Korenblum and Zhu19] consists of ![]() $f\in H(\mathbb{D})$ such that
$f\in H(\mathbb{D})$ such that
 \begin{equation*}
\|f\|_{L_a^p(\mathbb{D})}=\Big(\int_{\mathbb{D}}|f(z)|^p\,\mathrm{d}A(z)\Big)^{1/p} \lt \infty,
\end{equation*}
\begin{equation*}
\|f\|_{L_a^p(\mathbb{D})}=\Big(\int_{\mathbb{D}}|f(z)|^p\,\mathrm{d}A(z)\Big)^{1/p} \lt \infty,
\end{equation*} where  $\mathrm{d}A=\frac{1}{\pi}\,\mathrm{d}x\mathrm{d}y.$ To be convenient, we shall write Hp for
$\mathrm{d}A=\frac{1}{\pi}\,\mathrm{d}x\mathrm{d}y.$ To be convenient, we shall write Hp for ![]() $H^p(\mathbb{D}),$
$H^p(\mathbb{D}),$ ![]() $H^{\infty}$ for
$H^{\infty}$ for ![]() $H^{\infty}(\mathbb{D}),$ the algebra of bounded analytic functions on
$H^{\infty}(\mathbb{D}),$ the algebra of bounded analytic functions on ![]() $\mathbb{D}$, and
$\mathbb{D}$, and ![]() $L_a^p$ for
$L_a^p$ for ![]() $L_a^p(\mathbb{D}).$ Let
$L_a^p(\mathbb{D}).$ Let ![]() $\mathcal{D}^p$ denote the Dirichlet space, consisting of
$\mathcal{D}^p$ denote the Dirichlet space, consisting of ![]() $f\in H(\mathbb{D})$ such that
$f\in H(\mathbb{D})$ such that ![]() $f'\in L_a^p.$ Let
$f'\in L_a^p.$ Let ![]() $\mathcal{M}(\mathcal{D}^p)$ denote its multiplier algebra, that is,
$\mathcal{M}(\mathcal{D}^p)$ denote its multiplier algebra, that is, ![]() $h\in \mathcal{M}(\mathcal{D}^p)$ if and only if
$h\in \mathcal{M}(\mathcal{D}^p)$ if and only if ![]() $h f\in \mathcal{D}^p$ for each
$h f\in \mathcal{D}^p$ for each ![]() $f \in \mathcal{D}^p.$ For simplicity,
$f \in \mathcal{D}^p.$ For simplicity, ![]() $\mathcal{D}^2$ is shorthanded as
$\mathcal{D}^2$ is shorthanded as ![]() $\mathcal{D}.$ The Bloch space
$\mathcal{D}.$ The Bloch space ![]() $\mathcal{B}$ [Reference Anderson, Clunie and Pommerenke2] consists of
$\mathcal{B}$ [Reference Anderson, Clunie and Pommerenke2] consists of ![]() $f\in H(\mathbb{D})$ such that
$f\in H(\mathbb{D})$ such that ![]() $\sup_{z\in\mathbb{D}}(1-|z|^2)|f'(z)| \lt \infty$ and the little Bloch space
$\sup_{z\in\mathbb{D}}(1-|z|^2)|f'(z)| \lt \infty$ and the little Bloch space ![]() $\mathcal{B}_0$ the closure of polynomials in
$\mathcal{B}_0$ the closure of polynomials in ![]() $\mathcal{B}$.
$\mathcal{B}$.
Definition 6. A random variable X is called Rademacher if  $\mathbb{P}(X=1)=\mathbb{P}(X=-1)=\frac{1}{2}$, Steinhaus if it is uniformly distributed on the unit circle, standard real Gaussian if its density is
$\mathbb{P}(X=1)=\mathbb{P}(X=-1)=\frac{1}{2}$, Steinhaus if it is uniformly distributed on the unit circle, standard real Gaussian if its density is  $\frac{1}{\sqrt{2\pi}}\exp(-t^2/2)$ with
$\frac{1}{\sqrt{2\pi}}\exp(-t^2/2)$ with ![]() $t\in\mathbb{R}$ and standard complex Gaussian if its density is
$t\in\mathbb{R}$ and standard complex Gaussian if its density is  $\frac{1}{\pi}\exp(-|z|^2)$ with
$\frac{1}{\pi}\exp(-|z|^2)$ with ![]() $z\in\mathbb{C}.$ Moreover, let
$z\in\mathbb{C}.$ Moreover, let
Then, by a standard X-sequence, we mean a sequence of independent, identically distributed X variables. Lastly, a standard random sequence ![]() $\{X_n\}_{n\geq 0}$ refers to either a Rademacher, Steinhaus, standard real or complex Gaussian sequence, denoted by
$\{X_n\}_{n\geq 0}$ refers to either a Rademacher, Steinhaus, standard real or complex Gaussian sequence, denoted by
 \begin{equation*}\{\epsilon_n\}_{n\geq 0}, \ \ \{\mathrm{e}^{2\pi \mathrm{i}\alpha_n}\}_{n\geq 0}, \ \ \{\xi_n\}_{n\geq 0} \ \
\text{and} \ \ \{\gamma_n\}_{n\geq 0},\end{equation*}
\begin{equation*}\{\epsilon_n\}_{n\geq 0}, \ \ \{\mathrm{e}^{2\pi \mathrm{i}\alpha_n}\}_{n\geq 0}, \ \ \{\xi_n\}_{n\geq 0} \ \
\text{and} \ \ \{\gamma_n\}_{n\geq 0},\end{equation*}respectively.
We assume that all random variables are defined on a probability space ![]() $(\Omega, \mathcal{F}, \mathbb{P})$ with expectation denoted by
$(\Omega, \mathcal{F}, \mathbb{P})$ with expectation denoted by ![]() $\mathbb{E}(\cdot),$ where
$\mathbb{E}(\cdot),$ where ![]() $\mathcal{F}$ is a σ-algebra on Ω and
$\mathcal{F}$ is a σ-algebra on Ω and ![]() $\mathbb{P}$ is a probability measure defined on
$\mathbb{P}$ is a probability measure defined on ![]() $\mathcal{F}$. The probability of an event
$\mathcal{F}$. The probability of an event ![]() $\{\omega\in\Omega: X(\omega)\in A\}$, with
$\{\omega\in\Omega: X(\omega)\in A\}$, with ![]() $A\in \mathcal{F}$, is
$A\in \mathcal{F}$, is ![]() $\mathbb{P}(X\in A)$. The abbreviation ‘a.s.’ stands for ‘almost surely’. As usual, ‘A ≈ B’ implies that there exists a positive constant
$\mathbb{P}(X\in A)$. The abbreviation ‘a.s.’ stands for ‘almost surely’. As usual, ‘A ≈ B’ implies that there exists a positive constant ![]() $C \lt \infty$ such that
$C \lt \infty$ such that  $\frac{A}{C}\leq B\leq CA,$ ‘
$\frac{A}{C}\leq B\leq CA,$ ‘![]() $A\lesssim B$’ (resp. ‘
$A\lesssim B$’ (resp. ‘![]() $A \gt rsim B$’) means that there exists a positive constant
$A \gt rsim B$’) means that there exists a positive constant ![]() $C \lt \infty$ such that
$C \lt \infty$ such that ![]() $A\leq CB$ (resp.
$A\leq CB$ (resp. ![]() $A\geq CB$), and ‘
$A\geq CB$), and ‘![]() $\Leftrightarrow$’ stands for ‘if and only if’.
$\Leftrightarrow$’ stands for ‘if and only if’.
3. The symbol space  $\mathcal{X}_{\star}$
$\mathcal{X}_{\star}$
In this section, we prove Theorem A.
Proof of Theorem A
The proof of (i.1) is divided into three steps.
Step 1. ![]() $f\in \mathcal{X}_{\star} \ \Longrightarrow \ \mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}} \lt \infty.$
$f\in \mathcal{X}_{\star} \ \Longrightarrow \ \mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}} \lt \infty.$
By (iv) of Definition 2,  $
\sup\limits_{0\leq r \lt 1}\|(\mathcal{R} f)_r\|_{\mathcal{X}} = \|\mathcal{R} f\|_{\mathcal{X}} \lt \infty\ \text{a.s.}
$ Then, the Marcinkiewicz–Zygmund–Kahane theorem [Reference Li and Queffélec26, Theorem II.4, p. 240] implies that
$
\sup\limits_{0\leq r \lt 1}\|(\mathcal{R} f)_r\|_{\mathcal{X}} = \|\mathcal{R} f\|_{\mathcal{X}} \lt \infty\ \text{a.s.}
$ Then, the Marcinkiewicz–Zygmund–Kahane theorem [Reference Li and Queffélec26, Theorem II.4, p. 240] implies that  $\sup\limits_{N\geq 0} \|S_N(\mathcal{R} f)\|_{\mathcal{X}} \lt \infty\ \text{a.s.} $ since
$\sup\limits_{N\geq 0} \|S_N(\mathcal{R} f)\|_{\mathcal{X}} \lt \infty\ \text{a.s.} $ since ![]() $\mathcal{R} f$ is A-bounded in
$\mathcal{R} f$ is A-bounded in ![]() $\mathcal{X}$ with
$\mathcal{X}$ with ![]() $A=(r_n^m)_{n,m\in \mathbb{N}}$ and
$A=(r_n^m)_{n,m\in \mathbb{N}}$ and ![]() $r_n\to 1^-$ as
$r_n\to 1^-$ as ![]() $n\to\infty.$ Let
$n\to\infty.$ Let  $M = \sup\limits_{N\geq 0} \|S_N(\mathcal{R} f)\|_{\mathcal{X}}.$ Then, by Kahane’s inequality [Reference Li and Queffélec25, Theorem V.1, p. 139] (for Rademacher or Steinhaus sequences) and Fernique’s theorem [Reference Li and Queffélec25, Theorem V.26, p. 255] (for Gaussian sequences), we have
$M = \sup\limits_{N\geq 0} \|S_N(\mathcal{R} f)\|_{\mathcal{X}}.$ Then, by Kahane’s inequality [Reference Li and Queffélec25, Theorem V.1, p. 139] (for Rademacher or Steinhaus sequences) and Fernique’s theorem [Reference Li and Queffélec25, Theorem V.26, p. 255] (for Gaussian sequences), we have ![]() $
\mathbb{E}\big(\exp(\lambda M)\big) \lt \infty
$ for some small enough λ > 0. Now, we need the following lemma, which is a consequence of [Reference Arendt and Nikolski4, Theorem 3.1].
$
\mathbb{E}\big(\exp(\lambda M)\big) \lt \infty
$ for some small enough λ > 0. Now, we need the following lemma, which is a consequence of [Reference Arendt and Nikolski4, Theorem 3.1].
Lemma 7. Let ![]() $\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with
$\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with ![]() $p\in (0, 1),$ of homogeneous type; for the latter, we also assume
$p\in (0, 1),$ of homogeneous type; for the latter, we also assume  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1$. If
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1$. If ![]() $f\in \mathcal{X},$ then for each fixed
$f\in \mathcal{X},$ then for each fixed ![]() $0\leq r \lt 1,$
$0\leq r \lt 1,$  $
\lim\limits_{N\to\infty}\|S_Nf_r-f_r\|_{\mathcal{X}}=0.
$
$
\lim\limits_{N\to\infty}\|S_Nf_r-f_r\|_{\mathcal{X}}=0.
$
By Lemma 7 and (iv) of Definition 2, ![]() $\|\mathcal{R} f\|_{\mathcal{X}} \leq M$ a.s. Now, Step 1 follows from Kahane’s inequality [Reference Li and Queffélec25, Theorem V.1, p. 139] and Fernique’s theorem [Reference Li and Queffélec25, Theorem V.26, p. 255].
$\|\mathcal{R} f\|_{\mathcal{X}} \leq M$ a.s. Now, Step 1 follows from Kahane’s inequality [Reference Li and Queffélec25, Theorem V.1, p. 139] and Fernique’s theorem [Reference Li and Queffélec25, Theorem V.26, p. 255].
Step 2. ![]() $(\mathcal{X}_{\star}, \|\cdot\|_{\mathcal{X}_{\star}})$ is a Banach space.
$(\mathcal{X}_{\star}, \|\cdot\|_{\mathcal{X}_{\star}})$ is a Banach space.
Let ![]() $\{f_n\}_{n\geq 1}$ be a Cauchy sequence in
$\{f_n\}_{n\geq 1}$ be a Cauchy sequence in ![]() $\mathcal{X}_{\star}$ with
$\mathcal{X}_{\star}$ with  $f_n(z)=\sum\limits_{k=0}^{\infty}a_k^{(n)}z^k.$ Then, there exists
$f_n(z)=\sum\limits_{k=0}^{\infty}a_k^{(n)}z^k.$ Then, there exists  $F(z, \omega)=\sum\limits_{k=0}^{\infty}c_k(\omega)z^k\in L^1(\Omega; \mathcal{X})$ such that
$F(z, \omega)=\sum\limits_{k=0}^{\infty}c_k(\omega)z^k\in L^1(\Omega; \mathcal{X})$ such that  $
\lim\limits_{n\to\infty}\mathbb{E}\|\mathcal{R} f_n-F\|_{\mathcal{X}} \to 0.
$ By the Riesz lemma, there exists a subsequence
$
\lim\limits_{n\to\infty}\mathbb{E}\|\mathcal{R} f_n-F\|_{\mathcal{X}} \to 0.
$ By the Riesz lemma, there exists a subsequence ![]() $\{f_{n_i}\}_{i\geq 1}$ and
$\{f_{n_i}\}_{i\geq 1}$ and ![]() $\Omega_0\subset \Omega$ with
$\Omega_0\subset \Omega$ with ![]() $\mathbb{P}(\Omega_0)=1,$ such that for
$\mathbb{P}(\Omega_0)=1,$ such that for ![]() $\omega\in \Omega_0,$
$\omega\in \Omega_0,$
 \begin{equation}
\lim_{i\to\infty}\|\mathcal{R} f_{n_i}(z, \omega)-F(z, \omega)\|_{\mathcal{X}} = \lim_{i\to\infty}\Big\|\sum_{k=0}^{\infty}a_k^{(n_i)}X_k(\omega)z^k-\sum_{k=0}^{\infty}c_k(\omega)z^k\Big\|_{\mathcal{X}} = 0.
\end{equation}
\begin{equation}
\lim_{i\to\infty}\|\mathcal{R} f_{n_i}(z, \omega)-F(z, \omega)\|_{\mathcal{X}} = \lim_{i\to\infty}\Big\|\sum_{k=0}^{\infty}a_k^{(n_i)}X_k(\omega)z^k-\sum_{k=0}^{\infty}c_k(\omega)z^k\Big\|_{\mathcal{X}} = 0.
\end{equation} Since ![]() $\{\delta_z:\ z\in\mathbb{D}\}\subset \mathcal{X}^{\ast},$ for each fixed k and
$\{\delta_z:\ z\in\mathbb{D}\}\subset \mathcal{X}^{\ast},$ for each fixed k and ![]() $\omega\in\Omega_0,$ we have
$\omega\in\Omega_0,$ we have  $
\lim\limits_{i\to\infty}a_k^{(n_i)}X_k(\omega) = c_k(\omega).
$ Consequently, there exists a constant ak such that
$
\lim\limits_{i\to\infty}a_k^{(n_i)}X_k(\omega) = c_k(\omega).
$ Consequently, there exists a constant ak such that ![]() $c_k(\omega)=a_kX_k(\omega),\ \omega\in \Omega_0.$ Now, (2) implies that
$c_k(\omega)=a_kX_k(\omega),\ \omega\in \Omega_0.$ Now, (2) implies that ![]() $\mathcal{R} f_{n_i} \to \mathcal{R} f\ \text{a.s.}$ with
$\mathcal{R} f_{n_i} \to \mathcal{R} f\ \text{a.s.}$ with  $\mathcal{R} f(z)=\sum\limits_{k=0}^{\infty}a_kX_kz^k\in \mathcal{X}_{\star}.$ Then, for any
$\mathcal{R} f(z)=\sum\limits_{k=0}^{\infty}a_kX_kz^k\in \mathcal{X}_{\star}.$ Then, for any ![]() $\epsilon \gt 0,$
$\epsilon \gt 0,$
 \begin{eqnarray*}
\mathbb{E} \|\mathcal{R} f_{n_i}-\mathcal{R} f\|_{\mathcal{X}}
&\leq& \lim_{r\to 1^-}\liminf_{j\to\infty}\mathbb{E} \|(\mathcal{R} f_{n_i})_r-(\mathcal{R} f_{n_j})_r\|_{\mathcal{X}}\\
&\leq&\sup_{j\geq N}\mathbb{E}\|\mathcal{R} f_{n_i}-\mathcal{R} f_{n_j}\|_{\mathcal{X}}\\
& \lt &\epsilon
\end{eqnarray*}
\begin{eqnarray*}
\mathbb{E} \|\mathcal{R} f_{n_i}-\mathcal{R} f\|_{\mathcal{X}}
&\leq& \lim_{r\to 1^-}\liminf_{j\to\infty}\mathbb{E} \|(\mathcal{R} f_{n_i})_r-(\mathcal{R} f_{n_j})_r\|_{\mathcal{X}}\\
&\leq&\sup_{j\geq N}\mathbb{E}\|\mathcal{R} f_{n_i}-\mathcal{R} f_{n_j}\|_{\mathcal{X}}\\
& \lt &\epsilon
\end{eqnarray*} when i and N are large enough. Now, ![]() $\mathbb{E}\|\mathcal{R} f_{n}-\mathcal{R} f\|_{\mathcal{X}}\to 0$ as
$\mathbb{E}\|\mathcal{R} f_{n}-\mathcal{R} f\|_{\mathcal{X}}\to 0$ as ![]() $n\to\infty$ by the triangle inequality.
$n\to\infty$ by the triangle inequality.
Step 3. ![]() $(\mathcal{X}_{\star}, \|\cdot\|_{\mathcal{X}_{\star}})$ is of homogeneous type.
$(\mathcal{X}_{\star}, \|\cdot\|_{\mathcal{X}_{\star}})$ is of homogeneous type.
Firstly, let  $f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in \mathcal{X}_{\star}$. Then, there exists constant C > 0 such that
$f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in \mathcal{X}_{\star}$. Then, there exists constant C > 0 such that
 \begin{equation*}
|f(z)|\leq \sum_{n=0}^{\infty}|a_n||z|^n
\leq C\sum_{n=0}^{\infty}\frac{\|f\|_{\mathcal{X}_{\star}}}{\|z^n\|_{\mathcal{X}}}|z|^n
= C\Big(\sum_{n=0}^{\infty}\frac{|z|^n}{\|z^n\|_{\mathcal{X}}}\Big)\|f\|_{\mathcal{X}_{\star}},
\end{equation*}
\begin{equation*}
|f(z)|\leq \sum_{n=0}^{\infty}|a_n||z|^n
\leq C\sum_{n=0}^{\infty}\frac{\|f\|_{\mathcal{X}_{\star}}}{\|z^n\|_{\mathcal{X}}}|z|^n
= C\Big(\sum_{n=0}^{\infty}\frac{|z|^n}{\|z^n\|_{\mathcal{X}}}\Big)\|f\|_{\mathcal{X}_{\star}},
\end{equation*} where the second inequality follows from the contraction principle ([Reference Hytönen, van Neerven, Veraar and Weis21, Theorem 6.1.13, p. 9]) and Lemma 8 below, i.e., ![]() $
\|a_nz^n\|_{\mathcal{X}_{\star}} \leq C \|S_N f\|_{\mathcal{X}_{\star}} \leq C\|f\|_{\mathcal{X}_\star}
$ if
$
\|a_nz^n\|_{\mathcal{X}_{\star}} \leq C \|S_N f\|_{\mathcal{X}_{\star}} \leq C\|f\|_{\mathcal{X}_\star}
$ if ![]() $N \gt n.$ Since
$N \gt n.$ Since ![]() $\{\delta_z: \ z\in\mathbb{D}\}\subset \mathcal{X}^{\ast},$ one has
$\{\delta_z: \ z\in\mathbb{D}\}\subset \mathcal{X}^{\ast},$ one has  $\liminf\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{1/n}\geq 1,$ which yields
$\liminf\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{1/n}\geq 1,$ which yields  $\sum\limits_{n=0}^{\infty}\frac{|z|^n}{\|z^n\|_{\mathcal{X}}} \lt \infty$ for fixed
$\sum\limits_{n=0}^{\infty}\frac{|z|^n}{\|z^n\|_{\mathcal{X}}} \lt \infty$ for fixed ![]() $z\in\mathbb{D}.$ So
$z\in\mathbb{D}.$ So ![]() $\{\delta_z:\ z\in\mathbb{D}\}\subset (\mathcal{X}_{\star})^{\ast}.$ Secondly,
$\{\delta_z:\ z\in\mathbb{D}\}\subset (\mathcal{X}_{\star})^{\ast}.$ Secondly,
Thirdly, the continuity of F follows from [Reference Arendt and Nikolski4, Theorem 3.1]. Lastly, for ![]() $f\in \mathcal{X}_{\star},$
$f\in \mathcal{X}_{\star},$
 \begin{equation*}
\|f\|_{\mathcal{X}_{\star}} \ =\ \mathbb{E}\big\|\mathcal{R} f\big\|_{\mathcal{X}}\ =\ \mathbb{E}\Big(\sup_{0\leq r \lt 1}\big\|\mathcal{R} f_r\big\|_{\mathcal{X}}\Big)
\ =\ \sup_{0\leq r \lt 1}\mathbb{E}\big\|\mathcal{R} f_r\big\|_{\mathcal{X}}\ =\ \sup_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}_{\star}}.
\end{equation*}
\begin{equation*}
\|f\|_{\mathcal{X}_{\star}} \ =\ \mathbb{E}\big\|\mathcal{R} f\big\|_{\mathcal{X}}\ =\ \mathbb{E}\Big(\sup_{0\leq r \lt 1}\big\|\mathcal{R} f_r\big\|_{\mathcal{X}}\Big)
\ =\ \sup_{0\leq r \lt 1}\mathbb{E}\big\|\mathcal{R} f_r\big\|_{\mathcal{X}}\ =\ \sup_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}_{\star}}.
\end{equation*} Now, we turn to (i.2). If ![]() $\{X_n\}_{n\geq 0}$ is a standard Steinhaus or complex Gaussian sequence, then by the contraction principle ([Reference Hytönen, van Neerven, Veraar and Weis21, Theorem 6.1.13, p. 9]),
$\{X_n\}_{n\geq 0}$ is a standard Steinhaus or complex Gaussian sequence, then by the contraction principle ([Reference Hytönen, van Neerven, Veraar and Weis21, Theorem 6.1.13, p. 9]),
 \begin{eqnarray*}
\Big\|\sum_{n=0}^{N}\lambda_na_n\frac{z^n}{\|z^n\|_{\mathcal{X}}}\Big\|_{\mathcal{X}^{\star}}
&\leq& \mathbb{E}\Big\|\sum_{n=0}^{N}a_nX_n\frac{z^n}{\|z^n\|_{\mathcal{X}}}\Big\|_{\mathcal{X}}
\end{eqnarray*}
\begin{eqnarray*}
\Big\|\sum_{n=0}^{N}\lambda_na_n\frac{z^n}{\|z^n\|_{\mathcal{X}}}\Big\|_{\mathcal{X}^{\star}}
&\leq& \mathbb{E}\Big\|\sum_{n=0}^{N}a_nX_n\frac{z^n}{\|z^n\|_{\mathcal{X}}}\Big\|_{\mathcal{X}}
\end{eqnarray*} for ![]() $|\lambda_n|\leq 1,$
$|\lambda_n|\leq 1,$ ![]() $N\in\mathbb{N}$ and
$N\in\mathbb{N}$ and ![]() $a_n\in\mathbb{C}.$ Take
$a_n\in\mathbb{C}.$ Take ![]() $\mathcal{T}: \mathcal{X}_{\star}\to \mathfrak{S}$ as
$\mathcal{T}: \mathcal{X}_{\star}\to \mathfrak{S}$ as  $
f(z)=\sum\limits_{n=0}^{\infty}a_nz^n \longmapsto (a_n\|z^n\|_{\mathcal{X}})_{n\geq 0}.
$ Then
$
f(z)=\sum\limits_{n=0}^{\infty}a_nz^n \longmapsto (a_n\|z^n\|_{\mathcal{X}})_{n\geq 0}.
$ Then  $
P_Nf(z)=\sum\limits_{n=0}^N(\mathcal{T} f)_n\frac{z^n}{\|z^n\|_{\mathcal{X}}}=S_Nf(z).
$ It suffices to show that
$
P_Nf(z)=\sum\limits_{n=0}^N(\mathcal{T} f)_n\frac{z^n}{\|z^n\|_{\mathcal{X}}}=S_Nf(z).
$ It suffices to show that ![]() $\|S_N f\|_{\mathcal{X}_{\star}} \to \|f \|_{\mathcal{X}_{\star}},$ as
$\|S_N f\|_{\mathcal{X}_{\star}} \to \|f \|_{\mathcal{X}_{\star}},$ as ![]() $N\to\infty,$ for
$N\to\infty,$ for ![]() $f\in \mathcal{X}_{\star},$ which follows from (3) in Lemma 8 below.
$f\in \mathcal{X}_{\star},$ which follows from (3) in Lemma 8 below.
Now, (i.3) for a standard Rademacher or real Gaussian sequence, which are real symmetric, follows from the contraction principle ([Reference Hytönen, van Neerven, Veraar and Weis21, Theorem 6.1.13, p. 9]) just as case (i.2). The details are skipped.
The proof of (ii) is similar to that of (i); hence, we only indicate the differences briefly. For ![]() $f\in \mathcal{X}_{\star}\Longrightarrow \mathbb{E}(\|\mathcal{R} f\|^p_{\mathcal{X}}) \lt \infty,$ the Kahane’s inequality and Fernique’s theorem used in the proof of Theorem A (Step 1) still hold for p-Banach spaces; see [Reference Cheng, Fang and Liu11,
Theorem 28 and Theorem 31]. The other parts of the proof can be modified accordingly. That
$f\in \mathcal{X}_{\star}\Longrightarrow \mathbb{E}(\|\mathcal{R} f\|^p_{\mathcal{X}}) \lt \infty,$ the Kahane’s inequality and Fernique’s theorem used in the proof of Theorem A (Step 1) still hold for p-Banach spaces; see [Reference Cheng, Fang and Liu11,
Theorem 28 and Theorem 31]. The other parts of the proof can be modified accordingly. That ![]() $(\mathcal{X}_{\star}, \|\cdot\|_{\mathcal{X}_{\star}})$ is a functional p-Banach space can be proved by replacing
$(\mathcal{X}_{\star}, \|\cdot\|_{\mathcal{X}_{\star}})$ is a functional p-Banach space can be proved by replacing ![]() $\mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}}$ with
$\mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}}$ with ![]() $\mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}}^p.$ To check that
$\mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}}^p.$ To check that ![]() $(\mathcal{X}_{\star}, \|\cdot\|_{\mathcal{X}_{\star}})$ is of homogeneous type, the only difference is that the continuity of
$(\mathcal{X}_{\star}, \|\cdot\|_{\mathcal{X}_{\star}})$ is of homogeneous type, the only difference is that the continuity of ![]() $F: \mathbb{D} \to \mathcal{X}_{\star},$ defined by
$F: \mathbb{D} \to \mathcal{X}_{\star},$ defined by ![]() $F(z)=f_z,$ is a consequence of the assumption
$F(z)=f_z,$ is a consequence of the assumption  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ Then, (ii.2) follows from the contraction principle for p-Banach spaces (see [Reference Kalton23, Proposition 2.5]) and Lemma 8.
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ Then, (ii.2) follows from the contraction principle for p-Banach spaces (see [Reference Kalton23, Proposition 2.5]) and Lemma 8.
Remark. If ![]() $\mathcal{X}=\mathcal{X}_{\mathcal{P}}$ for a p-Banach space, the assumption
$\mathcal{X}=\mathcal{X}_{\mathcal{P}}$ for a p-Banach space, the assumption  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1$ in Theorem A (ii) can be dropped. In detail, by the claim in the proof of Lemma 10,
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1$ in Theorem A (ii) can be dropped. In detail, by the claim in the proof of Lemma 10, ![]() $f\in(\mathcal{X}_{\mathcal{P}})_{\star}$ implies that
$f\in(\mathcal{X}_{\mathcal{P}})_{\star}$ implies that ![]() $(\mathcal{R} f)_r$ converges to
$(\mathcal{R} f)_r$ converges to ![]() $\mathcal{R} f$ a.s. as
$\mathcal{R} f$ a.s. as ![]() $r\to1^{-}.$ Then, by the Marcinkiewicz–Zygmund–Kahane theorem [Reference Li and Queffélec26, Theorem II.4, p. 240],
$r\to1^{-}.$ Then, by the Marcinkiewicz–Zygmund–Kahane theorem [Reference Li and Queffélec26, Theorem II.4, p. 240], ![]() $S_N(\mathcal{R} f)$ converges to
$S_N(\mathcal{R} f)$ converges to ![]() $\mathcal{R} f$ a.s. as
$\mathcal{R} f$ a.s. as ![]() $N\to\infty.$
$N\to\infty.$ ![]() $S_N f$ converges to f in
$S_N f$ converges to f in ![]() $(\mathcal{X}_{\mathcal{P}})_{\star}$ as
$(\mathcal{X}_{\mathcal{P}})_{\star}$ as ![]() $N\to\infty$ by Kahane’s inequality [Reference Li and Queffélec25, Theorem V.1, p. 139] and Fernique’s theorem [Reference Li and Queffélec25, Theorem V.26, p. 255]. The rest of the proof is similar to the proof of part (i) of Theorem A. The same remark applies to part (i) of Lemma 9.
$N\to\infty$ by Kahane’s inequality [Reference Li and Queffélec25, Theorem V.1, p. 139] and Fernique’s theorem [Reference Li and Queffélec25, Theorem V.26, p. 255]. The rest of the proof is similar to the proof of part (i) of Theorem A. The same remark applies to part (i) of Lemma 9.
Remark. The role of M, appearing in Step 1 of the proof of (i), deserves further attention in the study of random analytic functions. We introduce a deterministic version
 \begin{equation*}
\mathcal{X}_T=\Big\{f(z)=\sum_{n=0}^{\infty}a_nz^n\in H(\mathbb{D}):\ \|f\|_{\mathcal{X}_T}=\sup_{N\geq 0}\Big\|\sum_{n=0}^Na_nz^n\Big\|_{\mathcal{X}} \lt \infty\Big\}.
\end{equation*}
\begin{equation*}
\mathcal{X}_T=\Big\{f(z)=\sum_{n=0}^{\infty}a_nz^n\in H(\mathbb{D}):\ \|f\|_{\mathcal{X}_T}=\sup_{N\geq 0}\Big\|\sum_{n=0}^Na_nz^n\Big\|_{\mathcal{X}} \lt \infty\Big\}.
\end{equation*} Then, ![]() $(\mathcal{X}_T)_{\star}$ is a solid space by Proposition 11 and
$(\mathcal{X}_T)_{\star}$ is a solid space by Proposition 11 and ![]() $\mathcal{X}^\mathrm{max}$ is identified as
$\mathcal{X}^\mathrm{max}$ is identified as ![]() $\mathcal{X}_T$ under certain conditions in Proposition 15.
$\mathcal{X}_T$ under certain conditions in Proposition 15.
We end this section with a supplemental property about the norm ![]() $\|f\|_{\mathcal{X}_{\star}}$ in Theorem A.
$\|f\|_{\mathcal{X}_{\star}}$ in Theorem A.
Lemma 8. Let ![]() $\{X_n\}_{n\geq 0}$ be a standard random sequence.
$\{X_n\}_{n\geq 0}$ be a standard random sequence.
(i) If
 $\mathcal{X}$ is a functional Banach space of homogeneous type and
$\mathcal{X}$ is a functional Banach space of homogeneous type and  $f\in \mathcal{X}_{\star},$ then
(3)
$f\in \mathcal{X}_{\star},$ then
(3) \begin{equation}
\|f\|_{\mathcal{X}_{\star}}=\sup_{N\geq 0}\|S_Nf\|_{\mathcal{X}_{\star}}=\lim_{N\to\infty}\|S_Nf\|_{\mathcal{X}_{\star}}.
\end{equation}
\begin{equation}
\|f\|_{\mathcal{X}_{\star}}=\sup_{N\geq 0}\|S_Nf\|_{\mathcal{X}_{\star}}=\lim_{N\to\infty}\|S_Nf\|_{\mathcal{X}_{\star}}.
\end{equation}(ii) If
 $\mathcal{X}$ is a functional p-Banach space of homogeneous type with
$\mathcal{X}$ is a functional p-Banach space of homogeneous type with  $p\in (0, 1),$ and
$p\in (0, 1),$ and  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1,$ then for each
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1,$ then for each  $f\in \mathcal{X}_{\star},$
$f\in \mathcal{X}_{\star},$  $
\|f\|_{\mathcal{X}_{\star}}\leq \sup\limits_{N\geq 0}\|S_Nf\|_{\mathcal{X}_{\star}}\leq 2^{\frac{1}{p}-1}\|f\|_{\mathcal{X}_{\star}}.
$
$
\|f\|_{\mathcal{X}_{\star}}\leq \sup\limits_{N\geq 0}\|S_Nf\|_{\mathcal{X}_{\star}}\leq 2^{\frac{1}{p}-1}\|f\|_{\mathcal{X}_{\star}}.
$
Proof. Let ![]() $g\in \mathcal{X}.$ Observe that, by (iv) of Definition 2, we have
$g\in \mathcal{X}.$ Observe that, by (iv) of Definition 2, we have ![]() $
\|g_{r_2}\|_{\mathcal{X}}\geq \|g_{r_1}\|_{\mathcal{X}}$ when
$
\|g_{r_2}\|_{\mathcal{X}}\geq \|g_{r_1}\|_{\mathcal{X}}$ when ![]() $ 0 \lt r_1 \lt r_2 \lt 1.$ If
$ 0 \lt r_1 \lt r_2 \lt 1.$ If ![]() $\mathcal{X}$ is a functional Banach space, then
$\mathcal{X}$ is a functional Banach space, then ![]() $\|S_Nf\|_{\mathcal{X}_{\star}}$ is increasing in N by [Reference Hytönen, van Neerven, Veraar and Weis21, Proposition 6.1.5, p. 5]. So it suffices to show that
$\|S_Nf\|_{\mathcal{X}_{\star}}$ is increasing in N by [Reference Hytönen, van Neerven, Veraar and Weis21, Proposition 6.1.5, p. 5]. So it suffices to show that  $\|f\|_{\mathcal{X}_{\star}}=\sup\limits_{N\geq 0}\|S_Nf\|_{\mathcal{X}_{\star}}.$ Note that
$\|f\|_{\mathcal{X}_{\star}}=\sup\limits_{N\geq 0}\|S_Nf\|_{\mathcal{X}_{\star}}.$ Note that
 \begin{equation*}
\|f\|_{\mathcal{X}_{\star}} = \mathbb{E}\big\|\mathcal{R} f\big\|_{\mathcal{X}}
\leq \sup_{N\geq 0} \lim_{r\to 1^-}\mathbb{E}\big\|S_N(\mathcal{R} f_r)\big\|_{\mathcal{X}} = \sup_{N\geq 0}\|S_Nf\|_{\mathcal{X}_{\star}}.
\end{equation*}
\begin{equation*}
\|f\|_{\mathcal{X}_{\star}} = \mathbb{E}\big\|\mathcal{R} f\big\|_{\mathcal{X}}
\leq \sup_{N\geq 0} \lim_{r\to 1^-}\mathbb{E}\big\|S_N(\mathcal{R} f_r)\big\|_{\mathcal{X}} = \sup_{N\geq 0}\|S_Nf\|_{\mathcal{X}_{\star}}.
\end{equation*}Conversely, by [Reference Hytönen, van Neerven, Veraar and Weis21, Proposition 6.1.5, p. 5],
 \begin{equation*}
\|S_Nf\|_{\mathcal{X}_{\star}} = \mathbb{E}\big\|S_N(\mathcal{R} f)\big\|_{\mathcal{X}} \leq \mathbb{E}\big\|S_N(\mathcal{R} f)+\big(\mathcal{R} f-S_N(\mathcal{R} f)\big)\big\|_{\mathcal{X}} =
\|f\|_{\mathcal{X}_{\star}}.
\end{equation*}
\begin{equation*}
\|S_Nf\|_{\mathcal{X}_{\star}} = \mathbb{E}\big\|S_N(\mathcal{R} f)\big\|_{\mathcal{X}} \leq \mathbb{E}\big\|S_N(\mathcal{R} f)+\big(\mathcal{R} f-S_N(\mathcal{R} f)\big)\big\|_{\mathcal{X}} =
\|f\|_{\mathcal{X}_{\star}}.
\end{equation*} If ![]() $\mathcal{X}$ is a functional p-Banach space, the proof of
$\mathcal{X}$ is a functional p-Banach space, the proof of  $\|f\|_{\mathcal{X}_{\star}}\leq \sup\limits_{N\geq 0}\|S_Nf\|_{\mathcal{X}_{\star}}$ is a modification of that for Banach spaces. For the other direction, arguing as in [Reference Hytönen, van Neerven, Veraar and Weis21, Proposition 6.1.5, p. 5],
$\|f\|_{\mathcal{X}_{\star}}\leq \sup\limits_{N\geq 0}\|S_Nf\|_{\mathcal{X}_{\star}}$ is a modification of that for Banach spaces. For the other direction, arguing as in [Reference Hytönen, van Neerven, Veraar and Weis21, Proposition 6.1.5, p. 5],
 \begin{eqnarray*}
\|S_Nf\|_{\mathcal{X}_{\star}}
&\leq& 2^{\frac{1}{p}-1} \big(\mathbb{E}\big\|S_N(\mathcal{R} f)+\big(\mathcal{R} f-S_N(\mathcal{R} f)\big)\big\|_{\mathcal{X}}^p\big)^{1/p}
=
2^{\frac{1}{p}-1} \|f\|_{\mathcal{X}_{\star}},
\end{eqnarray*}
\begin{eqnarray*}
\|S_Nf\|_{\mathcal{X}_{\star}}
&\leq& 2^{\frac{1}{p}-1} \big(\mathbb{E}\big\|S_N(\mathcal{R} f)+\big(\mathcal{R} f-S_N(\mathcal{R} f)\big)\big\|_{\mathcal{X}}^p\big)^{1/p}
=
2^{\frac{1}{p}-1} \|f\|_{\mathcal{X}_{\star}},
\end{eqnarray*}as desired.
4. Maximal homogeneous extension
In this section, we prove Theorem B, ending with three nuggets supplementary to Theorem B. The following lemma is not only needed in the proof of Theorem B but also of independent interest, whose proof can be referred in the Appendix in [Reference Cheng, Fang and Liu11].
Lemma 9. Let ![]() $\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with
$\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with ![]() $p\in (0, 1)$, of homogeneous type; for the latter, we also assume
$p\in (0, 1)$, of homogeneous type; for the latter, we also assume  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ Let
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ Let ![]() $\{X_n\}_{n\geq 0}$ be a standard random sequence, and
$\{X_n\}_{n\geq 0}$ be a standard random sequence, and ![]() $s=\min\{1, p\}.$
$s=\min\{1, p\}.$
(i) If
 $f\in \mathcal{X}_{\star},$ then
$f\in \mathcal{X}_{\star},$ then  $\mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}}^s \lt \infty.$ Moreover,
$\mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}}^s \lt \infty.$ Moreover,  $f\in (\mathcal{X}_T)_{\star}$ and
$f\in (\mathcal{X}_T)_{\star}$ and  $
\mathbb{E}\big(\exp(\lambda\|\mathcal{R} f\|_{\mathcal{X}}^s)\big) \lt \infty
$ for some small enough λ > 0. This implies, in particular,
$
\mathbb{E}\big(\exp(\lambda\|\mathcal{R} f\|_{\mathcal{X}}^s)\big) \lt \infty
$ for some small enough λ > 0. This implies, in particular,  $\mathbb{E} \|\mathcal{R} f\|_{\mathcal{X}}^t \lt \infty$ for all t > 0.
$\mathbb{E} \|\mathcal{R} f\|_{\mathcal{X}}^t \lt \infty$ for all t > 0.(ii) If
 $\mathcal{X}=\mathcal{X}^\mathrm{max}$ and now we also assume that
$\mathcal{X}=\mathcal{X}^\mathrm{max}$ and now we also assume that  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{1/n}=1$ for the Banach space case, then, for
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{1/n}=1$ for the Banach space case, then, for  $f\in H(\mathbb{D}),$
$f\in H(\mathbb{D}),$  $f\in \mathcal{X}_{\star}$ if and only if
$f\in \mathcal{X}_{\star}$ if and only if  $\mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}}^s \lt \infty.$
$\mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}}^s \lt \infty.$
Proof of Theorem B
(i) Let
 \begin{equation*}
\mathcal{X}^\mathrm{max}=\Big\{f\in H(\mathbb{D}):\ f_r\in \mathcal{X}\ \text{for}\ 0\leq r \lt 1,\ \|f\|_\mathrm{max}=\sup_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}} \lt \infty\Big\}.
\end{equation*}
\begin{equation*}
\mathcal{X}^\mathrm{max}=\Big\{f\in H(\mathbb{D}):\ f_r\in \mathcal{X}\ \text{for}\ 0\leq r \lt 1,\ \|f\|_\mathrm{max}=\sup_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}} \lt \infty\Big\}.
\end{equation*} We will show that ![]() $\mathcal{X}^\mathrm{max}$ is the unique maximal homogeneous extension of
$\mathcal{X}^\mathrm{max}$ is the unique maximal homogeneous extension of ![]() $\mathcal{X}.$ The proof for the case of p-Banach spaces is similar to that of Banach spaces and will be skipped. The proof is divided into three steps.
$\mathcal{X}.$ The proof for the case of p-Banach spaces is similar to that of Banach spaces and will be skipped. The proof is divided into three steps.
Step 1. ![]() $(\mathcal{X}^\mathrm{max}, \|\cdot\|_\mathrm{max})$ is a Banach space.
$(\mathcal{X}^\mathrm{max}, \|\cdot\|_\mathrm{max})$ is a Banach space.
Let ![]() $\{f_n\}_{n\geq 1}$ be a Cauchy sequence in
$\{f_n\}_{n\geq 1}$ be a Cauchy sequence in ![]() $\mathcal{X}^\mathrm{max}$ with
$\mathcal{X}^\mathrm{max}$ with  $f_n(z)=\sum\limits_{k=0}^{\infty}a_k^{(n)}z^k.$ Then,
$f_n(z)=\sum\limits_{k=0}^{\infty}a_k^{(n)}z^k.$ Then, ![]() $\{(f_n)_r\}_{n\geq 1}$ is also Cauchy in
$\{(f_n)_r\}_{n\geq 1}$ is also Cauchy in ![]() $\mathcal{X}$ for each
$\mathcal{X}$ for each ![]() $r\in (0, 1)$. Since
$r\in (0, 1)$. Since ![]() $\mathcal{X}$ is a Banach space, we assume that
$\mathcal{X}$ is a Banach space, we assume that  $(f_n)_r(z)=\sum\limits_{k=0}^{\infty}a_k^{(n)}r^kz^k$ converges to
$(f_n)_r(z)=\sum\limits_{k=0}^{\infty}a_k^{(n)}r^kz^k$ converges to  $\sum\limits_{k=0}^{\infty}a_{k,r}z^k$ in
$\sum\limits_{k=0}^{\infty}a_{k,r}z^k$ in ![]() $\mathcal{X}$ as
$\mathcal{X}$ as ![]() $n\to\infty.$ By (i) in Definition 2, for each fixed
$n\to\infty.$ By (i) in Definition 2, for each fixed ![]() $k\geq0,$
$k\geq0,$  $a_k^{(n)}r^k\to a_{k,r}$ as
$a_k^{(n)}r^k\to a_{k,r}$ as ![]() $n\to\infty.$ Then,
$n\to\infty.$ Then,  $a_k^{(n)}\to\frac{a_{k,r}}{r^k}\doteq a_k$ as
$a_k^{(n)}\to\frac{a_{k,r}}{r^k}\doteq a_k$ as ![]() $n\to\infty.$ Let
$n\to\infty.$ Let  $g(z)=\sum\limits_{k=0}^{\infty}a_kz^k.$ Then, for each
$g(z)=\sum\limits_{k=0}^{\infty}a_kz^k.$ Then, for each ![]() $r\in(0,1),$
$r\in(0,1),$  $g_r(z)=\sum\limits_{k=0}^{\infty}a_kr^kz^k=\sum\limits_{k=0}^{\infty}a_{k,r}z^k\in\mathcal{X}.$ By (i) in Definition 2 again, the point evaluation functionals are uniformly bounded on each compact subset in
$g_r(z)=\sum\limits_{k=0}^{\infty}a_kr^kz^k=\sum\limits_{k=0}^{\infty}a_{k,r}z^k\in\mathcal{X}.$ By (i) in Definition 2 again, the point evaluation functionals are uniformly bounded on each compact subset in ![]() $\mathbb{D}.$ So
$\mathbb{D}.$ So ![]() $\{f_n\}_{n\geq 1}$ converges uniformly to g on each compact subset in
$\{f_n\}_{n\geq 1}$ converges uniformly to g on each compact subset in ![]() $\mathbb{D}.$ This implies that
$\mathbb{D}.$ This implies that ![]() $g\in H(\mathbb{D})$. Then,
$g\in H(\mathbb{D})$. Then,
 \begin{equation*}
\|f_n-g\|_\mathrm{max} = \sup_{0\leq r \lt 1}\|(f_n)_r-g_r\|_{\mathcal{X}}
\leq \sup_{0\leq r \lt 1}\sup_{m\geq N}\|(f_n)_r-(f_m)_r\|_{\mathcal{X}} =\sup_{m\geq N}\|f_n-f_m\|_\mathrm{max},
\end{equation*}
\begin{equation*}
\|f_n-g\|_\mathrm{max} = \sup_{0\leq r \lt 1}\|(f_n)_r-g_r\|_{\mathcal{X}}
\leq \sup_{0\leq r \lt 1}\sup_{m\geq N}\|(f_n)_r-(f_m)_r\|_{\mathcal{X}} =\sup_{m\geq N}\|f_n-f_m\|_\mathrm{max},
\end{equation*} which is arbitrarily small. Hence, ![]() $g\in \mathcal{X}^\mathrm{max},$ as desired.
$g\in \mathcal{X}^\mathrm{max},$ as desired.
Step 2. ![]() $\mathcal{X}^\mathrm{max}$ is of homogeneous type.
$\mathcal{X}^\mathrm{max}$ is of homogeneous type.
Let ![]() $z\in \mathbb{D}$ and
$z\in \mathbb{D}$ and ![]() $f\in \mathcal{X}^\mathrm{max}.$ Then,
$f\in \mathcal{X}^\mathrm{max}.$ Then, ![]() $f_r\in \mathcal{X}$ with
$f_r\in \mathcal{X}$ with ![]() $0\leq r \lt 1,$ and
$0\leq r \lt 1,$ and
Letting ![]() $r\to 1^-,$ we see that
$r\to 1^-,$ we see that ![]() $\{\delta_z: z\in\mathbb{D}\}\subset (\mathcal{X}^\mathrm{max})^{\ast}.$ Now, let
$\{\delta_z: z\in\mathbb{D}\}\subset (\mathcal{X}^\mathrm{max})^{\ast}.$ Now, let ![]() $f\in \mathcal{X}^\mathrm{max}$ and
$f\in \mathcal{X}^\mathrm{max}$ and ![]() $\xi\in\mathbb{T}.$ Then,
$\xi\in\mathbb{T}.$ Then,  $
\|f\|_\mathrm{max}=\sup\limits_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}}=\sup\limits_{0\leq r \lt 1}\|(f_r)_{\xi}\|_{\mathcal{X}}=\|f_{\xi}\|_\mathrm{max},
$ as desired. For each
$
\|f\|_\mathrm{max}=\sup\limits_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}}=\sup\limits_{0\leq r \lt 1}\|(f_r)_{\xi}\|_{\mathcal{X}}=\|f_{\xi}\|_\mathrm{max},
$ as desired. For each ![]() $f\in \mathcal{X}^\mathrm{max},$ define
$f\in \mathcal{X}^\mathrm{max},$ define ![]() $F: \mathbb{D}\to \mathcal{X}^\mathrm{max}$ with
$F: \mathbb{D}\to \mathcal{X}^\mathrm{max}$ with ![]() $F(z)=f_z, z\in\mathbb{D}$. The proof of the continuity of F follows from similar arguments as those in the proof of Theorem A. Lastly, for
$F(z)=f_z, z\in\mathbb{D}$. The proof of the continuity of F follows from similar arguments as those in the proof of Theorem A. Lastly, for ![]() $f\in \mathcal{X}\mathrm{^{max}},$
$f\in \mathcal{X}\mathrm{^{max}},$  $\|f\|_\mathrm{max}= \sup\limits_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}}= \sup\limits_{0\leq r \lt 1}\|f_r\|_\mathrm{max}.
$
$\|f\|_\mathrm{max}= \sup\limits_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}}= \sup\limits_{0\leq r \lt 1}\|f_r\|_\mathrm{max}.
$
Step 3. ![]() $\mathcal{X}^\mathrm{max}$ is the maximal homogeneous extension of
$\mathcal{X}^\mathrm{max}$ is the maximal homogeneous extension of ![]() $\mathcal{X}.$
$\mathcal{X}.$
Clearly, ![]() $\mathcal{X}\subset \mathcal{X}\mathrm{^{max}},$ and
$\mathcal{X}\subset \mathcal{X}\mathrm{^{max}},$ and ![]() $f_r\in \mathcal{X}$ if
$f_r\in \mathcal{X}$ if ![]() $f\in \mathcal{X}\mathrm{^{max}},$
$f\in \mathcal{X}\mathrm{^{max}},$ ![]() $0 \leq r \lt 1.$ If
$0 \leq r \lt 1.$ If ![]() $f\in \mathcal{X},$ then
$f\in \mathcal{X},$ then  $\|f\|_\mathrm{max}=\sup\limits_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}} = \|f\|_{\mathcal{X}}.$ If
$\|f\|_\mathrm{max}=\sup\limits_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}} = \|f\|_{\mathcal{X}}.$ If ![]() $\mathcal{Y}$ is a homogeneous extension of
$\mathcal{Y}$ is a homogeneous extension of ![]() $\mathcal{X},$ and
$\mathcal{X},$ and ![]() $f\in \mathcal{Y},$ then
$f\in \mathcal{Y},$ then  $
\|f\|_{\mathcal{Y}}=\sup\limits_{0\leq r \lt 1}\|f_r\|_{\mathcal{Y}}=\sup\limits_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}} \lt \infty,
$ which implies that
$
\|f\|_{\mathcal{Y}}=\sup\limits_{0\leq r \lt 1}\|f_r\|_{\mathcal{Y}}=\sup\limits_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}} \lt \infty,
$ which implies that ![]() $f\in \mathcal{X}^\mathrm{max}.$
$f\in \mathcal{X}^\mathrm{max}.$
We now turn to (ii). Only the proof for Banach spaces will be given. ![]() $(\mathcal{X}_{\mathcal{P}})_{\star}$ is a solid space since Proposition 14 and Lemma 10 imply that
$(\mathcal{X}_{\mathcal{P}})_{\star}$ is a solid space since Proposition 14 and Lemma 10 imply that  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for ![]() $(\mathcal{X}_{\mathcal{P}})_{\star}$, which yields the solidity of
$(\mathcal{X}_{\mathcal{P}})_{\star}$, which yields the solidity of ![]() $(\mathcal{X}_{\mathcal{P}})_{\star}$ by [Reference Li and Queffélec25, Theorem II.7, p. 89]. Now, for
$(\mathcal{X}_{\mathcal{P}})_{\star}$ by [Reference Li and Queffélec25, Theorem II.7, p. 89]. Now, for ![]() $(\mathcal{X}^\mathrm{max})_{\star}$, we would like to prove
$(\mathcal{X}^\mathrm{max})_{\star}$, we would like to prove  $
(\mathcal{R} f)^{\lambda}(z)\doteq \sum\limits_{n=0}^{\infty}a_n\lambda_nX_nz^n\in \mathcal{X}^\mathrm{max}\ \text{a.s.}
$ if
$
(\mathcal{R} f)^{\lambda}(z)\doteq \sum\limits_{n=0}^{\infty}a_n\lambda_nX_nz^n\in \mathcal{X}^\mathrm{max}\ \text{a.s.}
$ if  $f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in (\mathcal{X}^\mathrm{max})_{\star}$ and
$f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in (\mathcal{X}^\mathrm{max})_{\star}$ and ![]() $\lambda=\{\lambda_n\}_{n\geq 0}\in\ell^{\infty}.$ By Lemma 7, for
$\lambda=\{\lambda_n\}_{n\geq 0}\in\ell^{\infty}.$ By Lemma 7, for ![]() $0\leq r \lt 1,$
$0\leq r \lt 1,$  $
\lim\limits_{N\to\infty}\|S_N(\mathcal{R} f)_r-(\mathcal{R} f)_r\|_{\mathcal{X}}=0\ \text{a.s.}
$ Lemma 9 and the dominated convergence theorem imply that
$
\lim\limits_{N\to\infty}\|S_N(\mathcal{R} f)_r-(\mathcal{R} f)_r\|_{\mathcal{X}}=0\ \text{a.s.}
$ Lemma 9 and the dominated convergence theorem imply that  $
\lim\limits_{N\to\infty}\mathbb{E}\big(\|S_N(\mathcal{R} f)_r-(\mathcal{R} f)_r\|_{\mathcal{X}}\big)=0.
$ By the contraction principle ([Reference Hytönen, van Neerven, Veraar and Weis21, Theorem 6.1.13, p. 9]),
$
\lim\limits_{N\to\infty}\mathbb{E}\big(\|S_N(\mathcal{R} f)_r-(\mathcal{R} f)_r\|_{\mathcal{X}}\big)=0.
$ By the contraction principle ([Reference Hytönen, van Neerven, Veraar and Weis21, Theorem 6.1.13, p. 9]),
which implies that  $\big\{S_N(\mathcal{R} f)_{r}^{\lambda}\big\}_{N\geq 0}$ converges in
$\big\{S_N(\mathcal{R} f)_{r}^{\lambda}\big\}_{N\geq 0}$ converges in ![]() $L^1(\Omega; \mathcal{X}),$ leading to a convergent subsequence. The subsequence principle [Reference Li and Queffélec25, Theorem III.5, p. 132] implies that
$L^1(\Omega; \mathcal{X}),$ leading to a convergent subsequence. The subsequence principle [Reference Li and Queffélec25, Theorem III.5, p. 132] implies that ![]() $S_N(\mathcal{R} f)_{r}^{\lambda}$ converges in
$S_N(\mathcal{R} f)_{r}^{\lambda}$ converges in ![]() $\mathcal{X}\ \text{a.s.}$ So
$\mathcal{X}\ \text{a.s.}$ So  $
(\mathcal{R} f)_{r}^{\lambda}(z)=\sum\limits_{n=0}^{\infty}\lambda_na_nr^nX_nz^n\in \mathcal{X}\ \text{a.s.}
$ Moreover, by (4) and the contraction principle ([Reference Hytönen, van Neerven, Veraar and Weis21, Theorem 6.1.13, p. 9]),
$
(\mathcal{R} f)_{r}^{\lambda}(z)=\sum\limits_{n=0}^{\infty}\lambda_na_nr^nX_nz^n\in \mathcal{X}\ \text{a.s.}
$ Moreover, by (4) and the contraction principle ([Reference Hytönen, van Neerven, Veraar and Weis21, Theorem 6.1.13, p. 9]),
 \begin{eqnarray*}
\mathbb{E}\|(\mathcal{R} f)_{r}^{\lambda}\|_{\mathcal{X}} &\lesssim& \|\lambda\|_{\ell^{\infty}}
\lim_{N\to\infty} \mathbb{E}\|S_N(\mathcal{R} f)_{r}\|_{\mathcal{X}}
\leq \|\lambda\|_{\ell^{\infty}} \mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}} \lt \infty.
\end{eqnarray*}
\begin{eqnarray*}
\mathbb{E}\|(\mathcal{R} f)_{r}^{\lambda}\|_{\mathcal{X}} &\lesssim& \|\lambda\|_{\ell^{\infty}}
\lim_{N\to\infty} \mathbb{E}\|S_N(\mathcal{R} f)_{r}\|_{\mathcal{X}}
\leq \|\lambda\|_{\ell^{\infty}} \mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}} \lt \infty.
\end{eqnarray*}Then,
 \begin{eqnarray*}
\mathbb{E}\|(\mathcal{R} f)^{\lambda}\|_\mathrm{max}&=& \sup_{0\leq r \lt 1}\mathbb{E}\|(\mathcal{R} f)_{r}^{\lambda}\|_{\mathcal{X}}\lesssim \|\lambda\|_{\ell^{\infty}} \mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}}\ =\
\|\lambda\|_{\ell^{\infty}} \mathbb{E}\|\mathcal{R} f\|_\mathrm{max} \lt \infty.
\end{eqnarray*}
\begin{eqnarray*}
\mathbb{E}\|(\mathcal{R} f)^{\lambda}\|_\mathrm{max}&=& \sup_{0\leq r \lt 1}\mathbb{E}\|(\mathcal{R} f)_{r}^{\lambda}\|_{\mathcal{X}}\lesssim \|\lambda\|_{\ell^{\infty}} \mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}}\ =\
\|\lambda\|_{\ell^{\infty}} \mathbb{E}\|\mathcal{R} f\|_\mathrm{max} \lt \infty.
\end{eqnarray*} It follows that ![]() $(\mathcal{R} f)^{\lambda}\in \mathcal{X}^\mathrm{max}$ a.s., as desired.
$(\mathcal{R} f)^{\lambda}\in \mathcal{X}^\mathrm{max}$ a.s., as desired.
Remark. In Theorem B (ii), the condition  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1$ can be dropped for the case
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1$ can be dropped for the case ![]() $(\mathcal{X}_{\mathcal{P}})_\star$ if
$(\mathcal{X}_{\mathcal{P}})_\star$ if ![]() $\mathcal{X}$ is a functional p-Banach space, since
$\mathcal{X}$ is a functional p-Banach space, since  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ form an unconditional basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ form an unconditional basis for ![]() $(\mathcal{X}_{\mathcal{P}})_\star.$ The same remark applies to Lemma 10.
$(\mathcal{X}_{\mathcal{P}})_\star.$ The same remark applies to Lemma 10.
The rest of this section contains three nuggets supplementary to Theorem B: a counterexample to the solidity of ![]() $\mathcal{X}_{\star}$, the commutativity of
$\mathcal{X}_{\star}$, the commutativity of ![]() $\mathcal{X}_{\mathcal{P}}$ and
$\mathcal{X}_{\mathcal{P}}$ and ![]() $\mathcal{X}^\mathrm{max}$ with
$\mathcal{X}^\mathrm{max}$ with ![]() $\mathcal{X}_{\star}$ and the solidity of
$\mathcal{X}_{\star}$ and the solidity of ![]() $(\mathcal{X}_T)_{\star}$.
$(\mathcal{X}_T)_{\star}$.
Example. We show that the symbol space ![]() $\mathcal{X}_{\star}$ is not always a solid space. Let
$\mathcal{X}_{\star}$ is not always a solid space. Let ![]() $\mathcal{X}_{\star}^{S}$ denote the symbol space under the randomization by the standard Steinhaus sequence. Let
$\mathcal{X}_{\star}^{S}$ denote the symbol space under the randomization by the standard Steinhaus sequence. Let ![]() $\mathcal{B}$ denote the Bloch space and
$\mathcal{B}$ denote the Bloch space and
 \begin{equation*}
\mathcal{X}=\Big\{f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{B}:\ \lim_{k\to\infty}|a_{2^k}|\ \text{exists}\Big\}.
\end{equation*}
\begin{equation*}
\mathcal{X}=\Big\{f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{B}:\ \lim_{k\to\infty}|a_{2^k}|\ \text{exists}\Big\}.
\end{equation*} Recall that  $\|f\|_{\mathcal{B}}=|f(0)|+\sup\limits_{z\in\mathbb{D}}(1-|z|^2)|f'(z)|$ for
$\|f\|_{\mathcal{B}}=|f(0)|+\sup\limits_{z\in\mathbb{D}}(1-|z|^2)|f'(z)|$ for ![]() $f\in\mathcal{X}$ and one can check that
$f\in\mathcal{X}$ and one can check that ![]() $\big(\mathcal{X}, \|\cdot\|_{\mathcal{B}}\big)$ is of homogeneous type. For
$\big(\mathcal{X}, \|\cdot\|_{\mathcal{B}}\big)$ is of homogeneous type. For ![]() $\big(\mathcal{X}, \|\cdot\|_{\mathcal{B}}\big)$, the hypotheses of Definition 2 are satisfied since
$\big(\mathcal{X}, \|\cdot\|_{\mathcal{B}}\big)$, the hypotheses of Definition 2 are satisfied since ![]() $\mathcal{B}$ is of homogeneous type. So, it is sufficient to prove that
$\mathcal{B}$ is of homogeneous type. So, it is sufficient to prove that ![]() $\big(\mathcal{X}, \|\cdot\|_{\mathcal{B}}\big)$ is complete. Let
$\big(\mathcal{X}, \|\cdot\|_{\mathcal{B}}\big)$ is complete. Let ![]() $\{f_m\}_{m\geq1}$ be a Cauchy sequence in
$\{f_m\}_{m\geq1}$ be a Cauchy sequence in ![]() $\mathcal{X}$ with
$\mathcal{X}$ with  $f_m(z)=\sum\limits_{n=0}^{\infty}a_n^{(m)}z^n$. Since
$f_m(z)=\sum\limits_{n=0}^{\infty}a_n^{(m)}z^n$. Since ![]() $\mathcal{B}$ is complete, there exists
$\mathcal{B}$ is complete, there exists  $f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in\mathcal{B}$ such that
$f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in\mathcal{B}$ such that  $\lim\limits_{m\to\infty}\|f_m-f\|_{\mathcal{B}}=0.$ By [Reference Hedenmalm, Korenblum and Zhu19, p. 16], for any
$\lim\limits_{m\to\infty}\|f_m-f\|_{\mathcal{B}}=0.$ By [Reference Hedenmalm, Korenblum and Zhu19, p. 16], for any  $g(z)=\sum\limits_{n=0}^{\infty}b_nz^n\in\mathcal{B},$
$g(z)=\sum\limits_{n=0}^{\infty}b_nz^n\in\mathcal{B},$ ![]() $|b_n|\leq2\|g\|_{\mathcal{B}}, \ \forall n\geq1.$ Then,
$|b_n|\leq2\|g\|_{\mathcal{B}}, \ \forall n\geq1.$ Then,
 \begin{eqnarray*}
\big||a_{2^k}|-|a_{2^j}|\big|&\leq&\big||a_{2^k}|-|a_{2^k}^{(m)}|\big|+
\big||a_{2^k}^{(m)}|-|a_{2^j}^{(m)}|\big|+\big||a_{2^j}^{(m)}|-|a_{2^j}|\big|\\
&\leq&4\|f_m-f\|_{\mathcal{B}}+\big||a_{2^k}^{(m)}|-|a_{2^j}^{(m)}|\big|.
\end{eqnarray*}
\begin{eqnarray*}
\big||a_{2^k}|-|a_{2^j}|\big|&\leq&\big||a_{2^k}|-|a_{2^k}^{(m)}|\big|+
\big||a_{2^k}^{(m)}|-|a_{2^j}^{(m)}|\big|+\big||a_{2^j}^{(m)}|-|a_{2^j}|\big|\\
&\leq&4\|f_m-f\|_{\mathcal{B}}+\big||a_{2^k}^{(m)}|-|a_{2^j}^{(m)}|\big|.
\end{eqnarray*} So  $\big\{|a_{2^k}|\big\}_{k\geq1}$ is a Cauchy sequence in
$\big\{|a_{2^k}|\big\}_{k\geq1}$ is a Cauchy sequence in ![]() $\mathbb{R},$ hence
$\mathbb{R},$ hence ![]() $f\in\mathcal{X}$. That is,
$f\in\mathcal{X}$. That is, ![]() $\big(\mathcal{X}, \|\cdot\|_{\mathcal{B}}\big)$ is of homogeneous type. Lastly, we point out that
$\big(\mathcal{X}, \|\cdot\|_{\mathcal{B}}\big)$ is of homogeneous type. Lastly, we point out that  $\sum\limits_{k=1}^{\infty}z^{2^k}\in \mathcal{X}_{\star}^{S}.$ By [Reference Hedenmalm, Korenblum and Zhu19, Theorem 1.14, p. 15], for any lacunary sequence
$\sum\limits_{k=1}^{\infty}z^{2^k}\in \mathcal{X}_{\star}^{S}.$ By [Reference Hedenmalm, Korenblum and Zhu19, Theorem 1.14, p. 15], for any lacunary sequence ![]() $\{n_k\}_{k\geq 1}$, that is,
$\{n_k\}_{k\geq 1}$, that is,  $\inf\limits_{k\geq1}\frac{n_{k+1}}{n_k} \gt 1$, the series
$\inf\limits_{k\geq1}\frac{n_{k+1}}{n_k} \gt 1$, the series  $\sum\limits_{k=1}^{\infty}a_kz^{n_k}$ belongs to
$\sum\limits_{k=1}^{\infty}a_kz^{n_k}$ belongs to ![]() $\mathcal{B}$ if and only if
$\mathcal{B}$ if and only if  $\sup\limits_{k\geq1}|a_k| \lt \infty.$ So the Steinhaus randomization
$\sup\limits_{k\geq1}|a_k| \lt \infty.$ So the Steinhaus randomization  $\sum\limits_{k=1}^{\infty}e^{2\pi i\alpha_k}z^{2^k}\in\mathcal{X}$ a.s., that is,
$\sum\limits_{k=1}^{\infty}e^{2\pi i\alpha_k}z^{2^k}\in\mathcal{X}$ a.s., that is,  $\sum\limits_{k=1}^{\infty}z^{2^k}\in \mathcal{X}_{\star}^{S}.$ But
$\sum\limits_{k=1}^{\infty}z^{2^k}\in \mathcal{X}_{\star}^{S}.$ But  $
\Big\{\sum\limits_{k=1}^{\infty}\lambda_kz^{2^k}:\ \{\lambda_k\}_{k\geq 1}\in \ell^{\infty}\Big\}\not\subset \mathcal{X}_{\star}^{S}.
$ For example, taking
$
\Big\{\sum\limits_{k=1}^{\infty}\lambda_kz^{2^k}:\ \{\lambda_k\}_{k\geq 1}\in \ell^{\infty}\Big\}\not\subset \mathcal{X}_{\star}^{S}.
$ For example, taking ![]() $\lambda_{2k}=1$ and
$\lambda_{2k}=1$ and ![]() $\lambda_{2k-1}=0$ for
$\lambda_{2k-1}=0$ for ![]() $k\geq1,$ one has
$k\geq1,$ one has  $\sum\limits_{k=1}^{\infty}\lambda_kz^{2^k}\notin\mathcal{X}_{\star}^{S}.$
$\sum\limits_{k=1}^{\infty}\lambda_kz^{2^k}\notin\mathcal{X}_{\star}^{S}.$
The above example shows that ![]() $\mathcal{X}_{\star}^{S}$ is not always a solid space. The same is true for
$\mathcal{X}_{\star}^{S}$ is not always a solid space. The same is true for ![]() $\mathcal{X}_{\star}^{R}$ obtained through the Rademacher sequence. For the standard real (or complex) Gaussian randomization, we now show that
$\mathcal{X}_{\star}^{R}$ obtained through the Rademacher sequence. For the standard real (or complex) Gaussian randomization, we now show that ![]() $\mathcal{X}_{\star}^{G}$ is a solid space. Here, we consider only the real Gaussian case, and the complex Gaussian case can be treated in a similar fashion. If
$\mathcal{X}_{\star}^{G}$ is a solid space. Here, we consider only the real Gaussian case, and the complex Gaussian case can be treated in a similar fashion. If  $f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in\mathcal{X}_{\star}^{G},$ then
$f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in\mathcal{X}_{\star}^{G},$ then  $\lim\limits_{k\to\infty}|a_{2^k}\xi_{2^k}|$ exists a.s., where
$\lim\limits_{k\to\infty}|a_{2^k}\xi_{2^k}|$ exists a.s., where ![]() $\{\xi_n\}_{n\geq0}$ is a standard real Gaussian sequence. By the Kolmogorov zero-one law,
$\{\xi_n\}_{n\geq0}$ is a standard real Gaussian sequence. By the Kolmogorov zero-one law,  $\lim\limits_{k\to\infty}|a_{2^k}\xi_{2^k}|=c$ a.s. for some constant
$\lim\limits_{k\to\infty}|a_{2^k}\xi_{2^k}|=c$ a.s. for some constant ![]() $c\geq0.$ Since
$c\geq0.$ Since  $\limsup\limits_{n\to\infty}\frac{|\xi_n|}{\sqrt{2\log n}}=1$ a.s. [Reference Li and Queffélec25, p. 43], one has
$\limsup\limits_{n\to\infty}\frac{|\xi_n|}{\sqrt{2\log n}}=1$ a.s. [Reference Li and Queffélec25, p. 43], one has ![]() $a_{2^k}\to0$ as
$a_{2^k}\to0$ as ![]() $k\to\infty.$ Furthermore, by a direct verification,
$k\to\infty.$ Furthermore, by a direct verification, ![]() $a_{2^k}\xi_{2^k}$ converges to 0 in distribution as
$a_{2^k}\xi_{2^k}$ converges to 0 in distribution as ![]() $k\to\infty.$ It follows that c = 0. Let
$k\to\infty.$ It follows that c = 0. Let ![]() $\{\lambda_n\}_{n\geq0}\in\ell^\infty.$ Then,
$\{\lambda_n\}_{n\geq0}\in\ell^\infty.$ Then,  $\sum\limits_{n=0}^{\infty}a_n\lambda_nz^n\in\mathcal{B}_{\star}^{G}$ by the remark after Theorem B, and
$\sum\limits_{n=0}^{\infty}a_n\lambda_nz^n\in\mathcal{B}_{\star}^{G}$ by the remark after Theorem B, and  $\lim\limits_{k\to\infty}a_{2^k}\lambda_{2^k}\xi_{2^k}=0$ a.s. That is,
$\lim\limits_{k\to\infty}a_{2^k}\lambda_{2^k}\xi_{2^k}=0$ a.s. That is,  $\sum\limits_{n=0}^{\infty}a_n\lambda_nz^n\in\mathcal{X}_{\star}^{G}.$
$\sum\limits_{n=0}^{\infty}a_n\lambda_nz^n\in\mathcal{X}_{\star}^{G}.$
Problem A. To characterize homogeneous ![]() $\mathcal{X}$ such that
$\mathcal{X}$ such that ![]() $\mathcal{X}_\star$ is a solid space.
$\mathcal{X}_\star$ is a solid space.
The second nugget is the following commutativity:
Lemma 10. Let ![]() $\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with
$\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with ![]() $p\in (0, 1),$ of homogeneous type; for the latter, we also assume
$p\in (0, 1),$ of homogeneous type; for the latter, we also assume  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ Let
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ Let ![]() $\{X_n\}_{n\geq 0}$ be a standard random sequence. Then,
$\{X_n\}_{n\geq 0}$ be a standard random sequence. Then,
Proof. We first claim that if ![]() $g\in \mathcal{X}_{\mathcal{P}},$ then
$g\in \mathcal{X}_{\mathcal{P}},$ then  $\lim\limits_{r\to 1^-}g_r=g$, where the convergence is in norm. Assume that
$\lim\limits_{r\to 1^-}g_r=g$, where the convergence is in norm. Assume that ![]() $p_n\to g$ as
$p_n\to g$ as ![]() $n\to\infty$ with
$n\to\infty$ with ![]() $p_n\in \mathcal{P}.$ Since
$p_n\in \mathcal{P}.$ Since  $\lim\limits_{r\to 1^-}\|(p_n)_r-p_n\|_{\mathcal{X}}=0$ for each n, the claim follows from
$\lim\limits_{r\to 1^-}\|(p_n)_r-p_n\|_{\mathcal{X}}=0$ for each n, the claim follows from
 \begin{eqnarray*}
\|g_r-g\|_{\mathcal{X}}^{p}
&\leq&\|g_r-(p_n)_r\|_{\mathcal{X}}^{p}+\|(p_n)_r-p_n\|_{\mathcal{X}}^{p}
+\|p_n-g\|_{\mathcal{X}}^{p}\\
&\leq& 2\|p_n-g\|_{\mathcal{X}}^{p} + \|(p_n)_r-p_n\|_{\mathcal{X}}^{p}
\end{eqnarray*}
\begin{eqnarray*}
\|g_r-g\|_{\mathcal{X}}^{p}
&\leq&\|g_r-(p_n)_r\|_{\mathcal{X}}^{p}+\|(p_n)_r-p_n\|_{\mathcal{X}}^{p}
+\|p_n-g\|_{\mathcal{X}}^{p}\\
&\leq& 2\|p_n-g\|_{\mathcal{X}}^{p} + \|(p_n)_r-p_n\|_{\mathcal{X}}^{p}
\end{eqnarray*} since ![]() $\mathcal{X}$ is of homogeneous type. In particular, if
$\mathcal{X}$ is of homogeneous type. In particular, if ![]() $\mathcal{X}$ is a Banach space, we take p = 1. Now let
$\mathcal{X}$ is a Banach space, we take p = 1. Now let ![]() $f\in (\mathcal{X}_{\mathcal{P}})_{\star}$. The claim implies that
$f\in (\mathcal{X}_{\mathcal{P}})_{\star}$. The claim implies that ![]() $(\mathcal{R} f)_r\to \mathcal{R} f\ \text{a.s.}$ as
$(\mathcal{R} f)_r\to \mathcal{R} f\ \text{a.s.}$ as ![]() $r\to 1^-.$ The Marcinkiewicz–Zygmund–Kahane theorem [Reference Li and Queffélec26, Theorem II.4, p. 240] implies that
$r\to 1^-.$ The Marcinkiewicz–Zygmund–Kahane theorem [Reference Li and Queffélec26, Theorem II.4, p. 240] implies that ![]() $S_N(\mathcal{R} f)\to \mathcal{R} f\ \text{a.s.}$ as
$S_N(\mathcal{R} f)\to \mathcal{R} f\ \text{a.s.}$ as ![]() $N\to\infty.$ By the dominated convergence theorem, one has
$N\to\infty.$ By the dominated convergence theorem, one has  $\lim\limits_{N\to\infty}\mathbb{E}\|S_N(\mathcal{R} f)-\mathcal{R} f\|_{\mathcal{X}}=0,$ which yields that
$\lim\limits_{N\to\infty}\mathbb{E}\|S_N(\mathcal{R} f)-\mathcal{R} f\|_{\mathcal{X}}=0,$ which yields that ![]() $f\in (\mathcal{X}_{\star})_{\mathcal{P}}.$ Conversely, let
$f\in (\mathcal{X}_{\star})_{\mathcal{P}}.$ Conversely, let ![]() $f\in (\mathcal{X}_{\star})_{\mathcal{P}}.$ By Theorem A, one has
$f\in (\mathcal{X}_{\star})_{\mathcal{P}}.$ By Theorem A, one has  $\lim\limits_{N\to\infty}S_Nf=f$ in
$\lim\limits_{N\to\infty}S_Nf=f$ in ![]() $\mathcal{X}_{\star}.$ So
$\mathcal{X}_{\star}.$ So ![]() $f\in (\mathcal{X}_{\mathcal{P}})_{\star},$ as desired.
$f\in (\mathcal{X}_{\mathcal{P}})_{\star},$ as desired.
For the second equality, if ![]() $f\in (\mathcal{X}_{\star})^\mathrm{max},$ then
$f\in (\mathcal{X}_{\star})^\mathrm{max},$ then ![]() $
(\mathcal{R} f)_{r}\in \mathcal{X}\ \text{a.s.}, \ 0\leq r \lt 1$ and
$
(\mathcal{R} f)_{r}\in \mathcal{X}\ \text{a.s.}, \ 0\leq r \lt 1$ and  $\sup\limits_{0\leq r \lt 1}\mathbb{E}\|(\mathcal{R} f)_r\|_{\mathcal{X}}=
\mathbb{E}\Big(\sup\limits_{0\leq r \lt 1}\|(\mathcal{R} f)_r\|_{\mathcal{X}}\Big) \lt \infty
$ since
$\sup\limits_{0\leq r \lt 1}\mathbb{E}\|(\mathcal{R} f)_r\|_{\mathcal{X}}=
\mathbb{E}\Big(\sup\limits_{0\leq r \lt 1}\|(\mathcal{R} f)_r\|_{\mathcal{X}}\Big) \lt \infty
$ since ![]() $\mathcal{X}$ is homogeneous. It follows that
$\mathcal{X}$ is homogeneous. It follows that  $\sup\limits_{0\leq r \lt 1}\|(\mathcal{R} f)_r\|_{\mathcal{X}} \lt \infty\ \text{a.s.},$ which implies that
$\sup\limits_{0\leq r \lt 1}\|(\mathcal{R} f)_r\|_{\mathcal{X}} \lt \infty\ \text{a.s.},$ which implies that ![]() $f\in (\mathcal{X}^\mathrm{max})_{\star}.$ Conversely, let
$f\in (\mathcal{X}^\mathrm{max})_{\star}.$ Conversely, let ![]() $f\in (\mathcal{X}^\mathrm{max})_{\star}.$ Then,
$f\in (\mathcal{X}^\mathrm{max})_{\star}.$ Then, ![]() $
(\mathcal{R} f)_{r}\in \mathcal{X}\ \text{a.s.},\ 0\leq r \lt 1$ and
$
(\mathcal{R} f)_{r}\in \mathcal{X}\ \text{a.s.},\ 0\leq r \lt 1$ and  $\sup\limits_{0\leq r \lt 1}\|(\mathcal{R} f)_r\|_{\mathcal{X}} \lt \infty\ \text{a.s.}
$ The Marcinkiewicz–Zygmund–Kahane theorem [Reference Li and Queffélec26, Theorem II.4, p. 240] implies
$\sup\limits_{0\leq r \lt 1}\|(\mathcal{R} f)_r\|_{\mathcal{X}} \lt \infty\ \text{a.s.}
$ The Marcinkiewicz–Zygmund–Kahane theorem [Reference Li and Queffélec26, Theorem II.4, p. 240] implies  $\sup\limits_{N\geq 0}\|S_N(\mathcal{R} f)\|_{\mathcal{X}} \lt \infty\ \text{a.s.}$ Moreover,
$\sup\limits_{N\geq 0}\|S_N(\mathcal{R} f)\|_{\mathcal{X}} \lt \infty\ \text{a.s.}$ Moreover,  $\lim\limits_{N\to\infty}S_N(\mathcal{R} f)_r = (\mathcal{R} f)_r\ \text{a.s.}$ by Lemma 7. By Kahane’s inequality [Reference Li and Queffélec25, Theorem V.1, p. 139] and Fernique’s theorem [Reference Li and Queffélec25, Theorem V.26, p. 255],
$\lim\limits_{N\to\infty}S_N(\mathcal{R} f)_r = (\mathcal{R} f)_r\ \text{a.s.}$ by Lemma 7. By Kahane’s inequality [Reference Li and Queffélec25, Theorem V.1, p. 139] and Fernique’s theorem [Reference Li and Queffélec25, Theorem V.26, p. 255],
 \begin{equation*}
\sup\limits_{0\leq r \lt 1}\mathbb{E} \|(\mathcal{R} f)_r\|_{\mathcal{X}} \leq \mathbb{E}\Big(\sup\limits_{0\leq r \lt 1}\|(\mathcal{R} f)_r\|_{\mathcal{X}}\Big)\leq \mathbb{E}\Big(\sup\limits_{N\geq 0}\|S_N(\mathcal{R} f)\|_{\mathcal{X}}\Big) \lt \infty.
\end{equation*}
\begin{equation*}
\sup\limits_{0\leq r \lt 1}\mathbb{E} \|(\mathcal{R} f)_r\|_{\mathcal{X}} \leq \mathbb{E}\Big(\sup\limits_{0\leq r \lt 1}\|(\mathcal{R} f)_r\|_{\mathcal{X}}\Big)\leq \mathbb{E}\Big(\sup\limits_{N\geq 0}\|S_N(\mathcal{R} f)\|_{\mathcal{X}}\Big) \lt \infty.
\end{equation*} So ![]() $f\in (\mathcal{X}_{\star})^\mathrm{max},$ as desired.
$f\in (\mathcal{X}_{\star})^\mathrm{max},$ as desired.
Lastly, as the third nugget, the following proposition should be compared with Proposition 15, which identifies ![]() $\mathcal{X}_T$ with
$\mathcal{X}_T$ with ![]() $\mathcal{X}^\mathrm{max}$ under certain conditions.
$\mathcal{X}^\mathrm{max}$ under certain conditions.
Proposition 11. Let ![]() $\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with
$\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with ![]() $p\in (0, 1)$, of homogeneous type. Let
$p\in (0, 1)$, of homogeneous type. Let ![]() $\{X_n\}_{n\geq 0}$ be a standard random sequence. Then,
$\{X_n\}_{n\geq 0}$ be a standard random sequence. Then, ![]() $(\mathcal{X}_T)_{\star}$ is a solid space.
$(\mathcal{X}_T)_{\star}$ is a solid space.
Proof. We shall only prove the Banach space case since the modification needed for p-Banach spaces is straightforward. Let ![]() $f(z)=\sum_{n=0}^{\infty}a_nz^n\in (\mathcal{X}_T)_{\star}.$ By Lemma 9,
$f(z)=\sum_{n=0}^{\infty}a_nz^n\in (\mathcal{X}_T)_{\star}.$ By Lemma 9, ![]() $(\mathcal{R} f)^{\lambda}\in \mathcal{X}_T\ \text{a.s.}$ if and only if
$(\mathcal{R} f)^{\lambda}\in \mathcal{X}_T\ \text{a.s.}$ if and only if  $\mathbb{E}\|(\mathcal{R} f)^{\lambda}\|_{\mathcal{X}_T} \lt \infty,$ where
$\mathbb{E}\|(\mathcal{R} f)^{\lambda}\|_{\mathcal{X}_T} \lt \infty,$ where ![]() $(\mathcal{R} f)^{\lambda}(z)= \sum_{n=0}^{\infty}a_n\lambda_nX_nz^n$ and
$(\mathcal{R} f)^{\lambda}(z)= \sum_{n=0}^{\infty}a_n\lambda_nX_nz^n$ and ![]() $\lambda=\{\lambda_n\}_{n \geq 0}\in\ell^{\infty}.$ Note that
$\lambda=\{\lambda_n\}_{n \geq 0}\in\ell^{\infty}.$ Note that
 \begin{eqnarray*}
\mathbb{E}\|(\mathcal{R} f)^{\lambda}\|_{\mathcal{X}_T}
&\lesssim&\lim_{N\to\infty}\int_0^{\infty}\mathbb{P}\big(\|(S_N(\mathcal{R} f))^{\lambda}\|_{\mathcal{X}} \gt t\big)\,\mathrm{d}t\\
&\lesssim& \sup_{n\geq 0}|\lambda_n| \ \lim_{N\to\infty}\mathbb{E}\|S_N (\mathcal{R} f)\|_{\mathcal{X}} \\
&\leq& \sup_{n\geq 0}|\lambda_n| \ \mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}_T} \lt \infty,
\end{eqnarray*}
\begin{eqnarray*}
\mathbb{E}\|(\mathcal{R} f)^{\lambda}\|_{\mathcal{X}_T}
&\lesssim&\lim_{N\to\infty}\int_0^{\infty}\mathbb{P}\big(\|(S_N(\mathcal{R} f))^{\lambda}\|_{\mathcal{X}} \gt t\big)\,\mathrm{d}t\\
&\lesssim& \sup_{n\geq 0}|\lambda_n| \ \lim_{N\to\infty}\mathbb{E}\|S_N (\mathcal{R} f)\|_{\mathcal{X}} \\
&\leq& \sup_{n\geq 0}|\lambda_n| \ \mathbb{E}\|\mathcal{R} f\|_{\mathcal{X}_T} \lt \infty,
\end{eqnarray*} where the first ‘![]() $\lesssim$’ follows from Lévy’s inequality [Reference Cheng, Fang and Liu11], and the second one holds by the contraction principle ([Reference Hytönen, van Neerven, Veraar and Weis21, Theorem 6.1.13, p. 9]).
$\lesssim$’ follows from Lévy’s inequality [Reference Cheng, Fang and Liu11], and the second one holds by the contraction principle ([Reference Hytönen, van Neerven, Veraar and Weis21, Theorem 6.1.13, p. 9]).
5. Relationship with unconditional bases
In this section, we first present the (rather short) proof of Theorem C. Then, we present four propositions to further illustrate the connection between solid bases/frames and unconditional bases.
Proof of Theorem C
(i.1) ![]() $\Rightarrow $ (i.2) is obvious. (i.2)
$\Rightarrow $ (i.2) is obvious. (i.2) ![]() $\Rightarrow $ (i.3) is by the fact that
$\Rightarrow $ (i.3) is by the fact that ![]() $\lim_{N\to\infty}S_Nf=f$ if and only if
$\lim_{N\to\infty}S_Nf=f$ if and only if ![]() $f\in \mathcal{X}_{\mathcal{P}}$ in the proof of Proposition 14. Next, (i.3)
$f\in \mathcal{X}_{\mathcal{P}}$ in the proof of Proposition 14. Next, (i.3) ![]() $\Rightarrow $ (i.4). Part (i) of Definition 1 is satisfied since
$\Rightarrow $ (i.4). Part (i) of Definition 1 is satisfied since  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for ![]() $\mathcal{X}_{\mathcal{P}}$ with constant 1. It suffices to show that
$\mathcal{X}_{\mathcal{P}}$ with constant 1. It suffices to show that ![]() $
\lim_{N\to\infty} \|S_Nf\|_\mathrm{max}=\|f\|_\mathrm{max}$ for
$
\lim_{N\to\infty} \|S_Nf\|_\mathrm{max}=\|f\|_\mathrm{max}$ for ![]() $ f\in \mathcal{X}^\mathrm{max}.$ Since
$ f\in \mathcal{X}^\mathrm{max}.$ Since ![]() $f_r\in \mathcal{X}_{\mathcal{P}}$ for each
$f_r\in \mathcal{X}_{\mathcal{P}}$ for each ![]() $0\leq r \lt 1$ by Lemma 7, one has
$0\leq r \lt 1$ by Lemma 7, one has
 \begin{equation}
\lim_{N\to\infty}\|S_Nf_r\|_{\mathcal{X}} = \sup_{N\geq 0}\|S_Nf_r\|_{\mathcal{X}} = \|f_r\|_{\mathcal{X}}
\end{equation}
\begin{equation}
\lim_{N\to\infty}\|S_Nf_r\|_{\mathcal{X}} = \sup_{N\geq 0}\|S_Nf_r\|_{\mathcal{X}} = \|f_r\|_{\mathcal{X}}
\end{equation} because ![]() $\|S_Nf_r\|_{\mathcal{X}}$ increases as
$\|S_Nf_r\|_{\mathcal{X}}$ increases as ![]() $N\to\infty.$ Then,
$N\to\infty.$ Then,
 \begin{equation}
\sup_{N\geq 0}\|S_Nf\|_\mathrm{max}=\sup_{N\geq 0}\sup_{0\leq r \lt 1}\|S_Nf_r\|_{\mathcal{X}}=\sup_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}}=\|f\|_\mathrm{max},
\end{equation}
\begin{equation}
\sup_{N\geq 0}\|S_Nf\|_\mathrm{max}=\sup_{N\geq 0}\sup_{0\leq r \lt 1}\|S_Nf_r\|_{\mathcal{X}}=\sup_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}}=\|f\|_\mathrm{max},
\end{equation} as desired. (i.4) ![]() $\Rightarrow $ (i.1) follows from the definition of the homogeneous extension. The proof for p-Banach spaces follows from a modification by replacing (5) with
$\Rightarrow $ (i.1) follows from the definition of the homogeneous extension. The proof for p-Banach spaces follows from a modification by replacing (5) with  $
\sup\limits_{N\geq 0}\|S_Nf_r\|_{\mathcal{X}} \approx \|f_r\|_{\mathcal{X}}.
$
$
\sup\limits_{N\geq 0}\|S_Nf_r\|_{\mathcal{X}} \approx \|f_r\|_{\mathcal{X}}.
$
Remark. In Theorem C (ii), the condition  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1$ can be dropped for the case
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1$ can be dropped for the case ![]() $\mathcal{X}=\mathcal{X}_{\mathcal{P}}$ if
$\mathcal{X}=\mathcal{X}_{\mathcal{P}}$ if ![]() $\mathcal{X}$ is a functional p-Banach space. This follows from the fact that
$\mathcal{X}$ is a functional p-Banach space. This follows from the fact that  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a Schauder basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a Schauder basis for ![]() $\mathcal{X}_{\mathcal{P}}$ if and only if
$\mathcal{X}_{\mathcal{P}}$ if and only if ![]() $\sup_{N\geq 0}\|S_N\| \lt \infty;$ see [Reference Zhu43, Proposition 1]. The same remark applies to Theorem E and Theorem F.
$\sup_{N\geq 0}\|S_N\| \lt \infty;$ see [Reference Zhu43, Proposition 1]. The same remark applies to Theorem E and Theorem F.
The rest of this section is to prove the following four propositions, which further illustrate the relationship between solid bases/frames and unconditional bases.
Proposition 12. Let E be a Banach space. Then, ![]() $\{{e}_n\}_{n\geq 1}$ is an unconditional basis for E with constant 1 if and only if it is both a solid basis and a Schauder basis for E.
$\{{e}_n\}_{n\geq 1}$ is an unconditional basis for E with constant 1 if and only if it is both a solid basis and a Schauder basis for E.
Recall that a sequence ![]() $\{{e}_n\}_{n\geq 1}$ in a Banach space E is said to be a basic sequence if it is a Schauder basis for the closure of its span. Let
$\{{e}_n\}_{n\geq 1}$ in a Banach space E is said to be a basic sequence if it is a Schauder basis for the closure of its span. Let ![]() $\mathbf{e}_n=(0, \cdots, 0, 1, 0, \cdots),\ n\geq 1.$
$\mathbf{e}_n=(0, \cdots, 0, 1, 0, \cdots),\ n\geq 1.$
Proposition 13. Let E be a Banach space and ![]() $\{{e}_n\}_{n\geq 1}$ be a basic sequence with
$\{{e}_n\}_{n\geq 1}$ be a basic sequence with ![]() $\|{e}_n\|_E=1,\ n\geq1.$ Let W denote the closure of finite linear combinations of
$\|{e}_n\|_E=1,\ n\geq1.$ Let W denote the closure of finite linear combinations of ![]() $\{{e}_n\}_{n\geq 1}.$ Then,
$\{{e}_n\}_{n\geq 1}.$ Then, ![]() $\{{e}_n\}_{n\geq 1}$ is an unconditional basis for W if and only if
$\{{e}_n\}_{n\geq 1}$ is an unconditional basis for W if and only if ![]() $\{\mathbf{e}_n\}_{n\geq 1}$ is a solid frame for
$\{\mathbf{e}_n\}_{n\geq 1}$ is a solid frame for ![]() $W^{\mathrm{s\text{-}max}}.$
$W^{\mathrm{s\text{-}max}}.$
Here, the sequential version of the maximal solid extension ![]() $E\mathrm{^{s\text{-}max}}$ is defined as
$E\mathrm{^{s\text{-}max}}$ is defined as
 \begin{equation}
E^{\mathrm{s\text{-}max}}=\Big\{a=(a_1, a_2, \cdots)\in \mathfrak{S}:\ \|a\|_\mathrm{s\text{-}max}=\sup_{N\geq 1}\Big\|\sum_{n=1}^Na_n{e}_n\Big\|_E \lt \infty\Big\},
\end{equation}
\begin{equation}
E^{\mathrm{s\text{-}max}}=\Big\{a=(a_1, a_2, \cdots)\in \mathfrak{S}:\ \|a\|_\mathrm{s\text{-}max}=\sup_{N\geq 1}\Big\|\sum_{n=1}^Na_n{e}_n\Big\|_E \lt \infty\Big\},
\end{equation}which is the unique maximal solid extension of E up to an isometric isomorphism; see Theorem G.
(i) Let E be a Banach space with a solid basis
 $\{{e}_n\}_{n\geq 1}.$ Then,
$\{{e}_n\}_{n\geq 1}.$ Then,  $\{{e}_n\}_{n\geq 1}$ is an unconditional basis for
$\{{e}_n\}_{n\geq 1}$ is an unconditional basis for  $E_{\mathcal{P}}$ with constant 1.
$E_{\mathcal{P}}$ with constant 1.(ii) Let E be a p-Banach space with
 $p\in (0, 1)$ and
$p\in (0, 1)$ and  $\{{e}_n\}_{n\geq 1}$ a solid frame. Then,
$\{{e}_n\}_{n\geq 1}$ a solid frame. Then,  $\{{e}_n\}_{n\geq 1}$ is an unconditional basis for
$\{{e}_n\}_{n\geq 1}$ is an unconditional basis for  $E_{\mathcal{P}}.$
$E_{\mathcal{P}}.$
Proposition 15. Let ![]() $\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with
$\mathcal{X}$ be a functional Banach space, or a functional p-Banach space with ![]() $p\in (0, 1),$ of homogeneous type; for the latter, we assume
$p\in (0, 1),$ of homogeneous type; for the latter, we assume  $\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ If
$\lim\limits_{n\to\infty}\|z^n\|_{\mathcal{X}}^{\frac{1}{n}}=1.$ If  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for ![]() $\mathcal{X}_{\mathcal{P}},$ then
$\mathcal{X}_{\mathcal{P}},$ then ![]() $
\mathcal{X}^\mathrm{max} = \mathcal{X}_{T}.
$
$
\mathcal{X}^\mathrm{max} = \mathcal{X}_{T}.
$
Proof of Proposition 12
If ![]() $\{{e}_n\}_{n\geq 1}$ is an unconditional basis with constant 1, then, by [Reference Li and Queffélec25, Proposition III.5, p.92], part (i) of Definition 1 is satisfied. Condition (ii) holds since it is a Schauder basis. Conversely, if
$\{{e}_n\}_{n\geq 1}$ is an unconditional basis with constant 1, then, by [Reference Li and Queffélec25, Proposition III.5, p.92], part (i) of Definition 1 is satisfied. Condition (ii) holds since it is a Schauder basis. Conversely, if ![]() $\{{e}_n\}_{n\geq 1}$ is a solid basis, then part (i) of Definition 1 ensures that
$\{{e}_n\}_{n\geq 1}$ is a solid basis, then part (i) of Definition 1 ensures that ![]() $\{{e}_n\}_{n\geq 1}$ is an unconditional basis with constant 1.
$\{{e}_n\}_{n\geq 1}$ is an unconditional basis with constant 1.
Proof of Proposition 13
This proof follows from the following lemma which is less sleek but covers a slightly more general situation.
Lemma 16. Let E be a Banach space and ![]() $\{e_n\}_{n\geq 1}$ be a sequence of unit vectors. Let W denote the closure of finite linear combinations of
$\{e_n\}_{n\geq 1}$ be a sequence of unit vectors. Let W denote the closure of finite linear combinations of ![]() $\{e_n\}_{n\geq 1}.$
$\{e_n\}_{n\geq 1}.$
(i) If
 $\{e_n\}_{n\geq 1}$ is an unconditional basis for
$\{e_n\}_{n\geq 1}$ is an unconditional basis for  $W,$ then
$W,$ then  $\{\mathbf{e}_n\}_{n\geq 1}$ is a solid frame for
$\{\mathbf{e}_n\}_{n\geq 1}$ is a solid frame for  $W^\mathrm{s\text{-}max}.$
$W^\mathrm{s\text{-}max}.$(ii) If
 $\{e_n\}_{n\geq 1}$ is a Schauder basis for W and
$\{e_n\}_{n\geq 1}$ is a Schauder basis for W and  $\{\mathbf{e}_n\}_{n\geq 1}$ is a solid frame for
$\{\mathbf{e}_n\}_{n\geq 1}$ is a solid frame for  $W^\mathrm{s\text{-}max},$ then
$W^\mathrm{s\text{-}max},$ then  $\{e_n\}_{n\geq 1}$ is an unconditional basis for
$\{e_n\}_{n\geq 1}$ is an unconditional basis for  $W.$
$W.$
Proof of Lemma 16
(i) If ![]() $\{e_n\}_{n\geq 1}$ is an unconditional basis for
$\{e_n\}_{n\geq 1}$ is an unconditional basis for ![]() $W,$ then
$W,$ then ![]() $\|\mathbf{e}_n\|_\mathrm{s\text{-}max}=\|e_n\|_E=1.$ Moreover,
$\|\mathbf{e}_n\|_\mathrm{s\text{-}max}=\|e_n\|_E=1.$ Moreover,
 \begin{eqnarray*}
\Big\|\sum_{k=1}^N\lambda_ka_k\mathbf{e}_k\Big\|_\mathrm{s\text{-}max} = \sup_{1\leq n\leq N}\Big\|\sum_{k=1}^n\lambda_ka_ke_k\Big\|_E
\ \lesssim\ \sup_{1\leq n\leq N}\Big\|\sum_{k=1}^na_ke_k\Big\|_E
= \Big\|\sum_{k=1}^Na_k\mathbf{e}_k\Big\|_\mathrm{s\text{-}max}
\end{eqnarray*}
\begin{eqnarray*}
\Big\|\sum_{k=1}^N\lambda_ka_k\mathbf{e}_k\Big\|_\mathrm{s\text{-}max} = \sup_{1\leq n\leq N}\Big\|\sum_{k=1}^n\lambda_ka_ke_k\Big\|_E
\ \lesssim\ \sup_{1\leq n\leq N}\Big\|\sum_{k=1}^na_ke_k\Big\|_E
= \Big\|\sum_{k=1}^Na_k\mathbf{e}_k\Big\|_\mathrm{s\text{-}max}
\end{eqnarray*} for all ![]() $|\lambda_k|\leq 1.$ For any
$|\lambda_k|\leq 1.$ For any ![]() $a\in W\mathrm{^{s\text{-}max}},$ let
$a\in W\mathrm{^{s\text{-}max}},$ let  $\widetilde{P}_Na = \sum_{k=1}^Na_k\mathbf{e}_k,$ then
$\widetilde{P}_Na = \sum_{k=1}^Na_k\mathbf{e}_k,$ then
 \begin{eqnarray*}
\|a\|_\mathrm{s\text{-}max}=\sup_{N\geq 1}\Big\|\sum_{k=1}^Na_ke_k\Big\|_E\ = \ \lim_{N\to\infty}
\sup_{1\leq n\leq N}\Big\|\sum_{k=1}^na_ke_k\Big\|_E
= \lim_{N\to\infty}\Big\|\widetilde{P}_Na \Big\|_\mathrm{s\text{-}max}.
\end{eqnarray*}
\begin{eqnarray*}
\|a\|_\mathrm{s\text{-}max}=\sup_{N\geq 1}\Big\|\sum_{k=1}^Na_ke_k\Big\|_E\ = \ \lim_{N\to\infty}
\sup_{1\leq n\leq N}\Big\|\sum_{k=1}^na_ke_k\Big\|_E
= \lim_{N\to\infty}\Big\|\widetilde{P}_Na \Big\|_\mathrm{s\text{-}max}.
\end{eqnarray*} So ![]() $\{\mathbf{e}_n\}_{n\geq 1}$ is a solid frame for
$\{\mathbf{e}_n\}_{n\geq 1}$ is a solid frame for ![]() $W^\mathrm{s\text{-}max}.$
$W^\mathrm{s\text{-}max}.$
(ii) Since ![]() $\{e_n\}_{n\geq 1}$ is a Schauder basis for W, there exists a coefficient map
$\{e_n\}_{n\geq 1}$ is a Schauder basis for W, there exists a coefficient map ![]() $\mathcal{T}_1: W \to W^\mathrm{s\text{-}max}$ with
$\mathcal{T}_1: W \to W^\mathrm{s\text{-}max}$ with ![]() $\mathcal{T}_1 x=\big((\mathcal{T} x)_1, \cdots, (\mathcal{T} x)_n, \cdots \big),$ and
$\mathcal{T}_1 x=\big((\mathcal{T} x)_1, \cdots, (\mathcal{T} x)_n, \cdots \big),$ and  $\sum\limits_{n=1}^{N}(\mathcal{T}_1 x)_ne_n$ converges to x in
$\sum\limits_{n=1}^{N}(\mathcal{T}_1 x)_ne_n$ converges to x in ![]() $W.$ By [Reference Li and Queffélec25, Theorem II.3, p. 48],
$W.$ By [Reference Li and Queffélec25, Theorem II.3, p. 48],
 \begin{equation*}
\|x\|_{E}\ \approx \ \sup_{N\geq1}\bigg\|\sum\limits_{n=1}^{N}(\mathcal{T}_1 x)_ne_n\bigg\|_E\ = \ \Big\|\big((\mathcal{T}_1 x)_n\big)_{n\geq1}\Big\|_\mathrm{s\text{-}max}.
\end{equation*}
\begin{equation*}
\|x\|_{E}\ \approx \ \sup_{N\geq1}\bigg\|\sum\limits_{n=1}^{N}(\mathcal{T}_1 x)_ne_n\bigg\|_E\ = \ \Big\|\big((\mathcal{T}_1 x)_n\big)_{n\geq1}\Big\|_\mathrm{s\text{-}max}.
\end{equation*} For each ![]() $(\theta_n)_{n\geq1}\in\{-1, 1\}^{\mathbb{N}},$ since
$(\theta_n)_{n\geq1}\in\{-1, 1\}^{\mathbb{N}},$ since ![]() $\{\mathbf{e}_n\}_{n\geq 1}$ is a solid frame for
$\{\mathbf{e}_n\}_{n\geq 1}$ is a solid frame for ![]() $W^\mathrm{s\text{-}max},$ one has
$W^\mathrm{s\text{-}max},$ one has
 \begin{eqnarray*}
\bigg\|\sum\limits_{n=N+1}^{M}\theta_n(\mathcal{T}_1 x)_ne_n\bigg\|_E
&\lesssim&\bigg\|\sum_{n=N+1}^{M}(\mathcal{T}_1 x)_n\mathbf{e}_n\bigg\|_\mathrm{s\text{-}max}
\approx\bigg\|\sum\limits_{n=N+1}^{M}(\mathcal{T}_1 x)_ne_n\bigg\|_E,
\end{eqnarray*}
\begin{eqnarray*}
\bigg\|\sum\limits_{n=N+1}^{M}\theta_n(\mathcal{T}_1 x)_ne_n\bigg\|_E
&\lesssim&\bigg\|\sum_{n=N+1}^{M}(\mathcal{T}_1 x)_n\mathbf{e}_n\bigg\|_\mathrm{s\text{-}max}
\approx\bigg\|\sum\limits_{n=N+1}^{M}(\mathcal{T}_1 x)_ne_n\bigg\|_E,
\end{eqnarray*} where ![]() $M \gt N.$ So
$M \gt N.$ So  $\sum\limits_{n=1}^{N}(\mathcal{T}_1 x)_ne_n$ converges unconditionally in
$\sum\limits_{n=1}^{N}(\mathcal{T}_1 x)_ne_n$ converges unconditionally in ![]() $W,$ as desired.
$W,$ as desired.
Proof of Proposition 14
(i) In order to show that ![]() $\{e_n\}_{n\geq 1}$ is a Schauder basis for
$\{e_n\}_{n\geq 1}$ is a Schauder basis for ![]() $E_{\mathcal{P}}$, we shall prove that for
$E_{\mathcal{P}}$, we shall prove that for ![]() $x\in E,$
$x\in E,$ ![]() $
\lim_{N\to\infty}P_N(x)=x \Longleftrightarrow x\in E_{\mathcal{P}}.
$ It suffices to show the sufficiency. Assume that
$
\lim_{N\to\infty}P_N(x)=x \Longleftrightarrow x\in E_{\mathcal{P}}.
$ It suffices to show the sufficiency. Assume that  $\lim\limits_{n\to\infty}x_n=x$ for
$\lim\limits_{n\to\infty}x_n=x$ for  $x_n=\sum_{j=1}^{k_n}c_{j}^{(n)}e_j,$ where
$x_n=\sum_{j=1}^{k_n}c_{j}^{(n)}e_j,$ where  $c_{j}^{(n)}\in \mathbb{C}.$ For
$c_{j}^{(n)}\in \mathbb{C}.$ For ![]() $\epsilon \gt 0,$ take n large enough so that
$\epsilon \gt 0,$ take n large enough so that ![]() $
\|x_n-x\|_E \lt \epsilon.
$ For any
$
\|x_n-x\|_E \lt \epsilon.
$ For any ![]() $N \gt k_n,$
$N \gt k_n,$ ![]() $
\|P_Nx -x\|_E \leq \|P_Nx-P_Nx_n\|_E+\|P_Nx_n-x_n\|_E+\|x_n-x\|_E \leq 2\epsilon.
$ Now the conclusion follows from [Reference Li and Queffélec25, Proposition III.3, p. 91] and Definition 1. The proof of part (ii) for p-Banach spaces follows from [Reference Albiac, Ansorena, Berná and Wojtaszczyk1, Theorem 1.10], together with a straightforward modification of the arguments in part (i).
$
\|P_Nx -x\|_E \leq \|P_Nx-P_Nx_n\|_E+\|P_Nx_n-x_n\|_E+\|x_n-x\|_E \leq 2\epsilon.
$ Now the conclusion follows from [Reference Li and Queffélec25, Proposition III.3, p. 91] and Definition 1. The proof of part (ii) for p-Banach spaces follows from [Reference Albiac, Ansorena, Berná and Wojtaszczyk1, Theorem 1.10], together with a straightforward modification of the arguments in part (i).
Proof of Proposition 15
If ![]() $f\in \mathcal{X}^\mathrm{max},$ then
$f\in \mathcal{X}^\mathrm{max},$ then ![]() $
\|f\|_{\mathcal{X}_T}\ =\ \sup_{N\geq 0}\|S_Nf\|_{\mathcal{X}} \ \approx\ \|f\|_\mathrm{max},
$ where ‘≈’ can be strengthened to an equality, by (6), if
$
\|f\|_{\mathcal{X}_T}\ =\ \sup_{N\geq 0}\|S_Nf\|_{\mathcal{X}} \ \approx\ \|f\|_\mathrm{max},
$ where ‘≈’ can be strengthened to an equality, by (6), if ![]() $\mathcal{X}$ is a Banach space. Hence,
$\mathcal{X}$ is a Banach space. Hence, ![]() $f\in \mathcal{X}_T.$ Conversely, let
$f\in \mathcal{X}_T.$ Conversely, let ![]() $f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{X}_T.$ We claim that
$f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{X}_T.$ We claim that ![]() $f_r\in \mathcal{X}$ for
$f_r\in \mathcal{X}$ for ![]() $0\leq r \lt 1.$ It suffices to show that
$0\leq r \lt 1.$ It suffices to show that  $\Big\{\sum_{k=0}^na_kr^kz^k\Big\}_{n\geq 0}$ is a Cauchy sequence in
$\Big\{\sum_{k=0}^na_kr^kz^k\Big\}_{n\geq 0}$ is a Cauchy sequence in ![]() $\mathcal{X}.$ Since
$\mathcal{X}.$ Since  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for ![]() $\mathcal{X}_{\mathcal{P}},$ by [Reference Li and Queffélec25, Proposition III.5, p. 92] or [Reference Albiac, Ansorena, Berná and Wojtaszczyk1, Theorem 1.10], for
$\mathcal{X}_{\mathcal{P}},$ by [Reference Li and Queffélec25, Proposition III.5, p. 92] or [Reference Albiac, Ansorena, Berná and Wojtaszczyk1, Theorem 1.10], for ![]() $m \gt n,$
$m \gt n,$
 \begin{equation*}
\Big\|\sum_{k=n}^ma_kr^kz^k\Big\|_{\mathcal{X}} \lesssim r^n\Big\|\sum_{k=n}^ma_kz^k\Big\|_{\mathcal{X}}
\lesssim r^n\sup_{N\geq 0}\Big\|\sum_{k=0}^Na_kz^k\Big\|_{\mathcal{X}} \lesssim r^n\|f\|_{\mathcal{X}_T} \to 0
\end{equation*}
\begin{equation*}
\Big\|\sum_{k=n}^ma_kr^kz^k\Big\|_{\mathcal{X}} \lesssim r^n\Big\|\sum_{k=n}^ma_kz^k\Big\|_{\mathcal{X}}
\lesssim r^n\sup_{N\geq 0}\Big\|\sum_{k=0}^Na_kz^k\Big\|_{\mathcal{X}} \lesssim r^n\|f\|_{\mathcal{X}_T} \to 0
\end{equation*} as ![]() $n\to\infty.$ Then,
$n\to\infty.$ Then, ![]() $f\in \mathcal{X}^\mathrm{max}$.
$f\in \mathcal{X}^\mathrm{max}$.
Example. For ![]() $0 \lt p \lt \infty,$ recall that
$0 \lt p \lt \infty,$ recall that ![]() $H^p,$
$H^p,$ ![]() $L_a^p,$
$L_a^p,$ ![]() $\mathcal{D}^p$,
$\mathcal{D}^p$, ![]() $\mathcal{B}$ and
$\mathcal{B}$ and ![]() $A(\mathbb{D})$ denote the Hardy space, the Bergman space, the Dirichet space, the Bloch space and the disk algebra, respectively. If
$A(\mathbb{D})$ denote the Hardy space, the Bergman space, the Dirichet space, the Bloch space and the disk algebra, respectively. If ![]() $\mathcal{X}=H^p, L_a^p, $ or
$\mathcal{X}=H^p, L_a^p, $ or ![]() $\mathcal{D}^{p}$, with
$\mathcal{D}^{p}$, with ![]() $1 \lt p \lt \infty,$ then
$1 \lt p \lt \infty,$ then ![]() $
\mathcal{X}_T=\mathcal{X}^\mathrm{max}=\mathcal{X}.
$ On the other hand, if
$
\mathcal{X}_T=\mathcal{X}^\mathrm{max}=\mathcal{X}.
$ On the other hand, if ![]() $\mathcal{X} = H^{\infty}, \mathcal{B}, \text{BMOA}, H^1, L_a^1,$ or
$\mathcal{X} = H^{\infty}, \mathcal{B}, \text{BMOA}, H^1, L_a^1,$ or ![]() $ A(\mathbb{D}),$ then
$ A(\mathbb{D}),$ then ![]() $
\mathcal{X}_T\subsetneq \mathcal{X}^\mathrm{max}=\mathcal{X}
$ since there exists
$
\mathcal{X}_T\subsetneq \mathcal{X}^\mathrm{max}=\mathcal{X}
$ since there exists ![]() $f_0\in \mathcal{X}$ such that
$f_0\in \mathcal{X}$ such that ![]() $\|S_Nf_0\|_{\mathcal{X}}\to \infty$ as
$\|S_Nf_0\|_{\mathcal{X}}\to \infty$ as ![]() $N\to\infty.$ See [Reference Bennett, Stegenga and Timoney5, Reference Zhu43] for more details.
$N\to\infty.$ See [Reference Bennett, Stegenga and Timoney5, Reference Zhu43] for more details.
Problem B. To characterize homogeneous ![]() $\mathcal{X}$ such that
$\mathcal{X}$ such that ![]() $\mathcal{X}^\mathrm{max}=\mathcal{X}_T$.
$\mathcal{X}^\mathrm{max}=\mathcal{X}_T$.
Remark. Let ![]() $\phi_n(x)=(\mathcal{T} x)_n,\ x\in E,$ the coordinate functional, if
$\phi_n(x)=(\mathcal{T} x)_n,\ x\in E,$ the coordinate functional, if ![]() $\{e_n\}_{n\geq1}$ form a solid basis for E, then
$\{e_n\}_{n\geq1}$ form a solid basis for E, then ![]() $\{\phi_n\}_{n\geq1}$ form an unconditional basic sequence in
$\{\phi_n\}_{n\geq1}$ form an unconditional basic sequence in ![]() $E^\ast$; that is,
$E^\ast$; that is, ![]() $\{\phi_n\}_{n\geq1}$ form an unconditional basis for
$\{\phi_n\}_{n\geq1}$ form an unconditional basis for ![]() $\overline{\text{span}}\big\{\phi_n: n\geq1\big\}.$
$\overline{\text{span}}\big\{\phi_n: n\geq1\big\}.$
Remark. Let ![]() $\mathcal{X}$ be a Banach space of analytic functions over
$\mathcal{X}$ be a Banach space of analytic functions over ![]() $\mathbb{D}$ with
$\mathbb{D}$ with  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ as a solid basis. If
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ as a solid basis. If ![]() $\mathcal{X}={\mathcal{Y}}^{\ast}$ for some separable Banach space
$\mathcal{X}={\mathcal{Y}}^{\ast}$ for some separable Banach space ![]() $\mathcal{Y}$ of analytic functions over
$\mathcal{Y}$ of analytic functions over ![]() $\mathbb{D}.$ Then,
$\mathbb{D}.$ Then, ![]() $\mathcal{X}=\mathcal{X}_T.$ It suffices to show that
$\mathcal{X}=\mathcal{X}_T.$ It suffices to show that ![]() $\mathcal{X}_T\subset \mathcal{X}.$ Let
$\mathcal{X}_T\subset \mathcal{X}.$ Let ![]() $f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{X}_T.$ Then,
$f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{X}_T.$ Then,  $
\sup_{N\geq 1}\Big\|\sum_{n=0}^Na_nz^n\Big\|_{\mathcal{X}} \lt \infty.
$ Since
$
\sup_{N\geq 1}\Big\|\sum_{n=0}^Na_nz^n\Big\|_{\mathcal{X}} \lt \infty.
$ Since ![]() $\mathcal{Y}$ is separable, the
$\mathcal{Y}$ is separable, the ![]() $w^{\ast}$-topology on
$w^{\ast}$-topology on ![]() $\mathcal{X}$ is metrizable. The Banach–Alaoglu theorem implies that there exists a subsequence
$\mathcal{X}$ is metrizable. The Banach–Alaoglu theorem implies that there exists a subsequence ![]() $\{N_k\}_{k\geq 1}$ such that
$\{N_k\}_{k\geq 1}$ such that  $
f_k=\sum_{n=0}^{N_k}a_nz^{n}
$ converges to some
$
f_k=\sum_{n=0}^{N_k}a_nz^{n}
$ converges to some ![]() $f\in \mathcal{X}$ in
$f\in \mathcal{X}$ in ![]() $w^{\ast}$-topology. By [Reference Brown and Shields9],
$w^{\ast}$-topology. By [Reference Brown and Shields9], ![]() $f_k(z)\to f(z)$ as
$f_k(z)\to f(z)$ as ![]() $k\to\infty.$ Then, for each fixed
$k\to\infty.$ Then, for each fixed ![]() $n,$ it can be checked that the nth Taylor coefficient of f is
$n,$ it can be checked that the nth Taylor coefficient of f is ![]() $a_n,$ as desired.
$a_n,$ as desired.
6. Weak-star convergence of Taylor polynomials
In this section, we prove Theorem D, which states that, in the presence of a solid basis, Taylor polynomials are ![]() $w^{\ast}$-convergent in the double dual. When
$w^{\ast}$-convergent in the double dual. When ![]() $E=E_{\mathcal{P}}$, Proposition 14 implies that the Taylor polynomials converge in norm. Hence, the strength of Theorem D lies in the non-separable case.
$E=E_{\mathcal{P}}$, Proposition 14 implies that the Taylor polynomials converge in norm. Hence, the strength of Theorem D lies in the non-separable case.
For any homogeneous functional Banach space ![]() $\mathcal{X},$ the Taylor polynomials are certainly pointwisely convergent, hence locally uniformly convergent by the principle of uniform boundedness. When
$\mathcal{X},$ the Taylor polynomials are certainly pointwisely convergent, hence locally uniformly convergent by the principle of uniform boundedness. When ![]() $\mathcal{X}=\mathcal{X}_{\mathcal{P}}$, the norm convergence of Taylor polynomials, which is equivalent to the weak convergence, is well understood; indeed, the following are equivalent:
$\mathcal{X}=\mathcal{X}_{\mathcal{P}}$, the norm convergence of Taylor polynomials, which is equivalent to the weak convergence, is well understood; indeed, the following are equivalent:
(i)
 $\{S_Nf\}_{N\geq 0}$ converges in norm for each
$\{S_Nf\}_{N\geq 0}$ converges in norm for each  $f\in \mathcal{X};$
$f\in \mathcal{X};$(ii)
 $\{S_Nf\}_{N\geq 0}$ converges in w-topology for each
$\{S_Nf\}_{N\geq 0}$ converges in w-topology for each  $f\in \mathcal{X};$
$f\in \mathcal{X};$(iii)
 $\sup_{N\geq 0}\|S_N\| \lt \infty.$
$\sup_{N\geq 0}\|S_N\| \lt \infty.$
We only need to check (ii) ![]() $\Rightarrow$ (iii) since the equivalence between (i) and (iii) follows from Proposition 1 in [Reference Zhu43]. It suffices to observe that the partial summation operator SN is bounded for each
$\Rightarrow$ (iii) since the equivalence between (i) and (iii) follows from Proposition 1 in [Reference Zhu43]. It suffices to observe that the partial summation operator SN is bounded for each ![]() $N \in \mathbb{N}$, for then the implication follows from the principle of uniform boundedness. Since the coefficient functionals are continuous,
$N \in \mathbb{N}$, for then the implication follows from the principle of uniform boundedness. Since the coefficient functionals are continuous,
 \begin{equation*}
\|S_Nf\|_{\mathcal{X}}
\leq \sum_{n=0}^N |a_n|\|z^n\|_{\mathcal{X}}
\leq \sum_{n=0}^Nc_n\|f\|_{\mathcal{X}}\|z^n\|_{\mathcal{X}}
= \Big(\sum_{n=0}^Nc_n\|z^n\|_{\mathcal{X}}\Big)\|f\|_{\mathcal{X}}
\end{equation*}
\begin{equation*}
\|S_Nf\|_{\mathcal{X}}
\leq \sum_{n=0}^N |a_n|\|z^n\|_{\mathcal{X}}
\leq \sum_{n=0}^Nc_n\|f\|_{\mathcal{X}}\|z^n\|_{\mathcal{X}}
= \Big(\sum_{n=0}^Nc_n\|z^n\|_{\mathcal{X}}\Big)\|f\|_{\mathcal{X}}
\end{equation*} for some positive sequence ![]() $\{c_n\}_{n\geq 0}.$
$\{c_n\}_{n\geq 0}.$
If ![]() $\mathcal{X} = \mathcal{Y}^*$ for some separable Banach space
$\mathcal{X} = \mathcal{Y}^*$ for some separable Banach space ![]() $\mathcal{Y}$, and still assuming that
$\mathcal{Y}$, and still assuming that ![]() $\mathcal{X}=\mathcal{X}_{\mathcal{P}}$, then
$\mathcal{X}=\mathcal{X}_{\mathcal{P}}$, then ![]() $\{S_Nf\}_{N\geq 0}$ is
$\{S_Nf\}_{N\geq 0}$ is ![]() $w^{\ast}$-convergent if and only if
$w^{\ast}$-convergent if and only if ![]() $\{S_Nf\}_{N\geq 0}$ converges uniformly on compacta in
$\{S_Nf\}_{N\geq 0}$ converges uniformly on compacta in ![]() $\mathbb{D}$ and
$\mathbb{D}$ and ![]() $\sup_{N\geq 0}\|S_N\| \lt \infty$; see [Reference Brown and Shields9].
$\sup_{N\geq 0}\|S_N\| \lt \infty$; see [Reference Brown and Shields9].
If ![]() $\mathcal{X}\ne \mathcal{X}_{\mathcal{P}}$, then almost nothing affirmative is known about the convergence of Taylor polynomials, at least from a Banach space viewpoint. For instance, in
$\mathcal{X}\ne \mathcal{X}_{\mathcal{P}}$, then almost nothing affirmative is known about the convergence of Taylor polynomials, at least from a Banach space viewpoint. For instance, in ![]() $H^\infty$, the Taylor polynomials are not convergent in norm, w-topology or
$H^\infty$, the Taylor polynomials are not convergent in norm, w-topology or ![]() $w^{\ast}$-topology.
$w^{\ast}$-topology.
Proof of Theorem D
Let ![]() $\{e_n\}_{n\geq 1}$ be a solid basis for a Banach space
$\{e_n\}_{n\geq 1}$ be a solid basis for a Banach space ![]() $E.$ Then, for any
$E.$ Then, for any ![]() $x\in E$ and
$x\in E$ and ![]() $\phi\in E^{\ast},$ we claim that
$\phi\in E^{\ast},$ we claim that
 \begin{equation}
\sum_{n=1}^{\infty}|(\mathcal{T} x)_n||\phi (e_n)| \lt \infty.
\end{equation}
\begin{equation}
\sum_{n=1}^{\infty}|(\mathcal{T} x)_n||\phi (e_n)| \lt \infty.
\end{equation} Indeed, by (i) of Definition 1, for every finite subset ![]() $\sigma,$
$\sigma,$  $
\sup\limits_{\theta_n=\pm 1}\big\|\sum\limits_{n\in\sigma}\theta_n(\mathcal{T} x)_ne_n\big\|_E\leq \|x\|_E.
$ Let
$
\sup\limits_{\theta_n=\pm 1}\big\|\sum\limits_{n\in\sigma}\theta_n(\mathcal{T} x)_ne_n\big\|_E\leq \|x\|_E.
$ Let ![]() $N\geq 1.$ Set
$N\geq 1.$ Set
 \begin{equation*}
\theta_n=
\begin{cases}
1,& \text{Re} \ \phi((\mathcal{T} x)_ne_n)\geq 0;\\
-1,& \text{Re}\ \phi((\mathcal{T} x)_ne_n) \lt 0.
\end{cases}
\end{equation*}
\begin{equation*}
\theta_n=
\begin{cases}
1,& \text{Re} \ \phi((\mathcal{T} x)_ne_n)\geq 0;\\
-1,& \text{Re}\ \phi((\mathcal{T} x)_ne_n) \lt 0.
\end{cases}
\end{equation*}Similarly, set
 \begin{equation*}
\theta_n'=
\begin{cases}
1,& \text{Im} \ \phi((\mathcal{T} x)_ne_n)\geq 0;\\
-1,& \text{Im} \ \phi ((\mathcal{T} x)_ne_n) \lt 0.
\end{cases}
\end{equation*}
\begin{equation*}
\theta_n'=
\begin{cases}
1,& \text{Im} \ \phi((\mathcal{T} x)_ne_n)\geq 0;\\
-1,& \text{Im} \ \phi ((\mathcal{T} x)_ne_n) \lt 0.
\end{cases}
\end{equation*}Then,
 \begin{eqnarray*}
\sum_{n=1}^N|\phi((\mathcal{T} x)_ne_n)|&\leq& \sum_{n=1}^N|\text{Re}\ \phi((\mathcal{T} x)_ne_n)|+\sum_{n=1}^N|\text{Im}\ \phi((\mathcal{T} x)_ne_n)|\\
&\leq& \|\phi\|_{E^{\ast}}\Big\|\sum_{n=1}^N\theta_n(\mathcal{T} x)_ne_n\Big\|_E+ \|\phi\|_{E^{\ast}}\Big\|\sum_{n=1}^N\theta_n'(\mathcal{T} x)_ne_n\Big\|_E\\
&\leq&2\|\phi\|_{E^{\ast}}\|x\|_E.
\end{eqnarray*}
\begin{eqnarray*}
\sum_{n=1}^N|\phi((\mathcal{T} x)_ne_n)|&\leq& \sum_{n=1}^N|\text{Re}\ \phi((\mathcal{T} x)_ne_n)|+\sum_{n=1}^N|\text{Im}\ \phi((\mathcal{T} x)_ne_n)|\\
&\leq& \|\phi\|_{E^{\ast}}\Big\|\sum_{n=1}^N\theta_n(\mathcal{T} x)_ne_n\Big\|_E+ \|\phi\|_{E^{\ast}}\Big\|\sum_{n=1}^N\theta_n'(\mathcal{T} x)_ne_n\Big\|_E\\
&\leq&2\|\phi\|_{E^{\ast}}\|x\|_E.
\end{eqnarray*} So the claim (8) holds. Then,  $
\sum\limits_{n=1}^{\infty}(\mathcal{T} x)_n (Je_n)(\phi)
$ exists. Let
$
\sum\limits_{n=1}^{\infty}(\mathcal{T} x)_n (Je_n)(\phi)
$ exists. Let
 \begin{equation*}
\Psi(\phi)\doteq\sum_{n=1}^{\infty}(\mathcal{T} x)_n(Je_n)(\phi)
=\sum_{n=1}^{\infty}(\mathcal{T} x)_n(\phi e_n),
\end{equation*}
\begin{equation*}
\Psi(\phi)\doteq\sum_{n=1}^{\infty}(\mathcal{T} x)_n(Je_n)(\phi)
=\sum_{n=1}^{\infty}(\mathcal{T} x)_n(\phi e_n),
\end{equation*} and then  $
\sum_{n=1}^{N}(\mathcal{T} x)_n (Je_n) = J(P_Nx)
$ converges to Ψ in
$
\sum_{n=1}^{N}(\mathcal{T} x)_n (Je_n) = J(P_Nx)
$ converges to Ψ in ![]() $w^{\ast}$-topology.
$w^{\ast}$-topology.
We let ![]() $\mathfrak {J}(x)$ denote the limit element
$\mathfrak {J}(x)$ denote the limit element ![]() $\Psi \in E^{\ast\ast},$ so we have a map
$\Psi \in E^{\ast\ast},$ so we have a map ![]() $\mathfrak {J}: \ E\longrightarrow E^{\ast\ast}$ which is easily seen to satisfy:
$\mathfrak {J}: \ E\longrightarrow E^{\ast\ast}$ which is easily seen to satisfy: ![]() $\|\mathfrak {J}\|=1,$ and
$\|\mathfrak {J}\|=1,$ and ![]() $\mathfrak {J}$ is injective. It appears interesting to compare this map with the canonical embedding
$\mathfrak {J}$ is injective. It appears interesting to compare this map with the canonical embedding ![]() $J: E \to E^{\ast\ast}$.
$J: E \to E^{\ast\ast}$.
Proposition 17. Let E be a Banach space with a solid basis ![]() $\{e_n\}_{n\geq 1}.$
$\{e_n\}_{n\geq 1}.$
(i)
 $J(x)=\mathfrak {J}(x)$ if and only if
$J(x)=\mathfrak {J}(x)$ if and only if  $x\in E_{\mathcal{P}}.$
$x\in E_{\mathcal{P}}.$(ii) If
 $E_{\mathcal{P}}\subsetneq E,$ then
$E_{\mathcal{P}}\subsetneq E,$ then  $\overline{\mathfrak {J} E}^{w^{\ast}}$ is a proper subspace in
$\overline{\mathfrak {J} E}^{w^{\ast}}$ is a proper subspace in  $E^{\ast\ast}$.
$E^{\ast\ast}$.
Remark. For the canonical map ![]() $J,$ it is known that
$J,$ it is known that  $\overline{JE}^{w^{\ast}}=E^{\ast\ast}.$
$\overline{JE}^{w^{\ast}}=E^{\ast\ast}.$
Proof. (i) Let ![]() $x\in E_{\mathcal{P}}.$ Then
$x\in E_{\mathcal{P}}.$ Then  $\lim\limits_{N\to\infty}P_Nx=x$ by Proposition 14. For
$\lim\limits_{N\to\infty}P_Nx=x$ by Proposition 14. For ![]() $\phi\in E^{\ast},$
$\phi\in E^{\ast},$
 \begin{equation*}
(Jx)(\phi)=\phi(x)\quad \text{and}\quad (\mathfrak {J} x)(\phi)=\lim_{N\to\infty}\phi(P_Nx)=\phi(x).
\end{equation*}
\begin{equation*}
(Jx)(\phi)=\phi(x)\quad \text{and}\quad (\mathfrak {J} x)(\phi)=\lim_{N\to\infty}\phi(P_Nx)=\phi(x).
\end{equation*} So ![]() $J(x)=\mathfrak {J}(x).$ Conversely, let
$J(x)=\mathfrak {J}(x).$ Conversely, let ![]() $x\in E\setminus E_{\mathcal{P}}.$ By the Hahn-Banach theorem there exists a nonzero
$x\in E\setminus E_{\mathcal{P}}.$ By the Hahn-Banach theorem there exists a nonzero ![]() $\phi\in E^{\ast}$ such that
$\phi\in E^{\ast}$ such that  $\phi|_{E_{\mathcal{P}}}=0, \ \text{and} \ \phi(x)\neq 0.$ Then,
$\phi|_{E_{\mathcal{P}}}=0, \ \text{and} \ \phi(x)\neq 0.$ Then, ![]() $
(\mathfrak {J} x)(\phi)=0,
$ and
$
(\mathfrak {J} x)(\phi)=0,
$ and ![]() $
(Jx)(\phi)=\phi(x)\neq 0.
$ (ii) Recall that
$
(Jx)(\phi)=\phi(x)\neq 0.
$ (ii) Recall that  $\overline{\mathfrak {J} E}^{w^{\ast}}=(^{\perp}\mathfrak {J} E)^{\perp}$ [Reference Rudin37, Theorem 4.7, p. 96], where ‘
$\overline{\mathfrak {J} E}^{w^{\ast}}=(^{\perp}\mathfrak {J} E)^{\perp}$ [Reference Rudin37, Theorem 4.7, p. 96], where ‘![]() $\perp$’ denotes the annihilators. We claim that
$\perp$’ denotes the annihilators. We claim that  $^{\perp}(\mathfrak {J} E)=\big\{\phi\in E^{\ast}:\ \phi|_{E_{\mathcal{P}}}=0\big\}.$ If
$^{\perp}(\mathfrak {J} E)=\big\{\phi\in E^{\ast}:\ \phi|_{E_{\mathcal{P}}}=0\big\}.$ If  $\phi\in \big\{\phi\in E^{\ast}:\ \phi|_{E_{\mathcal{P}}}=0\big\},$ then, for each
$\phi\in \big\{\phi\in E^{\ast}:\ \phi|_{E_{\mathcal{P}}}=0\big\},$ then, for each ![]() $x\in E,$
$x\in E,$  $
(\mathfrak {J} x)\phi=\lim\limits_{N\to\infty}\phi(P_Nx)=0.
$ So
$
(\mathfrak {J} x)\phi=\lim\limits_{N\to\infty}\phi(P_Nx)=0.
$ So ![]() $\phi\in ^{\perp}(\mathfrak {J} E).$ Conversely, let
$\phi\in ^{\perp}(\mathfrak {J} E).$ Conversely, let ![]() $\phi\in ^{\perp}(\mathfrak {J} E).$ Let
$\phi\in ^{\perp}(\mathfrak {J} E).$ Let  $x=\lim\limits_{n\to \infty} x_n \in E_{\mathcal{P}}$ with xn being a finite linear combination of
$x=\lim\limits_{n\to \infty} x_n \in E_{\mathcal{P}}$ with xn being a finite linear combination of ![]() $\{e_n\}_{n\geq 1}.$ For each
$\{e_n\}_{n\geq 1}.$ For each ![]() $n,$
$n,$  $
\phi(x_n)=\lim\limits_{N\to\infty}\phi(P_Nx_n)=0.
$ So the claim holds. It follows that
$
\phi(x_n)=\lim\limits_{N\to\infty}\phi(P_Nx_n)=0.
$ So the claim holds. It follows that  $
\big\{\phi\in E^{\ast}:\ \phi|_{E_{\mathcal{P}}}=0\big\}=^{\perp}(J E_{\mathcal{P}}).
$ Then,
$
\big\{\phi\in E^{\ast}:\ \phi|_{E_{\mathcal{P}}}=0\big\}=^{\perp}(J E_{\mathcal{P}}).
$ Then,
 \begin{equation*}
\overline{\mathfrak {J} E}^{w^{\ast}}=\overline{J E_{\mathcal{P}}}^{w^{\ast}}=\big(^{\perp}(J E_{\mathcal{P}})\big)^{\perp}=\big(^{\perp}(\mathfrak {J} E_{\mathcal{P}})\big)^{\perp},
\end{equation*}
\begin{equation*}
\overline{\mathfrak {J} E}^{w^{\ast}}=\overline{J E_{\mathcal{P}}}^{w^{\ast}}=\big(^{\perp}(J E_{\mathcal{P}})\big)^{\perp}=\big(^{\perp}(\mathfrak {J} E_{\mathcal{P}})\big)^{\perp},
\end{equation*} where the last ‘=’ follows from (i). In other words,  $
\overline{\mathfrak {J} E}^{w^{\ast}}=(E_{\mathcal{P}})^{\perp\perp}.
$ Since
$
\overline{\mathfrak {J} E}^{w^{\ast}}=(E_{\mathcal{P}})^{\perp\perp}.
$ Since ![]() $E_{\mathcal{P}}\subsetneq E,$ we can take
$E_{\mathcal{P}}\subsetneq E,$ we can take ![]() $x_0\in E\setminus E_{\mathcal{P}}$ and choose, by Hahn–Banach, a nonzero
$x_0\in E\setminus E_{\mathcal{P}}$ and choose, by Hahn–Banach, a nonzero ![]() $\phi_0\in E^{\ast}$ such that
$\phi_0\in E^{\ast}$ such that  $\phi_0|_{E_{\mathcal{P}}}=0$ and
$\phi_0|_{E_{\mathcal{P}}}=0$ and ![]() $\phi_0(x_0)=1.$ Then,
$\phi_0(x_0)=1.$ Then, ![]() $Jx_0\in E^{\ast\ast},$ but
$Jx_0\in E^{\ast\ast},$ but ![]() $(Jx_0)\phi_0=\phi_0(x_0)=1,$ so
$(Jx_0)\phi_0=\phi_0(x_0)=1,$ so ![]() $Jx_0\in E^{\ast\ast}\setminus (E_{\mathcal{P}})^{\perp\perp},$ as desired.
$Jx_0\in E^{\ast\ast}\setminus (E_{\mathcal{P}})^{\perp\perp},$ as desired.
Example. We give an explicit example of ![]() $J\neq \mathfrak {J}$ via the so-called Banach limit. Let
$J\neq \mathfrak {J}$ via the so-called Banach limit. Let ![]() $E=\ell^{\infty}$. There exists a bounded linear functional φ on
$E=\ell^{\infty}$. There exists a bounded linear functional φ on ![]() $\ell^{\infty}$ [Reference Conway14, p. 82] (the Banach limit) such that
$\ell^{\infty}$ [Reference Conway14, p. 82] (the Banach limit) such that
(i)
 $\varphi S(x)=\varphi(x)$; and
$\varphi S(x)=\varphi(x)$; and(ii)
 $x\in c,\ \varphi(x)=\lim\limits_{n\to\infty}x_n,$
$x\in c,\ \varphi(x)=\lim\limits_{n\to\infty}x_n,$
where ![]() $S(x_1, x_2, \cdots)=(x_2, x_3, \cdots),$ and c is the collection of sequences in
$S(x_1, x_2, \cdots)=(x_2, x_3, \cdots),$ and c is the collection of sequences in ![]() $\mathfrak{S}$ having limits. By (i), one has
$\mathfrak{S}$ having limits. By (i), one has ![]() $
\varphi(x_1, x_2, \cdots, x_n, 0, 0, \cdots)=0.
$ Let
$
\varphi(x_1, x_2, \cdots, x_n, 0, 0, \cdots)=0.
$ Let ![]() $x\in c\setminus c_0.$ Then
$x\in c\setminus c_0.$ Then  $
(Jx)\varphi=\varphi(x)=\lim\limits_{n\to\infty}x_n\neq 0,
$ and,
$
(Jx)\varphi=\varphi(x)=\lim\limits_{n\to\infty}x_n\neq 0,
$ and,  $
(\mathfrak {J} x)\varphi=\lim\limits_{n\to\infty}\varphi(x_1, x_2, \cdots, x_n, 0, 0, \cdots)=0.
$ Hence,
$
(\mathfrak {J} x)\varphi=\lim\limits_{n\to\infty}\varphi(x_1, x_2, \cdots, x_n, 0, 0, \cdots)=0.
$ Hence, ![]() $J\neq \mathfrak {J}$ on
$J\neq \mathfrak {J}$ on ![]() $c\setminus c_0.$ Moreover, by the proof of Proposition 17 (ii),
$c\setminus c_0.$ Moreover, by the proof of Proposition 17 (ii),  $
\overline{\mathfrak {J} E}^{w^{\ast}}=c_0^{\perp\perp},
$ which is isometrically isomorphic to
$
\overline{\mathfrak {J} E}^{w^{\ast}}=c_0^{\perp\perp},
$ which is isometrically isomorphic to ![]() $c_0^{\ast\ast},$ which is
$c_0^{\ast\ast},$ which is ![]() $\ell^{\infty}.$ In other words,
$\ell^{\infty}.$ In other words,  $
c_0^{\perp\perp}\simeq \big((\ell^{\infty})^{\ast}/c_0^{\perp}\big)^{\ast}\simeq c_0^{\ast\ast}.
$
$
c_0^{\perp\perp}\simeq \big((\ell^{\infty})^{\ast}/c_0^{\perp}\big)^{\ast}\simeq c_0^{\ast\ast}.
$
Example. Here is another example on functional spaces. Let ![]() $E=\mathcal{B}_{\star}^{S},$ the symbol space of the Bloch space under the Steinhaus randomization. Fix a lacunary sequence
$E=\mathcal{B}_{\star}^{S},$ the symbol space of the Bloch space under the Steinhaus randomization. Fix a lacunary sequence ![]() $\{n_k\}_{k\geq 1},$ i.e.,
$\{n_k\}_{k\geq 1},$ i.e.,  $\inf_{k\geq1}\frac{n_{k+1}}{n_k} \gt 1,$ and let
$\inf_{k\geq1}\frac{n_{k+1}}{n_k} \gt 1,$ and let
 \begin{equation*}
A=\Big\{f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{B}_{\star}^{S}:\ \lim_{k\to\infty}a_{n_k}\ \text{exists}\Big\}.
\end{equation*}
\begin{equation*}
A=\Big\{f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{B}_{\star}^{S}:\ \lim_{k\to\infty}a_{n_k}\ \text{exists}\Big\}.
\end{equation*} Then, A is a subspace of ![]() $\mathcal{B}_{\star}^{S}.$ Define a bounded linear functional φ on A by
$\mathcal{B}_{\star}^{S}.$ Define a bounded linear functional φ on A by  $
\varphi(f)=\lim\limits_{k\to\infty}a_{n_k}.
$ Note that
$
\varphi(f)=\lim\limits_{k\to\infty}a_{n_k}.
$ Note that  $|a_{n_k}|\lesssim \|a_{n_k}z^{n_k}\|_{\mathcal{B}_{\star}^{S}}\leq \|f\|_{\mathcal{B}_{\star}^{S}}.$ The extension of φ to
$|a_{n_k}|\lesssim \|a_{n_k}z^{n_k}\|_{\mathcal{B}_{\star}^{S}}\leq \|f\|_{\mathcal{B}_{\star}^{S}}.$ The extension of φ to ![]() $\mathcal{B}_{\star}^{S}$ is still denoted by
$\mathcal{B}_{\star}^{S}$ is still denoted by ![]() $\varphi.$ Now take any
$\varphi.$ Now take any  $f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in A$ with
$f(z)=\sum\limits_{n=0}^{\infty}a_nz^n\in A$ with  $\lim\limits_{k\to\infty}a_{n_k}\neq 0$. Then
$\lim\limits_{k\to\infty}a_{n_k}\neq 0$. Then  $
(Jf)(\varphi)=\varphi(f)=\lim\limits_{k\to\infty}a_{n_k}\neq 0
$ and
$
(Jf)(\varphi)=\varphi(f)=\lim\limits_{k\to\infty}a_{n_k}\neq 0
$ and  $
(\mathfrak {J} f)(\varphi)=\lim\limits_{N\to\infty}\varphi\Big(\sum\limits_{n=0}^Na_nz^n\Big)=0.
$
$
(\mathfrak {J} f)(\varphi)=\lim\limits_{N\to\infty}\varphi\Big(\sum\limits_{n=0}^Na_nz^n\Big)=0.
$
7. Transforming solid frames into solid bases
Proof of Theorem E
We shall prove that the following are equivalent:
(i)
 $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for  $\mathcal{X}.$
$\mathcal{X}.$(ii)
 $\|f\|_{\sharp}\approx \|f\|_{\mathcal{X}}, \ f\in\mathcal{X}.$
$\|f\|_{\sharp}\approx \|f\|_{\mathcal{X}}, \ f\in\mathcal{X}.$(iii) For each
 $f\in \mathcal{X},$
$f\in \mathcal{X},$  $\|f\|_{\sharp} \lt \infty.$
$\|f\|_{\sharp} \lt \infty.$(iv)
 $(\mathcal{X}, \|\cdot\|_{\sharp})$ is a Banach space (or p-Banach space), and
$(\mathcal{X}, \|\cdot\|_{\sharp})$ is a Banach space (or p-Banach space), and  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for  $(\mathcal{X}, \|\cdot\|_{\sharp}).$
$(\mathcal{X}, \|\cdot\|_{\sharp}).$
Also we only prove the Banach space case since it takes only a straightforward modification to treat p-Banach spaces. (i) ![]() $\Rightarrow$ (iii) is clear. Now, (iii)
$\Rightarrow$ (iii) is clear. Now, (iii) ![]() $\Rightarrow$ (iv). Since
$\Rightarrow$ (iv). Since ![]() $\mathcal{X}$ is of homogeneous type,
$\mathcal{X}$ is of homogeneous type,
 \begin{equation}
\|f\|_{\mathcal{X}}=\lim_{r\to 1^-}\|f_r\|_{\mathcal{X}}
\leq \sup_{N\geq 0}\sup_{0\leq r \lt 1} \Big\|\sum_{k=0}^Na_kr^kz^k\Big\|_{\mathcal{X}} \leq \|f\|_{\sharp}.
\end{equation}
\begin{equation}
\|f\|_{\mathcal{X}}=\lim_{r\to 1^-}\|f_r\|_{\mathcal{X}}
\leq \sup_{N\geq 0}\sup_{0\leq r \lt 1} \Big\|\sum_{k=0}^Na_kr^kz^k\Big\|_{\mathcal{X}} \leq \|f\|_{\sharp}.
\end{equation} It suffices to show that ![]() $(\mathcal{X}, \|\cdot\|_{\sharp})$ is a Banach space. Let
$(\mathcal{X}, \|\cdot\|_{\sharp})$ is a Banach space. Let ![]() $\{f_j\}_{j\geq 1}$ be a Cauchy sequence in
$\{f_j\}_{j\geq 1}$ be a Cauchy sequence in ![]() $(\mathcal{X}, \|\cdot\|_{\sharp})$ with
$(\mathcal{X}, \|\cdot\|_{\sharp})$ with  $f_j(z)=\sum_{n=0}^{\infty}a_n^{(j)}z^n$. By (9),
$f_j(z)=\sum_{n=0}^{\infty}a_n^{(j)}z^n$. By (9), ![]() $f_j\to f(z)=\sum_{n=1}^{\infty}a_nz^n$ in
$f_j\to f(z)=\sum_{n=1}^{\infty}a_nz^n$ in ![]() $(\mathcal{X}, \|\cdot\|_{\mathcal{X}}).$ Then,
$(\mathcal{X}, \|\cdot\|_{\mathcal{X}}).$ Then,
 \begin{eqnarray*}
\|f_j-f\|_{\sharp}
&=&\sup_{N\geq 0}\sup_{\|\lambda\|_{\ell^{\infty}}\leq 1}\sup_{\ell \gt M}\Big\|\sum_{k=0}^N\lambda_k(a_k^{(j)}-a_k^{(\ell)})z^k\Big\|_{\mathcal{X}}
\leq\sup_{\ell \gt M}\|f_j-f_{\ell}\|_{\mathcal{X}} \lt \epsilon
\end{eqnarray*}
\begin{eqnarray*}
\|f_j-f\|_{\sharp}
&=&\sup_{N\geq 0}\sup_{\|\lambda\|_{\ell^{\infty}}\leq 1}\sup_{\ell \gt M}\Big\|\sum_{k=0}^N\lambda_k(a_k^{(j)}-a_k^{(\ell)})z^k\Big\|_{\mathcal{X}}
\leq\sup_{\ell \gt M}\|f_j-f_{\ell}\|_{\mathcal{X}} \lt \epsilon
\end{eqnarray*} when M is large enough. So ![]() $f_j\to f$ in
$f_j\to f$ in ![]() $(\mathcal{X}, \|\cdot\|_{\sharp}).$ On the other hand, one can check directly that
$(\mathcal{X}, \|\cdot\|_{\sharp}).$ On the other hand, one can check directly that  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid basis for ![]() $(\mathcal{X}, \|\cdot\|_{\sharp}).$ (iv)
$(\mathcal{X}, \|\cdot\|_{\sharp}).$ (iv) ![]() $\Rightarrow$ (ii) is clear. (ii)
$\Rightarrow$ (ii) is clear. (ii) ![]() $\Rightarrow$ (i) is also straightforward now since
$\Rightarrow$ (i) is also straightforward now since ![]() $\|f\|_{\sharp} \approx \|f\|_{\mathcal{X}},\ f\in \mathcal{X},$ and one can verify directly that
$\|f\|_{\sharp} \approx \|f\|_{\mathcal{X}},\ f\in \mathcal{X},$ and one can verify directly that  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for ![]() $\mathcal{X}.$
$\mathcal{X}.$
Remark. An interesting fact from [Reference Megginson33, p. 376] allows us to establish a connection between solid frames and Banach algebras. If ![]() $\mathcal{X}$ is a functional Banach space of homogeneous type, and
$\mathcal{X}$ is a functional Banach space of homogeneous type, and  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame, then
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame, then ![]() $\mathcal{X}_{\mathcal{P}}$ and
$\mathcal{X}_{\mathcal{P}}$ and ![]() $\mathcal{X}^\mathrm{max}$ become Banach algebras when equipped with the norm
$\mathcal{X}^\mathrm{max}$ become Banach algebras when equipped with the norm  $
\|f\|_{\sharp} = \sup\limits_{N\geq 0}\sup\limits_{\|\lambda\|_{\ell^{\infty}}\leq 1}\Big\|\sum\limits_{n=0}^N\lambda_na_nz^n\Big\|_{\mathcal{X}},
$ with the product given by
$
\|f\|_{\sharp} = \sup\limits_{N\geq 0}\sup\limits_{\|\lambda\|_{\ell^{\infty}}\leq 1}\Big\|\sum\limits_{n=0}^N\lambda_na_nz^n\Big\|_{\mathcal{X}},
$ with the product given by ![]() $
(f\star g)(z)=\sum_{n=0}^{\infty}a_nb_n\|z^n\|_{\mathcal{X}}z^n.
$ Then,
$
(f\star g)(z)=\sum_{n=0}^{\infty}a_nb_n\|z^n\|_{\mathcal{X}}z^n.
$ Then, ![]() $\big(\mathcal{X}_{\mathcal{P}}, \ \|\cdot\|_{\sharp}, \ \star\big)$ is a commutative Banach algebra without identity. The space
$\big(\mathcal{X}_{\mathcal{P}}, \ \|\cdot\|_{\sharp}, \ \star\big)$ is a commutative Banach algebra without identity. The space ![]() $\big(\mathcal{X}^\mathrm{max}, \ \|\cdot\|_{\sharp}, \ \star\big)$ is also a commutative Banach algebra. Moreover, under the assumption that
$\big(\mathcal{X}^\mathrm{max}, \ \|\cdot\|_{\sharp}, \ \star\big)$ is also a commutative Banach algebra. Moreover, under the assumption that  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame, the followings are equivalent:
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame, the followings are equivalent:
(i)
 $\big(\mathcal{X}^\mathrm{max}, \ \|\cdot\|_{\sharp}, \ \star\big)$ has an identity;
$\big(\mathcal{X}^\mathrm{max}, \ \|\cdot\|_{\sharp}, \ \star\big)$ has an identity;(ii)
 $\sum\limits_{n=0}^{\infty}\frac{z^n}{\|z^n\|_{\mathcal{X}}}\in\mathcal{X}^\mathrm{max};$
$\sum\limits_{n=0}^{\infty}\frac{z^n}{\|z^n\|_{\mathcal{X}}}\in\mathcal{X}^\mathrm{max};$(iii)
 $\mathcal{X}^\mathrm{max}$ and
$\mathcal{X}^\mathrm{max}$ and  $\ell^\infty$ are isomorphic.
$\ell^\infty$ are isomorphic.
8. A characterization for monomials to be solid frames
Proof of Theorem F
We shall only prove the Banach space case. We first consider ![]() $\mathcal{X}=\mathcal{X}^\mathrm{max}.$ If
$\mathcal{X}=\mathcal{X}^\mathrm{max}.$ If  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n \geq 1}$ is a solid frame, then
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n \geq 1}$ is a solid frame, then ![]() $\sup_{N\geq 0}\|S_N\| \lt \infty$. Take any
$\sup_{N\geq 0}\|S_N\| \lt \infty$. Take any ![]() $\lambda=\{\lambda_n\}_{n\geq 0}\in \ell^{\infty},$ and
$\lambda=\{\lambda_n\}_{n\geq 0}\in \ell^{\infty},$ and ![]() $f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{X}^\mathrm{max}.$ Let
$f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{X}^\mathrm{max}.$ Let ![]() $g(z)=\sum_{n=0}^{\infty}\lambda_na_nz^n.$ For any
$g(z)=\sum_{n=0}^{\infty}\lambda_na_nz^n.$ For any ![]() $0\leq r \lt 1,$
$0\leq r \lt 1,$  $
\Big\|\sum_{k=N}^{M}\lambda_ka_kr^kz^k\Big\|_{\mathcal{X}} \lesssim \|\lambda\|_{\ell^{\infty}}\Big\|\sum_{k=N}^{M}a_kr^kz^k\Big\|_{\mathcal{X}}.
$ Hence,
$
\Big\|\sum_{k=N}^{M}\lambda_ka_kr^kz^k\Big\|_{\mathcal{X}} \lesssim \|\lambda\|_{\ell^{\infty}}\Big\|\sum_{k=N}^{M}a_kr^kz^k\Big\|_{\mathcal{X}}.
$ Hence, ![]() $g_r\in \mathcal{X}_{\mathcal{P}}.$ So
$g_r\in \mathcal{X}_{\mathcal{P}}.$ So
 \begin{equation*}
\|g\|_\mathrm{max} = \sup_{0\leq r \lt 1}\|g_r\|_{\mathcal{X}} \lesssim \|\lambda\|_{\ell^{\infty}} \sup_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}} =
\|\lambda\|_{\ell^{\infty}} \|f\|_\mathrm{max}.
\end{equation*}
\begin{equation*}
\|g\|_\mathrm{max} = \sup_{0\leq r \lt 1}\|g_r\|_{\mathcal{X}} \lesssim \|\lambda\|_{\ell^{\infty}} \sup_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}} =
\|\lambda\|_{\ell^{\infty}} \|f\|_\mathrm{max}.
\end{equation*} It follows ![]() $g\in \mathcal{X}^\mathrm{max}.$ For sufficiency, by Theorem E, it suffices to show that
$g\in \mathcal{X}^\mathrm{max}.$ For sufficiency, by Theorem E, it suffices to show that
 \begin{equation}
\sup_{N\geq 0}\sup_{\|\lambda\|_{\ell^{\infty}}\leq 1}\Big\|\sum_{k=0}^{N}\lambda_ka_kz^k\Big\|_{\mathcal{X}} \lt \infty
\end{equation}
\begin{equation}
\sup_{N\geq 0}\sup_{\|\lambda\|_{\ell^{\infty}}\leq 1}\Big\|\sum_{k=0}^{N}\lambda_ka_kz^k\Big\|_{\mathcal{X}} \lt \infty
\end{equation} for each ![]() $f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{X}^\mathrm{max}.$ Let
$f(z)=\sum_{n=0}^{\infty}a_nz^n\in \mathcal{X}^\mathrm{max}.$ Let ![]() $T_f: \ell^{\infty} \to \mathcal{X}^\mathrm{max}$ be defined by
$T_f: \ell^{\infty} \to \mathcal{X}^\mathrm{max}$ be defined by  $
T_f (\lambda) \doteq \sum\limits_{n=0}^{\infty}\lambda_na_nz^n.
$ The condition that
$
T_f (\lambda) \doteq \sum\limits_{n=0}^{\infty}\lambda_na_nz^n.
$ The condition that ![]() $\mathcal{X}^\mathrm{max}$ is a solid space ensures that Tf is well defined. The closed graph theorem and the condition
$\mathcal{X}^\mathrm{max}$ is a solid space ensures that Tf is well defined. The closed graph theorem and the condition ![]() $\sup_{N\geq 0}\|S_N\| \lt \infty$ imply that (10) holds. Now we treat the case
$\sup_{N\geq 0}\|S_N\| \lt \infty$ imply that (10) holds. Now we treat the case ![]() $\mathcal{X}=\mathcal{X}_{\mathcal{P}}.$ By [Reference Zhu43, Proposition 1],
$\mathcal{X}=\mathcal{X}_{\mathcal{P}}.$ By [Reference Zhu43, Proposition 1],  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a Schauder basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a Schauder basis for ![]() $\mathcal{X}$ if and only if
$\mathcal{X}$ if and only if ![]() $\sup_{N\geq 0}\|S_N\| \lt \infty.$ The proof of the sufficiency for
$\sup_{N\geq 0}\|S_N\| \lt \infty.$ The proof of the sufficiency for ![]() $\mathcal{X}^\mathrm{max}$ above can be modified to show that
$\mathcal{X}^\mathrm{max}$ above can be modified to show that  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is an unconditional basis for ![]() $\mathcal{X}.$ Conversely, if it is a solid frame, then by Proposition 14, it is also an unconditional basis for
$\mathcal{X}.$ Conversely, if it is a solid frame, then by Proposition 14, it is also an unconditional basis for ![]() $\mathcal{X}$.
$\mathcal{X}$.
Remark. For a functional Banach space of homogeneous type, the condition ![]() $\sup_{N\geq 0}\|S_N\| \lt \infty$ does not imply that
$\sup_{N\geq 0}\|S_N\| \lt \infty$ does not imply that  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ is a solid frame for ![]() $\mathcal{X}.$ An example is provided by
$\mathcal{X}.$ An example is provided by ![]() $\mathcal{X}=H^p \ (1 \lt p \lt 2)$ for which
$\mathcal{X}=H^p \ (1 \lt p \lt 2)$ for which ![]() $\{z^n\}_{n\geq 0}$ is a Schauder basis. If it were a solid frame, then it would be an unconditional basis as well. This is known to be false and can be shown quickly. Otherwise, take
$\{z^n\}_{n\geq 0}$ is a Schauder basis. If it were a solid frame, then it would be an unconditional basis as well. This is known to be false and can be shown quickly. Otherwise, take ![]() $f(z)=\sum_{n=0}^{\infty}a_nz^n\in H^p\setminus H^2.$ By Littlewood’s theorem [Reference Littlewood29], there exists a sequence
$f(z)=\sum_{n=0}^{\infty}a_nz^n\in H^p\setminus H^2.$ By Littlewood’s theorem [Reference Littlewood29], there exists a sequence ![]() $\{\theta_n\}_{n\geq 0} \in \{-1, 1\}^{\mathbb{N}}$ such that
$\{\theta_n\}_{n\geq 0} \in \{-1, 1\}^{\mathbb{N}}$ such that ![]() $
\sum_{n=0}^{\infty}\theta_na_nz^n\notin H^p,
$ contradicting the assumption that
$
\sum_{n=0}^{\infty}\theta_na_nz^n\notin H^p,
$ contradicting the assumption that ![]() $\{z^n\}_{n\geq 0}$ were an unconditional basis.
$\{z^n\}_{n\geq 0}$ were an unconditional basis.
9. The problem of a solid span
Proof of Theorem G
(i) Let
 \begin{equation}
E^\mathrm{s\text{-}max}=\Big\{a=(a_1, a_2, \cdots):\ \|a\|_\mathrm{s\text{-}max}=\sup_{N\geq 1}\Big\|\sum_{n=1}^Na_ne_n\Big\|_E \lt \infty\Big\}.
\end{equation}
\begin{equation}
E^\mathrm{s\text{-}max}=\Big\{a=(a_1, a_2, \cdots):\ \|a\|_\mathrm{s\text{-}max}=\sup_{N\geq 1}\Big\|\sum_{n=1}^Na_ne_n\Big\|_E \lt \infty\Big\}.
\end{equation} Then ![]() $I(x)=\big((\mathcal{T} x)_1, (\mathcal{T} x)_2, \cdots\big)$ is an isometric embedding from E into
$I(x)=\big((\mathcal{T} x)_1, (\mathcal{T} x)_2, \cdots\big)$ is an isometric embedding from E into ![]() $E^\mathrm{s\text{-}max},$ where
$E^\mathrm{s\text{-}max},$ where ![]() $\mathcal{T}: E\to \mathfrak{S}$ is the coefficient map. Note that
$\mathcal{T}: E\to \mathfrak{S}$ is the coefficient map. Note that ![]() $Ie_n=\mathbf{e}_n$,
$Ie_n=\mathbf{e}_n$, ![]() $n\geq 1.$ For
$n\geq 1.$ For ![]() $|\lambda_n|\leq 1$ and
$|\lambda_n|\leq 1$ and ![]() $c_n\in \mathbb{C},$
$c_n\in \mathbb{C},$
 \begin{equation*}
\Big\|\sum_{n=1}^N\lambda_nc_n\mathbf{e}_n\Big\|_\mathrm{s\text{-}max}= \Big\|\sum_{n=1}^N\lambda_nc_ne_n\Big\|_E
\leq \Big\|\sum_{n=1}^Nc_ne_n\Big\|_E
= \Big\|\sum_{n=1}^Nc_n\mathbf{e}_n\Big\|_\mathrm{s\text{-}max}.
\end{equation*}
\begin{equation*}
\Big\|\sum_{n=1}^N\lambda_nc_n\mathbf{e}_n\Big\|_\mathrm{s\text{-}max}= \Big\|\sum_{n=1}^N\lambda_nc_ne_n\Big\|_E
\leq \Big\|\sum_{n=1}^Nc_ne_n\Big\|_E
= \Big\|\sum_{n=1}^Nc_n\mathbf{e}_n\Big\|_\mathrm{s\text{-}max}.
\end{equation*} Also  $
\lim\limits_{N\to\infty}\|P_Na\|_\mathrm{s\text{-}max}=\lim\limits_{N\to\infty}\Big\|\sum\limits_{n=1}^Na_ne_n\Big\|_E=\|a\|_\mathrm{s\text{-}max}.
$ So
$
\lim\limits_{N\to\infty}\|P_Na\|_\mathrm{s\text{-}max}=\lim\limits_{N\to\infty}\Big\|\sum\limits_{n=1}^Na_ne_n\Big\|_E=\|a\|_\mathrm{s\text{-}max}.
$ So ![]() $\{\mathbf{e}_n\}_{n\geq 1}$ is a solid basis for
$\{\mathbf{e}_n\}_{n\geq 1}$ is a solid basis for ![]() $E^\mathrm{s\text{-}max}.$ To complete the proof, it suffices to show that F can be isometrically embedded into
$E^\mathrm{s\text{-}max}.$ To complete the proof, it suffices to show that F can be isometrically embedded into ![]() $E^\mathrm{s\text{-}max}$ if F is a solid extension of E (see Definition 5). Let
$E^\mathrm{s\text{-}max}$ if F is a solid extension of E (see Definition 5). Let ![]() $I': E\hookrightarrow F$ denote the isometric embedding from E into
$I': E\hookrightarrow F$ denote the isometric embedding from E into ![]() $F,$ with
$F,$ with ![]() $\{I'e_n\}_{n\geq 1}$ being a solid basis for
$\{I'e_n\}_{n\geq 1}$ being a solid basis for ![]() $F.$ For convenience, write
$F.$ For convenience, write ![]() $e_n'=I'e_n, n\geq 1,$ and
$e_n'=I'e_n, n\geq 1,$ and ![]() $\mathcal{T}': F\to \mathfrak{S}$ the corresponding coefficient map. We claim that
$\mathcal{T}': F\to \mathfrak{S}$ the corresponding coefficient map. We claim that ![]() $I'': F\to E^\mathrm{s\text{-}max}$ defined by
$I'': F\to E^\mathrm{s\text{-}max}$ defined by ![]() $I''(x)=\big((\mathcal{T}'x)_1, (\mathcal{T}'x)_2, \cdots\big),\ x\in F,$ is an isometric embedding. Note that
$I''(x)=\big((\mathcal{T}'x)_1, (\mathcal{T}'x)_2, \cdots\big),\ x\in F,$ is an isometric embedding. Note that
 \begin{equation*}
\Big\|\sum_{n=1}^N(\mathcal{T}'x)_ne_n'\Big\|_F = \Big\|I'\Big(\sum_{n=1}^N(\mathcal{T}'x)_ne_n\Big)\Big\|_F = \Big\|\sum_{n=1}^N(\mathcal{T}'x)_ne_n\Big\|_E
\end{equation*}
\begin{equation*}
\Big\|\sum_{n=1}^N(\mathcal{T}'x)_ne_n'\Big\|_F = \Big\|I'\Big(\sum_{n=1}^N(\mathcal{T}'x)_ne_n\Big)\Big\|_F = \Big\|\sum_{n=1}^N(\mathcal{T}'x)_ne_n\Big\|_E
\end{equation*} since ![]() $I': E\hookrightarrow F$ is isometric. Then, for
$I': E\hookrightarrow F$ is isometric. Then, for ![]() $x\in F,$
$x\in F,$
 \begin{equation*}
\|x\|_F = \lim_{N\to\infty}\Big\|\sum_{n=1}^N(\mathcal{T}'x)_ne_n'\Big\|_F
= \lim_{N\to\infty}\Big\|\sum_{n=1}^N(\mathcal{T}'x)_ne_n\Big\|_E
= \|I''(x)\|_\mathrm{s\text{-}max}.
\end{equation*}
\begin{equation*}
\|x\|_F = \lim_{N\to\infty}\Big\|\sum_{n=1}^N(\mathcal{T}'x)_ne_n'\Big\|_F
= \lim_{N\to\infty}\Big\|\sum_{n=1}^N(\mathcal{T}'x)_ne_n\Big\|_E
= \|I''(x)\|_\mathrm{s\text{-}max}.
\end{equation*} (ii) If ![]() $\{\imath e_n\}_{n\geq 1}$ is a solid basis for
$\{\imath e_n\}_{n\geq 1}$ is a solid basis for ![]() $W.$ Let
$W.$ Let ![]() $\mathcal{T}: W\to \mathfrak{S}$ be the corresponding coefficient map. Then, we can check that
$\mathcal{T}: W\to \mathfrak{S}$ be the corresponding coefficient map. Then, we can check that ![]() $\mathcal{T}$ is an isometric embedding from W into
$\mathcal{T}$ is an isometric embedding from W into ![]() $(E_{\mathcal{P}})^\mathrm{s\text{-}max}.$ Conversely,
$(E_{\mathcal{P}})^\mathrm{s\text{-}max}.$ Conversely, ![]() $\{\mathbf{e}_n\}_{n\geq 1}$ is a solid basis for
$\{\mathbf{e}_n\}_{n\geq 1}$ is a solid basis for ![]() $(E_{\mathcal{P}})^\mathrm{s\text{-}max},$ since
$(E_{\mathcal{P}})^\mathrm{s\text{-}max},$ since ![]() $\{e_n\}_{n\geq 1}$ is a solid basis for
$\{e_n\}_{n\geq 1}$ is a solid basis for ![]() $E_{\mathcal{P}}.$ Then, one can check that
$E_{\mathcal{P}}.$ Then, one can check that ![]() $\{\imath e_n\}_{n\geq 1}$ is a solid basis for
$\{\imath e_n\}_{n\geq 1}$ is a solid basis for ![]() $W,$ since
$W,$ since ![]() $\imath: E_{\mathcal{P}}\to W$ is an isometric embedding and
$\imath: E_{\mathcal{P}}\to W$ is an isometric embedding and ![]() $E_{\mathcal{P}}$ is embedded into
$E_{\mathcal{P}}$ is embedded into ![]() $(E_{\mathcal{P}})^\mathrm{s\text{-}max}$ isometrically.
$(E_{\mathcal{P}})^\mathrm{s\text{-}max}$ isometrically.
10. The role of c 0
Proof of Theorem H
(i) We first show that ![]() $
\mathcal{P}\subset c_0\cdot E \subset E_{\mathcal{P}},
$ which follows from Lemma 18 below. Here,
$
\mathcal{P}\subset c_0\cdot E \subset E_{\mathcal{P}},
$ which follows from Lemma 18 below. Here, ![]() $\mathcal{P}$ denotes the collection of finite linear combinations of
$\mathcal{P}$ denotes the collection of finite linear combinations of ![]() $\{e_n\}_{n\geq 1}.$
$\{e_n\}_{n\geq 1}.$
Lemma 18. Let E be a Banach space with a solid basis ![]() $\{e_n\}_{n\geq 1}.$ If
$\{e_n\}_{n\geq 1}.$ If ![]() $\{t_n\}_{n\geq 1}\in c_0$ and
$\{t_n\}_{n\geq 1}\in c_0$ and ![]() $x\in E,$ then the series
$x\in E,$ then the series  $
\sum\limits_{n=1}^{\infty}t_n(\mathcal{T} x)_ne_n
$ converges in norm in E.
$
\sum\limits_{n=1}^{\infty}t_n(\mathcal{T} x)_ne_n
$ converges in norm in E.
Proof. By (8),  $
\sum\limits_{n=1}^{\infty}|(\mathcal{T} x)_n||\phi(e_n)| \lt \infty, \ \phi\in E^{\ast}.
$ Then, for
$
\sum\limits_{n=1}^{\infty}|(\mathcal{T} x)_n||\phi(e_n)| \lt \infty, \ \phi\in E^{\ast}.
$ Then, for ![]() $x\in E,$ the mapping
$x\in E,$ the mapping ![]() $T: E^{\ast}\to \ell^1$ defined by
$T: E^{\ast}\to \ell^1$ defined by ![]() $
T\phi\doteq\{(\mathcal{T} x)_n\phi(e_n)\}_{n\geq 1},\ \phi\in E^{\ast}
$ is continuous by the closed graph theorem. Now, for
$
T\phi\doteq\{(\mathcal{T} x)_n\phi(e_n)\}_{n\geq 1},\ \phi\in E^{\ast}
$ is continuous by the closed graph theorem. Now, for ![]() $m\leq k\leq n,$
$m\leq k\leq n,$
 \begin{eqnarray*}
\Big\|\sum_{k=m}^nt_k(\mathcal{T} x)_ke_k\Big\|_E
&\leq& \sup_{\phi\in B_{E^{\ast}}}\Big(\big(\sup_{m\leq k\leq n}|t_k|\big)\sum_{k=m}^{n}|(\mathcal{T} x)_k\phi(e_k)|\Big)
\lesssim \sup_{m\leq k\leq n}|t_k| \to 0
\end{eqnarray*}
\begin{eqnarray*}
\Big\|\sum_{k=m}^nt_k(\mathcal{T} x)_ke_k\Big\|_E
&\leq& \sup_{\phi\in B_{E^{\ast}}}\Big(\big(\sup_{m\leq k\leq n}|t_k|\big)\sum_{k=m}^{n}|(\mathcal{T} x)_k\phi(e_k)|\Big)
\lesssim \sup_{m\leq k\leq n}|t_k| \to 0
\end{eqnarray*} as ![]() $n \gt m\to\infty,$ where
$n \gt m\to\infty,$ where ![]() $B_{E^{}\ast}$ denotes the unit ball of
$B_{E^{}\ast}$ denotes the unit ball of ![]() $E^{\ast}.$
$E^{\ast}.$
Next, we show that ![]() $c_0\cdot E$ is closed in norm. Let
$c_0\cdot E$ is closed in norm. Let ![]() $x_m\to x$ with
$x_m\to x$ with ![]() $x_m\in c_0\cdot E.$ Then, by Lemma 18,
$x_m\in c_0\cdot E.$ Then, by Lemma 18, ![]() $x_m\in E_{\mathcal{P}}$ and
$x_m\in E_{\mathcal{P}}$ and ![]() $x\in E_{\mathcal{P}}.$ Write
$x\in E_{\mathcal{P}}.$ Write  $
x_m=\sum\limits_{n=1}^{\infty}t_n^{(m)}(\mathcal{T} x_m)_ne_n
$ with
$
x_m=\sum\limits_{n=1}^{\infty}t_n^{(m)}(\mathcal{T} x_m)_ne_n
$ with  $\{t_n^{(m)}\}_{n\geq 1}\in c_0.$ Since
$\{t_n^{(m)}\}_{n\geq 1}\in c_0.$ Since ![]() $\{(\mathcal{T} x_m)_{n}\}_{n\geq 1}\in \ell^{\infty},$ one has
$\{(\mathcal{T} x_m)_{n}\}_{n\geq 1}\in \ell^{\infty},$ one has  $\big\{t_n^{(m)}(\mathcal{T} x_m)_n\big\}_{n\geq 1}
\in c_0.$ Since
$\big\{t_n^{(m)}(\mathcal{T} x_m)_n\big\}_{n\geq 1}
\in c_0.$ Since ![]() $\{e_n\}_{n\geq 1}$ is a solid basis, for fixed
$\{e_n\}_{n\geq 1}$ is a solid basis, for fixed ![]() $n,$
$n,$  $t_n^{(m)}(\mathcal{T} x_m)_n \to a_n$ as
$t_n^{(m)}(\mathcal{T} x_m)_n \to a_n$ as ![]() $m\to\infty$ for some
$m\to\infty$ for some ![]() $a_n\in\mathbb{C}.$ This implies that
$a_n\in\mathbb{C}.$ This implies that ![]() $
(\mathcal{T} x)_n=a_n,\ n\geq 1.
$ Moreover,
$
(\mathcal{T} x)_n=a_n,\ n\geq 1.
$ Moreover,
 \begin{eqnarray*}
|a_n| = \big|a_n-t_n^{(m)}(\mathcal{T} x_m)_n+t_n^{(m)}(\mathcal{T} x_m)_n\big|
\leq \|x_m-x\|_E+|t_n^{(m)}(\mathcal{T} x_m)_n|,
\end{eqnarray*}
\begin{eqnarray*}
|a_n| = \big|a_n-t_n^{(m)}(\mathcal{T} x_m)_n+t_n^{(m)}(\mathcal{T} x_m)_n\big|
\leq \|x_m-x\|_E+|t_n^{(m)}(\mathcal{T} x_m)_n|,
\end{eqnarray*} so ![]() $\{a_n\}_{n\geq 1}\in c_0$ and
$\{a_n\}_{n\geq 1}\in c_0$ and ![]() $x=\sum_{n=1}^{\infty}a_ne_n$ converges in norm. Then, there exists a subsequence of integers
$x=\sum_{n=1}^{\infty}a_ne_n$ converges in norm. Then, there exists a subsequence of integers ![]() $\{n_k\}_{k\geq 1}$ such that
$\{n_k\}_{k\geq 1}$ such that  $
\big\|\sum_{i=n_k}^{n_{k+1}-1}a_ie_i\big\|_E \lt \frac{1}{k^3}.
$ Take
$
\big\|\sum_{i=n_k}^{n_{k+1}-1}a_ie_i\big\|_E \lt \frac{1}{k^3}.
$ Take  $t_n=\frac{1}{\sqrt{k}}$ if
$t_n=\frac{1}{\sqrt{k}}$ if ![]() $n\in [n_k, n_{k+1}-1]$ and let
$n\in [n_k, n_{k+1}-1]$ and let ![]() $b_n=\frac{a_n}{t_n}.$ Then, by the contraction principle,
$b_n=\frac{a_n}{t_n}.$ Then, by the contraction principle,  $x'=\sum\limits_{n=1}^{\infty}b_ne_n\in E_{\mathcal{P}}.$ Hence,
$x'=\sum\limits_{n=1}^{\infty}b_ne_n\in E_{\mathcal{P}}.$ Hence,  $
x=\sum\limits_{n=1}^{\infty}t_nb_ne_n\in c_0\cdot E,
$ as desired.
$
x=\sum\limits_{n=1}^{\infty}t_nb_ne_n\in c_0\cdot E,
$ as desired.
(ii) If ![]() $a\in E^\mathrm{s\text{-}max},$ then (8) holds and Lemma 18 applies to
$a\in E^\mathrm{s\text{-}max},$ then (8) holds and Lemma 18 applies to ![]() $E^\mathrm{s\text{-}max},$ which implies the sufficiency. Now the necessity. For
$E^\mathrm{s\text{-}max},$ which implies the sufficiency. Now the necessity. For ![]() $\{t_n\}_{n\geq 1}\in c_0,$
$\{t_n\}_{n\geq 1}\in c_0,$  $\sum\limits_{n=1}^{\infty}t_na_ne_n\in E_{\mathcal{P}}$ implies that this series converges, so
$\sum\limits_{n=1}^{\infty}t_na_ne_n\in E_{\mathcal{P}}$ implies that this series converges, so  $\sup\limits_{N\geq 1}\Big\|\sum\limits_{n=1}^Nt_na_ne_n\Big\|_E \lt \infty.$ This yields that
$\sup\limits_{N\geq 1}\Big\|\sum\limits_{n=1}^Nt_na_ne_n\Big\|_E \lt \infty.$ This yields that  $\sup\limits_{N\geq 1}\Big\|\sum\limits_{n=1}^Na_ne_n\Big\|_E \lt \infty.$ Otherwise,
$\sup\limits_{N\geq 1}\Big\|\sum\limits_{n=1}^Na_ne_n\Big\|_E \lt \infty.$ Otherwise,  $\sup\limits_{N\geq 1}\Big\|\sum\limits_{n=1}^Na_ne_n\Big\|_E=\infty,$ and there exists a subsequence
$\sup\limits_{N\geq 1}\Big\|\sum\limits_{n=1}^Na_ne_n\Big\|_E=\infty,$ and there exists a subsequence ![]() $\{n_k\}_{k\geq 1}$ such that
$\{n_k\}_{k\geq 1}$ such that  $
\Big\|\sum\limits_{i=1}^{n_{k+1}}a_ie_i\Big\|_E-\Big\|\sum\limits_{i=1}^{n_{k}}a_ie_i\Big\|_E\geq k^2.
$ So
$
\Big\|\sum\limits_{i=1}^{n_{k+1}}a_ie_i\Big\|_E-\Big\|\sum\limits_{i=1}^{n_{k}}a_ie_i\Big\|_E\geq k^2.
$ So
 \begin{equation*}
\Big\|\sum_{i=n_k+1}^{n_{k+1}}a_ie_i\Big\|_E\geq \Big\|\sum_{i=1}^{n_{k+1}}
a_ie_i\Big\|_E-\Big\|\sum_{i=1}^{n_{k}}a_ie_i\Big\|_E\geq k^2.
\end{equation*}
\begin{equation*}
\Big\|\sum_{i=n_k+1}^{n_{k+1}}a_ie_i\Big\|_E\geq \Big\|\sum_{i=1}^{n_{k+1}}
a_ie_i\Big\|_E-\Big\|\sum_{i=1}^{n_{k}}a_ie_i\Big\|_E\geq k^2.
\end{equation*} If we take  $t_i=\frac{1}{k}$ when
$t_i=\frac{1}{k}$ when ![]() $i\in [n_k+1, n_{k+1}],$ then
$i\in [n_k+1, n_{k+1}],$ then ![]() $t=\{t_n\}_{n\geq 1}\in c_0,$ and
$t=\{t_n\}_{n\geq 1}\in c_0,$ and  $
\Big\|\sum\limits_{i=n_k+1}^{n_{k+1}}t_ia_ie_i\Big\|_E\geq k.
$ By
$
\Big\|\sum\limits_{i=n_k+1}^{n_{k+1}}t_ia_ie_i\Big\|_E\geq k.
$ By  $
\Big\|\sum\limits_{i=1}^{n_{k+1}}t_ia_ie_i\Big\|_E\geq \Big\|\sum\limits_{i=n_k+1}^{n_{k+1}}t_ia_ie_i\Big\|_E\geq k,
$ we conclude that
$
\Big\|\sum\limits_{i=1}^{n_{k+1}}t_ia_ie_i\Big\|_E\geq \Big\|\sum\limits_{i=n_k+1}^{n_{k+1}}t_ia_ie_i\Big\|_E\geq k,
$ we conclude that  $\sup\limits_{N\geq 1}\Big\|\sum\limits_{n=1}^Na_nt_ne_n\Big\|_E=\infty,$ a contradiction.
$\sup\limits_{N\geq 1}\Big\|\sum\limits_{n=1}^Na_nt_ne_n\Big\|_E=\infty,$ a contradiction.
Now, we come to the (very short) proof of Theorem I, which is an application of James’ theorem.
Proof of Theorem I
If ![]() $\{\mathbf{e}_n\}_{n\geq 1}$ is an unconditional basis for
$\{\mathbf{e}_n\}_{n\geq 1}$ is an unconditional basis for ![]() $E^\mathrm{s\text{-}max},$ then, by James’ theorem [Reference Li and Queffélec25, Theorem V.4, p. 98],
$E^\mathrm{s\text{-}max},$ then, by James’ theorem [Reference Li and Queffélec25, Theorem V.4, p. 98], ![]() $E^\mathrm{s\text{-}max}$ does not contain
$E^\mathrm{s\text{-}max}$ does not contain ![]() $c_0.$ Conversely, we show that
$c_0.$ Conversely, we show that ![]() $E^{s\text{-}max}=(E^\mathrm{s\text{-}max})_{\mathcal{P}}.$ Otherwise, there exists a nonzero
$E^{s\text{-}max}=(E^\mathrm{s\text{-}max})_{\mathcal{P}}.$ Otherwise, there exists a nonzero ![]() $a\in E^{s\text{-}max}$ such that
$a\in E^{s\text{-}max}$ such that ![]() $P_Na\not\to a$ as
$P_Na\not\to a$ as ![]() $N\to\infty.$ But
$N\to\infty.$ But  $\sup\limits_{N\geq 1}\|P_Na\|_{s\text{-}max}=\|a\|_{s\text{-}max} \lt \infty.$ So the conclusion follows from the Bessaga-Pełczyński theorem ([Reference Li and Queffélec25, Theorem IV.2, p. 94]).
$\sup\limits_{N\geq 1}\|P_Na\|_{s\text{-}max}=\|a\|_{s\text{-}max} \lt \infty.$ So the conclusion follows from the Bessaga-Pełczyński theorem ([Reference Li and Queffélec25, Theorem IV.2, p. 94]).
Corollary 19. Let ![]() $\mathcal{X}$ be a functional Banach space of homogeneous type with
$\mathcal{X}$ be a functional Banach space of homogeneous type with  $\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ as a solid basis. For
$\big\{\frac{z^n}{\|z^n\|_{\mathcal{X}}}\big\}_{n\geq 0}$ as a solid basis. For ![]() $f\in H(\mathbb{D}),$ we have
$f\in H(\mathbb{D}),$ we have ![]() $
c_0\cdot f\subset \mathcal{X}_{\mathcal{P}} \Longleftrightarrow f\in \mathcal{X}^{max}.
$
$
c_0\cdot f\subset \mathcal{X}_{\mathcal{P}} \Longleftrightarrow f\in \mathcal{X}^{max}.
$
Remark. By Proposition 15, we have ![]() $\mathcal{X}^{max}=\mathcal{X}_{T}$ in the above corollary.
$\mathcal{X}^{max}=\mathcal{X}_{T}$ in the above corollary.
The rest of this section is devoted to a characterization of ![]() $E_{\mathcal{P}}$ via compact operators, which is motivated by [Reference Li and Queffélec25, Proposition II.6, p. 88].
$E_{\mathcal{P}}$ via compact operators, which is motivated by [Reference Li and Queffélec25, Proposition II.6, p. 88].
Theorem 20. Let E be a Banach space with a solid basis ![]() $\{e_n\}_{n\geq 1},$ and
$\{e_n\}_{n\geq 1},$ and ![]() $x\in E.$ Then
$x\in E.$ Then ![]() $x\in E_{\mathcal{P}}$ if and only if the operator
$x\in E_{\mathcal{P}}$ if and only if the operator
 \begin{eqnarray*}
U:\ c_0&\longrightarrow& E\\
(t_n)_{n\geq 1}&\longmapsto& \sum_{n=1}^{\infty}t_n(\mathcal{T} x)_ne_n
\end{eqnarray*}
\begin{eqnarray*}
U:\ c_0&\longrightarrow& E\\
(t_n)_{n\geq 1}&\longmapsto& \sum_{n=1}^{\infty}t_n(\mathcal{T} x)_ne_n
\end{eqnarray*}is compact.
Combining Theorem H and Theorem 20, we have
Corollary 21. Let E be a Banach space with a solid basis ![]() $\{e_n\}_{n\geq 1},$ and
$\{e_n\}_{n\geq 1},$ and ![]() $x\in E.$ The following are equivalent:
$x\in E.$ The following are equivalent:
(i)
 $x\in E_{\mathcal{P}};$
$x\in E_{\mathcal{P}};$(ii) there exists
 $\{t_n\}_{n\geq 1}\in c_0$ and
$\{t_n\}_{n\geq 1}\in c_0$ and  $x'\in E$ such that
$x'\in E$ such that  $x=\sum_{n=1}^{\infty}
t_n(\mathcal{T} x')_ne_n;$
$x=\sum_{n=1}^{\infty}
t_n(\mathcal{T} x')_ne_n;$(iii) there exists
 $\{t_n\}_{n\geq 1}\in c_0$ and
$\{t_n\}_{n\geq 1}\in c_0$ and  $x'\in E_{\mathcal{P}}$ such that
$x'\in E_{\mathcal{P}}$ such that  $x=\sum_{n=1}^{\infty}
t_n(\mathcal{T} x')_ne_n;$
$x=\sum_{n=1}^{\infty}
t_n(\mathcal{T} x')_ne_n;$(iv) the operator
 $U:\ c_0\to E $ defined by
$U:\ c_0\to E $ defined by  $(t_n)_{n\geq 1}\mapsto \sum\limits_{n=1}^{\infty}t_n(\mathcal{T} x)_ne_n$ is compact.
$(t_n)_{n\geq 1}\mapsto \sum\limits_{n=1}^{\infty}t_n(\mathcal{T} x)_ne_n$ is compact.
Proof of Theorem 20
The operator U is well defined by Lemma 18. Also note that
 \begin{equation*}
\Big\|\sum_{k=1}^n t_k (\mathcal{T} x)_ke_k\Big\|_E\leq \sup_{k\geq 1}|t_k| \Big\|\sum_{k=1}^n (\mathcal{T} x)_ke_k\Big\|_E.
\end{equation*}
\begin{equation*}
\Big\|\sum_{k=1}^n t_k (\mathcal{T} x)_ke_k\Big\|_E\leq \sup_{k\geq 1}|t_k| \Big\|\sum_{k=1}^n (\mathcal{T} x)_ke_k\Big\|_E.
\end{equation*} Letting ![]() $n\to\infty,$ we see that
$n\to\infty,$ we see that ![]() $\|Ut\|_E\leq \|x\|_E\|t\|_{c_0};$ hence U is bounded.
$\|Ut\|_E\leq \|x\|_E\|t\|_{c_0};$ hence U is bounded.
Necessity: Let ![]() $x\in E_{\mathcal{P}}.$ Note that
$x\in E_{\mathcal{P}}.$ Note that
 \begin{eqnarray*}
V=U^{\ast}:\ E^{\ast}&\longrightarrow& \ell^1\\
\phi &\longmapsto& \big\{(\mathcal{T} x)_n\phi(e_n)\big\}_{n\geq 1}.
\end{eqnarray*}
\begin{eqnarray*}
V=U^{\ast}:\ E^{\ast}&\longrightarrow& \ell^1\\
\phi &\longmapsto& \big\{(\mathcal{T} x)_n\phi(e_n)\big\}_{n\geq 1}.
\end{eqnarray*} We show that V is compact. Given any sequence ![]() $\{\phi_k\}_{k\geq 1}\subset B_{E^{\ast}},$ we must extract, from
$\{\phi_k\}_{k\geq 1}\subset B_{E^{\ast}},$ we must extract, from ![]() $\{V\phi_k\}_{k\geq 1},$ a subsequence convergent in norm in
$\{V\phi_k\}_{k\geq 1},$ a subsequence convergent in norm in ![]() $\ell^1.$ Schur’s theorem [Reference Li and Queffélec25, Theorem III.10, p. 65] implies that it suffices to show that there exists a w-convergent subsequence. We may assume that E is separable by replacing, if necessary, E with
$\ell^1.$ Schur’s theorem [Reference Li and Queffélec25, Theorem III.10, p. 65] implies that it suffices to show that there exists a w-convergent subsequence. We may assume that E is separable by replacing, if necessary, E with ![]() $\overline{\text{span}}\{e_n:\ n\geq 1\}.$ Then the compact space
$\overline{\text{span}}\{e_n:\ n\geq 1\}.$ Then the compact space ![]() $(B_{E^{\ast}}, w^{\ast})$ is metrizable. Thus, we can extract a subsequence
$(B_{E^{\ast}}, w^{\ast})$ is metrizable. Thus, we can extract a subsequence  $\{\phi_{k_j}\}_{j\geq 1}$
$\{\phi_{k_j}\}_{j\geq 1}$ ![]() $w^{\ast}$-convergent to
$w^{\ast}$-convergent to ![]() $\phi\in B_{E^{\ast}}.$
$\phi\in B_{E^{\ast}}.$
Now we show that  $V\phi_{k_j}$ converges weakly to
$V\phi_{k_j}$ converges weakly to ![]() $V\phi.$ Let
$V\phi.$ Let ![]() $\chi_{\sigma}\in\ell^{\infty}$ with
$\chi_{\sigma}\in\ell^{\infty}$ with ![]() $\sigma\subset \mathbb{N}.$ Then,
$\sigma\subset \mathbb{N}.$ Then,
 \begin{eqnarray*}
\chi_{\sigma}(V\phi_{k_j})&=& \sum_{n\in\sigma} (V\phi_{k_j})(n) = \sum_{n\in\sigma}(\mathcal{T} x)_n\phi_{k_j}(e_n)\\
&=& \phi_{k_j}\Big(\sum_{n\in \sigma}(\mathcal{T} x)_ne_n\Big) \to \phi\Big(\sum_{n\in \sigma}(\mathcal{T} x)_ne_n\Big) = \chi_{\sigma}(V\phi)
\end{eqnarray*}
\begin{eqnarray*}
\chi_{\sigma}(V\phi_{k_j})&=& \sum_{n\in\sigma} (V\phi_{k_j})(n) = \sum_{n\in\sigma}(\mathcal{T} x)_n\phi_{k_j}(e_n)\\
&=& \phi_{k_j}\Big(\sum_{n\in \sigma}(\mathcal{T} x)_ne_n\Big) \to \phi\Big(\sum_{n\in \sigma}(\mathcal{T} x)_ne_n\Big) = \chi_{\sigma}(V\phi)
\end{eqnarray*} as ![]() $j\to\infty.$ The series
$j\to\infty.$ The series ![]() $\sum_{n\in \sigma}(\mathcal{T} x)_ne_n$ converges since
$\sum_{n\in \sigma}(\mathcal{T} x)_ne_n$ converges since ![]() $x\in E_{\mathcal{P}}$ and
$x\in E_{\mathcal{P}}$ and ![]() $\{e_n\}_{n\geq 1}$ is an unconditional basis for
$\{e_n\}_{n\geq 1}$ is an unconditional basis for ![]() $E_{\mathcal{P}}.$ Observe that
$E_{\mathcal{P}}.$ Observe that ![]() $
\overline{\text{span}}\{\chi_{\sigma}:\ \sigma\subset \mathbb{N}\}=\ell^{\infty}
$ and the sequence
$
\overline{\text{span}}\{\chi_{\sigma}:\ \sigma\subset \mathbb{N}\}=\ell^{\infty}
$ and the sequence  $\{V\phi_{k_j}\}_{j\geq 1}$ is bounded. It follows the desired convergence of
$\{V\phi_{k_j}\}_{j\geq 1}$ is bounded. It follows the desired convergence of  $V \phi_{k_j}$.
$V \phi_{k_j}$.
Sufficiency: Let ![]() $Q_n: \ell^1\to \ell^1$ be a natural projection such that
$Q_n: \ell^1\to \ell^1$ be a natural projection such that ![]() $Q_n(\alpha_1, \alpha_2, \cdots)=
(0, \cdots, 0, \alpha_{n+1}, \cdots),$ where
$Q_n(\alpha_1, \alpha_2, \cdots)=
(0, \cdots, 0, \alpha_{n+1}, \cdots),$ where ![]() $\alpha=(\alpha_1, \alpha_2, \cdots)\in\ell^1.$ Then
$\alpha=(\alpha_1, \alpha_2, \cdots)\in\ell^1.$ Then  $\lim\limits_{n\to\infty}Q_n(\alpha)=0$ for
$\lim\limits_{n\to\infty}Q_n(\alpha)=0$ for ![]() $\alpha\in\ell^1.$ Since the operator V is compact and the set
$\alpha\in\ell^1.$ Since the operator V is compact and the set ![]() $K=\overline{V(B_{E^{\ast}})}$ is compact, Qn converges to 0 uniformly in
$K=\overline{V(B_{E^{\ast}})}$ is compact, Qn converges to 0 uniformly in ![]() $K.$ It follows that
$K.$ It follows that  $\big\{\sum_{n=1}^N(\mathcal{T} x)_ne_n\big\}_{N\geq 1}$ is a Cauchy sequence in
$\big\{\sum_{n=1}^N(\mathcal{T} x)_ne_n\big\}_{N\geq 1}$ is a Cauchy sequence in ![]() $E,$ since
$E,$ since
 \begin{eqnarray*}
\Big\|\sum_{n=p}^q(\mathcal{T} x)_ne_n\Big\|_E
&\leq& \sup_{\phi\in B_{E^{\ast}}}\sum_{n=p}^q|(\mathcal{T} x)_n||\phi(e_n)|
= \sup_{\phi\in B_{E^{\ast}}}\big\|(Q_q-Q_p)(V\phi)\big\|_{\ell^1}.
\end{eqnarray*}
\begin{eqnarray*}
\Big\|\sum_{n=p}^q(\mathcal{T} x)_ne_n\Big\|_E
&\leq& \sup_{\phi\in B_{E^{\ast}}}\sum_{n=p}^q|(\mathcal{T} x)_n||\phi(e_n)|
= \sup_{\phi\in B_{E^{\ast}}}\big\|(Q_q-Q_p)(V\phi)\big\|_{\ell^1}.
\end{eqnarray*} This implies that ![]() $\sum_{n=1}^{\infty}(\mathcal{T} x)_ne_n$ converges in
$\sum_{n=1}^{\infty}(\mathcal{T} x)_ne_n$ converges in ![]() $E,$ and
$E,$ and ![]() $x\in E_{\mathcal{P}},$ as desired.
$x\in E_{\mathcal{P}},$ as desired.
11. A problem of A.E. Taylor
A common assumption imposed on Banach spaces of analytic functions over the unit disk is to ask
 \begin{equation}
\sup_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}}\leq C\|f\|_{\mathcal{X}}, \ \ f\in \mathcal{X}
\end{equation}
\begin{equation}
\sup_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}}\leq C\|f\|_{\mathcal{X}}, \ \ f\in \mathcal{X}
\end{equation}for some constant C > 0. Here, we essentially repeat a problem A. E. Taylor; see [Reference Taylor41, p. 151].
Problem C. Does there exist a functional Banach or p-Banach space ![]() $\mathcal{X}$ such that it satisfies the conditions of Definition 2 except for (iv), and there exists a constant C > 1 such that (12) holds but fails when C = 1?
$\mathcal{X}$ such that it satisfies the conditions of Definition 2 except for (iv), and there exists a constant C > 1 such that (12) holds but fails when C = 1?
Let ![]() $\mathcal{X}$ be a functional Banach space which satisfies the conditions of Definition 2 except for (iv). Then, for each
$\mathcal{X}$ be a functional Banach space which satisfies the conditions of Definition 2 except for (iv). Then, for each ![]() $f\in\mathcal{X}_{\mathcal{P}},$
$f\in\mathcal{X}_{\mathcal{P}},$ ![]() $\mathrm{e}^{\mathrm{i}\theta}\mapsto f(\cdot \mathrm{e}^{\mathrm{i}\theta})$ is Bochner measurable from
$\mathrm{e}^{\mathrm{i}\theta}\mapsto f(\cdot \mathrm{e}^{\mathrm{i}\theta})$ is Bochner measurable from ![]() $\mathbb{T}\to\mathcal{X};$ see [Reference Blasco and Stylogiannis8, Theorem 2.3]. Combining the Poisson integral expression for fr and the vectorial Jensen inequality [Reference Hytönen, van Neerven, Veraar and Weis20, Proposition 1.2.11, p. 19], one can prove the following:
$\mathbb{T}\to\mathcal{X};$ see [Reference Blasco and Stylogiannis8, Theorem 2.3]. Combining the Poisson integral expression for fr and the vectorial Jensen inequality [Reference Hytönen, van Neerven, Veraar and Weis20, Proposition 1.2.11, p. 19], one can prove the following:
Lemma 22. Let ![]() $\mathcal{X}$ be a functional Banach space which satisfies the conditions of Definition 2 except for (iv). Then, for each
$\mathcal{X}$ be a functional Banach space which satisfies the conditions of Definition 2 except for (iv). Then, for each ![]() $f\in\mathcal{X}_{\mathcal{P}},$ we have
$f\in\mathcal{X}_{\mathcal{P}},$ we have
(i)
 $r\mapsto\|f_r\|_{\mathcal{X}}$ is increasing for
$r\mapsto\|f_r\|_{\mathcal{X}}$ is increasing for  $r \in (0, 1)$; and
$r \in (0, 1)$; and(ii)
 $\lim_{r\to1^{-}}\|f_r\|_{\mathcal{X}}\leq\|f\|_{\mathcal{X}}.$
$\lim_{r\to1^{-}}\|f_r\|_{\mathcal{X}}\leq\|f\|_{\mathcal{X}}.$
This prompts us to raise the following question:
Problem D. Does there exist a functional Banach or p-Banach space ![]() $\mathcal{X}$ which satisfies the conditions of Definition 2 except for (iv), and there exists some function
$\mathcal{X}$ which satisfies the conditions of Definition 2 except for (iv), and there exists some function ![]() $f\in\mathcal{X}$ such that
$f\in\mathcal{X}$ such that  $\sup\limits_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}} \lt \|f\|_{\mathcal{X}}?$
$\sup\limits_{0\leq r \lt 1}\|f_r\|_{\mathcal{X}} \lt \|f\|_{\mathcal{X}}?$
Acknowledgement
G. Cheng is supported by NSFC (12371126). X. Fang is supported by NSTC of Taiwan (NSTC 112-2115-M-008-010-MY2). C. Liu is supported by NSFC (12101103). Y. Lu is supported by NSFC (12031002).