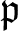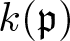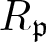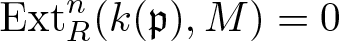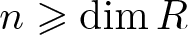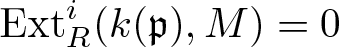1. Introduction
Over a commutative noetherian ring R, the injective and flat dimension of a module can be detected by vanishing of Ext and Tor with coefficients in residue fields ![]() $k(\mathfrak{p})$ at the prime ideals
$k(\mathfrak{p})$ at the prime ideals ![]() $\mathfrak{p}$ of R. This drives the interest in rigidity properties of Ext and Tor – here rigidity refers to the phenomenon that vanishing of, say,
$\mathfrak{p}$ of R. This drives the interest in rigidity properties of Ext and Tor – here rigidity refers to the phenomenon that vanishing of, say, ![]() $\mathrm{Ext}^n$ implies vanishing of
$\mathrm{Ext}^n$ implies vanishing of ![]() $\mathrm{Ext}^i$ for all
$\mathrm{Ext}^i$ for all ![]() $i\geqslant n$. Rigidity of Ext and Tor with coefficients in residue fields was studied by Christensen et al. [Reference Christensen, Iyengar and Marley7]. Here we push the investigation further in two directions: (1) We eliminate certain asymmetries in the rigidity statements for Ext/Tor and injective/flat dimension obtained in [Reference Christensen, Iyengar and Marley7]. (2) We establish and improve results on flat dimension that are conceptually dual to results on injective dimension already in the literature, including results obtained in [Reference Christensen, Iyengar and Marley7].
$i\geqslant n$. Rigidity of Ext and Tor with coefficients in residue fields was studied by Christensen et al. [Reference Christensen, Iyengar and Marley7]. Here we push the investigation further in two directions: (1) We eliminate certain asymmetries in the rigidity statements for Ext/Tor and injective/flat dimension obtained in [Reference Christensen, Iyengar and Marley7]. (2) We establish and improve results on flat dimension that are conceptually dual to results on injective dimension already in the literature, including results obtained in [Reference Christensen, Iyengar and Marley7].
We work with complexes of modules and our main result, found in § 3, is:
Theorem. Let R be a commutative noetherian ring and M an R-complex. If for an integer ![]() $n\geqslant\dim R+\operatorname{sup}{\mathrm H^\ast(M)}$ one has
$n\geqslant\dim R+\operatorname{sup}{\mathrm H^\ast(M)}$ one has ![]() $\operatorname{Ext}_R^{n}(k(\mathfrak{p}),M)=0$ for all prime ideals
$\operatorname{Ext}_R^{n}(k(\mathfrak{p}),M)=0$ for all prime ideals ![]() $\mathfrak{p}$ in R, then
$\mathfrak{p}$ in R, then ![]() $\operatorname{inj.\! dim}_R M \lt n$ holds.
$\operatorname{inj.\! dim}_R M \lt n$ holds.
This improves [Reference Christensen, Iyengar and Marley7, Theorem 5.7] and aligns perfectly with [Reference Christensen, Iyengar and Marley7, Theorem 4.1] on flat dimension. From the result of Christensen and Iyengar [Reference Christensen and Iyengar6, Theorem 1.1], the proof reduces to show, for complexes, the statement on Ext-rigidity made in the Abstract.
In § 4, we prove results on flat dimension of complexes which are dual to already established results on injective dimension. In one of these, we remove a boundedness assumption from [Reference Nakamura and Thompson12, Theorem 4.8], which is dual to [Reference Christensen, Iyengar and Marley7, Corollary 5.9]:
Theorem. Let R be a commutative noetherian ring of finite Krull dimension and M an R-complex. If M has finite flat dimesion, then the next equality holds,
 \begin{equation*} \operatorname{flat\, dim}_R M =\sup_{\mathfrak{p}\in\operatorname{Spec} R}\left\{\operatorname{depth}R_{\mathfrak p}-{\mathrm{depth}}_{R_{\mathfrak p}}R{\mathrm{Hom}}_R(R_{\mathfrak p},M)\right\}.\end{equation*}
\begin{equation*} \operatorname{flat\, dim}_R M =\sup_{\mathfrak{p}\in\operatorname{Spec} R}\left\{\operatorname{depth}R_{\mathfrak p}-{\mathrm{depth}}_{R_{\mathfrak p}}R{\mathrm{Hom}}_R(R_{\mathfrak p},M)\right\}.\end{equation*} A novel aspect of our arguments involves the notion of minimal semi-flat-cotorsion replacements. Recall first that a flat-cotorsion module is one which is both flat and right ![]() $\operatorname{Ext}^1$-orthogonal to flat modules. A semi-flat complex consisting of flat-cotorsion modules is called a semi-flat-cotorsion complex. Work of Gillespie [Reference Gillespie10] shows that every complex is isomorphic in the derived category to a semi-flat-cotorsion complex; such a complex is called a semi-flat-cotorsion replacement.
$\operatorname{Ext}^1$-orthogonal to flat modules. A semi-flat complex consisting of flat-cotorsion modules is called a semi-flat-cotorsion complex. Work of Gillespie [Reference Gillespie10] shows that every complex is isomorphic in the derived category to a semi-flat-cotorsion complex; such a complex is called a semi-flat-cotorsion replacement.
Minimality plays a crucial role in considerations of rigidity and homological dimensions. A complex M is minimal if every homotopy equivalence M → M is an isomorphism. Minimal semi-injective resolutions always exist, and they detect injective dimension; several proofs in [Reference Christensen, Iyengar and Marley7] rely on this. On the other hand, although semi-flat resolutions always exist, they may not contain a homotopically equivalent minimal summand that detects the flat dimension, see [Reference Christensen and Thompson8, Example 3.9]. Recently, Nakamura and Thompson [Reference Nakamura and Thompson12] showed that every complex over a commutative noetherian ring of finite Krull dimension has a minimal semi-flat-cotorsion replacement and that such a complex detects the flat dimension.
In this paper, we also take the opportunity to clarify a couple of statements in [Reference Christensen, Iyengar and Marley7]; see Remarks 2.4 and 5.3.
In this paper R is a commutative noetherian ring. We widely adopt the notation used in [Reference Christensen, Iyengar and Marley7]; in particular, we use both homological and cohomological notation.
1.1.
Let M be an R-complex.
For an integer s, we denote by ![]() $\Sigma^sM$ the complex with the module
$\Sigma^sM$ the complex with the module ![]() $M_{i-s}$ in degree i and differential
$M_{i-s}$ in degree i and differential  ${\rm d}^{\Sigma^sM}=(-1)^s{\rm d}^M$.
${\rm d}^{\Sigma^sM}=(-1)^s{\rm d}^M$.
Set ![]() $\inf \operatorname{H}_*(M):= \inf\{i \mid \operatorname{H}_i(M)\not=0\}$ and
$\inf \operatorname{H}_*(M):= \inf\{i \mid \operatorname{H}_i(M)\not=0\}$ and ![]() $\inf \operatorname{H}^*(M):= \inf\{i\mid \operatorname{H}^i(M)\not=0\}$, and define
$\inf \operatorname{H}^*(M):= \inf\{i\mid \operatorname{H}^i(M)\not=0\}$, and define ![]() $\sup\operatorname{H}_*(M)$ and
$\sup\operatorname{H}_*(M)$ and ![]() $\sup\operatorname{H}^*(M)$ similarly.
$\sup\operatorname{H}^*(M)$ similarly.
In case R is local with maximal ideal ![]() $\mathfrak{m}$, the right derived
$\mathfrak{m}$, the right derived ![]() $\mathfrak{m}$-torsion functor is denoted
$\mathfrak{m}$-torsion functor is denoted ![]() $\mathsf{R}\Gamma_\mathfrak{m}$ and
$\mathsf{R}\Gamma_\mathfrak{m}$ and ![]() $\mathsf{L}\Lambda^{\mathfrak{m}}$ is the left derived
$\mathsf{L}\Lambda^{\mathfrak{m}}$ is the left derived ![]() $\mathfrak{m}$-completion functor. The corresponding local (co)homology modules are denoted
$\mathfrak{m}$-completion functor. The corresponding local (co)homology modules are denoted ![]() $\operatorname{H}_\mathfrak{m}^*(M)$ and
$\operatorname{H}_\mathfrak{m}^*(M)$ and ![]() $\operatorname{H}^\mathfrak{m}_*(M)$. As always,
$\operatorname{H}^\mathfrak{m}_*(M)$. As always,
where k denotes the residue field ![]() $R/\mathfrak{m}$.
$R/\mathfrak{m}$.
We recall from [Reference Nakamura and Thompson12] some properties of minimal semi-flat-cotorsion complexes that will be used frequently.
1.2.
Assume that R has finite Krull dimension and let M be an R-complex. By [Reference Nakamura and Thompson12, Theorem 3.4], there exists a minimal semi-flat-cotorsion complex F isomorphic to M in the derived category: a minimal semi-flat-cotorsion replacement of M.
If M has finite flat dimension, then it follows from [Reference Nakamura and Thompson12, Lemma 4.1] that ![]() $F_i = 0$ holds for
$F_i = 0$ holds for ![]() $i \gt \operatorname{flat\,dim}_RM$.
$i \gt \operatorname{flat\,dim}_RM$.
If ![]() $\operatorname{H}_i(M) = 0$ holds for
$\operatorname{H}_i(M) = 0$ holds for ![]() $i \ll 0$, then
$i \ll 0$, then ![]() $F_i = 0$ for
$F_i = 0$ for ![]() $i \ll 0$ by [Reference Nakamura and Thompson12, Lemma 4.1].
$i \ll 0$ by [Reference Nakamura and Thompson12, Lemma 4.1].
For every prime ideal ![]() $\mathfrak{p}$ in R, the complex
$\mathfrak{p}$ in R, the complex ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F)$ is isomorphic in the derived category to
$\operatorname{Hom}_R(R_\mathfrak{p},F)$ is isomorphic in the derived category to ![]() $\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)$, see [Reference Nakamura and Thompson12, (A.1)]. Further, it consists by [Reference Thompson15, Lemma 2.2] of flat-cotorsion R-modules, so if
$\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)$, see [Reference Nakamura and Thompson12, (A.1)]. Further, it consists by [Reference Thompson15, Lemma 2.2] of flat-cotorsion R-modules, so if ![]() $F_i = 0$ for
$F_i = 0$ for ![]() $i \ll 0$, then
$i \ll 0$, then ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F)$ is a semi-flat-cotorsion replacement of
$\operatorname{Hom}_R(R_\mathfrak{p},F)$ is a semi-flat-cotorsion replacement of ![]() $\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)$ over both R and
$\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)$ over both R and ![]() $R_\mathfrak{p}$.
$R_\mathfrak{p}$.
2. Rigidity of Tor
The main result of this section, Theorem 2.2 below, removes a boundedness condition on ![]() $\operatorname{H}_*(M)$ from [Reference Christensen, Iyengar and Marley7, Proposition 3.3(1)] and aligns perfectly – see Remark 2.3 below – with [Reference Christensen, Iyengar and Marley7, Proposition 3.2] on rigidity of Ext.
$\operatorname{H}_*(M)$ from [Reference Christensen, Iyengar and Marley7, Proposition 3.3(1)] and aligns perfectly – see Remark 2.3 below – with [Reference Christensen, Iyengar and Marley7, Proposition 3.2] on rigidity of Ext.
Lemma 2.1. Let ![]() $(R,\mathfrak{m},k)$ be a local ring and F a minimal semi-flat-cotorsion R-complex. There is an isomorphism of R-complexes
$(R,\mathfrak{m},k)$ be a local ring and F a minimal semi-flat-cotorsion R-complex. There is an isomorphism of R-complexes ![]() $k\otimes_RF\cong k\otimes_R\Lambda^\mathfrak{m}(F)$, and both complexes have zero differential.
$k\otimes_RF\cong k\otimes_R\Lambda^\mathfrak{m}(F)$, and both complexes have zero differential.
Proof. The canonical map ![]() $F\to \Lambda^\mathfrak{m}(F)$ induces per [Reference Schenzel and Simon14, Theorem 2.2.2] an isomorphism of complexes
$F\to \Lambda^\mathfrak{m}(F)$ induces per [Reference Schenzel and Simon14, Theorem 2.2.2] an isomorphism of complexes ![]() $k\otimes_R F\to k\otimes_R \Lambda^\mathfrak{m}(F)$. Minimality of F implies per [Reference Nakamura and Thompson12, Theorem 2.3] that
$k\otimes_R F\to k\otimes_R \Lambda^\mathfrak{m}(F)$. Minimality of F implies per [Reference Nakamura and Thompson12, Theorem 2.3] that ![]() $k\otimes_R F$, and hence also
$k\otimes_R F$, and hence also ![]() $k\otimes_R \Lambda^\mathfrak{m}(F)$, has zero differential.
$k\otimes_R \Lambda^\mathfrak{m}(F)$, has zero differential.
Theorem 2.2. Let ![]() $(R,\mathfrak{m},k)$ be a local ring and M an R-complex. If one has
$(R,\mathfrak{m},k)$ be a local ring and M an R-complex. If one has  $\operatorname{Tor}^R_{n+1}(k,M)=0$ for an integer
$\operatorname{Tor}^R_{n+1}(k,M)=0$ for an integer ![]() $n \geqslant\sup\operatorname{H}^\mathfrak{m}_*(M)$, then
$n \geqslant\sup\operatorname{H}^\mathfrak{m}_*(M)$, then ![]() $\operatorname{Tor}^R_i(k,M)=0$ holds for all i > n and the next equality holds,
$\operatorname{Tor}^R_i(k,M)=0$ holds for all i > n and the next equality holds,
Proof. If the complex ![]() $k\otimes^{\mathsf{L}}_RM$ is acyclic, then one has
$k\otimes^{\mathsf{L}}_RM$ is acyclic, then one has ![]() $\sup\operatorname{Tor}^R_*(k,M)=-\infty$, so the assertion of the theorem is trivial, and so is the equality since
$\sup\operatorname{Tor}^R_*(k,M)=-\infty$, so the assertion of the theorem is trivial, and so is the equality since ![]() $\operatorname{depth}_RM=\infty$ holds in this case, see [Reference Foxby and Iyengar9, Definitions 2.3 and 4.3]. Hence, we may assume that
$\operatorname{depth}_RM=\infty$ holds in this case, see [Reference Foxby and Iyengar9, Definitions 2.3 and 4.3]. Hence, we may assume that ![]() $k\otimes^{\mathsf{L}}_RM$ is not acyclic. From [Reference Christensen, Iyengar and Marley7, (2.6)], it follows that
$k\otimes^{\mathsf{L}}_RM$ is not acyclic. From [Reference Christensen, Iyengar and Marley7, (2.6)], it follows that ![]() $\mathsf{L}\Lambda^\mathfrak{m}(M)$ is not acyclic. If
$\mathsf{L}\Lambda^\mathfrak{m}(M)$ is not acyclic. If ![]() $\sup\operatorname{H}^\mathfrak{m}_*(M)=\infty$ holds, then the statement is vacuously true. Thus, we may assume that
$\sup\operatorname{H}^\mathfrak{m}_*(M)=\infty$ holds, then the statement is vacuously true. Thus, we may assume that ![]() $\sup\operatorname{H}^\mathfrak{m}_*(M) \lt \infty$ holds, and set
$\sup\operatorname{H}^\mathfrak{m}_*(M) \lt \infty$ holds, and set ![]() $s := \sup\operatorname{H}^\mathfrak{m}_*(M)$.
$s := \sup\operatorname{H}^\mathfrak{m}_*(M)$.
Let F be a minimal semi-flat-cotorsion replacement of M, see 1.2, and set ![]() $P = \Lambda^\mathfrak{m}(F)$. As F is semi-flat, one has
$P = \Lambda^\mathfrak{m}(F)$. As F is semi-flat, one has ![]() $\mathsf{L}\Lambda^\mathfrak{m}(M)=P$, see for example [Reference Porta, Shaul and Yekutieli13, Proposition 3.6], and Lemma 2.1 yields the isomorphism
$\mathsf{L}\Lambda^\mathfrak{m}(M)=P$, see for example [Reference Porta, Shaul and Yekutieli13, Proposition 3.6], and Lemma 2.1 yields the isomorphism ![]() $k\otimes^{\mathsf{L}}_RM \simeq k\otimes_RP$ in the derived category. For every
$k\otimes^{\mathsf{L}}_RM \simeq k\otimes_RP$ in the derived category. For every ![]() $i\in\mathbb{Z}$, the
$i\in\mathbb{Z}$, the ![]() $\mathfrak{m}$-complete module
$\mathfrak{m}$-complete module ![]() $P_i = \Lambda^\mathfrak{m}(F_i)$ is flat-cotorsion, see [Reference Thompson15, Lemma 2.2]. The complex
$P_i = \Lambda^\mathfrak{m}(F_i)$ is flat-cotorsion, see [Reference Thompson15, Lemma 2.2]. The complex ![]() $\Sigma^s(P_{\geqslant s})$ is a semi-flat-cotorsion replacement of the module
$\Sigma^s(P_{\geqslant s})$ is a semi-flat-cotorsion replacement of the module ![]() $C = \operatorname{Coker}({P_{s+1}\rightarrow P_s})$. For every integer i > s, there are isomorphisms
$C = \operatorname{Coker}({P_{s+1}\rightarrow P_s})$. For every integer i > s, there are isomorphisms
 \begin{equation*}
\operatorname{Tor}_i^R(k,M) \cong \operatorname{H}_i(k\otimes_RP) \cong
\operatorname{H}_i(k\otimes_RP_{\geqslant s}) \cong \operatorname{Tor}_{i-s}^R(k,C).
\end{equation*}
\begin{equation*}
\operatorname{Tor}_i^R(k,M) \cong \operatorname{H}_i(k\otimes_RP) \cong
\operatorname{H}_i(k\otimes_RP_{\geqslant s}) \cong \operatorname{Tor}_{i-s}^R(k,C).
\end{equation*} Let ![]() $n\geqslant s$ and assume that
$n\geqslant s$ and assume that  $\operatorname{Tor}^R_{n+1}(k,M)=0$ holds. By the isomorphisms above, one has
$\operatorname{Tor}^R_{n+1}(k,M)=0$ holds. By the isomorphisms above, one has  $\operatorname{Tor}_{n+1-s}^R(k,C)=0$. The complex P, and hence the truncated complex
$\operatorname{Tor}_{n+1-s}^R(k,C)=0$. The complex P, and hence the truncated complex ![]() $P_{\geqslant s}$, is
$P_{\geqslant s}$, is ![]() $\mathfrak{m}$-complete, so the module C is derived
$\mathfrak{m}$-complete, so the module C is derived ![]() $\mathfrak{m}$-complete. It now follows from [Reference Christensen, Iyengar and Marley7, Lemma 2.1] that the module C has flat dimension at most n − s; in particular,
$\mathfrak{m}$-complete. It now follows from [Reference Christensen, Iyengar and Marley7, Lemma 2.1] that the module C has flat dimension at most n − s; in particular, ![]() $\operatorname{Tor}_i^R(k,M) = \operatorname{Tor}^R_{i-s}(k,C)=0$ holds for all
$\operatorname{Tor}_i^R(k,M) = \operatorname{Tor}^R_{i-s}(k,C)=0$ holds for all ![]() $i\geqslant n+1$. This proves the first claim.
$i\geqslant n+1$. This proves the first claim.
To prove the asserted equality, let E be the injective envelope of k. Adjunction yields
 \begin{equation*}
\operatorname{Hom}_R(\operatorname{Tor}_i^R(k,M),E) \cong \operatorname{Ext}^i_R(k,\operatorname{Hom}_R(M,E))\,,
\end{equation*}
\begin{equation*}
\operatorname{Hom}_R(\operatorname{Tor}_i^R(k,M),E) \cong \operatorname{Ext}^i_R(k,\operatorname{Hom}_R(M,E))\,,
\end{equation*} so ![]() $\operatorname{Ext}^i_R(k,\operatorname{Hom}_R(M,E)) = 0$ holds for
$\operatorname{Ext}^i_R(k,\operatorname{Hom}_R(M,E)) = 0$ holds for ![]() $i \gg 0$. Now faithful injectivity of E, together with [Reference Christensen, Iyengar and Marley7, Proposition 3.2], yields
$i \gg 0$. Now faithful injectivity of E, together with [Reference Christensen, Iyengar and Marley7, Proposition 3.2], yields
 \begin{align*}
\sup{\operatorname{Tor}^R_*(k,M)} &= \sup{\operatorname{Ext}_R^*(k,\operatorname{Hom}_R(M,E))} \\
& = \operatorname{depth} R- \operatorname{width}_R \operatorname{Hom}_R(M,E) \\
& = \operatorname{depth} R - \operatorname{depth}_R M ,
\end{align*}
\begin{align*}
\sup{\operatorname{Tor}^R_*(k,M)} &= \sup{\operatorname{Ext}_R^*(k,\operatorname{Hom}_R(M,E))} \\
& = \operatorname{depth} R- \operatorname{width}_R \operatorname{Hom}_R(M,E) \\
& = \operatorname{depth} R - \operatorname{depth}_R M ,
\end{align*}where the last equality is standard, see for example [Reference Foxby and Iyengar9, Proposition 4.4].
Remark 2.3. The bound on n in [Reference Christensen, Iyengar and Marley7, Proposition 3.2] appears to be 1 lower than the bound in Theorem 2.2, but as noted in the opening paragraph of [Reference Christensen, Iyengar and Marley7, Section 3], the lower bound cannot possibly be attained. We show below that one could similarly lower the bound in Theorem 2.2 by 1 as ![]() $\operatorname{Tor}_s^R(k,M) \ne 0$ holds for
$\operatorname{Tor}_s^R(k,M) \ne 0$ holds for ![]() $s = \sup\operatorname{H}^\mathfrak{m}_*(M)$.
$s = \sup\operatorname{H}^\mathfrak{m}_*(M)$.
Let M be an R-complex and F a minimal semi-flat-cotorsion replacement of M. Set ![]() $n=\sup \operatorname{H}^\mathfrak{m}_*(M)$. In degree n, the complex
$n=\sup \operatorname{H}^\mathfrak{m}_*(M)$. In degree n, the complex ![]() $\Lambda^\mathfrak{m}(F)$ is nonzero and Lemma 2.1 yields
$\Lambda^\mathfrak{m}(F)$ is nonzero and Lemma 2.1 yields ![]() $\operatorname{Tor}^R_n(k,M) = k\otimes_R \Lambda^\mathfrak{m}(F)_n$, which is nonzero, see [Reference Schenzel and Simon14, Observation 2.1.2].
$\operatorname{Tor}^R_n(k,M) = k\otimes_R \Lambda^\mathfrak{m}(F)_n$, which is nonzero, see [Reference Schenzel and Simon14, Observation 2.1.2].
Remark 2.4. The conclusion of [Reference Christensen, Iyengar and Marley7, Lemma 2.1] states that ![]() $\operatorname{Tor}_n^R(-,M)=0$ holds if M is a derived
$\operatorname{Tor}_n^R(-,M)=0$ holds if M is a derived ![]() $\mathfrak{a}$-complete complex with
$\mathfrak{a}$-complete complex with ![]() $\inf\operatorname{H}_*(M) \gt -\infty$ and
$\inf\operatorname{H}_*(M) \gt -\infty$ and ![]() $\operatorname{Tor}_n^R(R/\mathfrak{p},M)=0$ holds for all prime ideals
$\operatorname{Tor}_n^R(R/\mathfrak{p},M)=0$ holds for all prime ideals ![]() $\mathfrak{p}$ that contain
$\mathfrak{p}$ that contain ![]() $\mathfrak{a}$. We notice here that the proof in [Reference Christensen, Iyengar and Marley7] only demonstrates this for
$\mathfrak{a}$. We notice here that the proof in [Reference Christensen, Iyengar and Marley7] only demonstrates this for ![]() $\operatorname{Tor}_n^R(-,M)$ as a functor on the category of R-modules (not R-complexes). This is sufficient for the purposes of its use in both [Reference Christensen, Iyengar and Marley7] and the proof above. To see that the conclusion fails for Tor as a functor on complexes, let
$\operatorname{Tor}_n^R(-,M)$ as a functor on the category of R-modules (not R-complexes). This is sufficient for the purposes of its use in both [Reference Christensen, Iyengar and Marley7] and the proof above. To see that the conclusion fails for Tor as a functor on complexes, let ![]() $(R,\mathfrak{m},k)$ be a complete local ring and notice that though
$(R,\mathfrak{m},k)$ be a complete local ring and notice that though ![]() $\operatorname{Tor}_n^R(k,R) = 0$ holds for every
$\operatorname{Tor}_n^R(k,R) = 0$ holds for every ![]() $n \geqslant 1$, one has
$n \geqslant 1$, one has  $\operatorname{Tor}_n^R(\Sigma^nk,R) \cong k$.
$\operatorname{Tor}_n^R(\Sigma^nk,R) \cong k$.
3. Injective dimension
The next result improves the bound on n in [Reference Christensen, Iyengar and Marley7, Proposition 5.4 and Theorem 5.7].
Theorem 3.1. Let R be a commutative noetherian ring and M an R-complex. If for an integer ![]() $n \geqslant \dim R + \sup{\operatorname{H}^*(M)}$ one has
$n \geqslant \dim R + \sup{\operatorname{H}^*(M)}$ one has ![]() $\operatorname{Ext}_R^{n}(k(\mathfrak{p}),M)=0$ for all prime ideals
$\operatorname{Ext}_R^{n}(k(\mathfrak{p}),M)=0$ for all prime ideals ![]() $\mathfrak{p}$ in R, then
$\mathfrak{p}$ in R, then ![]() $\operatorname{inj.\! dim}_R M \lt n$ holds.
$\operatorname{inj.\! dim}_R M \lt n$ holds.
Proof. We may assume that R has finite Krull dimension and that M is not acyclic. We may also assume that ![]() $\operatorname{H}^i(M) = 0$ holds for
$\operatorname{H}^i(M) = 0$ holds for ![]() $i \gg 0$, otherwise the statement is vacuous. For every prime ideal
$i \gg 0$, otherwise the statement is vacuous. For every prime ideal ![]() $\mathfrak{p}$ in R, one has
$\mathfrak{p}$ in R, one has
 \begin{equation*}
0 = \operatorname{Ext}^{n}_R(k(\mathfrak{p}),M)
\cong \operatorname{Ext}^{n}_{R_\mathfrak{p}}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M))
\end{equation*}
\begin{equation*}
0 = \operatorname{Ext}^{n}_R(k(\mathfrak{p}),M)
\cong \operatorname{Ext}^{n}_{R_\mathfrak{p}}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M))
\end{equation*} by Hom–tensor adjunction in the derived category. It suffices, by [Reference Christensen and Iyengar6, Theorem 1.1] and [Reference Christensen, Iyengar and Marley7, Proposition 3.2], to show that  $\dim R + \sup \operatorname{H}^*(M) \geqslant \sup{\operatorname{H}^*_{\mathfrak{p}_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)}$ holds. For every
$\dim R + \sup \operatorname{H}^*(M) \geqslant \sup{\operatorname{H}^*_{\mathfrak{p}_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)}$ holds. For every ![]() $R_\mathfrak{p}$-complex X, there is an isomorphism
$R_\mathfrak{p}$-complex X, there is an isomorphism ![]() $\mathsf{R}\Gamma_{\mathfrak{p}_\mathfrak{p}}X \simeq \mathsf{R}\Gamma_\mathfrak{p} X$ in the derived category over
$\mathsf{R}\Gamma_{\mathfrak{p}_\mathfrak{p}}X \simeq \mathsf{R}\Gamma_\mathfrak{p} X$ in the derived category over ![]() $R_\mathfrak{p}$; this follows for example from [Reference Alonso Tarrío, Jeremías López and Lipman1, Lemma (3.2.3)] and explains the first and last isomorphisms in the next display. The second isomorphism holds by [Reference Alonso Tarrío, Jeremías López and Lipman11, Corollary (5.1.1)], while the third comes from [Reference Benson, Iyengar and Krause4, Proposition 8.3].
$R_\mathfrak{p}$; this follows for example from [Reference Alonso Tarrío, Jeremías López and Lipman1, Lemma (3.2.3)] and explains the first and last isomorphisms in the next display. The second isomorphism holds by [Reference Alonso Tarrío, Jeremías López and Lipman11, Corollary (5.1.1)], while the third comes from [Reference Benson, Iyengar and Krause4, Proposition 8.3].
 \begin{equation}
\begin{aligned}
\mathsf{R}\Gamma_{\mathfrak{p}_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M) & \simeq \mathsf{R}\Gamma_{\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)\\ &\simeq\mathsf{R}\Gamma_{\mathfrak{p}}\mathsf{L}\Lambda^{\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M) \\
& \simeq \mathsf{R}\Gamma_{\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},\mathsf{L}\Lambda^\mathfrak{p} M)\\
&\simeq\mathsf{R}\Gamma_{\mathfrak{p}_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},\mathsf{L}\Lambda^\mathfrak{p} M).
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\mathsf{R}\Gamma_{\mathfrak{p}_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M) & \simeq \mathsf{R}\Gamma_{\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)\\ &\simeq\mathsf{R}\Gamma_{\mathfrak{p}}\mathsf{L}\Lambda^{\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M) \\
& \simeq \mathsf{R}\Gamma_{\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},\mathsf{L}\Lambda^\mathfrak{p} M)\\
&\simeq\mathsf{R}\Gamma_{\mathfrak{p}_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},\mathsf{L}\Lambda^\mathfrak{p} M).
\end{aligned}
\end{equation} Let F be a minimal semi-flat-cotorsion replacement of M. In cohomological notation one has ![]() $F^i=0$ for
$F^i=0$ for ![]() $i \gg 0$, see 1.2, so the complex
$i \gg 0$, see 1.2, so the complex ![]() $\Lambda^\mathfrak{p} F \simeq \mathsf{L}\Lambda^\mathfrak{p} M$ is again a semi-flat-cotorsion R-complex, see [Reference Thompson15, Lemma 2.2]. In the derived category, the complex
$\Lambda^\mathfrak{p} F \simeq \mathsf{L}\Lambda^\mathfrak{p} M$ is again a semi-flat-cotorsion R-complex, see [Reference Thompson15, Lemma 2.2]. In the derived category, the complex ![]() $P = \operatorname{Hom}_R(R_\mathfrak{p},\Lambda^\mathfrak{p} F)$ is now isomorphic to
$P = \operatorname{Hom}_R(R_\mathfrak{p},\Lambda^\mathfrak{p} F)$ is now isomorphic to ![]() $\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},\mathsf{L}\Lambda^\mathfrak{p} M)$. Further [Reference Nakamura and Thompson12, Lemma 4.1] yields
$\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},\mathsf{L}\Lambda^\mathfrak{p} M)$. Further [Reference Nakamura and Thompson12, Lemma 4.1] yields ![]() $P^i = 0$ for
$P^i = 0$ for ![]() $i \gt \sup{\operatorname{H}^*(M)} + \dim R/\mathfrak{p}$, which explains the second inequality in the computation below. The first equality holds by (1), and the first inequality holds by [Reference Christensen, Iyengar and Marley7, (2.7)],
$i \gt \sup{\operatorname{H}^*(M)} + \dim R/\mathfrak{p}$, which explains the second inequality in the computation below. The first equality holds by (1), and the first inequality holds by [Reference Christensen, Iyengar and Marley7, (2.7)],
 \begin{align*}
\sup{\operatorname{H}^*_{\mathfrak{p}_\mathfrak{p}}(\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M))}
& = \sup{\operatorname{H}^*(\mathsf{R}\Gamma_{\mathfrak{p}_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},\mathsf{L}\Lambda^\mathfrak{p} M))} \\
& \leqslant \dim R_\mathfrak{p} + \sup{\operatorname{H}^*(\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},\mathsf{L}\Lambda^\mathfrak{p} M))} \\
& = \dim R_\mathfrak{p} + \sup{\operatorname{H}^*(P)} \\
& \leqslant \dim R_\mathfrak{p} + \dim R/\mathfrak{p} + \sup{\operatorname{H}^*(M)} \\
& \leqslant \dim R + \sup{\operatorname{H}^*(M)}.
\end{align*}
\begin{align*}
\sup{\operatorname{H}^*_{\mathfrak{p}_\mathfrak{p}}(\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M))}
& = \sup{\operatorname{H}^*(\mathsf{R}\Gamma_{\mathfrak{p}_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},\mathsf{L}\Lambda^\mathfrak{p} M))} \\
& \leqslant \dim R_\mathfrak{p} + \sup{\operatorname{H}^*(\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},\mathsf{L}\Lambda^\mathfrak{p} M))} \\
& = \dim R_\mathfrak{p} + \sup{\operatorname{H}^*(P)} \\
& \leqslant \dim R_\mathfrak{p} + \dim R/\mathfrak{p} + \sup{\operatorname{H}^*(M)} \\
& \leqslant \dim R + \sup{\operatorname{H}^*(M)}.
\end{align*}From the proof above one easily extracts the following rigidity result; for modules, it was stated in the Abstract.
Porism 3.2.
Let ![]() $\mathfrak{p}$ be a prime ideal in R and M an R-complex. If for an integer
$\mathfrak{p}$ be a prime ideal in R and M an R-complex. If for an integer ![]() $n \geqslant \dim R + \sup{\operatorname{H}^*(M)}$ one has
$n \geqslant \dim R + \sup{\operatorname{H}^*(M)}$ one has ![]() $\operatorname{Ext}_R^{n}(k(\mathfrak{p}),M)=0$, then
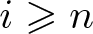
$\operatorname{Ext}_R^{n}(k(\mathfrak{p}),M)=0$, then ![]() $\operatorname{Ext}_R^{i}(k(\mathfrak{p}),M)=0$ holds for all
$\operatorname{Ext}_R^{i}(k(\mathfrak{p}),M)=0$ holds for all ![]() $i \geqslant n$.
$i \geqslant n$.
The bound on n in Theorem 3.1 and Porism 3.2 is sharp: Let ![]() $(R,\mathfrak{m},k)$ be a Cohen–Macaulay local ring that is not Gorenstein. One has
$(R,\mathfrak{m},k)$ be a Cohen–Macaulay local ring that is not Gorenstein. One has
This also shows that the bound on n in the next proposition is sharp. This statement is parallel to the first part of [Reference Christensen, Iyengar and Marley7, Theorem 4.1] and could have been made in [Reference Christensen, Iyengar and Marley7].
Proposition 3.3. Let R be a commutative noetherian ring and M an R-complex. If for a prime ideal ![]() $\mathfrak{p}$ and an integer
$\mathfrak{p}$ and an integer ![]() $n \geqslant \dim R_\mathfrak{p} + \sup{\operatorname{H}^*(\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M))}$ one has
$n \geqslant \dim R_\mathfrak{p} + \sup{\operatorname{H}^*(\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M))}$ one has ![]() $\operatorname{Ext}_R^{n}(k(\mathfrak{p}),M)=0$, then
$\operatorname{Ext}_R^{n}(k(\mathfrak{p}),M)=0$, then
 \begin{equation*}
\sup\operatorname{Ext}^*_R(k(\mathfrak{p}),M) = \operatorname{depth} R_\mathfrak{p} - \operatorname{width}_{R_\mathfrak{p}} \mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M) \lt n .
\end{equation*}
\begin{equation*}
\sup\operatorname{Ext}^*_R(k(\mathfrak{p}),M) = \operatorname{depth} R_\mathfrak{p} - \operatorname{width}_{R_\mathfrak{p}} \mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M) \lt n .
\end{equation*}Proof. Hom–tensor adjunction in the derived category yields for every integer n an isomorphism
 \begin{equation*}
\operatorname{Ext}_R^n(k(\mathfrak{p}),M) \cong \operatorname{Ext}_{R_\mathfrak{p}}^n(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}(R_\mathfrak{p},M)).
\end{equation*}
\begin{equation*}
\operatorname{Ext}_R^n(k(\mathfrak{p}),M) \cong \operatorname{Ext}_{R_\mathfrak{p}}^n(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}(R_\mathfrak{p},M)).
\end{equation*} Thus, the assertions follow immediately from [Reference Christensen, Iyengar and Marley7, Proposition 3.2] since one has  $n \geqslant \dim R_\mathfrak{p} + \sup{\operatorname{H}^*(\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M))} \geqslant
\sup\operatorname{H}_{\mathfrak{p}_\mathfrak{p}}^*(\mathsf{R}\mathrm{Hom}(R_\mathfrak{p},M))$; see [Reference Christensen, Iyengar and Marley7, (2.7)].
$n \geqslant \dim R_\mathfrak{p} + \sup{\operatorname{H}^*(\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M))} \geqslant
\sup\operatorname{H}_{\mathfrak{p}_\mathfrak{p}}^*(\mathsf{R}\mathrm{Hom}(R_\mathfrak{p},M))$; see [Reference Christensen, Iyengar and Marley7, (2.7)].
4. Flat dimension
In this section, we prove three statements that are dual to statements about injective dimension in the literature. Our proofs rely on the existence and structure of minimal semi-flat-cotorsion replacements, hence the assumption that the ring has finite Krull dimension. The first result below is a counterpart to [Reference Christensen, Iyengar and Marley7, Theorem 5.1] and could have been stated even in [Reference Nakamura and Thompson12].
Theorem 4.1. Let R be a commutative noetherian ring of finite Krull dimension and M an R-complex with ![]() $\inf\operatorname{H}_*(M) \gt -\infty$. If for an integer
$\inf\operatorname{H}_*(M) \gt -\infty$. If for an integer ![]() $n\geqslant\sup\operatorname{H}_*(M)$ one has
$n\geqslant\sup\operatorname{H}_*(M)$ one has
 \begin{equation*}
\operatorname{Tor}_{n+1}^{R_\mathfrak{p}}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M))=0\;{\rm for every
prime ideal }\mathfrak{p}\;\text{in }R ,
\end{equation*}
\begin{equation*}
\operatorname{Tor}_{n+1}^{R_\mathfrak{p}}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M))=0\;{\rm for every
prime ideal }\mathfrak{p}\;\text{in }R ,
\end{equation*}then the flat dimension of M is at most n.
Proof. Let F be a minimal semi-flat-cotorsion replacement of M; the assumption ![]() $\inf\operatorname{H}_*(M) \gt -\infty$ guarantees that
$\inf\operatorname{H}_*(M) \gt -\infty$ guarantees that ![]() $F_i=0$ holds for
$F_i=0$ holds for ![]() $i\ll0$, see 1.2. Per [Reference Nakamura and Thompson12, Remark 4.5], for every integer i, one has
$i\ll0$, see 1.2. Per [Reference Nakamura and Thompson12, Remark 4.5], for every integer i, one has
 \begin{equation*}
F_i = \prod_{\mathfrak{p}\in\operatorname{Spec} R}\Lambda^\mathfrak{p}\left(R_\mathfrak{p}^{(B^\mathfrak{p}_i)}\right) ,
\end{equation*}
\begin{equation*}
F_i = \prod_{\mathfrak{p}\in\operatorname{Spec} R}\Lambda^\mathfrak{p}\left(R_\mathfrak{p}^{(B^\mathfrak{p}_i)}\right) ,
\end{equation*} where the cardinality of ![]() $B_i^\mathfrak{p}$ is the
$B_i^\mathfrak{p}$ is the ![]() $\kappa(\mathfrak{p})$-dimension of
$\kappa(\mathfrak{p})$-dimension of  $\operatorname{Tor}^{R_\mathfrak{p}}_{i}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M))$. Thus, it follows from the assumption that
$\operatorname{Tor}^{R_\mathfrak{p}}_{i}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M))$. Thus, it follows from the assumption that  $|B^\mathfrak{p}_{n+1}|=0$ holds for all primes
$|B^\mathfrak{p}_{n+1}|=0$ holds for all primes ![]() $\mathfrak{p}$. As
$\mathfrak{p}$. As ![]() $n\geqslant\sup\operatorname{H}_*(M)$ holds, the flat dimension of M is at most n.
$n\geqslant\sup\operatorname{H}_*(M)$ holds, the flat dimension of M is at most n.
The boundedness condition in the next result, which is dual to [Reference Avramov and Foxby2, Proposition 5.3.I], is necessary, without it the flat dimension may grow under colocalization; see Example 5.1.
Proposition 4.2. Let R be a commutative noetherian ring of finite Krull dimension and M an R-complex with ![]() $\inf{\operatorname{H}_*(M)} \gt -\infty$. The next equalities hold
$\inf{\operatorname{H}_*(M)} \gt -\infty$. The next equalities hold
 \begin{align*}
\operatorname{flat\,dim}_R M &= \sup{\{i \in \mathbb{Z} \mid \operatorname{Tor}_i^{R_\mathfrak{p}}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}(R_\mathfrak{p},M))
\ne 0 {\rm for some } \mathfrak{p}\in\operatorname{Spec} R \}} \\
& = \sup_{\mathfrak{p}\in\operatorname{Spec} R}{\{\operatorname{flat\,dim}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M) \}} .
\end{align*}
\begin{align*}
\operatorname{flat\,dim}_R M &= \sup{\{i \in \mathbb{Z} \mid \operatorname{Tor}_i^{R_\mathfrak{p}}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}(R_\mathfrak{p},M))
\ne 0 {\rm for some } \mathfrak{p}\in\operatorname{Spec} R \}} \\
& = \sup_{\mathfrak{p}\in\operatorname{Spec} R}{\{\operatorname{flat\,dim}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M) \}} .
\end{align*}Proof. If M is acyclic, all three quantities equal ![]() $-\infty$, and so we may assume
$-\infty$, and so we may assume ![]() $\operatorname{H}_*(M)$ is nonzero. Set
$\operatorname{H}_*(M)$ is nonzero. Set ![]() $s := \sup\operatorname{H}_*(M)$, one has
$s := \sup\operatorname{H}_*(M)$, one has  $\operatorname{Tor}_s^{R_\mathfrak{p}}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}(R_\mathfrak{p},M)) \ne 0$ for some prime ideal
$\operatorname{Tor}_s^{R_\mathfrak{p}}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}(R_\mathfrak{p},M)) \ne 0$ for some prime ideal ![]() $\mathfrak{p}$ in R, see [Reference Nakamura and Thompson12, Remark 4.5]. The inequality
$\mathfrak{p}$ in R, see [Reference Nakamura and Thompson12, Remark 4.5]. The inequality
 \begin{equation*}
\operatorname{flat\,dim}_R M \leqslant \sup{\{i \in \mathbb{Z} \mid \operatorname{Tor}_i^{R_\mathfrak{p}}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}(R_\mathfrak{p},M))
\ne 0 \text{ for some } \mathfrak{p}\in\operatorname{Spec} R \}}
\end{equation*}
\begin{equation*}
\operatorname{flat\,dim}_R M \leqslant \sup{\{i \in \mathbb{Z} \mid \operatorname{Tor}_i^{R_\mathfrak{p}}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}(R_\mathfrak{p},M))
\ne 0 \text{ for some } \mathfrak{p}\in\operatorname{Spec} R \}}
\end{equation*} now follows immediately from Theorem 4.1. To verify the opposite inequality, assume that ![]() $f := \operatorname{flat\,dim}_R M$ is finite and let F be a minimal semi-flat-cotorsion replacement of M. As
$f := \operatorname{flat\,dim}_R M$ is finite and let F be a minimal semi-flat-cotorsion replacement of M. As ![]() $\inf\operatorname{H}_*(M) \gt -\infty$ holds, one has
$\inf\operatorname{H}_*(M) \gt -\infty$ holds, one has ![]() $F_i=0$ for i > f and
$F_i=0$ for i > f and ![]() $i\ll0$, see 1.2. For every prime ideal
$i\ll0$, see 1.2. For every prime ideal ![]() $\mathfrak{p}$ in R, the
$\mathfrak{p}$ in R, the ![]() $R_\mathfrak{p}$-complex
$R_\mathfrak{p}$-complex ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F)$ is semi-flat-cotorsion and isomorphic to
$\operatorname{Hom}_R(R_\mathfrak{p},F)$ is semi-flat-cotorsion and isomorphic to ![]() $\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)$ in the derived category over
$\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)$ in the derived category over ![]() $R_\mathfrak{p}$. Since
$R_\mathfrak{p}$. Since ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F)_i = \operatorname{Hom}_R(R_\mathfrak{p},F_i) = 0$ holds for i > f, one has
$\operatorname{Hom}_R(R_\mathfrak{p},F)_i = \operatorname{Hom}_R(R_\mathfrak{p},F_i) = 0$ holds for i > f, one has
 \begin{align*}
\sup{\{i\in\mathbb{Z} \mid
\operatorname{Tor}_i^{R_\mathfrak{p}}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}(R_\mathfrak{p},M)) \ne 0\}}
& \leqslant \operatorname{flat\,dim}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M) \\
& \leqslant \operatorname{flat\,dim}_R M .
\end{align*}
\begin{align*}
\sup{\{i\in\mathbb{Z} \mid
\operatorname{Tor}_i^{R_\mathfrak{p}}(k(\mathfrak{p}),\mathsf{R}\mathrm{Hom}(R_\mathfrak{p},M)) \ne 0\}}
& \leqslant \operatorname{flat\,dim}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M) \\
& \leqslant \operatorname{flat\,dim}_R M .
\end{align*}For complexes with bounded homology, the next result was proved in [Reference Nakamura and Thompson12, Theorem 4.8]; it compares to [Reference Christensen, Iyengar and Marley7, Proposition 5.2 and Corollary 5.9], and the proof is modeled on the proof of [Reference Christensen, Iyengar and Marley7, Proposition 5.2].
Theorem 4.3. Let R be a commutative noetherian ring of finite Krull dimension and M an R-complex. If M has finite flat dimension, then
 \begin{equation*}
\operatorname{flat\,dim}_R M = \sup_{\mathfrak{p}\in\operatorname{Spec} R}\{\operatorname{depth}{R_\mathfrak{p}} - \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)\} .
\end{equation*}
\begin{equation*}
\operatorname{flat\,dim}_R M = \sup_{\mathfrak{p}\in\operatorname{Spec} R}\{\operatorname{depth}{R_\mathfrak{p}} - \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)\} .
\end{equation*}Proof. The equality is trivial if M is acyclic, so assume that it is not and set ![]() $f := \operatorname{flat\,dim}_R M$. Let F be a semi-flat replacement of M with
$f := \operatorname{flat\,dim}_R M$. Let F be a semi-flat replacement of M with ![]() $F_i =0$ for i > f. To prove the asserted equality, it suffices to show that the inequality
$F_i =0$ for i > f. To prove the asserted equality, it suffices to show that the inequality
 \begin{equation}
\operatorname{flat\,dim}_R F \geqslant \operatorname{depth}{R_\mathfrak{p}} - \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F)
\end{equation}
\begin{equation}
\operatorname{flat\,dim}_R F \geqslant \operatorname{depth}{R_\mathfrak{p}} - \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F)
\end{equation} holds for every prime ![]() $\mathfrak{p}$ with equality for some
$\mathfrak{p}$ with equality for some ![]() $\mathfrak{p}$. For every
$\mathfrak{p}$. For every ![]() $n \leqslant f$, there is an exact sequence of complexes of flat R-modules
$n \leqslant f$, there is an exact sequence of complexes of flat R-modules
The complex ![]() $F_{\geqslant n}$ is a bounded complex of flat modules, so it is semi-flat and hence so is
$F_{\geqslant n}$ is a bounded complex of flat modules, so it is semi-flat and hence so is ![]() $F_{\leqslant n-1}$; see for example [Reference Christensen and Holm5, 6.1]. Evidently, one has
$F_{\leqslant n-1}$; see for example [Reference Christensen and Holm5, 6.1]. Evidently, one has
Now Proposition 4.2 and [Reference Christensen, Iyengar and Marley7, (2.3)] conspire to yield
 \begin{equation}
f = \sup_{\mathfrak{p}\in\operatorname{Spec} R}\{\operatorname{depth} R_\mathfrak{p} - \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\geqslant n})\}.
\end{equation}
\begin{equation}
f = \sup_{\mathfrak{p}\in\operatorname{Spec} R}\{\operatorname{depth} R_\mathfrak{p} - \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\geqslant n})\}.
\end{equation} To prove (2), we fix a prime ideal ![]() $\mathfrak{p}$. Without loss of generality, we can assume that
$\mathfrak{p}$. Without loss of generality, we can assume that  $\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F)$ is finite, set
$\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F)$ is finite, set  $d = -\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F)$. Now one has
$d = -\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F)$. Now one has
and, thus, ![]() $d \leqslant f$. As one now has
$d \leqslant f$. As one now has
 \begin{align*}
\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\leqslant d-1})
&\geqslant \inf \operatorname{H}^*(\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\leqslant d-1})) \\
&\geqslant \inf \operatorname{H}^*(F_{\leqslant d-1}) \\
&\geqslant 1-d\\
&= 1 + \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F),
\end{align*}
\begin{align*}
\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\leqslant d-1})
&\geqslant \inf \operatorname{H}^*(\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\leqslant d-1})) \\
&\geqslant \inf \operatorname{H}^*(F_{\leqslant d-1}) \\
&\geqslant 1-d\\
&= 1 + \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F),
\end{align*}the depth lemma yields
 \begin{equation*}
\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F) = \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\geqslant d}) .
\end{equation*}
\begin{equation*}
\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F) = \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\geqslant d}) .
\end{equation*}The inequality (2) follows from Equation (3) by taking n = d.
Now choose by (3) a prime ideal ![]() $\mathfrak{p}$ such that
$\mathfrak{p}$ such that
 \begin{equation}
f = \operatorname{depth} R_\mathfrak{p} - \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\geqslant f-1})
\end{equation}
\begin{equation}
f = \operatorname{depth} R_\mathfrak{p} - \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\geqslant f-1})
\end{equation} holds. The inequality (2) holds for every complex of finite flat dimension; applied to the truncated complex ![]() $F_{\leqslant f-2}$, it yields
$F_{\leqslant f-2}$, it yields
 \begin{equation}
f-2 \geqslant \operatorname{flat\,dim}_R F_{\leqslant f-2} \geqslant \operatorname{depth} R_\mathfrak{p} - \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\leqslant f-2}) .
\end{equation}
\begin{equation}
f-2 \geqslant \operatorname{flat\,dim}_R F_{\leqslant f-2} \geqslant \operatorname{depth} R_\mathfrak{p} - \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\leqslant f-2}) .
\end{equation} Elimination of ![]() $\operatorname{depth} R_\mathfrak{p}$ between (4) and (5) yields
$\operatorname{depth} R_\mathfrak{p}$ between (4) and (5) yields
 \begin{equation*}
\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\geqslant f-1}) + 2 \leqslant \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\leqslant f-2}).
\end{equation*}
\begin{equation*}
\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\geqslant f-1}) + 2 \leqslant \operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\leqslant f-2}).
\end{equation*}Now apply the depth lemma to the triangle
to get  $\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F)=\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\geqslant
f-1})$; substituting this into (4) yields the desired result.
$\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F)=\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},F_{\geqslant
f-1})$; substituting this into (4) yields the desired result.
Remark 4.4. For an R-complex M of finite flat dimension, the equality
 \begin{equation*}
\operatorname{flat\,dim}_R M = \sup_{\mathfrak{p}\in\operatorname{Spec} R}\{\operatorname{depth}{R_\mathfrak{p}} - \operatorname{depth}_{R_\mathfrak{p}}M_\mathfrak{p}\}
\end{equation*}
\begin{equation*}
\operatorname{flat\,dim}_R M = \sup_{\mathfrak{p}\in\operatorname{Spec} R}\{\operatorname{depth}{R_\mathfrak{p}} - \operatorname{depth}_{R_\mathfrak{p}}M_\mathfrak{p}\}
\end{equation*} holds, see [Reference Christensen, Iyengar and Marley7, (4.3)]. Echoing [Reference Christensen, Iyengar and Marley7, Remark 5.10], we remark that we do not know how the numbers  $\operatorname{depth}_{R_\mathfrak{p}}M_\mathfrak{p}$ and
$\operatorname{depth}_{R_\mathfrak{p}}M_\mathfrak{p}$ and  $\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)$ compare: If
$\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},M)$ compare: If ![]() $(R,\mathfrak{m},k)$ is local of positive Krull dimension and E is the injective envelope of k, then one has
$(R,\mathfrak{m},k)$ is local of positive Krull dimension and E is the injective envelope of k, then one has  $\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},E) = 0$ for every prime ideal
$\operatorname{depth}_{R_\mathfrak{p}}\mathsf{R}\mathrm{Hom}_R(R_\mathfrak{p},E) = 0$ for every prime ideal ![]() $\mathfrak{p}$ by the isomorphisms
$\mathfrak{p}$ by the isomorphisms
On the other hand, for ![]() $\mathfrak{p} \not = \mathfrak{m}$, the module
$\mathfrak{p} \not = \mathfrak{m}$, the module ![]() $E_\mathfrak{p}$ is zero and hence of infinite depth.
$E_\mathfrak{p}$ is zero and hence of infinite depth.
5. Examples
We close with a series of examples to show that boundedness conditions, such as the one in Proposition 4.2, are necessary in certain statements about semi-flat complexes. In particular, neither colocalization nor completion need preserve finiteness of flat dimension. The examples build on [Reference Nakamura and Thompson12, Example 5.11].
Example 5.1. Let k be a field and consider the local ring ![]() $R=k[[x,y]]/(x^2)$; it has only two prime ideals:
$R=k[[x,y]]/(x^2)$; it has only two prime ideals: ![]() $\mathfrak{p}=(x)$ and
$\mathfrak{p}=(x)$ and ![]() $\mathfrak{m}=(x,y)$. By [Reference Nakamura and Thompson12, Example 5.11], there exists a minimal semi-flat-cotorsion R-complex Y, called YP in [Reference Nakamura and Thompson12], such that
$\mathfrak{m}=(x,y)$. By [Reference Nakamura and Thompson12, Example 5.11], there exists a minimal semi-flat-cotorsion R-complex Y, called YP in [Reference Nakamura and Thompson12], such that ![]() $\operatorname{Hom}_R(R_\mathfrak{p},Y)$ is not semi-flat.
$\operatorname{Hom}_R(R_\mathfrak{p},Y)$ is not semi-flat.
Set ![]() $F=(Y)_{\leqslant 0}$ and
$F=(Y)_{\leqslant 0}$ and ![]() $F^{\prime}=(Y)_{\geqslant 1}$, the hard truncations of Y above at 0 and below at 1, respectively. There is an exact sequence
$F^{\prime}=(Y)_{\geqslant 1}$, the hard truncations of Y above at 0 and below at 1, respectively. There is an exact sequence ![]() $0 \to F \to Y \to F^{\prime} \to 0$, which is degreewise split. Application of
$0 \to F \to Y \to F^{\prime} \to 0$, which is degreewise split. Application of ![]() $\operatorname{Hom}_R(R_\mathfrak{p},-)$ now yields the exact sequence
$\operatorname{Hom}_R(R_\mathfrak{p},-)$ now yields the exact sequence
Since the complex ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F^{\prime})$ consists of flat modules and
$\operatorname{Hom}_R(R_\mathfrak{p},F^{\prime})$ consists of flat modules and ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F^{\prime})_i=0$ holds for
$\operatorname{Hom}_R(R_\mathfrak{p},F^{\prime})_i=0$ holds for ![]() $i\ll0$, it is semi-flat. Since
$i\ll0$, it is semi-flat. Since ![]() $\operatorname{Hom}_R(R_\mathfrak{p},Y)$ is not semi-flat, neither is the complex
$\operatorname{Hom}_R(R_\mathfrak{p},Y)$ is not semi-flat, neither is the complex ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F)$.
$\operatorname{Hom}_R(R_\mathfrak{p},F)$.
It follows from [Reference Nakamura and Thompson12, Theorem 2.3] that F is a minimal semi-flat-cotorsion complex; as ![]() $\operatorname{H}_0(F) \ne 0$, it has flat dimension 0. We claim, however, that
$\operatorname{H}_0(F) \ne 0$, it has flat dimension 0. We claim, however, that ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F)$ has infinite flat dimension. Suppose, to the contrary, that the complex
$\operatorname{Hom}_R(R_\mathfrak{p},F)$ has infinite flat dimension. Suppose, to the contrary, that the complex ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F)$ has finite flat dimension. Choose a semi-flat resolution
$\operatorname{Hom}_R(R_\mathfrak{p},F)$ has finite flat dimension. Choose a semi-flat resolution ![]() $P \to \operatorname{Hom}_R(R_\mathfrak{p},F)$ with
$P \to \operatorname{Hom}_R(R_\mathfrak{p},F)$ with ![]() $P_i=0$ for
$P_i=0$ for ![]() $i\gg0$ and let C be its mapping cone. Evidently, C is an acyclic complex of flat R-modules and
$i\gg0$ and let C be its mapping cone. Evidently, C is an acyclic complex of flat R-modules and ![]() $C_i=0$ holds for
$C_i=0$ holds for ![]() $i\gg0$. We argue that C is pure-acyclic; that is, all its cycle modules are flat: For every integer i, let
$i\gg0$. We argue that C is pure-acyclic; that is, all its cycle modules are flat: For every integer i, let ![]() $Z_i=\operatorname{Ker}(C_i\to C_{i-1})$ be the cycle module in degree i. There is an exact sequence
$Z_i=\operatorname{Ker}(C_i\to C_{i-1})$ be the cycle module in degree i. There is an exact sequence ![]() $0 \to Z_i \to C_i \to Z_{i-1} \to 0$. The ring R is Gorenstein of Krull dimension 1, so by a result of Bass [Reference Bass3, Corollary 5.6], the finitistic flat dimension of R is 1. As Ci is flat, it follows that Zi is flat. As i was arbitrary, this shows that C is pure-acyclic. It now follows from [Reference Christensen and Holm5, Theorem 7.3] that C is semi-flat. As C fits in a short exact sequence with the complexes P and
$0 \to Z_i \to C_i \to Z_{i-1} \to 0$. The ring R is Gorenstein of Krull dimension 1, so by a result of Bass [Reference Bass3, Corollary 5.6], the finitistic flat dimension of R is 1. As Ci is flat, it follows that Zi is flat. As i was arbitrary, this shows that C is pure-acyclic. It now follows from [Reference Christensen and Holm5, Theorem 7.3] that C is semi-flat. As C fits in a short exact sequence with the complexes P and ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F)$, of which the latter is not semi-flat, this is a contradiction. It follows that
$\operatorname{Hom}_R(R_\mathfrak{p},F)$, of which the latter is not semi-flat, this is a contradiction. It follows that ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F)$ has infinite flat dimension.
$\operatorname{Hom}_R(R_\mathfrak{p},F)$ has infinite flat dimension.
One can draw the same conclusion as in the previous example about the ![]() $\mathfrak{m}$-completion of F:
$\mathfrak{m}$-completion of F:
Example 5.2. Let R and F be as in Example 5.1. By [Reference Nakamura and Thompson12, (1.17)], there is an exact sequence
As F is semi-flat of finite flat dimension, equal to 0, but ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F)$ is not semi-flat and does not have finite flat dimension, it follows that the complex
$\operatorname{Hom}_R(R_\mathfrak{p},F)$ is not semi-flat and does not have finite flat dimension, it follows that the complex ![]() $\Lambda^{\mathfrak{m}}(F)$ is not semi-flat and does not have finite flat dimension.
$\Lambda^{\mathfrak{m}}(F)$ is not semi-flat and does not have finite flat dimension.
The examples above are dual to the examples in [Reference Christensen, Iyengar and Marley7, Section 6], and we take this opportunity to clarify one of the statements made there.
Remark 5.3. Let ![]() $(R,\mathfrak{m},k)$ be local. It is stated in [Reference Christensen, Iyengar and Marley7, Remark 6.2] that the support of the product
$(R,\mathfrak{m},k)$ be local. It is stated in [Reference Christensen, Iyengar and Marley7, Remark 6.2] that the support of the product ![]() $\operatorname{E}_R(k)^{\mathbb{N}}$ is all of
$\operatorname{E}_R(k)^{\mathbb{N}}$ is all of ![]() $\operatorname{Spec}{R}$, and that is correct though the argument provided in [Reference Christensen, Iyengar and Marley7] is too brief to be accurate. Here is a complete argument:
$\operatorname{Spec}{R}$, and that is correct though the argument provided in [Reference Christensen, Iyengar and Marley7] is too brief to be accurate. Here is a complete argument:
Set ![]() $E = \operatorname{E}_R(k)$, and for every
$E = \operatorname{E}_R(k)$, and for every ![]() $n \in {\mathbb{N}}$, let En denote the submodule
$n \in {\mathbb{N}}$, let En denote the submodule
It is the injective envelope of the artinian ring ![]() $R/\mathfrak{m}^n$, so one has
$R/\mathfrak{m}^n$, so one has ![]() $(0:_RE_n) = \mathfrak{m}^n$. Indeed, for x in R, the isomorphism
$(0:_RE_n) = \mathfrak{m}^n$. Indeed, for x in R, the isomorphism ![]() $R/\mathfrak{m}^n \cong \operatorname{Hom}_{R/\mathfrak{m}^n}(E_n,E_n) \cong \operatorname{Hom}_R(E_n,E_n)$ identifies the homothety
$R/\mathfrak{m}^n \cong \operatorname{Hom}_{R/\mathfrak{m}^n}(E_n,E_n) \cong \operatorname{Hom}_R(E_n,E_n)$ identifies the homothety ![]() $E_n \xrightarrow{x} E_n$ with the coset
$E_n \xrightarrow{x} E_n$ with the coset ![]() $x + \mathfrak{m}^n$ in
$x + \mathfrak{m}^n$ in ![]() $R/\mathfrak{m}^n$. Each submodule En has finite length; in particular, it is generated by elements
$R/\mathfrak{m}^n$. Each submodule En has finite length; in particular, it is generated by elements ![]() $e_{n,1},\ldots,e_{n,m_n}$. Now let e be the family of all these generators in the countable product
$e_{n,1},\ldots,e_{n,m_n}$. Now let e be the family of all these generators in the countable product ![]() $\prod_{n\in{\mathbb{N}}}\prod_{i=1}^{m_n}E$. It follows from Krull’s intersection theorem that the homomorphism
$\prod_{n\in{\mathbb{N}}}\prod_{i=1}^{m_n}E$. It follows from Krull’s intersection theorem that the homomorphism ![]() $R \to E^{\mathbb{N}}$ given by
$R \to E^{\mathbb{N}}$ given by ![]() $1 \mapsto e$ is injective, since an element in the kernel annihilates En for every
$1 \mapsto e$ is injective, since an element in the kernel annihilates En for every ![]() $n\in{\mathbb{N}}$ and hence belongs to the intersection
$n\in{\mathbb{N}}$ and hence belongs to the intersection ![]() $\bigcap_{n\in{\mathbb{N}}}\mathfrak{m}^n$. As localization is exact,
$\bigcap_{n\in{\mathbb{N}}}\mathfrak{m}^n$. As localization is exact, ![]() $R_\mathfrak{p}$ is now a nonzero submodule of
$R_\mathfrak{p}$ is now a nonzero submodule of ![]() $(E^{\mathbb{N}})_\mathfrak{p}$ for every prime ideal
$(E^{\mathbb{N}})_\mathfrak{p}$ for every prime ideal ![]() $\mathfrak{p}$ in R.
$\mathfrak{p}$ in R.
Let R be a commutative noetherian ring, P a projective R-module and F a semi-flat R-complex. As products of flat R-modules are flat, ![]() $\operatorname{Hom}_R(P,F)$ is a complex of flat R-modules. If
$\operatorname{Hom}_R(P,F)$ is a complex of flat R-modules. If ![]() $F_i=0$ holds for
$F_i=0$ holds for ![]() $i\ll0$, then the complex
$i\ll0$, then the complex ![]() $\operatorname{Hom}_R(P,F)$ satisfies the same boundedness condition, whence it is semi-flat. Without this boundedness condition, the conclusion may fail.
$\operatorname{Hom}_R(P,F)$ satisfies the same boundedness condition, whence it is semi-flat. Without this boundedness condition, the conclusion may fail.
Example 5.4. Let R be the ring and F the semi-flat R-complex from Example 5.1. There exist projective R-modules P such that ![]() $\operatorname{Hom}_R(P,F)$ is not semi-flat: As R is Gorenstein of Krull dimension 1, the finitistic projective dimension of R is 1 by [Reference Bass3, Corollary 5.6]. It follows that there is an exact sequence
$\operatorname{Hom}_R(P,F)$ is not semi-flat: As R is Gorenstein of Krull dimension 1, the finitistic projective dimension of R is 1 by [Reference Bass3, Corollary 5.6]. It follows that there is an exact sequence ![]() $0 \to P_1 \to P_0 \to R_\mathfrak{p} \to 0$, where P 1 and P 0 are projective R-modules. As F is a complex of flat-cotorsion modules, in particular modules that are
$0 \to P_1 \to P_0 \to R_\mathfrak{p} \to 0$, where P 1 and P 0 are projective R-modules. As F is a complex of flat-cotorsion modules, in particular modules that are ![]() $\mathrm{Ext}^1$-orthogonal to
$\mathrm{Ext}^1$-orthogonal to ![]() $R_\mathfrak{p}$, it yields an exact sequence
$R_\mathfrak{p}$, it yields an exact sequence
Assume towards a contradiction that ![]() $\operatorname{Hom}_R(P_1,F)$ and
$\operatorname{Hom}_R(P_1,F)$ and ![]() $\operatorname{Hom}_R(P_0,F)$ are both semi-flat R-complexes. As
$\operatorname{Hom}_R(P_0,F)$ are both semi-flat R-complexes. As ![]() $F_i = 0$ holds for i > 0, it follows that both complexes have finite flat dimension, at most 0, and hence so has
$F_i = 0$ holds for i > 0, it follows that both complexes have finite flat dimension, at most 0, and hence so has ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F)$. This contradicts the conclusion in Example 5.1 that
$\operatorname{Hom}_R(R_\mathfrak{p},F)$. This contradicts the conclusion in Example 5.1 that ![]() $\operatorname{Hom}_R(R_\mathfrak{p},F)$ has infinite flat dimension.
$\operatorname{Hom}_R(R_\mathfrak{p},F)$ has infinite flat dimension.
For the ring ![]() $R=k[[x,y]]/(x^2)$ with
$R=k[[x,y]]/(x^2)$ with ![]() $\mathfrak{p}=(x)$ from Example 5.1, one has
$\mathfrak{p}=(x)$ from Example 5.1, one has ![]() $R_\mathfrak{p} = R_y$, so it follows from [Reference Nakamura and Thompson12, Example 1.6] that the modules P 0 and P 1 can be chosen as countable direct sums of copies of R. Thus, F is an example of a semi-flat complex such that the product
$R_\mathfrak{p} = R_y$, so it follows from [Reference Nakamura and Thompson12, Example 1.6] that the modules P 0 and P 1 can be chosen as countable direct sums of copies of R. Thus, F is an example of a semi-flat complex such that the product ![]() $F^{\mathbb{N}}$ is not semi-flat. Compare this to the fact that for a semi-injective complex I, the coproduct
$F^{\mathbb{N}}$ is not semi-flat. Compare this to the fact that for a semi-injective complex I, the coproduct ![]() $I^{(\mathbb{N})}$ need not be semi-injective; see Iacob and Iyengar [Reference Iacob and Iyengar11, Theorem 2.8].
$I^{(\mathbb{N})}$ need not be semi-injective; see Iacob and Iyengar [Reference Iacob and Iyengar11, Theorem 2.8].
Acknowledgements
It is our pleasure to thank Srikanth Iyengar and Thomas Marley for discussions related to this work. We also thank the anonymous referee for their feedback, including the observation about the modules P 0 and P 1 recounted right above.
Funding Statement
L.W.C. was partly supported by Simons Foundation collaboration grant 428308.