Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-18T01:18:49.986Z Has data issue: false hasContentIssue false
  • English
  • Français

A Plane Quartic with Eight Undulations

Published online by Cambridge University Press:  20 January 2009

W. L. Edge
W. L. Edge
Affiliation:
Mathematical Institute, University of Edinburgh.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. The chief purpose of this paper is to demonstrate the existence of a plane quartic curve with eight undulations, an “undulation” being a point at which the tangent has four-point contact. It is shown that the curve

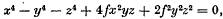
where (x, y, z) are homogeneous point-coordinates and f a constant, has undulations at the eight points

The curve has, in addition to these undulations, eight inflections which are; in general, distinct. But there are two geometrically different possibilities of their not being distinct, and in either instance they coincide in pairs at four further undulations. Thus two types of curve arise without any ordinary inflections at all, their 24 inflections coinciding in pairs at 12 undulations.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 8 , Issue 4 , October 1950 , pp. 147 - 162
Copyright
Copyright © Edinburgh Mathematical Society 1950

References

page 147 note 1 Rendiconto dell' accademia delle science Jisiche e matematiche, 21 (Naples, 1882) 45–69.Google Scholar

page 159 note 1 Math. Annalen, 17 (1880), 512.Google Scholar

page 160 note 1 Proc. Edinburgh Math. Soc. (2), 7 (1945), 154.Google Scholar