Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-25T02:12:29.345Z Has data issue: false hasContentIssue false
  • English
  • Français

A lower bound for the number of zeros of a meromorphic function and its second derivative

Published online by Cambridge University Press:  20 January 2009

J. K. Langley
J. K. Langley
Affiliation:
University of NottinghamNottinghamNG7 2RD E-mail: jkl@maths.nott.ac.uk.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that for a function f(z) transcendental and meromorphic in the plane and not of the form exp(az + b), we have either N(r, 1/ff″)≠0(T(r, f′/f)) or .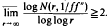

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 39 , Issue 1 , February 1996 , pp. 171 - 185
Copyright
Copyright © Edinburgh Mathematical Society 1996

References

REFERENCES

1. Anderson, J. M., Baker, I. N. and Clunie, J., The distribution of values of certain entire and meromorphic functions, Math. Z. 178 (1981), 509–525.CrossRefGoogle Scholar
2. Bergweiler, W., On the zeros of certain homogeneous differential polynomials, Arch. Math. (Basel) 64 (1995), 199–202.CrossRefGoogle Scholar
3. Bergweiler, W. and Eremenko, A., On the singularities of the inverse to a meromorphic function of finite order, Rev. Mat. Iberoamericana, to appear.Google Scholar
4. Eremenko, A., Meromorphic functions with small ramification, Indiana Univ. Math. J. 42 (1994), 1193–1218.CrossRefGoogle Scholar
5. Frank, G., Eine Vermutung von Hayman über Nullstellen meromorpher Funktionen, Math. Z. 149(1976), 29–36.Google Scholar
6. Frank, G. and Hellerstein, S., On the meromorphic solutions of nonhomogeneous linear differential equations with polynomial coefficients, Proc. London Math. Soc. (3) 53 (1986), 407–428.CrossRefGoogle Scholar
7. Frank, G., Hennekemper, W. and Polloczek, G., Über die Nullstellen meromorpher Funktionen and ihrer Ableitungen, Math. Ann. 225 (1977), 145–154.CrossRefGoogle Scholar
8. Hayman, W. K., Picard values of meromorphic functions and their derivatives, Ann. of Math. 70 (1959), 9–42.CrossRefGoogle Scholar
9. Hayman, W. K., The local growth of power series: a survey of the Wiman-Valiron method, Canad. Math. Bull. 17 (1974), 317–358.CrossRefGoogle Scholar
10. Hille, E., Ordinary Differential Equations in the Complex Domain (Wiley, New York, 1976).Google Scholar
11. Laine, I., Nevanlinna theory and complex differential equations (de Gruyter Studies in Math. 15, Walter de Gruyter, Berlin/New York 1993).CrossRefGoogle Scholar
12. Langley, J. K., Proof of a conjecture of Hayman concerning f and f″, J. London Math. Soc. (2)48(1993), 500–514.CrossRefGoogle Scholar
13. Langley, J. K., On the fixpoints of composite entire functions of finite order, Proc. Roy. Soc. Edinburgh 124A (1994), 995–1001.CrossRefGoogle Scholar
14. Langley, J. K., On the multiple points of certain meromorphic functions, Proc. Amer. Math. Soc., to appear.Google Scholar
15. Langley, J. K., On second order linear differential polynomials, Resultate Math. 26 (1994), 51–82.CrossRefGoogle Scholar
16. Mues, E., Über eine Vermutung von Hayman, Math. Z. 119 (1972), 11–20.CrossRefGoogle Scholar
17. Reinders, M., On the zeros of W(g, g′,…, g (n–1)), preprint.Google Scholar
18. Shea, D., On the frequency of multiple values of a meromorphic function of small order, Michigan Math. J. 32 (1985) 109–116.CrossRefGoogle Scholar