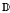An analytic function f in the unit disc belongs to F(p,q,s), if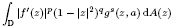

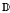is uniformly bounded for all a ∈ . Here 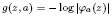is the Green function of 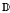, and φa(z)=(a−z)/(1−āz). It is shown that for 0 < γ < ∞ and |w|=1 the singular inner function exp(γ(z+w)/(z−w)) belongs to F(p,q,s), 0<s≤1, if and only if 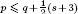. Moreover, it is proved that, if 0<s<1, then an inner function belongs to the Möbius invariant Besov-type space 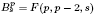for some (equivalently for all) p > max{s,1−s} if and only if it is a Blaschke product whose zero sequence {zn} satisfies .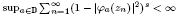