Article contents
Hecke C*-algebras and semi-direct products
Published online by Cambridge University Press: 02 February 2009
Abstract
We analyse Hecke pairs (G,H) and the associated Hecke algebra 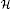 when G is a semi-direct product N ⋊ Q and H = M ⋊ R for subgroups M ⊂ N and R ⊂ Q with M normal in N. Our main result shows that, when (G,H) coincides with its Schlichting completion and R is normal in Q, the closure of
when G is a semi-direct product N ⋊ Q and H = M ⋊ R for subgroups M ⊂ N and R ⊂ Q with M normal in N. Our main result shows that, when (G,H) coincides with its Schlichting completion and R is normal in Q, the closure of 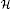 in C*(G) is Morita–Rieffel equivalent to a crossed product I⋊βQ/R, where I is a certain ideal in the fixed-point algebra C*(N)R. Several concrete examples are given illustrating and applying our techniques, including some involving subgroups of GL(2,K) acting on K2, where K = ℚ or K = ℤ[p−1]. In particular we look at the ax + b group of a quadratic extension of K.
in C*(G) is Morita–Rieffel equivalent to a crossed product I⋊βQ/R, where I is a certain ideal in the fixed-point algebra C*(N)R. Several concrete examples are given illustrating and applying our techniques, including some involving subgroups of GL(2,K) acting on K2, where K = ℚ or K = ℤ[p−1]. In particular we look at the ax + b group of a quadratic extension of K.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 52 , Issue 1 , February 2009 , pp. 127 - 153
- Copyright
- Copyright © Edinburgh Mathematical Society 2009
- 2
- Cited by


