Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-20T05:42:48.282Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of exponentially and superexponentially spatially localized breather solutions for nonlinear klein–gordon lattices in ℤd, d ≥ 1

Part of: Infinite-dimensional Hamiltonian systems Nonlinear operators and their properties

Published online by Cambridge University Press:  16 June 2022

Dirk Hennig  and
Nikos I. Karachalios Open the ORCID record for Nikos I. Karachalios [Opens in a new window]
Dirk Hennig
Affiliation:
Department of Mathematics, University of Thessaly, Lamia GR35100, Greece (dirkhennig@uth.gr, karan@uth.gr)
Nikos I. Karachalios
Affiliation:
Department of Mathematics, University of Thessaly, Lamia GR35100, Greece (dirkhennig@uth.gr, karan@uth.gr)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the existence of exponentially and superexponentially localized breather solutions for discrete nonlinear Klein–Gordon systems. Our approach considers $d$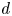-dimensional infinite lattice models with general on-site potentials and interaction potentials being bounded by an arbitrary power law, as well as, systems with purely anharmonic forces, cases which are much less studied particularly in a higher-dimensional set-up. The existence problem is formulated in terms of a fixed-point equation considered in weighted sequence spaces, which is solved by means of Schauder's Fixed-Point Theorem. The proofs provide energy bounds for the solutions depending on the lattice parameters and its dimension under physically relevant non-resonance conditions.

Keywords

discrete Klein–Gordonhigher-dimensional latticesbreathersexponential and superexponential localizationSchauder fixed-point theorem

MSC classification

Primary: 37K40: Soliton theory, asymptotic behavior of solutions
Secondary: 37K60: Lattice dynamics 47H10: Fixed-point theorems
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 2 , May 2022 , pp. 480 - 499
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achilleos, V., Álvarez, A., Cuevas, J., Frantzeskakis, D. J., Karachalios, N. I., Kevrekidis, P. G. and Sánchez-Rey, B., Escape dynamics in the discrete repulsive $\phi ^{4}$ model, Physica D 244 (2013), 1–24.CrossRefGoogle Scholar
Álvarez, A., Archilla, J. F. R., Cuevas, J. and Romero, F. R., Dark breathers in Klein-Gordon lattices. Band analysis of their stability properties, New J. Phys. 4 (2002), 72.CrossRefGoogle Scholar
Ahnert, K. and Pikovsky, A., Compactons and chaos in strongly nonlinear lattices, Phys. Rev. E 79 (2009), 02609.CrossRefGoogle ScholarPubMed
Akhmediev, N. and Ankiewicz, A., Modulation instability, Fermi-Pasta-Ulam recurrence, rogue waves, nonlinear phase shift, and exact solutions of the Ablowitz-Ladik equation, Phys. Rev. E 83 (2011), 046603.CrossRefGoogle ScholarPubMed
Ankiewicz, A., Akhmediev, N. and Soto-Crespo, J. M., Discrete rogue waves of the Ablowitz-Ladik and Hirota equations, Phys. Rev. E 82 (2010), 026602.CrossRefGoogle ScholarPubMed
Aubry, S., Discrete breathers in anharmonic models with acoustic phonons, Ann. Inst. H. Poincaré Phys. Théor. 68 (1998), 381–420.Google Scholar
Aubry, S., Kopidakis, G. and Kadelburg, V., Variational proof for hard discrete breathers in some classes of Hamiltonian dynamical systems, Discrete Contin. Dyn. Syst. Ser. B 1 (2001), 271–298.Google Scholar
Bazãrs, J., Eilbeck, J. C. and Leimkuhler, B., Nonlinear propagating localized modes in a 2D hexagonal crystal lattice, Phys. D 301–302 (2015), 8–20.Google Scholar
Bazãrs, J., Eilbeck, J. C. and Leimkuhler, B., Two-dimensional mobile breather scattering in a hexagonal crystal lattice, Phys. Rev. E 103 (2021), 022212.Google Scholar
Bambusi, D., Exponential stability of breathers in Hamiltonian networks of weakly coupled oscillators, Nonlinearity 9 (1996), 433–457.CrossRefGoogle Scholar
Bambusi, D., Asymptotic stability of breathers in some Hamiltonian networks of weakly coupled oscillators, Comm. Math. Phys. 324 (2013), 515–547.CrossRefGoogle Scholar
Bambusi, D., Paleari, S. and Penati, T., Existence and continuous approximation of small amplitude breathers in 1D and 2D Klein-Gordon lattices, Appl. Anal. 89 (2010), 1313–1334.CrossRefGoogle Scholar
Binder, P., Abraimov, D., Ustinov, A. V., Flach, S. and Zolotaryuk, Y., Observation of breathers in Josephson ladders, Phys. Rev. Lett. 84 (2000), 745.CrossRefGoogle ScholarPubMed
Boechler, N., Theocharis, G., Job, S. and Kevredikis, P. G., Discrete breathers in one-dimensional diatomic granular crystals, Phys. Rev. Lett. 104 (2010), 244302.CrossRefGoogle ScholarPubMed
Christiansen, P. L., Gaididei, Yu. B., Mezentsev, V. K., Musher, S. L., Rasmussen, K.Ø., Juul Rasmussen, J., Ryzhenkova, I. V. and Turitsyn, S. K., Discrete localized states and localization dynamics in discrete nonlinear Schrödinger equations, Phys. Scr. Vol. T 67 (1996), 160–166.CrossRefGoogle Scholar
Conway, J. B., A course in functional analysis, 2nd edn. (Springer-Verlag, 1990).Google Scholar
Cruzeiro-Hansson, L, Eilbeck, J. C., Marín, J. L. and Russell, F. M., Breathers in systems with intrinsic and extrinsic nonlinearities, Phys. D 142 (2000), 101–112.CrossRefGoogle Scholar
Cubero, D., Cuevas, J. and Kevrekidis, P. G., Nucleation of breathers via stochastic resonance in nonlinear lattices, Phys. Rev. Lett. 102 (2009), 205505.CrossRefGoogle ScholarPubMed
Cuevas, J. and Kevrekidis, P. G., Breather statics and dynamics in Klein-Gordon chains with a bend, Phys. Rev. E 69 (2004), 056609.CrossRefGoogle ScholarPubMed
Cuevas, J., Koukouloyannis, V., Kevrekidis, P. G. and Archilla, J. F. R., Multibreather and vortex breather stability in Klein–Gordon lattices: equivalence between two different approaches, Internat. J. Bifur. Chaos Appl. Sci. Engrg. 21 (2011), 2161–2177.CrossRefGoogle Scholar
Cuevas, J., Archilla, J. F. R. and Romero, F. R., Stability of non-time-reversible phonobreathers, J. Phys. A: Math. Theor. 44 (2011), 035102.CrossRefGoogle Scholar
Cuevas, J., English, L. Q., Kevrekidis, P. G. and Anderson, M., Discrete breathers in a forced famped array of coupled pendula: modeling, computation and experiment, Phys. Rev. Lett.. 102 (2009), 224101.CrossRefGoogle Scholar
Cuevas-Maraver, J., Kevrekidis, P. G. and Pelinovsky, D. E., Nonlinear instabilities of multi-site breathers in Klein–Gordon lattices, Stud. Appl. Math. 137 (2016), 214–237.CrossRefGoogle Scholar
Dorignac, J., Eilbeck, J. C., Salerno, M. and Scott, A. C., Quantum signatures of breather-breather interactions, Phys. Rev. Lett. 93 (2004), 025504.CrossRefGoogle ScholarPubMed
Eiermann, B., Anker, T., Albiez, M., Taglieber, M., Treutlein, P., Marzlin, K.-P. and Oberthaler, M. K., Bright Bose-Einstein gap solitons of atoms with repulsive interaction, Phys. Rev. Lett. 92 (2004), 23041.CrossRefGoogle ScholarPubMed
Eisenberg, H. S., Silberberg, Y., Morantotti, R., Boyd, A. R. and Atchinson, J. S., Discrete spatial optical solitons in waveguide arrays, Phys. Rev. Lett. 81 (1998), 3383.CrossRefGoogle Scholar
English, L. Q., Palmero, F., Stormes, J. F., Cuevas-Maraver, J., Carretero-González, R. and Kevrekidis, P. G., Nonlinear localized modes in two-dimensional electrical lattices, Phys. Rev. E 88 (2013), 022912.CrossRefGoogle ScholarPubMed
Flach, S. and Gorbach, A. V., Discrete breathers – Advances in theory and applications, Phys. Rep. 467 (2008), 1–116.CrossRefGoogle Scholar
Fleischer, J. W., Segev, M., Efremidis, N. K. and Christodoulides, D. N., Observation of two-dimensional discrete solitons in optically induced nonlinear photonic lattices, Nature 422 (2003), 147.CrossRefGoogle ScholarPubMed
Gorbach, A. V. and Flach, S., Compactlike discrete breathers in systems with nonlinear and nonlocal dispersive terms, Phys. Rev. E 72 (2005), 056607.CrossRefGoogle ScholarPubMed
Hennig, D., Existence and non-existence of breather solutions in damped and driven nonlinear lattices, AIP Advances 3 (2013), 102127.CrossRefGoogle Scholar
Hennig, D., Localised time-periodic solutions of discrete nonlinear Klein-Gordon systems with convex on-site potentials, J. Fixed Point Theory Appl. 23 (2021), 31.CrossRefGoogle Scholar
Hennig, D. and Karachalios, N. I., Existence of exponentially spatially localized breather solutions for lattices of nonlinearly coupled particles: Schauder's fixed-point theorem approach, J. Math. Phys. 62 (2021), 123506.CrossRefGoogle Scholar
James, G., Centre manifold reduction for quasilinear discrete systems, J. Nonlinear Sci. 13 (2003), 27–63.CrossRefGoogle Scholar
James, G., Sánchez-Rey, B. and Cuevas, J., Breathers in inhomogeneous nonlinear lattices: an analysis via center manifold reduction, Rev. Math. Phys. 21 (2009), 1–59.CrossRefGoogle Scholar
James, G., Kevrekidis, P. G. and Cuevas, J., Breathers in oscillator chains with Hertzian interactions, Physica D 251 (2013), 39–59.CrossRefGoogle Scholar
Kastner, M. and Sepulchre, J.-A., Effective Hamiltonian for traveling discrete breathers in the FPU chain, Discrete Contin. Dyn. Syst. Ser. B 5 (2005), 719–734.Google Scholar
Kevrekidis, P. G., Non-linear waves in lattices: past, present, future, IMA J. Appl. Math. 76 (2011), 389–423.CrossRefGoogle Scholar
Kevrekidis, P. G., Pelinovsky, D. E. and Saxena, A., When linear stability does not exclude nonlinear instability, Phys. Rev. Lett. 114 (2015), 214101.CrossRefGoogle Scholar
Kevrekidis, P. G., Cuevas-Maraver, J. and Pelinovsky, D. E., Energy criterion for the spectral stability of discrete breathers, Phys. Rev. Lett. 119 (2016), 094101.CrossRefGoogle Scholar
Kivshar, Y., Intrinsic localized modes as solitons with a compact support, Phys. Rev. E 48 (1993), R43(R).CrossRefGoogle ScholarPubMed
Koukouloyannis, V. and MacKay, R. S., Existence and stability of 3-site breathers in a triangular lattice, J. Phys. A: Math. Gen. 38 (2005), 1021.CrossRefGoogle Scholar
Koukouloyannis, V., Kevrekidis, P. G., Cuevas, J. and Rothos, V., Multibreathers in Klein–Gordon chains with interactions beyond nearest neighbors, Physica D 242 (2013), 16–29.CrossRefGoogle Scholar
MacKay, R. S. and Aubry, S., Proof of existence of breathers for time-reversible or Hamiltonian networks of weakly coupled oscillators, Nonlinearity 7 (1994), 1623–1643.CrossRefGoogle Scholar
Marín, J. L., Eilbeck, J. C. and Russell, F. M., 2-D breathers and applications, in Nonlinear science at the dawn of the 21st century (eds. P. L. Christiansen, M. P. Sørensen and A. C. Scott), Lecture Notes in Physics, Volume 542 (Springer, 2000).Google Scholar
Marín, J.L., Russell, F. M. and Eilbeck, J. C., Breathers in cuprate-like lattices, Phys. Lett. A 281 (2001), 21–25.CrossRefGoogle Scholar
Marín, J. L., Falo, F., Martínez, P. J. and Floría, L. M., Discrete breathers in dissipative lattices, Phys. Rev. E 63 (2001), 066603.CrossRefGoogle ScholarPubMed
Martínez, P. J., Meister, M., Floría, L. M. and Falo, F., Dissipative discrete breathers: periodic, quasiperiodic, chaotic, and mobile, Chaos 13 (2003), 610.CrossRefGoogle ScholarPubMed
Paleari, S. and Penati, T., Long time stability of small amplitude breathers in a mixed FPU-KG model, Z. Angew. Math. Phys. 67 (2016), 148.CrossRefGoogle Scholar
Palmero, F., English, L. Q., Cuevas, J., Carretero-González, R. and Kevrekidis, P. G., Discrete breathers in a nonlinear electric line: modeling, computation, and experiment, Phys. Rev. E 82 (2011), 026605.CrossRefGoogle Scholar
Pankov, A., Gap solitons in periodic discrete nonlinear Schrödinger equations, Nonlinearity 19 (2006), 27–40.CrossRefGoogle Scholar
Pankov, A., Solitary waves on nonlocal Fermi-Pasta-Ulam lattices: exponential localization, Nonlinear Anal. Real World Appl. 50 (2019), 603–612.CrossRefGoogle Scholar
Pelinovsky, D. E. and Sakovich, A., Multi-site breathers in Klein–Gordon lattices: stability, resonances and bifurcations, Nonlinearity 25 (2012), 3423–3451.CrossRefGoogle Scholar
Penati, T., Sansottera, M., Paleari, S., Koukouloyannis, V. and Kevrekidis, P. G., On the nonexistence of degenerate phase-shift discrete solitons in a dNLS nonlocal lattice, Physica D 370 (2018), 1–13.CrossRefGoogle Scholar
Remoissenet, M., Waves called solitons: concepts and experiments (Springer-Verlag, 2003).Google Scholar
Sato, M. and Sievers, A. J., Direct observation of the discrete character of intrinsic localized modes in an antiferromagnet, Nature 432 (2004), 486–488.CrossRefGoogle Scholar
Sato, M., Hubbard, B. E. and Sievers, A. J., Colloquium: nonlinear energy localization and its manipulation in micromechanical oscillator arrays, Rev. Mod. Phys. 78 (2006), 137.CrossRefGoogle Scholar
Schauder, J., Der Fixpunktsatz in Funktionalraümen, Studia Math. 2 (1930), 171–180.CrossRefGoogle Scholar
Schwarz, U. T., English, L. Q. and Sievers, A. J., Experimental generation and observation of intrinsic localized spin wave modes in an antiferromagnet, Phys. Rev. Lett. 83 (1999), 223.CrossRefGoogle Scholar
Sepulchre, J.-A. and MacKay, R. S., Localized oscillations in conservative or dissipative networks of weakly coupled autonomous oscillators, Nonlinearity 10 (1997), 679–713.CrossRefGoogle Scholar
Trombettoni, A. and Smerzi, A., Discrete solitons and breathers with dilute Bose-Einstein condensates, Phys. Rev. Lett. 86 (2001), 2353.CrossRefGoogle ScholarPubMed
Xu, H., Cuevas-Maraver, J., Kevrekidis, P. G. and Vainchtein, A., An energy-based stability criterion for solitary traveling waves in Hamiltonian lattices, Philos. Trans. Roy. Soc. A 376 (2018), 20170192.CrossRefGoogle ScholarPubMed
Zeidler, E., Nonlinear functional analysis and its applications IIA: linear monotone operators (Springer-Verlag, 1990).Google Scholar
Zeidler, E., Nonlinear functional analysis and its applications IIB: nonlinear monotone operators (Springer-Verlag, 1990).Google Scholar
Zhang, G., Breather solutions of the discrete nonlinear Schrödinger equations with unbounded potentials, J. Math. Phys. 50 (2009), 0131105.CrossRefGoogle Scholar