Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
Hostname: page-component-684899dbb8-ct24h Total loading time: 0.526 Render date: 2022-05-18T21:19:15.867Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "useRatesEcommerce": false, "useNewApi": true }
  • English
Proceedings of the Edinburgh Mathematical Society Proceedings of the Edinburgh Mathematical Society

Article contents

Extension and averaging operators for finite fields

Part of: Harmonic analysis in several variables Finite fields and commutative rings (number-theoretic aspects)

Published online by Cambridge University Press:  30 April 2013

Doowon Koh  and
Chun-Yen Shen
Doowon Koh
Affiliation:
Department of Mathematics, Chungbuk National University, Cheongju City, Chungbuk-Do 361-763, Republic of Korea (koh131@chungbuk.ac.kr)
Chun-Yen Shen
Affiliation:
Department of Mathematics and Statistics, McMaster University, Hamilton L8S 4K1, Canada (shenc@umail.iu.edu)
Get access Rights & Permissions[Opens in a new window]

Abstract

In this paper we study Lp−Lr estimates of both the extension operator and the averaging operator associated with the algebraic variety S = {x ∈ 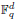: Q(x) = 0}, where Q(x) is a non-degenerate quadratic form over the finite field 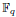with q elements. We show that the Fourier decay estimate on S is good enough to establish the sharp averaging estimates in odd dimensions. In addition, the Fourier decay estimate enables us to simply extend the sharp L2−L4 conical extension result in 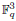, due to Mockenhaupt and Tao, to the L2−L2(d+1)/(d−1) estimate in all odd dimensions d ≥ 3. We also establish a sharp estimate of the mapping properties of the average operators in the case when the variety S in even dimensions d ≥ 4 contains a d/2-dimensional subspace.

Keywords

extension problemaveraging operatorfinite field

MSC classification

Secondary: 42B05: Fourier series and coefficients 11T24: Other character sums and Gauss sums
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 56 , Issue 2 , June 2013 , pp. 599 - 614
Copyright
Copyright © Edinburgh Mathematical Society 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bourgain, J., On the restriction and multiplier problem in ℝ3, Lecture Notes in Mathematics, Volume 1469 (Springer, 1991).Google Scholar
2.Carbery, A., Stones, B. and Wright, J., Averages in vector spaces over finite fields, Math. Proc. Camb. Phil. Soc. 144(13) (2008), 13–27.CrossRefGoogle Scholar
3.De Carli, L. and Iosevich, A., Some sharp restriction theorems for homogeneous manifolds, J. Fourier Analysis Applic. 1(4) (1998), 105–128.CrossRefGoogle Scholar
4.Iosevich, A. and Sawyer, E., Sharp Lp–Lq estimates for a class of averaging operators, Annales Inst. Fourier 46(5) (1996), 1359–1384.CrossRefGoogle Scholar
5.Iwaniec, H. and Kowalski, E., Analytic number theory, Collo quium Publications, Volume 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
6.Lidl, R. and Niederreiter, H., Finite fields (Cambridge University Press, 1997).Google Scholar
7.Littman, W., Lp–Lq estimates for singular integral operators, Proc. Symp. Pure Math. 23 (1973), 479–481.CrossRefGoogle Scholar
8.Mockenhaupt, G. and Tao, T., Restriction and Kakeya phenomena for finite fields, Duke Math. J. 121(1) (2004), 35–74.Google Scholar
9.Stein, E. M., Lpboundedness of certain convolution operators, Bull. Am. Math. Soc. 77 (1971), 404–405.CrossRefGoogle Scholar
10.Stein, E. M., Harmonic analysis (Princeton University Press, 1993).Google Scholar
11.Strichartz, R., Convolutions with kernels having singularities on the sphere, Trans. Am. Math. Soc. 148 (1970), 461–471.CrossRefGoogle Scholar
12.Tao, T., Recent progress on the restriction conjecture, in Fourier analysis and convexity (ed. Brandolini, L., Colzani, L., Iosevich, A. and Travaglini, G.), Applied and Numerical Harmonic Analysis, pp. 217–243 (Birkhäuser, Boston, MA, 2004).CrossRefGoogle Scholar
13.Wolff, T., A sharp bilinear cone restriction estimate, Annals Math. 153 (2001), 661–698.CrossRefGoogle Scholar
7
Cited by

Save article to Kindle

To save this article to your Kindle, first ensure coreplatform@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Extension and averaging operators for finite fields
Available formats
×

Save article to Dropbox

To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.

Extension and averaging operators for finite fields
Available formats
×

Save article to Google Drive

To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.

Extension and averaging operators for finite fields
Available formats
×
×

Reply to: Submit a response

Please enter your response.

Your details

Please enter a valid email address.

Conflicting interests

Do you have any conflicting interests? *