Hostname: page-component-7479d7b7d-rvbq7 Total loading time: 0 Render date: 2024-07-12T22:54:57.889Z Has data issue: false hasContentIssue false
  • English
  • Français

RINGS OF TETER TYPE

Part of: Local rings and semilocal rings Finite commutative rings

Published online by Cambridge University Press:  10 June 2022

OLEKSANDRA GASANOVA Open the ORCID record for OLEKSANDRA GASANOVA [Opens in a new window] ,
JÜRGEN HERZOG Open the ORCID record for JÜRGEN HERZOG [Opens in a new window] ,
TAKAYUKI HIBI Open the ORCID record for TAKAYUKI HIBI [Opens in a new window]  and
SOMAYEH MORADI Open the ORCID record for SOMAYEH MORADI [Opens in a new window]
OLEKSANDRA GASANOVA
Affiliation:
Department of Mathematics, Uppsala University, SE-75106 Uppsala, Sweden oleksandra.gasanova@math.uu.se
JÜRGEN HERZOG
Affiliation:
Fakultät für Mathematik, Universität Duisburg-Essen, 45117 Essen, Germany juergen.herzog@uni-essen.de
TAKAYUKI HIBI
Affiliation:
Department of Pure and Applied Mathematics, Graduate School of Information Science and Technology, Osaka University, Suita, Osaka 565-0871, Japan hibi@math.sci.osaka-u.ac.jp
SOMAYEH MORADI
Affiliation:
Department of Mathematics, School of Science, Ilam University, P.O.Box, 69315-516, Ilam, Iran so.moradi@ilam.ac.ir
Get access Rights & Permissions [Opens in a new window]

Abstract

Let R be a Cohen–Macaulay local K-algebra or a standard graded K-algebra over a field K with a canonical module 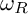$\omega _R$ . The trace of 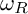$\omega _R$ is the ideal 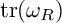$\operatorname {tr}(\omega _R)$ of R which is the sum of those ideals 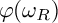$\varphi (\omega _R)$ with 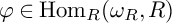${\varphi \in \operatorname {Hom}_R(\omega _R,R)}$ . The smallest number s for which there exist 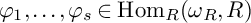$\varphi _1, \ldots , \varphi _s \in \operatorname {Hom}_R(\omega _R,R)$ with 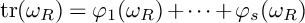$\operatorname {tr}(\omega _R)=\varphi _1(\omega _R) + \cdots + \varphi _s(\omega _R)$ is called the Teter number of R. We say that R is of Teter type if 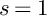$s = 1$ . It is shown that R is not of Teter type if R is generically Gorenstein. In the present paper, we focus especially on zero-dimensional graded and monomial K-algebras and present various classes of such algebras which are of Teter type.

MSC classification

Primary: 13H10: Special types (Cohen-Macaulay, Gorenstein, Buchsbaum, etc.)
Secondary: 13M05: Structure
Type
Article
Information
Nagoya Mathematical Journal , Volume 248 , December 2022 , pp. 1005 - 1033
Check for updates
Copyright
© (2022) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Oleksandra Gasanova’s stay was supported by Liljewalchs and Thelins travel scholarships from Uppsala University. Takayuki Hibi was partially supported by the Japan Society for the Promotion of Science Grants-in-Aid for Scientific Research Grant No. 19H00637. Somayeh Moradi was supported by the Centre International de Mathématiques Pures et Appliquées’ research in pairs fellowship and a partial grant from Ilam University.

References

Ananthnarayan, H., The Gorenstein colength of an Artinian local ring , J. Algebra 320 (2008), 3438–3446.CrossRefGoogle Scholar
Bruns, W. and Herzog, J., Cohen–Macaulay Rings, Cambridge Stud. Adv. Math. 39, Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar
Eisenbud, D., Commutative Algebra with a View Toward Algebraic Geometry, Grad. Texts in Math. 150, Springer Science & Business Media, Springer 2013.Google Scholar
Elias, J. and Takatuji, M. S., On Teter rings , Proc. Royal Soc. Edinburgh 147A (2017), 125–139.CrossRefGoogle Scholar
Herzog, J. and Hibi, T., Monomial Ideals, Grad. Texts in Math. 260, Springer, London, 2011.CrossRefGoogle Scholar
Herzog, J., Hibi, T., and Stamate, D., Canonical trace ideal and residue for numerical semigroup rings , Semigroup Forum 103 (2021), 550—566.CrossRefGoogle Scholar
Herzog, J. and Kunz, E., The canonical modulus of a Cohen-Macaulay ring, Vol. 238. Springer-Verlag, 2006.Google Scholar
Huneke, C. and Vraciu, A., Rings that are almost Gorenstein , Pac. J. Math. 225 (2006), 85–102.CrossRefGoogle Scholar
Kobayashi, T., Local rings with self-dual maximal ideal , Ill. J. Math. 64 (2020), 349–373.Google Scholar
Kunz, E., Almost complete intersections are not Gorenstein rings , J. Algebra 28 (1974), 111–115.Google Scholar
Teter, W., Rings which are a factor of a Gorenstein ring by its socle , Invent. Math. 23 (1974), 153–162.CrossRefGoogle Scholar
Vasconcelos, W. V., Computing the integral closure of an affine domain , Proc. Amer. Math. Soc. 113 (1991), 633–638.CrossRefGoogle Scholar