Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kantor, W. M.
1975.
Combinatorics.
p.
365.
Hirasaka, Mitsugu
2009.
On imprimitive multiplicity-free permutation groups the degree of which is the product of two distinct primes.
European Journal of Combinatorics,
Vol. 30,
Issue. 1,
p.
30.


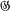 be a transitive permutation group on Ω such that
be a transitive permutation group on Ω such that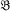 of index
of index 