Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-18T21:47:31.040Z Has data issue: false hasContentIssue false
  • English
  • Français

GLOBAL ATTRACTOR FOR WEAKLY DAMPED, FORCED mKdV EQUATION BELOW ENERGY SPACE

Part of: Equations of mathematical physics and other areas of application Partial differential equations Infinite-dimensional dissipative dynamical systems

Published online by Cambridge University Press:  20 June 2019

PRASHANT GOYAL Open the ORCID record for PRASHANT GOYAL [Opens in a new window]
PRASHANT GOYAL*
Affiliation:
Department of Mathematics, Graduate School of Science, Kyoto University, Kyoto 606-8501, Japan email goyalprashant194@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the existence of the global attractor in 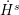${\dot{H}}^{s}$, 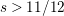$s>11/12$ for the weakly damped and forced mKdV on the one-dimensional torus. The existence of global attractor below the energy space has not been known, though the global well-posedness below the energy space has been established. We directly apply the 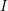$I$-method to the damped and forced mKdV, because the Miura transformation does not work for the mKdV with damping and forcing terms. We need to make a close investigation into the trilinear estimates involving resonant frequencies, which are different from the bilinear estimates corresponding to the KdV.

MSC classification

Primary: 35B41: Attractors
Secondary: 35Q53: KdV-like equations (Korteweg-de Vries) 37L50: Noncompact semigroups; dispersive equations; perturbations of Hamiltonian systems
Type
Article
Information
Nagoya Mathematical Journal , Volume 241 , March 2021 , pp. 171 - 203
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bourgain, J., Fourier transform restriction phenomena for certain lattice subsets and applications to nonlinear evolution equations, Geom. Funct. Anal. 3(3) (1993), 209–262.10.1007/BF01895688Google Scholar
Chen, W., Tian, L. and Deng, X., Global attractor of dissipative MKdV equation, J. Jiangsu Univ. Nat. Sci. 28(1) (2007), 89–92.Google Scholar
Chen, W., Tian, L. and Deng, X., The global attractor and numerical simulation of a forced weakly damped MKdV equation, Nonlinear Anal. Real World Appl. 10(3) (2009), 1822–1837.10.1016/j.nonrwa.2008.02.025Google Scholar
Colliander, J., Keel, M., Staffilani, G., Takaoka, H. and Tao, T., Sharp global well-posedness for KdV and modified KdV on ℝ and 𝕋, J. Amer. Math. Soc. 16(3) (2003), 705–749.10.1090/S0894-0347-03-00421-1Google Scholar
Colliander, J., Keel, M., Staffilani, G., Takaoka, H. and Tao, T., Multilinear estimates for periodic KdV equations, and applications, J. Funct. Anal. 211(1) (2004), 173–218.10.1016/S0022-1236(03)00218-0Google Scholar
Colliander, J., Keel, M., Staffilani, G., Takaoka, H. and Tao, T., Resonant decompositions and the I-method for cubic nonlinear Schrodinger on R 2, Discrete Contin. Dyn. Syst. 21(3) (2008), 665–686.10.3934/dcds.2008.21.665Google Scholar
Dlotko, T., Kania, M. B. and Yang, M., Generalized Korteweg–de Vries equation in H 1(ℝ), Nonlinear Anal. 71(9) (2009), 3934–3947.10.1016/j.na.2009.02.062Google Scholar
Ghidaglia, J. M., Finite-dimensional behavior for weakly damped driven Schrödinger equations, Ann. Inst. H. Poincaré Anal. Non Linéaire 5(4) (1988), 365–405.10.1016/S0294-1449(16)30343-2Google Scholar
Ghidaglia, J. M., Weakly damped forced Korteweg–de Vries equations behave as a finite-dimensional dynamical system in the long time, J. Differential Equations 74(2) (1988), 369–390.10.1016/0022-0396(88)90010-1Google Scholar
Ghidaglia, J. M., A note on the strong convergence towards attractors of damped forced KdV equations, J. Differential Equations 110(2) (1994), 356–359.10.1006/jdeq.1994.1071Google Scholar
Goubet, O., Regularity of the attractor for a weakly damped nonlinear Schrödinger equation, Appl. Anal. 60(1–2) (1996), 99–119. Harvard.10.1080/00036819608840420Google Scholar
Goubet, O. and Molinet, L., Global attractor for weakly damped Nonlinear Schrödinger equations in L 2(ℝ), Nonlinear Anal. 71(1–2) (2009), 317–320.10.1016/j.na.2008.10.078Google Scholar
Guo, B. and Li, Y., Attractor for dissipative Klein–Gordon–Schrödinger equations in ℝ3, J. Differential Equations 136(2) (1997), 356–377.Google Scholar
Haraux, A., Two remarks on dissipative hyperbolic problems, Res. Notes Math. 122 (1985), 161–179.Google Scholar
Kato, T., Quasi-linear equations of evolution, with applications to partial differential equations, Lect. Notes Math. 448 (1975), 25–70.10.1007/BFb0067080Google Scholar
Lu, K. and Wang, B., Global attractors for the Klein–Gordon–Schrödinger equation in unbounded domains, J. Differential Equations 170(2) (2001), 281–316.10.1006/jdeq.2000.3827Google Scholar
Miura, R. M., Korteweg–de Vries equation and generalizations. I. A remarkable explicit nonlinear transformation, J. Mathematical Phys. 9 (1968), 1202–1204.10.1063/1.1664700Google Scholar
Miura, R. M., The Korteweg–de Vries equation: a survey of results, SIAM Rev. 18(3) (1976), 412–459.10.1137/1018076Google Scholar
Miyaji, T. and Tsutsumi, Y., Existence of global solutions and global attractor for the third order Lugiato–Lefever equation on 𝕋, Ann. Inst. H. Poincaré Anal. Non Linéaire 34(7) (2017), 1707–1725.10.1016/j.anihpc.2016.12.004Google Scholar
Nakanishi, K., Takaoka, H. and Tsutsumi, Y., Local well-posedness in low regularity of the mKdV equation with periodic boundary condition, Discrete Contin. Dyn. Syst. 28(4) (2010), 1635–1654.10.3934/dcds.2010.28.1635Google Scholar
Takaoka, H. and Tsutsumi, Y., Well-posedness of the Cauchy problem for the modified KdV equation with periodic boundary condition, Int. Math. Res. Not. 56 (2004), 3009–3040.10.1155/S1073792804140555Google Scholar
Temam, R., Infinite-dimensional Dynamical Systems in Mechanics and Physics, 2nd ed. Springer-Verlag, New York, 1997.10.1007/978-1-4612-0645-3Google Scholar
Tsugawa, K., Existence of the global attractor for weakly damped, forced KdV equation on Sobolev spaces of negative index, Commun. Pure Appl. Anal. 3(2) (2004), 301–318.10.3934/cpaa.2004.3.301Google Scholar
Wang, M., Li, D., Zhang, C. and Tang, Y., Long time behavior of solutions of gKdV equations, J. Math. Anal. Appl. 390(1) (2012), 136–150.10.1016/j.jmaa.2012.01.031Google Scholar
Yang, X., Global attractor for the weakly damped forced KdV equation in Sobolev spaces of low regularity, Nonlinear Differ. Equ. Appl. 18(3) (2011), 273–285.10.1007/s00030-010-0095-9Google Scholar