Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-19T21:10:56.142Z Has data issue: false hasContentIssue false
  • English
  • Français

CONCAVITY PROPERTY OF MINIMAL 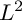$L^{2}$ INTEGRALS WITH LEBESGUE MEASURABLE GAIN

Part of: Genetics and population dynamics Differential operators in several variables Analytic continuation Holomorphic fiber spaces Holomorphic convexity Pluripotential theory

Published online by Cambridge University Press:  05 June 2023

QI’AN GUAN Open the ORCID record for QI’AN GUAN [Opens in a new window]  and
ZHENG YUAN Open the ORCID record for ZHENG YUAN [Opens in a new window]
QI’AN GUAN
Affiliation:
School of Mathematical Sciences Peking University Beijing 100871, China guanqian@math.pku.edu.cn
ZHENG YUAN*
Affiliation:
School of Mathematical Sciences Peking University Beijing 100871, China
*
zyuan@pku.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we present a concavity property of the minimal 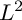$L^{2}$ integrals related to multiplier ideal sheaves with Lebesgue measurable gain. As applications, we give necessary conditions for our concavity degenerating to linearity, characterizations for 1-dimensional case, and a characterization for the holding of the equality in optimal 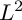$L^2$ extension problem on open Riemann surfaces with weights may not be subharmonic.

MSC classification

Primary: 32D15: Continuation of analytic objects
Secondary: 32E10: Stein spaces, Stein manifolds 32L10: Sheaves and cohomology of sections of holomorphic vector bundles, general results 32U05: Plurisubharmonic functions and generalizations 32W05: $overlinepartial$ and $overlinepartial$-Neumann operators
Type
Article
Information
Nagoya Mathematical Journal , Volume 252 , December 2023 , pp. 842 - 905
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Qi’an Guan was supported by the National Key R&D Program of China (Grant No. 2021YFA1003100) and the National Natural Science Foundation of China (Grant No. NSFC-11825101, NSFC-11522101, and NSFC-11431013).

References

Berndtsson, B., The openness conjecture for plurisubharmonic functions, preprint, arXiv:1305.5781Google Scholar
Demailly, J.-P., “On the Ohsawa–Takegoshi–Manivel ${L}^2$ extension theorem” in Proceedings of the Conference in Honour of the 85th birthday of Pierre Lelong, Paris, September 1997, Progr. Math., Birkhäuser, Basel, 2000.Google Scholar
Demailly, J-P., “Multiplier ideal sheaves and analytic methods in algebraic geometry” in School on Vanishing Theorems and Effective Results in Algebraic Geometry (Trieste, 2000), ICTP Lect. Notes 6, Abdus Salam Int. Cent. Theoret. Phys., Trieste, 2001, 1–148.Google Scholar
Demailly, J.-P., Analytic Methods in Algebraic Geometry, Higher Education Press, Beijing, 2010.Google Scholar
Demailly, J.-P., Complex analytic and differential geometry, electronically accessible at http://www-fourier.ujf-grenoble.fr/demailly/books.html.Google Scholar
Demailly, J.-P., Ein, L., and Lazarsfeld, R., A subadditivity property of multiplier ideals , Michigan Math. J. 48 (2000), 137–156.10.1307/mmj/1030132712CrossRefGoogle Scholar
Demailly, J.-P. and Kollár, J., Semi-continuity of complex singularity exponents and Kähler–Einstein metrics on Fano orbifolds . Ann. Sci. Éc. Norm. Supér. (4) 34 (2001), 525–556.10.1016/S0012-9593(01)01069-2CrossRefGoogle Scholar
Demailly, J.-P. and Peternell, T., A Kawamata–Viehweg vanishing theorem on compact Kähler manifolds . J. Differential Geom. 63 (2003), 231–277.10.4310/jdg/1090426678CrossRefGoogle Scholar
Favre, C. and Jonsson, M., Valuations and multiplier ideals , J. Amer. Math. Soc. 18 (2005), 655–684.10.1090/S0894-0347-05-00481-9CrossRefGoogle Scholar
Fornæss, J. E. and Narasimhan, R., The Levi problem on complex spaces with singularities , Math. Ann. 248 (1980), 47–72.10.1007/BF01349254CrossRefGoogle Scholar
Forster, O., Lectures on Riemann Surfaces, Grad. Texts in Math. 81, Springer, New York–Berlin, 1981.10.1007/978-1-4612-5961-9CrossRefGoogle Scholar
Grauert, H. and Remmert, R., Coherent Analytic Sheaves, Grundlehren Math. Wiss. 265, Springer, Berlin, 1984.10.1007/978-3-642-69582-7CrossRefGoogle Scholar
Guan, Q. A., Genneral concavity of minimal ${L}^2$ integrals related to multiplier sheaves, preprint, arXiv:1811.03261v4 Google Scholar
Guan, Q. A., A sharp effectiveness result of Demailly’s strong openness conjecture , Adv. Math. 348 (2019), 51–80.10.1016/j.aim.2019.03.017CrossRefGoogle Scholar
Guan, Q. A. and Mi, Z. T., Concavity of minimal ${L}^2$ integrals related to multiplier ideal sheaves, Peking Math. J. (2022). https://doi.org/10.1007/s42543-021-00047-5 CrossRefGoogle Scholar
Guan, Q. A. and Zhou, X. Y., Optimal constant problem in the ${L}^2\kern-2pt$ extension theorem , C. R. Acad. Sci. Paris. Ser. I 350 (2012), 753–756.10.1016/j.crma.2012.08.007CrossRefGoogle Scholar
Guan, Q. A. and Zhou, X. Y., Optimal constant in an ${L}^2\kern-1pt$ extension problem and a proof of a conjecture of Ohsawa , Sci. China Math. 58 (2015), 35–59.10.1007/s11425-014-4946-4CrossRefGoogle Scholar
Guan, Q. A. and Zhou, X. Y., A solution of an ${L}^2\kern-2pt$ extension problem with an optimal estimate and applications , Ann. of Math. (2) 181 (2015), 1139–1208.10.4007/annals.2015.181.3.6CrossRefGoogle Scholar
Guan, Q. A. and Zhou, X. Y., A proof of Demailly’s strong openness conjecture , Ann. of Math. (2) 182 (2015), 605–616; See also arXiv:1311.3781.10.4007/annals.2015.182.2.5CrossRefGoogle Scholar
Guan, Q. A. and Zhou, X. Y., Effectiveness of Demailly’s strong openness conjecture and related problems , Invent. Math. 202 (2015), no. 2, 635–676.10.1007/s00222-014-0575-3CrossRefGoogle Scholar
Jonsson, M. and Mustaţă, M., Valuations and asymptotic invariants for sequences of ideals , Ann. Inst. Fourier A (Grenoble) 62 (2012), 2145–2209.10.5802/aif.2746CrossRefGoogle Scholar
Lazarsfeld, R., Positivity in Algebraic Geometry. I. Classical Setting: Line Bundles and Linear Series, Ergeb. Math. Grenzgeb. (3) 48, Springer, Berlin, 2004; Positivity in Algebraic Geometry. II. Positivity for Vector Bundles, and Multiplier Ideals, Ergeb. Math. Grenzgeb. (3) 49.Google Scholar
Nadel, A., Multiplier ideal sheaves and Kähler–Einstein metrics of positive scalar curvature . Ann. of Math. (2) 132 (1990), 549–596.10.2307/1971429CrossRefGoogle Scholar
Ohsawa, T., On the extension of ${L}^2$ holomorphic functions. V. Effects of generalization . Nagoya Math. J. 161 (2001), 1–21. Erratum to: “On the extension of ${L}^2$ holomorphic functions. V. Effects of generalization” [Nagoya Math. J. 161 (2001), 1–21]. Nagoya Math. J. 163 (2001), 229.10.1017/S0027763000022108CrossRefGoogle Scholar
Sario, L. and Oikawa, K., Capacity Functions, Grundl. Math. Wissen. 149, Springer, New York, 1969.10.1007/978-3-642-46181-1CrossRefGoogle Scholar
Siu, Y. T., “The Fujita conjecture and the extension theorem of Ohsawa–Takegoshi” in Geometric Complex Analysis, World Scientific, Hayama, 1996, 577–592.Google Scholar
Siu, Y. T., Multiplier ideal sheaves in complex and algebraic geometry . Sci. China Ser. A 48 (2005), 1–31.10.1007/BF02884693CrossRefGoogle Scholar
Siu, Y. T., “Dynamic multiplier ideal sheaves and the construction of rational curves in Fano manifolds” in Complex Analysis and Digital Geometry, Acta Univ. Upsaliensis Skr. Uppsala Univ. C Organ. Hist. 86, Uppsala Universitet, Uppsala, 2009, 323–360.Google Scholar
Skoda, H., Sous-ensembles analytiques d’ordre fini ou infini dans ${\mathbb{C}}^n$ , Bull. Soc. Math. France 100 (1972), 353–408.10.24033/bsmf.1743CrossRefGoogle Scholar
Tian, G., On Kähler–Einstein metrics on certain Kähler manifolds with ${C}_1(M)>0$ , Invent. Math. 89 (1987), 225–246.10.1007/BF01389077CrossRefGoogle Scholar
Tsuji, M., Potential Theory in Modern Function Theory, Maruzen Co., Ltd., Tokyo, 1959.Google Scholar
Xu, W. and Zhou, X. Y., Optimal ${L}^2$ extensions of openness type, preprint, arXiv:2202.04791v2Google Scholar