Article contents
INTERTWINING SEMISIMPLE CHARACTERS FOR 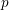 $p$-ADIC CLASSICAL GROUPS
$p$-ADIC CLASSICAL GROUPS
Published online by Cambridge University Press: 16 July 2018
Abstract
Let 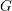 $G$ be an orthogonal, symplectic or unitary group over a non-archimedean local field of odd residual characteristic. This paper concerns the study of the “wild part” of an irreducible smooth representation of
$G$ be an orthogonal, symplectic or unitary group over a non-archimedean local field of odd residual characteristic. This paper concerns the study of the “wild part” of an irreducible smooth representation of 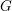 $G$, encoded in its “semisimple character”. We prove two fundamental results concerning them, which are crucial steps toward a complete classification of the cuspidal representations of
$G$, encoded in its “semisimple character”. We prove two fundamental results concerning them, which are crucial steps toward a complete classification of the cuspidal representations of 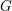 $G$. First we introduce a geometric combinatorial condition under which we prove an “intertwining implies conjugacy” theorem for semisimple characters, both in
$G$. First we introduce a geometric combinatorial condition under which we prove an “intertwining implies conjugacy” theorem for semisimple characters, both in 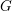 $G$ and in the ambient general linear group. Second, we prove a Skolem–Noether theorem for the action of
$G$ and in the ambient general linear group. Second, we prove a Skolem–Noether theorem for the action of  $G$ on its Lie algebra; more precisely, two semisimple elements of the Lie algebra of
$G$ on its Lie algebra; more precisely, two semisimple elements of the Lie algebra of 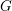 $G$ which have the same characteristic polynomial must be conjugate under an element of
$G$ which have the same characteristic polynomial must be conjugate under an element of 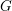 $G$ if there are corresponding semisimple strata which are intertwined by an element of
$G$ if there are corresponding semisimple strata which are intertwined by an element of 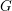 $G$.
$G$.
MSC classification
- Type
- Article
- Information
- Copyright
- © 2018 Foundation Nagoya Mathematical Journal
Footnotes
This research was funded by EPSRC grant EP/H00534X/1.
References
- 5
- Cited by


