Article contents
COHOMOLOGY OF THE BRUHAT–TITS STRATA IN THE UNRAMIFIED UNITARY RAPOPORT–ZINK SPACE OF SIGNATURE 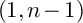 $(1,n-1)$
$(1,n-1)$
Published online by Cambridge University Press: 23 November 2022
Abstract
In their renowned paper (2011, Inventiones Mathematicae 184, 591–627), I. Vollaard and T. Wedhorn defined a stratification on the special fiber of the unitary unramified PEL Rapoport–Zink space with signature
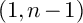 $(1,n-1)$
. They constructed an isomorphism between the closure of a stratum, called a closed Bruhat–Tits stratum, and a Deligne–Lusztig variety which is not of classical type. In this paper, we describe the
$(1,n-1)$
. They constructed an isomorphism between the closure of a stratum, called a closed Bruhat–Tits stratum, and a Deligne–Lusztig variety which is not of classical type. In this paper, we describe the
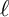 $\ell $
-adic cohomology groups over
$\ell $
-adic cohomology groups over
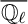 $\overline {{\mathbb Q}_{\ell }}$
of these Deligne–Lusztig varieties, where
$\overline {{\mathbb Q}_{\ell }}$
of these Deligne–Lusztig varieties, where
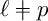 $\ell \not = p$
. The computations involve the spectral sequence associated with the Ekedahl–Oort stratification of a closed Bruhat–Tits stratum, which translates into a stratification by Coxeter varieties whose cohomology is known. Eventually, we find out that the irreducible representations of the finite unitary group which appear inside the cohomology contribute to only two different unipotent Harish-Chandra series, one of them belonging to the principal series.
$\ell \not = p$
. The computations involve the spectral sequence associated with the Ekedahl–Oort stratification of a closed Bruhat–Tits stratum, which translates into a stratification by Coxeter varieties whose cohomology is known. Eventually, we find out that the irreducible representations of the finite unitary group which appear inside the cohomology contribute to only two different unipotent Harish-Chandra series, one of them belonging to the principal series.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal
References
- 1
- Cited by



