Lone pairs and their stereochemistry

Students of high-school chemistry will be familiar with the molecular structures of simple molecules such as water and ammonia from the valence-shell electron pair repulsion (VSEPR) theory of Sidgwick and Powell,^{Reference Sidgwick and Powell8} later fine-tuned by Gillespie and Nyholm,^{Reference Gillespie and Nyholm9} as shown in Figure 1a. By counting electrons and assigning bond orders, one concludes that water has two lone pairs of electrons, leading to the familiar bent geometry, and to a substantial permanent dipole. Similarly, ammonia has one lone pair and adopts a distorted pyramidal geometry. In extended solids of heavier elements, similar principles apply. While competing long-range forces, relativistic contraction (expansion) of 6s (5d) orbitals, and effects of delocalization complicate the picture, they do not fundamentally alter it.^{Reference Galy, Meunier, Andersson and Åström10}

Figure 1. Molecular and crystal structures and associated symmetries (P.G.: point group; S.G.: space group) of (a) water and ammonia, (b)litharge PbO and rock-salt PbS, and (c) perovskites CsGeI₃ and CsSnBr₃ (both at ambient temperature). The lone pairs are schematically indicated. (d) Schematic double-well potential for lone pair-induced distortion of an octahedral coordination environment, parametrized by a generalized distortion coordinate, Q. The depth of the double-well, E _DW, relative to k_BT, determines whether the structure is crystallographically distorted (e.g., PbO, CsGeI₃) or locally distorted (PbS and CsSnBr₃).

In most semiconducting and insulating compounds of the main group elements (those of groups 1, 2, and 13–18 in the periodic table), the metal cations take on oxidation states reflecting completely empty ns and np orbitals, where n is the period. However, for heavier elements, another possibility becomes available and, indeed, is common. Elements such as tin, lead, antimony, and bismuth are instead oxidized only to 2 less than the group valence, holding onto their ns^{Reference Kulbak, Cahen and Hodes2} electrons as a lone pair. This is most prevalent in period 6 elements (Tl⁺, Pb²⁺, Bi³⁺), relatively common in period 5 elements (In⁺, Sn²⁺, Sb³⁺, Te⁴⁺), and less common in period 4 elements (Ga⁺, Ge²⁺, As³⁺, Se⁴⁺), reflecting increasing stabilization of the s orbital going down the table (and to the right).

In analogy with the more familiar previous examples of water and ammonia, the lone pairs in the heavier main group elements can be stereochemically expressed (i.e., they can occupy space as an acentric lobe of electron density, repelling other ligands). However, they can also appear in routine crystallography (i.e., temporally and spatially averaged) to maintain the spherical symmetry of the isolated s orbital, seemingly playing no structure-directing role. Taking the example of Pb, this is exemplified in Figure 1b by the distinct structures of litharge PbO with acentric Pb coordination, where the lone pair is stereochemically expressed, and rock-salt PbS, with ostensibly perfect octahedral coordination. The respective behavior is also observed in the structures of halide perovskites (Figure 1c); at room temperature, CsGeI₃ is rhombohedral and polar with three long and three short Ge–I bonds, whereas CsSnBr₃ is cubic.

However, in compounds such as PbS and CsSnBr₃, this crystallographically averaged view obscures some very interesting behavior. Several local structure experimental techniques, particularly pair distribution function (PDF) analysis from x-ray and neutron total scattering experiments, reveal large amplitude, hidden, local distortions in lone pair-containing rock-salt chalcogenides, bismuth pyrochlores, and halide perovskites in a manner similar to the hidden pseudo-Jahn–Teller distortions in the paraelectric phases of titanate and niobate ferroelectrics. Despite their apparent structure-directing innocence from the crystallographic view, the lone pairs in fact take up space, causing an anharmonic flat-bottomed or even double-well potential, such as the one shown schematically in Figure 1d. Whether a material adopts a crystallographically distorted structure is then simply a matter of energy scales. If the well is deep relative to thermal energy, a static distortion (usually coherent from unit cell to unit cell) results. On the other hand, if thermal energy is very large relative to the well depth, it mostly looks like the harmonic envelope encompassing the anharmonic potential. But for the intermediate case, when the energies are of similar order, interesting behavior results: highly anharmonic mechanical properties and elevated ionic dielectric response (vide infra).

In fact, ammonia is known to do something similar. The lone pair and the nitrogen nucleus “invert” through the plane of the hydrogen ligands. The depth of this double-well potential in ammonia is 250 meV—roughly ten times the thermal energy at room temperature,^{Reference Swalen and Ibers11} but quantum tunneling permits rapid inversion because the barrier is narrow.

This phenomenon of heavy main-group cations adopting lone-pair electron configurations, far from being simply a curiosity, has profound implications for the electronic and lattice dynamical properties observed in halide perovskites and myriad other functional materials, ranging from the first semiconductor diodes in early radio (PbS) to the first solid-state ion conductors (PbF₂) to thermoelectrics (PbTe) and topological insulators (Bi₂Se₃). Several of the important impacts of these lone-pair electrons on the properties and functionality of tin and lead halide perovskites are discussed.

Light holes and favorable band alignment inhalide perovskites

The electronic structure of the main-group halide perovskites is qualitatively different from that of the more familiar Group IV, III–V, and II–VI diamondoid semiconductors and is exemplified by the band structure of cubic CsPbBr₃ (shown in Figure2a). The 3D arrangement of linear Pb–Br–chains and the covalent interaction between halogen p states and the s states of Pb leads to a pair of bands with wide bandwidths (those with orange highlighting in the figure indicating their Pb s character). Because of the lone-pair electron count, the upper of these two bands is filled, constituting the VB, and its maximum is antibonding in character. Thus, the lone pair leads directly to a valence-band maximum (VBM), which is high in energy compared to conventional halide salts (Figure2a). This is qualitatively similar to the chalcogen p—metal d repulsion, which raises the VBM of Cu⁺ and Ag⁺-containing chalcopyrites.^{Reference Jaffe and Zunger12} This bonding type also creates high curvature at the VBM, which corresponds to a light effective mass for holes (≈0.1 m_e measured for the full exciton in CH₃NH₃PbI₃, where m_e is the rest mass of an electron).^{Reference Hirasawa, Ishihara, Goto, Uchida and Miura13,Reference Miyata, Mitioglu, Plochocka, Portugall, Wang, Stranks, Snaith and Nicholas14} This electronic structure is in many ways qualitatively similar to that of narrow-gap IV–VI semiconductors, such as PbS, which also contain lone-pair cations.

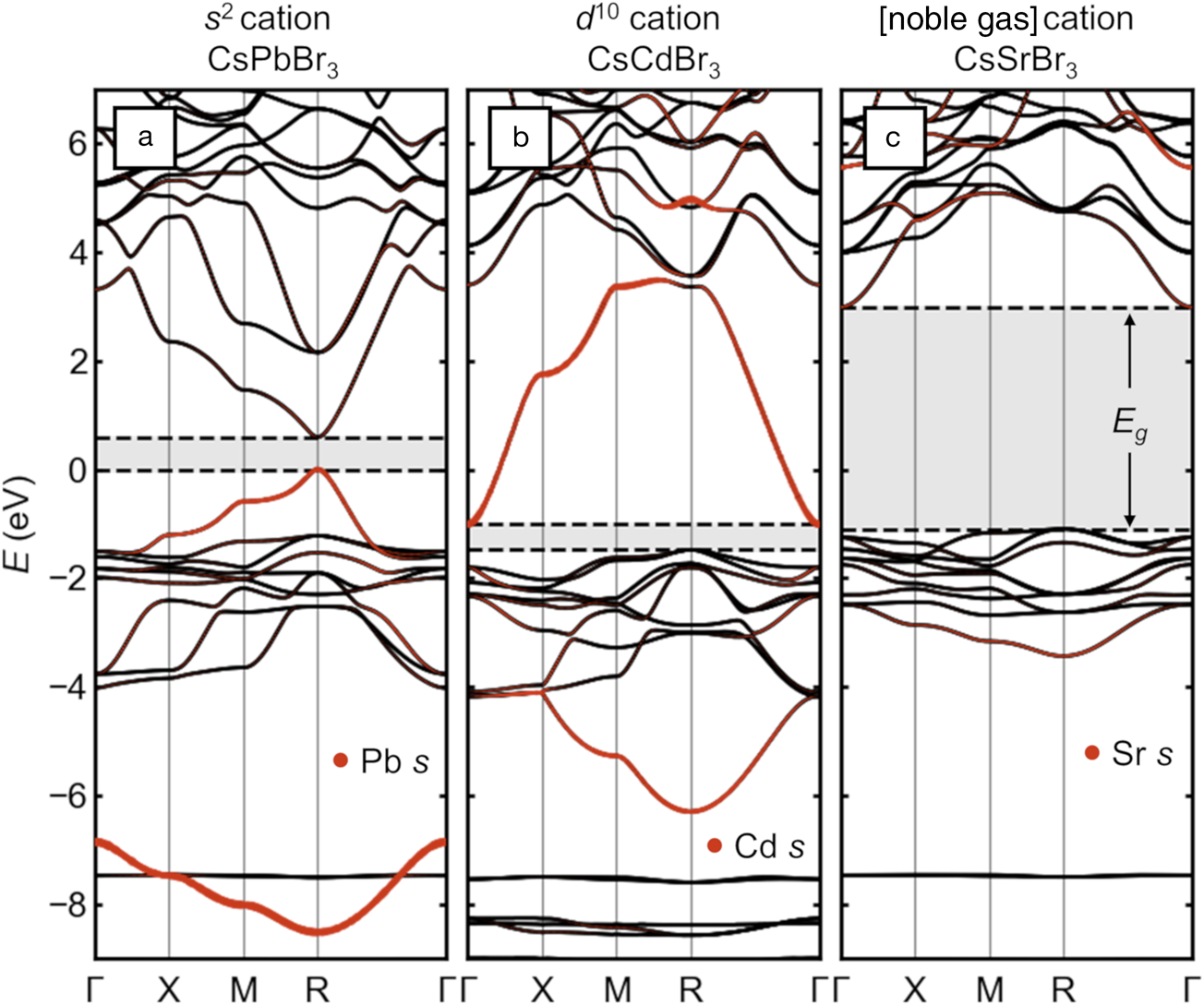
Figure 2. Electronic-band structures of cubic halide perovskites with different electronic configurations of the octahedral cation, presented on a common energy scale. (a) CsPbBr₃ with [Xe]4f ¹⁴5d ¹⁰6s ^{Reference Kulbak, Cahen and Hodes2} Pb²⁺ (“s ^{Reference Kulbak, Cahen and Hodes2}”). (b) Hypothetical “CsCdBr₃” with [Kr]4d ^{Reference Galy, Meunier, Andersson and Åström10}Cd²⁺ (“d ^{Reference Galy, Meunier, Andersson and Åström10}”). (c) CsSrBr₃ with [Kr]Sr²⁺ (“[noble gas]”). Bandgaps are indicated with shading and dashed lines. Projected s orbital character on the octahedral cation is shown as orange dots. The energy scales are aligned by the semi-core Cs 5s states (around –20 eV) and are referenced to the valence-band maximum of CsPbBr₃.

Several other studies have illustrated how decorating the perovskite lattice with s and p orbitals leads to the observed momentum-dependence of the frontier bands and location of the bandgap.^{Reference Huang and Lambrecht15–Reference Goesten and Hoffmann17} Rather than repeat these arguments, we show directly via ab initio calculations based on density functional theory (DFT) in Figure 2b–c the effects on the electronic structure of halide perovskites if the lone pair cation is replaced with one lacking this electron configuration. The A-site cation (Cs) and halogen (Br) are fixed across the series, and spin–orbit coupling is included.

If a “d ^{Reference Galy, Meunier, Andersson and Åström10}” cation such as Cd²⁺ (lacking a lone pair) with the [Kr]4d ^{Reference Galy, Meunier, Andersson and Åström10} electron configuration is substituted on the octahedral site, the band structure is radically altered, as shown in Figure 2b. Because of better energetic alignment, the empty Cd 5s and filled Br 4p orbital interaction is more covalent, leading to wider bandwidths for the corresponding pair of bands (orange highlighting). Crucially, the upper of these two bands is not occupied (no lone pair), so the VB (derived solely from the halogens) is now ≈1.5 eV deeper than that of CsPbBr₃ and much less dispersive, suggesting heavy holes, and the bandgap has become indirect. The high curvature of the conduction band (CB) suggests light electrons. Instead of balanced, small carrier masses and a direct bandgap such as in CsPbBr₃, the band structure of hypothetical “CsCdBr₃” (claimed once in the perovskite structure in 1928,^{Reference Natta and Passerini18} but subsequently reported always in the more plausible 1D BaNiO₃ structure) is analogous to that of n-type conductor BaSnO₃,^{Reference Scanlon19} but with a narrower gap.

For CsSrBr₃, as shown in Figure 2c, with the “empty shell” Sr²⁺ cation with the [Kr] electron configuration, the situation is taken to the extreme. The shallow 5s orbitals from highly electropositive Sr strongly reduce the covalency with the Br 4p, as seen in the narrower bandwidths and reduced Sr 5s weight in the bonding band around –3 eV. The VBM is again more than 1 eV deeper than in CsPbBr₃, and the hole effective mass is large. The higher band center and reduced bandwidth of the CB from this more ionic interaction creates a wide bandgap. As such, CsSrBr₃ is a colorless rare-earth ion scintillator host.

Given this limited space for chemical substitutions in “single” perovskites that maintain the favorable optoelectronic properties associated with Pb²⁺ and Sn²⁺, there has been much excitement about double perovskites with rock-salt-ordering of the octahedral cations (elpasolites) since the first reports of red Cs₂AgBiBr₆^{Reference Slavney, Hu, Lindenberg and Karunadasa20,Reference McClure, Ball, Windl and Woodward21} and the corresponding chloride.^{Reference McClure, Ball, Windl and Woodward21,Reference Volonakis, Filip, Haghighirad, Sakai, Wenger, Snaith and Giustino22} Expanding on a previous analysis,^{Reference Savory, Walsh and Scanlon16} we show here that while these compounds may be interesting for other reasons, there appear to be no practically feasible chemical substitutions that qualitatively maintain the favorable band structure of the lead and tin halide (single) perovskites. The electronic-band structures of double perovskites with various combinations of octahedral cation electron configurations are presented in Figure 3.

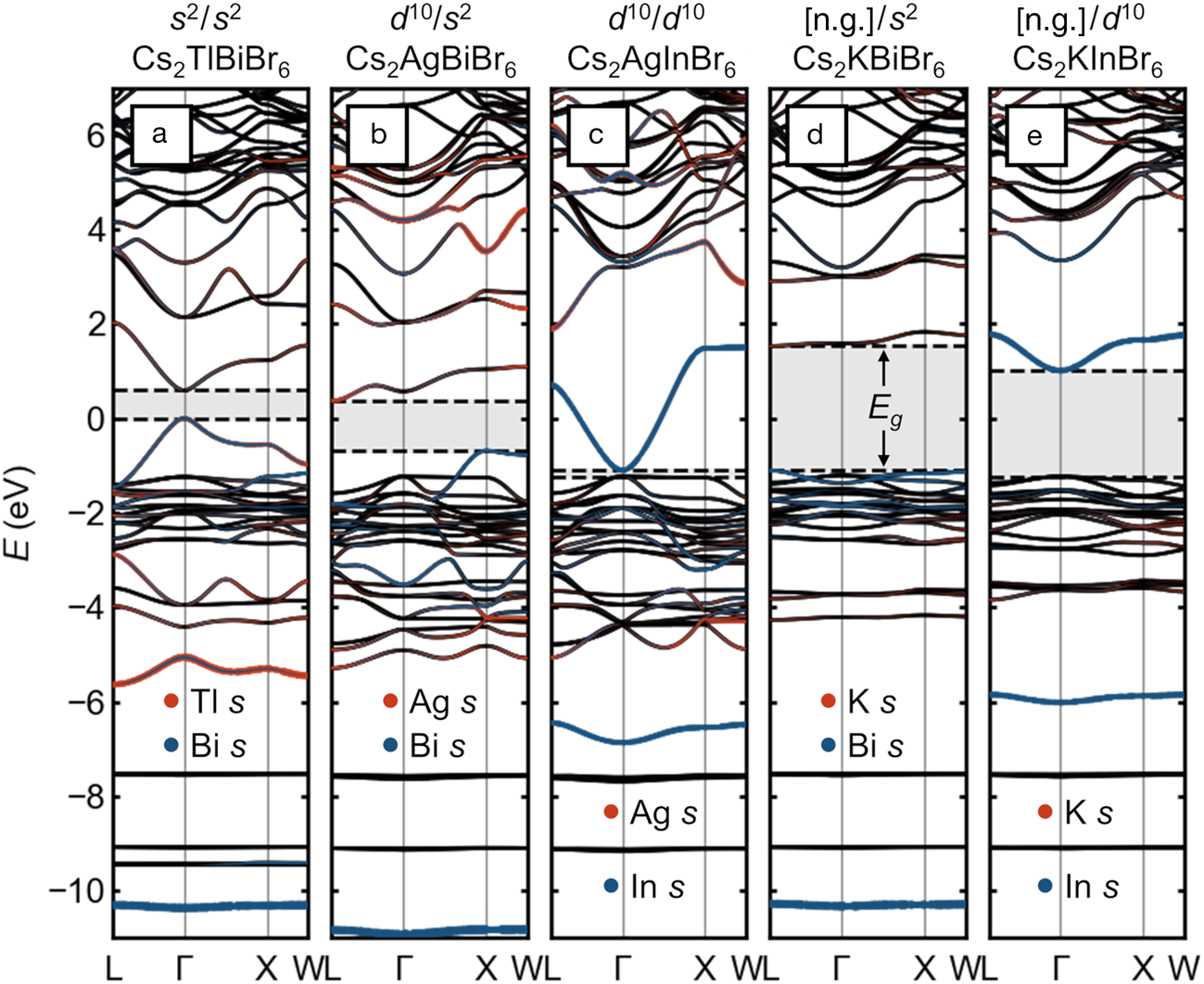
Figure 3. Electronic-band structures of rock-salt-ordered halide double perovskites (elpasolites) with different combinations of electronic configurations on the octahedral cations, presented on a common energy scale. (a) Hypothetical Cs₂TlBiBr₆ with s ^{Reference Kulbak, Cahen and Hodes2} Tl⁺ and s ^{Reference Kulbak, Cahen and Hodes2} Bi³⁺. (b) Cs₂AgBiBr₆ with d ^{Reference Galy, Meunier, Andersson and Åström10} Ag⁺ and s ^{Reference Kulbak, Cahen and Hodes2} Bi³⁺. (c) Hypothetical Cs₂AgInBr₆ with d ^{Reference Galy, Meunier, Andersson and Åström10} Ag⁺ and d ^{Reference Galy, Meunier, Andersson and Åström10} In³⁺. (d) Hypothetical Cs₂KBiBr₆ with [Ar] K⁺ and s ^{Reference Kulbak, Cahen and Hodes2} Bi³⁺. (e) Hypothetical Cs₂KInBr₆ with [Ar] K and d ^{Reference Galy, Meunier, Andersson and Åström10} In³⁺. Bandgaps are indicated with shading and dashed lines. Projected s orbital character on the octahedral cations is shown as orange and blue dots. The energy scales are aligned by the semi-core Cs 5s states (around –20 eV) and are referenced to the valence-band maximum of Cs₂TlBiBr₆. Note: [n.g.], noble gas electron configuration.

Figure 3a shows the case of the hypothetical “Cs₂TlBiBr₆,” with an ordering of two cations, Tl⁺ and Bi³⁺, which are isoelectronic to Pb²⁺. This compound thus represents only a small perturbation on CsPbBr₃, and the band structure appears similar to that of CsPbBr₃ simply back-folded into the FCC Brillouin zone, with a direct bandgap and a wide VB whose maximum exhibits high curvature and sits well above the (solely) Br p bands. Instead of a single bonding Pb 6s—Br 4p band centered roughly around –7.5 eV, we see two corresponding bands centered roughly around –5 eV (Tl) and –10.5 eV (Bi), reflecting the relative stability of the lone-pair s orbitals of the isolated cations, which increases in the order In⁺ < Tl⁺ < Sn²⁺ < Pb²⁺ < Sb³⁺ < Bi³⁺ < Te⁴⁺ < Po⁴⁺.^{Reference Stoltzfus, Woodward, Seshadri, Klepeis and Bursten23–Reference Xiao, Du, Meng, Wang, Mitzi and Yan25} While stoichiometric “Cs₂TlBiBr₆” has not been realized, (MA)₂TlBiBr₆ has been prepared, and exhibits a bandgap of ~2.2 eV.^{Reference Deng, Wei, Sun, Kieslich, Cheetham and Bristowe26} Unfortunately, Tl⁺ is exceedingly toxic (and appears too large to form a stable Cs-compound at full occupancy), and halides of In⁺ tend to be unstable against further oxidation or disproportionation to In₀ and In^{3+ Reference Tuck27–Reference McCall, Friedrich, Chica, Cai, Stoumpos, Alexander, Deemyad, Wessels and Kanatzidis29} and prone to severe lone-pair-driven distortions, which reduce orbital overlap and change connectivity,^{Reference Lin, Chen, Gao, Cai, Jin, Etman, Kang, Lei, Lin, Folgueras, Quan, Kong, Sherburne, Asta, Sun, Toney, Wu and Yang28–Reference Tan, Stephens, Hendrickx, Hadermann, Segre, Croft, Kang, Deng, Lapidus, Kim, Jin, Kotliar and Greenblatt30} seemingly rendering halide double perovskites that are electronically equivalent to lead halide single perovskites practically out of reach.

Replacing half of the lone-pair cations with d ^{Reference Galy, Meunier, Andersson and Åström10} cations such as Ag⁺ yields the now familiar case of Cs₂AgBiBr₆, as shown in Figure 3b. As noted previously,^{Reference Savory, Walsh and Scanlon16} the alternation of empty and filled s orbitals in the valence of the octahedral cations leads to a momentum dependence that moves the band edges from the zone center to two different locations on the zone boundary, resulting in an indirect gap. Though the gap remains in the visible, the VBM is significantly deeper and the hole-effective mass heavier than the all-lone-pair case. One consequence of the distinct gap nature is immediately evident in the laboratory: Powders of CsPbBr₃ are a brilliant luminescent orange, whereas those of Cs₂AgBiBr₆ are a much duller red.

The direct bandgap is recovered when the remaining lone-pair cation is replaced with another d ^{Reference Galy, Meunier, Andersson and Åström10} cation, as in the case of “Cs₂AgInBr₆,” shown in Figure 3c. However, similar to the case of “CsCdBr₃,” the VB derives primarily from the anions and lies quite deep in energy and has negligible dispersion along Γ–X, suggesting poor hole transport and unfavorable band alignment. The recovery of the direct bandgap by matching the orbital angular momentum of the frontier orbitals of the octahedral cations is illustrated in the alloying of Cs₂AgSb_1-xIn_xCl₆.^{Reference Thao Tran, Panella, Chamorro, Morey and McQueen31} While it appears “Cs₂AgInBr₆” has not been successfully prepared as a double perovskite, Cs₂AgInCl₆ has been prepared and has a wide gap of 3.3 eV.^{Reference Volonakis, Haghighirad, Milot, Sio, Filip, Wenger, Johnston, Herz, Snaith and Giustino32}

As shown in Figure 3d–e, substituting an empty shell cation such as K⁺ (with the [Ar] electron configuration) in “Cs₂KBiBr₆” uniformly produces deep VBMs, heavy holes, and wide bandgaps (e.g., (MA)₂KBiCl₆ has been prepared and exhibits a gap of ~3.0 eV^{Reference Wei, Deng, Sun, Xie, Kieslich, Evans, Carpenter, Bristowe and Cheetham33}). The gap when the other cation is d ^{Reference Galy, Meunier, Andersson and Åström10} like In³⁺ is somewhat narrower, but has significantly heavier electron mass than if both cations share this configuration. We note for completeness that other configurations are possible, for instance with rare-earth cations, but thus far, these appear to lead to compounds which are colorless.^{Reference Deng, Wie, Brivio, Wu, Sun, Bristowe and Cheetham34} These examples illustrate that uninterrupted main-group metal–halogen–main-group metal connectivity is also essential: When the connectivity is interrupted by electropositive alkali cations or by vacancies, the favorable wide valence bandwidth and the attendant band alignment and hole mass is lost. This can be seen as well in the flatter VBs and lower and deeper VBMs in low-dimensional compounds, such as PbI₂,^{Reference Brgoch, Lehner, Chabinyc and Seshadri35} BiI₃,^{Reference Lehner, Wang, Fabini, Liman, Hébert, Perry, Wang, Bazan, Chabinyc and Seshadri36} and ternary (chalco)halides of Sb and Bi.^{Reference Saparov, Hong, Sun, Duan, Meng, Cameron, Hill, Yan and Mitzi37–Reference Brandt, Poindexter, Gorai, Kurchin, Hoye, Nienhaus, Wilson, Polizzotti, Sereika, Zaltauskas, Lee, MacManus-Driscoll, Bawendi, Stevanovic and Buonassisi39}

Consistently, mismatch of the angular momentum of the frontier orbitals between the two octahedral cations gives an indirect bandgap, and the only combinations aside from the practically unfeasible (In,Tl)⁺/(Sb,Bi)³⁺, which match the frontier orbitals and maintain a direct gap (e.g., Ag⁺/In³⁺), suffer from deep VBMs and heavy holes and have not been successfully prepared for the heavier halogens. Therefore, the lone pair is essential for favorable band alignment, wide VB width, and light hole effective masses.

Thus far, other materials reproducing this qualitative electronic structure (but with wider bandgaps than the known IV–VI semiconductors) have eluded discovery, but such compounds, with heavy lone-pair cations in high symmetry coordination, moderately electronegative anions, and a high dimensionality of connectivity,^{Reference Xiao, Meng, Wang, Mitzi and Yan40} may yet be realized. In searching for such low-cost, defect-tolerant semiconductors beyond the perovskite structure, it is worth addressing how the energy of the lone-pair orbitals varies with chemistry. Pb²⁺ seems to exhibit a favorable compromise between stability and covalency (as noted previously, the energy of the lone-pair s orbital increases left-to-right and top-to-bottom of the heavy main group.^{Reference Stoltzfus, Woodward, Seshadri, Klepeis and Bursten23–Reference Xiao, Du, Meng, Wang, Mitzi and Yan25} In⁺ adopts severely distorted coordination environments, which reduce orbital overlap and alter connectivity, Tl⁺ is too toxic, and (meta)stable halides of Sn²⁺ in high symmetry coordination tend to display high concentrations of compensating defects because of their high energy VBM. On the other hand, halides, oxyhalides, and chalcohalides of Bi³⁺ are quite stable, but the more contracted lone pair and lower symmetry coordination environments lead to narrower VBs, deeper VBM, and heavier holes.^{Reference Lehner, Wang, Fabini, Liman, Hébert, Perry, Wang, Bazan, Chabinyc and Seshadri36–Reference Lehner, Fabini, Evans, Hébert, Smock, Hu, Wang, Zwanziger, Chabinyc and Seshadri38} Based on this compromise, new compounds with Sb³⁺ in high-symmetry coordination (akin to octahedral Pb²⁺ in halide perovskites or cuboctahedral Tl⁺ in rock-salt halides) and a high degree of connectivity are ripe for exploration.

Unconventional bandgap and defect tolerance

The lone-pair electron configuration causes an antibonding VB edge, which may aid in defect tolerance. In group IV and III–V semiconductors, the VB edge is bonding in character, and the CB edge is antibonding, and for most such compounds, the band extrema are both located at the Γ point of the Brillouin zone. The situation at the VB edge is reversed in many Cu⁺ and Ag⁺-containing compounds (e.g., chalcopyrite), where the filled d-shell is shallow enough in energy to interact with the anion p orbitals, pushing up the VB edge. This is precisely what occurs in lead and tin halide perovskites but because of the filled cation s orbitals (the lone pair) rather than the d orbitals, which are too deep in energy for these cations. This unusual electronic bandgap formed between an antibonding VB (metal s—halogen p) and an antibonding CB (metal p—halogen p) is exemplified by the electronic density of states, crystal orbital Hamilton population (COHP, which provides an energy-resolved view of chemical bonding),^{Reference Maintz, Deringer, Tchougreeff and Dronskowski41} and schematic bonding diagram for cubic CsPbBr₃ in Figure 4, shown here without spin–orbit coupling. The primary contribution from Pb 6s is in the bonding band with Br 4p around –8 eV, but the corresponding antibonding interaction produces the broad VB. The antibonding character of the VBM and the symmetry of the constituent orbitals ensures that this will occur away from the Γ point of the Brillouin zone. Though the CB is often erroneously labeled “nonbonding,” it derives from an antibonding interaction between Pb 6p and the halogens, as seen from the COHP in Figure 4 or from bandwidths in sublattice calculations.^{Reference Goesten and Hoffmann17} Goesten and Hoffmann^{Reference Goesten and Hoffmann17} give an excellent pedagogical discussion of the bonding in these compounds.

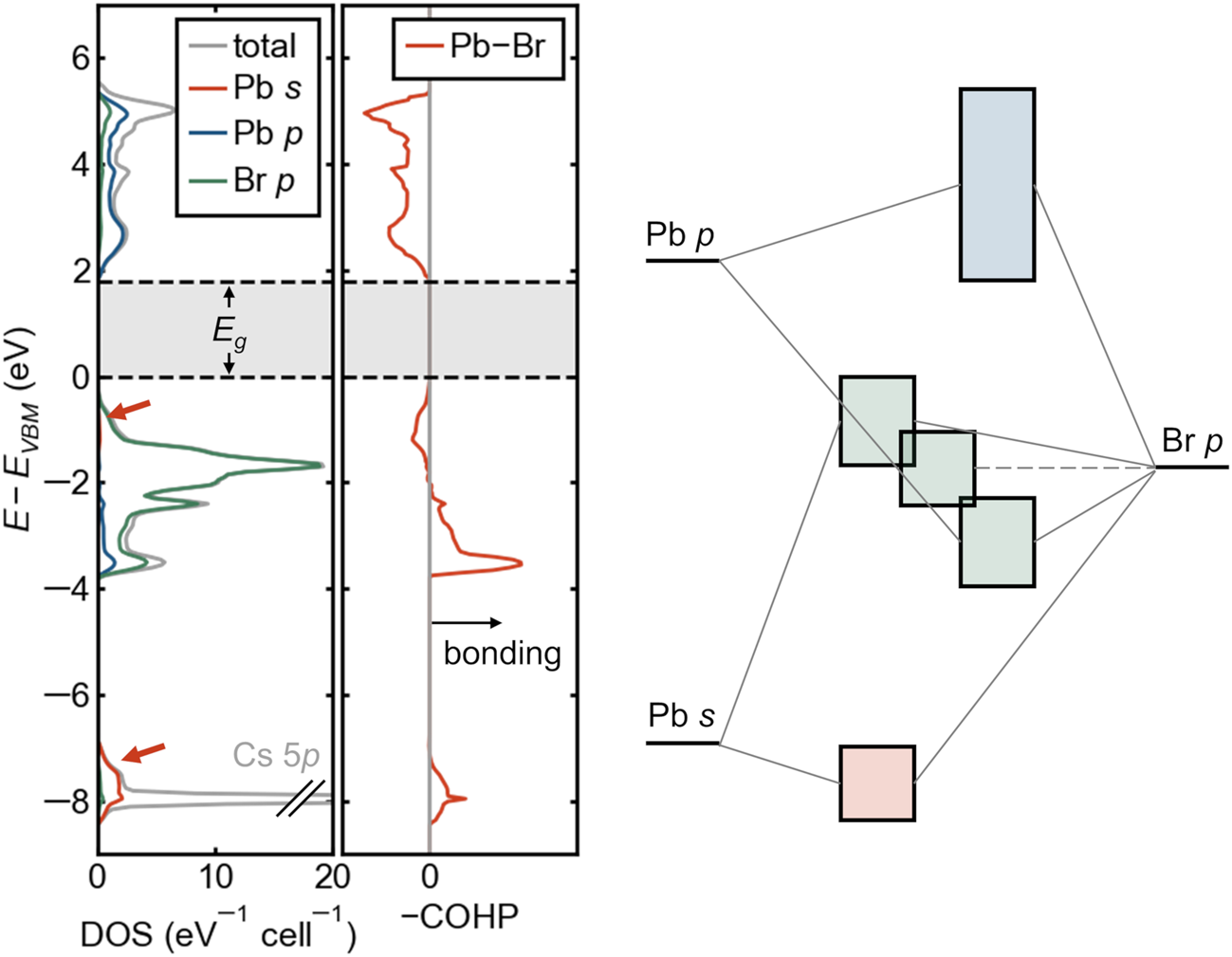
Figure 4. Orbital-projected electronic density of states (DOS), crystal orbital Hamilton population (COHP) for lead–halogen interactions, and schematic band diagram for cubic CsPbBr₃. Pb 6s contributions are indicated with orange arrows. Positive values of –COHP (to the right) are bonding, and negative values are antibonding. Both the valence-band maximum and the conduction-band minimum are seen to be antibonding, with consequences for defect energetics and temperature coefficient of the bandgap. Schematic bands are colored by the dominant orbital contribution following the colors in the DOS.

In the context of Cu⁺ compounds, an antibonding VB edge has been proposed to lead to shallow defects,^{Reference Zakutayev, Caskey, Fioretti, Ginley, Vidal, Stevanovic, Tea and Lany42} and this feature may be responsible for the shallow acceptors observed in lead halide perovskites. Because defect states would derive from atomic levels well below the VBM (e.g., Pb s and Br p in Figure 4), they would tend to form states close to the band edge or even resonant within the VB rather than deep, midgap states.^{Reference Yin, Shi and Yan43,Reference Brandt, Stevanovic, Ginley and Buonassisi44} Naturally, this argument does not extend directly to the (also) antibonding CB. Deep donors could form on the basis of the low-lying position of the Br p orbitals.

The relationship between chemistry, structural disorder, and electronic disorder in these compounds remains enigmatic, but this unusual antibonding VB may contribute to the defect tolerance, together with other factors such as compensatory ionic disorder^{Reference Walsh, Scanlon, Chen, Gong and Wei45} and lattice dynamical suppression of long-range correlations in the disorder potential.^{Reference Gehrmann and Egger46}

Unusual pressure- and temperature-dependence of the bandgap

Another consequence of these antibonding VBs and CBs is that the signs of ${{\partial E_g} \over {\partial T}}$ and ${{\partial E_g} \over {\partial P}}$ (via the associated deformation potentials) are opposite to those in most semiconductors—the bandgaps widen with rising temperature and narrow with pressure within one structural phase. This behavior with pressure was observed decades ago in germanium chlorides and bromides,^{Reference Schwarz, Wagner, Syassen and Hillebrecht47} and the behavior with temperature was observed more recently in CsSnI₃^{Reference Yu, Chen, Wang, Pfenninger, Vockic, Kenney and Shum48} and has been observed numerous times in lead and tin halide perovskites since.^{Reference Kontos, Kaltzoglou, Arfanis, McCall, Stoumpos, Wessels, Falaras and Kanatzidis49} Additionally, because of the large positive thermal expansion (vide infra) and small bulk moduli, these bandgap changes are quite significant. This strong temperature dependence suggests a very different temperature coefficient of performance in perovskite solar cells than their conventional cousins, although the overall effects in a single junction or tandem device are not yet known.

We have previously put forth a simple model for understanding the temperature dependence (with the same logic applying for pressure dependence) through a combination of ab initio calculations and photoluminescence measurements on CsSnBr₃ as an example.^{Reference Fabini, Laurita, Bechtel, Stoumpos, Evans, Kontos, Raptis, Falaras, Van der Ven, Kanatzidis and Seshadri50} Because VB and CB are both antibonding, both narrow and drop with thermal expansion on warming. However, the width of the VB is more sensitive to the degree of spatial overlap, so the net result is a widening of the bandgap. Beyond these dominant volume effects, nonlinearities in the observed bandgap temperature dependences suggest an additional impact from dynamic octahedral tilting and dynamic octahedral distortions.^{Reference Kontos, Kaltzoglou, Arfanis, McCall, Stoumpos, Wessels, Falaras and Kanatzidis49,Reference Fabini, Laurita, Bechtel, Stoumpos, Evans, Kontos, Raptis, Falaras, Van der Ven, Kanatzidis and Seshadri50} Although a fuller treatment of electron–phonon coupling is needed for quantitative agreement, this simple bonding-based picture appears to have qualitative predictive power.

Lone-pair effects on lattice dynamics: Anharmonicity and polar distortions

As discussed in the introduction, the presence of lone pairs on Pb and Sn provides a driving force for these cations to adopt distorted, acentric coordination environments, wherein the lone pair occupies space and repels the other ligands. Examining the reported crystal structure evolution of these compounds with temperature, one observes that all the Ge compounds adopt polar structures with crystallographically distorted, acentric Ge environments, whereas all the Pb compounds (except the fluorides, with strong lone-pair stereochemical activity and octahedral tilting) adopt centrosymmetric structures with nominally centric Pb coordination. The Sn compounds are intermediate, with iodides and some bromides adopting crystallographically centric Sn environments (except for CH₃NH₃SnBr₃, which adopts the polar Pmc2₁ (#26) space group at intermediate temperatures and an unknown, likely triclinic, ground state structure^{Reference Swainson, Chi, Her, Cranswick, Stephens, Winkler, Wilson and Milman51}), while the chlorides and fluorides are nonperovskite salts with [SnX ₃]^– pyramidal anions, because of the stronger stereochemical activity of the lone pair with these harder ligands. Despite numerous reports of ferroelectricity in perovskite lead iodides and bromides (particularly CH₃NH₃PbI₃), a preponderance of evidence suggests the bulk is centrosymmetric in these compounds,^{Reference Govinda, Kore, Bokdam, Mahale, Kumar, Pal, Bhattacharyya, Lahnsteiner, Kresse, Franchini, Pandey and Sarma52,Reference Frohna, Deshpande, Harter, Peng, Barker, Neaton, Louie, Bakr, Hsieh and Bernardi53} ruling out piezo-, pyro-, and ferroelectricity.

But this is only part of the story. Obscured in this average structure view are local, dynamic, polar distortions of the octahedral cation environments evident from vibrational spectroscopy,^{Reference Smit, Dirksen and Stufkens54} x-ray absorption spectroscopy,^{Reference Ishida, Maeda, Hirano, Kubozono and Furukawa55} pair distribution functions (PDFs) from total scattering,^{Reference Fabini, Laurita, Bechtel, Stoumpos, Evans, Kontos, Raptis, Falaras, Van der Ven, Kanatzidis and Seshadri50,Reference Worhatch, Kim, Swainson, Yonkeu and Billinge56,Reference Laurita, Fabini, Stoumpos, Kanatzidis and Seshadri57} and ab initio calculations.^{Reference Fabini, Laurita, Bechtel, Stoumpos, Evans, Kontos, Raptis, Falaras, Van der Ven, Kanatzidis and Seshadri50,Reference Marronnier, Lee, Geffroy, Even, Bonnassieux and Roma58–Reference Remsing and Klein60} Raman spectroscopy^{Reference Yaffe, Guo, Tan, Egger, Hull, Stoumpos, Zheng, Heinz, Kronik, Kanatzidis, Owen, Rappe, Pimenta and Brus61} has indicated the fluid-like dynamical nature of the perovskite lattices of CsPbBr₃ and MAPbBr_3, part of which is accounted for by the lone-pair activity of Pb²⁺. The lattice dynamics seem unique to these perovskites, and although they may not promote huge carrier mobilities, they could reduce electron–hole recombination rates, prolonging excited state carrier lifetimes. Pump-probe electron total scattering studies^{Reference Wu, Tan, Shen, Hu, Miyata, Trinh, Li, Coffee, Liu, Egger, Makasyuk, Zheng, Fry, Robinson, Smith, Guzelturk, Karunadasa, Wang, Zhu, Kronik, Rappe and Lindenberg62} indicate significant structural distortions upon photoexcitation in several of these compounds as well, although it is unclear as of yet if these are connected to the same lone-pair-driven instability.

These severe local distortions are exemplified by the x-ray pair distribution functions (PDFs) for hybrid tin and lead iodide perovskites in Figure 5a–d.^{Reference Laurita, Fabini, Stoumpos, Kanatzidis and Seshadri57} From the crystallographically cubic structures for all four compounds at this temperature,^{Reference Laurita, Fabini, Stoumpos, Kanatzidis and Seshadri57} one would expect a single, symmetric peak just above r = 3 Å, reflecting a single metal–iodide bond distance. Instead, all four exhibit asymmetric peaks, from the moderately asymmetric metal–I correlation in MAPbI₃ (Figure 5c) to the nearly bifurcated one in FASnI₃ (Figure 5b). Modeling these PDFs (and those for hybrid lead bromides and CsSnBr₃) with a small-box rhombohedral distortion, as observed crystallographically in the Ge halide perovskites, offers a simple way to understand the underlying chemical trends, as shown in Figure 5e. The magnitude of the local, polar distortions can be tuned by chemical substitution on all three sites, with lighter Sn²⁺, harder Br^–, and larger A-site cations all enhancing this effect.^{Reference Laurita, Fabini, Stoumpos, Kanatzidis and Seshadri57} Indeed, these chemical rules are precisely in line with those enumerated for rock-salt chalcogenides based on ab initio studies.^{Reference Waghmare, Spaldin, Kandpal and Seshadri63}

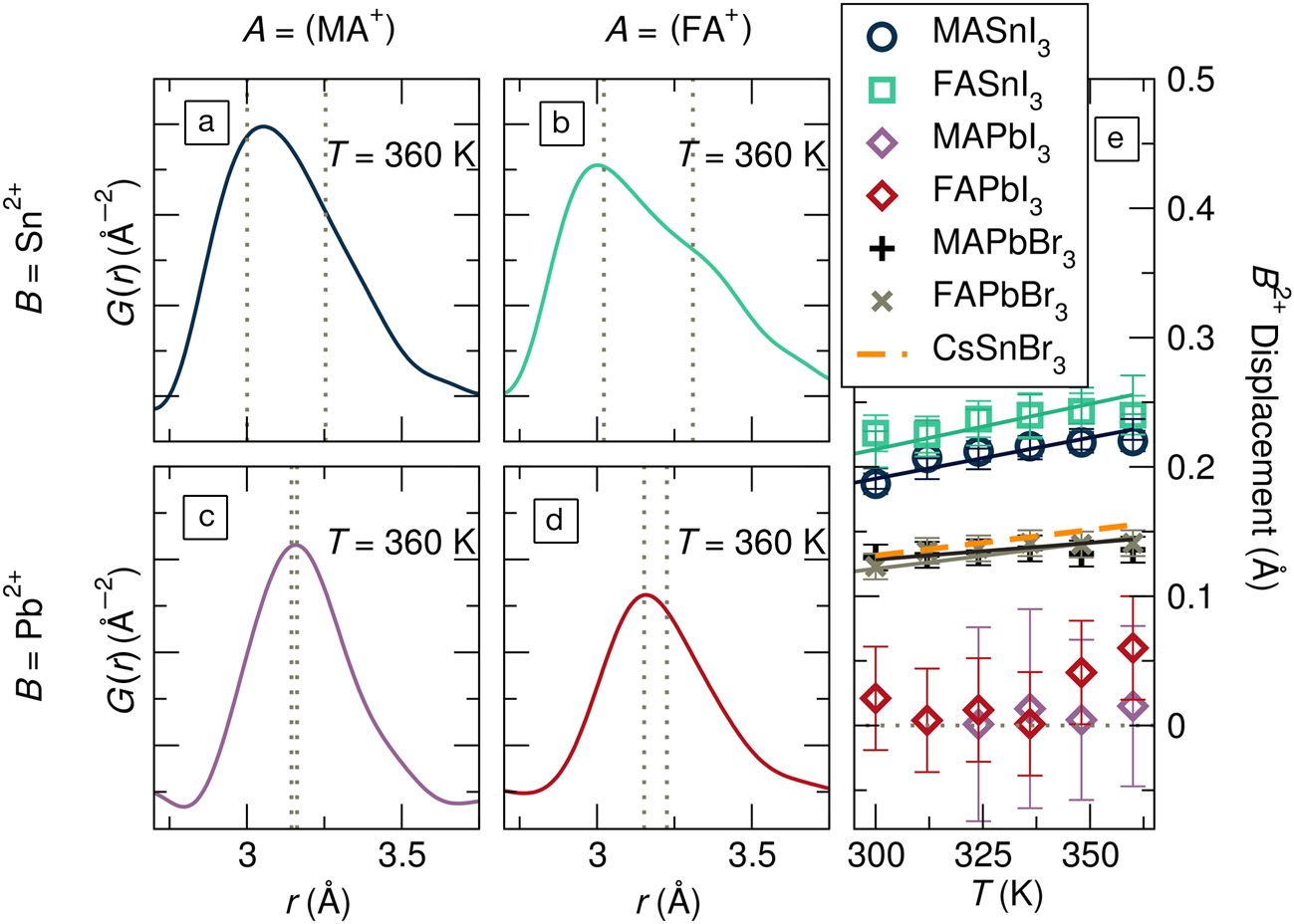
Figure 5. The x-ray pair distribution function (PDF), represented by G(r), at 360 K for (a) MASnI₃, (b) FASnI₃, (c) MAPbI₃, (d) FAPbI₃ revealing severely distorted MI₆ octahedra in these crystallographically cubic phases (MA = [CH₃NH₃]⁺; FA = [CH(NH₂)₂]⁺). (e)Displacements of the octahedral cations from small-box modeling of the PDF with a rhombohedral distortion. Values for MAPbBr₃, FAPbBr₃, and CsSnBr₃ are additionally shown. The severe asymmetry in the metal-halogen PDF peak is seen for all compounds but is strongest for tin iodides and more moderate for lead iodides. Reproduced with permission from Reference 57. © 2017 Royal Society of Chemistry.

Notably, these polar distortions are distinct from the well-known nonpolar dynamic tilting of rigid octahedra in high-temperature phases, which is driven by ionic size considerations rather than bonding and covalency and is ubiquitous in perovskites with undersized A-cations. Because of their polar nature, the lone-pair-driven distortions also impact dielectric properties (vide infra) and possibly allow for dynamic relativistic spin polarization^{Reference Kim, Im, Freeman, Ihm and Jin64} in these crystallographically centrosymmetric phases. Additionally, the anharmonicity associated with this bonding naturally has the effect of reducing lattice thermal conductivity, a point which has been covered extensively in the literature on thermoelectrics with lone-pair cations. Aside from the impacts on dielectric and thermomechanical properties, one expects that these unusual lattice dynamics would be linked to the electronic disorder in these structurally soft materials,^{Reference Egger, Bera, Cahen, Hodes, Kirchartz, Kronik, Lovrincic, Rappe, Reichman and Yaffe1,Reference Gehrmann and Egger46} which in turn dictates many excited state properties.

Large ionic dielectric response

The anharmonic potential for polar octahedral distortions underlying this observed “hidden” local structure should also manifest in an elevated ionic dielectric response, independent of the reorientation of dipolar molecular cations in the hybrid compounds. This is because the nominal, crystallographic, high-symmetry coordination of the lone-pair-bearing cation is a metastable saddle point in the potential energy landscape. Accordingly, a small applied field is sufficient to induce a large dipole from the distorted, acentric coordination because of the stereochemically active lone pair. As seen in Figure 6a, all the compounds in this class which have been measured to date have low-frequency dielectric constants two to three times those of silicon, III–Vs, kesterites, and chalcopyrites, even when molecular dipole contributions are removed.^{Reference Govinda, Kore, Bokdam, Mahale, Kumar, Pal, Bhattacharyya, Lahnsteiner, Kresse, Franchini, Pandey and Sarma52,Reference Wilson, Frost, Wallace and Walsh65–Reference Almond and Bowen75} Without the molecular dipole contributions, the dielectric constants of the inorganic and hybrid compounds are nearly identical, as illustrated by Govinda and co-workers for the case of lead bromides in Figure 6b. The schematic frequency dependence of the dielectric function (modeled after Young and Frederikse^{Reference Young and Frederikse76} and based off of reported molecular reorientation rates and optical phonon frequencies) is depicted in Figure 6c.

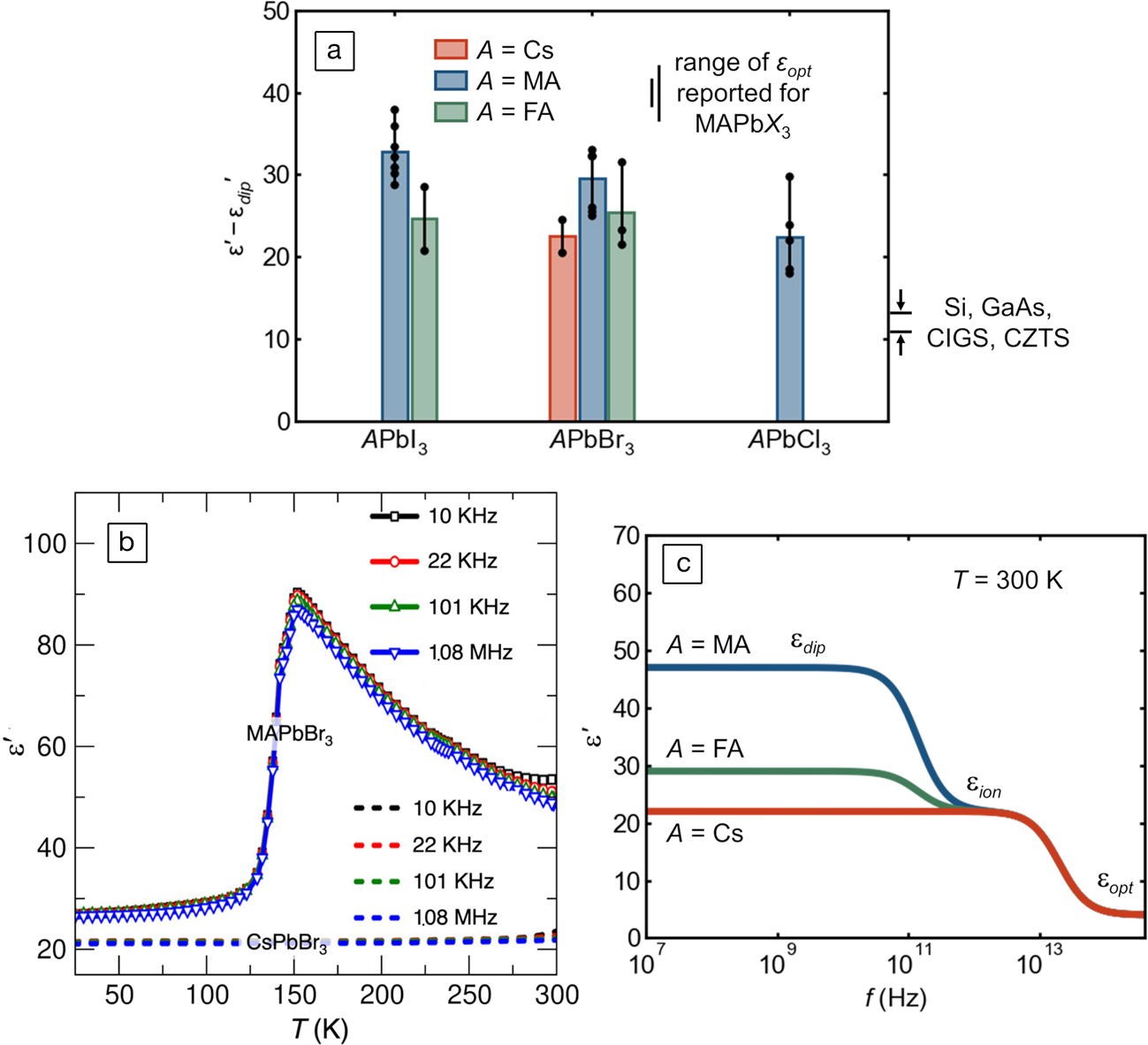
Figure 6. (a) Reported experimental static dielectric permittivity without molecular dipole contributions, εʹ—ε_dipʹ, compiled from the literature, in units of the vacuum permittivity, ε₀. These values are isolated via kHz or MHz capacitance measurements in the low temperature limit^{Reference Govinda, Kore, Bokdam, Mahale, Kumar, Pal, Bhattacharyya, Lahnsteiner, Kresse, Franchini, Pandey and Sarma52,Reference Onoda-Yamamuro, Matsuo and Suga67–Reference Fabini, Hogan, Evans, Stoumpos, Kanatzidis and Seshadri69,Reference Anusca, Balčiūnas, Gemeiner, Svirskas, Sanlialp, Lackner, Fettkenhauer, Belovickis, Samulionis, Ivanov, Dkhil, Banys, Shvartsman and Lupascu71–Reference Schueller, Laurita, Fabini, Stoumpos, Kanatzidis and Seshadri74} or at room temperature using GHz⁶⁶ or THz^{Reference Sendner, Nayak, Egger, Beck, Müller, Epding, Kowalsky, Kronik, Snaith, Pucci and Lovrincic70} radiation. Individual values (black dots) are shown, and bar height is the average value. The range of values for typical photovoltaic semiconductors is shown on the right-hand side (CIGS: Cu[In,Ga][S,Se]₂; CZTS: Cu₂ZnSnS₄). The range of reported optical dielectric constants, ε_opt, for MAPb(Cl,Br,I)₃ is also indicated.^{Reference Wilson, Frost, Wallace and Walsh65} (b) Low-frequency dielectric response of CsPbBr₃ and MAPbBr₃, showing that the ionic response of the two compounds is similar when reorientation of the molecular dipole is frozen out. Adapted with permission from Reference 52. © 2017 American Chemical Society. (c) Schematic of the frequency dependence of the dielectric response of halide perovskites at room temperature, illustrating static, ionic, and (sub-bandgap) optical regimes.

This elevated lattice polarizability (high static dielectric constant), because of the lone pairs, is far from a curiosity. Rather, it is the likely microscopic mechanism behind the hypothesized formation of large polarons in these materials.^{Reference Zhu and Podzorov77} In principle, a higher dielectric response (on the relevant time scale) should screen the Coulomb interaction between charge carriers and other carriers or charged defects, reducing scattering and recombination rates. Although focused study of the impacts of unusually strong dielectric screening on carrier transport appears to be in its infancy,^{Reference Du and Singh78,Reference Du79} an early result from doped ferroelectric complex oxides is quite intriguing.^{Reference Siemons, McGuire, Cooper, Biegalski, Ivanov, Jellison, Boatner, Sales and Christen80} In halide perovskites, there is ample circumstantial evidence, although direct proof remains challenging, as it can be difficult in practice to isolate the stimulus of interest (e.g., chemical substitution simultaneously alters the chemical bonding, ionic sizes, and defect energetics).

Notably, this phenomenon of a large ionic dielectric response should be fully general to compounds with lone-pair cations in relatively high symmetry environments (if the coordination is severely distorted, this may indicate that the double well is quite deep, akin to a polar phase whose polarization cannot be ferroelectrically switched before dielectric breakdown). An instructive example in simple binary compounds can be found in comparing PbS (in which lone-pair-driven dynamic distortions have been observed^{Reference Božin, Malliakas, Souvatzis, Proffen, Spaldin, Kanatzidis and Billinge81}) and CdS (without a lone-pair cation): PbS has a static dielectric constant more than one order of magnitude higher than that of CdS (even when accounting for the difference in optical dielectric constants from the rather different bandgaps).^{Reference Young and Frederikse76} Several other semiconductors with lone-pair cations have high dielectric constants, including Sb³⁺ sulfides and selenides, SbSI (with a ferroelectric transition around room temperature), and Tl⁺ halides.^{Reference Young and Frederikse76}

Enormous positive thermal expansion

As a purely anharmonic effect, thermal expansion behavior offers another window into the unusual lattice dynamics of these compounds—though we note that this property reflects both the polar modes discussed previously and the more familiar, nonpolar anharmonic modes associated with octahedral tilting in perovskites with undersized A-cations. The experimentally reported values of the volumetric thermal expansion coefficient, ${\rm \alpha }_{\rm V} = {1 \over V}\left({{{\partial V} \over {\partial T}}} \right)_p$, for tin and lead bromides and iodides are presented in Figure 7a (reliable figures are not yet available for FASnBr₃ and most of the corresponding chlorides). Though lattice parameters can be determined to high precision, such expansion coefficients necessitate taking finite differences of volumes, amplifying greatly any systematic error in lattice parameters across studies, laboratories, and instruments. As such, in almost every instance, lattice parameters at different temperatures have been taken from the same publication. Additionally, the volumetric thermal expansion of these materials seems generally not to be linear over wide temperature ranges,^{Reference Fabini, Laurita, Bechtel, Stoumpos, Evans, Kontos, Raptis, Falaras, Van der Ven, Kanatzidis and Seshadri50,Reference Fabini, Stoumpos, Laurita, Kaltzoglou, Kontos, Falaras, Kanatzidis and Seshadri88} even at temperatures well above any quantum effects, so α_V has been computed near room temperature whenever possible. Values derived from neutron diffraction, or older values that deviate significantly from those based on modern diffractometers, have been excluded.

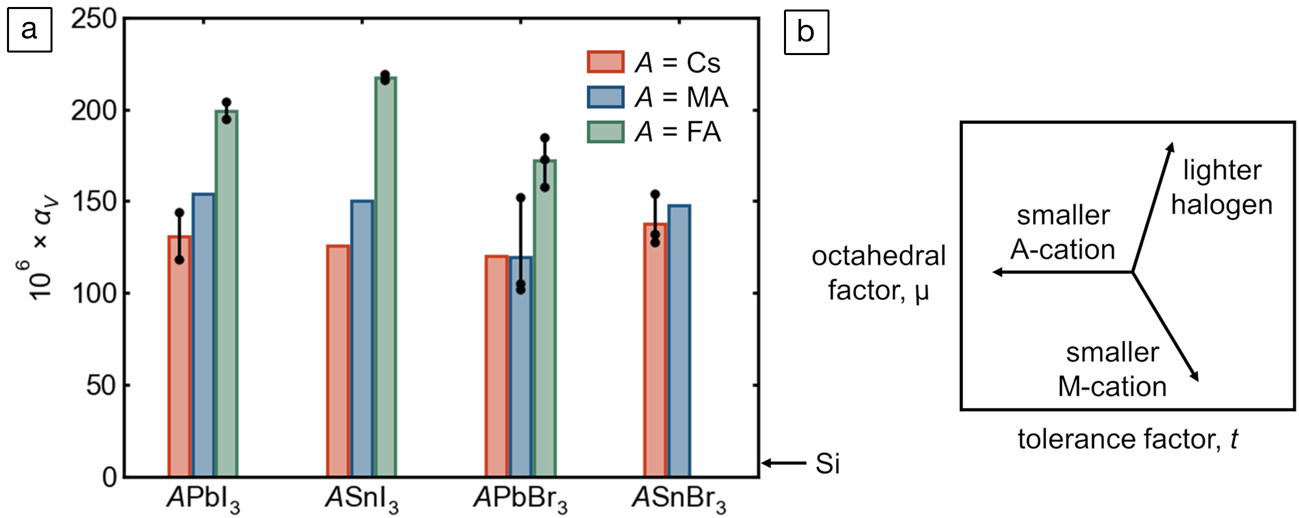
Figure 7. (a) Volumetric thermal expansion coefficients, α_V, of perovskite tin and lead bromides and iodides compiled from the literature.^{Reference Fabini, Laurita, Bechtel, Stoumpos, Evans, Kontos, Raptis, Falaras, Van der Ven, Kanatzidis and Seshadri50,Reference Worhatch, Kim, Swainson, Yonkeu and Billinge56,Reference Schueller, Laurita, Fabini, Stoumpos, Kanatzidis and Seshadri74,Reference Chung, Song, Im, Androulakis, Malliakas, Li, Freeman, Kenney and Kanatzidis82–Reference Fabini, Stoumpos, Laurita, Kaltzoglou, Kontos, Falaras, Kanatzidis and Seshadri88} Where multiple reliable values are available (e.g., different temperature ranges), individual points and the corresponding range are shown, and the bar height is the average value. The value for c-Si is shown for comparison. (b) Schematic μ–t phase space (μ = octahedral factor; t = tolerance factor) illustrating the purely geometric effects of chemical substitution on each of the three sites.

Several features are evident from Figure 7. Most glaringly, across all the iodides and bromides of tin and lead, the coefficients of volumetric thermal expansion are extremely large, more than one order of magnitude larger than that of c-Si (~8 × 10⁶).^{Reference Becker, Seyfried and Siegert89} As noted in previous reports from the authors, α_V for FAPbI₃ and FASnI₃ appear to be the largest values known for any 3D-extended crystalline solids near room temperature^{Reference Schueller, Laurita, Fabini, Stoumpos, Kanatzidis and Seshadri74,Reference Fabini, Stoumpos, Laurita, Kaltzoglou, Kontos, Falaras, Kanatzidis and Seshadri88} (at least one framework cyanide, and likely other compounds, appear to have a larger value at low temperatures^{Reference Goodwin, Calleja, Conterio, Dove, Evans, Keen, Peters and Tucker90}). Although this is remarkable from a fundamental perspective, this suggests significant challenges in applications, such as the possibility of fatigue cracking or substrate delamination because of diurnal temperature cycling in solar cells—though the “soft” kinetics of these materials and the corresponding high homologous temperatures may in fact allow self-healing.

Strikingly, in most cases, values of α_V of the tin halides appear to be comparable to or even somewhat higher than those of the corresponding lead halides. This includes the case of FASnI₃ and FAPbI₃, for which values are reported by the same group at comparable temperatures based on measurements at the same high-resolution synchrotron diffractometer.^{Reference Schueller, Laurita, Fabini, Stoumpos, Kanatzidis and Seshadri74,Reference Fabini, Stoumpos, Laurita, Kaltzoglou, Kontos, Falaras, Kanatzidis and Seshadri88} This is striking for two reasons. First, one typically expects “stiffening” of (thermo)mechanical properties as one ascends a group in the periodic table, such as higher bulk moduli and higher Debye temperatures (though we must not conflate stiffer harmonicity with reduced anharmonicity). Second, substituting tin for lead corresponds to a smaller octahedral factor and a larger tolerance factor (illustrated in Figure 7b)—the latter implying that tilting anharmonicity is reduced in making this substitution. Even in the face of a lighter divalent cation and lesser octahedral tilting (and lesser anharmonicity of those modes), tin halides have greater coefficients of thermal expansion, suggesting extreme anharmonicity of the Sn–X bond.

This is in line with the expectations based on lone-pair stereochemistry and the acute local distortions observed in tin halides by x-ray PDF discussed previously. We note, however, that at this time, one cannot rule out the possibility that a higher tolerance factor suppresses a negative contribution from rigid octahedral rocking modes as observed in ScF₃ and ReO₃—the nonlinear temperature-dependence of α_V through tilting phase transitions observed in CsSnBr₃^{Reference Fabini, Laurita, Bechtel, Stoumpos, Evans, Kontos, Raptis, Falaras, Van der Ven, Kanatzidis and Seshadri50} and FAPbI₃^{Reference Fabini, Stoumpos, Laurita, Kaltzoglou, Kontos, Falaras, Kanatzidis and Seshadri88} indicates this is a possibility. The lone pair (in part) causes these materials to have among the highest thermal expansion coefficients known for 3D-bonded extended solids.

Summary

The electronic configuration of Pb (Sn) in halide perovskites––with a 6s ^{Reference Kulbak, Cahen and Hodes2} (5s ^{Reference Kulbak, Cahen and Hodes2}) lone pair––imparts several unusual properties to these compounds, many of which are favorable for their optoelectronic applications. Via its interaction with the anions, the lone pair directly produces a wide VB, suitable band alignments for the absorption of visible light and the injection of carriers to common hole transport layers, and a light effective mass for holes. The antibonding nature of states at the VB edge may contribute to the defect tolerance of these materials and produces a large positive (negative) bandgap temperature (pressure) coefficient. The lattice dynamics are also profoundly affected: The tendency for the lone pair to express its stereochemistry and “take up space” produces a highly anharmonic energy landscape for polar distortions of the octahedral cation environments. This, in turn, results in crystallographically hidden, local distortions, enhanced dynamic behavior, elevated ionic dielectric response, reduced lattice thermal conductivity, and (in part) to positive thermal expansion that is among the largest known for 3D extended solids.

While the trajectory of solar-cell performance based on lead halide perovskites in the last decade has been remarkable, practical challenges for widespread adoption and the possibility of other uses motivate the continued and expanded exploration of applications beyond photovoltaics. These include those in light emission and detection, quantum behavior, thermoelectrics, photocatalysis, and devices that couple charge and spin in relativistic, noncentrosymmetric systems.

Equipped with these chemical insights into the myriad effects of lone pairs coupled with the wealth of predictions from recent computer-aided materials discovery efforts,^{Reference Brandt, Stevanovic, Ginley and Buonassisi44,Reference Kuhar, Pandey, Thygesen and Jacobsen91–Reference Jin, Zhang, Li, Wang, Wan, Guo and Wei93} there is an opportunity for materials scientists and inorganic chemists to fill in the gaps in the existing phase diagrams of pnictides, chalcogenides, halides, and mixed-anion systems of the heavy main group. Similarly remarkable new semiconductors may yet be found.