Introduction
The current information revolution has been driven by computing using electrons in silicon-based devices and optical communication through silica fibers, yet a fundamental incompatibility exists between them. Light wave diffraction limits the size of optical waveguides to the size of the wavelength (micron scale at the telecommunication wavelength), prohibiting seamless interfacing to nanoscale electron circuitry. By coupling light to the free electrons of metals, which are readily available in modern circuits, subdiffraction light confinement and propagation is possible with dense networks of plasmonic nanowaveguides.Reference Atwater, Maier, Polman, Dionne and Sweatlock1 It was recently shown that these propagating plasmon polaritons also emerge as a natural choice to carry non-classical information for future quantum networks.Reference Akimov, Mukherjee, Yu, Chang, Zibrov, Hemmer, Park and Lukin2 The control and manipulation of quantum phenomena can lead to a new paradigm for secure communication and advanced computing.Reference Nielsen and Chuang3 This intense area of research rests on principles of quantum mechanics, which requires matter to have a “wave” nature and light to have “particle” properties. At macroscopic scales of matter and large intensities of light, it is difficult to observe either of these wave-particle dualities. Progress in nanofabrication and characterization allow us to probe light-matter interactions and study unique quantum properties in the solid state. Furthermore, plasmon polaritons in particular have a key role to play to address many challenges in the seemingly disconnected field of quantum information technology.
This article reviews recent developments in the field of quantum plasmonics, where the quantum nature of either light or matter leads to unique properties not captured in the conventional classical description of plasmons.Reference Jacob and Shalaev4 Surface plasmon polaritons can lead to non-classical light sources as well as assist in quantum information transfer. Another pertinent problem in this regard is the wave nature of matter manifested in the localized version of this plasmonic excitation found in metallic nanoparticles. This is important to accurately quantify plasmon resonances and field enhancements for applications such as single molecule sensing using nanoplasmonic particles with sizes below 10 nm, where a simple classical model of the optical properties of metals breaks down.
Finally, we review the unique properties of plasmonic metamaterials, artificial media with optical properties that cannot be found in nature. The exotic electromagnetic response that can be tailored at will using metamaterials provides a new playground for understanding and controlling light-matter interaction. It was recently shown that the class of metamaterials that has an extremely anisotropic dielectric response can support an infinite number of electromagnetic states.Reference Jacob, Kim, Naik, Boltasseva, Narimanov and Shalaev5, Reference Jacob, Smolyaninov and Narimanov6 This greatly enhances light-matter interaction for applications, such as single photon sources, and also leads to optical equivalents of abrupt phase-transition behavior conventionally studied only in condensed matter systems.Reference Krishnamoorthy, Jacob, Narimanov, Kretzschmar and Menon7
Quantum light
Single photon sources
Sources of coherent electromagnetic radiation across the entire spectrum, from a classical microwave antenna to an optical laser, have the common property of a high intensity. This translates to the light being made of a large number of photons, fundamental energy packets of light waves that arise in the quantum theory of electromagnetic radiation. Attenuating a laser beam can lead to a low intensity and hence a small photon number, but a truly non-classical source with deterministic single photon emission can lead to revolutionary applications in quantum communications and quantum computing.Reference Altewischer, Van Exter and Woerdman8–Reference Lounis and Orrit11
Spontaneous emission lies at the heart of all light-emitting devices, including light-emitting diodes and lasers as well as single photon sources. Instead of a large collection of emitters, as in the gain medium of a laser, isolated emitters lead to single photon emission, but the efficiency is often low for practical applications. The key to achieving efficient and deterministic single photon emission is to enhance spontaneous emission through the Purcell effect. This effect is achieved by engineering the environment surrounding the emitter since spontaneous emission, as given by Fermi’s golden rule, depends on the number of decay routes available to the emitter. By placing quantum dots inside a cavity, the density of modes is enhanced at resonance, and reliable single photon sources have been achieved.Reference Grangier, Sanders and Vuckovic12 The nature of this cavity-based approach places stringent restrictions on the line width of the quantum dot, achievable only at low temperatures (below 5 K), which limits the applicability of this approach.
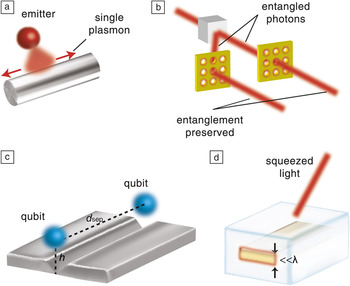
Recently, interest has shifted toward coupling isolated emitters to plasmonic nanostructures.Reference Akimov, Mukherjee, Yu, Chang, Zibrov, Hemmer, Park and Lukin2 The ability to confine plasmons down to the nanoscale also increases the interaction with the tiny isolated light emitters causing preferential and exclusive coupling of spontaneously emitted photons to plasmonic modes instead of propagating modes in vacuum. A major advantage of plasmonic approaches for enhancing single photon emission is their broad bandwidth. The fundamental plasmonic mode of a metal nanowire occurs for a broad range of frequencies, enabling coupling to single photons even at room temperature. Such broadband coupling is absolutely essential for emitters such as nitrogen vacancy (NV) centers in diamond, which have a broad bandwidth of emissionReference Babinec, Hausmann, Khan, Zhang, Maze, Hemmer and Loncar13 (Figure 1a).

Figure 1. Plasmons generated using non-classical light. (a) Broadband coupling of an isolated quantum emitter to a plasmon on a metal nanowire. The low mode volume leads to preferential coupling of spontaneously emitted single photons to plasmons on the nanowire.Reference Akimov, Mukherjee, Yu, Chang, Zibrov, Hemmer, Park and Lukin2 (b) Conventional enhanced transmission experiment through metallic nanohole arrays repeated with entangled photons showed that entanglement is preserved by excited surface plasmons.Reference Altewischer, Van Exter and Woerdman8 (c) Entanglement between qubits mediated by V-groove plasmon waveguides.Reference Gonzalez-Tudela, Martin-Cano, Moreno, Martin-Moreno, Tejedor and García-Vidal9 (d) Long range surface plasmon polaritons (LRSPP) of a gold metal stripe excited using “squeezed” vacuum. The outcoupled photons preserve the non-classical properties present in the light used to excite the LRSPP.Reference Huck, Smolka, Lodahl, Sorensen, Boltasseva, Janousek and Andersen10d sep, separation of the two quantum emitters; h, the distance of the quantum emitter from the nanogroove; λ, the wavelength of light used in the experiment.
NV centers in diamond have emerged as a natural choice for the solid-state quantum bit (qubit), not only because of their single photon emission, but also because of their spin coherence properties.Reference Aharonovich, Greentree and Prawer14 This is important in the field of quantum computing since the fundamental issue prohibiting the storage and retrieval of quantum bits is the decoherence (loss of information) caused by the environment. This unique platform that allows communication and computation using qubits of a different nature (spin and light) can lead to scalability of qubits for practical quantum computing. The ability to make these two degrees of freedom interact rests on the availability of single photons from NV centers beyond that available in bulk diamond.Reference Choy, Hausmann, Babinec, Bulu, Khan, Maletinsky, Yacoby and Lončar15 Conventional cavity-based approaches are not suited to these emitters with a broad bandwidth therefore low mode volume plasmons form a viable route to enhance spontaneous emission.Reference Huck, Kumar, Shakoor and Andersen16 Thus nanoplasmonic networks could assist in overcoming one of the main challenges in the field of quantum computing: scalability of qubits.
Quantum information transfer
The concept of a quantum bit is central to quantum computing and communication and rests on the fact that information encoded into quantum degrees of freedom show behavior distinct from the simple 1s and 0s of classical bits. For example, a quantum bit can exist in superposed states of 1 and 0 at the same time and collapses to either one only when measured. A question that naturally arises before one can choose the plasmon polariton for quantum applications is whether it can preserve non-classical information. Electrons in the solid comprising the plasmon inevitably undergo millions of collisions with ions that could lead to decoherence and loss of quantum information. Surprisingly, plasmon polaritons not only preserve the quantum properties of light used to generate them but also allow the reliable recovery of this non-classical information once the plasmon is scattered back into propagating photons.
Experiments have demonstrated that plasmons have the same exotic properties of photons such as entanglementReference Fasel, Robin, Moreno, Erni, Gisin and Zbinden17 and squeezing,Reference Huck, Smolka, Lodahl, Sorensen, Boltasseva, Janousek and Andersen10 which have no classical analogue.Reference Gerry, Knight and Beck18 Entangled photon pairs have a correlated quantum identity and are represented by a single wave function even when the physical separation between them is large. The conventional nanohole array experiment repeated with entangled photons has shown that the transmission on the output side, enhanced by a surface plasmon mechanism, also shows the same entanglement.Reference Altewischer, Van Exter and Woerdman8, Reference Moreno, García-Vidal, Erni, Cirac and Martín-Moreno19 This directly implies that the surface plasmons on the nanohole array can demonstrate non-local entanglement behavior of photons (Figure 1b). Recently, it was also proposed that one-dimensional plasmonic nano-waveguides can act as a mediator of entanglement between qubits (Figure 1c).
Another experiment showed that long range plasmon polaritons of a gold metal stripe can be excited using “squeezed vacuum,” a non-classical state of light consisting of just quantum noise. Careful mapping of the quantum state of the outcoupled light showed conclusive evidence that the plasmon polariton itself must have retained the “squeezed vacuum” properties (Figure 1d). Furthermore, a single quantum of the plasmon oscillation on a metal nanowire was excited using a single photon from an isolated quantum dot and a diamond NV center in separate experiments (Figure 1a). This was verified using the anti-bunching photon statisticsReference Akimov, Mukherjee, Yu, Chang, Zibrov, Hemmer, Park and Lukin2 (proof that only one photon is emitted a time) and wave-particle dualityReference Kolesov, Grotz, Balasubramanian, Stöhr, Nicolet, Hemmer, Jelezko and Wrachtrup20 from the outcoupled light.
For quantum information networks, switching and routing of single photons would be a necessary component. But light interacts well with itself only when assisted by nonlinearities. The low intensity of single photons makes this nonlinear interaction very weak, but efforts have also been focused on using nanowire plasmon-polariton-mediated single photon routing.Reference Chang, Sorensen, Demler and Lukin21 With the multitude of recent developments in quantum properties, the plasmon polariton is set to play a significant role in future nanoscale quantum circuits as a carrier of non-classical information.
Coherent sources
Another research direction dealing with quantum properties of localized plasmons is related to the SPASER (surface plasmon amplification by stimulated emission of radiation), a device for coherent generation and amplification of surface plasmons.Reference Bergman and Stockman22, Reference Noginov, Zhu, Belgrave, Bakker, Shalaev, Narimanov, Stout, Herz, Suteewong and Wiesner23 The nanoscale plasmon mode volumes cause coupling of a large collection of emitters to a single plasmonic mode, overcoming the detrimental effects of absorption of light in the metal. This nano-equivalent of the laser is expected to usher in a number of applications using a coherent amplified surface plasmon field (see the Khurgin and Boltasseva article in this issue).
Quantum matter
While the previous section emphasized the quantum behavior of light in propagating plasmon polaritons, we now focus on research that addresses the quantum aspects of matter comprising the localized plasmon. The classical description of the plasmon includes the Drude model for the free electrons of a metal coupled with the electric field of electromagnetic radiation.Reference García de Abajo24–Reference Scholl, Koh and Dionne27 All the advantages and limitations of this assumption are summarized by the dielectric constant of the metal
where ω is the frequency of light, ωp is the plasma frequency of the metal that depends on the density of free electrons, ![]() is the contribution to the dielectric constant due to core electrons, and Γ = Γbulk is the bulk collision rate of free electrons with positive ion cores. This model works exceptionally well to describe localized plasmon resonances of large particles, but for nanoscale metallic particles (diameter D < 10 nm), where the free electrons “feel” the nanoparticle boundary even before an electron collides with an ion (D < l mfp, where l mfp is the mean free path of electrons in the metal), an additional size-dependent collision mechanism at the surface (Γsurface) has to be included in the Drude model: Γ = Γbulk + Γsurface. Another approach is to use a spatially dispersive model for the dielectric constant such that it depends on the wave vector of light, k,
is the contribution to the dielectric constant due to core electrons, and Γ = Γbulk is the bulk collision rate of free electrons with positive ion cores. This model works exceptionally well to describe localized plasmon resonances of large particles, but for nanoscale metallic particles (diameter D < 10 nm), where the free electrons “feel” the nanoparticle boundary even before an electron collides with an ion (D < l mfp, where l mfp is the mean free path of electrons in the metal), an additional size-dependent collision mechanism at the surface (Γsurface) has to be included in the Drude model: Γ = Γbulk + Γsurface. Another approach is to use a spatially dispersive model for the dielectric constant such that it depends on the wave vector of light, k, ![]() .Reference García de Abajo24
.Reference García de Abajo24
There are aspects of localized plasmons on nanoparticles that even such modified models cannot capture. In the case of closely spaced metallic nanoparticles, tunneling of electrons between the nanoparticles can considerably affect the plasmon resonance as well as the field hotspots. Such “wave” effects of matter necessarily require a quantum mechanical model for the electron density of the metallic nanoparticle.Reference Zuloaga, Prodan and Nordlander25, Reference Zuloaga, Prodan and Nordlander26
As nanoparticle sizes shrink, the electrons closely resemble particles inside a box, and the quantization of their energy becomes evident. Such effects necessarily manifest when the de Broglie wavelength of the electron is of the size of the confinement, and electrons form standing waves in a confined space instead of bouncing around like particles. For semiconductor systems, such effects are relatively easier to observe in quantum wells and quantum dots since the de Broglie wavelength ranges from 10 to 100 nm. But in metals, where the Fermi energy (hence the Fermi momentum or Fermi wave vector k F) is large, the de Broglie wavelength (![]() ) is very short (approximately a nanometer or less). This makes it considerably more difficult to observe quantum effects in metals, yet a recent careful experiment has clearly isolated the role of quantized electron levels on localized plasmons of nanoparticles with a mean diameter of 8 nm.Reference Scholl, Koh and Dionne27
) is very short (approximately a nanometer or less). This makes it considerably more difficult to observe quantum effects in metals, yet a recent careful experiment has clearly isolated the role of quantized electron levels on localized plasmons of nanoparticles with a mean diameter of 8 nm.Reference Scholl, Koh and Dionne27
Future applications such as high sensitivity single molecule sensing using ultra-small nanoparticles or active devices such as SPASERS will rely on a complete description of nanoparticle plasmons beyond a classical model for the electrons on a metal. Incorporating a variety of effects stemming from quantization of the electron levels in metallic nanoparticles and tunneling effects between coupled dimers using a quantum description of the electron density will be necessary.
Quantum nanophotonics with metamaterials
We now turn our attention to nanoengineered plasmons in metamaterialsReference Cai and Shalaev28 (artificial media) that can increase light-matter interaction for a variety of quantum applications. The properties of a medium imprint themselves on waves passing through it, an effect that can be used to control light or, in turn, probe matter. For waves in general, it is the surface of allowed wave vectors inside a medium, the isofrequency surface, which governs this interaction. Metamaterials can allow unprecedented control of the electromagnetic response and hence the isofrequency surface.
Hyperbolic metamaterials
For waves in an isotropic medium, the spherical dispersion relation constrains the allowed wave vectors to lie on a sphere. Metal-dielectric composites can achieve an extreme anisotropy not available in nature at visible frequencies such that the dielectric constant in one direction becomes negative (reflective/metallic) but stays positive (transparent/dielectric) in the perpendicular direction. This control arises due to the ability to nanostructure the metal inclusions (negative dielectric constant) in a dielectric host medium (positive dielectric constant). Such a uniaxial medium can be described by a dielectric tensor (![]() with
with ![]() ) where the dielectric components are defined along the respective principal axes. This medium allows propagating solutions to Maxwell’s equations unlike a metal. For extraordinary waves (similar to transverse magnetic polarized) inside such a medium the dispersion relation takes the form
) where the dielectric components are defined along the respective principal axes. This medium allows propagating solutions to Maxwell’s equations unlike a metal. For extraordinary waves (similar to transverse magnetic polarized) inside such a medium the dispersion relation takes the form
where ![]() and
and ![]() . The wave vector of light is resolved along the principal axes
. The wave vector of light is resolved along the principal axes ![]() and k 0 = ω/c where ω is the frequency and c is the speed of light in vacuum. The extreme anisotropy leads to hyperbolic isofrequency surfaces since
and k 0 = ω/c where ω is the frequency and c is the speed of light in vacuum. The extreme anisotropy leads to hyperbolic isofrequency surfaces since ![]() . This class of optical metamaterials, known as hyperbolic metamaterials (HMM),Reference Smith, Kolinko and Schurig29, Reference Podolskiy and Narimanov30 is among the most promising for practical applications due to their high figure of merit, ease of nanofabrication, bulk three-dimensional non-resonant response, deeply subwavelength unit cells, and tunability across the visible and mid-infrared spectrum.Reference Noginov, Barnakov, Zhu, Tumkur, Li and Narimanov31–Reference Hoffman, Alekseyev, Howard, Franz, Wasserman, Podolskiy, Narimanov, Sivco and Gmachl33 Two forms of the hyperboloid are possible depending on the number of negative components of the dielectric tensor. We have Type I (εxx = εyy > 0 while εzz < 0) or Type II (εxx = εyy < 0 and εzz > 0) hyperbolic metamaterials.
. This class of optical metamaterials, known as hyperbolic metamaterials (HMM),Reference Smith, Kolinko and Schurig29, Reference Podolskiy and Narimanov30 is among the most promising for practical applications due to their high figure of merit, ease of nanofabrication, bulk three-dimensional non-resonant response, deeply subwavelength unit cells, and tunability across the visible and mid-infrared spectrum.Reference Noginov, Barnakov, Zhu, Tumkur, Li and Narimanov31–Reference Hoffman, Alekseyev, Howard, Franz, Wasserman, Podolskiy, Narimanov, Sivco and Gmachl33 Two forms of the hyperboloid are possible depending on the number of negative components of the dielectric tensor. We have Type I (εxx = εyy > 0 while εzz < 0) or Type II (εxx = εyy < 0 and εzz > 0) hyperbolic metamaterials.
The most striking feature of the hyperbolic metamaterials is that they allow waves with unbounded wave vectors. In vacuum, these large wave vector waves (high-k waves) are evanescent and simply decay away (Figure 2). This property has led to many device applications from subdiffraction imaging in the hyperlensReference Jacob, Alekseyev and Narimanov34, Reference Liu, Lee, Xiong, Sun and Zhang35 to subwavelength mode confinement in metamaterial photonic funnels.Reference Govyadinov and Podolskiy36

Figure 2. Dispersion curves at constant frequency. The isofrequency curve for (a) an isotropic dielectric is a sphere and (b) extraordinary waves in a uniaxial medium with extreme anisotropy εxx = εyy > 0 and εzz < 0 is a hyperboloid (Type I metamaterial). (c) Hyperboloid of Type II metamaterial when two components of the dielectric tensor are negative (εxx = εyy < 0 and εzz > 0). The metamaterials in (b) and (c) can support waves with unbounded wave vectors (dashed red arrows), which are evanescent and simply decay away in any isotropic medium. These high-k states contribute to the photonic density of states causing a divergence in the effective medium limit. kx, ky, and kz, components of the wave vector tensor along the x, y, and z axes, respectively; εxx, εyy, and εzz, components of the dielectric tensors along the x, y, and z axes, respectively; k min, the wave vector below which waves do not propagate in the Type II metamaterial.
Singularity in the photonic density of states
Recently it was pointed out that hyperbolic metamaterials support a broadband singularity in the photonic density of states (PDOS), the physical quantity governing quantum optical phenomena.Reference Jacob, Smolyaninov and Narimanov6, Reference Jacob37 This was later confirmed experimentallyReference Jacob, Kim, Naik, Boltasseva, Narimanov and Shalaev5, Reference Noginov, Li, Barnakov, Dryden, Nataraj, Zhu, Bonner, Mayy, Jacob and Narimanov38 paving the route for controlling spontaneous emission and related phenomena using metamaterials. The PDOS, like its electronic counterpart, can be understood intuitively by calculating the volume enclosed between the isofrequency contours at ω(k) and ω(k) + ∆ω where Δω is a small increase in frequency. For an isotropic medium, this is the volume of an infinitesimally thin spherical shell. In stark contrast, for the HMM, we get a hyperboloidal shell that has infinite volume in the effective medium limit, leading to a singularity in the density of states. The divergence occurs because the metamaterial supports a large number of electromagnetic states (high-k modes) with unbounded wave vectors in the effective medium limit.
The peculiar property, which sets it apart from conventional approaches to PDOS engineering such as optical microcavities and slow light waveguides,Reference Yao, Van Vlack, Reza, Patterson, Dignam and Hughes39 is the broad bandwidth in which the PDOS is enhanced. A direct consequence of this is the broadband Purcell effect, which can enhance the spontaneous emission from quantum emitters. Thus hyperbolic metamaterials would be excellent candidates to enhance the broadband emission from NV centers in diamond.
There are two approaches to achieving the extreme anisotropy required for hyperbolic isofrequency curves: metal-dielectric composites in either a multilayered structure or a periodic array of nanowires in a dielectric host with a subwavelength unit cell size (a << λ). Effective medium theory predicts that both these structures achieve a uniaxial dielectric response with required anisotropy (Figure 3b–c).Reference Milton40 The physical origin of the large number of high-k modes are the coupled plasmonic Bloch modes of the nanowire array or multilayer structure.Reference Elser, Podolskiy, Salakhutdinov and Avrutsky41 This clearly places an upper cut off to the highest allowable wave vector given by the inverse of the unit cell size (![]() ). But with current fabrication techniques that can achieve continuous 10 nm thin films of metal and dielectric, or 40 nm diameter metal nanorods,
). But with current fabrication techniques that can achieve continuous 10 nm thin films of metal and dielectric, or 40 nm diameter metal nanorods, ![]() can be easily achieved for visible light, where k 0 is the free space wave vector. Decreasing the unit cell size further leads to issues due to the higher absorption in nanostructured metal.
can be easily achieved for visible light, where k 0 is the free space wave vector. Decreasing the unit cell size further leads to issues due to the higher absorption in nanostructured metal.

Figure 3. A materials perspective of hyperbolic media. (a) Hyperbolic metamaterials (HMM) can be made using plasmonic materials tailored to different wavelength regions from the visible to mid-infrared ranges. (b) Multilayer realization consists of alternating subwavelength layers of metal and dielectric. (c) HMM based on metal nanorods in a dielectric host. Multiple experiments have probed the spontaneous emission from dye molecules near these metamaterials.Reference Jacob, Kim, Naik, Boltasseva, Narimanov and Shalaev5, Reference Noginov, Li, Barnakov, Dryden, Nataraj, Zhu, Bonner, Mayy, Jacob and Narimanov38 This has become an exciting area of research of quantum nanophotonics using hyperbolic metamaterials.Reference Cortes, Newman, Molesky and Jacob44 UV, ultraviolet; IR, infrared.
The hyperbolic response of the two structures in the previous section occurs in a broad bandwidth with very low loss as compared to other optical metamaterials. Furthermore, the response can be tuned from the ultraviolet (UV) to mid-infrared (mid-IR) wavelength ranges using an appropriate plasmonic metal. At UV and visible wavelengths, silver and gold form the obvious choice for the metal, but the situation is different at larger wavelengths. The transmission of light through the metamaterials is an important factor for which impedance matching has to be achieved. The large negative real part of conventional plasmonic metals limits their usefulness for hyperbolic metamaterials at near-IR and mid-IR wavelength ranges. Alternate plasmonic materialsReference Naik, Kim and Boltasseva42 (transparent conducting oxides and transition metal nitrides) in the near-IR and doped semiconductors (III–V) in the mid-IR have emerged as the best candidates for hyperbolic metamaterials. It also has to be noted that the highest possible index for the dielectric leads to the best tunability, broad bandwidth, and impedance matching. A summary of possible materials for HMMs are shown in Figure 3a.
The near-field thermal and spontaneous emission properties of such metamaterials are modified due to the presence of unique high-k modes. This is best understood by analyzing the near-field local density of states (LDOS).Reference Novotny and Hecht43 In Figure 4, we plot the wave vector-resolved local density of states (WLDOS) for a multilayer structure consisting of 16 layers of silver (Ag) and alumina (Al2O3). The WLDOS shows the contribution of various modes (specified by their lateral wave vector at a given wavelength) to the local density of states (LDOS) in the near-field of the metamaterial. A bright band denotes a set of states with specified frequency and wave vector that couple efficiently to an isolated emitter. It is seen that this practical realization of the hyperbolic metamaterial supports high-k states (coupled plasmonic Bloch modes) in a broad bandwidth, in agreement with effective medium theory. Spontaneous emission properties of R6G dye molecules have been experimentally studied using both nanowireReference Noginov, Li, Barnakov, Dryden, Nataraj, Zhu, Bonner, Mayy, Jacob and Narimanov38 and multilayerReference Jacob, Kim, Naik, Boltasseva, Narimanov and Shalaev5 HMM (Figure 3b–c). A significant decrease of lifetime of the dye molecules was observed particularly for the low loss nanowire realization. Future work will address key challenges of enhancing the transmission to study non-classical light interaction with metamaterials.

Figure 4. Wave vector-resolved local density of states (WLDOS) in the near-field of a hyperbolic metamaterial (HMM) calculated for an effective medium slab and practical multilayer realization taking all non-idealities into account.Reference Cortes, Newman, Molesky and Jacob44 The color bar is in a logarithmic scale normalized to the photonic density of states of vacuum. (a) Effective medium theory (EMT) predicts the existence of a large number of high-k states in a broad bandwidth. (b) Result for a 16 layer Ag/Al2O3, 15 nm/15 nm practical system, which achieves the same response predicted by EMT. For large wave vectors, the WLDOS is different since the enhancement in the density of states is curtailed by the finite unit cell size. kx, the lateral wave vector along the planar interface of the metamaterial; k 0, the free space wave vector.
Optical phase diagram
In Figure 5, we plot the optical phase diagram for a metal-dielectric (Ag/TiO2) multilayer structure as predicted by effective medium theory for different fill fractions of the metal at UV and visible wavelengths.Reference Cortes, Newman, Molesky and Jacob44 EMT predicts this metal-dielectric composite to have a rich variation of dielectric constants behaving as an effectively anisotropic dielectric, a metal, a Type I HMM, or a Type II HMM. The central meeting point of the optical phases at a fill fraction of 0.5 and wavelength of around 510 nm corresponds to the bulk metamaterial plasmon resonance of the metal-dielectric composite, where the effective components reach a singular limit of εxx → 0 and |εzz| → ∞.

Figure 5. Optical phase diagram. Effective medium theory predicts a multilayer structure consisting of nanolayers of Ag and TiO2 to behave as an effective dielectric, metal, Type I hyperbolic metamaterials (HMM), or Type II HMM, depending on the wavelength and fill fraction of the metal. The most interesting feature occurs along the phase boundaries, where the topology of the isofrequency surface can change from an ellipsoid to a hyperboloid, leading to a sudden increase in light-matter interaction.Reference Krishnamoorthy, Jacob, Narimanov, Kretzschmar and Menon7 The red dashed arrows are the light wave vectors.
Topological transitions
The most interesting phenomenon occurs at the phase boundaries where the wavelength dispersion of the metal causes the metamaterial structure to change from an effective dielectric to a HMM (Figure 5). The isofrequency surface therefore changes from an ellipsoid to a hyperboloid at the transition wavelength. The role of the isofrequency surface in optics is analogous to the Fermi surface in electronics and, not surprisingly, such changes in topology of the Fermi surface (known as Lifshitz transitions) occur in electronic systems with dramatic consequences on electron transport properties.Reference Lifshitz45 In the optical equivalent, the transition is characterized by the sudden appearance of the high-k states, since the closed ellipsoidal isofrequency surface does not support these modes. Such topological transitions in the optical isofrequency surface lead to increased light matter-interaction beyond the transition wavelength. They were studied using the lifetime of broadband quantum emitters placed in the vicinity of a multilayer HMM. The sample was carefully designed to have a εxx ≈ 0 transition within the bandwidth of the dye,Reference Krishnamoorthy, Jacob, Narimanov, Kretzschmar and Menon7 and a decrease in lifetime was observed beyond the transition wavelength. This unique metamaterial effect should lead to applications in controllable switching of light-matter interaction.
Summary and future
The departure from the classical description of plasmons and plasmonic metamaterials leads to not only unique quantum phenomena but also applications in single photon sources, coherent generator of surface plasmons (SPASERS), and single molecule sensing. These are fueled in turn by advances in synthesis and unprecedented precision to characterize and probe light-matter interaction. Future progress in the field would be on both the fundamental and applied fronts. A complete description of quantum plasmonics in the future would incorporate the non-classical properties of light as well as matter leading to possibly fundamental advances. On the other hand, many challenges in the field of quantum information technology could be addressed by plasmonics and metamaterials.
Acknowledgments
Z.J. acknowledges C. Cortes and W. Newman for their input. This work was supported in part by the National Science and Engineering Research Council of Canada, Canadian School of Energy and Environment and University of Alberta’s Nanobridge initiative.