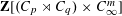In the paper [Reference Evans1] I claimed to show that there are no non-trivial stably free modules over integral group rings of the groups
![]() $\,(C_{p}\rtimes C_{q})\times C_{\infty }^{m}$
. Unfortunately there are a number of erroneous statements in [Reference Evans1] which vitiate the attempted proof. To explain where these occur, recall that in [Reference Evans1] two Milnor fibre squares
$\,(C_{p}\rtimes C_{q})\times C_{\infty }^{m}$
. Unfortunately there are a number of erroneous statements in [Reference Evans1] which vitiate the attempted proof. To explain where these occur, recall that in [Reference Evans1] two Milnor fibre squares
![]() $\,(\clubsuit )\,$
and
$\,(\clubsuit )\,$
and
![]() $\,(\heartsuit )\,$
were introduced as follows:
$\,(\heartsuit )\,$
were introduced as follows:

Here
![]() $\unicode[STIX]{x1D6E4}=C_{\infty }^{m}$
, and
$\unicode[STIX]{x1D6E4}=C_{\infty }^{m}$
, and
![]() ${\mathcal{T}}_{q}={\mathcal{T}}_{q}(A,\unicode[STIX]{x1D70B})$
is the ring of quasi-triangular
${\mathcal{T}}_{q}={\mathcal{T}}_{q}(A,\unicode[STIX]{x1D70B})$
is the ring of quasi-triangular
![]() $q\times q$
matrices where
$q\times q$
matrices where
![]() $A=\mathbf{Z}[\unicode[STIX]{x1D701}_{p}]^{C_{q}}$
is the subring of the cyclotomic integers
$A=\mathbf{Z}[\unicode[STIX]{x1D701}_{p}]^{C_{q}}$
is the subring of the cyclotomic integers
![]() $\mathbf{Z}[\unicode[STIX]{x1D701}_{p}]$
fixed under the Galois action of
$\mathbf{Z}[\unicode[STIX]{x1D701}_{p}]$
fixed under the Galois action of
![]() $C_{q}$
and
$C_{q}$
and
![]() $\unicode[STIX]{x1D70B}\in \text{Spec}(A)$
is the unique prime over
$\unicode[STIX]{x1D70B}\in \text{Spec}(A)$
is the unique prime over
![]() $p$
.
$p$
.
The most obvious errors [Reference Evans1, Corollary 3.4] include a misdescription of the unit group
![]() $U(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])$
, and the possibility of non-trivial rank-one stably free modules over
$U(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])$
, and the possibility of non-trivial rank-one stably free modules over
![]() ${\mathcal{T}}_{2}[\unicode[STIX]{x1D6E4}]$
. A slightly less obvious but more significant error concerns the possibility of lifting units from
${\mathcal{T}}_{2}[\unicode[STIX]{x1D6E4}]$
. A slightly less obvious but more significant error concerns the possibility of lifting units from
![]() $\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}]$
to
$\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}]$
to
![]() ${\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}]$
. In consequence we must amend the original statement of [Reference Evans1] as follows.
${\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}]$
. In consequence we must amend the original statement of [Reference Evans1] as follows.
Theorem A. Let
![]() $S$
be a stably free module of rank
$S$
be a stably free module of rank
![]() $n$
over
$n$
over
![]() $\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{m}]$
where
$\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{m}]$
where
![]() $m\geqslant 2$
. Then:
$m\geqslant 2$
. Then:
∙ if
 $q$
is an odd prime,
$q$
is an odd prime,
 $S$
is free provided
$S$
is free provided
 $n\neq 2$
; and
$n\neq 2$
; and∙ if
 $q=2$
,
$q=2$
,
 $S$
is free provided
$S$
is free provided
 $n\geqslant 3$
.
$n\geqslant 3$
.
Nevertheless, when
![]() $m=1$
the original statement continues to hold:
$m=1$
the original statement continues to hold:
Theorem B. Any stably free module over
![]() $\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }]$
is free.
$\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }]$
is free.
Rather than try to patch up the proof in [Reference Evans1] piecemeal we give a more straightforward approach which isolates the real difficulty and avoids it where possible. We first establish four propositions.
Proposition 1.
![]() $U(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
is finite; in fact
$U(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
is finite; in fact
Proof. As
![]() $q$
is a divisor of
$q$
is a divisor of
![]() $p-1$
, we have
$p-1$
, we have
Consequently
Observe that
![]() $U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
contains a copy of
$U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
contains a copy of
![]() $\unicode[STIX]{x1D6E4}^{(q)}=\underbrace{\unicode[STIX]{x1D6E4}\times \cdots \times \unicode[STIX]{x1D6E4}}_{q}$
, namely the diagonal matrices
$\unicode[STIX]{x1D6E4}^{(q)}=\underbrace{\unicode[STIX]{x1D6E4}\times \cdots \times \unicode[STIX]{x1D6E4}}_{q}$
, namely the diagonal matrices
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{q})=\left(\begin{smallmatrix}\unicode[STIX]{x1D6FE}_{1}\\ & \unicode[STIX]{x1D6FE}_{2} & \\ & & \ddots \\ & & & \unicode[STIX]{x1D6FE}_{q}\end{smallmatrix}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{q})=\left(\begin{smallmatrix}\unicode[STIX]{x1D6FE}_{1}\\ & \unicode[STIX]{x1D6FE}_{2} & \\ & & \ddots \\ & & & \unicode[STIX]{x1D6FE}_{q}\end{smallmatrix}\right),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FE}_{i}\in \unicode[STIX]{x1D6E4}$
. Combining this with the obvious inclusion
$\unicode[STIX]{x1D6FE}_{i}\in \unicode[STIX]{x1D6E4}$
. Combining this with the obvious inclusion
![]() $U({\mathcal{T}}_{q})\subset U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
gives an injection
$U({\mathcal{T}}_{q})\subset U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
gives an injection
![]() $U({\mathcal{T}}_{q})\times \unicode[STIX]{x1D6E4}^{(q)}{\hookrightarrow}U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
. Hence we now have a surjection
$U({\mathcal{T}}_{q})\times \unicode[STIX]{x1D6E4}^{(q)}{\hookrightarrow}U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
. Hence we now have a surjection
The ring isomorphism (*) now gives an isomorphism of unit groups
Now
![]() $\unicode[STIX]{x1D6E4}=C_{\infty }^{m}$
is a t.u.p. group so
$\unicode[STIX]{x1D6E4}=C_{\infty }^{m}$
is a t.u.p. group so
![]() $\mathbf{F}_{p}[\unicode[STIX]{x1D6E4}]$
has only trivial units (cf. [Reference Johnson2, Appendix C]). Hence
$\mathbf{F}_{p}[\unicode[STIX]{x1D6E4}]$
has only trivial units (cf. [Reference Johnson2, Appendix C]). Hence
 $$\begin{eqnarray}\displaystyle U(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}]) & \cong & \displaystyle \underbrace{(U(\mathbf{F}_{p})\times \unicode[STIX]{x1D6E4})\times \cdots \times (U(\mathbf{F}_{p})\times \unicode[STIX]{x1D6E4})}_{q}\nonumber\\ \displaystyle & \cong & \displaystyle \underbrace{U(\mathbf{F}_{p})\times \cdots \times U(\mathbf{F}_{p})}_{q}\times \unicode[STIX]{x1D6E4}^{(q)}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}]) & \cong & \displaystyle \underbrace{(U(\mathbf{F}_{p})\times \unicode[STIX]{x1D6E4})\times \cdots \times (U(\mathbf{F}_{p})\times \unicode[STIX]{x1D6E4})}_{q}\nonumber\\ \displaystyle & \cong & \displaystyle \underbrace{U(\mathbf{F}_{p})\times \cdots \times U(\mathbf{F}_{p})}_{q}\times \unicode[STIX]{x1D6E4}^{(q)}\nonumber\end{eqnarray}$$
so that, by (*), there are bijections
From (**) we obtain a surjection
![]() $U(\mathbf{F}_{p}[C_{q}])/U({\mathcal{T}}_{q}){\twoheadrightarrow}U(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/U$
$U(\mathbf{F}_{p}[C_{q}])/U({\mathcal{T}}_{q}){\twoheadrightarrow}U(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/U$
![]() $({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
. The stated result now follows as
$({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
. The stated result now follows as
![]() $U(\mathbf{F}_{p}[C_{q}])/U({\mathcal{T}}_{q})$
is finite.◻
$U(\mathbf{F}_{p}[C_{q}])/U({\mathcal{T}}_{q})$
is finite.◻
Proposition 2. Let
![]() $p$
be an odd prime and
$p$
be an odd prime and
![]() $q$
be a divisor of
$q$
be a divisor of
![]() $p-1$
. Then, for all
$p-1$
. Then, for all
![]() $n\geqslant 3$
,
$n\geqslant 3$
,
Proof. Given rings
![]() $A,B$
such that
$A,B$
such that
![]() $\text{GL}_{n}(A)=U(A)E_{n}(A)$
and
$\text{GL}_{n}(A)=U(A)E_{n}(A)$
and
![]() $\text{GL}_{n}(B)=U(B)E_{n}(B)$
, we have
$\text{GL}_{n}(B)=U(B)E_{n}(B)$
, we have
![]() $\text{GL}_{n}(A\times B)=U(A\times B)E_{n}(A\times B)$
. The result thus follows from (*) by induction on
$\text{GL}_{n}(A\times B)=U(A\times B)E_{n}(A\times B)$
. The result thus follows from (*) by induction on
![]() $q$
, the case
$q$
, the case
![]() $q=1$
being Suslin’s theorem [Reference Suslin3], namely that
$q=1$
being Suslin’s theorem [Reference Suslin3], namely that
for any field
![]() $\mathbf{F}$
and any integer
$\mathbf{F}$
and any integer
![]() $k\geqslant 3$
.◻
$k\geqslant 3$
.◻
Proposition 3.
![]() $\text{GL}_{n}(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/\text{GL}_{n}({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
is finite for
$\text{GL}_{n}(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/\text{GL}_{n}({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
is finite for
![]() $n\geqslant 3$
; in fact
$n\geqslant 3$
; in fact
Proof. Evidently
![]() $U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])E_{n}({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])\subset \text{GL}_{n}({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
and so there is a natural surjection
$U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])E_{n}({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])\subset \text{GL}_{n}({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
and so there is a natural surjection
![]() $\text{GL}_{n}(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])E_{n}({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}]){\twoheadrightarrow}\text{GL}_{n}(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/\text{GL}_{n}({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
. Also, the ring homomorphism
$\text{GL}_{n}(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])E_{n}({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}]){\twoheadrightarrow}\text{GL}_{n}(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/\text{GL}_{n}({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
. Also, the ring homomorphism
![]() $\natural :{\mathcal{T}}_{q}(A,\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}]\rightarrow \mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}]$
is surjective and so induces surjections
$\natural :{\mathcal{T}}_{q}(A,\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}]\rightarrow \mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}]$
is surjective and so induces surjections
![]() $\natural _{\ast }:E_{k}({\mathcal{T}}_{q}(A,\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])\rightarrow E_{k}(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])$
for all
$\natural _{\ast }:E_{k}({\mathcal{T}}_{q}(A,\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])\rightarrow E_{k}(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])$
for all
![]() $k\geqslant 2$
. By Proposition 2 we may write
$k\geqslant 2$
. By Proposition 2 we may write
We obtain a surjection
![]() $U(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}]){\twoheadrightarrow}\text{GL}_{n}(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/\text{GL}_{n}$
$U(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/U({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}]){\twoheadrightarrow}\text{GL}_{n}(\mathbf{F}_{p}[C_{q}\times \unicode[STIX]{x1D6E4}])/\text{GL}_{n}$
![]() $({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
and so the stated result now follows from Proposition 1.◻
$({\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}])$
and so the stated result now follows from Proposition 1.◻
Proposition 4. Let
![]() $p$
be an odd prime and
$p$
be an odd prime and
![]() $q$
be a divisor of
$q$
be a divisor of
![]() $p-1$
. Then, for all
$p-1$
. Then, for all
![]() $n\geqslant 1$
,
$n\geqslant 1$
,
Proof. We follow the same line of argument as Proposition 2 with the exception that, in establishing the induction base, we do not use Suslin’s theorem. Instead we note that, as
![]() $\mathbf{F}_{p}[C_{\infty }]$
is a Euclidean domain, we may use the Smith normal form to show that
$\mathbf{F}_{p}[C_{\infty }]$
is a Euclidean domain, we may use the Smith normal form to show that
![]() $\text{GL}_{k}(\mathbf{F}_{p}[C_{\infty }])=U(\mathbf{F}_{p}[C_{\infty }])\cdot$
$\text{GL}_{k}(\mathbf{F}_{p}[C_{\infty }])=U(\mathbf{F}_{p}[C_{\infty }])\cdot$
![]() $E_{k}(\mathbf{F}_{p}[C_{\infty }])$
.◻
$E_{k}(\mathbf{F}_{p}[C_{\infty }])$
.◻
As in [Reference Evans1], we denote the set of isomorphism classes of locally free
![]() $\mathbf{Z}[C_{p}\rtimes C_{q}]$
-modules of rank
$\mathbf{Z}[C_{p}\rtimes C_{q}]$
-modules of rank
![]() $k$
by
$k$
by
![]() ${\mathcal{L}}{\mathcal{F}}_{k}(\clubsuit )$
. By Milnor’s classification, this corresponds to the two-sided quotient
${\mathcal{L}}{\mathcal{F}}_{k}(\clubsuit )$
. By Milnor’s classification, this corresponds to the two-sided quotient
Likewise, the locally free
![]() $\mathbf{Z}[(C_{p}\rtimes C_{q})\times \unicode[STIX]{x1D6E4}]$
-modules of rank
$\mathbf{Z}[(C_{p}\rtimes C_{q})\times \unicode[STIX]{x1D6E4}]$
-modules of rank
![]() $k$
correspond to the quotient
$k$
correspond to the quotient
In particular, if neither
![]() $\mathbf{Z}[C_{q}]$
nor
$\mathbf{Z}[C_{q}]$
nor
![]() ${\mathcal{T}}_{q}$
admits non-trivial stably free modules of rank
${\mathcal{T}}_{q}$
admits non-trivial stably free modules of rank
![]() $k$
, then any stably free module of rank
$k$
, then any stably free module of rank
![]() $k$
over
$k$
over
![]() $\mathbf{Z}[C_{p}\rtimes C_{q}]$
is locally free. Consequently, the set
$\mathbf{Z}[C_{p}\rtimes C_{q}]$
is locally free. Consequently, the set
![]() ${\mathcal{S}}{\mathcal{F}}_{k}(\mathbf{Z}[C_{p}\rtimes C_{q}])$
of stably free modules of rank
${\mathcal{S}}{\mathcal{F}}_{k}(\mathbf{Z}[C_{p}\rtimes C_{q}])$
of stably free modules of rank
![]() $k$
over
$k$
over
![]() $\mathbf{Z}[C_{p}\rtimes C_{q}]$
is a subset of
$\mathbf{Z}[C_{p}\rtimes C_{q}]$
is a subset of
![]() ${\mathcal{L}}{\mathcal{F}}_{k}(\clubsuit )$
. Similarly,
${\mathcal{L}}{\mathcal{F}}_{k}(\clubsuit )$
. Similarly,
![]() ${\mathcal{S}}{\mathcal{F}}_{k}(\mathbf{Z}[(C_{p}\rtimes C_{q})\times \unicode[STIX]{x1D6E4}])$
is a subset of
${\mathcal{S}}{\mathcal{F}}_{k}(\mathbf{Z}[(C_{p}\rtimes C_{q})\times \unicode[STIX]{x1D6E4}])$
is a subset of
![]() ${\mathcal{L}}{\mathcal{F}}_{k}(\heartsuit )$
if neither
${\mathcal{L}}{\mathcal{F}}_{k}(\heartsuit )$
if neither
![]() $\mathbf{Z}[C_{q}\times \unicode[STIX]{x1D6E4}]$
nor
$\mathbf{Z}[C_{q}\times \unicode[STIX]{x1D6E4}]$
nor
![]() ${\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}]$
admits non-trivial stably free modules of rank
${\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}]$
admits non-trivial stably free modules of rank
![]() $k$
.
$k$
.
There are obvious mappings of fibre squares
![]() $i:(\clubsuit ){\hookrightarrow}(\heartsuit )$
and
$i:(\clubsuit ){\hookrightarrow}(\heartsuit )$
and
![]() $r:(\heartsuit )\rightarrow (\clubsuit )$
such that
$r:(\heartsuit )\rightarrow (\clubsuit )$
such that
![]() $r\circ i=\text{Id}$
. Consequently, there is a commutative ladder of mappings
$r\circ i=\text{Id}$
. Consequently, there is a commutative ladder of mappings

where
![]() $s_{k,1}$
and
$s_{k,1}$
and
![]() $\unicode[STIX]{x1D70E}_{k,1}$
are the obvious stabilization mappings. We note that the mappings
$\unicode[STIX]{x1D70E}_{k,1}$
are the obvious stabilization mappings. We note that the mappings
![]() $i_{k}$
are injective in view of the fact that
$i_{k}$
are injective in view of the fact that
![]() $r\circ i=\text{Id}$
.
$r\circ i=\text{Id}$
.
The argument is now divided into two cases:
![]() $q$
is odd, and
$q$
is odd, and
![]() $q=2$
. First, suppose
$q=2$
. First, suppose
![]() $q$
is an odd prime dividing
$q$
is an odd prime dividing
![]() $p-1$
. As noted in [Reference Evans1], in
$p-1$
. As noted in [Reference Evans1], in
![]() $(\clubsuit )$
, the rings
$(\clubsuit )$
, the rings
![]() $\mathbf{Z}[C_{q}]$
and
$\mathbf{Z}[C_{q}]$
and
![]() ${\mathcal{T}}_{q}$
both have property SFC. Consequently,
${\mathcal{T}}_{q}$
both have property SFC. Consequently,
![]() ${\mathcal{S}}{\mathcal{F}}_{k}(\mathbf{Z}[C_{p}\rtimes C_{q}])$
is a subset of
${\mathcal{S}}{\mathcal{F}}_{k}(\mathbf{Z}[C_{p}\rtimes C_{q}])$
is a subset of
![]() ${\mathcal{L}}{\mathcal{F}}_{k}(\clubsuit )$
for all
${\mathcal{L}}{\mathcal{F}}_{k}(\clubsuit )$
for all
![]() $k\geqslant 1$
. Similarly, in the fibre square
$k\geqslant 1$
. Similarly, in the fibre square
![]() $(\heartsuit )$
, the rings
$(\heartsuit )$
, the rings
![]() $\mathbf{Z}[C_{q}\times \unicode[STIX]{x1D6E4}]$
and
$\mathbf{Z}[C_{q}\times \unicode[STIX]{x1D6E4}]$
and
![]() ${\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}]$
also have SFC and once again
${\mathcal{T}}_{q}[\unicode[STIX]{x1D6E4}]$
also have SFC and once again
![]() ${\mathcal{S}}{\mathcal{F}}_{k}(\mathbf{Z}[(C_{p}\rtimes C_{q})\times \unicode[STIX]{x1D6E4}])$
is a subset of
${\mathcal{S}}{\mathcal{F}}_{k}(\mathbf{Z}[(C_{p}\rtimes C_{q})\times \unicode[STIX]{x1D6E4}])$
is a subset of
![]() ${\mathcal{L}}{\mathcal{F}}_{k}(\heartsuit )$
for all
${\mathcal{L}}{\mathcal{F}}_{k}(\heartsuit )$
for all
![]() $k\geqslant 1$
. The essence of the argument now consists of the following five statements.
$k\geqslant 1$
. The essence of the argument now consists of the following five statements.
(I) For all
 $n$
,
$n$
,
 ${\mathcal{L}}{\mathcal{F}}_{n}(\clubsuit )$
is finite and
${\mathcal{L}}{\mathcal{F}}_{n}(\clubsuit )$
is finite and
 $s_{n,1}:{\mathcal{L}}{\mathcal{F}}_{n}(\clubsuit )\rightarrow {\mathcal{L}}{\mathcal{F}}_{n+1}(\clubsuit )$
is bijective.
$s_{n,1}:{\mathcal{L}}{\mathcal{F}}_{n}(\clubsuit )\rightarrow {\mathcal{L}}{\mathcal{F}}_{n+1}(\clubsuit )$
is bijective.(II)
 $i_{1}:{\mathcal{L}}{\mathcal{F}}_{1}(\clubsuit )\rightarrow {\mathcal{L}}{\mathcal{F}}_{1}(\heartsuit )$
is bijective.
$i_{1}:{\mathcal{L}}{\mathcal{F}}_{1}(\clubsuit )\rightarrow {\mathcal{L}}{\mathcal{F}}_{1}(\heartsuit )$
is bijective.(III)
 $i_{n}:{\mathcal{L}}{\mathcal{F}}_{n}(\clubsuit )\rightarrow {\mathcal{L}}{\mathcal{F}}_{n}(\heartsuit )$
is bijective for all
$i_{n}:{\mathcal{L}}{\mathcal{F}}_{n}(\clubsuit )\rightarrow {\mathcal{L}}{\mathcal{F}}_{n}(\heartsuit )$
is bijective for all
 $n\geqslant 3$
.
$n\geqslant 3$
.(IV)
 $\unicode[STIX]{x1D70E}_{n,1}:{\mathcal{L}}{\mathcal{F}}_{n}(\heartsuit )\rightarrow {\mathcal{L}}{\mathcal{F}}_{n+1}(\heartsuit )$
is injective provided
$\unicode[STIX]{x1D70E}_{n,1}:{\mathcal{L}}{\mathcal{F}}_{n}(\heartsuit )\rightarrow {\mathcal{L}}{\mathcal{F}}_{n+1}(\heartsuit )$
is injective provided
 $n\neq 2$
.
$n\neq 2$
.(V) If
 $m=1$
(that is,
$m=1$
(that is,
 $\unicode[STIX]{x1D6E4}\;=\;C_{\infty }$
) then
$\unicode[STIX]{x1D6E4}\;=\;C_{\infty }$
) then
 $i_{2}:{\mathcal{L}}{\mathcal{F}}_{2}(\clubsuit )\rightarrow {\mathcal{L}}{\mathcal{F}}_{2}(\heartsuit )$
is bijective.
$i_{2}:{\mathcal{L}}{\mathcal{F}}_{2}(\clubsuit )\rightarrow {\mathcal{L}}{\mathcal{F}}_{2}(\heartsuit )$
is bijective.
To prove (I) we note that, as
![]() $C_{p}\rtimes C_{q}$
is finite, the finiteness of
$C_{p}\rtimes C_{q}$
is finite, the finiteness of
![]() ${\mathcal{L}}{\mathcal{F}}_{n}(\clubsuit )$
follows from the Jordan–Zassenhaus theorem, together with Milnor’s classification of projectives. Moreover, as
${\mathcal{L}}{\mathcal{F}}_{n}(\clubsuit )$
follows from the Jordan–Zassenhaus theorem, together with Milnor’s classification of projectives. Moreover, as
![]() $\mathbf{Z}[C_{p}\rtimes C_{q}]$
satisfies the Eichler condition, the Swan–Jacobinski theorem shows that each
$\mathbf{Z}[C_{p}\rtimes C_{q}]$
satisfies the Eichler condition, the Swan–Jacobinski theorem shows that each
![]() $s_{k,1}:{\mathcal{L}}{\mathcal{F}}_{k}(\clubsuit )\rightarrow {\mathcal{L}}{\mathcal{F}}_{k+1}(\clubsuit )$
is bijective. It follows from Proposition 1 that
$s_{k,1}:{\mathcal{L}}{\mathcal{F}}_{k}(\clubsuit )\rightarrow {\mathcal{L}}{\mathcal{F}}_{k+1}(\clubsuit )$
is bijective. It follows from Proposition 1 that
![]() $|{\mathcal{L}}{\mathcal{F}}_{1}(\heartsuit )|\leqslant |{\mathcal{L}}{\mathcal{F}}_{1}(\clubsuit )|$
. Thus (II) is true as
$|{\mathcal{L}}{\mathcal{F}}_{1}(\heartsuit )|\leqslant |{\mathcal{L}}{\mathcal{F}}_{1}(\clubsuit )|$
. Thus (II) is true as
![]() $i_{1}$
is injective and
$i_{1}$
is injective and
![]() ${\mathcal{L}}{\mathcal{F}}_{1}(\clubsuit )$
is finite. Likewise it follows from Proposition 3 that
${\mathcal{L}}{\mathcal{F}}_{1}(\clubsuit )$
is finite. Likewise it follows from Proposition 3 that
![]() $|{\mathcal{L}}{\mathcal{F}}_{n}(\heartsuit )|\leqslant |{\mathcal{L}}{\mathcal{F}}_{n}(\clubsuit )|$
for
$|{\mathcal{L}}{\mathcal{F}}_{n}(\heartsuit )|\leqslant |{\mathcal{L}}{\mathcal{F}}_{n}(\clubsuit )|$
for
![]() $n\geqslant 3$
. Thus (III) is true as
$n\geqslant 3$
. Thus (III) is true as
![]() $i_{n}$
is injective and
$i_{n}$
is injective and
![]() ${\mathcal{L}}{\mathcal{F}}_{n}(\clubsuit )$
is finite; (IV) now follows from (I), (II) and (III) by diagram chasing using the fact that
${\mathcal{L}}{\mathcal{F}}_{n}(\clubsuit )$
is finite; (IV) now follows from (I), (II) and (III) by diagram chasing using the fact that
![]() $i_{2}$
is injective. Finally, (V) follows by the same argument as (III) on substituting Proposition 4 for Proposition 2.
$i_{2}$
is injective. Finally, (V) follows by the same argument as (III) on substituting Proposition 4 for Proposition 2.
To proceed with the proof of Theorem A, put
![]() $\unicode[STIX]{x1D70E}_{n,k}=\unicode[STIX]{x1D70E}_{n+k-1,1}\circ \ldots \circ \unicode[STIX]{x1D70E}_{n,1}$
whenever
$\unicode[STIX]{x1D70E}_{n,k}=\unicode[STIX]{x1D70E}_{n+k-1,1}\circ \ldots \circ \unicode[STIX]{x1D70E}_{n,1}$
whenever
![]() $k\geqslant 1$
. It follows from (IV) that
$k\geqslant 1$
. It follows from (IV) that
![]() $\unicode[STIX]{x1D70E}_{n,k}$
is injective provided
$\unicode[STIX]{x1D70E}_{n,k}$
is injective provided
![]() $n\geqslant 3$
. A straightforward diagram chase using (I), (II) and (III) also shows that each
$n\geqslant 3$
. A straightforward diagram chase using (I), (II) and (III) also shows that each
![]() $\unicode[STIX]{x1D70E}_{1,k}$
is injective. Now suppose that
$\unicode[STIX]{x1D70E}_{1,k}$
is injective. Now suppose that
![]() $S$
is a stably free module of rank
$S$
is a stably free module of rank
![]() $n\neq 2$
over
$n\neq 2$
over
![]() $\unicode[STIX]{x1D6EC}=\mathbf{Z}[(C_{p}\rtimes C_{q})\times \unicode[STIX]{x1D6E4}])$
and denote its class in
$\unicode[STIX]{x1D6EC}=\mathbf{Z}[(C_{p}\rtimes C_{q})\times \unicode[STIX]{x1D6E4}])$
and denote its class in
![]() ${\mathcal{L}}{\mathcal{F}}_{n}(\heartsuit )$
by
${\mathcal{L}}{\mathcal{F}}_{n}(\heartsuit )$
by
![]() $[S]$
. Then
$[S]$
. Then
![]() $S\oplus \unicode[STIX]{x1D6EC}^{k}\cong \unicode[STIX]{x1D6EC}^{n+k}$
for some
$S\oplus \unicode[STIX]{x1D6EC}^{k}\cong \unicode[STIX]{x1D6EC}^{n+k}$
for some
![]() $k\geqslant 1$
so that
$k\geqslant 1$
so that
![]() $\unicode[STIX]{x1D70E}_{n,k}[S]=\unicode[STIX]{x1D70E}_{n,k}[\unicode[STIX]{x1D6EC}^{n}]$
. As
$\unicode[STIX]{x1D70E}_{n,k}[S]=\unicode[STIX]{x1D70E}_{n,k}[\unicode[STIX]{x1D6EC}^{n}]$
. As
![]() $\unicode[STIX]{x1D70E}_{n,k}$
is injective,
$\unicode[STIX]{x1D70E}_{n,k}$
is injective,
![]() $S\cong \unicode[STIX]{x1D6EC}^{n}$
. Consequently, when
$S\cong \unicode[STIX]{x1D6EC}^{n}$
. Consequently, when
![]() $n\neq 2$
there are no non-trivial stably free modules of rank
$n\neq 2$
there are no non-trivial stably free modules of rank
![]() $n$
over
$n$
over
![]() $\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{m}]$
, and this proves the first part of Theorem A.
$\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{m}]$
, and this proves the first part of Theorem A.
In the case
![]() $q=2$
(i.e. dihedral groups) we cannot claim
$q=2$
(i.e. dihedral groups) we cannot claim
![]() ${\mathcal{T}}_{2}[\unicode[STIX]{x1D6E4}]$
has property SFC. To see why, consider the square
${\mathcal{T}}_{2}[\unicode[STIX]{x1D6E4}]$
has property SFC. To see why, consider the square

As
![]() $(A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}]$
is commutative, we have
$(A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}]$
is commutative, we have
![]() $\text{GL}_{2}((A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])=U((A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])\cdot \text{SL}_{2}((A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])$
. The unit group
$\text{GL}_{2}((A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])=U((A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])\cdot \text{SL}_{2}((A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])$
. The unit group
![]() $U((A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])$
lifts back to
$U((A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])$
lifts back to
![]() ${\mathcal{T}}_{2}((A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])$
. However, it is not clear whether we can lift the elements of
${\mathcal{T}}_{2}((A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])$
. However, it is not clear whether we can lift the elements of
![]() $\text{SL}_{2}((A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])$
. Thus, it is conceivable that
$\text{SL}_{2}((A/\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}])$
. Thus, it is conceivable that
![]() ${\mathcal{T}}_{2}(A,\,\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}]$
has non-trivial stably free modules of rank 1. Nevertheless, using Suslin’s theorem as before, it is clear that
${\mathcal{T}}_{2}(A,\,\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}]$
has non-trivial stably free modules of rank 1. Nevertheless, using Suslin’s theorem as before, it is clear that
![]() ${\mathcal{T}}_{2}(A,\,\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}]$
admits no non-trivial stably free module of rank
${\mathcal{T}}_{2}(A,\,\unicode[STIX]{x1D70B})[\unicode[STIX]{x1D6E4}]$
admits no non-trivial stably free module of rank
![]() ${\geqslant}2$
. Consequently, we observe that
${\geqslant}2$
. Consequently, we observe that
![]() ${\mathcal{S}}{\mathcal{F}}_{k}(\mathbf{Z}[(C_{p}\rtimes C_{q})\times \unicode[STIX]{x1D6E4}])$
is a subset of
${\mathcal{S}}{\mathcal{F}}_{k}(\mathbf{Z}[(C_{p}\rtimes C_{q})\times \unicode[STIX]{x1D6E4}])$
is a subset of
![]() ${\mathcal{L}}{\mathcal{F}}_{k}(\heartsuit )$
for all
${\mathcal{L}}{\mathcal{F}}_{k}(\heartsuit )$
for all
![]() $k\geqslant 2$
. We now proceed as above.
$k\geqslant 2$
. We now proceed as above.
Finally, the proof of Theorem B follows exactly the same lines except that now, in the case where
![]() $m=1$
and
$m=1$
and
![]() $\unicode[STIX]{x1D6E4}=C_{\infty }$
, we see from (V) that
$\unicode[STIX]{x1D6E4}=C_{\infty }$
, we see from (V) that
![]() $\unicode[STIX]{x1D70E}_{2,1}$
is also injective. Consequently, each
$\unicode[STIX]{x1D70E}_{2,1}$
is also injective. Consequently, each
![]() $\unicode[STIX]{x1D70E}_{2,k}$
is injective. Thus, there are no non-trivial stably free modules of any rank over
$\unicode[STIX]{x1D70E}_{2,k}$
is injective. Thus, there are no non-trivial stably free modules of any rank over
![]() $\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }]$
.
$\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }]$
.