Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-17T23:35:55.656Z Has data issue: false hasContentIssue false
  • English
  • Français

On packings and coverings of unit density

Published online by Cambridge University Press:  26 February 2010

H. Groemer
H. Groemer
Affiliation:
Department of Mathematics, The University of Arizona, Tucson, AZ 85721, USA.
Get access

Abstract

Let (C1, C2, …) be a sequence of convex bodies in n-dimensional euclidean space En, and let υ(Ci) denote the volume and d(Ci) the diameter of Ci. It is shown that the conditions

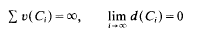
imply that the sets Ci can be rearranged by the application of rigid motions so that the resulting sets form a packing in En of density 1. A corresponding result for coverings of En is also proved.

Type
Research Article
Information
Mathematika , Volume 35 , Issue 2 , December 1988 , pp. 172 - 179
Copyright
Copyright © University College London 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bezdek, A.. Ausfüllung und Überdeckung der Ebene durch Kreise. Ann. Univ. Sci. Budap. Eötvös Sect. Math., 28 (1985), 173–177.Google Scholar
2.Groemer, H.. Covering and packing properties of bounded sequences of convex sets. Mathematika, 29 (1982), 18–31.CrossRefGoogle Scholar
3.Groemer, H.. Coverings and packings by sequences of convex sets. Annals of the N. Y. Acad. of Sci., 440 (1985), 262–278.CrossRefGoogle Scholar