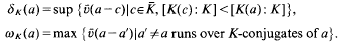Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bhatia, Saurabh
and
Khanduja, Sudesh K.
2002.
A CHARACTERIZATION OF KRASNER'S CONSTANT.
Communications in Algebra,
Vol. 30,
Issue. 6,
p.
2975.
Bhatia, Saurabh
and
Khanduja, Sudesh K.
2002.
On extensions generated by roots of lifting polynomials.
Mathematika,
Vol. 49,
Issue. 1-2,
p.
107.
Khanduja, Sudesh K.
Popescu, N.
and
Roggenkamp, K. W.
2002.
On minimal pairs and residually transcendental extensions of valuations.
Mathematika,
Vol. 49,
Issue. 1-2,
p.
93.
Aghigh, Kamal
and
Khanduja, Sudesh K.
2005.
On Chains Associated with Elements Algebraic over a Henselian Valued Field.
Algebra Colloquium,
Vol. 12,
Issue. 04,
p.
607.
Bhatia, Saurabh
and
Khanduja, Sudesh K.
2005.
On Limits of Sequences of Algebraic Elements over a Complete Field.
Algebra Colloquium,
Vol. 12,
Issue. 04,
p.
617.
Khanduja, Sudesh K.
2010.
On Brown’s constant associated with irreducible polynomials over henselian valued fields.
Journal of Pure and Applied Algebra,
Vol. 214,
Issue. 12,
p.
2294.
BISHNOI, ANUJ
KUMAR, SANJEEV
and
KHANDUJA, SUDESH K.
2013.
ON LIFTINGS OF POWERS OF IRREDUCIBLE POLYNOMIALS.
Journal of Algebra and Its Applications,
Vol. 12,
Issue. 05,
p.
1250222.
Aghigh, Kamal
and
Nikseresht, Azadeh
2015.
Characterizing Distinguished Pairs by Using Liftings of Irreducible Polynomials.
Canadian Mathematical Bulletin,
Vol. 58,
Issue. 2,
p.
225.
Aghigh, Kamal
and
Nikseresht, Azadeh
2015.
Constructing complete distinguished chains with given invariants.
Journal of Algebra and Its Applications,
Vol. 14,
Issue. 03,
p.
1550026.
Jakhar, Anuj
Khanduja, Sudesh K.
and
Sangwan, Neeraj
2018.
On factorization of polynomials in henselian valued fields.
Communications in Algebra,
Vol. 46,
Issue. 7,
p.
3205.




 of
of