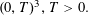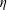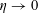1 Introduction
The behaviour of systems (of Maxwell equations) with periodic coefficients in the regime of “high contrast” or “large coupling”, that is, when the ratio between material properties of some of the constituents within the composite is large, is understood to be of special interest in applications. This is due to the improved band-gap properties of the spectra for such materials compared to the usual moderate-contrast composites. A series of recent studies have analysed asymptotic limits of scalar high-contrast problems, either in the strong
![]() $L^{2}$
sense (see [Reference Zhikov11, Reference Zhikov12]) or in the norm-resolvent
$L^{2}$
sense (see [Reference Zhikov11, Reference Zhikov12]) or in the norm-resolvent
![]() $L^{2}$
sense (see [Reference Cherednichenko and Cooper2]). These have resulted in sharp operator convergence estimates in the homogenization of such problems (i.e. in the limit as the period tends to zero) and have provided a link between the study of effective properties of periodic media and the behaviour of waves in such media, in particular their scattering characteristics. The studies have also highlighted the need to extend the classical compactness techniques in homogenization to cases where the symbol of the operator involved is no longer uniformly positive definite, thus leading to “degenerate” problems. The work [Reference Kamotski and Smyshlyaev6] has opened a way to one such extension procedure, based on a “generalized Weyl decomposition”, from the perspective of the strong
$L^{2}$
sense (see [Reference Cherednichenko and Cooper2]). These have resulted in sharp operator convergence estimates in the homogenization of such problems (i.e. in the limit as the period tends to zero) and have provided a link between the study of effective properties of periodic media and the behaviour of waves in such media, in particular their scattering characteristics. The studies have also highlighted the need to extend the classical compactness techniques in homogenization to cases where the symbol of the operator involved is no longer uniformly positive definite, thus leading to “degenerate” problems. The work [Reference Kamotski and Smyshlyaev6] has opened a way to one such extension procedure, based on a “generalized Weyl decomposition”, from the perspective of the strong
![]() $L^{2}$
convergence.
$L^{2}$
convergence.
The set of tools developed in the literature is now poised for the treatment of vector problems with degeneracies such as the linearized elasticity equations and the Maxwell equations; these examples are typically invoked in the physics and applications literature, and are prototypes for wider varieties of partial differential equations. The recent work [Reference Zhikov and Pastukhova10] has studied the spectral behaviour of periodic operators with rapidly oscillating coefficients in the context of linearized elasticity. It shows that the related spectrum exhibits the phenomenon of “partial” wave propagation, depending on the number of eigenmodes available at each given frequency. This is close in spirit to the work [Reference Smyshlyaev7], where “partial wave propagation” was studied for a wider class of vector problems, with a general high-contrast anisotropy.
The high-contrast system of Maxwell equations poses an analytic challenge in view of the special structure of the “space of microscopic variations” (using the terminology of [Reference Kamotski and Smyshlyaev6]), which consists of functions that are curl-free on the “stiff” component, in the case of a two-component composite of a “stiff” matrix and “soft” inclusions. In the work [Reference Cherednichenko and Cooper1] the authors analysed the two-scale structure of solutions to the high-contrast system of Maxwell equations in the low-frequency limit, and derived the corresponding system of homogenized equations, by developing an appropriate compactness argument on the basis of the general theory of [Reference Kamotski and Smyshlyaev6]. In the present paper we consider the associated wave propagation problem for monochromatic waves of a given frequency by constructing two-scale asymptotic series for eigenfunctions. We justify these asymptotic series by demonstrating that for each element of the spectrum of the homogenized equations there exist convergent eigenvalues and eigenfunctions for the original heterogeneous problem. Our analysis is set in the context of a “supercell” spectral problem, that is, the problem of vibrations of a square-shaped domain with periodicity conditions on the boundary (equivalently seen as a torus). The problem of the “spectral completeness” of the homogenized description in question remains open: it is not known, for the full-space problem, whether there may exist sequences of eigenvalues converging to a point outside the spectrum of the homogenized problem. This will be addressed in a future publication, using the method developed in [Reference Cherednichenko and Cooper2].
2 Problem formulation and main results
In this paper we consider Maxwell equations for a three-dimensional two-component periodic dielectric composite when the dielectric properties of the constituent materials exhibit a high degree of contrast. We assume that the reference cell
![]() $Q:= [\!0,1\!)^{3}$
contains an inclusion
$Q:= [\!0,1\!)^{3}$
contains an inclusion
![]() $Q_{0},$
which is an open set with sufficiently smooth boundary. We also assume that the “matrix”
$Q_{0},$
which is an open set with sufficiently smooth boundary. We also assume that the “matrix”
![]() $Q_{1}:=Q\backslash \overline{Q_{0}}$
is simply connected Lipschitz set.
$Q_{1}:=Q\backslash \overline{Q_{0}}$
is simply connected Lipschitz set.
We consider a composite with high contrast in the dielectric permittivity
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D702}}=\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D702}}(x/\unicode[STIX]{x1D702})$
at points
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D702}}=\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D702}}(x/\unicode[STIX]{x1D702})$
at points
![]() $x\in \unicode[STIX]{x1D702}(Q_{1}+m)$
,
$x\in \unicode[STIX]{x1D702}(Q_{1}+m)$
,
![]() $m\in \mathbb{Z}^{3},$
and
$m\in \mathbb{Z}^{3},$
and
![]() $x\in \unicode[STIX]{x1D702}(Q_{0}+m),$
$x\in \unicode[STIX]{x1D702}(Q_{0}+m),$
![]() $m\in \mathbb{Z}^{3},$
namely
$m\in \mathbb{Z}^{3},$
namely
where
![]() $\unicode[STIX]{x1D702}\in (0,1)$
is the period and
$\unicode[STIX]{x1D702}\in (0,1)$
is the period and
![]() $\unicode[STIX]{x1D716}_{0}$
,
$\unicode[STIX]{x1D716}_{0}$
,
![]() $\unicode[STIX]{x1D716}_{1}$
are continuously differentiable
$\unicode[STIX]{x1D716}_{1}$
are continuously differentiable
![]() $Q$
-periodic positive-definite scalar functions.
$Q$
-periodic positive-definite scalar functions.
We also assume moderate contrast in the magnetic permeability, and for simplicity of exposition we shall set
![]() $\unicode[STIX]{x1D707}\equiv 1$
. We consider the open cube
$\unicode[STIX]{x1D707}\equiv 1$
. We consider the open cube
![]() $\mathbb{T}:=(0,T)^{3}$
and those values of the parameter
$\mathbb{T}:=(0,T)^{3}$
and those values of the parameter
![]() $\unicode[STIX]{x1D702}$
for which
$\unicode[STIX]{x1D702}$
for which
![]() $T/\unicode[STIX]{x1D702}\in \mathbb{N}.$
By rescaling the spatial variable (which can also be viewed as non-dimensionalization) we assume that
$T/\unicode[STIX]{x1D702}\in \mathbb{N}.$
By rescaling the spatial variable (which can also be viewed as non-dimensionalization) we assume that
![]() $T=1$
and that
$T=1$
and that
![]() $\unicode[STIX]{x1D702}^{-1}\in \mathbb{N}.$
We shall study the behaviour of the magnetic component
$\unicode[STIX]{x1D702}^{-1}\in \mathbb{N}.$
We shall study the behaviour of the magnetic component
![]() $H^{\unicode[STIX]{x1D702}}$
of the electromagnetic wave of frequency
$H^{\unicode[STIX]{x1D702}}$
of the electromagnetic wave of frequency
![]() $\unicode[STIX]{x1D714}$
propagating through the domain
$\unicode[STIX]{x1D714}$
propagating through the domain
![]() $\mathbb{T}$
occupied by a dielectric material with permittivity
$\mathbb{T}$
occupied by a dielectric material with permittivity
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D702}}(x/\unicode[STIX]{x1D702}).$
More precisely, we consider pairs
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D702}}(x/\unicode[STIX]{x1D702}).$
More precisely, we consider pairs
![]() $(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D702}},H^{\unicode[STIX]{x1D702}})\in \mathbb{R}_{+}\times [H_{\#}^{1}(\mathbb{T})]^{3}$
satisfying the system of equations
$(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D702}},H^{\unicode[STIX]{x1D702}})\in \mathbb{R}_{+}\times [H_{\#}^{1}(\mathbb{T})]^{3}$
satisfying the system of equations
Notice that solutions of (2.1) are automatically solenoidal, that is,
![]() $\text{div}\,H^{\unicode[STIX]{x1D702}}=0$
.
$\text{div}\,H^{\unicode[STIX]{x1D702}}=0$
.
We seek solutions to the above problem in the form of an asymptotic expansion
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\displaystyle H^{\unicode[STIX]{x1D702}}(x)=H^{0}\biggl(x,\frac{x}{\unicode[STIX]{x1D702}}\biggr)+\unicode[STIX]{x1D702}H^{1}\biggl(x,\frac{x}{\unicode[STIX]{x1D702}}\biggr)+\unicode[STIX]{x1D702}^{2}H^{2}\biggl(x,\frac{x}{\unicode[STIX]{x1D702}}\biggr)+\cdots \,,\\ \displaystyle \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D702}}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D702}^{2}\unicode[STIX]{x1D714}_{2}+\cdots \,,\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\displaystyle H^{\unicode[STIX]{x1D702}}(x)=H^{0}\biggl(x,\frac{x}{\unicode[STIX]{x1D702}}\biggr)+\unicode[STIX]{x1D702}H^{1}\biggl(x,\frac{x}{\unicode[STIX]{x1D702}}\biggr)+\unicode[STIX]{x1D702}^{2}H^{2}\biggl(x,\frac{x}{\unicode[STIX]{x1D702}}\biggr)+\cdots \,,\\ \displaystyle \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D702}}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D702}\unicode[STIX]{x1D714}_{1}+\unicode[STIX]{x1D702}^{2}\unicode[STIX]{x1D714}_{2}+\cdots \,,\end{array} & & \displaystyle\end{eqnarray}$$
where the vector functions
![]() $H^{j}(x,y)$
,
$H^{j}(x,y)$
,
![]() $j=0,1,2,\ldots ,$
are
$j=0,1,2,\ldots ,$
are
![]() $Q$
-periodic in the variable
$Q$
-periodic in the variable
![]() $y$
. (Note that the terms of order
$y$
. (Note that the terms of order
![]() $O(\unicode[STIX]{x1D702})$
and higher in the expansion for
$O(\unicode[STIX]{x1D702})$
and higher in the expansion for
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D702}}$
will be of no importance in what follows.) Substituting (2.2) into (2.1) and gathering the coefficients for each power of the parameter
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D702}}$
will be of no importance in what follows.) Substituting (2.2) into (2.1) and gathering the coefficients for each power of the parameter
![]() $\unicode[STIX]{x1D702}$
results in a system of recurrence relations for
$\unicode[STIX]{x1D702}$
results in a system of recurrence relations for
![]() $H^{j},$
$H^{j},$
![]() $j=0,1,2,\ldots$
; see §4. In particular, the function
$j=0,1,2,\ldots$
; see §4. In particular, the function
![]() $H^{0}$
is an eigenfunction of a limit (“homogenized”) system of partial differential equations, as described in the following theorem.
$H^{0}$
is an eigenfunction of a limit (“homogenized”) system of partial differential equations, as described in the following theorem.
Theorem 2.1. Consider the constant matrix
where the vector function
![]() $N$
is a solution to the “unit-cell problem”
$N$
is a solution to the “unit-cell problem”
in which
![]() $n$
is the exterior normal to
$n$
is the exterior normal to
![]() $\unicode[STIX]{x2202}Q_{0}$
.
$\unicode[STIX]{x2202}Q_{0}$
.
Suppose that
![]() $\unicode[STIX]{x1D714}\in \mathbb{R}_{+}$
and
$\unicode[STIX]{x1D714}\in \mathbb{R}_{+}$
and
![]() $H^{0}(x,y)=u(x)+\unicode[STIX]{x1D6FB}_{y}v(x,y)+z(x,y),$
where the tripletFootnote
1
$H^{0}(x,y)=u(x)+\unicode[STIX]{x1D6FB}_{y}v(x,y)+z(x,y),$
where the tripletFootnote
1
![]() $(u,v,z)\in [H_{\#\text{curl}}^{1}(\mathbb{T})]^{3}\times L^{2}(\mathbb{T};H_{\#}^{2}(Q))\times [L^{2}(\mathbb{T};H_{0}^{1}(Q_{0}))]^{3}$
satisfies the system of equations
$(u,v,z)\in [H_{\#\text{curl}}^{1}(\mathbb{T})]^{3}\times L^{2}(\mathbb{T};H_{\#}^{2}(Q))\times [L^{2}(\mathbb{T};H_{0}^{1}(Q_{0}))]^{3}$
satisfies the system of equations
Then:
(1) There exists at least one eigenfrequency
 $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D702}}$
for (2.1) such that (2.7)with an
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D702}}$
for (2.1) such that (2.7)with an $$\begin{eqnarray}|\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D702}}-\unicode[STIX]{x1D714}|<C\unicode[STIX]{x1D702},\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D702}}-\unicode[STIX]{x1D714}|<C\unicode[STIX]{x1D702},\end{eqnarray}$$
 $\unicode[STIX]{x1D702}$
-independent constant
$\unicode[STIX]{x1D702}$
-independent constant
 $C>0$
.
$C>0$
.(2) Consider the finite-dimensional vector space
There exists an $$\begin{eqnarray}X_{\unicode[STIX]{x1D702}}:=\text{span}\{H^{\unicode[STIX]{x1D702}}:\text{(2.1) holds, where }\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D702}}\text{ satisfies (2.7)}\}.\end{eqnarray}$$
$$\begin{eqnarray}X_{\unicode[STIX]{x1D702}}:=\text{span}\{H^{\unicode[STIX]{x1D702}}:\text{(2.1) holds, where }\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D702}}\text{ satisfies (2.7)}\}.\end{eqnarray}$$
 $\unicode[STIX]{x1D702}$
-independent constant
$\unicode[STIX]{x1D702}$
-independent constant
 $\widehat{C}>0$
such that
$\widehat{C}>0$
such that  $$\begin{eqnarray}\inf _{H\in X_{\unicode[STIX]{x1D702}}}\biggl\|H^{0}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)-H(\cdot )\biggr\|_{L^{2}(\mathbb{T})}<\widehat{C}\unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}\inf _{H\in X_{\unicode[STIX]{x1D702}}}\biggl\|H^{0}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)-H(\cdot )\biggr\|_{L^{2}(\mathbb{T})}<\widehat{C}\unicode[STIX]{x1D702}.\end{eqnarray}$$
The matrix
![]() $A^{\text{hom}}$
is described by solutions to certain degenerate “cell problems”, as follows. Consider the spaces
$A^{\text{hom}}$
is described by solutions to certain degenerate “cell problems”, as follows. Consider the spaces
and
![]() $V^{\bot },$
the orthogonal complement of
$V^{\bot },$
the orthogonal complement of
![]() $V$
in
$V$
in
![]() $[H_{\#}^{1}(Q)]^{3}$
with respect to the equivalent
$[H_{\#}^{1}(Q)]^{3}$
with respect to the equivalent
![]() $H^{1}(Q)$
-norm
$H^{1}(Q)$
-norm
associated with the inner product
Then
where
![]() $N_{\unicode[STIX]{x1D709}}$
,
$N_{\unicode[STIX]{x1D709}}$
,
![]() $\unicode[STIX]{x1D709}\in \mathbb{R}^{3}$
, is the unique (weak) solution in
$\unicode[STIX]{x1D709}\in \mathbb{R}^{3}$
, is the unique (weak) solution in
![]() $V^{\bot }$
to the problem (2.3), that is,
$V^{\bot }$
to the problem (2.3), that is,
Existence and uniqueness of
![]() $N_{\unicode[STIX]{x1D709}}$
are discussed in §4.
$N_{\unicode[STIX]{x1D709}}$
are discussed in §4.
Notice that
Indeed, for the functional
we find
![]() $F_{\unicode[STIX]{x1D709}}(U)=F_{\unicode[STIX]{x1D709}}(P_{V^{\bot }}U)$
for all
$F_{\unicode[STIX]{x1D709}}(U)=F_{\unicode[STIX]{x1D709}}(P_{V^{\bot }}U)$
for all
![]() $U\in [H_{\#}^{1}(Q)]^{3}$
, where
$U\in [H_{\#}^{1}(Q)]^{3}$
, where
![]() $P_{V^{\bot }}$
is the orthogonal projection onto
$P_{V^{\bot }}$
is the orthogonal projection onto
![]() $V^{\bot }$
. Therefore, without loss of generality,
$V^{\bot }$
. Therefore, without loss of generality,
![]() $F_{\unicode[STIX]{x1D709}}$
can be minimized on
$F_{\unicode[STIX]{x1D709}}$
can be minimized on
![]() $V^{\bot }$
for which (2.10) is the corresponding Euler–Lagrange equation.
$V^{\bot }$
for which (2.10) is the corresponding Euler–Lagrange equation.
The variational formulation (2.11) allows one to obtain a representation for the matrix
![]() $\unicode[STIX]{x1D716}_{\text{stiff}}^{\text{hom}}$
such that
$\unicode[STIX]{x1D716}_{\text{stiff}}^{\text{hom}}$
such that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}_{\text{stiff}}^{\text{hom}}\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D709}:=\inf _{\substack{ u\in H_{\#}^{1}(Q), \\ \unicode[STIX]{x1D6FB}u=-\unicode[STIX]{x1D709}\text{in }Q_{0}}}\int _{Q_{1}}\unicode[STIX]{x1D716}_{1}(\unicode[STIX]{x1D6FB}u+\unicode[STIX]{x1D709})\cdot (\unicode[STIX]{x1D6FB}u+\unicode[STIX]{x1D709}),\quad \unicode[STIX]{x1D709}\in \mathbb{R}^{3}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}_{\text{stiff}}^{\text{hom}}\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D709}:=\inf _{\substack{ u\in H_{\#}^{1}(Q), \\ \unicode[STIX]{x1D6FB}u=-\unicode[STIX]{x1D709}\text{in }Q_{0}}}\int _{Q_{1}}\unicode[STIX]{x1D716}_{1}(\unicode[STIX]{x1D6FB}u+\unicode[STIX]{x1D709})\cdot (\unicode[STIX]{x1D6FB}u+\unicode[STIX]{x1D709}),\quad \unicode[STIX]{x1D709}\in \mathbb{R}^{3}, & & \displaystyle\end{eqnarray}$$
which arises in the homogenization of periodic problems with stiff inclusions; see [Reference Jikov, Kozlov and Oleinik5, §3.2].Footnote 2
Indeed, as shown in [Reference Jikov, Kozlov and Oleinik5, p. 101], the following representation holds:
Notice that for each vector
![]() $v$
in (2.13) there exists
$v$
in (2.13) there exists
![]() $U_{v}\in [H_{\#}^{1}(Q)]^{3}$
such that
$U_{v}\in [H_{\#}^{1}(Q)]^{3}$
such that
![]() $v=\text{curl}\,U_{v}$
(see [Reference Jikov, Kozlov and Oleinik5, pp. 6–7]), and hence
$v=\text{curl}\,U_{v}$
(see [Reference Jikov, Kozlov and Oleinik5, pp. 6–7]), and hence
It follows that for all
![]() $\unicode[STIX]{x1D709}\in \mathbb{R}^{3}$
one has
$\unicode[STIX]{x1D709}\in \mathbb{R}^{3}$
one has
 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D716}_{\text{stiff}}^{\text{hom}})^{-1}\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D709} & = & \displaystyle \inf _{U\in [H_{\#}^{1}(Q)]^{3}}\int _{Q_{1}}\unicode[STIX]{x1D716}_{1}^{-1}(\text{curl}(P_{V^{\bot }}U)+\unicode[STIX]{x1D709})\cdot (\text{curl}(P_{V^{\bot }}U)+\unicode[STIX]{x1D709})\nonumber\\ \displaystyle & = & \displaystyle A^{\text{hom}}\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D709}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D716}_{\text{stiff}}^{\text{hom}})^{-1}\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D709} & = & \displaystyle \inf _{U\in [H_{\#}^{1}(Q)]^{3}}\int _{Q_{1}}\unicode[STIX]{x1D716}_{1}^{-1}(\text{curl}(P_{V^{\bot }}U)+\unicode[STIX]{x1D709})\cdot (\text{curl}(P_{V^{\bot }}U)+\unicode[STIX]{x1D709})\nonumber\\ \displaystyle & = & \displaystyle A^{\text{hom}}\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D709}.\nonumber\end{eqnarray}$$
3 On the spectrum of the limit problem
In this section we study the set of values
![]() $\unicode[STIX]{x1D714}^{2}$
such that there exists a non-trivial triple
$\unicode[STIX]{x1D714}^{2}$
such that there exists a non-trivial triple
![]() $(u,v,z)$
solving the two-scale limit spectral problem (2.4)–(2.6).
$(u,v,z)$
solving the two-scale limit spectral problem (2.4)–(2.6).
3.1 Equivalent formulation and spectral decomposition of the limit problem
Let
![]() $G$
be the Green function for the scalar periodic Laplacian, that is, for all
$G$
be the Green function for the scalar periodic Laplacian, that is, for all
![]() $y\in Q$
, one has
$y\in Q$
, one has
where
![]() $\unicode[STIX]{x1D6FF}_{0}$
is the Dirac delta function supported at zero, on
$\unicode[STIX]{x1D6FF}_{0}$
is the Dirac delta function supported at zero, on
![]() $Q$
considered as a torus. Then, as the functions
$Q$
considered as a torus. Then, as the functions
![]() $v$
,
$v$
,
![]() $z$
solve (2.5), we have
$z$
solve (2.5), we have
![]() $v(x,\cdot )=G\ast (\text{div}_{y}\,z)(x,\cdot ),$
and (2.6) takes the form
$v(x,\cdot )=G\ast (\text{div}_{y}\,z)(x,\cdot ),$
and (2.6) takes the form
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{curl}_{y}(\unicode[STIX]{x1D716}_{0}^{-1}(y)\text{curl}_{y}\,z(x,y))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D714}^{2}\biggl(u(x)+\unicode[STIX]{x1D6FB}_{y}\int _{Q_{0}}G(y-y^{\prime })\,\text{div}_{y^{\prime }}\,z(x,y^{\prime })\,dy^{\prime }+z(x,y)\biggr),\nonumber\\ \displaystyle & & \displaystyle \qquad (x,y)\in \mathbb{T}\times Q_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{curl}_{y}(\unicode[STIX]{x1D716}_{0}^{-1}(y)\text{curl}_{y}\,z(x,y))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D714}^{2}\biggl(u(x)+\unicode[STIX]{x1D6FB}_{y}\int _{Q_{0}}G(y-y^{\prime })\,\text{div}_{y^{\prime }}\,z(x,y^{\prime })\,dy^{\prime }+z(x,y)\biggr),\nonumber\\ \displaystyle & & \displaystyle \qquad (x,y)\in \mathbb{T}\times Q_{0}.\end{eqnarray}$$
For the case
![]() $\unicode[STIX]{x1D714}=0$
the set of solutions
$\unicode[STIX]{x1D714}=0$
the set of solutions
![]() $z$
to (3.1) subject to the condition
$z$
to (3.1) subject to the condition
![]() $z(x,y)=0$
,
$z(x,y)=0$
,
![]() $x\in \mathbb{T},$
$x\in \mathbb{T},$
![]() $y\in \unicode[STIX]{x2202}Q_{0},$
is clearly given by
$y\in \unicode[STIX]{x2202}Q_{0},$
is clearly given by
![]() $L^{2}(\mathbb{T},{\mathcal{H}}_{0}),$
where
$L^{2}(\mathbb{T},{\mathcal{H}}_{0}),$
where
![]() ${\mathcal{H}}_{0}:=\{u\in [H_{0}^{1}(Q_{0})]^{3}:\text{curl}\,u=0\}.$
${\mathcal{H}}_{0}:=\{u\in [H_{0}^{1}(Q_{0})]^{3}:\text{curl}\,u=0\}.$
Further, for
![]() $\unicode[STIX]{x1D714}\neq 0,$
as (3.1) is linear in
$\unicode[STIX]{x1D714}\neq 0,$
as (3.1) is linear in
![]() $u(x)$
and
$u(x)$
and
![]() $\text{curl}_{y}\unicode[STIX]{x1D6FB}_{y}=0$
, we set
$\text{curl}_{y}\unicode[STIX]{x1D6FB}_{y}=0$
, we set
where
![]() $B$
is a
$B$
is a
![]() $3\times 3$
matrix function whose column vectors
$3\times 3$
matrix function whose column vectors
![]() $B^{j}$
,
$B^{j}$
,
![]() $j=1,2,3,$
are solutions in
$j=1,2,3,$
are solutions in
![]() $[H_{\#}^{1}(Q)]^{3}$
to the system
$[H_{\#}^{1}(Q)]^{3}$
to the system
where
![]() $e_{j}$
,
$e_{j}$
,
![]() $j=1,2,3,$
are the Euclidean basis vectors and
$j=1,2,3,$
are the Euclidean basis vectors and
![]() $a(B^{j})$
is the “circulation” of
$a(B^{j})$
is the “circulation” of
![]() $B^{j},$
that is defined as the continuous extension, in the sense of the
$B^{j},$
that is defined as the continuous extension, in the sense of the
![]() $H^{1}$
norm, of the map given by
$H^{1}$
norm, of the map given by
![]() $a(\unicode[STIX]{x1D719})_{i}=\int _{0}^{1}\unicode[STIX]{x1D719}_{i}(te_{i})\,dt$
,
$a(\unicode[STIX]{x1D719})_{i}=\int _{0}^{1}\unicode[STIX]{x1D719}_{i}(te_{i})\,dt$
,
![]() $i=1,2,3$
, for
$i=1,2,3$
, for
![]() $\unicode[STIX]{x1D719}\in [C^{\infty }(Q)]^{3}$
. Note that, since
$\unicode[STIX]{x1D719}\in [C^{\infty }(Q)]^{3}$
. Note that, since
![]() $B^{j}\in [H^{1}(Q)]^{3}$
, equation (3.4) implies
$B^{j}\in [H^{1}(Q)]^{3}$
, equation (3.4) implies
![]() $\unicode[STIX]{x1D716}_{0}^{-1}\text{curl}_{}\,B^{j}\times n|_{-}=0$
on
$\unicode[STIX]{x1D716}_{0}^{-1}\text{curl}_{}\,B^{j}\times n|_{-}=0$
on
![]() $\unicode[STIX]{x2202}Q_{0}$
. Furthermore, the system (3.3)–(3.6) implies the variational problem of finding
$\unicode[STIX]{x2202}Q_{0}$
. Furthermore, the system (3.3)–(3.6) implies the variational problem of finding
![]() $B^{j}\in [H_{\#}^{1}(Q)]^{3},$
subject to the constraints (3.4)–(3.6), such that the following identity holds:
$B^{j}\in [H_{\#}^{1}(Q)]^{3},$
subject to the constraints (3.4)–(3.6), such that the following identity holds:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}\,\text{curl}\,B^{j}\cdot \text{curl}\,\unicode[STIX]{x1D711}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q}e_{j}\cdot \unicode[STIX]{x1D711}+\unicode[STIX]{x1D714}^{2}\int _{Q}B^{j}\cdot \unicode[STIX]{x1D711}\quad \text{for all }\unicode[STIX]{x1D711}\in [H_{\#}^{1}(Q)]^{3}\text{ satisfying (3.4){-}(3.6).}\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}\,\text{curl}\,B^{j}\cdot \text{curl}\,\unicode[STIX]{x1D711}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q}e_{j}\cdot \unicode[STIX]{x1D711}+\unicode[STIX]{x1D714}^{2}\int _{Q}B^{j}\cdot \unicode[STIX]{x1D711}\quad \text{for all }\unicode[STIX]{x1D711}\in [H_{\#}^{1}(Q)]^{3}\text{ satisfying (3.4){-}(3.6).}\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Indeed, functions
![]() $\unicode[STIX]{x1D711}\in [H_{\#}^{1}(Q)]^{3}$
which satisfy (3.4) and (3.6) admit (see Lemma 4.1 below) the representation
$\unicode[STIX]{x1D711}\in [H_{\#}^{1}(Q)]^{3}$
which satisfy (3.4) and (3.6) admit (see Lemma 4.1 below) the representation
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D6FB}p+\unicode[STIX]{x1D713}$
,
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D6FB}p+\unicode[STIX]{x1D713}$
,
![]() $p\in H_{\#}^{2}(Q)$
,
$p\in H_{\#}^{2}(Q)$
,
![]() $\unicode[STIX]{x1D713}\in [H_{0}^{1}(Q_{0})]^{3}$
. Therefore, it is straightforward to show (3.7) holds for
$\unicode[STIX]{x1D713}\in [H_{0}^{1}(Q_{0})]^{3}$
. Therefore, it is straightforward to show (3.7) holds for
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D713}$
if and only if (3.3) holds. Similarly, one can show (3.7) holds for
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D713}$
if and only if (3.3) holds. Similarly, one can show (3.7) holds for
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D6FB}p$
if and only if (3.5) holds.
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D6FB}p$
if and only if (3.5) holds.
Substituting the representation (3.2) into (2.4) and using the fact that
leads to the operator-pencil spectral problem
where
![]() $\unicode[STIX]{x1D6E4}$
is a matrix-valued function that vanishes at
$\unicode[STIX]{x1D6E4}$
is a matrix-valued function that vanishes at
![]() $\unicode[STIX]{x1D714}=0,$
and for
$\unicode[STIX]{x1D714}=0,$
and for
![]() $\unicode[STIX]{x1D714}\neq 0$
has elements
$\unicode[STIX]{x1D714}\neq 0$
has elements
We denote by
![]() ${\mathcal{H}}_{1}$
the space of vector fields in
${\mathcal{H}}_{1}$
the space of vector fields in
![]() $[H_{\#}^{1}(Q)]^{3}$
that satisfy conditions (3.4)–(3.6). It can be shownFootnote
3
that there exist countably many pairs
$[H_{\#}^{1}(Q)]^{3}$
that satisfy conditions (3.4)–(3.6). It can be shownFootnote
3
that there exist countably many pairs
![]() $(\unicode[STIX]{x1D6FC}^{k},r^{k})\in \mathbb{R}\times {\mathcal{H}}_{1}$
such that
$(\unicode[STIX]{x1D6FC}^{k},r^{k})\in \mathbb{R}\times {\mathcal{H}}_{1}$
such that
![]() $\Vert r^{k}\Vert _{[L^{2}(Q)]^{3}}=1$
and
$\Vert r^{k}\Vert _{[L^{2}(Q)]^{3}}=1$
and
Moreover, the sequence
![]() $(r^{k})_{k\in \mathbb{N}}$
can be chosen to form an orthonormal basis of the closure
$(r^{k})_{k\in \mathbb{N}}$
can be chosen to form an orthonormal basis of the closure
![]() $\overline{{\mathcal{H}}}_{1}$
of
$\overline{{\mathcal{H}}}_{1}$
of
![]() ${\mathcal{H}}_{1}$
in
${\mathcal{H}}_{1}$
in
![]() $[L^{2}(Q)]^{3}$
and, upon a suitable rearrangement, one has
$[L^{2}(Q)]^{3}$
and, upon a suitable rearrangement, one has
Performing a decompositionFootnote
4
of the functions
![]() $B^{j}$
,
$B^{j}$
,
![]() $j=1,2,3,$
with respect to the above basis yields
$j=1,2,3,$
with respect to the above basis yields
where
![]() $r_{j}^{k}$
,
$r_{j}^{k}$
,
![]() $j=1,2,3,$
are the components of the vector
$j=1,2,3,$
are the components of the vector
![]() $r^{k},$
$r^{k},$
![]() $k\in \mathbb{N}$
.
$k\in \mathbb{N}$
.
Consider the functions
![]() $\unicode[STIX]{x1D719}^{k}\in [H_{0}^{1}(Q_{0})]^{3}$
,
$\unicode[STIX]{x1D719}^{k}\in [H_{0}^{1}(Q_{0})]^{3}$
,
![]() $k\in \mathbb{N},$
that solve the non-local problems
$k\in \mathbb{N},$
that solve the non-local problems
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{curl}_{}(\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{}\unicode[STIX]{x1D719}^{k}(y))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FC}^{k}\biggl(\unicode[STIX]{x1D6FB}\int _{Q_{0}}G(y-y^{\prime })\,\text{div}\,\unicode[STIX]{x1D719}^{k}(y^{\prime })\,dy^{\prime }+\unicode[STIX]{x1D719}^{k}(y)\biggr),\quad y\in Q_{0},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{curl}_{}(\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{}\unicode[STIX]{x1D719}^{k}(y))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FC}^{k}\biggl(\unicode[STIX]{x1D6FB}\int _{Q_{0}}G(y-y^{\prime })\,\text{div}\,\unicode[STIX]{x1D719}^{k}(y^{\prime })\,dy^{\prime }+\unicode[STIX]{x1D719}^{k}(y)\biggr),\quad y\in Q_{0},\end{eqnarray}$$
and satisfy the orthonormality conditions
where
![]() $\unicode[STIX]{x1D6FB}^{2}G$
is the Hessian matrix of
$\unicode[STIX]{x1D6FB}^{2}G$
is the Hessian matrix of
![]() $G.$
Using the formula
$G.$
Using the formula
we obtain the following representation for
![]() $\unicode[STIX]{x1D6E4}$
:
$\unicode[STIX]{x1D6E4}$
:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{ij}(\unicode[STIX]{x1D714}) & = & \displaystyle \unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FF}_{ij}+\unicode[STIX]{x1D714}^{4}\mathop{\sum }_{k=1}^{\infty }\frac{(\int _{Q_{0}}\unicode[STIX]{x1D719}_{i}^{k})(\int _{Q_{0}}\unicode[STIX]{x1D719}_{j}^{k})}{\unicode[STIX]{x1D6FC}^{k}-\unicode[STIX]{x1D714}^{2}},\nonumber\\ \displaystyle & & \displaystyle i,j=1,2,3,\quad \unicode[STIX]{x1D714}^{2}\notin \{0\}\cup \{\unicode[STIX]{x1D6FC}^{k}\}_{k=1}^{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{ij}(\unicode[STIX]{x1D714}) & = & \displaystyle \unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D6FF}_{ij}+\unicode[STIX]{x1D714}^{4}\mathop{\sum }_{k=1}^{\infty }\frac{(\int _{Q_{0}}\unicode[STIX]{x1D719}_{i}^{k})(\int _{Q_{0}}\unicode[STIX]{x1D719}_{j}^{k})}{\unicode[STIX]{x1D6FC}^{k}-\unicode[STIX]{x1D714}^{2}},\nonumber\\ \displaystyle & & \displaystyle i,j=1,2,3,\quad \unicode[STIX]{x1D714}^{2}\notin \{0\}\cup \{\unicode[STIX]{x1D6FC}^{k}\}_{k=1}^{\infty }.\end{eqnarray}$$
3.2 Analysis of the limit spectrum
Consider the Fourier expansion for the function
![]() $u$
in (3.8):
$u$
in (3.8):
where the integral is taken componentwise. As
![]() $u$
solves (3.8), the coefficients
$u$
solves (3.8), the coefficients
![]() $\hat{u} (m)$
satisfy the equation
$\hat{u} (m)$
satisfy the equation
with the matrix-valued function
![]() ${\mathcal{M}}$
given by
${\mathcal{M}}$
given by
 $$\begin{eqnarray}\displaystyle {\mathcal{M}}_{lp}(m) & = & \displaystyle 4\unicode[STIX]{x1D70B}^{2}\mathop{\sum }_{i,j,s,t=1}^{3}\unicode[STIX]{x1D700}_{ils}m_{s}A_{ij}^{\text{hom}}\unicode[STIX]{x1D700}_{jpt}m_{t}\nonumber\\ \displaystyle & = & \displaystyle 4\unicode[STIX]{x1D70B}^{2}(e_{l}\times m)\cdot A^{\text{hom}}(e_{p}\times m),\quad m\in \mathbb{Z}^{3},l,p=1,2,3,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{M}}_{lp}(m) & = & \displaystyle 4\unicode[STIX]{x1D70B}^{2}\mathop{\sum }_{i,j,s,t=1}^{3}\unicode[STIX]{x1D700}_{ils}m_{s}A_{ij}^{\text{hom}}\unicode[STIX]{x1D700}_{jpt}m_{t}\nonumber\\ \displaystyle & = & \displaystyle 4\unicode[STIX]{x1D70B}^{2}(e_{l}\times m)\cdot A^{\text{hom}}(e_{p}\times m),\quad m\in \mathbb{Z}^{3},l,p=1,2,3,\nonumber\end{eqnarray}$$
where
![]() $e_{j}$
,
$e_{j}$
,
![]() $j=1,2,3$
are the Euclidean basis vectors. Here
$j=1,2,3$
are the Euclidean basis vectors. Here
![]() $\unicode[STIX]{x1D700}$
is the Levi-Civita symbol:
$\unicode[STIX]{x1D700}$
is the Levi-Civita symbol:
 $$\begin{eqnarray}\unicode[STIX]{x1D700}_{jkl}=\left\{\begin{array}{@{}ll@{}}1, & (jkl)=(123),(231),(312),\\ -1, & (jkl)=(132),(321),(213),\\ 0 & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{jkl}=\left\{\begin{array}{@{}ll@{}}1, & (jkl)=(123),(231),(312),\\ -1, & (jkl)=(132),(321),(213),\\ 0 & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
Notice that, for all
![]() $m\in \mathbb{Z}^{3}\setminus \{0\},$
zero is a simple eigenvalue of
$m\in \mathbb{Z}^{3}\setminus \{0\},$
zero is a simple eigenvalue of
![]() ${\mathcal{M}}(m)$
with eigenvector
${\mathcal{M}}(m)$
with eigenvector
![]() $m,$
and since the matrix
$m,$
and since the matrix
![]() $A^{\text{hom}}$
is symmetric and positive definite, the values of
$A^{\text{hom}}$
is symmetric and positive definite, the values of
![]() ${\mathcal{M}}$
are also symmetric and positive definite on vectors
${\mathcal{M}}$
are also symmetric and positive definite on vectors
![]() $\unicode[STIX]{x1D709}$
such that
$\unicode[STIX]{x1D709}$
such that
![]() $\unicode[STIX]{x1D709}\cdot m=0.$
In particular, for all
$\unicode[STIX]{x1D709}\cdot m=0.$
In particular, for all
![]() $m\in \mathbb{Z}^{3},$
one has
$m\in \mathbb{Z}^{3},$
one has
whenever
![]() $\hat{u} (m)$
is a solution to (3.12). Denote
$\hat{u} (m)$
is a solution to (3.12). Denote
![]() $\tilde{m}:=|m|^{-1}m$
and notice that
$\tilde{m}:=|m|^{-1}m$
and notice that
![]() ${\mathcal{M}}(m)=|m|^{2}{\mathcal{M}}(\tilde{m})$
. Further, we denote by
${\mathcal{M}}(m)=|m|^{2}{\mathcal{M}}(\tilde{m})$
. Further, we denote by
![]() $\tilde{e}_{1}(\tilde{m})=(\tilde{e}_{11}(\tilde{m}),\tilde{e}_{12}(\tilde{m}),\tilde{e}_{13}(\tilde{m}))$
and
$\tilde{e}_{1}(\tilde{m})=(\tilde{e}_{11}(\tilde{m}),\tilde{e}_{12}(\tilde{m}),\tilde{e}_{13}(\tilde{m}))$
and
![]() $\tilde{e}_{2}(\tilde{m})=(\tilde{e}_{21}(\tilde{m}),\tilde{e}_{22}(\tilde{m}),\tilde{e}_{23}(\tilde{m}))$
the normalized eigenvectors of the matrix
$\tilde{e}_{2}(\tilde{m})=(\tilde{e}_{21}(\tilde{m}),\tilde{e}_{22}(\tilde{m}),\tilde{e}_{23}(\tilde{m}))$
the normalized eigenvectors of the matrix
![]() ${\mathcal{M}}(\tilde{m})$
corresponding to its two positive eigenvalues
${\mathcal{M}}(\tilde{m})$
corresponding to its two positive eigenvalues
![]() $\unicode[STIX]{x1D706}_{1}(\tilde{m})$
and
$\unicode[STIX]{x1D706}_{1}(\tilde{m})$
and
![]() $\unicode[STIX]{x1D706}_{2}(\tilde{m})$
, respectively.
$\unicode[STIX]{x1D706}_{2}(\tilde{m})$
, respectively.
We write
![]() $\hat{u} (m)$
in terms of the basis
$\hat{u} (m)$
in terms of the basis
![]() $(\tilde{e}_{1}(\tilde{m}),\tilde{e}_{2}(\tilde{m}),\tilde{m}),$
as follows:
$(\tilde{e}_{1}(\tilde{m}),\tilde{e}_{2}(\tilde{m}),\tilde{m}),$
as follows:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\displaystyle \hat{u} (m)=C(\tilde{m})^{\top }\tilde{u} (\tilde{m})+\unicode[STIX]{x1D6FC}(\tilde{m})\tilde{m},\quad \tilde{u} (\tilde{m})\in \mathbb{R}^{2},\unicode[STIX]{x1D6FC}(\tilde{m})\in \mathbb{R},\\ \displaystyle C(\tilde{m})=\left(\begin{array}{@{}ccc@{}}\tilde{e}_{11}(\tilde{m}) & \tilde{e}_{12}(\tilde{m}) & \tilde{e}_{13}(\tilde{m})\\ \tilde{e}_{21}(\tilde{m}) & \tilde{e}_{22}(\tilde{m}) & \tilde{e}_{23}(\tilde{m})\end{array}\right).\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}\displaystyle \hat{u} (m)=C(\tilde{m})^{\top }\tilde{u} (\tilde{m})+\unicode[STIX]{x1D6FC}(\tilde{m})\tilde{m},\quad \tilde{u} (\tilde{m})\in \mathbb{R}^{2},\unicode[STIX]{x1D6FC}(\tilde{m})\in \mathbb{R},\\ \displaystyle C(\tilde{m})=\left(\begin{array}{@{}ccc@{}}\tilde{e}_{11}(\tilde{m}) & \tilde{e}_{12}(\tilde{m}) & \tilde{e}_{13}(\tilde{m})\\ \tilde{e}_{21}(\tilde{m}) & \tilde{e}_{22}(\tilde{m}) & \tilde{e}_{23}(\tilde{m})\end{array}\right).\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
Finding a non-trivial solution to problem (3.12)–(3.13) is equivalent to determining
![]() $(\tilde{u} (\tilde{m}),\unicode[STIX]{x1D6FC}(\tilde{m}))\in \mathbb{R}^{3}\setminus \{0\}$
such that
$(\tilde{u} (\tilde{m}),\unicode[STIX]{x1D6FC}(\tilde{m}))\in \mathbb{R}^{3}\setminus \{0\}$
such that
where
We have thus proved the following statement.
Proposition 3.1. The spectrum of the problem (2.4)–(2.6) is the union of the following sets.
(1) The elements of
 $\{\unicode[STIX]{x1D6FC}^{k}:k\in \mathbb{Z}\}$
such that the corresponding
$\{\unicode[STIX]{x1D6FC}^{k}:k\in \mathbb{Z}\}$
such that the corresponding
 $r^{k}$
has zero mean over
$r^{k}$
has zero mean over
 $Q.$
These are eigenvalues of infinite multiplicity and the corresponding eigenfunctions
$Q.$
These are eigenvalues of infinite multiplicity and the corresponding eigenfunctions
 $H^{0}(x,y)$
are of the form
$H^{0}(x,y)$
are of the form
 $w(x)r^{k}(y)$
for an arbitrary
$w(x)r^{k}(y)$
for an arbitrary
 $w\in L^{2}(\mathbb{T})$
.
$w\in L^{2}(\mathbb{T})$
.(2) The set
 $\{\!\unicode[STIX]{x1D714}^{2}:\exists m\in \mathbb{Z}^{3}$
such that (3.14) holds
$\{\!\unicode[STIX]{x1D714}^{2}:\exists m\in \mathbb{Z}^{3}$
such that (3.14) holds
 $\}$
, with the corresponding eigenfunctions
$\}$
, with the corresponding eigenfunctions
 $H^{0}(x,y)$
of (2.4)–(2.6) having the form
$H^{0}(x,y)$
of (2.4)–(2.6) having the form
 $u(x)+\unicode[STIX]{x1D6FB}_{y}v(x,y)\,+z(x,y)$
, where
$u(x)+\unicode[STIX]{x1D6FB}_{y}v(x,y)\,+z(x,y)$
, where
 $u(x)=\exp (2\unicode[STIX]{x1D70B}\text{i}m\cdot x)\hat{u} (m)$
is an eigenfunction of macroscopic problem (3.8) and that is,
$u(x)=\exp (2\unicode[STIX]{x1D70B}\text{i}m\cdot x)\hat{u} (m)$
is an eigenfunction of macroscopic problem (3.8) and that is, $$\begin{eqnarray}\unicode[STIX]{x1D6FB}_{y}v(x,y)+z(x,y)=\unicode[STIX]{x1D714}^{2}B(y)u(x)\quad \text{a.e. }(x,y)\in \mathbb{T}\times Q,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}_{y}v(x,y)+z(x,y)=\unicode[STIX]{x1D714}^{2}B(y)u(x)\quad \text{a.e. }(x,y)\in \mathbb{T}\times Q,\end{eqnarray}$$
 $H^{0}(x,y)=(I+\unicode[STIX]{x1D714}^{2}B(y))\exp (2\unicode[STIX]{x1D70B}\text{i}m\cdot x)\hat{u} (m)$
.
$H^{0}(x,y)=(I+\unicode[STIX]{x1D714}^{2}B(y))\exp (2\unicode[STIX]{x1D70B}\text{i}m\cdot x)\hat{u} (m)$
.
An immediate consequence of the above analysis is the following result.
Corollary 3.1. If the matrix
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
is negative definite, the value
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
is negative definite, the value
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D714}^{2}$
does not belong to the spectrum of (2.4)–(2.6).
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D714}^{2}$
does not belong to the spectrum of (2.4)–(2.6).
Proof. Since
![]() ${\mathcal{M}}(\tilde{m})$
admits the spectral decomposition
${\mathcal{M}}(\tilde{m})$
admits the spectral decomposition
![]() $C^{\prime }(\tilde{m})\unicode[STIX]{x1D6EC}^{\prime }(\tilde{m})C^{\prime }(\tilde{m})^{\top },$
where
$C^{\prime }(\tilde{m})\unicode[STIX]{x1D6EC}^{\prime }(\tilde{m})C^{\prime }(\tilde{m})^{\top },$
where
 $$\begin{eqnarray}C^{\prime }(\tilde{m}):=\left(\begin{array}{@{}ccc@{}}\tilde{e}_{11}(\tilde{m}) & \tilde{e}_{12}(\tilde{m}) & \tilde{e}_{13}(\tilde{m})\\ \tilde{e}_{21}(\tilde{m}) & \tilde{e}_{22}(\tilde{m}) & \tilde{e}_{23}(\tilde{m})\\ \tilde{m}_{1} & \tilde{m}_{2} & \tilde{m}_{3}\end{array}\right),\qquad \unicode[STIX]{x1D6EC}^{\prime }(\tilde{m}):=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D706}_{1}(\tilde{m}) & 0 & 0\\ 0 & \unicode[STIX]{x1D706}_{2}(\tilde{m}) & 0\\ 0 & 0 & 0\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}C^{\prime }(\tilde{m}):=\left(\begin{array}{@{}ccc@{}}\tilde{e}_{11}(\tilde{m}) & \tilde{e}_{12}(\tilde{m}) & \tilde{e}_{13}(\tilde{m})\\ \tilde{e}_{21}(\tilde{m}) & \tilde{e}_{22}(\tilde{m}) & \tilde{e}_{23}(\tilde{m})\\ \tilde{m}_{1} & \tilde{m}_{2} & \tilde{m}_{3}\end{array}\right),\qquad \unicode[STIX]{x1D6EC}^{\prime }(\tilde{m}):=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D706}_{1}(\tilde{m}) & 0 & 0\\ 0 & \unicode[STIX]{x1D706}_{2}(\tilde{m}) & 0\\ 0 & 0 & 0\end{array}\right),\end{eqnarray}$$
a necessary condition for pairs
![]() $(m,\unicode[STIX]{x1D714})$
such that (3.12) has a solution is as follows:
$(m,\unicode[STIX]{x1D714})$
such that (3.12) has a solution is as follows:
This is not possible since
![]() $\unicode[STIX]{x1D6EC}^{\prime }(\tilde{m})$
is positive semidefinite and, by assumption, the matrix
$\unicode[STIX]{x1D6EC}^{\prime }(\tilde{m})$
is positive semidefinite and, by assumption, the matrix
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
is negative definite, and consequently the matrix
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
is negative definite, and consequently the matrix
![]() $C^{\prime }(\tilde{m})^{\top }\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})C^{\prime }(\tilde{m})$
is also negative definite.◻
$C^{\prime }(\tilde{m})^{\top }\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})C^{\prime }(\tilde{m})$
is also negative definite.◻
3.3 Examples of different admissible wave propagation regimes for the effective spectral problem
In this section we explore the effective wave propagation properties of high-contrast electromagnetic media. We demonstrate that the sign-indefinite nature of the matrix-valued function
![]() $\unicode[STIX]{x1D6E4}$
gives rise to phenomena not present in the case of polarized waves.
$\unicode[STIX]{x1D6E4}$
gives rise to phenomena not present in the case of polarized waves.
Suppose that the inclusion is symmetric under a rotation by
![]() $\unicode[STIX]{x1D70B}$
around at least two of the three coordinate axes. Then the matrices
$\unicode[STIX]{x1D70B}$
around at least two of the three coordinate axes. Then the matrices
![]() $A^{\text{hom}}$
and
$A^{\text{hom}}$
and
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
are diagonal (see Appendix):
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
are diagonal (see Appendix):
![]() $4\unicode[STIX]{x1D70B}^{2}A^{\text{hom}}=\text{diag}(a_{1},a_{2},a_{3}),$
$4\unicode[STIX]{x1D70B}^{2}A^{\text{hom}}=\text{diag}(a_{1},a_{2},a_{3}),$
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})=\text{diag}(\unicode[STIX]{x1D6FD}_{1}(\unicode[STIX]{x1D714}),\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714}),\unicode[STIX]{x1D6FD}_{3}(\unicode[STIX]{x1D714}))$
. Here
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})=\text{diag}(\unicode[STIX]{x1D6FD}_{1}(\unicode[STIX]{x1D714}),\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714}),\unicode[STIX]{x1D6FD}_{3}(\unicode[STIX]{x1D714}))$
. Here
![]() $a_{i}$
,
$a_{i}$
,
![]() $i=1,2,3,$
are positive constants and
$i=1,2,3,$
are positive constants and
![]() $\unicode[STIX]{x1D6FD}_{i}$
,
$\unicode[STIX]{x1D6FD}_{i}$
,
![]() $i=1,2,3,$
are real-valued scalar functions. Notice that, since
$i=1,2,3,$
are real-valued scalar functions. Notice that, since
![]() $|\tilde{m}|=1$
, the eigenvalues
$|\tilde{m}|=1$
, the eigenvalues
![]() $\unicode[STIX]{x1D706}_{1,2}(\tilde{m})$
of
$\unicode[STIX]{x1D706}_{1,2}(\tilde{m})$
of
![]() ${\mathcal{M}}(\tilde{m})$
are the solutions to the quadratic equation
${\mathcal{M}}(\tilde{m})$
are the solutions to the quadratic equation
We will now solve the eigenvalue problem (3.12), equivalently (3.14), for particular examples of such inclusions.
3.3.1 Isotropic propagation (no “weak” band gaps)
If the inclusion
![]() $Q_{0}$
is symmetric by a
$Q_{0}$
is symmetric by a
![]() $\unicode[STIX]{x1D70B}/2$
-rotation around at least two of the three axes, say
$\unicode[STIX]{x1D70B}/2$
-rotation around at least two of the three axes, say
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{2},$
then
$x_{2},$
then
![]() $a=a_{1}=a_{2}=a_{3}$
and
$a=a_{1}=a_{2}=a_{3}$
and
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D6FD}_{1}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D6FD}_{3}(\unicode[STIX]{x1D714})$
. Equation (3.15) takes the form
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D6FD}_{1}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D6FD}_{3}(\unicode[STIX]{x1D714})$
. Equation (3.15) takes the form
![]() $(\unicode[STIX]{x1D706}-a)^{2}=0,$
and therefore
$(\unicode[STIX]{x1D706}-a)^{2}=0,$
and therefore
![]() $\unicode[STIX]{x1D706}_{1}(\tilde{m})=\unicode[STIX]{x1D706}_{2}(\tilde{m})=a$
is an eigenvalue of multiplicity two of
$\unicode[STIX]{x1D706}_{1}(\tilde{m})=\unicode[STIX]{x1D706}_{2}(\tilde{m})=a$
is an eigenvalue of multiplicity two of
![]() ${\mathcal{M}}(\tilde{m}),$
with orthonormal eigenvectors given by
${\mathcal{M}}(\tilde{m}),$
with orthonormal eigenvectors given by
and
As before, the
![]() $e_{j}$
,
$e_{j}$
,
![]() $j=1,2,3,$
are the Euclidean basis vectors. The system (3.14) takes the form
$j=1,2,3,$
are the Euclidean basis vectors. The system (3.14) takes the form
Notice that if
![]() $\unicode[STIX]{x1D714}$
is a zero of
$\unicode[STIX]{x1D714}$
is a zero of
![]() $\unicode[STIX]{x1D6FD}$
then necessarily
$\unicode[STIX]{x1D6FD}$
then necessarily
![]() $\tilde{u} (\tilde{m})$
is the zero vector. For such values of
$\tilde{u} (\tilde{m})$
is the zero vector. For such values of
![]() $\unicode[STIX]{x1D714},$
the above system is satisfied for any
$\unicode[STIX]{x1D714},$
the above system is satisfied for any
![]() $\unicode[STIX]{x1D6FC}(\tilde{m}),$
that is, the non-trivial eigenvectors to (3.12) are parallel to
$\unicode[STIX]{x1D6FC}(\tilde{m}),$
that is, the non-trivial eigenvectors to (3.12) are parallel to
![]() $\tilde{m}$
. On the other hand, if
$\tilde{m}$
. On the other hand, if
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D714})\neq 0$
, then
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D714})\neq 0$
, then
![]() $\unicode[STIX]{x1D6FC}(\tilde{m})=0$
and
$\unicode[STIX]{x1D6FC}(\tilde{m})=0$
and
![]() $\unicode[STIX]{x1D714}$
is an eigenvalue of (3.12) if and only if it solves the equation
$\unicode[STIX]{x1D714}$
is an eigenvalue of (3.12) if and only if it solves the equation
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D714})=a|m|^{2}.$
In this case
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D714})=a|m|^{2}.$
In this case
![]() $\tilde{u} (\tilde{m})$
is an arbitrary element of
$\tilde{u} (\tilde{m})$
is an arbitrary element of
![]() $\mathbb{R}^{2}$
and
$\mathbb{R}^{2}$
and
![]() $\hat{u} (m)=C(\tilde{m})^{\top }\tilde{u} (\tilde{m})$
is an arbitrary vector of the (two-dimensional) eigenspace spanned by the vectors
$\hat{u} (m)=C(\tilde{m})^{\top }\tilde{u} (\tilde{m})$
is an arbitrary vector of the (two-dimensional) eigenspace spanned by the vectors
![]() $\tilde{e}_{1}(\tilde{m})$
and
$\tilde{e}_{1}(\tilde{m})$
and
![]() $\tilde{e}_{2}(\tilde{m}).$
Finally, there are no non-trivial solutions
$\tilde{e}_{2}(\tilde{m}).$
Finally, there are no non-trivial solutions
![]() $\hat{u}$
when
$\hat{u}$
when
![]() $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D714})<0.$
$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D714})<0.$
3.3.2 Directional propagation (existence of “weak” band gaps)
If the inclusion
![]() $Q_{0}$
is symmetric by a
$Q_{0}$
is symmetric by a
![]() $\unicode[STIX]{x1D70B}/2$
-rotation around one of the three coordinate axis, say
$\unicode[STIX]{x1D70B}/2$
-rotation around one of the three coordinate axis, say
![]() $x_{1},$
and by a
$x_{1},$
and by a
![]() $\unicode[STIX]{x1D70B}$
-rotation around another axis, say
$\unicode[STIX]{x1D70B}$
-rotation around another axis, say
![]() $x_{2},$
one has
$x_{2},$
one has
![]() $a=a_{1}$
,
$a=a_{1}$
,
![]() $b=a_{2}=a_{3}$
and
$b=a_{2}=a_{3}$
and
![]() $\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D6FD}_{3}(\unicode[STIX]{x1D714})$
. Here, recalling
$\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D6FD}_{3}(\unicode[STIX]{x1D714})$
. Here, recalling
![]() $|\tilde{m}|=1$
, (3.15) takes the form
$|\tilde{m}|=1$
, (3.15) takes the form
whence
![]() $\unicode[STIX]{x1D706}_{1}(\tilde{m})=a(1-\tilde{m}_{1}^{2})+b\tilde{m}_{1}^{2}$
,
$\unicode[STIX]{x1D706}_{1}(\tilde{m})=a(1-\tilde{m}_{1}^{2})+b\tilde{m}_{1}^{2}$
,
![]() $\unicode[STIX]{x1D706}_{2}(\tilde{m})=b$
. There are now two separate cases to consider.
$\unicode[STIX]{x1D706}_{2}(\tilde{m})=b$
. There are now two separate cases to consider.
Case 1. Assume that
![]() $|\tilde{m}_{1}|=1$
, that is, the vector
$|\tilde{m}_{1}|=1$
, that is, the vector
![]() $\tilde{m}$
is parallel to the axis of higher symmetry. Here,
$\tilde{m}$
is parallel to the axis of higher symmetry. Here,
![]() ${\mathcal{M}}(\tilde{m})=\text{diag}(0,b,b)$
and
${\mathcal{M}}(\tilde{m})=\text{diag}(0,b,b)$
and
![]() $b$
is an eigenvalue of multiplicity two with the eigenspace spanned by the vectors (3.16). The system (3.14) takes the form
$b$
is an eigenvalue of multiplicity two with the eigenspace spanned by the vectors (3.16). The system (3.14) takes the form
Here, if
![]() $\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714})<0,$
then necessarily
$\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714})<0,$
then necessarily
![]() $\tilde{u} (\tilde{m})=0$
and non-trivial solutions
$\tilde{u} (\tilde{m})=0$
and non-trivial solutions
![]() $\hat{u} (m)=\unicode[STIX]{x1D6FC}(\tilde{m})\tilde{m}$
exist if and only if
$\hat{u} (m)=\unicode[STIX]{x1D6FC}(\tilde{m})\tilde{m}$
exist if and only if
![]() $\unicode[STIX]{x1D6FD}_{1}(\unicode[STIX]{x1D714})=0.$
On the other hand, if
$\unicode[STIX]{x1D6FD}_{1}(\unicode[STIX]{x1D714})=0.$
On the other hand, if
![]() $\unicode[STIX]{x1D6FD}_{1}(\unicode[STIX]{x1D714})<0,$
then necessarily
$\unicode[STIX]{x1D6FD}_{1}(\unicode[STIX]{x1D714})<0,$
then necessarily
![]() $\unicode[STIX]{x1D6FC}(\tilde{m})=0$
and non-trivial solutions
$\unicode[STIX]{x1D6FC}(\tilde{m})=0$
and non-trivial solutions
![]() $\hat{u} (m)=C(\tilde{m})^{\top }\tilde{u} (\tilde{m})$
exist if and only if
$\hat{u} (m)=C(\tilde{m})^{\top }\tilde{u} (\tilde{m})$
exist if and only if
![]() $\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714})>0.$
The first situation only occurs at a discrete set of values
$\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714})>0.$
The first situation only occurs at a discrete set of values
![]() $\unicode[STIX]{x1D714},$
while, unlike in the isotropic case, the second situation can give rise to intervals each of which contains a sequence of admissible
$\unicode[STIX]{x1D714},$
while, unlike in the isotropic case, the second situation can give rise to intervals each of which contains a sequence of admissible
![]() $\unicode[STIX]{x1D714},$
obtained from the condition
$\unicode[STIX]{x1D714},$
obtained from the condition
![]() $\sqrt{\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714})/b}\in \mathbb{N},$
with a reduced number of eigenmodes. In the case of the full-space problem these intervals form part of the continuous spectrum of the problem with a reduced number of propagating modes (“weak band gaps”; cf. [Reference Smyshlyaev7, Reference Zhikov and Pastukhova9, Reference Zhikov and Pastukhova10]).
$\sqrt{\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714})/b}\in \mathbb{N},$
with a reduced number of eigenmodes. In the case of the full-space problem these intervals form part of the continuous spectrum of the problem with a reduced number of propagating modes (“weak band gaps”; cf. [Reference Smyshlyaev7, Reference Zhikov and Pastukhova9, Reference Zhikov and Pastukhova10]).
Case 2. Assume
![]() $|\tilde{m}_{1}|<1,$
that is, the vector
$|\tilde{m}_{1}|<1,$
that is, the vector
![]() $\tilde{m}$
is not parallel to the axis of higher symmetry. In this case the eigenvectors corresponding to
$\tilde{m}$
is not parallel to the axis of higher symmetry. In this case the eigenvectors corresponding to
![]() $\unicode[STIX]{x1D706}_{1}(\tilde{m}),$
$\unicode[STIX]{x1D706}_{1}(\tilde{m}),$
![]() $\unicode[STIX]{x1D706}_{2}(\tilde{m})$
are given by
$\unicode[STIX]{x1D706}_{2}(\tilde{m})$
are given by
![]() $\tilde{e}_{1}(\tilde{m}),$
$\tilde{e}_{1}(\tilde{m}),$
![]() $\tilde{e}_{2}(\tilde{m})$
in (3.17). By setting
$\tilde{e}_{2}(\tilde{m})$
in (3.17). By setting
it is easy to see that the system (3.14) takes the form

If
![]() $\tilde{m}_{1}=0$
, that is, the vector
$\tilde{m}_{1}=0$
, that is, the vector
![]() $\tilde{m}$
is perpendicular to the direction of higher symmetry, then the system (3.18) fully decouples and reduces to
$\tilde{m}$
is perpendicular to the direction of higher symmetry, then the system (3.18) fully decouples and reduces to
Suppose
![]() $\unicode[STIX]{x1D6FD}_{1}(\unicode[STIX]{x1D714})$
(respectively,
$\unicode[STIX]{x1D6FD}_{1}(\unicode[STIX]{x1D714})$
(respectively,
![]() $\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714})$
) is negative for some
$\unicode[STIX]{x1D6FD}_{2}(\unicode[STIX]{x1D714})$
) is negative for some
![]() $\unicode[STIX]{x1D714}$
. Then the above system implies that
$\unicode[STIX]{x1D714}$
. Then the above system implies that
![]() $\tilde{u} _{2}(\tilde{m})=0$
(respectively,
$\tilde{u} _{2}(\tilde{m})=0$
(respectively,
![]() $\tilde{u} _{1}(\tilde{m})=0$
). In this case, we see that propagation is restricted solely to the direction of
$\tilde{u} _{1}(\tilde{m})=0$
). In this case, we see that propagation is restricted solely to the direction of
![]() $\tilde{e}_{1}(\tilde{m})$
(respectively,
$\tilde{e}_{1}(\tilde{m})$
(respectively,
![]() $\tilde{e}_{2}(\tilde{m})$
), which is orthogonal to the eigenvector(s) corresponding to the negative eigenvalue of
$\tilde{e}_{2}(\tilde{m})$
), which is orthogonal to the eigenvector(s) corresponding to the negative eigenvalue of
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
. In both situations weak band gaps are present in the similar full-space problem.
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
. In both situations weak band gaps are present in the similar full-space problem.
Remark 3.1. Recently there have been several works on the analysis of problems with “partial” or “directional” wave propagation in the context of elasticity, where at some frequencies, propagation occurs for some but not for all values of the wave vector: the analysis of the vector problems for thin structures of critical thickness [Reference Zhikov and Pastukhova9], the analysis of high-contrast [Reference Zhikov and Pastukhova10], and partially high-contrast [Reference Smyshlyaev7] periodic elastic composites. To our knowledge, the effect we describe here is the first example of a similar kind for Maxwell equations.
Remark 3.2. When the “size”
![]() $T$
of the domain
$T$
of the domain
![]() $\mathbb{T}$
increases to infinity (equivalently, for a given macroscopic domain, the parameter by which its size is scaled (see §2) tends to zero), the spectrum of (2.4)–(2.6) converges to a union of intervals (“bands”) separated by intervals of those values
$\mathbb{T}$
increases to infinity (equivalently, for a given macroscopic domain, the parameter by which its size is scaled (see §2) tends to zero), the spectrum of (2.4)–(2.6) converges to a union of intervals (“bands”) separated by intervals of those values
![]() $\unicode[STIX]{x1D714}^{2}$
for which the matrix
$\unicode[STIX]{x1D714}^{2}$
for which the matrix
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
is negative definite (“gaps” or “lacunae”). As above, we say that
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
is negative definite (“gaps” or “lacunae”). As above, we say that
![]() $\unicode[STIX]{x1D714}^{2}$
belongs to a weak band gap (in the spectrum of (2.4)–(2.6)) if at least one eigenvalue of
$\unicode[STIX]{x1D714}^{2}$
belongs to a weak band gap (in the spectrum of (2.4)–(2.6)) if at least one eigenvalue of
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
is positive semidefinite and at least one eigenvalue of
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
is positive semidefinite and at least one eigenvalue of
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
is negative.
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
is negative.
4 Two-scale asymptotic expansion of the eigenfunctions
Here we give the details of the recurrent procedure for the construction of the series (2.2). We use
![]() $|_{+}$
and
$|_{+}$
and
![]() $|_{-}$
to denote the limit values of the expressions to which these symbols are attached, on the outside and on the inside of the boundary of the inclusion
$|_{-}$
to denote the limit values of the expressions to which these symbols are attached, on the outside and on the inside of the boundary of the inclusion
![]() $Q_{0}$
, respectively.
$Q_{0}$
, respectively.
Substituting the expansions (2.2) into (2.1) and equating coefficients on
![]() $\unicode[STIX]{x1D702}^{-2},\unicode[STIX]{x1D702}^{-1}$
and
$\unicode[STIX]{x1D702}^{-2},\unicode[STIX]{x1D702}^{-1}$
and
![]() $\unicode[STIX]{x1D702}^{0},$
we arrive at the following sets of equations, where
$\unicode[STIX]{x1D702}^{0},$
we arrive at the following sets of equations, where
![]() $x\in \mathbb{T}$
is a parameter:
$x\in \mathbb{T}$
is a parameter:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{curl}_{y}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y))\nonumber\\ \displaystyle & & \displaystyle \quad =-(\text{curl}_{y}\,\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}+\text{curl}_{x}\,\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y})H^{1}(x,y)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\text{curl}_{x}\,\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{0}(x,y)+\unicode[STIX]{x1D714}^{2}H^{0}(x,y),\quad y\in Q_{1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{curl}_{y}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y))\nonumber\\ \displaystyle & & \displaystyle \quad =-(\text{curl}_{y}\,\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}+\text{curl}_{x}\,\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y})H^{1}(x,y)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\text{curl}_{x}\,\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{0}(x,y)+\unicode[STIX]{x1D714}^{2}H^{0}(x,y),\quad y\in Q_{1},\end{eqnarray}$$
and
Multiplying equation (4.1) by
![]() $H^{0}$
, integrating by parts over
$H^{0}$
, integrating by parts over
![]() $Q_{1}$
and using (4.2) shows that
$Q_{1}$
and using (4.2) shows that
![]() $\text{curl}_{y}\,H^{0}(x,y)=0$
,
$\text{curl}_{y}\,H^{0}(x,y)=0$
,
![]() $y\in Q_{1}.$
More precisely, for all
$y\in Q_{1}.$
More precisely, for all
![]() $x\in \mathbb{T}$
, we seek
$x\in \mathbb{T}$
, we seek
![]() $H^{0}(x,\cdot )$
from the space
$H^{0}(x,\cdot )$
from the space
![]() $V$
; see (2.8). Before proceeding, we recall a characterization of the space
$V$
; see (2.8). Before proceeding, we recall a characterization of the space
![]() $V$
(see [Reference Cherednichenko and Cooper1]) that proves useful in the analysis of the term
$V$
(see [Reference Cherednichenko and Cooper1]) that proves useful in the analysis of the term
![]() $H^{0}$
.
$H^{0}$
.
Lemma 4.1 (Characterization of
 $V$
).
$V$
).
A function
![]() $v\in [H_{\#}^{1}(Q)]^{3}$
is an element of the space
$v\in [H_{\#}^{1}(Q)]^{3}$
is an element of the space
![]() $V$
if and only if
$V$
if and only if
for some
![]() $a\in \mathbb{R}^{3}$
,
$a\in \mathbb{R}^{3}$
,
![]() $b\in H_{\#}^{2}(Q)$
,
$b\in H_{\#}^{2}(Q)$
,
![]() $c\in [H_{0}^{1}(Q_{0})]^{3}$
.
$c\in [H_{0}^{1}(Q_{0})]^{3}$
.
Taking into account, via Lemma 4.1, that the leading-order term
![]() $H^{0}$
is of the form
$H^{0}$
is of the form
and substituting (4.9) into equations (4.3)–(4.4), we find that the coefficient
![]() $H^{1}$
has the representation
$H^{1}$
has the representation
![]() $H^{1}(x,y)=N(y)\,\text{curl}\,u(x)+\widetilde{H}^{1}(x,y),$
up to the addition of an element of
$H^{1}(x,y)=N(y)\,\text{curl}\,u(x)+\widetilde{H}^{1}(x,y),$
up to the addition of an element of
![]() $V$
. Here the term
$V$
. Here the term
![]() $\widetilde{H}^{1}(x,y)$
satisfies
$\widetilde{H}^{1}(x,y)$
satisfies
and
![]() $N=N(y)$
is a
$N=N(y)$
is a
![]() $Q$
-periodic matrix-valued function whose columns
$Q$
-periodic matrix-valued function whose columns
![]() $N^{r}=N^{r}(y)$
,
$N^{r}=N^{r}(y)$
,
![]() $r=1,2,3,$
are solutions to the problems
$r=1,2,3,$
are solutions to the problems
where
![]() $e^{r}$
is the
$e^{r}$
is the
![]() $r$
th Euclidean basis vector. It is shown [Reference Cooper4, Reference Kamotski and Smyshlyaev6] that (4.12) admits a unique solution in
$r$
th Euclidean basis vector. It is shown [Reference Cooper4, Reference Kamotski and Smyshlyaev6] that (4.12) admits a unique solution in
![]() $V^{\bot },$
the orthogonal complement to
$V^{\bot },$
the orthogonal complement to
![]() $V$
in the space
$V$
in the space
![]() $[H_{\#}^{1}(Q)]^{3}.$
$[H_{\#}^{1}(Q)]^{3}.$
Looking for
![]() $H^{1}(x,\cdot )\in [H_{\#}^{1}(Q)]^{3}$
and taking into account the identity
$H^{1}(x,\cdot )\in [H_{\#}^{1}(Q)]^{3}$
and taking into account the identity
![]() $\text{curl}_{x}\unicode[STIX]{x1D6FB}_{y}=-\text{curl}_{y}\unicode[STIX]{x1D6FB}_{x}$
together with (4.10)–(4.11), we infer that for all
$\text{curl}_{x}\unicode[STIX]{x1D6FB}_{y}=-\text{curl}_{y}\unicode[STIX]{x1D6FB}_{x}$
together with (4.10)–(4.11), we infer that for all
![]() $x\in \mathbb{T}$
the function
$x\in \mathbb{T}$
the function
![]() $h(x,\cdot ):=\widetilde{H}^{1}(x,\cdot )-\unicode[STIX]{x1D6FB}_{x}v(x,\cdot )$
is a solution in
$h(x,\cdot ):=\widetilde{H}^{1}(x,\cdot )-\unicode[STIX]{x1D6FB}_{x}v(x,\cdot )$
is a solution in
![]() $[H_{\#}^{1}(Q)]^{3}$
to
$[H_{\#}^{1}(Q)]^{3}$
to
In particular, the function
![]() $h$
belongs to the space
$h$
belongs to the space
![]() $V$
. Therefore, one has
$V$
. Therefore, one has
up to the addition of an element of
![]() $V$
. (As we discuss in Remark 5.1 below, one can specify the divergence
$V$
. (As we discuss in Remark 5.1 below, one can specify the divergence
![]() $\text{div}_{y}H^{1}(x,y).$
This, along with the condition that the
$\text{div}_{y}H^{1}(x,y).$
This, along with the condition that the
![]() $y$
-average of
$y$
-average of
![]() $H^{1}$
vanishes, defines this additional element of
$H^{1}$
vanishes, defines this additional element of
![]() $V$
in a unique way.)
$V$
in a unique way.)
Further, multiplying equation (4.5) by an arbitrary test function
![]() $\unicode[STIX]{x1D719}\in V$
and integrating over
$\unicode[STIX]{x1D719}\in V$
and integrating over
![]() $Q_{1}$
yields
$Q_{1}$
yields
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q_{1}}\text{curl}_{y}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y))\cdot \unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q_{1}}\unicode[STIX]{x1D714}^{2}H^{0}(x,y)\cdot \unicode[STIX]{x1D719}(y)\,dy-\int _{Q_{1}}\text{curl}_{y}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{1}(x,y))\cdot \unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\biggl(\int _{Q_{1}}\text{curl}_{x}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{0}(x,y))\cdot \unicode[STIX]{x1D719}(y)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\text{curl}_{x}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{1}(x,y))\cdot \unicode[STIX]{x1D719}(y)\,dy\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q_{1}}\text{curl}_{y}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y))\cdot \unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q_{1}}\unicode[STIX]{x1D714}^{2}H^{0}(x,y)\cdot \unicode[STIX]{x1D719}(y)\,dy-\int _{Q_{1}}\text{curl}_{y}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{1}(x,y))\cdot \unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\biggl(\int _{Q_{1}}\text{curl}_{x}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{0}(x,y))\cdot \unicode[STIX]{x1D719}(y)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\text{curl}_{x}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{1}(x,y))\cdot \unicode[STIX]{x1D719}(y)\,dy\biggr).\end{eqnarray}$$
We integrate in the left-hand side of (4.14) by parts to determine that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q_{1}}\text{curl}_{y}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y))\cdot \unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\unicode[STIX]{x2202}Q_{0}}\unicode[STIX]{x1D716}_{1}^{-1}(y)(\text{curl}_{y}\,H^{2}(x,y)\times n(y)|_{+})\cdot \unicode[STIX]{x1D719}(y)\,dS(y).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q_{1}}\text{curl}_{y}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y))\cdot \unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\unicode[STIX]{x2202}Q_{0}}\unicode[STIX]{x1D716}_{1}^{-1}(y)(\text{curl}_{y}\,H^{2}(x,y)\times n(y)|_{+})\cdot \unicode[STIX]{x1D719}(y)\,dS(y).\end{eqnarray}$$
Now we perform integration by parts on the individual terms on the right-hand side of (4.14).
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\int _{Q_{1}}\text{curl}_{y}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{1}(x,y))\unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{\unicode[STIX]{x2202}Q_{0}}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{1}(x,y)\times n(y)|_{+})\cdot \unicode[STIX]{x1D719}(y)\,dS(y)\nonumber\\ \displaystyle & & \displaystyle \,\quad \overset{\text{by (4.6)}}{=}\int _{\unicode[STIX]{x2202}Q_{0}}\{(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y)\times n(y)|_{+})\cdot \unicode[STIX]{x1D719}(y)\nonumber\\ \displaystyle & & \displaystyle \quad \qquad -\,(\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{y}\,H^{0}(x,y)\times n(y)|_{-})\cdot \unicode[STIX]{x1D719}(y)\!\}\,dS(y)\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{\unicode[STIX]{x2202}Q_{0}}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y)\times n(y)|_{+})\cdot \unicode[STIX]{x1D719}(y)\,dS(y)\nonumber\\ \displaystyle & & \displaystyle \quad \qquad +\,\int _{Q_{0}}\text{curl}_{y}(\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{y}\,H^{0}(x,y))\cdot \unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad \qquad -\,\int _{Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{y}\,H^{0}(x,y)\cdot \text{curl}_{y}\,\unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \,\quad \overset{\text{by (4.7)}}{=}\int _{\unicode[STIX]{x2202}Q_{0}}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y)\times n(y)|_{+})\cdot \unicode[STIX]{x1D719}(y)\,dS(y)\nonumber\\ \displaystyle & & \displaystyle \quad \qquad +\,\int _{Q_{0}}\unicode[STIX]{x1D714}^{2}H^{0}(x,y)\cdot \unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad \qquad -\,\int _{Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{y}\,H^{0}(x,y)\cdot \text{curl}_{y}\,\unicode[STIX]{x1D719}(y)\,dy.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\int _{Q_{1}}\text{curl}_{y}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{1}(x,y))\unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \qquad =-\int _{\unicode[STIX]{x2202}Q_{0}}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{1}(x,y)\times n(y)|_{+})\cdot \unicode[STIX]{x1D719}(y)\,dS(y)\nonumber\\ \displaystyle & & \displaystyle \,\quad \overset{\text{by (4.6)}}{=}\int _{\unicode[STIX]{x2202}Q_{0}}\{(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y)\times n(y)|_{+})\cdot \unicode[STIX]{x1D719}(y)\nonumber\\ \displaystyle & & \displaystyle \quad \qquad -\,(\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{y}\,H^{0}(x,y)\times n(y)|_{-})\cdot \unicode[STIX]{x1D719}(y)\!\}\,dS(y)\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{\unicode[STIX]{x2202}Q_{0}}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y)\times n(y)|_{+})\cdot \unicode[STIX]{x1D719}(y)\,dS(y)\nonumber\\ \displaystyle & & \displaystyle \quad \qquad +\,\int _{Q_{0}}\text{curl}_{y}(\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{y}\,H^{0}(x,y))\cdot \unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad \qquad -\,\int _{Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{y}\,H^{0}(x,y)\cdot \text{curl}_{y}\,\unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \,\quad \overset{\text{by (4.7)}}{=}\int _{\unicode[STIX]{x2202}Q_{0}}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y)\times n(y)|_{+})\cdot \unicode[STIX]{x1D719}(y)\,dS(y)\nonumber\\ \displaystyle & & \displaystyle \quad \qquad +\,\int _{Q_{0}}\unicode[STIX]{x1D714}^{2}H^{0}(x,y)\cdot \unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad \qquad -\,\int _{Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{y}\,H^{0}(x,y)\cdot \text{curl}_{y}\,\unicode[STIX]{x1D719}(y)\,dy.\end{eqnarray}$$
Taking into account the representations (4.9) and (4.13), we find that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q_{1}}\{\!\text{curl}_{x}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{0}(x,y))\cdot \unicode[STIX]{x1D719}(y)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\text{curl}_{x}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{1}(x,y))\cdot \unicode[STIX]{x1D719}(y)\!\}\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q_{1}}\text{curl}_{x}\!\{\!\unicode[STIX]{x1D716}_{1}^{-1}(y)(\,(I+\text{curl}\,N(y))\,\text{curl}_{x}\,u(x)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\text{curl}_{x}\unicode[STIX]{x1D6FB}_{y}v(x,y)+\text{curl}_{y}\unicode[STIX]{x1D6FB}_{x}v(x,y))\!\}\cdot \,\unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q_{1}}\text{curl}_{x}\{\unicode[STIX]{x1D716}_{1}^{-1}(y)(I+\text{curl}\,N(y))\,\text{curl}_{x}\,u(x)\}\cdot \unicode[STIX]{x1D719}(y)\,dy,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q_{1}}\{\!\text{curl}_{x}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{0}(x,y))\cdot \unicode[STIX]{x1D719}(y)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\text{curl}_{x}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{1}(x,y))\cdot \unicode[STIX]{x1D719}(y)\!\}\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q_{1}}\text{curl}_{x}\!\{\!\unicode[STIX]{x1D716}_{1}^{-1}(y)(\,(I+\text{curl}\,N(y))\,\text{curl}_{x}\,u(x)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\text{curl}_{x}\unicode[STIX]{x1D6FB}_{y}v(x,y)+\text{curl}_{y}\unicode[STIX]{x1D6FB}_{x}v(x,y))\!\}\cdot \,\unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q_{1}}\text{curl}_{x}\{\unicode[STIX]{x1D716}_{1}^{-1}(y)(I+\text{curl}\,N(y))\,\text{curl}_{x}\,u(x)\}\cdot \unicode[STIX]{x1D719}(y)\,dy,\end{eqnarray}$$
where we again make use of the identity
![]() $\text{curl}_{x}\unicode[STIX]{x1D6FB}_{y}=-\text{curl}_{y}\unicode[STIX]{x1D6FB}_{x}.$
Finally, equations (4.14)–(4.17) imply
$\text{curl}_{x}\unicode[STIX]{x1D6FB}_{y}=-\text{curl}_{y}\unicode[STIX]{x1D6FB}_{x}.$
Finally, equations (4.14)–(4.17) imply
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q_{1}}\text{curl}_{x}\{\unicode[STIX]{x1D716}_{1}^{-1}(y)(I+\text{curl}\,N(y))\,\text{curl}_{x}\,u(x)\}\cdot \unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{y}H^{0}(x,y)\cdot \text{curl}_{y}\,\unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q}\unicode[STIX]{x1D714}^{2}H^{0}(x,y)\cdot \unicode[STIX]{x1D719}(y)\,dy\quad \text{for all }\unicode[STIX]{x1D719}\in V.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q_{1}}\text{curl}_{x}\{\unicode[STIX]{x1D716}_{1}^{-1}(y)(I+\text{curl}\,N(y))\,\text{curl}_{x}\,u(x)\}\cdot \unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{y}H^{0}(x,y)\cdot \text{curl}_{y}\,\unicode[STIX]{x1D719}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q}\unicode[STIX]{x1D714}^{2}H^{0}(x,y)\cdot \unicode[STIX]{x1D719}(y)\,dy\quad \text{for all }\unicode[STIX]{x1D719}\in V.\end{eqnarray}$$
In what follows we derive the system (2.4)–(2.6) by considering different choices of the test function
![]() $\unicode[STIX]{x1D719}$
in the identity (4.18).
$\unicode[STIX]{x1D719}$
in the identity (4.18).
Step 1. Choosing test functions
![]() $\unicode[STIX]{x1D719}\in [C_{0}^{\infty }(Q_{0})]^{3}$
in (4.18), we find that
$\unicode[STIX]{x1D719}\in [C_{0}^{\infty }(Q_{0})]^{3}$
in (4.18), we find that
Using the representation (4.9) and the identity
![]() $\text{curl}_{y}\unicode[STIX]{x1D6FB}_{y}=0$
, we arrive at (2.6).
$\text{curl}_{y}\unicode[STIX]{x1D6FB}_{y}=0$
, we arrive at (2.6).
Step 2. Choosing
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D6FB}_{y}\unicode[STIX]{x1D713}$
in (4.18), performing integration by parts, using the identity
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D6FB}_{y}\unicode[STIX]{x1D713}$
in (4.18), performing integration by parts, using the identity
![]() $\text{div}_{y}\,\text{curl}_{x}=-\text{div}_{x}\,\text{curl}_{y}$
and recalling (4.12) gives
$\text{div}_{y}\,\text{curl}_{x}=-\text{div}_{x}\,\text{curl}_{y}$
and recalling (4.12) gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q}\unicode[STIX]{x1D714}^{2}H^{0}(x,y)\cdot \unicode[STIX]{x1D6FB}_{y}\unicode[STIX]{x1D713}\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q_{1}}\text{curl}_{x}\{\unicode[STIX]{x1D716}_{1}^{-1}(y)(I+\text{curl}\,N(y))\,\text{curl}_{x}\,u(x)\}\cdot \unicode[STIX]{x1D6FB}_{y}\unicode[STIX]{x1D713}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =-\int _{Q_{1}}\text{div}_{y}\,\text{curl}_{x}\{\unicode[STIX]{x1D716}_{1}^{-1}(y)(I+\text{curl}\,N(y))\,\text{curl}_{x}\,u(x)\}\cdot \unicode[STIX]{x1D713}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q_{1}}\text{div}_{x}\,\text{curl}_{y}\{\unicode[STIX]{x1D716}_{1}^{-1}(y)(I+\text{curl}\,N(y))\,\text{curl}_{x}\,u(x)\}\cdot \unicode[STIX]{x1D713}(y)\,dy=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q}\unicode[STIX]{x1D714}^{2}H^{0}(x,y)\cdot \unicode[STIX]{x1D6FB}_{y}\unicode[STIX]{x1D713}\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q_{1}}\text{curl}_{x}\{\unicode[STIX]{x1D716}_{1}^{-1}(y)(I+\text{curl}\,N(y))\,\text{curl}_{x}\,u(x)\}\cdot \unicode[STIX]{x1D6FB}_{y}\unicode[STIX]{x1D713}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =-\int _{Q_{1}}\text{div}_{y}\,\text{curl}_{x}\{\unicode[STIX]{x1D716}_{1}^{-1}(y)(I+\text{curl}\,N(y))\,\text{curl}_{x}\,u(x)\}\cdot \unicode[STIX]{x1D713}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q_{1}}\text{div}_{x}\,\text{curl}_{y}\{\unicode[STIX]{x1D716}_{1}^{-1}(y)(I+\text{curl}\,N(y))\,\text{curl}_{x}\,u(x)\}\cdot \unicode[STIX]{x1D713}(y)\,dy=0.\nonumber\end{eqnarray}$$
Therefore, we deduce that
and, taking into account (4.9), we obtain the equation (2.5).
Step 3. Choosing
![]() $\unicode[STIX]{x1D719}(y)\equiv 1$
in the identity (4.18), we find, using the representation (4.9) once more, that (2.4) holds, where the matrix
$\unicode[STIX]{x1D719}(y)\equiv 1$
in the identity (4.18), we find, using the representation (4.9) once more, that (2.4) holds, where the matrix
![]() $A^{\text{hom}}$
emerges as the result of integrating the expression
$A^{\text{hom}}$
emerges as the result of integrating the expression
![]() $\unicode[STIX]{x1D716}_{1}^{-1}(y)(\text{curl}\,N(y)+I)$
with respect to
$\unicode[STIX]{x1D716}_{1}^{-1}(y)(\text{curl}\,N(y)+I)$
with respect to
![]() $y\in Q_{1}.$
$y\in Q_{1}.$
In the next section we use the above formal construction of the series (2.2) to justify the two claims of Theorem 2.1.
5 Proof of Theorem 2.1
For each
![]() $\unicode[STIX]{x1D702}>0,$
denote by
$\unicode[STIX]{x1D702}>0,$
denote by
![]() ${\mathcal{A}}_{\unicode[STIX]{x1D702}}$
the operator in the spaceFootnote
5
${\mathcal{A}}_{\unicode[STIX]{x1D702}}$
the operator in the spaceFootnote
5
![]() $L_{\#\text{sol}}^{2}(\mathbb{T})$
defined in a standard way by the bilinear form (cf. (2.1))
$L_{\#\text{sol}}^{2}(\mathbb{T})$
defined in a standard way by the bilinear form (cf. (2.1))
For fixed
![]() $\unicode[STIX]{x1D714}$
in the spectrum of (2.4)–(2.6), let
$\unicode[STIX]{x1D714}$
in the spectrum of (2.4)–(2.6), let
![]() $H^{0}$
be a corresponding eigenfunction. Consider the (unique) solution
$H^{0}$
be a corresponding eigenfunction. Consider the (unique) solution
![]() $\widetilde{H}^{\unicode[STIX]{x1D702}}\in {\mathcal{H}}$
to the problem
$\widetilde{H}^{\unicode[STIX]{x1D702}}\in {\mathcal{H}}$
to the problem
Denote also
and (cf. (2.2))
where
![]() $H^{j}$
,
$H^{j}$
,
![]() $j=1,2,$
are solutions of the system of recurrence relations described in §4. The existence of solutions
$j=1,2,$
are solutions of the system of recurrence relations described in §4. The existence of solutions
![]() $H^{1}$
,
$H^{1}$
,
![]() $H^{2}$
is guaranteed by a result established in [Reference Cherednichenko and Cooper1, Lemma 3.4]. As these solutions are unique up to the addition of an element from
$H^{2}$
is guaranteed by a result established in [Reference Cherednichenko and Cooper1, Lemma 3.4]. As these solutions are unique up to the addition of an element from
![]() $V$
, we shall choose them as in Remark 5.1.
$V$
, we shall choose them as in Remark 5.1.
Proposition 5.1. There exists a constant
![]() $\widehat{C}>0$
such that the estimate
$\widehat{C}>0$
such that the estimate
holds for all
![]() $\unicode[STIX]{x1D711}\in [H_{\#}^{1}(\mathbb{T})]^{3}.$
$\unicode[STIX]{x1D711}\in [H_{\#}^{1}(\mathbb{T})]^{3}.$
Proof. Using the definition of the function
![]() $\widetilde{H}^{\unicode[STIX]{x1D702}}$
and the recurrence relations (4.1)–(4.8) yields
$\widetilde{H}^{\unicode[STIX]{x1D702}}$
and the recurrence relations (4.1)–(4.8) yields
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathfrak{b}_{\unicode[STIX]{x1D702}}(\widetilde{H}^{\unicode[STIX]{x1D702}}-H^{(2)}(\cdot ,\unicode[STIX]{x1D702}),\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\mathbb{T}}\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D702}}^{-1}\biggl(\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)\text{curl}\,\widetilde{H}^{\unicode[STIX]{x1D702}}\cdot \text{curl}\,\unicode[STIX]{x1D711}+\int _{\mathbb{T}}\widetilde{H}^{\unicode[STIX]{x1D702}}\cdot \unicode[STIX]{x1D711}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\int _{\mathbb{T}}\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D702}}^{-1}\biggl(\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)\,\text{curl}\biggl(H^{0}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)+\unicode[STIX]{x1D702}H^{1}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)+\unicode[STIX]{x1D702}^{2}H^{2}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)\biggr)\cdot \text{curl}\,\unicode[STIX]{x1D711}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\int _{\mathbb{T}}\biggl(H^{0}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)+\unicode[STIX]{x1D702}H^{1}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)+\unicode[STIX]{x1D702}^{2}H^{2}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)\biggr)\cdot \unicode[STIX]{x1D711}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\mathbb{T}}F^{1}(\cdot ,\unicode[STIX]{x1D702})\cdot \unicode[STIX]{x1D711}+\int _{\mathbb{T}}F^{2}(\cdot ,\unicode[STIX]{x1D702})\cdot \unicode[STIX]{x1D702}\,\text{curl}_{}\unicode[STIX]{x1D711}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathfrak{b}_{\unicode[STIX]{x1D702}}(\widetilde{H}^{\unicode[STIX]{x1D702}}-H^{(2)}(\cdot ,\unicode[STIX]{x1D702}),\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\mathbb{T}}\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D702}}^{-1}\biggl(\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)\text{curl}\,\widetilde{H}^{\unicode[STIX]{x1D702}}\cdot \text{curl}\,\unicode[STIX]{x1D711}+\int _{\mathbb{T}}\widetilde{H}^{\unicode[STIX]{x1D702}}\cdot \unicode[STIX]{x1D711}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\int _{\mathbb{T}}\unicode[STIX]{x1D700}_{\unicode[STIX]{x1D702}}^{-1}\biggl(\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)\,\text{curl}\biggl(H^{0}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)+\unicode[STIX]{x1D702}H^{1}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)+\unicode[STIX]{x1D702}^{2}H^{2}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)\biggr)\cdot \text{curl}\,\unicode[STIX]{x1D711}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\int _{\mathbb{T}}\biggl(H^{0}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)+\unicode[STIX]{x1D702}H^{1}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)+\unicode[STIX]{x1D702}^{2}H^{2}\biggl(\cdot ,\frac{\cdot }{\unicode[STIX]{x1D702}}\biggr)\biggr)\cdot \unicode[STIX]{x1D711}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\mathbb{T}}F^{1}(\cdot ,\unicode[STIX]{x1D702})\cdot \unicode[STIX]{x1D711}+\int _{\mathbb{T}}F^{2}(\cdot ,\unicode[STIX]{x1D702})\cdot \unicode[STIX]{x1D702}\,\text{curl}_{}\unicode[STIX]{x1D711}.\end{eqnarray}$$
Here,
![]() $F^{1},F^{2}$
are elements of
$F^{1},F^{2}$
are elements of
![]() $L^{2}(\mathbb{T})$
defined for a.e.
$L^{2}(\mathbb{T})$
defined for a.e.
![]() $x\in \mathbb{T}$
by
$x\in \mathbb{T}$
by
 $$\begin{eqnarray}\displaystyle F^{1}(x,\unicode[STIX]{x1D702}) & = & \displaystyle -\unicode[STIX]{x1D702}(\unicode[STIX]{x1D712}_{0}(y)\,\text{curl}_{x}(\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{y}\,H^{0}(x,y))\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D712}_{1}(y)\{\!\text{curl}_{x}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{1}(x,y))\nonumber\\ \displaystyle & & \displaystyle +\,\text{curl}_{x}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y))\!\}+H^{1}(x,y)+\unicode[STIX]{x1D702}H^{2}(x,y))\!|_{y=x/\unicode[STIX]{x1D702}},\nonumber\\ \displaystyle F^{2}(x,\unicode[STIX]{x1D702}) & = & \displaystyle -\unicode[STIX]{x1D702}(\unicode[STIX]{x1D712}_{0}(y)\unicode[STIX]{x1D716}_{0}^{-1}(y)\{\!\text{curl}_{x}\,H^{0}(x,y)\nonumber\\ \displaystyle & & \displaystyle +\,\text{curl}_{y}\,H^{1}(x,y)+\unicode[STIX]{x1D702}\,\text{curl}_{x}\,H^{1}(x,y)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D702}\,\text{curl}_{y}\,H^{2}(x,y)+\unicode[STIX]{x1D702}^{2}\,\text{curl}_{x}\,H^{2}(x,y)\!\}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D712}_{1}(y)\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{2}(x,y))\!|_{y=x/\unicode[STIX]{x1D702}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F^{1}(x,\unicode[STIX]{x1D702}) & = & \displaystyle -\unicode[STIX]{x1D702}(\unicode[STIX]{x1D712}_{0}(y)\,\text{curl}_{x}(\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}_{y}\,H^{0}(x,y))\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D712}_{1}(y)\{\!\text{curl}_{x}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{1}(x,y))\nonumber\\ \displaystyle & & \displaystyle +\,\text{curl}_{x}(\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{y}\,H^{2}(x,y))\!\}+H^{1}(x,y)+\unicode[STIX]{x1D702}H^{2}(x,y))\!|_{y=x/\unicode[STIX]{x1D702}},\nonumber\\ \displaystyle F^{2}(x,\unicode[STIX]{x1D702}) & = & \displaystyle -\unicode[STIX]{x1D702}(\unicode[STIX]{x1D712}_{0}(y)\unicode[STIX]{x1D716}_{0}^{-1}(y)\{\!\text{curl}_{x}\,H^{0}(x,y)\nonumber\\ \displaystyle & & \displaystyle +\,\text{curl}_{y}\,H^{1}(x,y)+\unicode[STIX]{x1D702}\,\text{curl}_{x}\,H^{1}(x,y)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D702}\,\text{curl}_{y}\,H^{2}(x,y)+\unicode[STIX]{x1D702}^{2}\,\text{curl}_{x}\,H^{2}(x,y)\!\}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D712}_{1}(y)\unicode[STIX]{x1D716}_{1}^{-1}(y)\,\text{curl}_{x}\,H^{2}(x,y))\!|_{y=x/\unicode[STIX]{x1D702}}.\end{eqnarray}$$
Notice that the functions
![]() $H^{0}=H^{0}(x,y),H^{1}=H^{1}(x,y),H^{2}=H^{2}(x,y)$
all belong to the space
$H^{0}=H^{0}(x,y),H^{1}=H^{1}(x,y),H^{2}=H^{2}(x,y)$
all belong to the space
![]() $C_{\#}^{\infty }(\mathbb{T},H_{\#}^{1}(Q))$
. Indeed, this is seen to be true for
$C_{\#}^{\infty }(\mathbb{T},H_{\#}^{1}(Q))$
. Indeed, this is seen to be true for
![]() $H^{0}$
by Proposition 3.1; in the case of
$H^{0}$
by Proposition 3.1; in the case of
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FC}^{k}$
we choose
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FC}^{k}$
we choose
![]() $w\in C_{\#}^{\infty }(\mathbb{T})$
. The assertions for
$w\in C_{\#}^{\infty }(\mathbb{T})$
. The assertions for
![]() $H^{1}$
and
$H^{1}$
and
![]() $H^{2}$
now follow from formula (4.13) for the corrector
$H^{2}$
now follow from formula (4.13) for the corrector
![]() $H^{1}(x,y),$
and the boundary-value problem (4.5)–(4.6) for the function
$H^{1}(x,y),$
and the boundary-value problem (4.5)–(4.6) for the function
![]() $H^{2}(x,y).$
It then follows from (5.5) (see, for example, [Reference Cherednichenko and Smyshlyaev3, p. 1353]) that
$H^{2}(x,y).$
It then follows from (5.5) (see, for example, [Reference Cherednichenko and Smyshlyaev3, p. 1353]) that
![]() $\Vert F^{1}(\cdot ,\unicode[STIX]{x1D702})\Vert _{L^{2}(\mathbb{T})}\leqslant C\unicode[STIX]{x1D702}$
,
$\Vert F^{1}(\cdot ,\unicode[STIX]{x1D702})\Vert _{L^{2}(\mathbb{T})}\leqslant C\unicode[STIX]{x1D702}$
,
![]() $\Vert F^{2}(\cdot ,\unicode[STIX]{x1D702})\Vert _{L^{2}(\mathbb{T})}\leqslant C\unicode[STIX]{x1D702}$
, and by applying the Hölder inequality to (5.4) we deduce that
$\Vert F^{2}(\cdot ,\unicode[STIX]{x1D702})\Vert _{L^{2}(\mathbb{T})}\leqslant C\unicode[STIX]{x1D702}$
, and by applying the Hölder inequality to (5.4) we deduce that
as required.◻
The above proposition implies the following statement.
Theorem 5.1. There exists a constant
![]() $C$
such that the estimate
$C$
such that the estimate
holds for all
![]() $\unicode[STIX]{x1D702}.$
$\unicode[STIX]{x1D702}.$
Proof. Setting
![]() $\unicode[STIX]{x1D711}=\widetilde{H}^{\unicode[STIX]{x1D702}}-H^{(2)}(\cdot ,\unicode[STIX]{x1D702})$
in the estimate (5.3) yields
$\unicode[STIX]{x1D711}=\widetilde{H}^{\unicode[STIX]{x1D702}}-H^{(2)}(\cdot ,\unicode[STIX]{x1D702})$
in the estimate (5.3) yields
The claim of the theorem now follows by noting that in view of (5.2), we have
for some
![]() $\widetilde{C}>0,$
and hence
$\widetilde{C}>0,$
and hence
as required. ◻
The claims of Theorem 2.1 now follow from the estimate
where we used the definition (5.1) of the function
![]() $\widetilde{H}^{\unicode[STIX]{x1D702}}$
and Theorem 5.1. Indeed, from [Reference Vishik and Lyusternik8, p. 109], we infer that the quantities
$\widetilde{H}^{\unicode[STIX]{x1D702}}$
and Theorem 5.1. Indeed, from [Reference Vishik and Lyusternik8, p. 109], we infer that the quantities
![]() $\text{dist}((\unicode[STIX]{x1D714}^{2}+1)^{-1},\text{Sp}(({\mathcal{A}}_{\unicode[STIX]{x1D702}}+1)^{-1}))$
and
$\text{dist}((\unicode[STIX]{x1D714}^{2}+1)^{-1},\text{Sp}(({\mathcal{A}}_{\unicode[STIX]{x1D702}}+1)^{-1}))$
and
![]() $\text{dist}((\unicode[STIX]{x1D714}^{2}+1)^{-1}H^{0}(\cdot ,\cdot /\unicode[STIX]{x1D702}),X_{\unicode[STIX]{x1D702}})$
are controlled above by the right-hand side of (5.6), which completes the proof of Theorem 2.1.
$\text{dist}((\unicode[STIX]{x1D714}^{2}+1)^{-1}H^{0}(\cdot ,\cdot /\unicode[STIX]{x1D702}),X_{\unicode[STIX]{x1D702}})$
are controlled above by the right-hand side of (5.6), which completes the proof of Theorem 2.1.
Remark 5.1. Note that
![]() $H^{(2)}$
is not solenoidal in general, but can be defined in such a way that it is “close” to a solenoidal field, thanks to equation (4.19) (equivalently, (2.5)) and the special choice of the function
$H^{(2)}$
is not solenoidal in general, but can be defined in such a way that it is “close” to a solenoidal field, thanks to equation (4.19) (equivalently, (2.5)) and the special choice of the function
![]() $H^{1}$
so that
$H^{1}$
so that
The function
![]() $H^{(2)}$
thus defined is
$H^{(2)}$
thus defined is
![]() $\unicode[STIX]{x1D702}$
-close to the eigenspace
$\unicode[STIX]{x1D702}$
-close to the eigenspace
![]() $X_{\unicode[STIX]{x1D702}}$
in the norm of
$X_{\unicode[STIX]{x1D702}}$
in the norm of
![]() $[H_{\#}^{1}(Q)]^{3}$
.
$[H_{\#}^{1}(Q)]^{3}$
.
Acknowledgements
K.D.C. and S.C. are grateful for the financial support of the Leverhulme Trust (Grant RPG–167 “Dissipative and non-self-adjoint problems”) and the Engineering and Physical Sciences Research Council (Grant EP/L018802/2 “Mathematical foundations of metamaterials: homogenisation, dissipation and operator theory”, and Grant EP/M017281/1 “Operator asymptotics, a new approach to length-scale interactions in metamaterials”).
We would also like to thank Valery Smyshlyaev for helpful discussions on the subject of this manuscript as well as the referee for the careful revision and a number of insightful suggestions.
A. Appendix. Symmetry of
 $A^{\text{hom}}$
and
$A^{\text{hom}}$
and
 $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
under rotations
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
under rotations
Suppose that
![]() $A\in [L^{\infty }(Q)]^{3\times 3}$
is symmetric such that
$A\in [L^{\infty }(Q)]^{3\times 3}$
is symmetric such that
![]() $A\geqslant \unicode[STIX]{x1D708}I$
on
$A\geqslant \unicode[STIX]{x1D708}I$
on
![]() $Q_{1}$
,
$Q_{1}$
,
![]() $\unicode[STIX]{x1D708}>0,$
and
$\unicode[STIX]{x1D708}>0,$
and
![]() $A\equiv 0$
on
$A\equiv 0$
on
![]() $Q_{0}$
. Consider the matrix
$Q_{0}$
. Consider the matrix
where
![]() $N^{q}$
is the unique solution to the problem (cf. [Reference Kamotski and Smyshlyaev6], [Reference Cherednichenko and Cooper1, Lemma 3.4] and (4.12) above for
$N^{q}$
is the unique solution to the problem (cf. [Reference Kamotski and Smyshlyaev6], [Reference Cherednichenko and Cooper1, Lemma 3.4] and (4.12) above for
![]() $A=\unicode[STIX]{x1D716}_{1}^{-1}\unicode[STIX]{x1D712}_{1},$
where
$A=\unicode[STIX]{x1D716}_{1}^{-1}\unicode[STIX]{x1D712}_{1},$
where
![]() $\unicode[STIX]{x1D712}_{1}$
is the characteristic function of
$\unicode[STIX]{x1D712}_{1}$
is the characteristic function of
![]() $Q_{1}$
)
$Q_{1}$
)
Here the superscript “
![]() $\bot$
” denotes the orthogonal complement in
$\bot$
” denotes the orthogonal complement in
![]() $[H_{\#}^{1}(Q)]^{3}.$
Notice that if, for fixed
$[H_{\#}^{1}(Q)]^{3}.$
Notice that if, for fixed
![]() $\unicode[STIX]{x1D701}\in \mathbb{R}^{3}$
, we multiply each of the above equations by
$\unicode[STIX]{x1D701}\in \mathbb{R}^{3}$
, we multiply each of the above equations by
![]() $\unicode[STIX]{x1D701}_{q},$
then we obtain
$\unicode[STIX]{x1D701}_{q},$
then we obtain
where the vector
![]() $N_{\unicode[STIX]{x1D701}}$
, whose components are
$N_{\unicode[STIX]{x1D701}}$
, whose components are
![]() $\sum _{q}N_{p}^{q}\unicode[STIX]{x1D701}_{q}$
,
$\sum _{q}N_{p}^{q}\unicode[STIX]{x1D701}_{q}$
,
![]() $p=1,2,3,$
is the unique solution to the problem
$p=1,2,3,$
is the unique solution to the problem
It is clear that the matrix representation of the bounded linear mapping
![]() $\unicode[STIX]{x1D701}\mapsto \int _{Q}A(\text{curl}\,N_{\unicode[STIX]{x1D701}}+\unicode[STIX]{x1D701})$
is equal to
$\unicode[STIX]{x1D701}\mapsto \int _{Q}A(\text{curl}\,N_{\unicode[STIX]{x1D701}}+\unicode[STIX]{x1D701})$
is equal to
![]() $A^{\text{hom}}$
. The following property holds.
$A^{\text{hom}}$
. The following property holds.
Proposition A.1. Suppose that
![]() $\unicode[STIX]{x1D70E}$
is a rotation such that
$\unicode[STIX]{x1D70E}$
is a rotation such that
![]() $\unicode[STIX]{x1D70E}Q=Q$
and assume that
$\unicode[STIX]{x1D70E}Q=Q$
and assume that
Then
![]() $A^{\text{hom}}$
inherits the same symmetry, that is, one has
$A^{\text{hom}}$
inherits the same symmetry, that is, one has
In particular, if (A.3) holds for all
![]() $\unicode[STIX]{x1D70B}/2$
-rotations, then one has
$\unicode[STIX]{x1D70B}/2$
-rotations, then one has
![]() $A_{kl}^{\text{hom}}=A_{lk}^{\text{hom}}=0$
for all
$A_{kl}^{\text{hom}}=A_{lk}^{\text{hom}}=0$
for all
![]() $l\neq k$
.
$l\neq k$
.
Proof. For each
![]() $u\in [H_{\#}^{1}(Q)]^{3}$
let
$u\in [H_{\#}^{1}(Q)]^{3}$
let
![]() $w$
be the solution of the vector equation
$w$
be the solution of the vector equation
in the space
It is clear that such a solution exists. We denote by
![]() $\hat{u}$
the vector field
$\hat{u}$
the vector field
![]() $\text{curl}\,w$
. A direct calculation, using the property
$\text{curl}\,w$
. A direct calculation, using the property
![]() $\unicode[STIX]{x1D70E}^{-1}=\unicode[STIX]{x1D70E}^{\top }$
, yields
$\unicode[STIX]{x1D70E}^{-1}=\unicode[STIX]{x1D70E}^{\top }$
, yields
Therefore, for all
![]() $\unicode[STIX]{x1D711}\in [H_{\#}^{1}(Q)]^{3}$
, the above equality and the assumption (A.3) imply
$\unicode[STIX]{x1D711}\in [H_{\#}^{1}(Q)]^{3}$
, the above equality and the assumption (A.3) imply
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q}A(y^{\prime })\,\text{curl}_{y^{\prime }}\,u(\unicode[STIX]{x1D70E}^{-1}y^{\prime })\cdot \text{curl}_{y^{\prime }}\,\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70E}^{-1}y^{\prime })\,dy^{\prime }\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q}A(\unicode[STIX]{x1D70E}y)\unicode[STIX]{x1D70E}\,\text{curl}_{}\,\hat{u} (y)\cdot \unicode[STIX]{x1D70E}\,\text{curl}_{}\,\hat{\unicode[STIX]{x1D711}}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q}A(y)\,\text{curl}_{}\,\hat{u} (y)\cdot \text{curl}_{}\,\hat{\unicode[STIX]{x1D711}}(y)\,dy.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q}A(y^{\prime })\,\text{curl}_{y^{\prime }}\,u(\unicode[STIX]{x1D70E}^{-1}y^{\prime })\cdot \text{curl}_{y^{\prime }}\,\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70E}^{-1}y^{\prime })\,dy^{\prime }\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q}A(\unicode[STIX]{x1D70E}y)\unicode[STIX]{x1D70E}\,\text{curl}_{}\,\hat{u} (y)\cdot \unicode[STIX]{x1D70E}\,\text{curl}_{}\,\hat{\unicode[STIX]{x1D711}}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q}A(y)\,\text{curl}_{}\,\hat{u} (y)\cdot \text{curl}_{}\,\hat{\unicode[STIX]{x1D711}}(y)\,dy.\nonumber\end{eqnarray}$$
Hence, a function
![]() $u\in [H_{\#}^{1}(Q)]^{3}$
solves
$u\in [H_{\#}^{1}(Q)]^{3}$
solves
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q}A(y^{\prime })\,\text{curl}_{y^{\prime }}\,u(\unicode[STIX]{x1D70E}^{-1}y^{\prime })\cdot \text{curl}_{y^{\prime }}\,\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70E}^{-1}y^{\prime })\,dy^{\prime }\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q}f(y^{\prime })\cdot \text{curl}_{y^{\prime }}\,\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70E}^{-1}y^{\prime })\,dy^{\prime }\quad \text{for all }\unicode[STIX]{x1D711}\in [H_{\#}^{1}(Q)]^{3},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q}A(y^{\prime })\,\text{curl}_{y^{\prime }}\,u(\unicode[STIX]{x1D70E}^{-1}y^{\prime })\cdot \text{curl}_{y^{\prime }}\,\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70E}^{-1}y^{\prime })\,dy^{\prime }\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q}f(y^{\prime })\cdot \text{curl}_{y^{\prime }}\,\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70E}^{-1}y^{\prime })\,dy^{\prime }\quad \text{for all }\unicode[STIX]{x1D711}\in [H_{\#}^{1}(Q)]^{3},\end{eqnarray}$$
if and only if
![]() $\hat{u}$
solves
$\hat{u}$
solves
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q}A(y)\,\text{curl}_{}\,\hat{u} (y)\cdot \text{curl}_{}\,\hat{\unicode[STIX]{x1D711}}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q}\unicode[STIX]{x1D70E}^{-1}f(\unicode[STIX]{x1D70E}y)\cdot \text{curl}_{}\,\hat{\unicode[STIX]{x1D711}}(y)\,dy\quad \text{for all }\hat{\unicode[STIX]{x1D711}}\in [H_{\#}^{1}(Q)]^{3}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q}A(y)\,\text{curl}_{}\,\hat{u} (y)\cdot \text{curl}_{}\,\hat{\unicode[STIX]{x1D711}}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q}\unicode[STIX]{x1D70E}^{-1}f(\unicode[STIX]{x1D70E}y)\cdot \text{curl}_{}\,\hat{\unicode[STIX]{x1D711}}(y)\,dy\quad \text{for all }\hat{\unicode[STIX]{x1D711}}\in [H_{\#}^{1}(Q)]^{3}.\end{eqnarray}$$
Let us now prove (A.4). For fixed
![]() $\unicode[STIX]{x1D709},\unicode[STIX]{x1D701}\in \mathbb{R}^{3}$
let
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D701}\in \mathbb{R}^{3}$
let
![]() $N_{\unicode[STIX]{x1D709}}$
be the unique solution to (A.2) and set
$N_{\unicode[STIX]{x1D709}}$
be the unique solution to (A.2) and set
![]() $u(y):=N_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70E}y)$
,
$u(y):=N_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70E}y)$
,
![]() $y\in Q$
. By (A.1), assumption (A.3) and (A.5) we deduce that
$y\in Q$
. By (A.1), assumption (A.3) and (A.5) we deduce that
 $$\begin{eqnarray}\displaystyle A^{\text{hom}}\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D701} & = & \displaystyle \int _{Q}A(y^{\prime })(\text{curl}_{y^{\prime }}\,N_{\unicode[STIX]{x1D709}}(y^{\prime })+\unicode[STIX]{x1D709})\cdot \unicode[STIX]{x1D701}\,dy^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \int _{Q}A(y^{\prime })(\text{curl}_{y^{\prime }}\,u(\unicode[STIX]{x1D70E}^{-1}y^{\prime })+\unicode[STIX]{x1D709})\cdot \unicode[STIX]{x1D701}\,dy^{\prime }\nonumber\\ \displaystyle & \overset{(A.5)}{=} & \displaystyle \int _{Q}A(y^{\prime })(\unicode[STIX]{x1D70E}\,\text{curl}\,\hat{u} (\unicode[STIX]{x1D70E}^{-1}y^{\prime })+\unicode[STIX]{x1D709})\cdot \unicode[STIX]{x1D701}\,dy^{\prime }\nonumber\\ \displaystyle & \overset{y^{\prime }=\unicode[STIX]{x1D70E}y}{=} & \displaystyle \int _{Q}A(\unicode[STIX]{x1D70E}y)(\unicode[STIX]{x1D70E}\,\text{curl}\,\hat{u} (y)+\unicode[STIX]{x1D709})\cdot \unicode[STIX]{x1D701}\,dy\nonumber\\ \displaystyle & \overset{(A.3)}{=} & \displaystyle \int _{Q}A(y)(\text{curl}\,\hat{u} (y)+\unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D709})\cdot \unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D701}\,dy.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A^{\text{hom}}\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D701} & = & \displaystyle \int _{Q}A(y^{\prime })(\text{curl}_{y^{\prime }}\,N_{\unicode[STIX]{x1D709}}(y^{\prime })+\unicode[STIX]{x1D709})\cdot \unicode[STIX]{x1D701}\,dy^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \int _{Q}A(y^{\prime })(\text{curl}_{y^{\prime }}\,u(\unicode[STIX]{x1D70E}^{-1}y^{\prime })+\unicode[STIX]{x1D709})\cdot \unicode[STIX]{x1D701}\,dy^{\prime }\nonumber\\ \displaystyle & \overset{(A.5)}{=} & \displaystyle \int _{Q}A(y^{\prime })(\unicode[STIX]{x1D70E}\,\text{curl}\,\hat{u} (\unicode[STIX]{x1D70E}^{-1}y^{\prime })+\unicode[STIX]{x1D709})\cdot \unicode[STIX]{x1D701}\,dy^{\prime }\nonumber\\ \displaystyle & \overset{y^{\prime }=\unicode[STIX]{x1D70E}y}{=} & \displaystyle \int _{Q}A(\unicode[STIX]{x1D70E}y)(\unicode[STIX]{x1D70E}\,\text{curl}\,\hat{u} (y)+\unicode[STIX]{x1D709})\cdot \unicode[STIX]{x1D701}\,dy\nonumber\\ \displaystyle & \overset{(A.3)}{=} & \displaystyle \int _{Q}A(y)(\text{curl}\,\hat{u} (y)+\unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D709})\cdot \unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D701}\,dy.\end{eqnarray}$$
Since
![]() $N_{\unicode[STIX]{x1D709}}(y^{\prime })$
solves (A.2),
$N_{\unicode[STIX]{x1D709}}(y^{\prime })$
solves (A.2),
![]() $u(\unicode[STIX]{x1D70E}^{-1}y^{\prime })$
solves (A.6) for
$u(\unicode[STIX]{x1D70E}^{-1}y^{\prime })$
solves (A.6) for
![]() $f(y^{\prime })=-A(y^{\prime })\unicode[STIX]{x1D709}$
and therefore
$f(y^{\prime })=-A(y^{\prime })\unicode[STIX]{x1D709}$
and therefore
![]() $\hat{u}$
solves (A.7) where, by (A.3),
$\hat{u}$
solves (A.7) where, by (A.3),
![]() $\unicode[STIX]{x1D70E}^{-1}f(\unicode[STIX]{x1D70E}y)=-\unicode[STIX]{x1D70E}^{-1}A(\unicode[STIX]{x1D70E}y)\unicode[STIX]{x1D709}=-A(y)\unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D709}$
. Hence, the solution
$\unicode[STIX]{x1D70E}^{-1}f(\unicode[STIX]{x1D70E}y)=-\unicode[STIX]{x1D70E}^{-1}A(\unicode[STIX]{x1D70E}y)\unicode[STIX]{x1D709}=-A(y)\unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D709}$
. Hence, the solution
![]() $N_{\unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D709}}$
to (A.2), for
$N_{\unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D709}}$
to (A.2), for
![]() $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D709}$
, is the projection of
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D709}$
, is the projection of
![]() $\hat{u}$
onto the space
$\hat{u}$
onto the space
![]() $\{u\in [H_{\#}^{1}(Q)]^{3}:A\,\text{curl}\,u=0\}^{\bot }$
and the expression in (A.8) equals
$\{u\in [H_{\#}^{1}(Q)]^{3}:A\,\text{curl}\,u=0\}^{\bot }$
and the expression in (A.8) equals
![]() $A^{\text{hom}}\unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D701}.$
The assertion (A.4) follows, in view of the arbitrary choice of
$A^{\text{hom}}\unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D70E}^{-1}\unicode[STIX]{x1D701}.$
The assertion (A.4) follows, in view of the arbitrary choice of
![]() $\unicode[STIX]{x1D709},$
$\unicode[STIX]{x1D709},$
![]() $\unicode[STIX]{x1D701},$
and the equality
$\unicode[STIX]{x1D701},$
and the equality
![]() $\unicode[STIX]{x1D70E}A^{\text{hom}}\unicode[STIX]{x1D70E}^{-1}=\unicode[STIX]{x1D70E}^{-1}A^{\text{hom}}\unicode[STIX]{x1D70E}$
which holds since
$\unicode[STIX]{x1D70E}A^{\text{hom}}\unicode[STIX]{x1D70E}^{-1}=\unicode[STIX]{x1D70E}^{-1}A^{\text{hom}}\unicode[STIX]{x1D70E}$
which holds since
![]() $\unicode[STIX]{x1D70E}$
is unitary and
$\unicode[STIX]{x1D70E}$
is unitary and
![]() $A^{\text{hom}}$
is symmetric.◻
$A^{\text{hom}}$
is symmetric.◻
Corollary A.1. If (A.3) holds for
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{k},$
where
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{k},$
where
![]() $\unicode[STIX]{x1D70E}_{k}$
is the rotation by
$\unicode[STIX]{x1D70E}_{k}$
is the rotation by
![]() $\unicode[STIX]{x1D70B}$
around the
$\unicode[STIX]{x1D70B}$
around the
![]() $x_{k}$
-axis, then
$x_{k}$
-axis, then
![]() $A_{kl}^{\text{hom}}=0$
, for all
$A_{kl}^{\text{hom}}=0$
, for all
![]() $l\neq k.$
$l\neq k.$
Proof. Indeed, say for
![]() $k=1$
, (A.4) takes the form
$k=1$
, (A.4) takes the form
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}A_{11}^{\text{hom}} & A_{12}^{\text{hom}} & A_{13}^{\text{hom}}\\ A_{21}^{\text{hom}} & A_{22}^{\text{hom}} & A_{23}^{\text{hom}}\\ A_{31}^{\text{hom}} & A_{32}^{\text{hom}} & A_{33}^{\text{hom}}\end{array}\right)=\left(\begin{array}{@{}ccc@{}}A_{11}^{\text{hom}} & -A_{12}^{\text{hom}} & -A_{13}^{\text{hom}}\\ -A_{21}^{\text{hom}} & A_{22}^{\text{hom}} & A_{23}^{\text{hom}}\\ -A_{31}^{\text{hom}} & A_{32}^{\text{hom}} & A_{33}^{\text{hom}}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}A_{11}^{\text{hom}} & A_{12}^{\text{hom}} & A_{13}^{\text{hom}}\\ A_{21}^{\text{hom}} & A_{22}^{\text{hom}} & A_{23}^{\text{hom}}\\ A_{31}^{\text{hom}} & A_{32}^{\text{hom}} & A_{33}^{\text{hom}}\end{array}\right)=\left(\begin{array}{@{}ccc@{}}A_{11}^{\text{hom}} & -A_{12}^{\text{hom}} & -A_{13}^{\text{hom}}\\ -A_{21}^{\text{hom}} & A_{22}^{\text{hom}} & A_{23}^{\text{hom}}\\ -A_{31}^{\text{hom}} & A_{32}^{\text{hom}} & A_{33}^{\text{hom}}\end{array}\right),\end{eqnarray}$$
and hence
![]() $A_{12}^{\text{hom}}=A_{21}^{\text{hom}}=A_{13}^{\text{hom}}=A_{31}^{\text{hom}}=0.$
◻
$A_{12}^{\text{hom}}=A_{21}^{\text{hom}}=A_{13}^{\text{hom}}=A_{31}^{\text{hom}}=0.$
◻
Similarly, direct calculation proves the following statement.
Corollary A.2. If (A.3) holds for
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{k},$
where
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{k},$
where
![]() $\unicode[STIX]{x1D70E}_{k}$
is the rotation by
$\unicode[STIX]{x1D70E}_{k}$
is the rotation by
![]() $\unicode[STIX]{x1D70B}/2$
around the
$\unicode[STIX]{x1D70B}/2$
around the
![]() $x_{k}$
-axis, then
$x_{k}$
-axis, then
![]() $A_{kl}^{\text{hom}}=0$
, for all
$A_{kl}^{\text{hom}}=0$
, for all
![]() $l\neq k$
and
$l\neq k$
and
![]() $A_{\mathit{ii}}^{\text{hom}}=A_{\mathit{jj}}^{\text{hom}}$
,
$A_{\mathit{ii}}^{\text{hom}}=A_{\mathit{jj}}^{\text{hom}}$
,
![]() $i,j\neq k$
.
$i,j\neq k$
.
Proposition A.2. Let
![]() $\unicode[STIX]{x1D712}_{0}$
be the characteristic function of the set
$\unicode[STIX]{x1D712}_{0}$
be the characteristic function of the set
![]() $Q_{0}$
. Suppose that the set
$Q_{0}$
. Suppose that the set
![]() $Q$
and the coefficient
$Q$
and the coefficient
![]() $A=\unicode[STIX]{x1D716}_{0}^{-1}\unicode[STIX]{x1D712}_{0}I$
are invariant under a rotation
$A=\unicode[STIX]{x1D716}_{0}^{-1}\unicode[STIX]{x1D712}_{0}I$
are invariant under a rotation
![]() $\unicode[STIX]{x1D70E}$
, that is,
$\unicode[STIX]{x1D70E}$
, that is,
![]() $\unicode[STIX]{x1D70E}Q=Q$
and
$\unicode[STIX]{x1D70E}Q=Q$
and
![]() $A=\unicode[STIX]{x1D716}_{0}^{-1}\unicode[STIX]{x1D712}_{0}I$
satisfies (A.3), or equivalently,
$A=\unicode[STIX]{x1D716}_{0}^{-1}\unicode[STIX]{x1D712}_{0}I$
satisfies (A.3), or equivalently,
Then for all
![]() $\unicode[STIX]{x1D714}^{2}\notin \{0\}\cup \{\unicode[STIX]{x1D6FC}^{k}\}_{k=1}^{\infty }$
the matrix
$\unicode[STIX]{x1D714}^{2}\notin \{0\}\cup \{\unicode[STIX]{x1D6FC}^{k}\}_{k=1}^{\infty }$
the matrix
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714}),$
defined by (3.9) and (3.3)–(3.6), satisfies the property
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714}),$
defined by (3.9) and (3.3)–(3.6), satisfies the property
Proof. We make use of the representation (3.11) for
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
and of the equations (3.10) for the functions
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
and of the equations (3.10) for the functions
![]() $\unicode[STIX]{x1D719}^{k}.$
$\unicode[STIX]{x1D719}^{k}.$
Multiplying (3.10) by
![]() $\unicode[STIX]{x1D713}\in [C_{0}^{\infty }(Q_{0})]^{3}$
and integrating by parts yields
$\unicode[STIX]{x1D713}\in [C_{0}^{\infty }(Q_{0})]^{3}$
and integrating by parts yields
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}\,\unicode[STIX]{x1D719}^{k}(y)\cdot \text{curl}\,\unicode[STIX]{x1D713}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FC}^{k}\int _{Q_{0}}\int _{Q_{0}}G(y-y^{\prime })\,\text{div}\,\unicode[STIX]{x1D719}^{k}(y^{\prime })\,\text{div}\,\unicode[STIX]{x1D713}(y)\,dy^{\prime }\,dy\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D6FC}^{k}\int _{Q_{0}}\unicode[STIX]{x1D719}^{k}(y)\cdot \unicode[STIX]{x1D713}(y)\,dy.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}\,\unicode[STIX]{x1D719}^{k}(y)\cdot \text{curl}\,\unicode[STIX]{x1D713}(y)\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FC}^{k}\int _{Q_{0}}\int _{Q_{0}}G(y-y^{\prime })\,\text{div}\,\unicode[STIX]{x1D719}^{k}(y^{\prime })\,\text{div}\,\unicode[STIX]{x1D713}(y)\,dy^{\prime }\,dy\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D6FC}^{k}\int _{Q_{0}}\unicode[STIX]{x1D719}^{k}(y)\cdot \unicode[STIX]{x1D713}(y)\,dy.\end{eqnarray}$$
We claim that the functions
![]() $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}\cdot )$
satisfy the identity (A.10) with
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}\cdot )$
satisfy the identity (A.10) with
![]() $Q_{0}$
replaced by
$Q_{0}$
replaced by
![]() $\unicode[STIX]{x1D70E}Q_{0}:=\{y\in Q:\unicode[STIX]{x1D70E}^{-1}y\in Q_{0}\}.$
We show this by treating each term in (A.10) separately. It is clear that
$\unicode[STIX]{x1D70E}Q_{0}:=\{y\in Q:\unicode[STIX]{x1D70E}^{-1}y\in Q_{0}\}.$
We show this by treating each term in (A.10) separately. It is clear that
 $$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D70E}Q_{0}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}})\cdot \unicode[STIX]{x1D70E}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}})\,d{\tilde{y}} & = & \displaystyle \int _{\unicode[STIX]{x1D70E}Q_{0}}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}})\cdot \unicode[STIX]{x1D713}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}})\,d{\tilde{y}}\nonumber\\ \displaystyle & \stackrel{{\tilde{y}}=\unicode[STIX]{x1D70E}y}{=} & \displaystyle \int _{Q_{0}}\unicode[STIX]{x1D719}^{k}(y)\cdot \unicode[STIX]{x1D713}(y)\,dy.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D70E}Q_{0}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}})\cdot \unicode[STIX]{x1D70E}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}})\,d{\tilde{y}} & = & \displaystyle \int _{\unicode[STIX]{x1D70E}Q_{0}}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}})\cdot \unicode[STIX]{x1D713}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}})\,d{\tilde{y}}\nonumber\\ \displaystyle & \stackrel{{\tilde{y}}=\unicode[STIX]{x1D70E}y}{=} & \displaystyle \int _{Q_{0}}\unicode[STIX]{x1D719}^{k}(y)\cdot \unicode[STIX]{x1D713}(y)\,dy.\end{eqnarray}$$
Furthermore, by utilizing the identity
which holds due to the fact that
![]() $\unicode[STIX]{x1D70E}$
is a rotation, as well as property (A.9), we obtain
$\unicode[STIX]{x1D70E}$
is a rotation, as well as property (A.9), we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70E}Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}({\tilde{y}})\,\text{curl}_{{\tilde{y}}}(\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}}))\cdot \text{curl}_{{\tilde{y}}}(\unicode[STIX]{x1D70E}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}}))\,d{\tilde{y}}\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{{\tilde{y}}=\unicode[STIX]{x1D70E}y}{=}\int _{Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}\,\unicode[STIX]{x1D719}^{k}(y)\cdot \text{curl}\,\unicode[STIX]{x1D713}(y)\,dy.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70E}Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}({\tilde{y}})\,\text{curl}_{{\tilde{y}}}(\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}}))\cdot \text{curl}_{{\tilde{y}}}(\unicode[STIX]{x1D70E}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}}))\,d{\tilde{y}}\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{{\tilde{y}}=\unicode[STIX]{x1D70E}y}{=}\int _{Q_{0}}\unicode[STIX]{x1D716}_{0}^{-1}(y)\,\text{curl}\,\unicode[STIX]{x1D719}^{k}(y)\cdot \text{curl}\,\unicode[STIX]{x1D713}(y)\,dy.\end{eqnarray}$$
Finally, it is clear that
![]() $\text{div}\,(\unicode[STIX]{x1D70E}F(\unicode[STIX]{x1D70E}^{-1}\cdot ))=(\text{div}\,F)(\unicode[STIX]{x1D70E}^{-1}\cdot )$
for vector fields
$\text{div}\,(\unicode[STIX]{x1D70E}F(\unicode[STIX]{x1D70E}^{-1}\cdot ))=(\text{div}\,F)(\unicode[STIX]{x1D70E}^{-1}\cdot )$
for vector fields
![]() $F$
and therefore
$F$
and therefore
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70E}Q_{0}}\int _{\unicode[STIX]{x1D70E}Q_{0}}G({\tilde{y}}-{\tilde{y}}^{\prime })\,\text{div}_{{\tilde{y}}}(\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}}))\,\text{div}_{{\tilde{y}}}(\unicode[STIX]{x1D70E}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}}^{\prime }))\,d{\tilde{y}}^{\prime }\,d{\tilde{y}}\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\substack{ {\tilde{y}}=\unicode[STIX]{x1D70E}y, \\ {\tilde{y}}^{\prime }=\unicode[STIX]{x1D70E}y^{\prime }}}{=}\int _{Q_{0}}\int _{Q_{0}}G(\unicode[STIX]{x1D70E}(y-y^{\prime }))\,\text{div}\,\unicode[STIX]{x1D719}^{k}(y)\,\text{div}\,\unicode[STIX]{x1D713}(y^{\prime })\,dy^{\prime }\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q_{0}}\int _{Q_{0}}G(y-y^{\prime })\,\text{div}\,\unicode[STIX]{x1D719}^{k}(y)\,\text{div}\,\unicode[STIX]{x1D713}(y^{\prime })\,dy^{\prime }\,dy,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70E}Q_{0}}\int _{\unicode[STIX]{x1D70E}Q_{0}}G({\tilde{y}}-{\tilde{y}}^{\prime })\,\text{div}_{{\tilde{y}}}(\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}}))\,\text{div}_{{\tilde{y}}}(\unicode[STIX]{x1D70E}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70E}^{-1}{\tilde{y}}^{\prime }))\,d{\tilde{y}}^{\prime }\,d{\tilde{y}}\nonumber\\ \displaystyle & & \displaystyle \quad \stackrel{\substack{ {\tilde{y}}=\unicode[STIX]{x1D70E}y, \\ {\tilde{y}}^{\prime }=\unicode[STIX]{x1D70E}y^{\prime }}}{=}\int _{Q_{0}}\int _{Q_{0}}G(\unicode[STIX]{x1D70E}(y-y^{\prime }))\,\text{div}\,\unicode[STIX]{x1D719}^{k}(y)\,\text{div}\,\unicode[STIX]{x1D713}(y^{\prime })\,dy^{\prime }\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{Q_{0}}\int _{Q_{0}}G(y-y^{\prime })\,\text{div}\,\unicode[STIX]{x1D719}^{k}(y)\,\text{div}\,\unicode[STIX]{x1D713}(y^{\prime })\,dy^{\prime }\,dy,\nonumber\end{eqnarray}$$
where the invariance of the Green function
![]() $G$
under the rotation
$G$
under the rotation
![]() $\unicode[STIX]{x1D70E}$
holds due to the assumption
$\unicode[STIX]{x1D70E}$
holds due to the assumption
![]() $\unicode[STIX]{x1D70E}Q=Q.$
$\unicode[STIX]{x1D70E}Q=Q.$
The proof is concluded by combining the definition of
![]() $\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
via (3.9), (3.3)–(3.6) and formula (3.11) applied twice, namely for the inclusion
$\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})$
via (3.9), (3.3)–(3.6) and formula (3.11) applied twice, namely for the inclusion
![]() $\unicode[STIX]{x1D70E}Q_{0},$
which coincides with
$\unicode[STIX]{x1D70E}Q_{0},$
which coincides with
![]() $Q_{0}$
due to (A.9), and the inclusion
$Q_{0}$
due to (A.9), and the inclusion
![]() $Q_{0}$
itself:
$Q_{0}$
itself:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714}) & = & \displaystyle \unicode[STIX]{x1D714}^{2}+\unicode[STIX]{x1D714}^{4}\mathop{\sum }_{k=1}^{\infty }\frac{(\int _{\unicode[STIX]{x1D70E}Q_{0}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}\cdot ))\otimes (\int _{\unicode[STIX]{x1D70E}Q_{0}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}\cdot ))}{\unicode[STIX]{x1D6FC}^{k}-\unicode[STIX]{x1D714}^{2}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70E}^{-1}+\unicode[STIX]{x1D714}^{4}\mathop{\sum }_{k=1}^{\infty }\frac{(\int _{Q_{0}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k})\otimes (\int _{Q_{0}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k})}{\unicode[STIX]{x1D6FC}^{k}-\unicode[STIX]{x1D714}^{2}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70E}\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})\unicode[STIX]{x1D70E}^{-1},\quad \unicode[STIX]{x1D714}^{2}\notin \{0\}\cup \{\unicode[STIX]{x1D6FC}^{k}\}_{k=1}^{\infty },\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714}) & = & \displaystyle \unicode[STIX]{x1D714}^{2}+\unicode[STIX]{x1D714}^{4}\mathop{\sum }_{k=1}^{\infty }\frac{(\int _{\unicode[STIX]{x1D70E}Q_{0}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}\cdot ))\otimes (\int _{\unicode[STIX]{x1D70E}Q_{0}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k}(\unicode[STIX]{x1D70E}^{-1}\cdot ))}{\unicode[STIX]{x1D6FC}^{k}-\unicode[STIX]{x1D714}^{2}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70E}^{-1}+\unicode[STIX]{x1D714}^{4}\mathop{\sum }_{k=1}^{\infty }\frac{(\int _{Q_{0}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k})\otimes (\int _{Q_{0}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D719}^{k})}{\unicode[STIX]{x1D6FC}^{k}-\unicode[STIX]{x1D714}^{2}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70E}\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D714})\unicode[STIX]{x1D70E}^{-1},\quad \unicode[STIX]{x1D714}^{2}\notin \{0\}\cup \{\unicode[STIX]{x1D6FC}^{k}\}_{k=1}^{\infty },\nonumber\end{eqnarray}$$
as required. ◻
By analogy with Corollaries A.1 and A.2 we obtain the following statement.
Corollary A.3. Under the conditions of Proposition A.2 with
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{k},$
where
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{k},$
where
![]() $\unicode[STIX]{x1D70E}_{k}$
is a rotation by
$\unicode[STIX]{x1D70E}_{k}$
is a rotation by
![]() $\unicode[STIX]{x1D70B}$
around the
$\unicode[STIX]{x1D70B}$
around the
![]() $x_{k}$
-axis,
$x_{k}$
-axis,
![]() $\unicode[STIX]{x1D6E4}_{kl}(\unicode[STIX]{x1D714})=0$
for all
$\unicode[STIX]{x1D6E4}_{kl}(\unicode[STIX]{x1D714})=0$
for all
![]() $l\neq k,$
$l\neq k,$
![]() $\unicode[STIX]{x1D714}^{2}\notin \{0\}\cup \{\unicode[STIX]{x1D6FC}^{k}\}_{k=1}^{\infty }.$
Moreover, if
$\unicode[STIX]{x1D714}^{2}\notin \{0\}\cup \{\unicode[STIX]{x1D6FC}^{k}\}_{k=1}^{\infty }.$
Moreover, if
![]() $\unicode[STIX]{x1D70E}_{k}$
is a rotation by
$\unicode[STIX]{x1D70E}_{k}$
is a rotation by
![]() $\unicode[STIX]{x1D70B}/2$
around the
$\unicode[STIX]{x1D70B}/2$
around the
![]() $x_{k}$
-axis, then
$x_{k}$
-axis, then
![]() $\unicode[STIX]{x1D6E4}_{\mathit{ii}}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D6E4}_{\mathit{jj}}(\unicode[STIX]{x1D714})$
for
$\unicode[STIX]{x1D6E4}_{\mathit{ii}}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D6E4}_{\mathit{jj}}(\unicode[STIX]{x1D714})$
for
![]() $i,j\neq k$
.
$i,j\neq k$
.