Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-18T10:56:31.026Z Has data issue: false hasContentIssue false
  • English
  • Français

Tight closure of powers of ideals and tight hilbert polynomials

Part of: General commutative ring theory Arithmetic rings and other special rings Local rings and semilocal rings Commutative algebra: Homological methods

Published online by Cambridge University Press:  12 July 2019

KRITI GOEL ,
J. K. VERMA  and
VIVEK MUKUNDAN
KRITI GOEL
Affiliation:
Indian Institute of Technology Bombay, Mumbai400076, India. Department of Mathematics, IIT Bombay, Mumbai-400076 India e-mail: kriti@math.iitb.ac.in, jkv@math.iitb.ac.in
J. K. VERMA
Affiliation:
Indian Institute of Technology Bombay, Mumbai400076, India. Department of Mathematics, IIT Bombay, Mumbai-400076 India e-mail: kriti@math.iitb.ac.in, jkv@math.iitb.ac.in
VIVEK MUKUNDAN
Affiliation:
University of Virginia, Charlottesville, VA 22904, USA Department of Mathematics, University of Virginia, 141 Cabell Drive, ICERCHOF Hall, P.O. Box 40087 - Charlottesville e-mail: vm6y@virginia.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let (R, 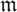) be an analytically unramified local ring of positive prime characteristic p. For an ideal I, let I* denote its tight closure. We introduce the tight Hilbert function 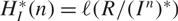$$H_I^*\left( n \right) = \Im \left( {R/\left( {{I^n}} \right)*} \right)$$ and the corresponding tight Hilbert polynomial 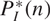$$P_I^*\left( n \right)$$, where I is an m-primary ideal. It is proved that F-rationality can be detected by the vanishing of the first coefficient of 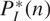$$P_I^*\left( n \right)$$. We find the tight Hilbert polynomial of certain parameter ideals in hypersurface rings and Stanley-Reisner rings of simplicial complexes.

MSC classification

Primary: 13A35: Characteristic $p$ methods (Frobenius endomorphism) and reduction to characteristic $p$; tight closure 13D40: Hilbert-Samuel and Hilbert-Kunz functions; Poincaré series
Secondary: 13F55: Stanley-Reisner face rings; simplicial complexes 13H10: Special types (Cohen-Macaulay, Gorenstein, Buchsbaum, etc.)
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 169 , Issue 2 , September 2020 , pp. 335 - 355
Copyright
© Cambridge Philosophical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by a UGC fellowship, Govt. of India.

References

REFERENCES

Bruns, W. and Erzog, J. H. Cohen–Macaulay rings, volume 39 of Cambridge Studies in Advanced Mathematics. (Cambridge University Press, Cambridge, 1993).Google Scholar
Corso, A., Polini, C. and Rossi, M.E.. Bounds on the normal Hilbert coefficients. Proc. Amer. Math. Soc. 144(5) (2016), 1919–1930.10.1090/proc/12858CrossRefGoogle Scholar
Hochster, M.. Tight closure theory and characteristic p methods. In Trends in commutative algebra, Math.Sci.Res.Inst. Publ. vol, 51. (Cambridge University Press, Cambridge, 2004), page 181–210. With an appendix by Graham, J. Leuschke.10.1017/CBO9780511756382.007CrossRefGoogle Scholar
Hochster, M. and Huneke, C.. Tight closure in equal characteristic zero. Preprint Available at: http://www.math.lsa.umich.edu/hochster/msr.html (1999).Google Scholar
Hong, J. and Ulrich, B.. Specialisation and integral closure. J. Lond. Math. Soc. (2), 90(3) (2014), 861–878.10.1112/jlms/jdu053CrossRefGoogle Scholar
Huckaba, S.. A d-dimensional extension of a lemma of Huneke’s and formulas for the Hilbert coefficients. Proc. Amer. Math. Soc. 124(5) (1996), 1393–1401.10.1090/S0002-9939-96-03182-6CrossRefGoogle Scholar
Huckaba, S. and Marley, T.. Hilbert coefficients and the depths of associated graded rings. J. London Math. Soc., 56(1) (1997), 64–76.10.1112/S0024610797005206CrossRefGoogle Scholar
Itoh, S.. Integral closures of ideals generated by regular sequences. J. Algebra 117(2) (1988), 390–401.10.1016/0021-8693(88)90114-7CrossRefGoogle Scholar
Itoh, S.. Coefficients of normal Hilbert polynomials. J. Algebra 150(1) (1992), 101–117.10.1016/S0021-8693(05)80052-3CrossRefGoogle Scholar
Kummini, M. and Masuti, S.. On conjectures of Itoh and of Lipman on the cohomology of normalised blow ups. arxiv (2015), pages 1–17.Google Scholar
Marley, T.J.. Hilbert functions of ideals in Cohen—Macaulay rings. ProQuest LLC, Ph.D. Thesis purdue university (Ann Arbor, MI, 1989).Google Scholar
Masuti, S.K., Puthenpurakal, T.J., and Verma, J.K.. Local cohomology of multi-Rees algebras with applications to joint reductions and complete ideals. Acta Math. Vietnam. 40(3) (2015), 479–510.CrossRefGoogle Scholar
Matsumura, H.. Commutative ring theory, Camb. Stud. Adv. Math., vol. 8 (Cambridge University Press, Cambridge, second edition, 1989). Translated from the Japanese by Reid, M..Google Scholar
Rees, D.. A note on analytically unramified local rings. J. London Math. Soc. 1(1) (1961), 24–28.10.1112/jlms/s1-36.1.24CrossRefGoogle Scholar
Rees, D.. Hilbert functions and pseudo-rational local rings of dimension two. J. London Math. Soc., 2(3) (1981), 467–479.10.1112/jlms/s2-24.3.467CrossRefGoogle Scholar
Sullivant, S.. Tight closure of monomial ideals in Fermat rings. Available at: www4.ncsu.edu/smsulli2/Pubs/tc.ps.Google Scholar
Valabrega, P. and Valla, G.. Form rings and regular sequences. Nagoya Math. J. 72 (1978), 93–101.10.1017/S0027763000018225CrossRefGoogle Scholar