Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zotter, Bruno
1962.
Die Berechnung der Nullstellen der Zylinderringfunktionen durch Potenzreihen.
Zeitschrift für angewandte Mathematik und Physik ZAMP,
Vol. 13,
Issue. 6,
p.
604.
HOWARD, ROGER
CURZON, F. L.
and
POWELL, E. H.
1963.
TE omn Modes of a Quasi-co-axial Resonant Cavity†.
Journal of Electronics and Control,
Vol. 14,
Issue. 5,
p.
513.
Chow, Chuen-Yen
and
Uberoi, Mahinder S.
1965.
Hydromagnetic Instability of Fluid between Two Coaxial Cylinders.
The Physics of Fluids,
Vol. 8,
Issue. 3,
p.
413.
Knowles, James K.
and
Sternberg, Eli
1966.
On Saint-Venant's principle and the torsion of solids of revolution.
Archive for Rational Mechanics and Analysis,
Vol. 22,
Issue. 2,
p.
100.
Chow, Chuen-Yen
and
Uberoi, Mahinder S.
1966.
Further Results on Hydromagnetic Instability of Fluid between Two Coaxial Cylinders.
The Physics of Fluids,
Vol. 9,
Issue. 1,
p.
216.
Naylor, D.
1966.
On a Sturm-Liouville expansion in series of Bessel functions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 62,
Issue. 1,
p.
61.
Weil, Joyce
Murty, Tadepalli S.
and
Rao, Desiraju B.
1967.
Zeros of 𝐽_{𝑛}(𝜆)𝑌_{𝑛}(𝜂𝜆)-𝐽_{𝑛}(𝜂𝜆)𝑌_{𝑛}(𝜆).
Mathematics of Computation,
Vol. 21,
Issue. 100,
p.
722.
Martynov, Yu. V.
1978.
Axially symmetric vortical flow of a nonviscous liquid in the semiinfinite gap between two coaxial circular cylinders.
Fluid Dynamics,
Vol. 12,
Issue. 5,
p.
673.
Ekardt, W
and
Thoai, D B Tran
1982.
Collective Excitations in Atomic Shells.
Physica Scripta,
Vol. 26,
Issue. 3,
p.
194.
Abdelraheem, S. K.
1993.
The Turning Point of Bessel Functions and Applications to the Electronic Eigenvalues in Wedge‐Shaped Films.
physica status solidi (b),
Vol. 178,
Issue. 1,
Maurya, J. P.
Yadav, Shyam Lal
and
Singh, A. K.
2020.
Analysis of magnetohydrodynamics transient flow in a horizontal annular duct.
International Journal of Dynamics and Control,
Vol. 8,
Issue. 3,
p.
730.


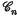 (λ
(λ