No CrossRef data available.
Article contents
Random fractals and their intersection with winning sets
Published online by Cambridge University Press: 07 July 2021
Abstract
We show that fractal percolation sets in 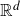 $\mathbb{R}^{d}$ almost surely intersect every hyperplane absolutely winning (HAW) set with full Hausdorff dimension. In particular, if
$\mathbb{R}^{d}$ almost surely intersect every hyperplane absolutely winning (HAW) set with full Hausdorff dimension. In particular, if 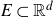 $E\subset\mathbb{R}^{d}$ is a realisation of a fractal percolation process, then almost surely (conditioned on
$E\subset\mathbb{R}^{d}$ is a realisation of a fractal percolation process, then almost surely (conditioned on 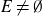 $E\neq\emptyset$), for every countable collection
$E\neq\emptyset$), for every countable collection 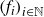 $\left(f_{i}\right)_{i\in\mathbb{N}}$ of
$\left(f_{i}\right)_{i\in\mathbb{N}}$ of 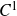 $C^{1}$ diffeomorphisms of
$C^{1}$ diffeomorphisms of 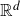 $\mathbb{R}^{d}$,
$\mathbb{R}^{d}$, 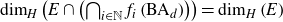 $\dim_{H}\left(E\cap\left(\bigcap_{i\in\mathbb{N}}f_{i}\left(\text{BA}_{d}\right)\right)\right)=\dim_{H}\left(E\right)$, where
$\dim_{H}\left(E\cap\left(\bigcap_{i\in\mathbb{N}}f_{i}\left(\text{BA}_{d}\right)\right)\right)=\dim_{H}\left(E\right)$, where 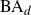 $\text{BA}_{d}$ is the set of badly approximable vectors in
$\text{BA}_{d}$ is the set of badly approximable vectors in 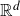 $\mathbb{R}^{d}$. We show this by proving that E almost surely contains hyperplane diffuse subsets which are Ahlfors-regular with dimensions arbitrarily close to
$\mathbb{R}^{d}$. We show this by proving that E almost surely contains hyperplane diffuse subsets which are Ahlfors-regular with dimensions arbitrarily close to 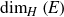 $\dim_{H}\left(E\right)$.
$\dim_{H}\left(E\right)$.
We achieve this by analysing Galton–Watson trees and showing that they almost surely contain appropriate subtrees whose projections to 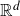 $\mathbb{R}^{d}$ yield the aforementioned subsets of E. This method allows us to obtain a more general result by projecting the Galton–Watson trees against any similarity IFS whose attractor is not contained in a single affine hyperplane. Thus our general result relates to a broader class of random fractals than fractal percolation.
$\mathbb{R}^{d}$ yield the aforementioned subsets of E. This method allows us to obtain a more general result by projecting the Galton–Watson trees against any similarity IFS whose attractor is not contained in a single affine hyperplane. Thus our general result relates to a broader class of random fractals than fractal percolation.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 172 , Issue 3 , May 2022 , pp. 655 - 684
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society


